일래스토메릭 부싱의 회전 방향 모드에 대한 Modified Pipkin-Rogers 모델링

1. 서론

자동차는 현대사회에서는 누구나 편리하게 사용하는 도구가 되었으며, 성능에 있어서는 어떠한 제품이라도 신뢰성이 담보되어 있을 만큼 발전되어 왔다. 하지만, 아직도 자동차에 있어서 승차감이라고 하는 요소는 탑승자와 관련된 가장 민감한 부분이므로 이와 관련된 연구는 지속적으로 수행되어 왔다. 이러한 승차감과 관련된 자동차의 주요 부품으로는 현가장치(Suspension System)가 있으며, 이 현가장치는 차축과 차체를 연결하여 차체의 중량을 지지하면서, 노면에서 전달되는 진동이나 충격으로부터 차체가 손상되는 것을 방지함과 동시에 탑승자의 승차감을 좋게 하는 역할을 한다.

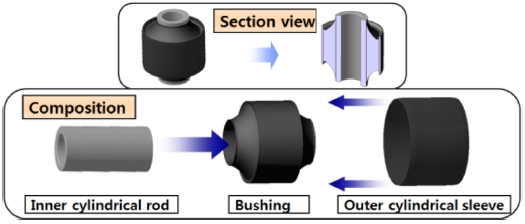
자동차의 부싱(Bushing)은 현가장치에 포함되는 작은 부품이지만, 자동차의 현가장치에서 부싱을 통하여 전달되는 하중은 자동차의 부품들에 대한 피로수명 예측 및 동특성에 직접 관련되어 중요하므로, 자동차 부싱에 대한 연구가 꾸준하게 진행되어 왔다. 자동차의 부싱은 여러 다양한 형상을 가지고 있고, 전달되는 하중의 형태도 다양하게 존재한다. 자동차의 일래스토메릭 부싱의 가장 단순한 형상은 바깥쪽의 실린더형 슬리브와 안쪽의 실린더형 축 사이에서 가운데가 비어있는 실린더의 형상이다.

Lee와 Wineman^1-3 등은 미국 미시간대학교 기계공학과의 자동차구조내구성센터(Center for Automotive Structural Durability Simulation)에서 수행한 일차원 반경 방향 변위 제어 실험으로부터 주어진 하중과 변위와의 관계가 비압축성, 비선형 점탄성 성질을 보임을 확인시켜주었으며, 이로부터 점탄성학 이론이 실제 부싱 제품에 본격적으로 활용되기 시작하였다.

점탄성에 대한 개념은 144년 전 등방성 물질에 대한 연구를 수행하였던 Boltzman⁴으로부터 유래를 찾아볼 수 있으나, 점탄성학에 대한 보편적인 연구가 수행된 것은 1950년대부터라고 할 수 있다. Gross⁵는 실험에서 얻어진 물질함수를 사용하여 일차원에서의 점탄성 이론의 수학적 구조를 설명하였으며, Adkins와 Gent⁶는 부싱에 대한 실험을 이용하여 하중과 변형과의 관계를 설명하였다. Adkins와 Gent⁶의 부싱연구는 중요한 성과는 있었으나 기본적으로 선형(Linearity)에 기초하고 탄성론(Elasticity)에 입각한 것이어서, 물질의 비선형성(Nonlinearity)과 점탄성 성질(Viscoelastic Property)을 설명하기에는 한계가 있었다.

Coleman과 Noll⁷은 근사적 구성방정식을 완성하기 위하여 페이딩 메모리 개념(Fading Memory Concept)을 이용하여 등방성 점탄성 고체에 대한 3차원 구성방정식을 완성하였으며, McGuirt와 Lianis⁸는 스티렌-부타디엔 고무(Styrene-Butadiene Rubber)에 대한 실험을 통하여 비선형 점탄성 구성방정식을 실험식으로 완성하였고, 이 식은 Lianis식으로 명명되어 지금까지도 사용되고 있다. 또한, Pipkin과 Rogers⁹는 점탄성 거동에 대한 비선형 적분 형태의 식을 보여주었다.

앞서 언급한 바와 같이, 점탄성학에 대한 이론은 Wineman과 Lee¹에 의하여 미국 포드자동차의 현가장치에 부착되어있는 부싱에 적용되었고, Wineman과 Lee¹는 Lianis의 실험데이터를 활용한 구성방정식을 이용하여 핍킨-라저스모델(Pipkin-Rogers Model)을 완성하고 이름도 명명하였다.

핍킨-라저스모델은 Lianis가 제안한 실험식에 비하여 간단히 정리된 장점이 있으므로 오랫동안 사용되어 왔으나 현장에서 사용되기에는 여전히 복잡한 성질을 가지고 있으므로, 일래스토메릭 부싱에 대하여 더욱 편리하게 적용할 수 있는 새로운 모델이 필요로 하게 되었다. 이러한 필요성으로 Lee¹⁰는 일래스토메릭 부싱의 축 방향 모드에 대하여, 기존의 리아니스의 실험식으로부터 완성된 핍킨-라저스모델의 데이터를 활용하여 새로이 수정된 핍킨-라저스모델(Modified Pipkin-Rogers Model)을 제안하였으며, 이를 검증하여 새로운 모델인 축 방향 모드에 대한 Modified Pipkin-Rogers Model이 사용될 수 있음을 보여주었다.

2. Lianis식과 Pipkin-Rogers Model

2.1 Lianis식

다음의 내용은 Lee¹⁰에도 기술되어 있으나, 본 논문의 진행과 직접 관련이 되는 내용이므로 여기에 다시 언급한다. 퍼듀대학교(Purdue University)의 McGuirt와 Lianis⁸는 스티렌-부타디엔 고무(Styrene-Butadiene Rubber)에 대한 실험을 통하여, 응력과 변형률 간의 구성방정식을 만들었고, 실험을 통하여 제안한 기본식을 응력과 변형률의 관계로 나타내면 다음 식(1)과 같다.

$\[ \begin{array}{c}\sigma \left(t\right)=-p\left(t\right)I+\left[a+\frac{b}{{\left(I_1-2\right)}^2}+I_1\left\{c+d\left(I_2-3\right)\right\}\right]B\hfill \\ -\left[c+d\left(I_2-3\right)\right]B^2\hfill \\ +2{\int }_{-\infty }^t\left[\left\{P_0\left(t-s\right)+\left(I_2-3\right)Q_0\left(t-s\right)\right\}\frac{d{C}_t\left(s\right)}{ds}\right]ds\hfill \\ +{\int }_{-\infty }^t\left[\left\{P_1\left(t-s\right)+\frac{Q_1\left(t-s\right)}{{\left(I_1-2\right)}^2}\right\}\left\{B\frac{d{C}_t\left(s\right)}{ds}+\frac{d{C}_t\left(s\right)}{ds}B\right\}\right]ds\hfill \end{array} \]$

(1)

σ(t)는 응력텐서(Stress Tensor)이며, p(t)는 비압축성의 제한으로부터 온 압력(Pressure)이며, t는 현재의 시간, s는 과거에서 현재까지의 시간, B는 왼쪽 코시-그린 텐서(Left Cauchy-Green Tensor), C_t(s)는 오른쪽 상대 코시-그린 텐서(Right Relative Cauchy-Green Tensor), I₁과 I₂는 B의 스트레인불변량(Strain Invariants)이고, I는 3 × 3 항등행렬(Identity Matrix)이며, 실험값인 P₀(t), Q₀(t), P₁(t), Q₁(t)은 스티렌-부타디엔 고무의 0^oC에서 시간에 따라 변하는 물질의 특성이며, a, b, c, d는 일정한 값을 갖는 물질의 특성으로, 실험에서 구해진 값들은 Table 1에 표기하였다.

Table 1

Material functions for SBR at 0oC

3. 자동차 현가장치의 일래스토메릭 부싱

3.1 일래스토메릭 부싱의 형상

자동차 현가장치의 일래스토메릭 부싱은 다양한 형상을 가지고 있으나, 본 연구에서 고려한 형상은 가장 단순한 형태인 바깥쪽의 실린더형 슬리브와 안쪽의 실린더형 축 사이에서 가운데가 비어있는 실린더의 형태를 가지고 있으며, Lee¹⁰에 있는 그림을 Fig. 1에 다시 나타내었다.

Fig. 1

Configurations of the elastomeric bushing1 (Adapted from Ref. 1 on the basis of OA)

3.2 회전 방향 모드에 대한 Lianis식

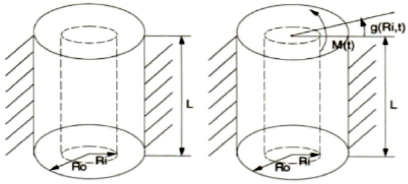
일래스토메릭 부싱은 가운데가 비어있는 실린더로 가정되어 축 방향 대칭이며, Lee¹에 있는 변형 전과 변형 후의 형상을 Fig. 2에 다시 나타내었다.

Fig. 2

Reference and current configurations in torsional mode

본 연구에서는 바깥쪽 슬리브를 고정시키고, 가장 큰 변형이 발생하는 안쪽의 회전변형각도와 주어진 모멘트와의 관계를 가지는 회전 방향 모드를 고려하였으며, 경계조건으로 외부에서의 회전 방향의 회전변형각도를 0으로 놓고, 내부 반지름에서의 회전 방향의 변형각도와 주어진 모멘트와의 관계를 구하였다. Lianis가 제안한 식(1)을 회전 방향 모드에 대하여 정리하면 다음 식(3)과 같다.

$\[ \begin{array}{c}M\left(r,t\right)=\left[a+\frac{1}{{\left\{1+h^2\left(r,t\right)\right\}}^2}\right.\hfill \\ \left. +\left\{3+h^2\left(r,t\right)\right\}\left\{c+d{h}^2\left(r,t\right)\right\}\right]h\left(r,t\right)\hfill \\ -\left\{c+d{h}^2\left(r,t\right)\right\}\left\{2+h^2\left(r,t\right)\right\}h\left(r,t\right)\hfill \\ +2h\left(r,0^{+}\right)\left\{P_0\left(t\right)+h^2\left(r,t\right)Q_0\left(t\right)\right\}\hfill \\ +2{\int }_{0^{+}}^t\left\{P_0\left(t-s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds\hfill \\ +2h^2\left(r,t\right){\int }_{0^{+}}^t\left\{Q_0\left(t-s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds\hfill \\ +h\left(r,0^{+}\right)\left[P_1\left(t\right)+\frac{Q_1\left(t\right)}{\left\{1+h^2\left(r,t\right)\right\}}\right]\left\{2+h\left(r,0^{+}\right)h\left(r,t\right)\right.\hfill \\ \left. -h^2\left(r,t\right)\right\}+2h\left(r,t\right){\int }_{0^{+}}^t\left\{P_1\left(t-s\right)h\left(r,s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds\hfill \\ +\left\{{2-h}^{2}h\left(r,t\right)\right\}{\int }_{0^{+}}^t\left\{P_1\left(t-s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds\hfill \\ +\frac{2h\left(r,t\right)}{{\left\{{1+h}^2\left(r,t\right)\right\}}^2}{\int }_{0^{+}}^t\left\{Q_1\left(t-s\right)h\left(r,s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds\hfill \\ +\frac{2-h^2\left(r,t\right)}{{\left\{{1+h}^2\left(r,t\right)\right\}}^2}{\int }_{0^{+}}^t\left\{Q_1\left(t-s\right)\frac{\partial h\left(r,s\right)}{\partial s}\right\}ds,\hfill \\ h\left(r,s\right)=r\frac{\partial g\left(r,s\right)}{\partial r}\hfill \end{array} \]$

(3)

3.3 회전 방향 모드에 대한 Modified Pipkin-Rogers Modeling

Lee¹는 주어진 모멘트 M(t)과 내부 반지름에서의 회전 방향 변형각도 g(s)의 관계를 구하고자 하였으며, 시간 s < 0에서는 주어진 모멘트가 없으며, 회전 방향의 변형각도도 발생하지 않는 것으로 가정하였다. Lianis의 실험식을 이용하여 완성된 회전 방향 모드에 대한 Pipkin-Rogers Model인 식(2)를 이용하여, Ramp-to-Constant Rotational Angle Control Test를 수행하여 모의실험 데이터를 확보하였으며, 모멘트에 대한 외삽법(Moment Extrapolation Method)과 최소자승법(Least Squares Method)을 이용하여 회전 방향의 변형각도에 의존하는 모멘트완화함수(Rotational Angle Dependent Moment Relaxation Function)를 구하여 소수점 넷째 자리까지 완성한 회전 방향 모드에 대한 핍킨-라저스모델은 다음 식(4)와 같다.

$\[ \begin{array}{c}M\left(t\right)=H\left(g\left(0\right),t\right)+{\int }_{0^{+}}^t\frac{\partial H\left(g\left(s\right),t-s\right)}{\partial g\left(s\right)}\frac{dg\left(s\right)}{\partial s}ds,\hfill \\ H\left(g\left(s\right),t\right)=\left[1.6114+0.2448e^{-\frac{t}{15.6895}}+0.24e^{-\frac{t}{2.0877}}\right]g\left(s\right)+\hfill \\ \left[-0.4951-0.102e^{-\frac{t}{12.3654}}-0.1387e^{-\frac{t}{2.8285}}\right]{\left\{g\left(s\right)\right\}}^3+\hfill \\ \left[0.1839+0.1238e^{-\frac{t}{2.4729}}-0.017e^{-\frac{t}{0.5733}}\right]{\left\{g\left(s\right)\right\}}^5\hfill \end{array} \]$

(4)

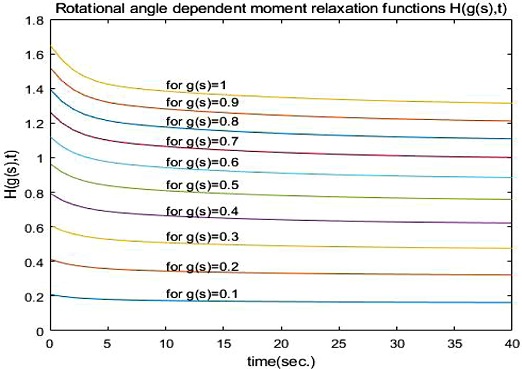
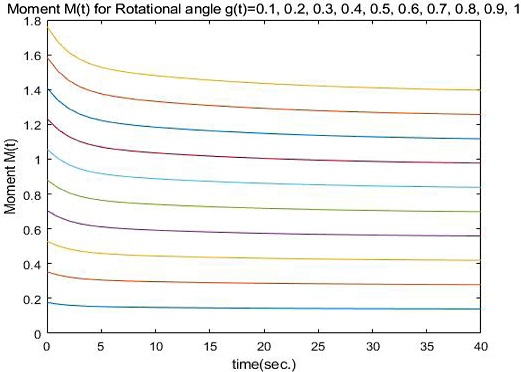
식(4)로부터 g(s) = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0에 대한 Step Rotational Angle Control Test의 결과인 모멘트(Moment)는 회전변형각도에 의존하는 모멘트 완화함수(Rotational Angle Dependent Moment Relaxation Function)로서 H(g(s), t)로 나타내며, Fig. 3에 나타내었다.

Fig. 3

Rotational angle dependent moment relaxation function

모멘트완화함수(Moment Relaxation Function) H(g(s), t)는 식(4)와 같이 내부 반지름에서의 회전 방향 변형각도인 g(s)의 홀수의 거듭제곱들의 합의 형태로 식(5)와 같이 표현된다.

$\[ H\left(g\left(s\right),t\right)=G_1\left(t\right)g\left(s\right)+G_3\left(t\right){\left\{g\left(s\right)\right\}}^3+G_5\left(t\right){\left\{g\left(s\right)\right\}}^5 \]$

(5)

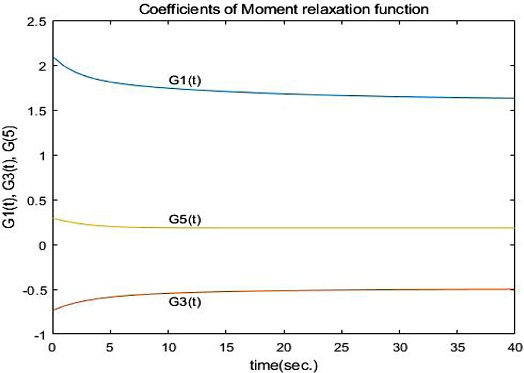
식(5)는 널리 이용되고 있으며, Fig. 4는 Fig. 3의 데이터에 선형최소자승법을 적용하여 구한 불연속 데이터 G₁(t), G₃(t), G₅(t)를 나타내고 있다.

Fig. 4

Coefficients of moment relaxation function

고무물질에 대한 점탄성 현상을 포함하는 시뮬레이션을 단순화하기 위해서는 기존의 식보다는 단순한 식이 필요하게 되며, 본 연구에서는 모멘트완화함수(Moment Relaxation Function) H(g(s), t)을 내부 반지름에서의 회전 방향 변형각도인 g(s)와 현재 시간 t의 함수인 G(t)와의 곱인 선형관계의 식을 이용한 수정된 핍킨-라저스모델(Modified Pipkin-Rogers Model)로 제안하였다.

$\[ M\left(t\right)=G\left(t\right)g\left(0\right)+{\int }_{0^{+}}^{t}G\left(t-s\right)\frac{dg\left(s\right)}{\partial s}ds \]$

(6)

식(6)은 구성된 식의 단순성으로 그 효용성이 증대될 수 있으며, 그동안 오차를 조절하지 못하여 제안되지 못하였으나, 컴퓨터와 수치해석의 발전으로 인하여 본 연구에서는 고무 물질에 대한 오차범위 내에서 충분히 사용 가능함이 증명되었다.

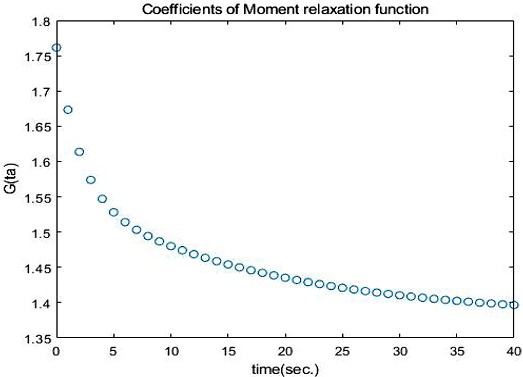
Fig. 5는 Fig. 3의 데이터에 선형최소자승법을 적용한 불연속 데이터 G(t)를 나타내고 있으며, 시간에 대한 불연속성을 표현하고자 Fig. 5에서는 G(t_a)로 표기하였다.

Fig. 5

Coefficients of moment relaxation function

Fig. 5에서의 시간 t_a(a = 1, 2, 3, ..., 41)에 대한 G(t_a)를 다음과 같이 시간 t에 대한 다항식 함수(Polynomial Function)을 이용하여 Curve Fitting하였으며 식(7)에 나타내었다.

$\[ G\left(t\right)={\sum }_{i=1}^n{C}_{n-1}{t}^{n-1} \]$

(7)

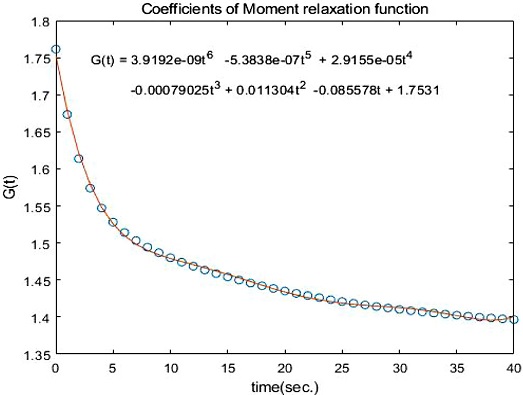
본 연구에서는 n = 7을 이용한 6차 다항식을 이용하였으며, 수정된 핍킨-라저스모델에 필요한 함수 G(t)는 다음 식(8)과 같다.

$\[ \begin{array}{c}G\left(t\right)=3.9192\times {10}^{-9}{t}^6-5.3838\times {10}^{-7}{t}^5\hfill \\ +2.9155\times {10}^{-5}{t}^4-7.9025\times {10}^{-4}{t}^3\hfill \\ +0.011304t^2-0.085578t+1.7531\hfill \end{array} \]$

(8)

Fig. 6은 Fig. 5의 불연속데이터와 식(8)의 결과를 실선으로 표기하여 함께 나타낸 것이다.

Fig. 6

Coefficients of moment relaxation function

G(t)와 G(t_a)를 비교하기 위하여, G(t)의 G(t_a)에 대한 상대오차를 2-Norm 개념을 도입하여 다음 식(9)와 같이 정의하였다.

$\[ \mathrm{R}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}=\frac{{‖G\left(t\right)-G\left(t_a\right)‖}_2}{{‖G\left(t_a\right)‖}_2}, \left(a=\mathrm{1,2},\cdots ,41\right) \]$

(9)

G(t)의 G(t_a)에 대한 상대오차는 0.21%이며, 점탄성 모델을 축 방향 모드에 대하여 완성한 Modified Pipkin-Rogers Model은 다음 식(10)과 같다.

$\[ \begin{array}{c}M\left(t\right)=G\left(t\right)g\left(0\right)+{\int }_{0^{+}}^{t}G\left(t-s\right)\frac{dg\left(s\right)}{\partial s}ds,\hfill \\ \begin{array}{c}G\left(t\right)=3.9192\times {10}^{-9}{t}^6-5.3838\times {10}^{-7}{t}^5\hfill \\ +2.9155\times {10}^{-5}{t}^4-7.9025\times {10}^{-4}{t}^3\hfill \\ +0.011304t^2-0.085578t+1.7531\hfill \end{array}\hfill \end{array} \]$

(10)

3.4 Pipkin-Rogers Model과 Modified Pipkin-Rogers Model의 결과 비교

Pipkin-Rogers Model과 Modified Pipkin-Rogers Model에 대하여, 주어진 동일한 회전변형각도로부터 구하여진 모멘트 M(t)의 결과를 비교하였으며, Fig. 3은 Pipkin-Rogers Model의 결과로 나온 모멘트 M(t)를 나타내고 있으며, Fig. 7은 Fig. 3과 동일하게 주어진 회전변형각도에 대하여 Modified Pipkin-Rogers Model을 이용한 결과를 보여주고 있다.

Fig. 7

Moment from modified pipkin-rogers model

두 모델의 결과인 M(t)를 비교하기 위하여, 식(9)와 같이 상대오차를 놈(Norm)을 이용하여, 다음 식(11)과 같이 정의하였다.

$\[ \mathrm{R}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}=\frac{\text{Modified PR result}-\text{PR result}}{\text{PR result}} \]$

(11)

식(11)로부터, g(s) = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0에 대한 Modified Pipkin-Rogers Model의 Pipkin-Rogers Model에 대한 상대오차는 각각 14.61, 13.81, 12.48, 10.65, 8.33, 5.58, 2.51, 0.72, 3.87, 6.6%로 평균 15% 이내의 상대오차를 가지고 있는데 이는 점탄성학의 특성상 유효한 범위이므로, 제안한 점탄성 부싱모델(Modified Pipkin-Rogers Model)이 새로운 부싱 모델로서 사용 가능함을 알 수 있으며, 고무 부싱의 점탄성 성질의 어려움을 고려하여 볼 때 모든 구간에서 15% 미만의 오차는 유효하다고 할 수 있으며, 새로이 완성된 Modified Pipkin-Rogers Model은 회전 방향 모드에서 사용이 가능하다.

4. 결론

본 연구에서는 자동차 부싱의 회전 방향 모드에 대하여 모멘트와 회전변형각도와의 관계를 알아보는데 있어서, 두 가지의 모델을 사용하였다. Lianis식을 이용한 기존의 응용역학방법을 이용한 후, 결과로 나온 모멘트에 대한 외삽법을 활용한 Pipkin-Rogers Model은 Lianis식이 가지고 있는 관련식들이 음함수로 연결됨으로 인하여 동역학적 모의실험에 이용하기에 어려운 문제는 해결하였으나, 여전히 수식의 복잡성으로 인하여 현장에서 사용하기에는 어려움이 있었다.

따라서 본 연구에서는 Lianis식을 활용하고 Ramp-to-Constant Rotational Angle Control Test를 이용하여 모멘트에 대한 외삽법을 이용한 Pipkin-Rogers Model로부터의 결과와 새로이 제안된 Modified Pipkin-Rogers Model의 결과를 비교하여 오차범위 내에서의 좋은 결과를 얻었다.

본 연구의 목적은 자동차의 회전 방향 모드에 대하여 현장에서 사용 가능한 점탄성 모델을 완성하는 것이며, Modified Pipkin-Rogers Model의 결과는 원하는 오차범위 내에서 사용이 가능함을 알 수 있었다. 이는 Modified Pipkin-Rogers Model이 기존의 Pipkin-Rogers Model을 대치할 수 있다는 것을 검증하고 있으므로, 부싱에 대한 새로운 점탄성 모델로서 Modified Pipkin-Rogers Model을 사용할 수 있는 근거를 제시한다.

향후에는 본 연구 방법을 실험에 근거한 연구에 적용해보아야 할 것이다. 또한 축 방향 모드, 반경 방향 모드, 회전 방향 모드의 복합 모드에 대한 연구가 필요하다.

Acknowledgments

본 논문은 2018학년도 인제대학교 학술연구조성비 보조에 의한 것임.

REFERENCES

• Lee, S. B., “A Study of a Nonlinear Viscoelastic Model of Elastomeric Bushing Response,” Ph.D. Thesis, University of Michigan, 1997.
• Wineman, A., Van Dyke, T., and Shi, S., “A Nonlinear Viscoelastic Model for One Dimensional Response of Elastomeric Bushings,” International Journal of Mechanical Sciences, Vol. 40, No. 12, pp. 1295-1305, 1998. [https://doi.org/10.1016/S0020-7403(98)00023-X]
• Lee, S. B. and Wineman, A., “A Model for Nonlinear Viscoelastic Torsional Response of AN Elastomeric Bushing,” Acta Mechanica, Vol. 135, Nos. 3-4, pp. 199-218, 1999. [https://doi.org/10.1007/BF01305752]
• Boltzmann, L., “Zur Theorie der Elastischen Nachwirkung,” Annalen der Physik, Vol. 241, No. 11, pp. 430-432, 1878.
• Gross, B., “Mathematical Structure of the Theories of Viscoelasticity,” Hermann, 1953.
• Adkins, J. and Gent, A., “Load-Deflexion Relations of Rubber Bush Mountings,” British Journal of Applied Physics, Vol. 5, No. 10, p. 354, 1954. [https://doi.org/10.1088/0508-3443/5/10/305]
• Coleman, B. D. and Noll, W., “Foundations of Linear Viscoelasticity,” Reviews of Modern Physics, Vol. 33, No. 2, pp. 239-249, 1961. [https://doi.org/10.1103/RevModPhys.33.239]
• McGuirt, C. W. and Lianis, G., “Constitutive Equations for Viscoelastic Solids under Finite Uniaxial and Biaxial Deformations,” Transactions of the Society of Rheology, Vol. 14, No. 2, pp. 117-134, 1970. [https://doi.org/10.1122/1.549182]
• Pipkin, A. and Rogers, T., “A Non-Linear Integral Representation for Viscoelastic Behaviour,” Journal of the Mechanics and Physics of Solids, Vol. 16, No. 1, pp. 59-72, 1968. [https://doi.org/10.1016/0022-5096(68)90016-1]
• Lee, S. B., “Modified Pipkin-Rogers Modeling of Elastomeric Bushing in Axial Mode,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 9, pp. 653-658, 2017. [https://doi.org/10.7736/KSPE.2017.34.9.653]