초정밀 장비의 진동 저감을 위한 능동형 동조질량감쇠기

1. 서론

반도체·디스플레이 산업은 우리나라의 대표적인 수출 상품으로 전 세계적인 IT 산업의 발전, 소비자의 고급화 요구에 따라 고집적화, 고해상도의 추세로 매년 급격히 발전하고 있다. 이에 대응하여 반도체·디스플레이 생산 장비 등과 같은 초정밀 생산 장비 또한 높은 정밀도와 더불어 대량 생산을 요구되고 있다. 특히 반도체·디스플레이 장비가 가동되는 Fab. 내부는 클린룸(Cleanroom) 환경을 유지하기 위해 수많은 공조 장치가 작동하고 있다. 이때 발생하는 진동에 의해 건물에 전역적인 미세 진동이 필연적으로 존재한다. 또한 장비 근처에 설치된 높은 동하중을 갖는 로봇의 구동, 작업자의 걸음 등 다양한 요인으로 진동이 유발된다. 이는 초정밀 장비가 설치된 바닥에서 유입되어 심각한 생산 불량과 수율 저하를 유발하게 된다. 한편, 장비 내부의 구동기가 거동하여 발생하는 동하중은 장비의 동특성에 따라 다양한 진동을 발생시킨다.

이러한 대부분의 진동은 바람직하지 않으므로 이를 저감시키기 위해 다양한 방법이 지속적으로 연구되어 왔다. 그 중 동조질량감쇠기(Tuned Mass Damper, TMD)는 구조물의 변경 없이 국부적으로 진동을 저감시킬 수 있는 장치이다. 동조질량감쇠기는 크게 수동형(Passive)와 능동형(Active)로 구분할 수 있다. 수동형 동조질량감쇠기는 진동이 큰 구조물에 추가적인 질량과 스프링, 감쇠기를 부착하여 구조물의 동특성을 변경함으로써 낮은 진동을 유도한다. 1994년 R. Villaverde는 2차원 및 3차원 구조물 모델에 지진 기록 데이터를 재현하며 수동형 동조질량감쇠기의 성능을 비교하였다.¹ 2006년 안상경 등은 실제 동조질량감쇠기를 설계하여 건물 바닥 슬래브(Slab)의 진동을 제어하는 실험을 진행했다.² 또한 수동형 동조질량감쇠기의 최적 성능을 유도하는 질량, 강성, 감쇠비를 결정하는 방법에 대한 연구가 많이 진행되었다.^3-6

수동형 동조질량감쇠기는 이론적으로 비교적 좋은 진동 저감효과를 보이나 기계요소를 이용하여 질량, 강성, 감쇠 상수 등 민감한 매개변수의 정교한 조절이 요구되어 선정된 값과 정확히 일치하는 구조물의 제작 및 시공이 어려운 문제가 있다. 이러한 단점을 보완하며, 제어 알고리즘을 이용하여 더 높은 성능을 유도할 수 있는 능동형 동조질량감쇠기에 대한 많은 연구 또한 진행되었다. 이는 수동형 동조질량감쇠기에 센서와 구동기, 제어장치를 추가하여 제어시스템을 구축하고 적절한 알고리즘을 이용하여 구동기를 작동시켜 진동을 저감시키는 장치이다. 이를 위한 제어 방법으로는 퍼지(Fuzzy) 제어, H_∞ 제어, 슬라이딩 모드 제어 등 다양한 알고리즘이 제안되었다.^7-9 2019년 S. Chesne 등은 2중 루프 PID 제어기를 이용하여 능동형 동조질량감쇠기를 제어하는 방법을 소개하였고, 1자유도 구조물에 적용하여 시뮬레이션 및 실험을 통해 검증하였다.¹⁰ 본 연구에서는 초정밀 장비의 국부적인 진동 저감을 목표로 2중 루프 PID 제어기를 개선하여 더욱 높은 진동 저감 성능을 보이는 능동형 동조질량감쇠기를 개발하였다.

2. 수동형 동조질량감쇠기의 설계 방법

2.1 동조질량감쇠기의 구조

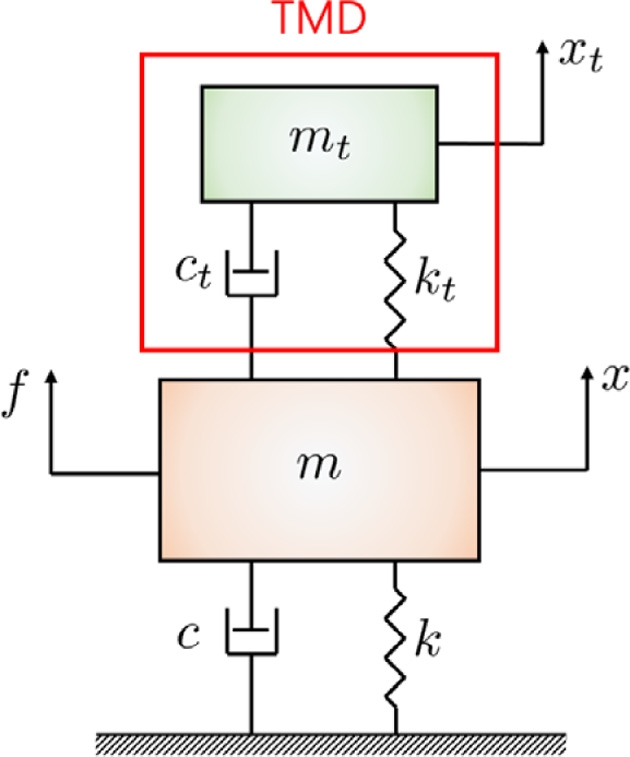
수동형 동조질량감쇠기가 포함된 구조물의 구성도를 Fig. 1에 나타내었다. m, c, k는 각각 진동에 취약한 구조물의 질량, 감쇠상수, 강성을 나타내며, x는 구조물의 변위, f는 구조물에 작용하여 진동을 발생시키는 외력을 나타낸다. 구조물 상단에 1자유도진동 시스템으로 구성된 동조질량감쇠가가 부착되어 있으며, 이의 매개변수는 각각 m_t, c_t, k_t로 나타내었다. x_t는 마찬가지로 동조질량감쇠기의 변위를 나타낸다. 이에 뉴턴 제2법칙을 적용하면 본 시스템의 운동방정식은 식(1)과 식(2)와 같이 유도된다.

$\[ m\ddot{x}+\left(c+C_t\right)\dot{x}+\left(k+k_t\right)x-c_t{\dot{x}}_t-k_t{x}_t=f \]$

(1)

$\[ m_t{\ddot{x}}_t+c_t{x}_t+k_t{x}_t-c_t\dot{x}-k_{t}x=0 \]$

(2)

Fig. 1

Schematic diagram of structure with passive TMD

위 운동방정식에 각각 라플라스 변환(Laplace Transform)을 수행한 후 자유도별로 정리하면 식(3)과 같이 전달행렬의 역행렬과 벡터 형식으로 표현할 수 있다. 행렬 [G(s)]^-1의 구성은 식(4)에 나타내었다.

$\[ {\left[G\left(s\right)\right]}^{-1}\left\{\begin{array}{c}X\left(s\right)\\ X_t\left(s\right)\end{array}\right\}=\left\{\begin{array}{c}F\left(s\right)\\ 0\end{array}\right\} \]$

(3)

$\[ {\left[G\left(s\right)\right]}^{-1}=\left[\begin{array}{cc}m{s}^2+\left(c+c_t\right)s+\left(k+k_t\right)& -c_{t}s-k_t\\ -c_{t}s-k_t& m_t{s}^2+c_{t}s+k_t\end{array}\right] \]$

(4)

행렬[G(s)]는 식(5)와 같이 외력 입력 F(s)에 따른 각부의 출력을 나타내는 시스템의 전달행렬(Transfer Matrix)을 의미한다. 이는 외력에 대한 각 자유도의 변위를 정의하는 4개의 전달함수로 구성된다.

$\[ \left\{\begin{array}{c}X\left(s\right)\\ X_t\left(s\right)\end{array}\right\}=\left[G\left(s\right)\right]\left\{\begin{array}{c}F\left(s\right)\\ 0\end{array}\right\} \]$

(5)

2.2 최적의 매개변수 결정

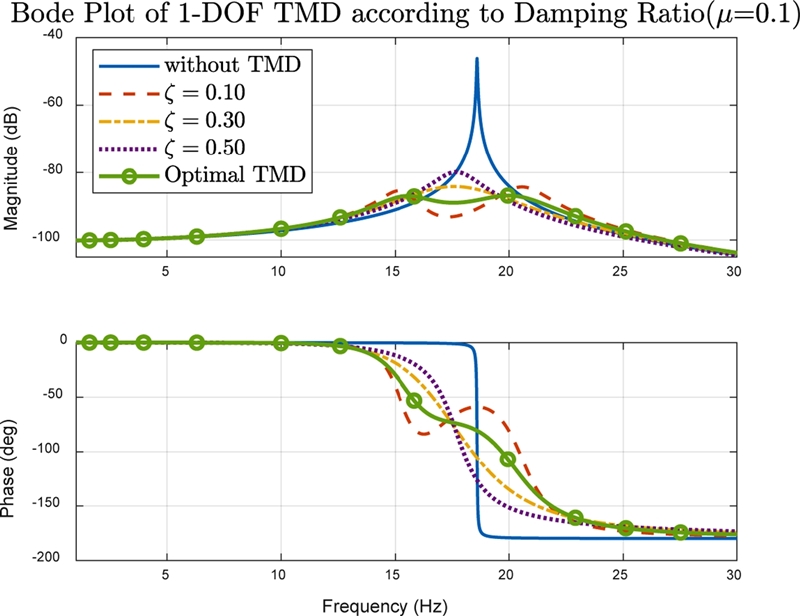
수동형 동조질량감쇠기는 구조물의 질량과 강성에 따라 설계변수가 달라지며, 최적의 설계 변수를 결정하는 방법 또한 다양하게 연구되었다. 그 중에서 Table 1에 나타낸 Den Hartog의 방법이 좋은 효과를 보임이 알려져 있다.⁶ 이에 따르면 구조물의 고유진동수를 파악한 후 유효 질량과 동조질량감쇠기의 질량간의 질량비(Mass Ratio, μ)를 결정하면 나머지 매개변수는 자동으로 결정된다. Fig. 2는 동조질량감쇠기의 질량비를 0.1로 고정하고 최적의 강성을 선택한 후 감쇠비에 따른 주파수 응답을 Bode 선도로 나타낸 것이다. 동조질량감쇠기가 부착되면 1자유도시스템이 2자유도로 변경되므로 2개의 고유진동수를 가지게 된다. 또한 감쇠비에 따라 민감한 반응을 보이며 최적의 감쇠비에서 가장 낮은 크기를 보이는 것을 확인할 수 있다.

Table 1

Optimal TMD parameters by Den Hartog’s method

Fig. 2

Bode plot of passive TMD with respect to changing damping ratio

3. 능동형 동조질량감쇠기의 개발

3.1 구동기를 고려한 모델링

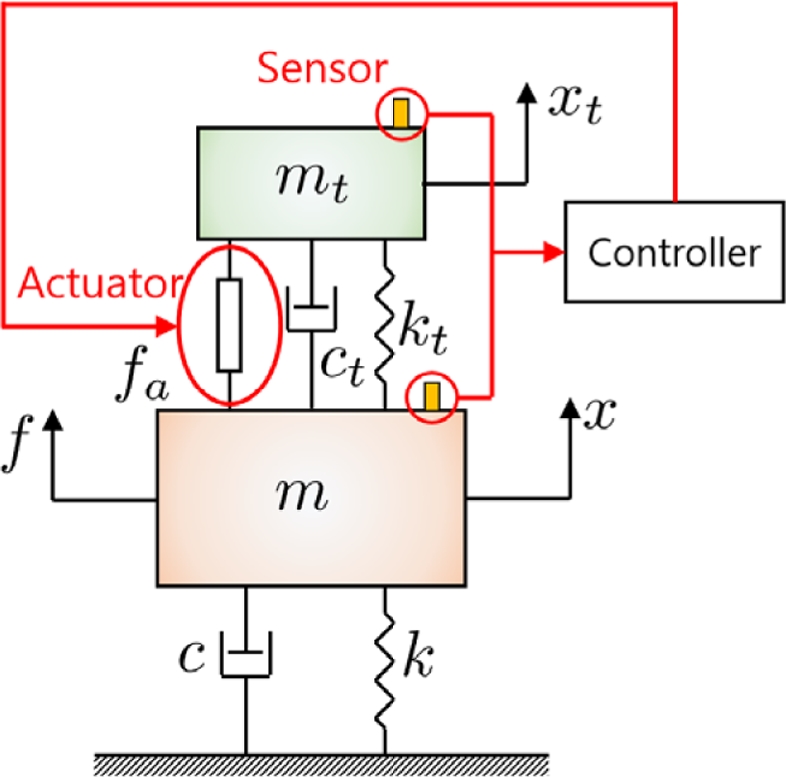
능동형 동조질량감쇠기는 Fig. 3과 같이 기존의 수동형 동조질량감쇠기에 센서, 구동기, 제어장치를 추가한 형태를 가진다. 이는 제어 알고리즘을 통하여 시스템의 동특성을 효과적으로 조정할 수 있으므로 수동형 동조질량감쇠기에 비하여 좋은 성능을 기대할 수 있으며 소프트웨어적으로 미세 조절이 가능하므로 현장 적용성도 매우 뛰어난 특징을 기대할 수 있다.

Fig. 3

Schematic diagram of structure with active TMD

식(6)과 식(7)은 능동형 동조질량감쇠기의 운동방정식을 나타낸 것이다. 이는 수동형 동조질량감쇠기와 매우 유사하지만, 구동기의 구동력(f_a)을 추가한 차이가 있다.

$\[ m\ddot{x}+\left(c+c_t\right)\dot{x}+\left(k+k_t\right)x-c_t{\dot{x}}_t-k_t{x}_t=f-f_a \]$

(6)

$\[ m_t{\ddot{x}}_t+c_t{\dot{x}}_t+k_t{x}_t-c_t\dot{x}-k_{t}x=f_a \]$

(7)

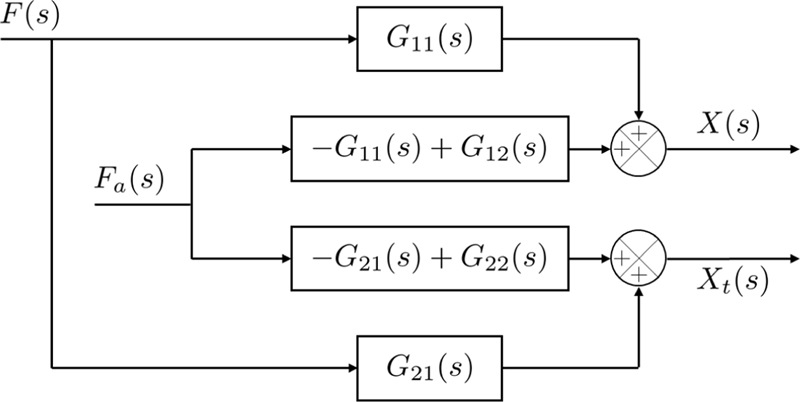
마찬가지로 라플라스 변환을 수행하면 식(5)와 동일한 전달행렬 [G(s)]가 구해지며 구동기를 고려한 각부의 응답은 식(8)로 나타낼 수 있다. 이를 블록선도로 표현하면 Fig. 4와 같다.

$\[ \left\{\begin{array}{c}X\left(s\right)\\ X_t\left(s\right)\end{array}\right\}\begin{array}{l}=\left[G\left(s\right)\right]\left\{\begin{array}{c}F\left(s\right)-F_a\left(s\right)\\ F_a\left(s\right)\end{array}\right\}\\ =\left[\begin{array}{cc}{G}_{11}\left(s\right)& G_{12}\left(s\right)\\ G_{21}\left(s\right)& G_{22}\left(s\right)\end{array}\right]\left\{\begin{array}{c}F\left(s\right)-F_a\left(s\right)\\ F_a\left(s\right)\end{array}\right\}\end{array} \]$

(8)

Fig. 4

Block diagram of the active TMD structure

3.2 2중 루프 제어기의 적용

앞서 언급한 기존의 2중 루프 PID 제어기의 제어 구조는 P I 제어기와 P 제어기를 이용하여 2중 루프를 구성하고 이의 우수한 성능을 보였다. 그러나 피드백을 위한 속도 센서에서 발생한 영점과 P I 제어기의 극점이 원점에서 일치하게 되며 해석상으로 소거되나 실제 제어시스템을 구현할 때는 불안정한 극점의 소거(Pole-Zero Cancellation)를 유발할 수 있다. 이는 긴 시간동안 지속되는 잔류 진동의 원인이 되곤 한다. 본 연구에서는 이를 회피하고자 P I 제어기를 식(9)와 같은 비최소위상시스템(Non-Minimum Phase System)으로 대체한다. 이는 제어기의 극점을 원점으로부터 약간 왼쪽으로 이동하여 속도 센서와 결합된 극점의 소거를 회피하며 제어기의 이득에 따른 극점의 배치를 용이하게 한다.

$\[ C_1\left(s\right)=k_{p1}\left(\frac{s-T_s}{s+T_s∕\beta }\right) \]$

(9)

일반적으로 구조물의 절대 속도의 P 제어를 이용해 능동형 동조질량감쇠기를 제어하는 것은 안정도 여유(Stability Margin)가 매우 낮다고 알려져 있다.¹¹ 이는 제어기의 이득이 조금만 높아져도 시스템의 극점이 복소평면의 허수축을 기준으로 우측 반평면으로 이동하여 불안정해지기 때문이다. 내부 루프 제어기는 이러한 안정도 여유를 높이기 위하여 허수축으로부터 극점을 좌측으로 멀리 떨어뜨리는 역할을 수행한다. 외부 루프 제어기는 구조물의 절대 속도에 P 제어를 수행하여 시스템의 두 극점의 감쇠비가 같아지는 제어 이득을 선택한다.

외부 루프 제어기는 구조물의 절대 속도에 P 제어를 적용하며, 제어기의 전달함수는 식(10)과 같이 나타낼 수 있다.

$\[ C_2\left(s\right)=-k_{p2} \]$

(10)

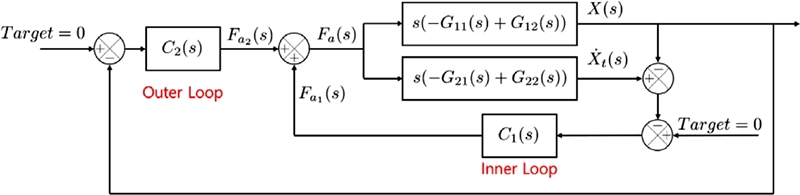
내부 루프 제어기와 외부 루프 제어기가 포함된 전체 시스템의 블록선도를 Fig. 5에 나타내었다. 앞서 Fig. 4에서 동조질량감쇠기가 포함된 구조물의 블록선도를 나타내었다. 여기서 F(s)는 구조물의 외부 가진력으로 이를 외란으로 간주하고 평상시 입력되는 힘은 0이라고 가정한다. 따라서 F(s)에 대한 입력을 제외하고 내부 루프 제어기가 포함된 블록선도를 Fig. 5와 같이 나타낼 수 있다. 또한 속도 센서 사용을 표현하기 위해 미분기(s)를 추가하였다. 내부 루프 제어기에서 생성된 구동기의 출력을 F_a1(s)라고 정의하였고, 외부 루프 제어기의 출력은 F_a2(s)라고 정의하였다. 최종적으로 구동기가 발생시는 출력은 두 제어기의 출력의 합으로 결정된다.

Fig. 5

Block diagram of the dual loop control for active TMD

3.3 제어기 이득 조정 및 해석적 평가

능동형 동조질량감쇠기의 거동을 분석하기 위해 MATLAB을 이용해 해석을 진행하였다. 해석에 사용한 구조물과 동조질량감쇠기의 매개변수는 Table 2에 나타내었다.

Table 2

Parameters of main and TMD structures

수동형 동조질량감쇠기는 Den Hartog의 방법에 따라 최적의 매개변수로 선정한다.⁶ 능동형 동조질량감쇠기의 감쇠비를 0.1%로 매우 낮게 가정하였고, 고유진동수 또한 수동형보다 낮게 설정하여 제어 알고리즘을 통해 이를 보완하도록 하였다. 내부 루프 제어기와 외부 루프 제어기의 이득을 설정하기 위해 T_s, β, k_p1을 변경하며 내부 루프 제어기를 조정하였고, 이를 폐루프로 구성한 후 k_p2를 변경하며 외부 루프제어기를 조정하였다. 제어기 이득 조정 방법으로는 근궤적선도를 사용하였고, 조정 결과 중 감쇠비를 Table 3에 나타내었다.

Table 3

Damping ratio along gain tuning

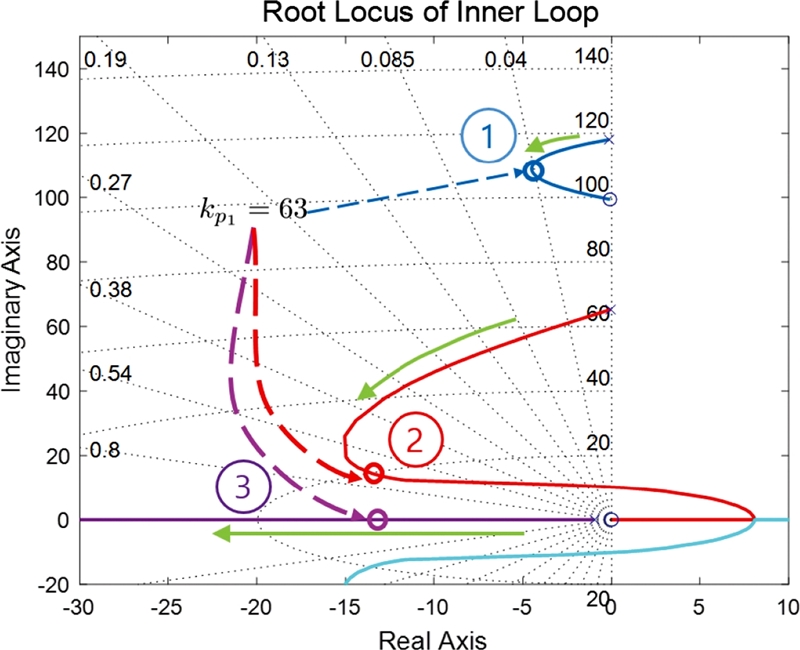
Table 3에서 감쇠비가 가장 높은 경우에 대해서 내부 루프제어기의 근궤적선도를 Fig. 6에 나타내었다. 앞서 설명한대로 제어기의 이득이 증가함에 따라 두 번째 극점의 위치가 허수축으로부터 멀어지는 것을 볼 수 있다. 첫 번째 극점과 세 번째 극점은 모든 제어 이득에서 허수축 기준 오른쪽 반평면을 침범하지 않기 때문에 항상 안정하다.

Fig. 6

Root locus plot of inner loop controller

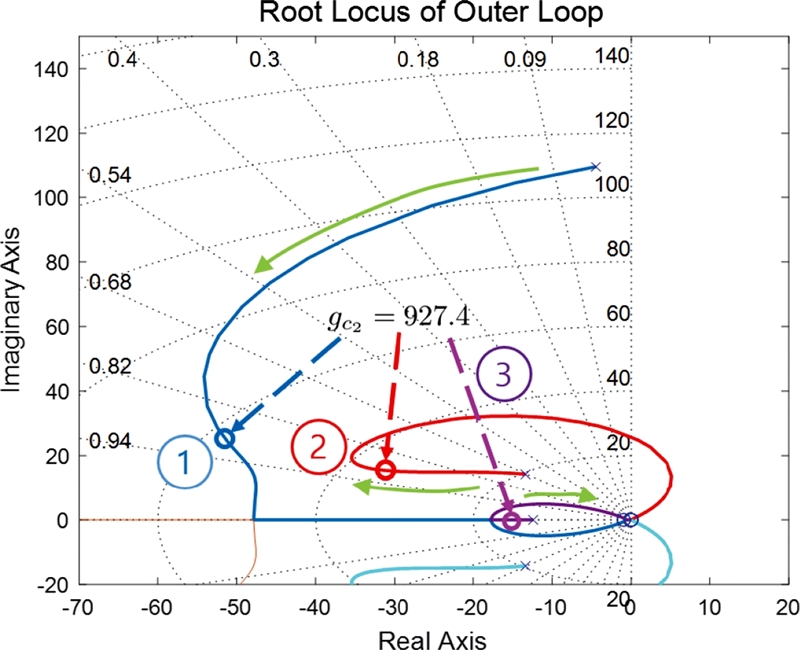
내부 루프 제어기의 이득을 63으로 설정하고 외부 루프 제어기를 구성한 후 근궤적 선도를 그린 결과를 Fig. 7에 나타내었다. 제어기의 이득이 927.4인 지점에서 첫 번째 극점과 두 번째 극점의 감쇠비가 0.8935로 매우 높은 것을 알 수 있다. 세 번째 극점은 실수축상에 있어서 감쇠비가 1이므로 낮은 진동을 유발한다.

Fig. 7

Root locus plot of outer loop controller

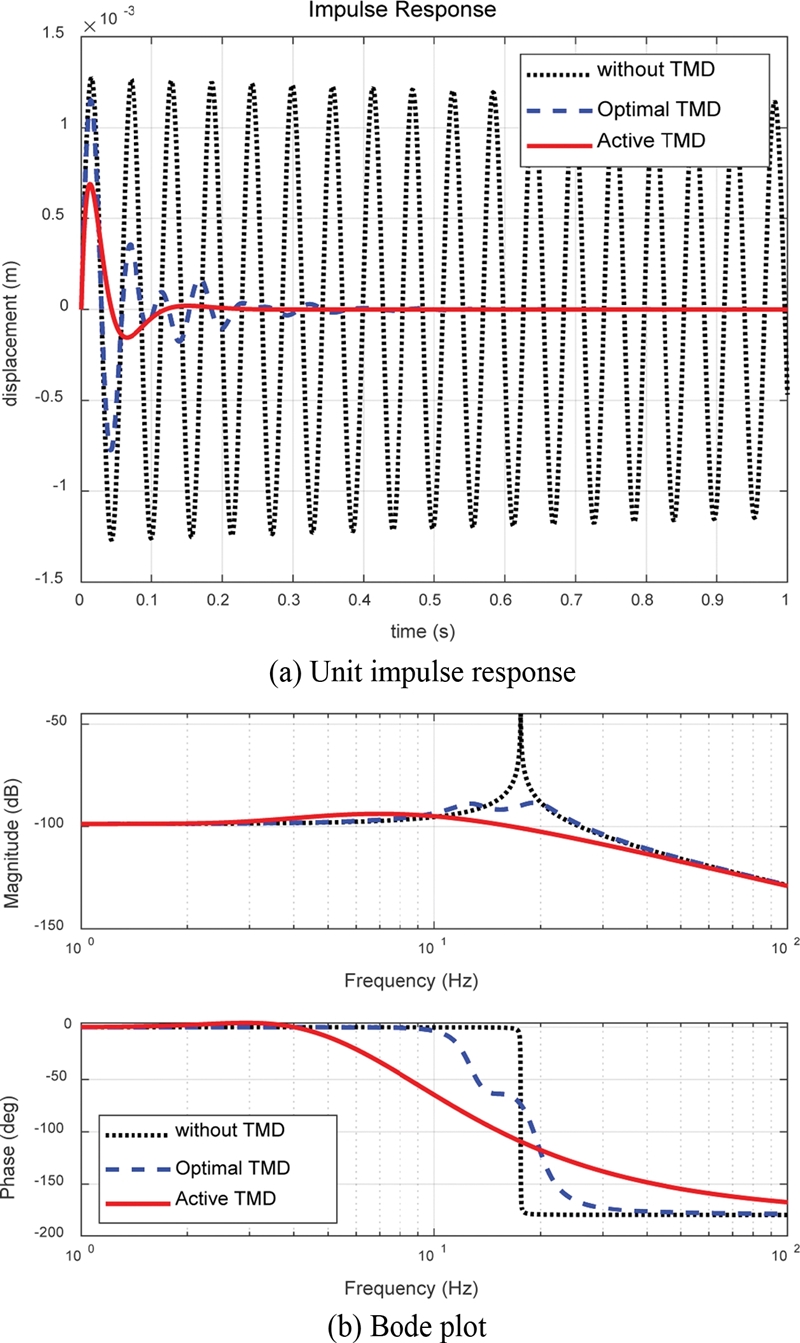
제어기의 튜닝 결과에 대해서 해석적인 단위 충격 응답과 주파수 응답을 각각 Figs. 8(a)와 8(b)에 나타내었다. 단위 충격입력 응답에서 수동형 동조질량감쇠기를 적용하면 0.4초만에 진동이 사라지며, Bode 선도에서 피크주파수에서의 크기가 44 dB만큼 작아졌다. 그러나 능동형 동조질량감쇠기를 적용하면 0.2초만에 진동이 사라지는 것을 확인할 수 있으며 Bode 선도에서 피크주파수에서의 크기가 49 dB만큼 작아지는 것을 보이고 있다. 이를 통해 2중 루프 제어기를 적용한 능동형 동조질량감쇠기는 최적화된 수동형 동조질량감쇠기보다 매우 우수한 진동저감 성능을 가짐을 확인할 수 있다.

Fig. 8

Comparison of simulation results between active and passive TMD

4. 실험적 성능 평가

Fig. 9(a)는 실험을 하기 위한 구조물의 상단 사진을 나타내었다. 진동 저감의 대상이 되는 구조물은 양단이 고정되어 있는 얇은 철재 평판 형태의 보를 이용하였다. 양단 고정보 상단에 동조질량감쇠기 구조물을 결합하였고, 이의 속도 측정을 위한 속도 센서가 부착되어 있다. 또한 성능 평가를 위한 가속도 센서를 동조질량감쇠기 구조물 측면에 부착하였다.

Fig. 9

Picture of the test structures

구조물의 하단부 사진은 Fig. 9(b)에 나타내었다. 진동 저감의 대상이 되는 구조물의 속도 측정을 위한 속도 센서가 하단 중앙에 부착되어 있다. 충격 해머(Impact Hammer)를 이용해 구조물의 하단을 가진하여 모달 테스트(Modal Test)를 진행하였다.

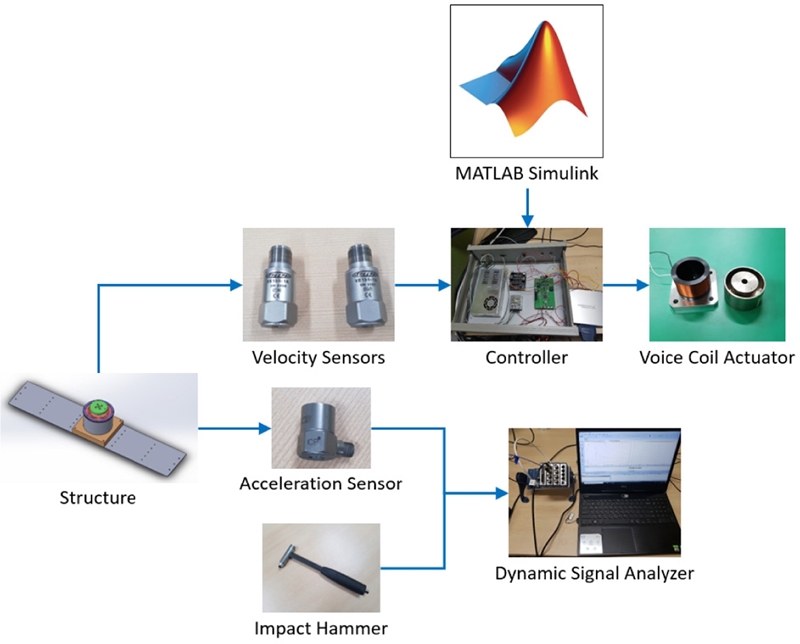
능동형 동조질량감쇠기의 실험적 성능 평가를 위한 장치의 구성도를 Fig. 10에 나타내었다. 제어 알고리즘을 위한 속도 센서 2개가 각각 구조물과 동조질량감쇠기의 질량에 부착된다. 구동기는 선형 보이스 코일 모터(Voice Coil Motor, VCM)를 이용한다. 속도 센서 되먹임 및 제어 신호의 출력을 위하여 DAQ Board를 사용하였고, PC에서 MATLAB Simulink를 사용하여 2중 루프 제어 알고리즘을 구현하였다. 그의 결과인 제어 신호는 선형 구동기에 전류를 공급하는 전류 증폭기로 PWM 신호가 전달된다. 한편 시스템의 진동 저감 효과를 확인하기 위해 모달 테스트 기법을 이용한다. 충격 해머를 이용한 충격 입력은 구조물에 가해지고 그의 응답은 가속도센서로 측정된다. 동적 신호분석기(Dynamic Signal Analyzer)는 두 신호를 받아 구조물의 주파수 응답 함수(Frequency Response Function, FRF)를 구하여 성능 평가에 사용된다.

Fig. 10

Evaluation system of active TMD using modal test

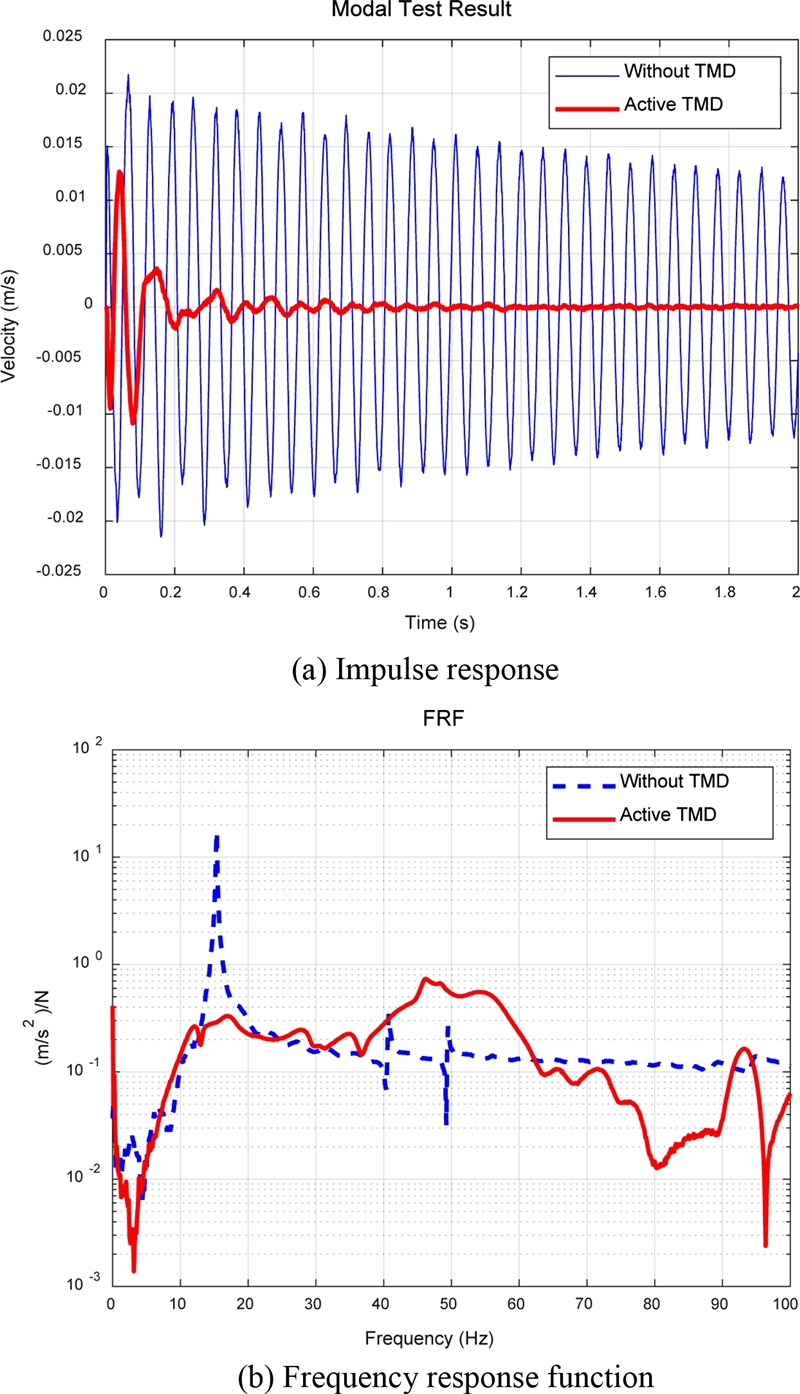
Fig. 11(a)는 충격 입력에 대한 응답을 시간 영역에서 나타낸 것이다. 능동형 동조질량감쇠기가 없는 구조물은 감쇠비가 매우 작기 때문에 진동이 10초 이상 지속된다. 그러나 능동형 동조질량감쇠기가 적용된 구조물은 약 1초 내외에서 진동이 제거되는 우수한 효과를 확인할 수 있다.

Fig. 11

Experimental result for evaluation of active TMD

또한 주파수 응답 함수를 이용한 비교는 Fig. 11(b)에 나타내었다. 동조질량감쇠기가 없을 때 피크주파수 15.34 Hz에서 17.45 (m/s²)/N의 크기를 가지고 있었지만, 능동형 동조질량감쇠기를 적용하면 17Hz에서 0.33 (m/s²)/N으로 약 52배 감소하였음을 알 수 있다. 40-50 Hz 구간의 피크는 실험에 사용된 보의 비틀림 모드의 효과로 수직 방향 진동에는 큰 영향이 없는 것으로 판단된다.

이를 통해 2중 루프 제어기를 사용한 능동형 동조질량감쇠기의 우수한 성능을 확인할 수 있었다. 모달 테스트를 통해 확인한 1자유도 구조물의 진동 제어 실험 결과를 Table 4에 나타내었다.

Table 4

Result of modal test

5. 결론

본 연구에서는 반도체·디스플레이 장비와 같은 초정밀 장비의 동특성을 개선하여 진동을 효과적으로 제거하기 위하여 기존의 수동형 동조질량감쇠기에 구동기를 적용한 능동형 동조질량감쇠기를 설계, 개발하였다. 이를 위하여 기존의 수동형 동조질량감쇠기에 센서와 선형 구동기를 장착하고 제어 시스템을 구성하였다. 이의 안정성 확보와 높은 감쇠비를 구현하기 위하여 2중 루프 제어기를 적용하였으며 제어기는 내부 루프에서 비최소위상 시스템을, 외부 루프 제어기에서는 P 제어기를 적용 하였으며 근궤적 선도를 이용하여 효과적인 제어기의 이득을 조절하였다.

시스템의 진동 저감 성능을 실험적으로 검증하기 위해 제작된 구조물에 모달 테스트를 진행하였고, 능동형 동조질량감쇠기는 시간 영역에서 정착시간 96.8% 감소, 주파수 응답 함수의 피크 크기를 기준으로 98.1% 이상 감소의 매우 우수한 진동 저감효과를 확인하였다. 본 연구의 결과는 반도체·디스플레이 장비와 같은 고정밀 장비의 진동을 획기적으로 저감하여 시스템의 정밀도와 수율 향상에 큰 도움이 될 것으로 예상된다.

Acknowledgments

본 논문은 2018년도 한국기술교육대학교 교수 교육연구진흥 과제 지원에 의하여 연구되었음.

References

• Villaverde, R., “Seismic Control of Structures with Damped Resonant Appendages,” http://www.taylordevices.com/custom/pdf/tech-papers/18-SeismicControlStructures.pdf, (Accessed 14 DECEMBER 2020)
• Ahn, S. K., “Vibration Control for Floor Slabs Using Tuned Mass Damper,” Journal of the Korean Association for Spatial Structures, Vol. 12, No. 2, pp. 24-29, 2012.
• Lin, C. C., Hu, C. M., Wang, J. F., and Hu, R. Y., “Vibration Control Effectiveness of Passive Tuned Mass Dampers,” Journal of the Chinese Institute of Engineers, Vol. 17, No. 3, pp. 367-376, 1994. [https://doi.org/10.1080/02533839.1994.9677600]
• Tsai, H. C. and Lin, G. C., “Explicit Formulae for Optimum Absorber Parameters for Force-Excited and Viscously Damped Systems,” Journal of Sound and Vibration, Vol. 176, No. 5, pp. 585-596, 1994. [https://doi.org/10.1006/jsvi.1994.1400]
• Bakre, S. and Jangid, R., “Optimum Parameters of Tuned Mass Damper for Damped Main System,” Structural Control and Health Monitoring: The Official Journal of the International Association for Structural Control and Monitoring and of the European Association for the Control of Structures, Vol. 14, No. 3, pp. 448-470, 2007. [https://doi.org/10.1002/stc.166]
• Nigdeli, S. M. and Bekdas, G., “Performance Comparison of Location of Optimum TMD on Seismic Structures,” International Journal of Theoretical and Applied Mechanics, Vol. 3, pp. 99-106, 2018.
• Battaini, M., Casciati, F., and Faravelli, L., “Implementing a Fuzzy Controller into an Active Mass Damper Device,” Proc. of the American Control Conference, pp. 888-892, 1997. [https://doi.org/10.1109/ACC.1997.609654]
• Baoya, C. and Chunxiang, L., “Design of Active Tuned Mass Damper based on Robust Control,” Proc. of the IEEE International Conference on Computer Science and Automation Engineering, pp. 760-764, 2012. [https://doi.org/10.1109/CSAE.2012.6272877]
• Thenozhi, S. and Yu, W., “Fuzzy Sliding Surface Control of Wind-Induced Vibration,” Proc. of the IEEE International Conference on Fuzzy Systems, pp. 895-900, 2014. [https://doi.org/10.1109/FUZZ-IEEE.2014.6891623]
• Chesne, S., Inquieté, G., Cranga, P., Legrand, F., and Petitjean, B., “Innovative Hybrid Mass Damper for Dual-Loop Controller,” Mechanical Systems and Signal Processing, Vol. 115, pp. 514-523, 2019. [https://doi.org/10.1016/j.ymssp.2018.06.023]
• Chesné, S. and Collette, C., “Experimental Validation of Fail-Safe Hybrid Mass Damper,” Journal of Vibration and Control, Vol. 24, No. 19, pp. 4395-4406, 2018. [https://doi.org/10.1177/1077546317724949]