내부공간의 방향성으로 인한 이방성을 고려한 셀룰러 구조 최적설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Additive manufacturing (AM) had a significant influence on the geometry design of products. It became possible to replace the full solid material with cellular structures for the optimal design of AM parts. Various types of cellular structures have been developed and studied for different purposes. However, many studies have focused on an optimal design using cellular structures having near-isotropic properties, such as cube or honeycomb structures. This paper presents the effect of the anisotropic material property on the optimal design by generating cellular structure with anisotropic material property induced by internal void geometry. Kriging metamodel-based material property model is proposed for modeling anisotropy induced by the rotation of internal void. This material model is then applied to the optimal design process. Three types of void geometry, circular, non-rotating, and rotating elliptical void, are considered to demonstrate the effect of anisotropic cellular structure on the optimal design. Due to the anisotropy induced by complex internal void geometry, Kriging metamodel-based material property models are utilized as the material property model. The effect of the anisotropic property and the material property model on the optimized structures is confirmed through two numerical examples in the perspectives of structure performance and density distribution.
Keywords:
Anisotropic material property, Cellular structure, Elliptical void, Kriging metamodel, Optimal design키워드:
이방성 물성치, 셀룰러 구조, 타원형 내부공간, 크리깅 메타 모델, 최적설계1. 서론
적층 제조 기술의 발전은 제품의 설계에서부터 제조까지 이르는 제조 방식에 큰 영향을 미쳤다. 특히, 기존 절삭 가공으로는 제작하기 어려웠던 복잡한 형상의 제작이 가능해졌다. 대표적으로 기존 솔리드 형상의 재료를 대체하는 셀룰러 구조를 그 예로 들 수 있다. 셀룰러 구조는 기존 솔리드 형상의 재료에 비해 무게 대비 성능이 좋으며 설계자의 의도에 따라 다양한 형상의 셀룰러 구조를 활용할 수 있다.1 실제 적층 제조 기술을 활용하여 벨로와 덕트 같은 자동차 부품2뿐만 아니라 제트 엔진의 연료 노즐과 같은 항공 부품3의 설계 및 제작되고 있다.
최근 30년간 기하학적으로 단순한 사각형 모양의 셀룰러 구조4,5와 정육각형의 허니콤 구조,5,6 불규칙한 보로노이 구조5,7 등의 다양한 셀룰러 구조에 대한 연구가 진행되어 왔다. Fig. 1과 같이 대부분의 셀룰러 구조는 방향성이 없는 직교이방성을 가지는 형상이거나 등방성을 갖도록 설계되고 있다. 설계 조건에서 벗어난 방향의 하중이 가해질 경우 동일 조건으로 설계된 방향성이 없는 직교이방성 셀룰러 구조는 이방성 셀룰러 구조에 비해 안정적이지만 이방성 셀룰러 구조에 비해서 높은 밀도를 가진다. 따라서 하중의 방향이 일정한 구조물 또는 제품의 경우 다른 종류의 셀룰러 구조보다 이방성 셀룰러 구조를 활용하여 설계하는 것이 무게 대비 효율적이다.8 하지만 이방성 셀룰러구조를 활용한 최적설계와 이방성 셀룰러 구조가 최적설계 결과에 미치는 영향에 대한 연구는 현재까지 많이 이루어지지 않고 있다.
많은 연구에서 Asymptotic 균질화법(Homogenization)을 이용해 계산된 셀룰러 구조의 유효 탄성행렬(Effective Elastic Matrix)을 기반으로 물성 모델을 생성하고, 물성 모델을 최적설계 프로세스에 적용하였다. 많은 물성 모델들이 셀룰러 구조의 밀도를 단일변수로 하고 있으며, Solid Isotropic Material with Penalization (SIMP)9,10와 다항식14-16을 기반으로 하고 있다. SIMP는 멱급수를 이용하여 물성 모델을 생성하는 방법이며, 다항식에 비해 간단하지만 정확도는 낮은 편이다. SIMP와 회전행렬을 이용하여 Li et al.8와 Grogen and Sigmound10는 회전하는 셀룰러 구조의 유효 탄성행렬을, Nguyen et al.11,12은 프린팅 방향에 따른 셀룰러 구조의 유효 탄성행렬을 예측하였다. Kozuch and Jasiuk13는 다항식과 회전행렬을 이용하여 회전하는 타원형 내부 구조를 가지는 셀룰러 구조의 물성 모델을 생성하고 최적 설계에 적용하였다. 그들의 연구에서는 총 세 가지의 변수, 타원형 한 축의 길이와 축 길이의 종횡비, 내부 구조의 회전각을 셀룰러 구조의 설계 변수로 설정하였다. 다만, 그들은 최적설계 과정에서 3개의 변수를 동시에 고려하지 않고, 2개의 변수를 특정 값으로 고정한 상태에서 나머지 1개의 변수에 대해서만 최적설계를 진행하였다. 따라서, 몇 가지 수치예제를 통해 내부 구조의 형상과 회전각이 최적설계 결과에 미치는 영향에 대해 제한적으로 확인하였다.
또 다른 물성 모델로는 크리깅 메타 모델을 이용한 경우가 있다.17,18 크리깅 메타 모델을 이용한 물성 모델은 다변수 또는 복합적 셀룰러 구조의 유효 탄성 계수를 하나의 물성 모델로 정확하게 표현할 수 있는 장점이 있다. 특히, 주어진 변수와 시뮬레이션 결과를 이용하여 그 둘 사이의 관계식을 찾는 도구로 많이 활용되고 있다.19 대부분의 셀룰러 구조는 형상이 단순하고 형상을 결정하는 변수인 밀도에 따라 유효 탄성행렬의 값이 단조 증가하기 때문에, 많은 연구에서는 처리 속도가 상대적으로 긴 크리깅 메타 모델을 이용한 물성 모델보다는 처리 속도가 빠르고 단순한 SIMP와 다항식 기반의 모델 등을 많이 사용하고 있다.9,10
본 논문에서는 1) 타원형 내부 구조를 이용하여 2차원 이방성 셀룰러 구조를 정의하고, 2) 다항식 기반의 물성 모델과 크리깅 메타 모델을 이용한 물성 모델을 생성 후, 3) 이방성 셀룰러 구조와 두 물성 모델이 최적설계 결과에 미치는 영향을 구조의 성능과 요소의 밀도 분포의 관점에서 논의하고자 한다. 이어지는 2절에서는 이방성 셀룰러 구조를 정의하고 셀룰러 구조에 대한 두 물성 모델의 정확성을 비교한다. 3절에서는 최적설계 문제를 정의하고 최적설계 문제에 이방성 셀룰러 구조와 두 물성 모델을 적용하여 최적설계 결과를 도출한다. 도출된 결과를 토대로 이방성 셀룰러 구조와 두 물성 모델이 최적설계 결과에 미치는 영향을 확인한다.
2. 이방성 셀룰러 구조와 물성치 모델
본 절에서는 이방성 셀룰러 구조를 정의하고 해당 셀룰러 구조의 탄성행렬 예측을 위한 두 종류의 물성 모델을 검토한다. 물성 모델로는 일반적으로 사용되고 있는 다항식 기반 모델과 크리깅 메타 모델을 선정하였다.17,18 본 절에서 사용된 셀룰러구조 재료의 탄성 계수와 포아송 비는 일반적인 티타늄 합금의 물성치인 100 GPa과 0.3으로 설정하였다.
2.1 타원형 내부 구조를 가지는 이방성 셀룰러 구조
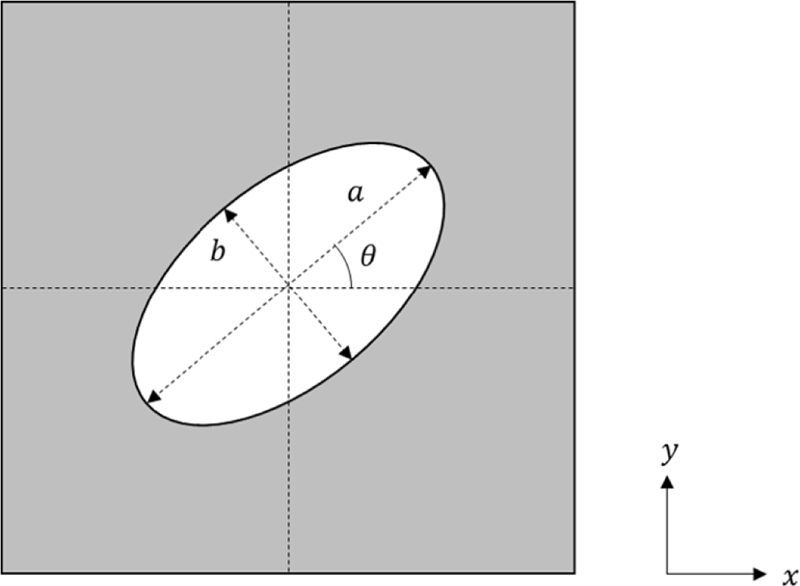
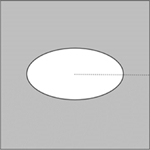
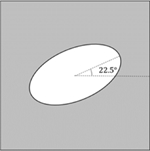
Fig. 2는 타원형 내부공간을 가지는 단위 셀룰러 구조를 표현한 그림이다. 단위 셀룰러 구조 중앙에 위치한 타원형 내부공간은 두 축의 길이 a와 b를 가지며 x축을 기준으로 회전각 θ만큼 회전된 상태이다. 이러한 단위 셀룰러 구조는 a와 b, θ값에 따라 내부공간의 형상과 셀룰러 구조 물성의 방향성을 제공할 수 있을 뿐만 아니라 내부공간에 날카로운 모서리가 존재하지 않아 응력 집중 문제가 다른 셀룰러 구조에 비해 적다는 장점이 있다. 또한, 형상이 회전된 각축에 대해 대칭이기 때문에 구성방정식 변수의 개수를 줄일 수 있다. 하지만 타원형으로 정의되는 내부공간으로 인해 a와 b값이 1을 초과할 수 없으며, 셀룰러 구조의 최소 밀도는 a와 b값이 각각 1인 원형 내부 구조를 가지는 셀룰러 구조의 밀도인 0.2146이 된다.
많은 연구에서 셀룰러 구조의 탄성행렬을 수치적으로 도출하기 위해 균질화법을 활용해왔다. Asymptotic 균질화법은 균질화법 중 하나이며, 셀룰러 구조뿐만 아니라 복합 재료의 유효 탄성물성 계산 등에 사용되고 있다.20-23 해당 균질화법은 다음과 같이 세 가지의 가정을 기반으로 하고있다. 1) 셀룰러 구조의 경계 조건은 규칙적이며, 2) 셀룰러 구조를 구성하는 서로 다른 소재는 완벽하게 결속되어 있으며, 3) 셀룰러 구조의 크기는 설계 영역의 크기에 비해 충분히 작아야 한다.24 본 논문의 셀룰러 구조가 이러한 세 가지의 가정을 만족하는지에 대해서는 3.1절에서 자세히 설명하였다.
타원형 내부공간을 가지는 단위 셀룰러 구조의 CH는 Dong et al.20이 제안한 균질화법 알고리즘을 활용하여 수치적으로 계산하였다. 평면변형 조건하에서 직교이방성 셀룰러 구조의 구성방정식은 식(1)과 같다.
| (1) |
여기서 σ와 ε는 각각 직교좌표계에서의 응력과 변형률이며, 소재의 C는 강성행렬이다. 유효 탄성행렬 CH는 식(2)와 같이 이산화된 형태로 표현된다.
| (2) |
여기서 N은 요소의 총 개수이며, B는 변형-변위행렬, I는 6 × 6 단위행렬이다. V와 Ve는 각각 구조물의 총 부피와 요소의 부피이다. 이때 아래첨자 e는 각 요소를 의미한다. 요소의 미소 변위벡터(Microscopic Displacement Vector) χe는 식(3)을 통해 계산할 수 있다.
| (3) |
여기서 변형행렬 εij는 식(4)와 같다.
| (4) |
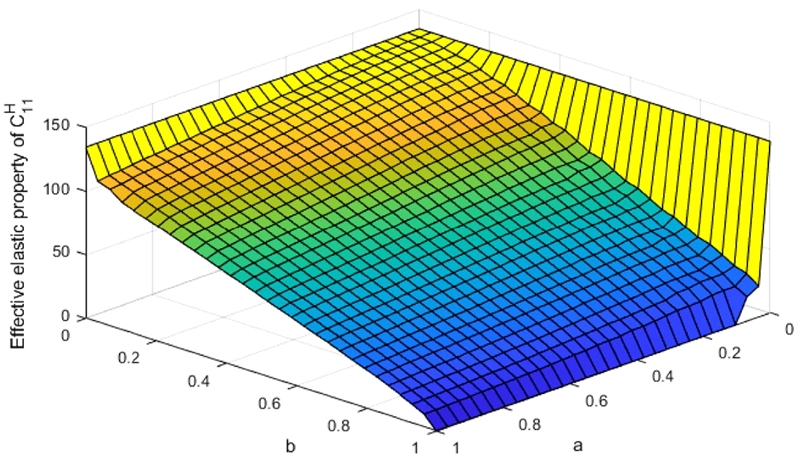
Fig. 3은 Asymptotic 균질화법으로 계산된 유효 탄성행렬의 한 요소 값을 a와 b값에 따라 표현한 그래프이다. 값은 대체적으로 a와 b값에 선형적으로 반비례하며, a와 b값이 0과 1에 근사한 경우 큰 폭으로 증가 또는 감소하였다. 와 모두 a와 b값에 대해 선형적으로 반비례하는 경향을 보였다. 이때, 내부공간의 형상이 x와 y축에 대해 서로 대칭이므로 과 값은 0이었다.
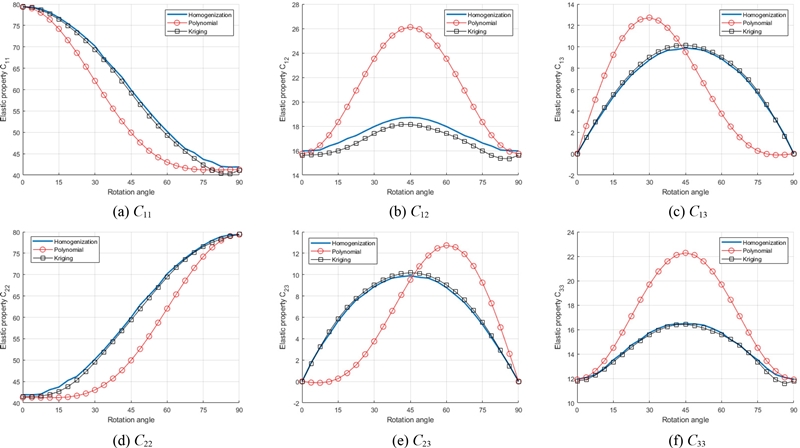
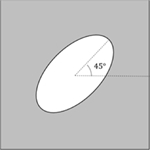
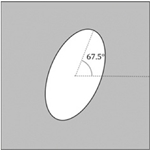
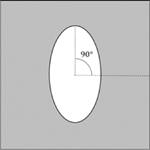
내부공간의 회전이 유효 탄성행렬의 각 요소값에 미치는 영향을 확인하기 위해, Table 1와 같이 a와 b 값이 각각 0.4와 0.8인 타원형 내부공간을 0, 22.5, 45, 67.5, 90°로 회전시키며 단위 셀룰러 구조의 유효 탄성행렬을 계산하였다. 회전각이 0과 90°인 경우, 내부공간의 형상에 따라 와 의 값이 바뀌었다. 즉, θ가 0° 경우에는 값이 값보다 크고, θ가 90°인 경우에는 값이 값보다 컸다. 두 경우 모두 내부공간의 형상이 x와 y축에 대칭되므로 과 값은 0이었다. 하지만, θ가 0에서 90° 사이의 값을 가지는 경우 과 값은 0이 아닌 값을 보여주었으며, 그 값들은 θ가 45°일 때 최대가 되었다. 이러한 내부공간 회전에 따른 유효 탄성행렬 요소값의 변화는 Figs. 4(c)와 4(d)에서 명확히 확인할 수 있으며, Fig. 4는 Table 1에 동일 조건에서 회전각의 수를 증가시켜가며 계산한 유효 탄성행렬의 각 요소의 값을 그래프로 표현한 것이다.
2.2 내부공간의 회전을 고려한 물성치 모델
많은 연구에서 식(5)와 같이 다항식 기반 물성 모델에 회전행렬을 적용하여 회전을 고려한 단위 셀룰러 구조의 물성 모델을 정의하였다.8,10-13
| (5) |
여기서 Cpoly(x)는 설계변수 x에서 다항식 기반 물성 모델로 예측한 탄성행렬이며, 는 Cpoly(x)에 회전행렬 R을 적용하여 예측한 탄성 행렬이다. 이때 x는 셀룰러 구조를 설계하는 일반적인 변수이며, 본 연구에서는 x를 a와 b로 나누어 표현할 수 있다.
식(5)에서 확인할 수 있듯이, 는 회전행렬을 이용하여 Cpoly(x)를 θ값만큼 회전시킨 행렬이다. 본 논문에서 정의하고 있는 이방성 셀룰러 구조는 구조 자체가 회전하는 것이 아닌 내부 구조가 회전하기 때문에 와는 개념적 차이가 있다. Fig. 4에서 빨간색 선으로 표현된 그래프와 파란색 선으로 표현된 유효 탄성행렬의 그래프는 명확한 차이를 보이고 있다. 이러한 결과를 볼 때, Cpoly(a, b)에 회전행렬을 적용한 는 회전하는 타원형 내부 구조를 가지는 셀룰러 구조의 물성 모델로 적합하지 않을 수 있다. 따라서, 회전행렬이 적용된 다항식 기반 물성 모델의 대안으로서 크리깅 메타 모델의 사용을 제안한다.
크리깅 메타 모델은 지질학자 Krige25에 의해 소개된 수치 모델로 최적의 광물질 등급 분포를 표현하기 위해 개발되었다. 일반적인 크리깅 메타 모델은 식(6)과 같이 표현된다.
| (6) |
여기서 f(x)Tβ는 데이터의 회귀 모델을, Z(x)는 회귀 모델에 대한 에러의 보간 모델을 나타낸다. x는 벡터형식 변수이다. 크리깅 메타 모델은 밀도와 같은 단일변수 모델뿐만 아니라 다변수 모델 생성에 활용 가능한 장점이 있다. 본 연구에서는 a와 b, θ값을 변수로 하는 크리깅 메타 모델 Y(a, b, θ)을 생성하였다.
Fig. 4에서는 유효 탄성행렬의 요소값(파란색 선)과 값(빨간색 선)과 Y(a, b, θ) 값(검정색 선)이 그래프로 표현되고 있다. 2.1절에서도 설명했듯이, 과 값은 회전각이 45°일 때 가장 큰 값을 보이고 있다. Y(a, b, θ)값은 이러한 경향을 상당히 정확하게 예측하고 있지만, 값은 회전각이 30과 60°일 때 가장 큰 값을 보이고 있다. 이러한 차이는 이 회전행렬을 이용하여 물성치를 예측했기 때문으로 추정된다. Fig. 4에서 유효 탄성행렬에 대한 값과 Y(a, b, θ)값의 평균 제곱근 오차는 각각 4.47과 0.59이었다.
3. 수치예제에 의한 이방성 물성 모델 검증
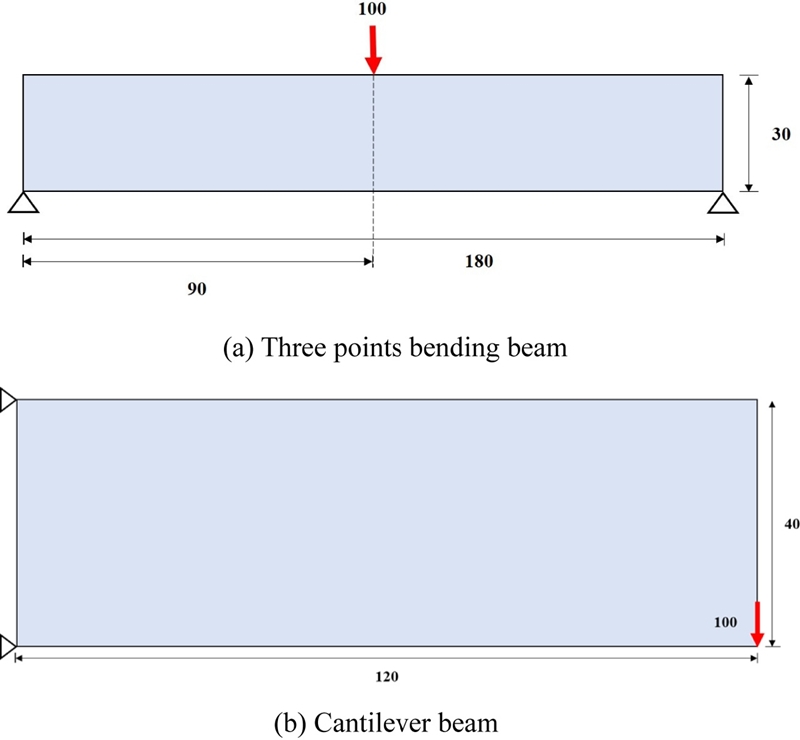
본 절에서는 2차원 3점 굽힘보와 단순지지된 평판 구조의 변형에너지를 목적 함수로 하는 최적설계 문제를 이용하여 이방성 물성 모델의 유효성을 검증하고 이방성 물성 모델이 최적설계 결과에 미치는 영향을 확인하다. 2차원 3점 굽힘보와 단순지된 평판 구조는 대표적인 수치예제로 많은 연구에서도 활용되고 있다.8-12 최적설계에는 Asymptotic 균질화법으로 도출된 유효 탄성행렬을 기반으로 생성된 두 물성 모델과 변화율(Gradient)기반의 위상 최적화 알고리즘이 사용되었다.11,12,21
3.1 최적설계 문제 정의
최적설계 문제는 목적함수를 최소화하는 동시에 주어진 구속 조건을 만족하는 최적의 설계변수값을 찾는 것으로 정의된다. 본 논문에서는 물성 모델 검증과 최적설계 결과에 대한 이방성셀룰러 구조의 영향을 확인하기 위한 최적설계 문제를 Table 2와 같이 정의하였다:
여기서 c(x)는 구조물의 변형에너지를, U(x)와 K(x)는 각각 전체변위벡터와 전체강성행렬을 나타낸다. v(x)는 각 요소 밀도의 총 합이며 사용자가 정의한 목표 평균 밀도 보다 작거나 같은 값이여야 한다. 2.1절에서 설명한 것과 같이, 아래첨자 e는 각 요소의 인덱스를 ae와 be, θe, ve는 각 요소의 타원형 내부공간 각 축의 길이와 회전각, 부피를 나타낸다. 변수 ae와 be, ve는 각각 최솟값과 최댓값을 가지며 ae와 be의 최댓값은 요소의 한변의 길이 lele을 초과할 수 없다. 주어진 최적설계 문제는 설계 영역에 규칙적으로 배치된 요소의 타원형 내부공간의 설계변수를 주어진 조건과 목적에 맞도록 수정하는 문제로 간주할 수 있다.9,21
최적설계 과정은 Hassani and Hinton21이 최적설계를 위해 제안한 최적정기준(Optimality Criteria)법과 위상 최적화 알고리즘을 이용하여 타원형 내부공간의 설계변수를 수정하고 내부공간을 회전한다. 이때 각 요소의 내부공간은 요소에 작용하는 주응력 방향으로 회전시킨다.21,23
이방성과 등방성 물성 모델에 따른 최적설계 결과를 확인하고 물성 모델의 적합성을 평가하기 위해 각 내부공간을 아래와 같이 세 가지로 분류하였다. 1) 원형 내부공간, 2) 회전이 고려되지 않은 타원형 내부공간, 3) 회전이 고려된 기하학적 내부공간 물성 모델의 정확성 검증에는 Zhang et al.17이 활용한 물성모델 정확성 검증 방법을 확장하여 적용하였다.
3.2 수치예제 정의
이방성 셀룰러 구조와 물성 모델이 구조물의 최적설계에 미치는 영향을 확인하기 위해 Fig. 5와 같이 두 수치예제에 대한 최적설계를 수행하였다. 모든 수치예제에서는 셀룰러 구조 소재의 탄성 계수와 포아송 비를 각각 100 GPa과 0.3으로 설정하였다. 타원형 내부공간에는 소재가 없는 상태, 즉 공기로 채워져 있으며, 각 요소의 크기는 설계 영역에 비해 충분히 작다고 가정한다.
Ameen et al.24에 따르면 각 설계 영역의 최대 크기에 대한 요소의 크기의 비 α가 8분에 1 이하일 경우, 각 요소의 크기가 충분히 작으며 균질화법을 적용하기에 적합하다. 본 논문에서는 3점 굽힘보와 단순지지된 평판 수치예제에서 사용된 요소의 크기 lele는 모두 5로 정의하였다. 이 경우 Ameen et al.24이 제안한 설계 영역의 최대 크기에 대한 요소의 크기의 비를 만족했다. 위에서 언급된 최적설계 조건들은 2.1절에서 언급한 Asymptotic 균질화법의 세 가지 가정을 만족시킨다고 할 수 있다.
각 수치예제에는 두 가지의 물성 모델과 세 가지의 셀룰러 구조를 활용하여 최적설계를 진행하였다. 물성 모델은 회전행렬이 적용된 다항식 기반 물성 모델과 크리깅 메타 모델을, 셀룰러 구조는 원형, 회전이 고려되지 않은 타원형, 회전이 고려된 타원형 내부 구조를 가지는 셀룰러 구조를 활용하였다. 원형 내부공간은 a와 b값이 같은 타원형 내부공간으로 간주한다.
최적설계 제한 조건은 Table 3과 같이 정의하였다. Fig. 3에서 확인되었던 큰 폭으로 물성치가 변화하는 영역을 제외하기 위해 ae와 be의 최대, 최솟값을 각각 0.9와 0.1로 설정하였다. vmin은 타원형 내부 구조의 기하학적 특징을 고려하여 0.4로, vmax는 Nugyen et al.12에서 사용된 0.8로 정의하였다. 셀룰러 구조를 이용한 최적설계에서 일반적으로 사용되는 구조의 목표 평균 밀도 는 0.5-0.6 사이의 값이며,8,11,12 본 논문에서는 를 0.6으로 설정하여 각 요소간 밀도 분배의 자유도를 높여 주었다.
3.3 변형에너지 비교를 통한 물성 모델의 정확성 검증
물성 모델의 정확성을 검증하기 위해 Zhang et al.17은 균질화법으로 계산한 셀룰러 구조의 유효 탄성행렬의 요소값과 물성 모델로 예측한 값을 비교함으로써 자신들이 제안한 물성 모델의 정확성을 검증하였다. 본 논문에서는 Zhang et al.17이 활용한 물성 모델 정확성 검증 방법을 구조물로 확장하여 아래와 같이 계산된 두 값의 비교를 통해 물성 모델의 정확성을 검증한다.
(1) 주어진 물성 모델을 이용한 최적설계 결과의 변형에너지
(2) 최적설계 결과로서 얻어진 각 요소들의 설계변수를 기반으로 계산된 유효 탄성행렬로부터 도출된 구조물의 변형에너지
여기서 (1)의 값은 물성 모델을 이용한 구조물의 변형에너지로, (2)의 값은 요소의 내부 형상 정보를 이용해 계산한 구조물의 변형에너지로 명명한다. 수치예제의 최적설계 결과에서 두 변형에너지 값의 차이가 작은 경우, 사용된 물성 모델이 정확하게 셀룰러 구조의 유효 탄성행렬을 예측했다고 간주할 수 있다.
Table 4는 두 수치예제에 대한 최적설계 결과의 변형에너지를 비교한 표이며, Table 4에 표기된 Model-Based는 물성 모델을 이용한 구조물의 변형에너지를, Homogenization-Based는 요소의 형상 정보를 이용한 구조물의 변형에너지를 나타낸다. Diff.로 표현된 두 변형에너지 차이는 Homogenization-Based 값과 Model-Based 값의 차이를 Homogenization-Based 값으로 나눈 값이다. Diff.값이 작을수록 주어진 형상 정보에 대해 물성 모델이 유효 탄성행렬을 정확하게 예측했다고 할 수 있다.17

Structural compliance of the optimal design with respect to two material property models and three different cellular types
원형과 회전이 고려되지 않은 셀룰러 구조와 회전행렬을 적용한 다항식 기반 물성 모델을 이용한 최적설계 결과의 경우, 두 변형에너지 차이가 3점 굽힘보 예제에서 0.19와 0.51%, 평판 예제에서 0.11와 0.23%였다. 물성 모델로 크리깅 메타 모델을 활용한 경우, 두 변형에너지의 차이가 3점 굽힘보 예제에서 0.15와 0.37%, 평판 예제에서 0.51과 0.04%였다. 이러한 결과는 두 물성 모델 모두 원형과 회전이 고려되지 않은 타원형 내부공간을 가지는 셀룰러 구조의 유효 탄성행렬을 정확하게 예측했다는 것을 보여준다.
회전이 고려된 타원형 내부공간을 가지는 셀룰러 구조와 크리깅 메타 모델을 활용한 최적설계인 경우, 두 수치예제에서 변형에너지의 차이가 각각 0.49와 0.15%였다. 반면, 다항식 기반의 물성치 모델을 활용한 경우에서는 25.67와 23.09%의 큰 차이를 보였다. 이러한 결과는 회전행렬이 적용된 다항식 기반 물성 모델이 크리깅 메타 모델에 비해 회전하는 타원형 내부 구조의 유효 탄성행렬 예측이 부정확함을 보여주고 있다.
결과적으로, 세 가지 종류의 셀룰러 구조에 대한 다항식 기반물성 모델은 주어진 두 수치예제에서 최대 25.67%의 변형에너지 차이를 보인 반면, 크리깅 메타 모델 기반 물성 모델은 최대 0.51%의 차이를 보였다. 이를 통해 크리깅 메타 모델 기반 물성 모델이 다항식 기반 물성 모델에 비해 회전하는 타원형 내부공간을 가지는 셀룰러 구조의 물성을 정확하게 예측함을 확인할 수 있었다.
3.4 이방성 셀룰러 구조가 최적설계 결과에 미치는 영향
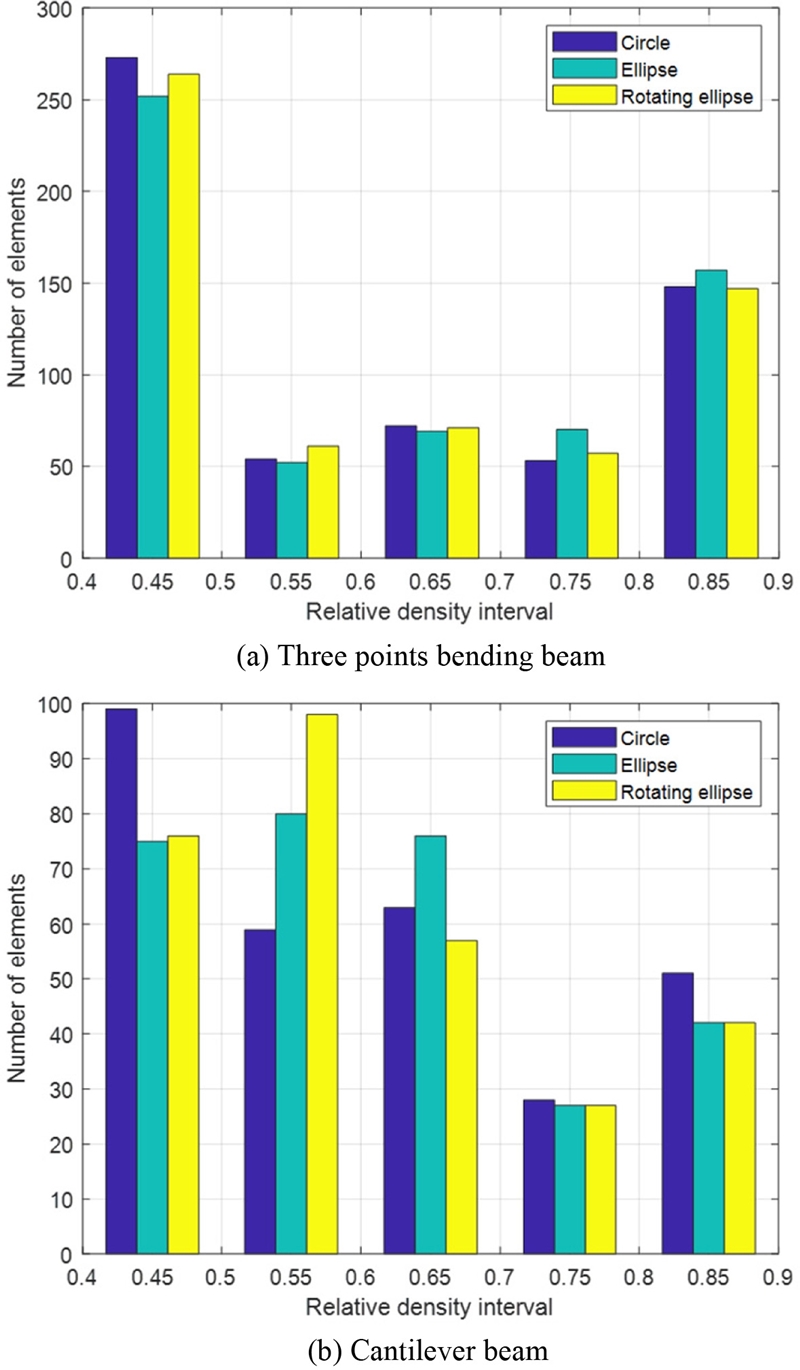
세 가지의 셀룰러 구조를 이용한 최적설계 결과의 형상은 Table 5와 같다. 최적설계 과정에는 크리깅 메타 모델을 물성 모델로 사용하였으며, 각 요소의 그레이 스케일은 요소의 밀도를, 요소 중심 흰 영역은 내부공간의 형상을 나타낸다. 3점 굽힘보 예제의 경우, 셀룰러 구조의 형상이 힘이 가해지는 점의 위치를 기준으로 대칭이므로 설계 영역의 절반만을 가시화하였다.
단순지지된 평판 예제를 통해 보았을 때, 회전이 고려된 타원형 내부공간을 이용한 최적설계의 변형에너지는 원형 및 회전이 고려되지 않은 타원형 내부공간을 이용한 경우에 비해 4.5와 1.2%의 성능 향상을 보였다. 3점 굽힘보 예제에서는 6.1과 3.0%의 성능 향상을 보였다. 이러한 결과는 이방성 셀룰러 구조를 이용한 최적설계의 장점을 보여주고 있다.
두 수치예제를 통해 확인한 이방성 셀룰러 구조를 이용한 최적설계 결과의 성능 향상은 요소에 작용하는 응력의 크기와 방향에 따라 내부공간 형상과 방향을 조절함으로써 효율적인 재료의 분배가 가능했기 때문이다. Fig. 6은 최적설계 결과의 요소별 밀도 분포를 통해 이방성 셀룰러 구조의 효율적 재료 분배를 보여주고 있다. 원형 내부공간을 이용한 경우, 다른 내부공간을 이용한 결과에 비해 0.8-0.9 사이의 높은 밀도를 가지는 요소의 비율이 상대적으로 높다. 셀룰러 구조의 이방성이 높아질수록 높은 밀도를 가지는 요소의 비율은 낮아지고, 0.4-0.7 사이의 낮은 밀도를 가지는 요소의 비율이 높아졌다. 그럼에도 불구하고 더 높은 성능이 보이는 이유는 요소에 작용하는 응력의 방향과 크기에 따라 재료를 효율적으로 분배했기 때문이다.
4. 결론
본 연구에서는 타원형 내부 구조를 가지는 이방성 셀룰러 구조를 정의하고 최적설계에 적용하였다. 최적설계에는 변화율 기반 위상 최적화와 최적정기준법이 사용되었다. 두 가지의 수치 예제를 통해 이방성 셀룰러 구조는 등방성 혹은 방향성이 없는 직교이방성 셀룰러 구조에 비해 높은 설계 자유도를 가지며, 그로 인해 높은 효율의 최적설계 결과를 얻을 수 있음을 확인하였다. 타원형 내부공간의 회전으로 인한 셀룰러 구조의 이방성은 일반적으로 많이 사용되고 있는 물성 모델 중 하나인 다항식 기반 모델과 회전행렬로는 예측이 부정확했다. 따라서 본 논문에서는 크리깅 메타 모델을 그 대안으로 제안하였다. 수치예제를 통해 이방성 셀룰러 구조 기반 최적설계 결과의 전반적인 밀도 분포와 더불어 셀룰러 구조의 최대 밀도 변수에 따른 밀도 분포 특징을 확인하였다. 이방성 셀룰러 구조를 이용하여 최적 설계를 진행할 경우, 등방성 셀룰러 구조를 이용한 경우에 비해 높은 밀도를 가지는 요소의 개수가 줄어들었으며 동시에 중간 수준의 밀도를 가지는 요소의 개수가 증가하였다. 이를 통해 이방성 셀룰러 구조를 이용한 최적설계 과정에서 재료의 분배가 응력의 방향과 크기에 따라 효율적으로 진행되었음을 확인하였다. 또한, 셀룰러 구조의 최대 밀도가 낮아질수록 이방성 셀룰러 구조를 이용한 최적설계의 결과가 등방성 셀룰러 구조를 이용한 경우 대비 더 높은 효율을 보였다. 실제 적층 제조 과정에서는 해상도 등으로 인해 제조할 수 있는 셀룰러 구조의 최대 밀도가 존재하기 때문에 본 연구의 결과는 제조 환경을 고려한 셀룰러 구조의 최대 밀도 결정에 좋은 지표가 될 것으로 기대된다.
본 논문에서 사용된 이방성 셀룰러 구조의 형상이 단순하고, 3차원 셀룰러 구조에 적용할 경우 제작이 어렵다는 한계를 가지고 있다. 추후 연구에서는 이방성 셀룰러 구조의 개념을 3차원으로 확장시키고자 한다.
NOMENCLATURE
| a and b : | Length of Axis of an Elliptical Void |
| θ : | Rotation Angle of an Elliptical Void |
| B : | Strain-Displacement Matrix |
| I : | Identification Matrix |
| σ : | Stress Vector |
| ε : | Strain Vector |
| C : | Stiffness Matrix |
| CH : | Effective Elastic Matrix |
| Cpoly : | Material Property Model based on Polynomial Regression Model |
| e : | Element Index |
| x : | Design Variables in Vector Foam |
| Y : | Predicted Value of Kriging Metamodel |
| c : | Total Compliance of Structure |
| K : | Stiffness Matrix of Elements |
| U : | Displacement Matrix of Elements |
| N : | Total Number of Elements |
| V : | Total Volume of Elements |
| v : | Volume of Elements |
| : | Volume Constraint |
Acknowledgments
This research was supported by the Chung-Ang University research grant in 2020 and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2019R1A2C1002010).
References
-
Helou, M. and Kara, S., “Design, Analysis and Manufacturing of Cellular Structures: An Overview,” International Journal of Computer Integrated Manufacturing, Vol. 31, No. 3, pp. 243-261, 2018.
[https://doi.org/10.1080/0951192X.2017.1407456]

- Lyons, B., “Additive Manufacturing in Aerospace: Examples and Research Outlook,” The Bridge, Vol. 44, No. 3, pp. 13-19, 2014.
- Sarvankar, S. G. and Yewale, S. N., “Additive Manufacturing in Automobile Industry,” International Journal of Research in Aeronautical and Mechanical Engineering, Vol. 7, No. 4, pp. 1-10, 2019.
- Hassani, B. and Hinton, E., “Homogenization and Structural Topology Optimization: Theory, Practice and Software,” Springer Science & Business Media, pp. 9-64, 2012.
- Gibson, L. J. and Ashby, M. F., “Cellular Solids: Structure and Properties,” Cambridge University Press, pp. 15-51, 1999.
-
Zhang, Q., Yang, X., Li, P., Huang, G., Feng, S., et al., “Bioinspired Engineering of Honeycomb Structure-Using Nature to Inspire Human Innovation,” Progress in Materials Science, Vol. 74, pp. 332-400, 2015.
[https://doi.org/10.1016/j.pmatsci.2015.05.001]

-
Lei, H. Y., Li, J. R., Xu, Z. J., and Wang, Q. H., “Parametric Design of Voronoi-Based Lattice Porous Structures,” Materials & Design, Vol. 191, Paper No. 108607, 2020.
[https://doi.org/10.1016/j.matdes.2020.108607]

-
Li, D., Liao, W., Dai, N., and Xie, Y. M., “Anisotropic Design and Optimization of Conformal Gradient Lattice Structures,” Computer-Aided Design, Vol. 119, Paper No. 102787, 2020.
[https://doi.org/10.1016/j.cad.2019.102787]

-
Bendsøe, M. P., “Optimal Shape Design as a Material Distribution Problem,” Structural Optimization, Vol. 1, No. 4, pp. 193-202, 1989.
[https://doi.org/10.1007/BF01650949]

-
Groen, J. P., Wu, J., and Sigmund, O., “Homogenization-Based Stiffness Optimization and Projection of 2D Coated Structures with Orthotropic Infill,” Computer Methods in Applied Mechanics and Engineering, Vol. 349, pp. 722-742, 2019.
[https://doi.org/10.1016/j.cma.2019.02.031]

- Nguyen, C. H. P., Kim, Y., and Choi, Y., “Design for Additive Manufacturing of Functionally Graded Lattice Structures: A Design Method with Process Induced Anisotropy Consideration,” International Journal of Precision Engineering and Manufacturing-Green Technology, 2019. (DOI: https://doi.org/ 10.1007/s40684-019-00173-7)
-
Nguyen, C. H. P. and Choi, Y., “Concurrent Density Distribution and Build Orientation Optimization of Additively Manufactured Functionally Graded Lattice Structures,” Computer-Aided Design, Vol. 127, Paper No. 102884, 2020.
[https://doi.org/10.1016/j.cad.2020.102884]

-
Kozuch, C. D. and Jasiuk, I. M., “Optimization of Structures Made from Composites with Elliptical Inclusions,” Journal of Applied Mechanics, Vol. 85, No. 12, Paper No. 121006, 2018.
[https://doi.org/10.1115/1.4041225]

- Jiang, D. and Smith, D., “Topology Optimization for 3D Material Distribution and Orientation in Additive Manufacturing,” Proc. of the 28th Annual International Solid Freeform Fabrication Symposium, pp. 7-9, 2017.
-
Wang, Y., Zhang, L., Daynes, S., Zhang, H., Feih, S., et al., “Design of Graded Lattice Structure with Optimized Mesostructures for Additive Manufacturing,” Materials & Design, Vol. 142, pp. 114-123, 2018.
[https://doi.org/10.1016/j.matdes.2018.01.011]

-
Stanković, T., Mueller, J., and Shea, K., “The Effect of Anisotropy on the Optimization of Additively Manufactured Lattice Structures,” Additive Manufacturing, Vol. 17, pp. 67-76, 2017.
[https://doi.org/10.1016/j.addma.2017.07.004]

-
Zhang, Y., Gao, L., and Xiao, M., “Maximizing Natural Frequencies of Inhomogeneous Cellular Structures by Kriging-Assisted Multiscale Topology Optimization,” Computers & Structures, Vol. 230, Paper No. 106197, 2020.
[https://doi.org/10.1016/j.compstruc.2019.106197]

-
Zhang, Y., Xiao, M., Gao, L., Gao, J., and Li, H., “Multiscale Topology Optimization for Minimizing Frequency Responses of Cellular Composites with Connectable Graded Microstructures,” Mechanical Systems and Signal Processing, Vol. 135, Paper No. 106369, 2020.
[https://doi.org/10.1016/j.ymssp.2019.106369]

-
Zhou, H., Zhou, Q., Liu, C., and Zhou, T., “A Kriging Metamodel-Assisted Robust Optimization Method based on a Reverse Model,” Engineering Optimization, Vol. 50, No. 2, pp. 253-272, 2018.
[https://doi.org/10.1080/0305215X.2017.1307355]

-
Dong, G., Tang, Y., and Zhao, Y. F., “A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in Matlab,” Journal of Engineering Materials and Technology, Vol. 141, No. 1, Paper No. 011005, 2019.
[https://doi.org/10.1115/1.4040555]

- Hassani, B. and Hinton, E., “Homogenization and Structural Topology Optimization: Theory, Practice and Software,” Springer Science & Business Media, 2012.
-
Suzuki, K. and Kikuchi, N., “A Homogenization Method for Shape and Topology Optimization,” Vol. 93, No. 3, pp. 291-318, 1991.
[https://doi.org/10.1016/0045-7825(91)90245-2]

-
Dfaz, A. and Bendsøe, M., “Shape Optimization of Multipurpose Structures by a Homogenization Method,” Structural Optimization, Vol. 4, pp. 17-22, 1992.
[https://doi.org/10.1007/BF01894077]

-
Ameen, M. M., Peerlings, R., and Geers, M., “A Quantitative Assessment of the Scale Separation Limits of Classical and Higher-Order Asymptotic Homogenization,” European Journal of Mechanics-A/Solids, Vol. 71, pp. 89-100, 2018.
[https://doi.org/10.1016/j.euromechsol.2018.02.011]

- Krige, D. G., “A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand,” Journal of the Southern African Institute of Mining and Metallurgy, Vol. 52, No. 6, pp. 119-139, 1951.

Ph.D candidate in the Graduate school of Chung-Ang University. His research interest includes CAD and design for additive manufacturing.
E-mail: yaedi5589@gmail.com

Ph.D candidate in the Graduate school of Chung-Ang University. His research interest includes CAD, machine learning, and design for additive manufacturing.
E-mail: phongch90@gmail.com

Professor in the Department of Mechanical Engineering, Chung-Ang University. His research interest includes CAD, geometric algorithm, and 3D shape representation.
E-mail: yychoi@cau.ac.kr