DMD와 초점 가변 렌즈를 이용한 유연 대처 패턴 조사 현미경 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this investigation, we propose a flexible structured illumination microscope (FSIM) to eliminate mechanical moving parts for the phase shifts in the spatial pattern and longitudinal scanning of the specimen. In order to prevent these mechanical motions, we adopt a focus-tunable lens and digital micromirror device (DMD) to replace the lateral motion of the pattern and the scanning of the specimen, respectively, which leads to the enhancement of rapid and precise measurement results for measuring the 3D surface profile of specimens. To realize the proposed system, two types of flexible structured illumination microscopes, Macro and micro types, were constructed and their performances were verified with a plane mirror and step height specimens.
Keywords:
Flexible structured illumination microscope, Digital micromirror device, Focus-tunable lens, Fourier transformation키워드:
유연 대처 패턴 조사 현미경, DMD, 초점 가변 렌즈, 푸리에 변환1. 서론
패턴 조사 현미경(Structured Illumination Microscope, SIM)은 조명의 공간적인 패턴을 이용하여 시편의 3차원 형상을 측정한다.1 이때 조명의 공간적인 패턴은 일반적으로 Ronchi 격자와 같은 진폭 변조 격자(Amplitude Modulation Grid)를 이용하여 생성하며, 생성된 조명 패턴은 광학계를 통해 시편의 표면에 결상(Imaging)된다. 그러면 패턴 조사 현미경의 조명 패턴과 시편의 표면, 카메라의 촬상면(Imaging Plane)은 광학적으로 서로 공액 관계(Conjugate)에 놓이게 되며, 이로 인해 카메라에서 획득되는 패턴의 가시도(Visibility)는 시편 표면의 높이에 따라 변화한다. 즉, 시편의 표면이 대물 렌즈의 초점 위치에 놓이게 되는 경우 패턴의 가시도가 가장 크게 나타나며, 이를 이용하면 시편의 높이 정보를 추출할 수 있다.2,3
이러한 원리의 패턴 조사 현미경은 대물 렌즈의 초점 위치에 해당하는 시편의 높이를 측정하는 관점에서 산업계에서 널리 활용되고 있는 공초점 주사 현미경(Confocal Scanning Microscopy)과 매우 유사하다. 또한 시스템 성능을 확인하기 위한 이론적인 변조 전달 함수(Modulation Transfer Function, MTF)의 유도 및 해석, 평가도 동일한 방법 및 과정으로 이루어진다.4 그러나 패턴 조사 현미경은 일반적인 점측정 방식(Point Measurement)인 공초점 주사 현미경과 달리 면적에 대한 높이, 즉 3차원 형상을 바로 획득할 수 있다는 점에서 큰 차이를 보인다. 비록 마이크로 렌즈 배열(Micro-lens Array)이나 Nipkow Disk 등을 통해 공초점 주사 현미경도 3차원 형상 측정이 가능하지만,5 이와 같이 특별히 제작된 부가 장치는 시스템 비용을 증가시킨다. 그래서 패턴 조사 현미경은 수 마이크로미터 이하의 측정 분해능을 가지는 동시에 높은 경제성으로 3차원 형상 측정 분야에서 널리 응용하고 있다.6 그러나 패턴 조사 현미경은 시편의 광축 방향 주사(Scanning) 및 조명 패턴의 위상 천이(Phase Shifting)를 위해 기계적 구동부가 필수적인 한계를 가진다.
한편, 최근 들어 광학 시스템이 점차 소형화되면서 다양한 광전자 부품 및 미세 구동 광부품들을 개발하고 있으며, 이러한 부품들은 기존의 광학 시스템의 크기를 줄일 수 있을 뿐 아니라, 기계적인 구동부 등을 전기, 전자적인 구동으로 대체하여 시편의 사양에 따른 측정 시스템의 변경을 가능하게 한다.
본 연구에서는 이러한 광전자 부품 및 미세 구동 광부품들을 이용하여 패턴 조사 현미경의 기계적 구동부를 최소화하고, 다양한 패턴을 조사할 수 있는 유연 대처 패턴 조사 현미경(Flexible Structured Illumination Microscope, FSIM)을 제안한다. 제안하는 유연 대처 패턴 조사 현미경은 DMD (Digital Micromirror Device)와 초점 가변 렌즈(Focus-tunable Lens)를 통해 각각 조명 패턴의 생성 및 위상 천이, 광축 방향의 주사가 가능하도록 구성하고, 이를 통해 본 연구에서는 3차원 형상 측정을 수행하고 성능을 검증한다.
2. 유연 대처 패턴 조사 현미경
2.1 패턴 조사 현미경
패턴 조사 현미경의 광학 구성은 일반적으로 Fig. 1(a)와 같이 나타낼 수 있다. 광원에서 출사한 광은 공간 패턴을 생성하기 위한 격자에 입사한 후, 렌즈(L)와 대물 렌즈(OL)를 통해 시편(Specimen)에 조사된다. 이후, 시편에서 반사된 광은 대물 렌즈와 결상 렌즈(IL)를 통해 CCD 카메라에서 검출되며, CCD 카메라에서는 시편의 높이에 따라 가시도가 변화하는 패턴을 관찰할 수 있다. 이때 조명 패턴은 사인파(Sinusoidal Wave) 형태의 패턴을 사용하며, 시편의 높이에 따른 패턴의 가시도(V)는 시편의 고정된 위치에서 패턴을 위상 천이하여 식(1)을 통해 계산할 수 있다.1
| (1) |
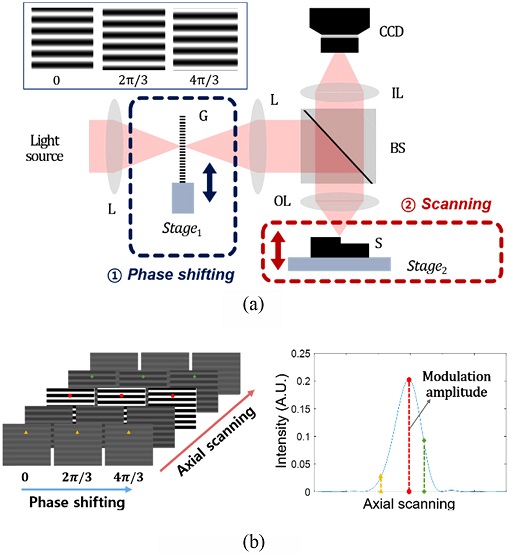
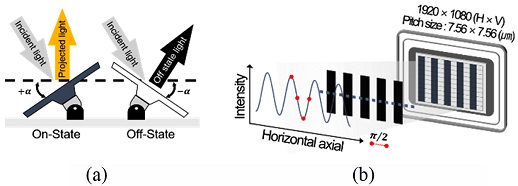
(a) Optical configuration of a typical structured illumination microscope (SIM); L: Lens, G: Ronchi grating, BS: Beam splitter, OL: Objective, S: Specimen, IL: Imaging lens, and (b) Operating principle of SIM
여기서 I1, I2, I3는 각각 패턴을 120o로 위상 천이하면서 획득한 광강도를 나타낸다.
이때 시편을 광축 방향으로 주사시키면서 식(1)을 이용하여 가시도를 각각 계산하면, Fig. 1(b)와 같이 시편의 광축 위치에 따른 전체 가시도 그래프를 획득할 수 있고, 가시도 그래프의 정점(Peak) 위치를 통해 시편의 높이를 측정할 수 있다. 또한, 전체 카메라 픽셀에 대해서 같은 과정을 반복하여 시편의 3차원 형상을 복원한다. 그러나 이러한 기본 원리의 패턴 조사 현미경은 광축 주사와 위상 천이가 비동기화되어 있기 때문에 오랜 측정 시간이 필요한 단점이 있다. 이를 보완하기 위해 연속 주사 패턴 조사 현미경(Continuously Scanned Structured Illumination Microscopy, CSSIM)을 제안하였고, 광축 주사와 위상 천이를 동기화(Synchronization)하여 보다 빠른 측정이 가능해졌다.2,3 그러나 연속 주사 패턴 조사 현미경의 경우에도 광축 주사와 위상 천이를 위해 기계적 구동부가 필요하고, 이로 인해 측정 시스템은 성능의 한계를 가진다.
2.2 유연 대처 패턴 조사 현미경
Fig. 2는 본 연구에서 제안하는 유연 대처 패턴 조사 현미경을 나타낸다. 전체적인 광학 구성은 기존의 패턴 조명 현미경과 유사하나, 조명의 패턴을 생성하는 부분이 기계적인 격자 구동에서 DMD로 대체되었으며, 광축 방향의 구동은 초점 가변 렌즈로 대체되었다. 또한 DMD의 구동은 초점 가변 렌즈의 구동과 동기화되어 있기 때문에 연속 주사 패턴 조사 현미경의 원리를 적용할 수 있는 동시에, 기존의 패턴 조사 현미경의 기계적 구동을 최소화할 수 있다.
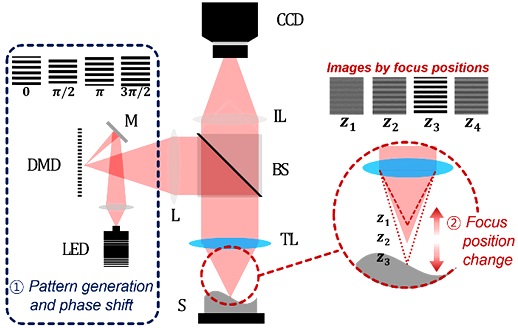
Optical configuration of the flexible structured illumination microscope (FSIM); DMD: Digital micromirror device, M: Mirror, L: Lens, BS: Beam splitter, TL: Focus-tunable lens, S: Specimen, IL: Imaging lens
DMD는 수 마이크로 크기를 가지는 수백만 개의 미세 거울이 바둑판 형태로 배열되어 있으며, 이 미세 거울을 통해 반사되는 광을 스위칭(Switching)하여, 임의의 조명 패턴을 생성할 수 있다. 각각의 거울들은 작동 전에는 기판(Substrate)과 평행한 상태로 위치하고 있지만, Fig. 3(a)와 같이 미세한 전압을 통해 거울을 기준 상태의 +α° 혹은 −α°로 기울여 On/Off할 수 있다. 유연 대처 패턴 조사 현미경에서는 이러한 DMD의 원리를 통해 Fig. 3(b)와 같이 일정 간격으로 거울을 On/Off하여 패턴을 생성한다. 위상 천이를 위해 사전에 준비된 4장의 위상 천이된 사인파 형태의 이미지들을 이용하며, 이들을 통해 순차적으로 DMD를 구동시킨다. 그래서 유연 대처 패턴 조사 현미경은 기존의 고정된 격자 패턴과는 달리 시편 및 대물 렌즈의 배율에 따라 다양한 간격과 모양의 패턴을 생성할 수 있다. 또한, 기존에는 임의의 패턴 격자를 횡 방향으로 구동시켜 패턴의 위상 천이를 수행했지만, DMD는 정해진 패턴으로 구동되기 때문에 기계적 구동에 의한 위상 오차를 최소화할 수 있다.
초점 가변 렌즈는 Fig. 4(a)와 같이 막(Membrane) 내부로 광학적 유체(Optical Fluid)가 채워져 있으며, 유체 주위로는 코일(Coil)로 구성된 미세 구동 장치(Actuator)가 둘러져 있다.
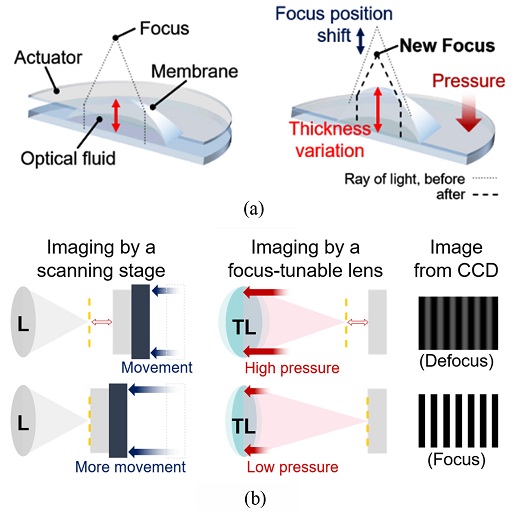
(a) Schematic diagram of a focus-tunable lens and working principle, and (b) Scanning by a focus-tunable lens
구동 시에는 미세 구동 장치의 코일을 통해 전류가 흐르며, 유체 렌즈 주위로 전류량에 비례하는 압력이 가해진다. 이때 압력에 의해 렌즈의 중심 두께가 변화하기 때문에 렌즈의 초점 거리가 변화하므로, 이를 이용하면 초점 가변 렌즈의 전류 제어를 통해 고정된 시편을 주사할 수 있다. 기존 패턴 조사 현미경에서는 Fig. 4(b)와 같이 시편의 광축 주사를 위해 기계적 구동 장치를 사용하여 대물 렌즈의 고정된 초점 위치로 이동시켰지만, 유연 대처 패턴 조사 현미경은 초점 가변 렌즈 속 코일을 통한 전류 제어만으로 렌즈의 초점 위치를 변경하여 고정된 시편의 위치별 이미지를 획득할 수 있다. 그래서 유연 대처 패턴 조사 현미경은 기존의 기계 구동으로 인한 오차를 줄일 수 있을 뿐만 아니라, 구동기로 인한 시스템의 물리적 크기를 줄일 수 있는 장점이 있다.
유연 대처 패턴 조사 현미경에서는 DMD를 통해 조사되는 조명 패턴의 위상 천이와 초점 가변 렌즈의 구동이 동기화되어 있으며, 이를 통해 카메라에서 획득되는 이미지들의 한 점에서의 광강도 신호는 조명 패턴에 의한 변조 신호(Modulation Signal)와 가시도에 의한 포락선 신호(Envelope Signal)의 조합으로 나타낼 수 있다. 이러한 신호는 푸리에-역푸리에 변환(Fourier Transformation-Inverse Fourier Transformation)을 이용하여 해석하면 해당 점의 가시도 정점을 추출하여 높이값을 구할 수 있다.2 일반적으로 패턴 조사 현미경에서 획득되는 이미지들의 한 점에서의 신호(I(z))를 수식적으로 표현하면 식(2)와 같다.
| (2) |
여기서 I0는 신호의 평균 광강도를 의미하고, G(h−z)는 초점 가변 렌즈에 의한 종축 구동(z)에 따른 높이(h)에 대한 포락선 함수이다. 그리고 cos(2πfsz)는 DMD에 의한 패턴과 초점 가변 렌즈의 구동에 의해 생성되는 신호의 변조 성분이다. fs는 신호의 공간 주파수(Spatial Frequency)를 가리킨다. 식(2)에서 높이 정보 h를 추출하기 위해 식(2)를 푸리에 변환하고, 주파수 대역통과 필터(Band Pass Filter)를 적용한 이후, 역푸리에 변환하면 식(3)과 같이 나타낼 수 있다.
| (3) |
이때 식(3)의 IF(z)의 절댓값(Absolute Value)은 획득된 신호의 포락선, 즉 패턴 조사 현미경에서 획득되는 패턴의 가시도를 나타내기 때문에, 이를 통해 가시도의 정점을 무게 중심법(Center of Gravity)으로 추출할 수 있다. 또한, 같은 과정을 이미지의 모든 점에서 반복하면 시편의 3차원 형상을 복원할 수 있다.
3. 실험 결과
본 연구에서는 제안하는 유연 대처 패턴 조사 현미경의 원리 및 성능을 검증하기 위해 넓은 영역을 측정하기 위한 Macro 타입과 좁은 영역을 확대 측정하기 위한 Micro 타입의 유연 대처 패턴 조사 현미경을 구성하였으며, 이를 통해 평면 거울과 게이지 블록으로 구성한 단차 시편을 측정하였다. 광원으로는 400-700 nm 대역의 백색 LED를 사용하였으며, 7.56 μm 크기를 갖는 미세 거울(픽셀, Pixel)이 (1,920 × 1,080)로 배열되어 있는 DMD를 이용하여 패턴을 생성하고 위상 천이를 수행하였다. 각각의 시스템은 횡 방향으로 각각 (6.7 × 5.0) mm2, (1.0 × 0.76) mm2의 측정 영역 및 이론적으로 12.4, 2.4 μm의 분해능을 가지도록 구성하였다.
3.1 Macro 타입 유연 대처 패턴 조사 현미경
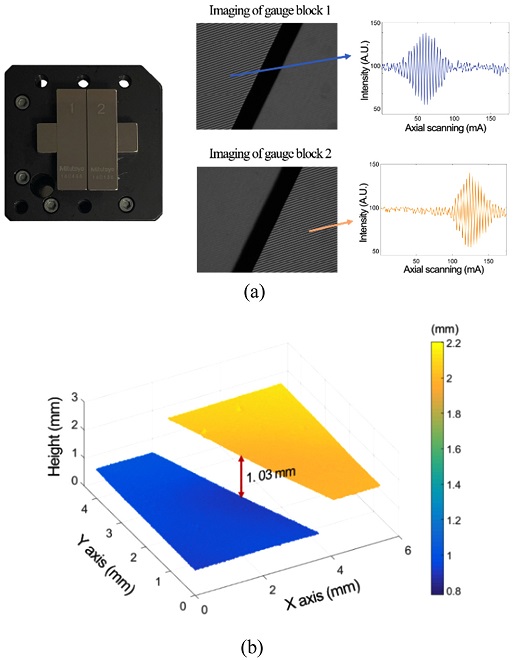
Fig. 5는 본 연구에서 구성한 Macro 타입 유연 대처 패턴 조사 현미경의 실제 모습을 나타낸다. 초점 가변 렌즈로는 100 mm의 작동 거리를 갖는 Edmund Optics사의 0.75x 초점 가변 텔레센트릭(Telecentric) 렌즈를 사용하였으며, 조명부와 CCD 카메라 부분에 각각 동일한 렌즈를 설치하였다. 이는 단일 초점 가변 텔레센트릭 렌즈를 이용하는 경우, 광분할기가 렌즈의 상(Image) 부분에 설치되어야 하고, 이로 인해 텔레센트릭 렌즈의 작동거리가 짧아져서 시편의 위치가 렌즈의 안쪽 부분으로 들어와야 하는 문제점이 발생하기 때문이다. 또한, 이 경우 텔레센트릭 렌즈의 성능도 저하되는 한계가 발생하기 때문에, 이를 해결하기 위해 2개의 초점 가변 텔레센트릭 렌즈(TTL1, TTL2)를 각각 설치하고 동기화하여 작동하였다.
실험을 수행하기에 앞서, 초점 가변 텔레센트릭 렌즈에 인가하는 전류와 실제 거리 변화의 관계를 확인하기 위해, 마이크로 스텝 모터 구동기(Micro Stepping Motorized Stage)를 구동하면서 패턴의 가시도가 가장 크게 나타나는 전류값을 측정하였다. 측정 결과, 초점 가변 텔레센트릭 렌즈의 전류 변화와 초점 거리 변화는 선형적인 관계를 가짐을 확인하였으며, 80.3 μm/mA의 변환값을 획득하였다. 이를 통해 실험에서 초점 가변 렌즈에 인가하는 전류값으로부터 초점 거리 변화를 보정하였다. 한편, DMD에서 생성한 패턴의 주기는 한 주기당 4개 픽셀이 되도록 설정하였다.
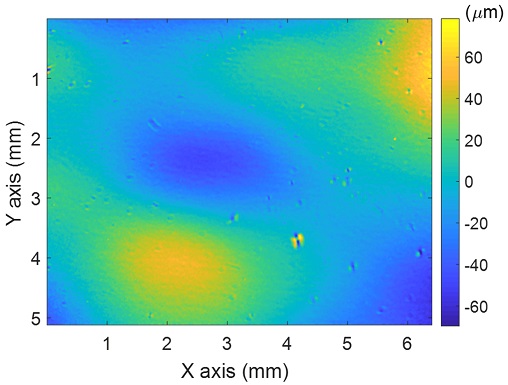
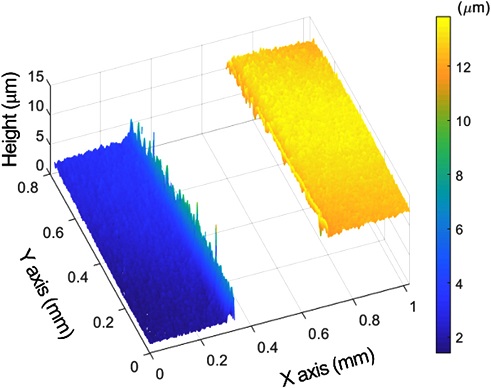
Fig. 6은 Macro 타입 유연 대처 패턴 조사 현미경을 이용하여 평면 거울을 측정한 결과를 나타낸다. 측정 결과, 전체 형상이 평면에서 크게 휘어진 형태로 측정됨을 확인하였으며, 이는 광학계에서 발생하는 수차와 더불어 패턴 형상의 기준이 되는 DMD의 형상에 의한 오차로 판단하였다. 이때, 측정된 형상의 PV (Peak to Valley)값은 133.9 μm로 측정되었으며, Sa (Arithmetical Mean Height)값은 18 μm임을 확인하였다. 20번의 반복 측정 결과, 전체 면적에 대한 표준편차의 평균으로 정의한 반복능(Repeatability)은 1.1 μm로 계산하였다. 참고로, 평면 거울에서 측정된 결과는 본 연구에서 구성한 광학 구성에서의 시스템 오차에 해당하기 때문에, 이를 이용하여 다른 측정 시편의 측정 결과를 보정하였다. Fig. 7은 게이지 블록을 이용하여 구성한 단차 시편의 측정 결과를 보여준다. Fig. 7(a)는 게이지 블록을 이용하여 구성한 1 mm 단차 시편의 실제 모습과 시편의 표면에 패턴이 생성되었을 때의 이미지를 나타낸다. Fig. 7(a)에서 알 수 있듯이, 각 면의 높이에 따라 광강도 신호의 정점 위치가 다르며, 이를 통해 Fig. 7(b)와 같이 단차 시편의 형상을 복원하였다. 측정 결과, 단차는 1.03 mm로 측정되었다.
3.2 Micro 유연 대처 패턴 조사 현미경
Fig. 8은 Micro 타입의 유연 대처 패턴 조사 현미경의 실제 구성 사진을 보여준다. Micro 타입 구성은 Macro 타입의 구성과는 달리 5x의 배율을 가지는 현미경 대물 렌즈 및 이미징 렌즈(무한 보정 광학계)를 이용하여 구성하였으며, 전체 시스템의 부피를 최소화하기 위해 초점 가변 렌즈는 대물 렌즈와 시편의 사이에 위치시켰다. 이 경우 초점 가변 렌즈의 초점 변화에 따라 미세하게 현미경 배율의 변화가 발생할 수 있으나, 측정 형상의 높이 차이가 상대적으로 작기 때문에 배율 변화로 인한 측정 오차는 매우 작다고 가정하였다.
우선, Macro 타입의 유연 대처 패턴 조사 현미경과 유사하게 초점 가변 렌즈의 전류 변화와 초점 거리 간의 관계를 확인하였으며, 그 결과 8 μm/mA의 변환값을 획득하였다. 또한, 이때 생성한 패턴의 주기는 한 주기당 DMD의 4개 픽셀이 되도록 설정하였다.
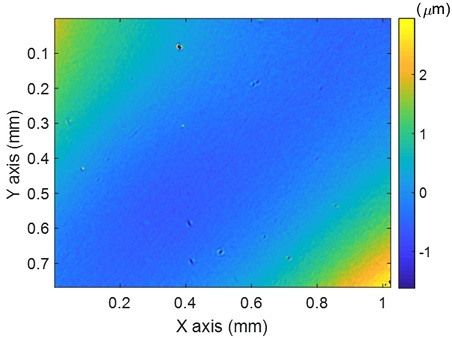
Fig. 9는 Micro 타입의 구성을 통해 측정한 평면 거울의 형상을 나타낸다. Macro 타입의 측정 결과와 같이 측정된 형상은 휘어져 있는 형태를 보였으며, PV값은 4.6, Sa값은 0.46 μm로 계산되었다. 20번의 반복 측정 결과, 반복능은 0.15 μm로 계산되었다. 이와 같은 형상의 왜곡이 발생한 이유는 Macro 타입과 마찬가지로 광학계의 수차와 DMD의 형상 오차로 인한 결과로 판단하였고, 또한 평면 거울의 측정 결과는 다른 시편의 형상 복원을 위한 보정용 데이터로 활용하였다.
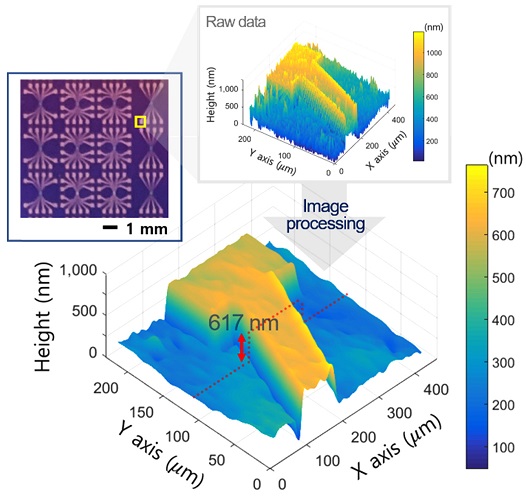
Fig. 10은 Micro 타입의 유연 대처 패턴 조사 현미경을 이용하여 10 μm 단차를 가지는 게이지 블록 시편을 측정한 결과를 나타낸다. 측정 결과 단차는 10.04 μm로 측정되어, Micro 타입의 유연 대처 패턴 조사 현미경은 Macro 타입의 시스템에 비해 작은 높이의 시편을 보다 정밀하게 측정할 수 있음을 확인하였다. 이와 더불어 Micro 타입의 시스템은 보다 높은 고배율로 미세 패턴을 측정할 수 있기 때문에 Fig. 11과 같은 반도체 시편에 대한 실험을 수행하였으며, 측정 결과 600 nm 설계값을 가지는 미세 패턴에 대해 617 nm의 단차를 측정하였다. 이때 대물 렌즈의 배율은 10x였으며, 생성한 패턴의 주기는 한 주기당 DMD의 8개 픽셀이 되도록 설정하였다. 이는 10x 대물 렌즈를 통해 패턴을 시편에 조사하기 위한 최대 공간 주파수의 한계로 인하여, DMD의 미세한 패턴이 시편에 조사되지 못하기 때문이다. 참고로 측정 시편으로는 실리콘(Si) 기판 위에 크롬(Cr)과 금(Au)로 패턴이 생성되어있는 TFT 시편을 이용하였다. 참고로, 측정된 시편은 단차가 비교적 매우 작아서 Fig. 11의 윗부분과 같이 패턴의 모서리 부분에서 Batwing 효과 등으로 인한 잡음과 같은 측정 결과들이 나타났으며, 시편의 형상을 보다 분명하게 드러내기 위해 영상 처리를 통해 시편의 3차원 형상을 복원하였다.
4. 논의
본 연구에서 제안하는 유연 대처 패턴 조사 현미경은 기존의 패턴 조사 현미경의 한계인 기계적 구동부를 최소화함으로써, 측정 시 발생하는 진동을 줄이고, 구동에 의한 측정 시간을 최소화할 수 있다. 초점 가변 렌즈와 DMD의 빠른 응답 특성(수 ms)으로, 제안하는 시스템의 측정 시간은 카메라의 이미지 획득 시간으로 결정한다. 이는 기존의 패턴 조사 현미경의 측정 시간이 구동부의 구동 시간과 카메라의 이미지 획득 시간에 의해 결정되는 것과 비교한다. 예를 들어, 본 연구에서 구성한 시스템의 경우, 45 ms (카메라 노출 시간 40 ms + 초점가변 렌즈와 DMD 구동 5 ms) × 100(영상 획득 개수) = 4.5 s의 시간으로 측정이 가능하다. 이와 달리 기존의 패턴 조사 현미경은 70 ms (카메라 노출시간 40 ms +스테이지 구동시간 30 ms) × 3 × 100 = 21 s의 측정 시간이 걸린다.
그러나 측정 결과 측면에서 유연 대처 패턴 조사 현미경은 기존의 시스템에 비해 DMD의 형상 균일도 및 초점 가변 렌즈에서 발생하는 수차로 인하여 Figs. 6과 9와 같이 측정된 형상의 휨 현상이 발생하였다. 이를 제거하기 위해서는 보다 정밀하게 제조된 DMD의 이용과 광학 수차를 제거하기 위한 전체 시스템의 세밀한 광학 설계가 필요하다. 그에 비해, 본 연구에서는 모아레 간섭계(Moiré Interferometer)7 및 광편향기(Deflectometry)8 등에서 사용하는 형상 왜곡 보정 방법을 적용하였다. 이를 위해 기준이 될 수 있는 평면 거울을 측정하여 시스템 오차를 확인하였고, 그 결과를 이용하여 다른 측정 시편들의 측정 결과를 보정하였다.
한편, 유연 대처 패턴 조사 현미경은 시편의 광축 주사를 초점 가변 렌즈로 대체하였기 때문에, 광축 방향의 높이 측정 범위는 초점 가변 렌즈에 의해 결정되며, 본 연구에서는 Macro 타입의 경우 16 mm, Micro 타입의 경우에는 570 μm였다. 이러한 측정 범위는 기존의 패턴 조사 현미경과는 달리 전체 광학 시스템의 성능에 따라 달라지는 특징이 있다. 또한, 정밀 측정을 위해 초점 가변 렌즈의 보정이 필수적이며, 또한 인가하는 전류와 초점 변화에 대한 선형성이 매우 중요하다. 본 연구에서 이용한 Macro 타입 구성의 초점 가변 텔레센트릭 렌즈와 Micro 타입 구성의 초점 가변 렌즈의 비선형성은 실험 결과, PV값 기준으로 각각 ±30 μm, ±3 μm 수준이었으며, 이러한 비선형성은 측정 오차로 작용하여 반복능에 영향을 주었다고 판단한다. 또한, 초점 가변 렌즈에 인가하는 전류에 잡음으로 인한 측정 오차도 반복능 저하의 요인으로 작용하였다.
본 연구에서 제안한 시스템에서 조명 패턴을 생성시키는 DMD는 기존의 물리적인 격자에 비해 다양한 패턴의 형성이 가능한 동시에 위상 천이가 가능한 장점이 있다. 특히, Micro 타입의 패턴 조사 현미경의 경우에는 대물 렌즈의 배율에 따라 시편에 조사되는 조명의 패턴이 변화해야 한다. 이를 위해 기존의 시스템에서는 격자를 변경하여 측정을 수행하였으나, 본 연구에서 제안하는 시스템에서는 이러한 변경없이 유연하게 패턴 변경이 가능하였다.
5. 결론
본 연구에서는 기존 패턴 조사 현미경의 기계적 구동을 최소화하기 위한 유연 대처 패턴 조사 현미경을 제안하였다. 제안한 시스템은 물리적인 구동 장치를 DMD 및 초점 가변 렌즈로 대체하여 구동 범위를 최소화하였고, 이를 통해 측정 시 발생하는 진동을 제거하고, 측정 속도를 개선하였다. 제안하는 시스템을 검증하기 위해 넓은 영역을 측정하기 위한 Macro 타입과 미세 영역 측정을 위한 Micro 타입의 유연 대처 패턴 조사 현미경을 구성하였고, 평면 거울과 단차 시편 등을 측정하여 성능을 검증하였다.
Nomenclature
| V : | Visibility of the Spatial Pattern |
| I : | Intensity of the Image Obtained by Structured Illumination Microscope |
| IF : | Filtered Intensity via Fourier and Inverse Fourier Transforms |
| h : | Height of the Specimen |
| z : | Longitudinal Scanning Coordinate |
| G(h-z) : | Envelope Function of the Signal |
| fs : | Spatial Frequency by the Spatial Pattern |
Acknowledgments
이 논문은 2019년도 조선대학교 연구비의 지원을 받아 연구되었음.
REFERENCES
-
Neil, M. A., Juškaitis, R., and Wilson, T., “Method of Obtaining Optical Sectioning by Using Structured Light in a Conventional Microscope,” Optics Letters, Vol. 22, No. 24, pp. 1905-1907, 1997.
[https://doi.org/10.1364/OL.22.001905]

-
Joo, K. N., “Fourier Domain Analysis on Continuously Scanned Structured Illumination Microscopy,” Measurement Science and Technology, Vol. 23, No. 5, Paper No. 057002, 2012.
[https://doi.org/10.1088/0957-0233/23/5/057002]

- Park, H. M. and Joo, K. N., “Endoscopic Precise 3D Surface Profiler based on Continuously Scanning Structured Illumination Microscopy,” Current Optics and Photonics, Vol. 2, No. 2, pp. 172-178, 2018.
-
Karadaglić, D. and Wilson, T., “Image Formation in Structured Illumination Wide-Field Fluorescence Microscopy,” Micron, Vol. 39, No. 7, pp. 808-818, 2008.
[https://doi.org/10.1016/j.micron.2008.01.017]

-
Tanaami, T., Otsuki, S., Tomosada, N., Kosugi, Y., Shimizu, M., et al., “High-Speed 1-frame/ms Scanning Confocal Microscope with a Microlens and Nipkow Disks,” Applied Optics, Vol. 41, No. 22, pp. 4704-4708, 2002.
[https://doi.org/10.1364/AO.41.004704]

-
Vogel, M., Yang, Z., Kessel, A., Kranitzky, C., Faber, C., et al., “Structured-Illumination Microscopy on Technical Surfaces: 3D Metrology with Nanometer Sensitivity,” Proc. of the Optical Measurement Systems for Industrial Inspection VII, Vol. 8082, 2011.
[https://doi.org/10.1117/12.889428]

-
Wang, L., Cao, Y., Li, C., Wan, Y., Li, H., et al., “Improved Computer-Generated Moire Profilometry with Flat Image Calibration,” Applied Optics, Vol. 60, No. 5, pp. 1209-1216, 2021.
[https://doi.org/10.1364/AO.412291]

-
Han, H., Wu, S., and Song, Z., “An Accurate Calibration Means for the Phase Measuring Deflectometry System,” Sensors, Vol. 19, No. 24, Paper No. 5377, 2019.
[https://doi.org/10.3390/s19245377]


MS. candidate in the Department of Photonic Engineering, Chosun University. Her research interest is optical 3D surface metrology.
E-mail: hbin0106@naver.com

Professor in the Department of Photonic Engineering, Chosun University. His research interest is optical metrology and instrumentation.
E-mail: knjoo@chosun.ac.kr