Vibration Analysis for Developing Ultrasonic Kitchen Knife for Cutting Foods
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Ultrasonic cutting is used not only for cutting various materials such as metals and non-metals, but also for bone cutting of the human body or for various surgical operations. In recent, ultrasonic cutting technology is being applied for cutting various food products such as cakes, pizza, and cheese. It is shown that ultrasonic vibrations for cutting food products enables high-precision and high-quality cutting, and the quality of the cutting surface is affected by the shape of food products and cutting conditions. However, most of the studies have been on industrial cutting horns that can be used in large-scale grocery factories, but these cutting horns are very different from the shape of knives used in the households. Accordingly, research or technology development for ultrasonic cutting knives that can be used in household has not been studied. Therefore, this study developed a knife that can cut or process food by applying ultrasonic vibration while having a shape similar to the existing knife as possible so that it can be used in general. To develop such a knife, a modal analysis was performed using the finite element method for knife models of various shapes, and a suitable model for a kitchen knife was proposed.
Keywords:
Food cutting, Ultrasonic knife, Modal analysis, Resonant frequency키워드:
식료품 커팅, 초음파 칼, 모달 해석, 공진주파수1. Introduction
Ultrasound technology has long been used in various industrial fields, i.e., non-contact distance measurement, flow or level measurement, non-destructive testing, medical fields such as ultrasonic imaging or cancer diagnosis and treatment, ultrasonic cleaning and ultrasonic welding, etc. One of the fields of application that is receiving attention again in recent years is ultrasonic welding and ultrasonic cutting. Ultrasonic welding is widely used for welding of plastics and metals, and a lot of related studies are being conducted, especially in recent years, it is widely used for ultrasonic metal welding for welding secondary battery terminal welding of electric vehicles.1,2
Ultrasonic cutting is used not only for cutting various materials such as metals and non-metals, but also for bone cutting of the human body or for various surgical operations. In recent years, ultrasonic technology has attracted great attention in cutting food products such as cakes, pizza, and cheese. It has been shown that the use of ultrasound when cutting human bones can reduce cutting power and greatly improve cutting precision compared to using conventional cutting tools.3
Various types of kitchen knives have been used for cutting or processing food products. When cutting food products such as meat that is difficult to cut, it requires great power from the cutting worker, so there is a problem in the supply and demand of manpower in the food processing industry. Even in the average home, women are having great difficulty preparing food. The working speed is also slow due to the difficulty of cutting, and the cutting surface of the food products is not cut cleanly, and safety issues such as injury to the operator's fingers are raised. Another problem is that debris sticks to the blade or remains in the workplace, which is an unnecessary waste of food.
Although there are differences in the type of food to be cut according to the eastern and western food culture, a lot of forces is applied to the cook's wrist when cutting tough ingredients such as beef or pork. The number of housewives suffering from Carpal Tunnel Syndrome every day is increasing because these tasks are repeated during cooking.
Therefore, there is a desperate need for a new type of tool that can efficiently and safely cut or process food products. That is, in order to efficiently and safely perform cutting or processing regardless of the type of food and not leave food residue, a cutting tool that is more economical, more hygienic and easier to work with than conventional cutting must be developed urgently.
Many studies have been made to utilize ultrasonic waves in cutting food. According to their studies, high-precision and high-quality cutting was possible when ultrasound was applied to the cutting of food products.4 Also, a finite element model of ultrasonic cutting of a multi-layer product was proposed.5 McCulloch proposed a FE analysis model for cutting food products, and proposed cutting horns with resonant frequencies of 20 and 35 kHz, and experimentally investigated its characteristics.6 In addition, studies on the quality of ultrasonic cutting according to the characteristics of food products were conducted. It was shown that the quality of the cutting surface was affected by the type, shape and cutting conditions of food products,7,8 and a study on ultrasonic cutting of cheese or apple was also conducted.9
Much of the research on the cutting horns (Knife) in food products has so far been mainly related to the horns for automated cutting systems in the food industry. However, the shape of the knife used in the general kitchen is significantly different from that of the industrial cutting horn, so it is necessary to interpret or design a kitchen knife.
Therefore, in this study, a knife that can cut or process food by applying ultrasonic vibration while having a shape similar to that of a conventional kitchen knife was developed so that it can be used in general homes rather than in the existing industry.
To this end, the length of the knife was first obtained from the vibration equation, and then modal analysis was performed using the finite element method for various types of knife models. By changing the dimensions of the proposed knife model, the FE analysis was performed to obtain the final shape in which the resonant frequency of 20 kHz was satisfied and the desired longitudinal vibration mode appeared on the knife blade.
2. Proposed Ultrasonic Cutting System
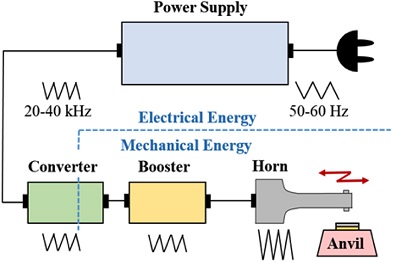
Fig. 1 shows an example of an ultrasonic cutting system for food products currently used for industrial use, and most of these systems use ultrasonic vibrations of 20 to 40 kHz. The horn (Cutting Tool) amplifies the vibration of the transducer and cuts while applying an appropriate force to cutting materials such as food products. The general shape of the horn currently used for cutting food is shown in Fig. 2. It can be seen that it is completely different from the general kitchen knife.
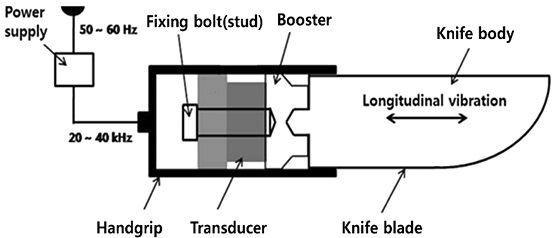
Fig. 3 shows the components and the operating principle of the ultrasonic welding system. The ultrasonic vibration of the transducer is amplified by a horn or a booster, and welding is performed by applying an appropriate clamping force to the welding material with the horn. Food cutting systems can also work on the same principle as the ultrasonic welding system by using a knife instead of a horn. Fig. 4 shows a schematic diagram of a cutting system proposed to be used for ultrasonic cutting of food products.
3. Design and Manufacturing Process
3.1 Design and Manufacturing Process of the Knife
A knife for cutting and processing food products with ultrasonic vibration should have a resonant frequency of 20 kHz, and a longitudinal vibration mode and maximum vibration amplitude should appear at the knife blade that is cut by direct contact with the food products. In addition, it should basically be suitable for the shape or size of the food products.
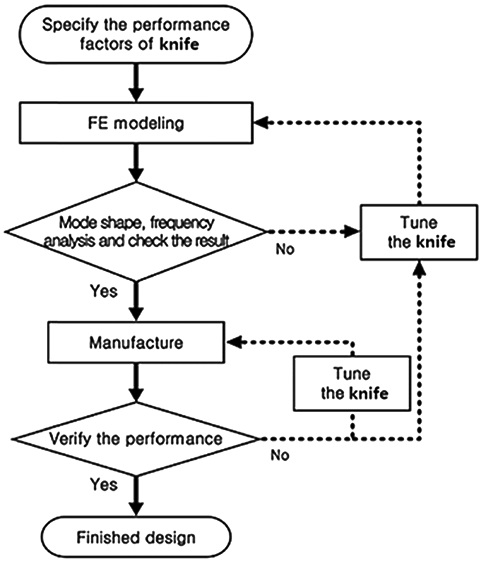
First, the approximate length of the cutting knife is determined using the vibration equation. Other final shapes or dimensions are determined by changing the shape of the knife and performing modal analysis in a trial & error method. Since there may be a difference between the theoretical analysis results and the vibration characteristics of the actually manufactured knife, the vibration performance must be verified through a vibration test on the manufactured knife. Proper tuning may be required in the manufacturing process until the required vibration characteristics are obtained. Fig. 5 shows the overall vibration analysis and manufacturing processes.
3.2 Calculation of the Overall Knife Length
Since the knife blade cuts the material with vibration parallel to the food products, the longitudinal vibration mode must appear and the frequency separation should also be clear to have only one natural frequency in the resonant frequency band. Using the longitudinal vibration equation of the elastic rod, the length of the horn can be calculated as follows.6
When vibration is applied to a rod with a uniform cross section, longitudinal vibration occurs. The vibration equation of an isotropic uniform elastic rod with free boundary conditions can be defined as the following Eq. (1).
| (1) |
Where u(x,t) is the displacement at time t, c is the sound velocity propagating through the rod, E is the Young's modulus, and ρ is the density. Using the variable separation method, the solution can be obtained as follows.
| (2) |
The cylindrical horn transmits the vibration displacement U0 of the booster at x = 0 and x = L, and the displacement becomes maximum at both ends of the rod, so the boundary condition can be written as the follows.
| (3) |
Using these boundary conditions Eq. (3), the solution of the vibration equation can be summarized by the follows.
| (4) |
| (5) |
| (6) |
| (7) |
Therefore, the characteristic equation can be obtained as follows.
| (8) |
Since the length of the knife is an integer multiple of the half wavelength of the sound wave, the length L of the knife at a specific frequency can be obtained by the following Eq. (9).
| (9) |
Where λ is the wavelength of sound wave.
4. Vibration Analysis of Ultrasonic Cutting System
4.1 Selection of Material of the Knife
As for the material of the knife, strength and hardness are the most important depending on the shape or cutting object. It should also be considered that the length of the wavelength is determined by the sound velocity of the wave in the material. This is because the length of the wavelength has a great influence on determining the length of the ultrasonic knife.
The ultrasonic knife should be a half-wavelength resonator, and the material is generally aluminum alloy or titanium alloy. Among them, titanium alloy is widely used because it has excellent acoustic and strength properties. In this study, Ti-6Al-4V alloy is used as the knife material, and its mechanical properties used in vibration analysis are shown in Table 1.
4.2 Boundary Conditions for FE Analysis
To develop the ultrasonic cutting system, modal analysis was performed by using ANSYS tool for validation via the FE modeling approach. As the transducer, the booster and the knife body are fastened by stud bolts each, boundary conditions must be given accordingly. As constraints on FE analysis, radial and tangential displacements of the cylindrical surface of all stud bolts holes were restrained and only longitudinal displacements were allowed. The number and the shape of meshes were automatically generated by ANSYS tool. The modal analysis was repeated to obtain the most efficient design of each part.
4.3 Modal Analysis of the Knife Model 1
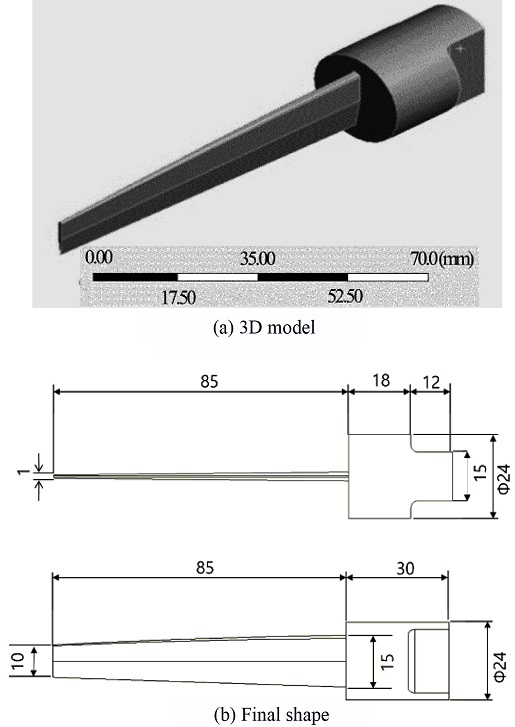
Fig. 6 shows the knife model 1 proposed in this study. Modal analysis was performed while varying dimensions such as the thickness and length of the knife. The final shape of the knife that satisfies the required resonant frequency 20 kHz and longitudinal vibration mode were derived. (The content of this study was submitted for a patent, so only the critical dimensions were noted here.)
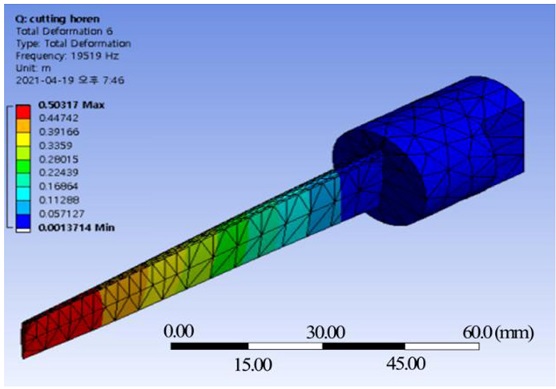
Table 2 shows the modal analysis results for the shape of Fig. 6. It can be seen that the longitudinal vibration mode satisfying the resonance frequency of 20 kHz ±500 Hz is the 3rd mode and the natural frequency is 19,519 Hz. In addition, as shown in the mode shape in Fig. 7, the maximum amplitude occurs at the front end of the knife blade, and although smaller than that, longitudinal vibration occurs at the rest of the blade. This means that cutting can be the easiest at the front end of the knife blade. As the vibration amplitude decreases toward the rear of the knife, the cutting performance may be degraded. Considering that it is impossible to obtain a uniform amplitude across the knife blade due to the characteristics of ultrasonic vibration, it is judged that the proposed design model 1 can be sufficiently used for cutting food products.
4.4 Modal Analysis of the Knife Model 2
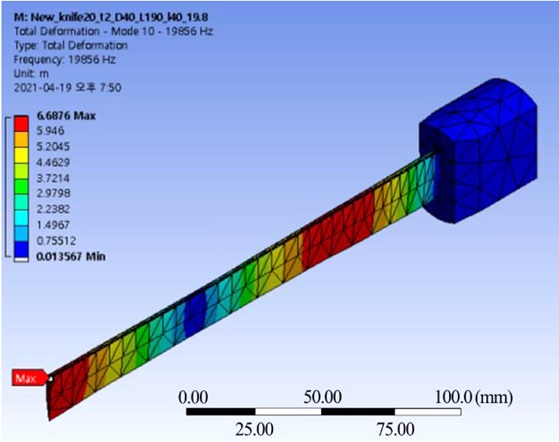
The overall length of the knife of the model 1 was 115 mm. In consideration of the convenience of use, the length of the blade of the model 2 was doubled. Table 3 shows the results of modal analysis while changing the remaining dimensions. The longitudinal vibration mode with a resonant frequency of 20 kHz ±500 Hz is the 3rd mode and the natural frequency is 19,856 Hz. However, as shown in the vibration mode of Fig. 8, the maximum amplitude occurs at the both front and middle blades, and a part without vibration appears between them. This vibration mode is judged not to be desirable because a problem such as non-uniform cutting may occur depending on the position of the knife blade.
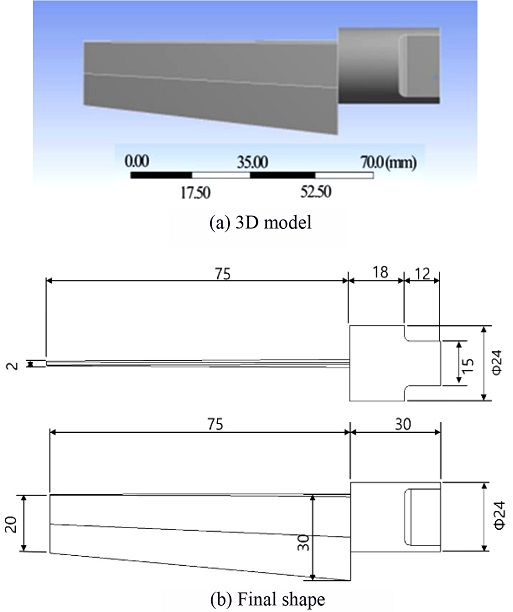
4.5 Modal Analysis of the Knife Model 3
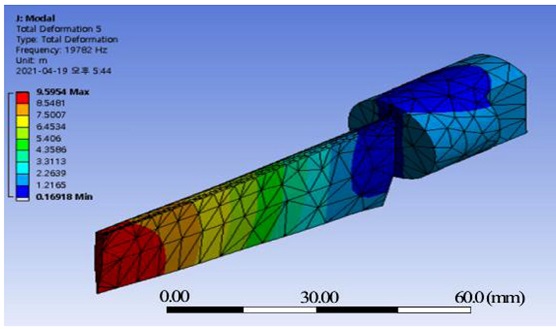
The blade of a commonly used kitchen knife is located below the handgrip. In consideration of this and the user's convenience, previous knife models were modified to a new model similar to the existing knife. As a result of repeating the modal analysis, the final shape of the new knife model is obtained as shown in Fig. 9. The modal analysis results for this shape are shown in Table 4. In mode 3, longitudinal vibration with a natural frequency of 19,782 Hz appears, and the remaining vibration modes are bending vibration modes. Fig. 10 shows the mode shape. As in model 1, the vibration amplitude decreases toward the rear, so the cutting performance may deteriorate. Considering that it is impossible to obtain a uniform amplitude across the knife due to the characteristics of ultrasonic vibration, it is judged that the proposed design model can be used for cutting food products while enhancing user convenience.
4.6 Modal Analysis of the Transducer and Booster Assembly
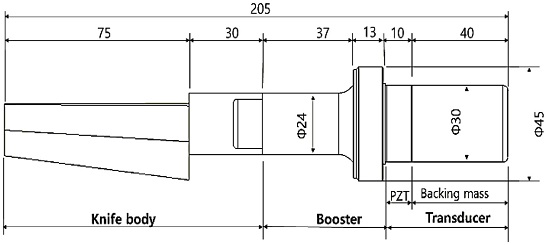
The transducer and booster assembly shown in Fig. 4 generates longitudinal vibration and transmits it to the knife. The assembly should have the resonant frequency of 20 kHz and longitudinal vibration mode too. The dimensions of this assembly (Right Rear Part of the Whole System) are shown in Fig. 12. The Transducer is composed of PZT and backing mass generally. For the FE analysis, the materials of the backing mass, PZT and booster were assumed to be SUS316, PZT8, and titanium alloy Ti-6Al-4V, respectively. Table 5 shows the mechanical properties of each material.
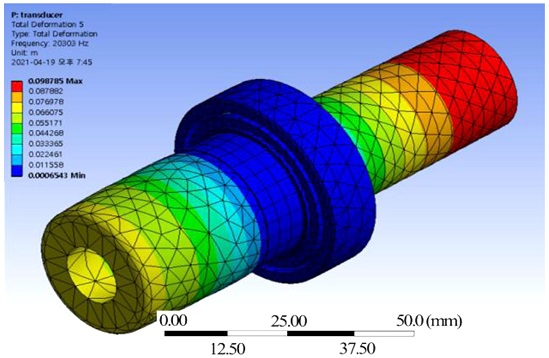
The results of the modal analysis of this assembly are shown in Table 6 and Fig. 11. From Table 6, it is found that the longitudinal vibration of the third mode satisfies the resonant frequency of 20 kHz ±500 Hz. In addition, the maximum amplitude occurs at the left end of the booster where the knife is fixed by a stud bolt. It is shown that vibration is minimized where the knife handgrip is fixed. This means the generated ultrasonic vibration is not transmitted to the user’s hand, so there are no problems in use. These results indicate that the proposed assembly model can be used effectively in an ultrasonic cutting knife system.
4.7 Modal Analysis of the Proposed Ultrasonic Cutting System
The proposed cutting system consists of a knife body, a booster and a transducer as shown in Fig. 12. The knife body uses the model 3 (Fig. 9) because it is similar to a real kitchen knife and has high user convenience. The assembly of the booster and transducer described above are fixed to the knife body via a stud bolt. The overall system is 205 mm long, which is similar to the length of a knife commonly used at home.
The result of modal analysis of this system is shown in Table 7. A desirable longitudinal vibration mode appears in the third mode with a resonant frequency of 20,652 Hz. Normally, the frequency of FE analysis is designed to be slightly higher than 20 kHz, but since it is tuned to the working frequency during manufacturing, the vibration characteristics of the entire system are judged to have no problem in use.
The mode shape is shown in Fig. 13. The magnitude of the vibration amplitude increases toward the left end of the blade, and there is little vibration at the right end of the blade. In addition, the vibration of the knife body does not show a uniform longitudinal vibration that is symmetrical vertically, which is an inevitable phenomenon that appears because the entire cutting system is not vertically symmetrical. The longitudinal vibration is minimized where the knife handgrip is fixed.
Considering these results, it is judged that the cutting system proposed in this study can be sufficiently practical at home. In addition, it plans to apply for a patent that reflects these results.
5. Conclusions
In this study, we tried to develop an ultrasonic knife that has a similar shape to a conventional kitchen knife and can conveniently cut or process food products using ultrasonic vibration. Considering the working frequency of 20 kHz, several types of knives were modeled for FE analysis and their vibration characteristics were analyzed, and the final knife model was derived using vibration equations and modal analysis.
The basic length of the knife was calculated as 115 mm using the vibration equations, and modal analysis was performed by adjusting the dimensions of various parts of the knife. Modal analysis was performed using ANSYS for the FE analysis approach. As constraints on FE analysis, radial and tangential displacements of the cylindrical surface of all stud bolts holes were restrained and only longitudinal displacements were allowed. The modal analysis was repeated to obtain the most efficient design of each part.
As a result of performing the modal analysis for the proposed cutting system, longitudinal vibration mode with resonant frequency of 20,652 Hz appeared. The frequency of FE analysis is designed to be slightly higher than 20 kHz, but since it is tuned to the working frequency during manufacturing, the vibration characteristics of the proposed system were judged to have no problem in use.
The mode shape showed the magnitude of the vibration amplitude increased toward the free end of the blade, and there was little vibration at the end of the blade fixed to the booster. Although the vibration of the knife body did not show a uniform longitudinal vibration, this is an inevitable phenomenon that appears because the entire cutting system is not vertically symmetrical. The longitudinal vibration was minimized where the knife handgrip is fixed. Considering these results, it is judged that the cutting system proposed in this study can be sufficiently practical at home.
Since it takes a lot of costs to produce a transducer, booster, and horn, this study has a limitation of performing only vibration analysis. In future study, the proposed ultrasonic cutting system will be fabricated to verify the vibration performance as well as the quality of the cut surface of food products with the support of an ultrasonic equipment product company.
Acknowledgments
This work was supported by Incheon National University Research Grant in 2017.
REFERENCES
-
Lee, S. S., Kim, T. H., Hu, S. J., Cai, W. W., and Abell, J. A., “Joining Technologies for Automotive Lithium-Ion Battery Manufacturing: A Review,” Proc. of the International Manufacturing Science and Engineering Conference, pp. 541-549, 2010.
[https://doi.org/10.1115/MSEC2010-34168]

-
Kang, B., Cai, W., and Tan, C. A., “Dynamic Response of Battery Tabs under Ultrasonic Welding,” Journal of Manufacturing Science and Engineering, Vol. 135, No. 5, Paper No. 051013, 2013.
[https://doi.org/10.1115/1.4024535]

-
Lucas, M. and Mathieson, A., “Ultrasonic Cutting for Surgical Applications,” Power Ultrasonics, pp. 695-721, 2015.
[https://doi.org/10.1016/B978-1-78242-028-6.00023-5]

- Rawson, F., “An Introduction to Ultrasonic Food Cutting,” Blackie Academic& Professional, pp. 254-269, 1998.
-
Lucas, M., MacBeath, A., McCulloch, E., and Cardoni, A., “A Finite Element Model for Ultrasonic Cutting,” Ultrasonics, Vol. 44, pp. e503-e509, 2006.
[https://doi.org/10.1016/j.ultras.2006.05.115]

- McCulloch, E., “Experimental and Finite Element Modelling of Ultrasonic Cutting of Food,” Ph.D. Thesis, University of Glasgow, 2008.
-
Brown, T., James, S. J., and Purnell, G. L., “Cutting Forces in Foods: Experimental Measurements,” Journal of Food Engineering, Vol. 70, No. 2, pp. 165-170, 2005.
[https://doi.org/10.1016/j.jfoodeng.2004.09.022]

-
Arnold, G., Leiteritz, L., Zahn, S., and Rohm, H., “Ultrasonic Cutting of Cheese: Composition Affects Cutting Work Reduction and Energy Demand,” International Dairy Journal, Vol. 19, No. 5, pp. 314-320, 2009.
[https://doi.org/10.1016/j.idairyj.2008.11.007]

- Yildiz, G., “Ultrasonic Cutting of Cheese and Apples Effect on Quality Attributes during Storage,” M.Sc. Thesis, University of Illinois at Urbana-Champaign, 2013.
- COSMO System, “The Innovation Supplier for Plastic and Metal Assembly Technology,” https://www.cosmo-stm.com/foodcutter/foodcut.html, (Accessed 20 MAY 2021)
- DUKANE, “Ultrasonic Food Cutting Products,” https://www.dukane.com/plastic-weldingproducts/ultrasonic-food-cutting-products/, (Accessed 13 MAY 2021)

M.S. candidate in the Department of Mechanical Engineering, Graduate School of Education, Incheon National University. His research interest is ultrasonic cutting.
E-mail: dhwan465@naver.com

M.S. candidate in the Department of Mechanical Engineering, Graduate school, Incheon National University. His research interest is ultrasonic welding.
E-mail: kooi45645@naver.com

Professor in the Department of Mechanical Engineering, Incheon National University. His research interest is ultrasonic welding and cutting.
E-mail: dspark@inu.ac.kr