하모닉 드라이브용 올댐 커플링 비틀림 성능해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The robot industry has greatly improved over the past 50 years. It is expected that in the era of the 4th industrial revolution the field of applying robots will expand. Motors are essential in order to operate and control robots. However, robots’ precision requires the application of robot reducers. In particular, many types of harmonic drive reducers have been applied to robots. Harmonic drive reducers have theoretically zero-backlash, but they actually exist for tolerances of Oldham coupling parts. In this paper, dynamic analysis adapted dimensional tolerances of oldham coupling was used to figure out the system backlash characteristics of harmonic drives.
Keywords:
Oldham coupling, Harmonic drive, Dynamic analysis, Tolerance, Backlash, DAFUL키워드:
올댐 커플링, 하모닉 드라이브, 동역학해석, 공차, 백래시, 다풀1. 서론
지난 반세기 동안 로봇 관련 기술은 발전을 거듭해 왔으며, 4차 산업혁명을 대표하는 인공지능, 사물인터넷 등과 융합하여 초연결 사회로의 진입을 앞두고 있다. 이는 산업용 및 협동 로봇의 수요가 증가하는 미래를 예상할 수 있다. 이러한 로봇의 동력 전달 구동계로는 하모닉 드라이브가 주로 사용되고 있는데, 무게 및 부피 대비 큰 감속비와 높은 정밀도를 얻을 수 있는 장치이며, 이 감속기 역시 점점 수요가 증가할 것으로 예상하고 있다.1
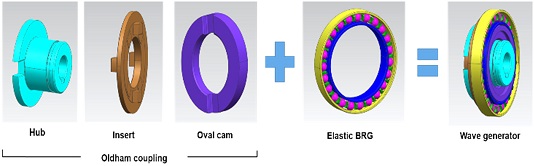
하모닉 드라이브는 3개의 주요 서브시스템으로 구성하고 있는데, 웨이브 제네레이터(Wave Generator), 플렉스 스플라인(Flex Spline) 그리고 서큘러 스플라인(Circular Spline)으로 구성되어 있다. 동력의 인풋을 전달받는 웨이브 제네레이터는 타원형 캠과 유연한 내외륜을 가지는 볼 베어링이며, 이는 타원 운동을 발생시키는 장치이다. 플렉스 스플라인은 유연한 재질의 컵과 같은 형상이며, 그 끝부분에는 기어가 생성되어 있다. 플렉스 스플라인과 조립이 되는 서큘러 스플라인은 안쪽에 기어 형상을 가지고 있으며, 플렉스 스플라인보다 강체 특성을 가지고 있다. 웨이브 제네레이터 시스템에 존재하는 올댐 커플링의 역할은 로봇의 인풋 회전 축과 하모닉 드라이브간 회전축이 일치하지 않는 상황이라 하더라도 회전력을 전달할 수 있으며, 이러한 축 공차에 의한 영향을 줄일 수 있는 부품이다.
하모닉 드라이브 관련 연구 동향을 살펴보면, 1955년 C. Walton Musser에 의해 고안된 이래로, 플렉스 스플라인의 치형, 탄성 베어링의 구조, 감속기의 마찰 및 기어물림, 플렉스 스플라인의 재료, 플렉스 스플라인의 구조 및 내구해석과 진동 특성에 관련한 연구가 주로 이루어져 왔다.2-6
그러나 실제로 구동축의 첫 부분인 올댐 커플링에 대한 연구사례를 찾아보기가 어려웠다. 아마도 메인 구성품들에 비해 연구 중요성은 낮을 수 밖에 없을 것이라 생각한다. 하지만 하모닉 드라이브의 백래시는 구동 시스템적인 관점에서 봤을 때 올댐 커플링의 부품별 공차에 의한 영향성이 높다고 판단하였다.
그 이유로는 서큘러 스플라인은 주로 축이 고정되어 있으며, 보통은 플렉스 스플라인이 회전하면서 상하 방향으로 변위 중첩이 발생하며, 그로 인해 백래시가 상쇄되는 시스템적 특성을 가지고 있기 때문이다.
따라서 본 논문에서는 웨이브 제네레이터의 한 서브시스템인 올댐 커플링 시스템의 부품 공차에 따른 하모닉 드라이브의 백래시값에 대한 영향도를 확인하기 위해 시스템 동역학 해석을 수행하였으며 그 결과를 검토하였다.
2. 하모닉 드라이브용 올댐 커플링
2.1 하모닉 드라이브 구성
하모닉 드라이브 시스템은 Fig. 1과 같이 웨이브 제네레이터, 플렉스 스플라인 그리고 서큘러 스플라인으로 크게 3가지의 서브시스템으로 구성되어 있다.
웨이브 제네레이터는 플렉스 스플라인이 조화 운동을 할 수 있도록 타원의 형태로 되어 있으며, 외륜이 유연한 특수한 베어링이 탑재되어 있다. 플렉스 스플라인은 탄성을 가지는 컵 형상의 기어로 되어 있으며, 이 역시 탄성 변형 운동을 쉽게 할 수 있도록 연신율이 높은 재질로 되어 있다. 마지막으로 플렉스 스플라인의 외치차 기능을 하는 서큘러 스플라인은 플렉스 스플라인에 비해 강한 재질의 특성을 가지고 있다.
2.2 웨이브 제네레이터의 구성
하모닉 드라이브의 웨이브 제네레이터를 구성하는 부품은, 올댐 커플링(인서트, 허브, 플러그 및 커브드 와셔로)과 타원 베어링으로 구성되어 있다.
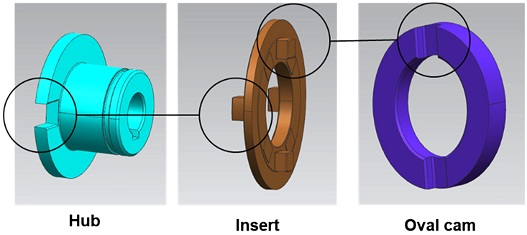
그 중에서 올댐 커플링을 구성하는 부품으로 Fig. 2와 같이 허브, 인서트, 그리고 타원 캠이다. 추가적으로 회전축 방향으로 미세한 복원력을 주는 커브드 와셔가 1개 존재하고 있으며, 이것의 기능은 웨이브 제네레이터 조립체가 밀착시키는 기능을 담당하는 역할을 하고 있다.
3. 올댐 커플링 시스템 해석 모델링
3.1 해석 모델링 구성
하모닉 드라이브 CSG/F 타입에 적용된 올댐 커플링을 선정하였으며, 허브(Hub), 인서트(Insert), 오발 캠(Oval Cam)을 유연체(Flexible Body)로 생성하였다. 이는 백래시를 확인하기 위해 부품의 거동 특성 뿐만 아니라 변형에 의한 효과를 고려하기 위한 목적이다.
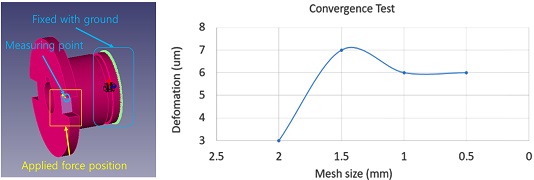
유연체 모델의 검증을 위해 해석 모델의 메쉬 사이즈를 0.5/1.0/1.5/2.0 mm로 선정하였고, 그 수렴성 검증을 위해 허브를 선정하였다.
검증해석 모델은 허브의 끝쪽을 그라운드(Ground)와 구속하고, 키홈의 한 부분에 단위 하중(Force)을 인가했을 때, 메쉬 사이즈에 따른 변형량에 대한 수렴성 검토를 Fig. 3과 같이 수행하였다.
한쪽이 구속되고 다른 한 쪽에 힘을 주게 되었을 때, 가장 변형이 많이 일어나는 지점을 선정하였으며, 그 변형량을 측정하였다.
1.0 mm 이하의 메쉬 사이즈를 적용 시 변형량이 일정하게 수렴하는 특성을 나타내고 있기 때문에 해석상에 문제는 없으나, 단위 하중이 적용되는 키홈 부분을 모델링할 때 접촉 정밀도를 고려하여 최소 3개 이상의 레이어가 있는 것이 시스템 접촉 측면에서 안정적이므로 메쉬 사이즈를 0.5 mm로 적용하였다.
그리고 허브, 인서트, 오발 캠은 공통적으로 키와 홈의 구조로 토크를 전달하는데, 허브와 인서트, 인서트와 오발 캠 사이에는 각각의 위상차가 180o로 되어 있으며, 이 두 부분의 접촉력에 의해 병진 조인트의 효과를 얻을 수 있다.
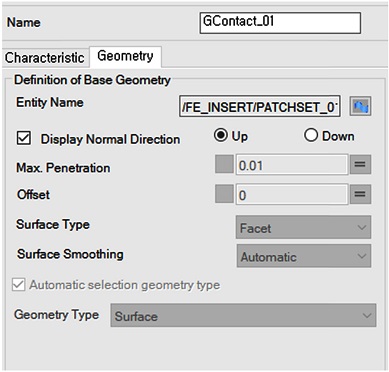
Fig. 4와 같이 각 부분의 접촉 서피스를 정의하고, 실제 접촉이 일어나는 부분들에 대해서 접촉 요소로 모델링하였고, 허브와 인서트는 알루미늄 계열, 오발 캠은 스틸 계열로 Table 1과 같이 물성치를 적용하였다.
3.2 해석 구동 조건
여러 가지 구동 시스템의 비틀림 특성을 확인하기 위해 인풋(Input)쪽을 구속하고, 아웃풋(Output)쪽에는 토크를 인가하여 토크-각도 선도를 주로 검토하고 있다.
해석 모델에서 인풋쪽은 허브의 키홈 부분에 노드를 정의한 뒤 그라운드와 구속하여 움직이지 않도록 한다. 아웃풋쪽은 오발 캠의 외곽부의 노드와 회전 조인트를 그라운드와 연결한다.
하모닉 드라이브에서 오발 캠은 탄성 베어링(Elastic Bearing)의 내륜(Inner Raceway)과 압입하여 회전하게 된다. 해석 모델에서 출력쪽의 구동 조건을 선정하기 위해 하모닉 드라이브사의 카탈로그 데이터를 활용하였다.7
구동 토크는 CSG/F 타입 사이즈 17의 자료를 참고하여 기어비 80대 1의 조건 구동 시 적용 토크는 24 Nm임을 알 수 있었다. 하지만 이 토크를 그대로 해석에 적용할 수 없다. 그 이유는 올댐 커플링에 적용되는 토크는 감속비로 나눈 값의 토크가 작용하게 된다.
그 이유는, 올댐 커플링은 단지축의 엇갈림이 있을 경우 그 공차를 흡수하는 역할을 하기 때문에, 하모닉 드라이브 시스템에서 감속기능을 나타내지 않고, 단지축의 동력 전달 역할만 수행하고 있으며, 감속이 이루어지는 부분은 플렉스 스플라인과 서큘러 스플라인 부분에서 발생한다.
그리고 구동 조건을 부여할 때는 아웃풋쪽에 0.3 Nm의 토크를 식(1)과 같이 사인파의 조합 형태로 구동시킨다.
| (1) |
3.3 공차를 고려한 해석 조건
실크햇 및 컵 타입의 하모닉 드라이브의 백래시는 올댐 커플링에서 발생하는 시스템이다. 특히 앞서 허브와 인서트, 그리고 인서트와 오발 캠이 접촉하는 키홈 부분의 공차의 설계 공차에 따라 백래시의 값이 발생하게 된다.
17형번의 감속비 80 기준을 적용할 경우, 백래시는 13 arc.sec (1 arc.sec는 1/3,600o를 의미)의 값을 가지게 된다. 올댐 커플링의 아웃풋측에서의 백래시는 이 값에 감속비를 곱한 17.333 arc.min (1 arc.min은 1/60o를 의미)로 예상할 수 있다. 이 값을 나타내는 최대 공차값을 해석을 통해 찾아보고자 한다.
실제 캐드 모델에는 공차가 없으며, 공차 효과를 주기 위해, 해석 모델링 시 접촉 부분을 공차만큼 이동(Offset)시키는 기능을 활용하면 공차의 효과를 볼 수 있다. Fig. 5에서 “Offset” 부분의 값인데, 0 부터 22 μm까지 증가하면서 해석 조건을 실시해 보았다.
4. 시스템 해석 결과
4.1 백래시의 정의
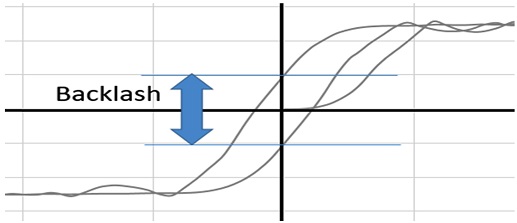
회전하는 기구의 백래시는 기어에서의 백래시와 다른 개념의 내용이다. 입력축을 고정한 상태에서 고정축에 사인파의 토크를 인가하면, 이론적으로는 히스테리시스가 발생하지 않는다. 하지만 실제 시스템에서는 공차에 의해 발생하는 히스테리 시스를 백래시라고 정의한다. 또한 이 백래시는 토크-각도 선도를 Fig. 6과 같이 세로축의 값의 차로 정의한다.8
4.2 공차에 따른 해석 결과
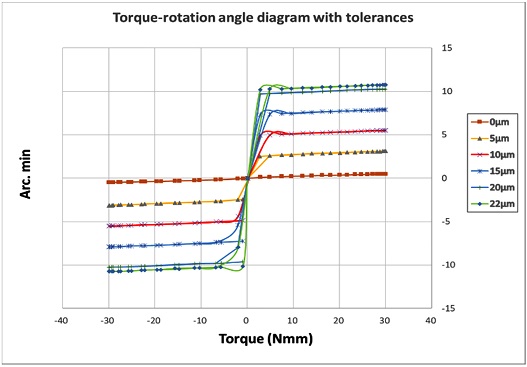
올댐 커플링에서 접촉이 일어나는 키와 홈 부분의 공차가 0인 경우 이론적으로 백래시는 0이 된다. 다만 입력축을 고정하고, 출력축에 가해진 토크에 의한 비틀림 강성이 나오는 것을 확인하였다. 그리고 하모닉 드라이브사에서 제공하고 있는 백래시값을 만족시키는 공차값을 찾기 위해 22 μm의 값을 해석 모델에 적용하였을 경우, 백래시값이 17.4 arc.min을 나타나는 것을 확인하였으며, 공차에 따른 백래시의 경향성은 선형 특성을 나타내고 있다.
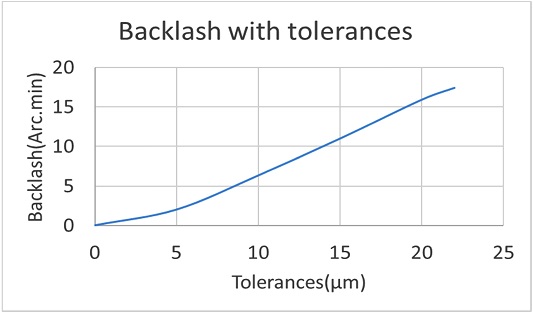
Fig. 7의 데이터를 바탕으로 공차에 따른 백래시를 정리하면 Table 2와 같은 데이터를 얻을 수 있다.
Fig. 8과 Table 2로부터 공차에 따른 백래시값은 거의 선형 함수를 나타내는 것을 확인할 수 있다. 이 결과로부터 하모닉 드라이브의 출력축의 최대 백래시값은 22 μm일 때 발생한다.
그리고 감속비를 역산하여 검토해보면 감속비가 클수록 백래시값이 작아지는 경향이 나오는데, 이는 인풋쪽의 백래시값이 감속비로 나누어지기 때문문에 역으로 저감속비인 30대 1의 경우가 가장 백래시가 크고, 고감속비를 적용할 경우 150대 1의 경우라 가정하면 실제 30대 1의 1/5 수준으로 백래시가 작아진 것을 알 수 있다.
5. 결론
하모닉 드라이브 시스템을 구성하고 있는 부품 중에서 탄성변형이 일어나는 플렉스 스플라인 그리고 서큘러 스플라인의 특성에 대해서 연구한 사례는 많았지만, 이번에는 입력 부분의 올댐 커플링에 대해서 연구하였다.
하모닉 드라이브에서 발생하는 백래시는 올댐 커플링의 기구 공차에 기인하여 발생하는 것을 해석 결과로부터 확인할 수 있었다.
하모닉 드라이브사의 카탈로그 자료와 해석 검증을 통해 알게 된 사실은 하모닉 드라이브 시스템에서 발생하는 백래시의 값은 매우 작은 값이며, 만일 발생하더라도 하모닉 드라이브 시스템에서는 플렉스 스플라인이 상하 운동을 하며 상쇄되는 부분이 있고, 최종 감속비가 큰 시스템이기 때문에 입력단에서 발생하는 백래시의 영향은 작게 된다.
하모닉 드라이브사에서는 감속비에 따른 올댐 커플링 사양을 따로 만드는 것이 아닌, 동일 형번에서는 동일한 올댐 커플링을 적용하는 것을 해석 결과로부터 추정할 수 있다. 따라서 하모닉 드라이브 시스템의 기구적 백래시를 최소화하기 위해서는 가급적 고감속비 모델을 적용하는 것이 백래시 측면에서 유리하다고 할 수 있다.
REFERENCES
- Korea Association of Robot Industry, “Korea Robot Industry Technology Roadmap 2017,” http://www.korearobot.or.kr/wp/wp-content/uploads/2017/10/%EB%8C%80%ED%95%9C%EB%AF%BC%EA%B5%AD-%EB%A1%9C%EB%B4%87%EC%82%B0%EC%97%85-%EA%B8%B0%EC%88%A0%EB%A1%9C%EB%93%9C%EB%A7%B5-%EC%B5%9C%EC%A2%85%EB%B0%B0%ED%8F%AC%EC%9A%A9.pdf, (Accessed 17 AUGUST 2021)
- Oh, S. H., Lee., C. W., Jeon, H. S., and Im, S. J., “Stress and Vibration Analysis of Flexspline for Harmonic Drive,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 23, No. 8, pp. 1253-1260, 1999.
-
Nam, W., Ham, S., and Oh, S., “Structural Analysis for Silk Hat Type of the Harmonic Drive for Precision Robot,” Journal of the Korea Society for Power System Engineering, Vol. 15, No. 5, pp. 61-66, 2011.
[https://doi.org/10.9726/kspse.2011.15.5.061]

-
Heo, M., Ham, S., Nam, W., and Oh, S., “Study on the Design Program for Non-Standard Plastic Gear,” Journal of the Korea Society for Power System Engineering, Vol. 15, No. 4, pp. 54-59, 2011.
[https://doi.org/10.9726/kspse.2011.15.4.054]

- Ahn, H. J., Choi, M., Kim, B. S., and Jin, S. H., “Design Program of Gear Tooth of a Harmonic Drive,” Proc. of the KSPE Conference, pp. 33-34, 2020.
- Kim, I. K., Park, I. G., and Choi, W., “Study on Controlling of Vibration Characteristic of the Harmonic Drive to Obtain the Best Performance,” Proc. of the Institute of Control, Robotics and Systems Conference, pp. 221-222, 2015.
- Harmonic Drive, “Reducer Catalog,” https://www.harmonicdrive.net/_hd/content/documents1/reducer_catalog.pdf, (Accessed 17 AUGUST 2021)
-
Wang, B., Liu, J., and Wang, C., “Measurement and Analysis of Backlash on Harmonic Drive,” Proc. of the IOP Conference Series: Materials Science and Engineering, Paper No. 012005, 2019.
[https://doi.org/10.1088/1757-899X/542/1/012005]


Ph.D. candidate in the Department of Mechanical Design Engineering, Hanyang University. His research interest is multibody dynamics.
E-mail: highself@hanyang.ac.kr

Professor in the Department of Mechanical Engineering, Hanyang University. His research interest is multibody dynamics.
E-mail: dsbae@hanyang.ac.kr

Professor in the Department of Mechanical Engineering, Myongji University. His research interest is automative engineering, torsional vibration isolation damper, multibody dynamics.
E-mail: jdjang@mju.ac.kr