전기화학 임피던스 분광법 기반 과도 상태 리튬 이온 배터리 고장 인자 선정 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Lithium-ion batteries are one of the main parts of electrical devices and are widely used in various applications. To safely use lithium-ion batteries, fault diagnosis and prognosis are significant. This paper analyzes resistance parameters from electrochemical impedance spectroscopy (EIS) to detect the fault of lithium-ion batteries. The internal fault mechanisms of batteries are so complex; it is difficult to detect abnormalities by direct current-based methods. However, by using alternating-current-based impedance by EIS, the internal degradation processes of the batteries can be detected. Impedance variation from EIS is verified under accelerated degradation test conditions and normal cycling test conditions. The results showed a significant relationship between fault and increase in resistance.
Keywords:
Electrochemical impedance spectroscopy, Lithium-ion battery, Fault diagnosis and prognosis, Accelerated degradation experiment키워드:
전기화학 임피던스 분광법, 리튬 이온 배터리, 고장 진단 및 예측, 가속 열화 실험1. 서론
정부의 환경 규제 정책에 따라 내연기관차에서 전기차로 이동이 급격하게 이루어지고 있다. 국토교통부 자료에 따르면 2020년 기준 국내에 상용화되고 있는 친환경차는 689,495대로 그 비중이 전년 동기 대비 2.3%에서 2.9%로 0.6%p 증가하였고, 18년 1.9, 19년 2.5%로 그 비중이 지속적으로 증가하고 있다.1 그러나 전기차의 급격한 증가는 화재 및 폭발 사고로 이어지고 있으며, 전기차 화재 사고에 대한 주요 원인으로 배터리 결함이 조사되었다.2 이로 인해 안전한 배터리 사용에 대한 연구가 요구된다. 현재 국내외적으로 배터리의 안전성 연구를 위해 배터리 고장을 모사하여 파괴적인 방법을 이용한 분석 연구가 진행되고 있다. 전자 주사 현미경(Scanning Electron Microscopy, SEM), X-선 회절 분광법(X-Ray Diffraction Spectroscopy, XRD)이 이러한 방법에 속한다.3 그러나 파괴적 방법을 통한 배터리의 고장 진단 및 예측은 실시간으로 배터리 상태를 탐지할 수 없기 때문에 비파괴적으로 고장을 진단하는 방법이 요구된다.4
배터리는 사용 중 고장에 의해 용량이 급격히 감소하거나 저항이 급격히 증가하는 과도 상태가 발생하기 때문에, 이러한 과도 상태 탐지를 위해 진단 및 예측 인자를 선정해 고장 상황에 대처해야 한다.5,6 배터리의 과도 상태에서 변화가 두드러지는 파라미터를 통해 열화 혹은 고장과 관계가 높은 인자를 선정할 수 있다. 파라미터는 일반적으로 등가회로 모델을 기반으로 하여 전기적 방법 및 전기화학적 방법으로 추출할 수 있다. 전기적 방법의 파라미터 추출 방법은 직류 전류를 인가해 전압의 변화를 통해 저항 및 캐패시턴스 파라미터를 추출한다.7 기존 전기적 방법에 따른 저항 추출의 경우 직관적이고 빠른 시간 내에 추출할 수 있는 장점이 있지만, 배터리 내부의 전기화학적 현상에 의한 저항과 캐패시턴스 특성을 모사하기 어렵다는 한계가 있다. 반면, 전기화학 임피던스 분광법(Electrochemical Impedance Spectroscopy, EIS)을 이용하면 내부 전기화학적인 상태에 대한 분석이 가능하기 때문에 기존 전기적 모델의 한계를 보완할 수 있다. EIS는 고주파수 영역에서 저주파수 영역까지 미소한 정현파 전류 및 전압 신호를 인가해 배터리의 전기적 평형 상태와 열적 평형 상태를 벗어나지 않는 범위에서 응답된 전압 및 전류 신호를 통해 진폭과 위상의 변화를 측정하여 임피던스를 분석하는 방법이다.8 정현파 신호는 고주파수에서 저주파수까지 인가되며 각 주파수별 임피던스가 도출된다. 주파수 영역을 이용하여 내부 메커니즘을 분석하는 방법이기 때문에, 배터리 시스템을 구성하는 성분, 즉 양극, 음극, 분리막, 전해질 등의 상태를 주파수 영역별로 분리해서 분석할 수 있다는 장점이 있다. 이는 전기적 방법과 비교하였을 때, 배터리의 고장 요소를 진단할 수 있으며, 고장 원인 분석에 용이하다.9,10 그러나, 기존 연구에서는 임피던스 특성을 기반으로 용량 감소, 내부 온도 추정, 수명 예측 등에 대한 연구를 주로 진행하였으며,11-17 고장 진단과 예측에 대한 연구 수행은 미비하다. 임피던스 데이터를 기반으로 수명, 온도 등을 추정하기 위해 실험 장비에 내장된 소프트웨어, 이중 분극 모델(Dual Polarization Model), 랜들스 모델(Randles Model), 커브 피팅 방식을 사용하였다.15-17 그러나 소프트웨어 방식, 커브 피팅 방식은 임피던스값 도출 과정에 있어 전기화학적 특성 반영에 대한 당위성이 부족하다. 이중 분극 모델의 경우 연산량이 높아 실시간 적용이 어렵다. 반면, 랜들스 모델의 경우 상대적으로 낮은 연산량과 높은 정확도를 통해 EIS 데이터 분석에 용이하다.
본 논문은 배터리 고장에 대한 사전 징후 인자 선정하기 위해 고장 상황에서 EIS 기반 저항 파라미터의 변화를 연구하였다. 가속 열화 시험 조건(60oC)에서 충전 및 방전을 통해 노화시험을 수행하고, 실험 도중 배터리 충전 및 방전이 불가한 고장 상황에서 임피던스 변화를 분석하였다. 정상 사이클 시험 조건(25oC)의 노화 시험 중 저항 파라미터 변화와 비교 분석을 통해 선정한 고장 인자를 검증하였다.
2. 전기화학 임피던스 분광법 분석 방법 및 모델 인자 추출
2.1 전기화학 임피던스 분광법
전기화학 임피던스 분광법은 전류 혹은 전압을 정현파로 인가하여 신호에 따른 임피던스 반응을 분석하는 방법이다. Fig. 1과 같이 인가된 신호에 의해 입력값과 출력값 사이에 상 차이가 나타나고, 실수부와 허수부가 나뉘게 된다.9,10,18,19 도출된 임피던스를 주파수 영역에 따라 복소 좌표계로 도식화해 나이키스트 선도를 나타낼 수 있다.
| (1) |
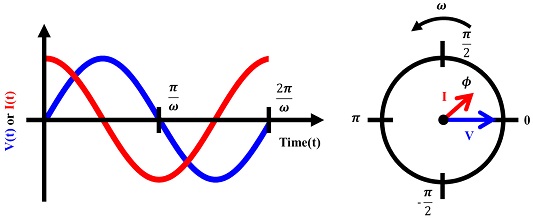
The relationship between sinusodial voltage and current curve and AC voltage with angular frequency ω
주파수별 임피던스는 진폭과 위상 특성 변화를 복소수 체계로 표현하게 되는데, 허수를 통해 위상 변화를 나타내고, 이다. 인가되는 정현파 전압에 따른 응답된 전류 신호는 식(1)로 계산된다. 교류 신호에 의한 전압 및 전류는 위상차로 인해 변화하는 값이기 때문에 ω의 함수로 표현된다. 교류 신호에 의한 전압 및 전류는 교류 회로 모델에 대해 옴의 법칙을 만족하며 임피던스를 식(2)와 같이 표현할 수 있다.
| (2) |
식(2)는 오일러 공식, exp(jΦ) = cos(Φ) + jsin(Φ)에 의해 식(3)과 같이 변환된다.
| (3) |
식(3)을 허수부와 실수부로 구분하여 나타내면 다음 식(4)와 같이 나타낼 수 있다.
| (4) |
임피던스는 교류 신호를 회로에 인가 시, 입력 및 출력 신호의 진폭 및 위상을 변화하는 성분으로 정의되며, 저항, 인덕턴스, 캐패시턴스 성분으로 구성된다.19 Zreal = Z0cos(Φ)는 저항 성분을 나타내고, Zimg = Z0jsin(Φ)는 허수부 j성분으로 인해 캐패시턴스(C) 성분과 인덕턴스(L) 성분을 갖는다.19
2.2 등가회로 모델
배터리의 내부 전기화학적 상태를 회로 소자를 통해 나타내 상태 추정을 용이하게 하기 위해 전기적 등가회로 모델을 적용한다.8 전기적 등가회로 모델은 전기화학 모델보다 정확도가 낮지만, 상대적으로 낮은 연산량과 정확도로 배터리의 내부 전기화학적 거동을 모사할 수 있다. 또한 전기화학적 메커니즘으로 기인한 분극 저항을 모사할 수 있기 때문에 실시간 진단에 용이하다.20,21
본 논문에서 사용한 등가회로 모델은 랜들스 모델로 배터리의 열화에 따라 변화하는 내부 상태를 저항과 캐패시터 조합으로 나타내었다.
Fig. 2에 배터리의 내부 전기화학적 상태를 분석하기 위해 주로 사용되는 등가회로 모델인 랜들스 모델이다. 랜들스 모델을 기반으로 응답 임피던스를 나이키스트 선도로 표현한 것을 Fig. 3에 나타내었다. 랜들스 모델에서 배터리의 전기화학적 프로세스에 의한 특성은 다음과 같이 표현된다.19-21
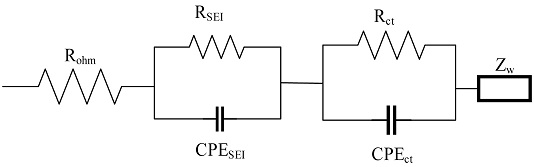
Randles model composed of ohmic resistance (Rohm), SEI resistance (RSEI), charge transfer resistance (Rct), constant phase element (CPESEI, CPEct) and Warburg impedance (Zw)
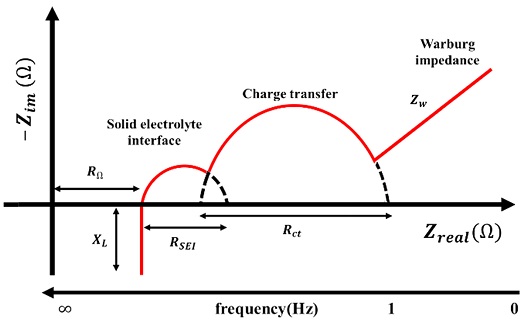
Analysis method of nyquist plot of Randles model composed of ohmic resistance (Rohm), SEI resistance (RSEI), charge transfer resistance (Rct), constant phase element (CPESEI, CPEct) and Warburg impedance (Zw)
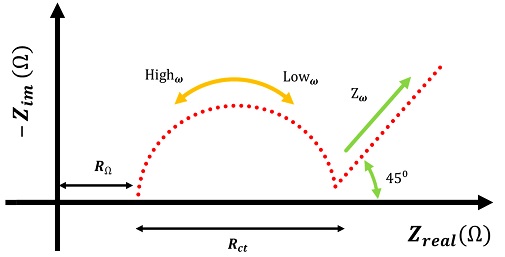
(1) Fig. 3의 실수 임피던스축 절편인 옴 저항(Rohm)은 전해질 저항으로 전해질의 이온 전도도의 특성을 나타낸다.
(2) Fig. 3의 첫 번째 반원은 고체 전해질 필름(Solid Electrolyte Interphase, SEI)에 의한 저항(RSEI)이다. 열화가 진행될 때, 전해질 분해로 인해 전극 표면에 생성된 SEI에 의한 저항을 나타낸다.
(3) Fig. 3의 두 번째 반원은 전극 계면에서 전하가 이동할 때 나타나는 현상인 전하 전달 저항(Rct) 및 Fig. 3의 Constant Phase Element (CPE)는 전극과 SEI, SEI와 전해질 계면에서 발생하는 전기 이중층에 대한 현상을 나타낸다.
(4) Fig. 3의 저주파수 영역에서 나타나는 45o 직선은 와버그 임피던스(Zw)로 배터리 내 리튬 이온의 확산 현상을 나타낸다.
Fig. 4의 변형 랜들스 모델(Modified Randles Model)은 기존 랜들스 모델을 간략화한 등가회로 모델로, 필름층 저항(RSEI)에 대한 특성을 고려하지 않는다. 고체 전해질 필름의 영향이 약한 경우, 필름층에 의한 저항(RSEI) 및 캐패시턴스 성분이 뚜렷하게 측정되지 않기 때문에 생략할 수 있으며, Fig. 5에 SEI가 측정되지 않았을 때의 나이키스트 선도를 도시하였다. 본 연구에서 사용한 니켈 코발트 알루미늄(Nickel-Cobalt-Aluminum, NCA) 배터리의 경우 고온에서 구조적인 성능 감소가 급격히 나타난다. 따라서, SEI 형성에 의한 저항 및 전기 이중층 현상이 측정되기 전 배터리의 수명이 감소하는 경향을 보이기 때문에, 본 연구에서 위의 사항을 고려한 변형 랜들스 모델을 통해 인자를 추출하였다.
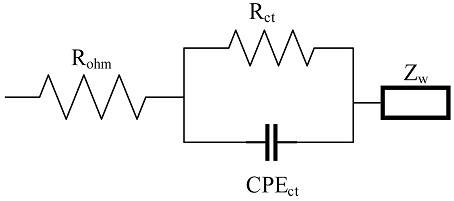
Modified Randles model composed of ohmic resistance (Rohm), charge transfer resistance (Rct), constant phase element (CPEct) and Warburg impedance (Zw)
2.3 모델 인자 추출
Fig. 4에서 직렬 저항으로 표현되는 옴 저항(Rohm)은 전해질, 집전체, 분리막 등에서 나타나는 모든 저항 성분을 더한 저항이다. 옴 저항(Rohm)은 캐패시턴스 혹은 인덕턴스 성분이 없는 저항이기 때문에 허수 임피던스를 나타낸 수직 축의 값은 0이며, Fig. 5에서 수평축 교차지점으로 나타난다.9,18,19
| (5) |
옴 저항(Rohm)은 전해질에 큰 영향을 받기 때문에 온도가 증가하면 전해질의 이온 전도도가 증가하여 옴 저항(Rohm)이 감소하는 현상을 보인다.12 배터리 열화 시 전해질 분해로 인한 부반응이 발생되고, 전해질 감소로 이온 전도도가 저하되어 옴 저항(Rohm)이 증가하는 현상이 나타나므로, 열화에 대한 지표로 사용할 수 있다.19
Fig. 5의 나이키스트 선도에서 반원 형태로 측정되는 전하 전달 현상은 배터리 내 전기화학 반응에 대한 현상이다. 전해질 용액과 전극 계면에서 에너지 교환 혹은 상변화를 통해 리튬 이온이 이동한다. 식(6)을 통해 수직축 값이 최대인 지점이 캐패시턴스가 최대인 지점이며, 수평축 성분에서 옴 저항(Rohm)을 뺀 값에 2배를 하여 전하 전달 저항(Rct)을 산출할 수 있다.22 전기 이중층에 의한 캐패시턴스는 나이키스트 선도에서 y축이 가장 높은 지점의 주파수를 통해 계산된다.19,20,23 식(7)은 전기 이중층에 의한 캐패시턴스 계산 수식이다.
| (6) |
| (7) |
Fig. 5의 45o 기울기를 나타낸 직선 형태의 와버그 임피던스(Zw)는 저주파수 영역에서 나타나는 현상으로 리튬 이온의 확산 현상을 나타내는 인자이다. 확산 현상은 농도차에 의해 기전력이 형성되어 과전압이 나타나는 현상이다.20 확산 현상은 외부 전기장이 아닌 내부 농도차에 의해 나타나며, 충전과 방전을 진행함에 따라 리튬 이온이 전극 내부를 이동하며 발생한다. 이러한 화학종의 농도 차이 때문에 나타나는 확산 현상을 Zw로 표현한다. 확산 현상의 지표인 Zw는 캐패시턴스와 저항을 통해 표현된다.24
| (8) |
식(8)에서 Rω는 확산 저항으로 허수부가 최솟값을 갖는 지점에서의 수평축 값이며, ω는 상이 -45o로 포화되었을 때의 주파수를 나타낸다. 이는 리튬 이온 배터리에서 Zw의 상이 –45o가 되었을 때 확산 현상이 포화된 것으로 추정하기 때문이다.24
3. 실험
3.1 실험 구성 및 방법
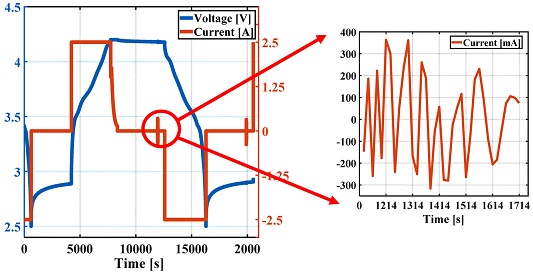
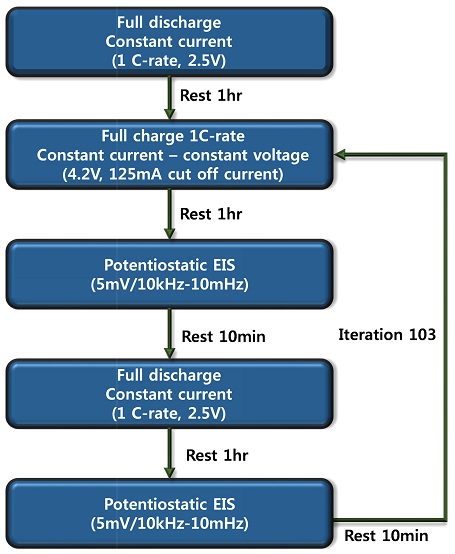
본 논문에서는 전기차용 기기 적용을 위해 INR18650-25R 고출력 배터리를 사용하였다. Fig. 6에 실험에 사용한 장비 및 배터리의 자세한 사양을 나타내었다. 실험에 사용된 장비는 Bio-Logic사의 BCS-815를 사용하였고, 장비의 전류 사양은 10 A-1 mA이며 전압 사양은 2-9 V이다. 실험 방식은 정현파 전압을 인가하여 임피던스를 측정하는 방법인 정전압 EIS (Potentiostatic EIS, PEIS) 방법을 이용하였다. 전압 진폭 5 mV의 정현파 전압을 인가하여 EIS 시험 중 배터리 내부 평형 상태를 유지하였다.12 Fig. 7의 오른쪽 그래프는 정현파 전압 신호에 대한 전류 응답 신호 측정값이다. 실제 측정된 전류의 경우, 1 s Sampling Time으로 측정되어 정확한 정현파는 보이지 않으나, 전압이 인가됨에 따라 전류의 변화를 확인할 수 있다. 실험의 환경 조건은 Jeio-Tech사의 온도 챔버에서 고온 환경(60oC)을 설정하여 진행하였으며, 온도 챔버의 사양은 0에서 100oC까지 운용이 가능하며, 0.3oC 수준의 오차를 보인다. 배터리를 완전히 충전 및 방전시킨 후 열 평형 상태를 형성하기 위해 1시간의 휴지 시간을 취한 후 전기화학 임피던스 분광법을 수행하였다. Fig. 8은 자세한 실험 방법 및 조건이다.
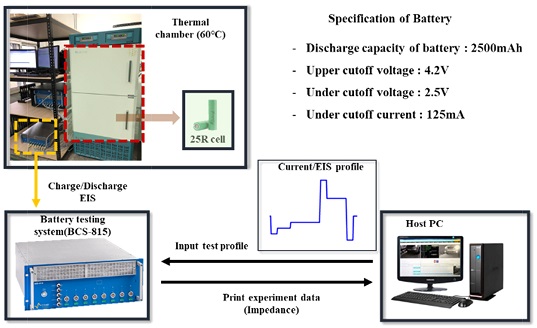
Electrochemical impedance spectroscopy experimental setup and specification of Nickel-Cobalt-Aluminum battery
3.2 실험 결과
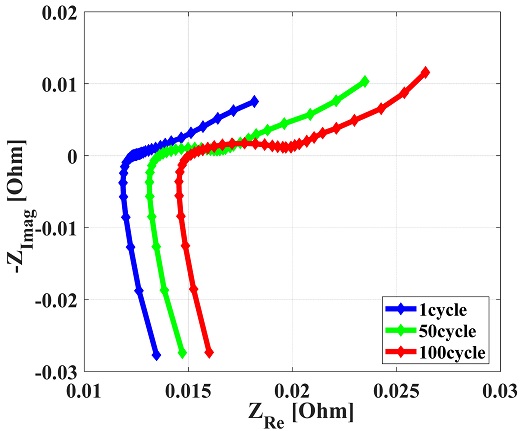
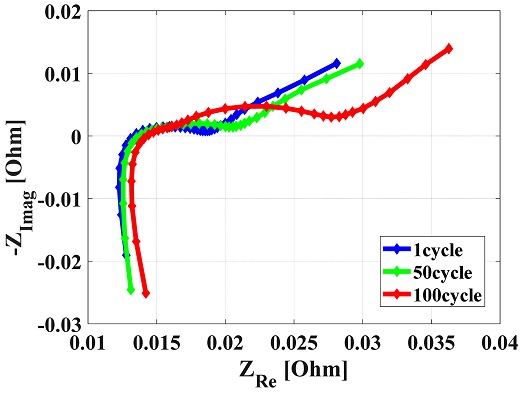
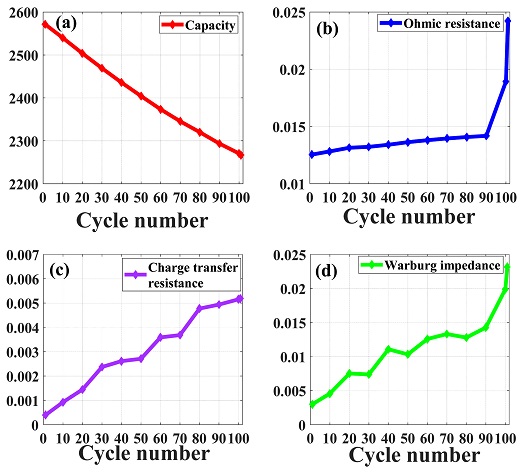
Fig. 9에 고온(60oC)에서 열화시킨 배터리의 1, 50, 100 충전 및 방전에 따른 나이키스트 선도를 도시하였다. 본 실험에서는 10 kHz에서 10 mHz 주파수 영역에서 총 36개의 주파수 지점을 선정하여 주파수에 따른 실수부와 허수부를 복소 평면에 도시하였으며, 열화에 따라 나이키스트 선도가 수평축으로 이동하는 경향을 보인다. 비교를 위해 상온 조건에서 열화시킨 배터리의 1, 50, 100 충전 및 방전에 따른 나이키스트 선도를 Fig. 10에 도시하였다. Figs. 9와 10을 통해 온도에 따라 노화되면서 변화하는 나이키스트 선도의 형태가 다름을 확인할 수 있다. 온도가 상이한 조건에서 열화하는 경우, 내부 상태의 변화가 달라져 임피던스의 변화 경향성도 달라진다. 고온에서 노화가 진행된 경우 옴 저항이 눈에 띄게 증가하고, 상온에서 노화가 진행된 경우 전하 전달 저항이 옴 저항 대비 상대적으로 많이 증가한다. Fig. 11은 고온 환경에서 열화에 따른 용량 및 모델 파라미터인 옴 저항(Rohm), 전하 전달 저항(Rct), 와버그 임피던스(Zw)의 변화이다. 충전 및 방전을 진행함에 따라 배터리가 열화되어 용량 감소 및 저항 증가 현상이 나타난다. 배터리의 열화는 Fig. 11(a)와 같이 선형적인 용량 감소와 모델 파라미터의 증가로 나타난다. 초기 용량 2.58 Ah에서 지속적인 용량 감소와 저항 증가 현상이 나타나며, 이는 열화에 따라 용량 및 출력이 감소한다는 기존 연구 내용들과 부합한다.10 실험을 진행하는 도중 수명 종료 시점(초기 용량 대비 80% 용량이 되는 시점)에 도달하기 전배터리 충전 및 방전이 진행되지 않는 현상이 발생하였다. 전류를 인가해도 배터리의 전압이 계측되지 않았기 때문에 고장으로 진단할 수 있다. 이때, 모델 파라미터 중 일부는 고장 발생 전 특정 지점에서 급격히 변화함을 보인다. 고장과 모델 파라미터 사이의 관계성을 분석하여 고장 사전 인자를 선정하기 위해 상온 열화 데이터의 모델 인자와 비교하였다.
4. 결과 및 분석
4.1 모델 인자 분석
고온 환경(60oC)에서 충전 및 방전에 따른 배터리 고장 발생에 대한 인자를 선정하기 위해 인자 분석을 수행하였다. 상온(25oC)에서 열화 시 용량 감소에 따른 모델 인자 변화와 고장 시 모델 인자 변화를 비교하여 고장 진단에 적합한 인자를 선정하였다.
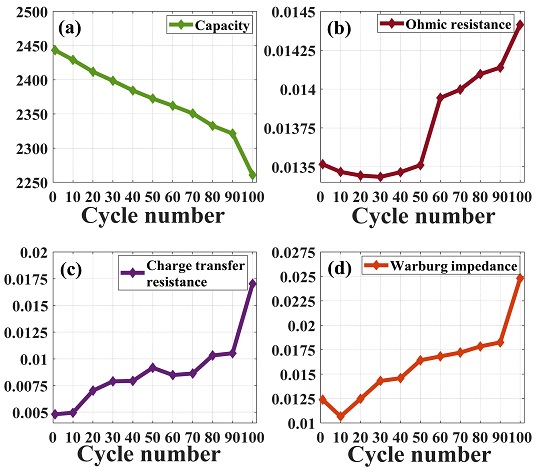
Fig. 11(a)를 통해 열화에 따른 배터리의 용량이 선형적으로 감소함을 확인할 수 있다. 반면 Fig. 11(b)에 도시한 옴 저항(Rohm)은 고장 2단계 전에서 초기 데이터 대비 92%로 급격하게 증가함을 확인할 수 있다. 선형적인 용량 감소와 달리 급격한 저항의 증가는 고장에 의한 현상으로 진단할 수 있다. Figs. 13(a) 및 13(b)의 고장이 발생하지 않은 상온 열화 데이터의 경우, 용량 감소와 옴 저항(Rohm)의 증가 정도가 초기 데이터 대비 10% 내외로 비슷한 경향을 띠고 있기 때문이다. 즉, 상온에서 열화에 따른 옴 저항(Rohm) 증가는 용량 감소와 비슷한 경향을 보이나, 고온에서 옴 저항(Rohm)의 거동은 용량 감소와 상이한 지점이 발생한다. 또한, 고장 발생 데이터의 옴 저항(Rohm)은 상온에서 진행한 열화에 대한 저항 증가보다 86% 높음을 확인하였다.
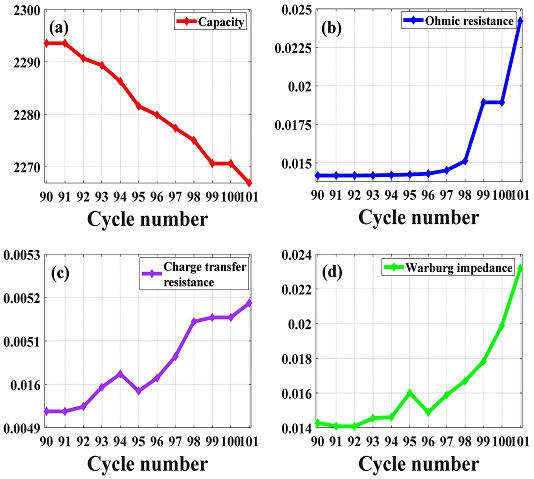
Cycle-parameters (a) Capacity, (b) Ohmic resistance, Rohm (c) Charge transfer resistance, Rct, and (d) Warburg impedance, Zw plot in 10 intervals, respectively (cycle 91-101) at 60 degree Celsius
Fig. 11(c)에 도시한 전하 전달 저항(Rct)의 증가는 초기 충전 및 방전 결과 대비 10% 증가 정도로, 열화에 따른 용량 감소 경향과 동일한 경향을 보인다. Figs. 13(a) 및 13(c)의 상온 데이터와 비교한 결과, 용량 감소와 전하 전달 저항(Rct)의 증가 역시 유사한 경향성을 나타냄을 확인할 수 있다. 따라서 전하 전달 저항(Rct)은 열화에 따른 용량 변화와 연관성이 있으며, 고장 상황과 낮은 관련성을 가지는 것을 확인할 수 있다.
Figs. 11(d)에 도시한 와버그 임피던스(Zw)의 증가는, 11(a)의 용량 감소와 같이 선형적으로 증가하나 90번째에서 급격한 기울기 변화를 보인다. Fig. 12(d)에 91번째에서 101번째까지 와버그 임피던스(Zw)의 변화를 도시하였으며, 고장 5단계 전에서 초기 대비 약 600%의 급격한 증가를 보임을 확인할 수 있다. 이는 옴 저항(Rohm)과 유사하게 용량 감소에 의한 영향이 아닌 고장에 의한 증가로 진단할 수 있다.
4.2 고장 인자 선정
고장과 무관하게 고온 및 상온에서 열화에 따라 용량이 일정하게 감소함을 확인하였다. 옴 저항(Rohm)과 와버그 임피던스(Zw)는 각각 고장 상황 2단계, 5단계 이전에서 직전(103번째) 대비 92, 400% 정도의 급격한 저항 증가를 보였다. 따라서 용량 감소에 대한 영향 외에 고장에 대한 영향을 반영하고 있음을 확인할 수 있다. 반면, 전하 전달 저항(Rct)의 증가는 노화 중 10%가량 일정하게 증가하며, 이는 용량 감소의 경향과 일치해 고온 노화에 의한 고장 진단 인자로 고려되기 어렵다. 따라서 고장 사전 진단을 위한 인자로써, 전하 전달 저항(Rct)을 배제하고, 와버그 임피던스(Zw)와 옴 저항(Rohm)만을 고려하여 분석하는 것이 타당하다.
5. 결론 및 향후 연구 계획
본 연구에서는 전기차 배터리의 고장을 사전에 진단하기 위해 고온 환경(60oC)에서 배터리 열화 실험을 수행하여 고장 상황을 모사하였다. 배터리 내부 상태의 전기화학적 거동을 진단할 수 있는 전기화학 임피던스 분광법 기반 등가회로 모델로 배터리의 내부 상태를 모사하여 모델 파라미터를 분석하였다. 고장과 모델 파라미터 사이의 관계성을 분석하기 위해 상온의 동일한 조건 하에서 열화 실험을 진행하였고, 고장이 발생하지 않은 상온 열화 데이터와 비교하였다. 결론적으로 세 가지 임피던스 파라미터 비교 분석을 통해 와버그 임피던스(Zw)가 고장 5단계 전에 가장 급격한 증가 경향을 보여주기 때문에 고장 진단 및 예측을 위한 주요 인자로 고려될 수 있다. 향후 실시간 진단을 위해 저주파수 영역에서 분석할 수 있는 와버그 임피던스(Zw)를 주요 파라미터로 사용하여 고장 사전 진단이 가능한 예측 모델을 개발하는 연구를 수행할 것이다.
Acknowledgments
이 연구는 충남대학교 학술연구비에 의해 지원되었음.
REFERENCES
- Ministry of Land, Infrastructure and Transport, “South Korea Has One Car per 2.1 People, Surpassing 24 Million Cars Registered in the First Half of this Year,” https://www.molit.go.kr/USR/viewer.do?mode=mb&type=NEWS&id=211158&num=1, (Accessed 27 SEPTEMBER 2021)
- Ministry of Land, Infrastructure and Transport, “Additional Voluntary Defect Correction (Recall) of 26,699 Vehicles including Hyundai and Kona (EV),” (Accessed 24 FEB 2021) https://www.molit.go.kr/USR/viewer.do?mode=mb&type=NEWS&id=218677&num=1, (Accessed 27 SEPTEMBER 2021)
-
Wang, L., Zhang, B., Hu, Y., Li, X., and Zhao, T., “Failure Analysis of LiNi0.83Co0.12Mn0.05O2/Graphite-SiOx Pouch Batteries Cycled at High Temperature,” Journal of Power Sources, Vol. 482, Paper No. 228978, 2021.
[https://doi.org/10.1016/j.jpowsour.2020.228978]

-
Abada, S., Marlair, G., Lecocq, A., Petit, M., Sauvant-Moynot, V., et al., “Safety Focused Modeling of Lithium-Ion Batteries: A Review,” Journal of Power Sources, Vol. 306, pp. 178-192, 2016.
[https://doi.org/10.1016/j.jpowsour.2015.11.100]

-
Liu, D., Zhou, J., Liao, H., Peng, Y., and Peng, X., “A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, Vol. 45, No. 6, pp. 915-928, 2015.
[https://doi.org/10.1109/TSMC.2015.2389757]

-
Song, Y., Peng, Y., and Liu, D., “Model-Based Health Diagnosis for Lithium-Ion Battery Pack in Space Applications,” IEEE Transactions on Industrial Electronics, Vol. 68, No. 12, pp. 12375-12384, 2020.
[https://doi.org/10.1109/TIE.2020.3045745]

-
Zhang, L., Peng, H., Ning, Z., Mu, Z., and Sun, C., “Comparative Research on RC Equivalent Circuit Models for Lithium-Ion Batteries of Electric Vehicles,” Applied Sciences, Vol. 7, No. 10, Paper No. 1002, 2017.
[https://doi.org/10.3390/app7101002]

-
Kampouris, D. K., Ji, X., Randviir, E. P., and Banks, C. E., “A New Approach for the Improved Interpretation of Capacitance Measurements for Materials Utilised in Energy Storage,” RSC Advances, Vol. 5, No. 17, pp. 12782-12791, 2015.
[https://doi.org/10.1039/C4RA17132B]

-
Osaka, T., Mukoyama, D., and Nara, H., “Development of Diagnostic Process for Commercially Available Batteries, Especially Lithium Ion Battery, by Electrochemical Impedance Spectroscopy,” Journal of the Electrochemical Society, Vol. 162, No. 14, Paper No. A2529, 2015.
[https://doi.org/10.1149/2.0141514jes]

-
Huang, Q. A., Shen, Y., Huang, Y., Zhang, L., and Zhang, J., “Impedance Characteristics and Diagnoses of Automotive Lithium-Ion Batteries at 7.5% to 93.0% State of Charge,” Electrochimica Acta, Vol. 219, pp. 751-765, 2016.
[https://doi.org/10.1016/j.electacta.2016.09.154]

-
Maheshwari, A., Heck, M., and Santarelli, M., “Cycle Aging Studies of Lithium Nickel Manganese Cobalt Oxide-Based Batteries Using Electrochemical Impedance Spectroscopy,” Electrochimica Acta, Vol. 273, pp. 335-348, 2018.
[https://doi.org/10.1016/j.electacta.2018.04.045]

-
Waag, W., Käbitz, S., and Sauer, D. U., “Experimental Investigation of the Lithium-Ion Battery Impedance Characteristic at Various Conditions and Aging States and Its Influence on the Application,” Applied Energy, Vol. 102, pp. 885-897, 2013.
[https://doi.org/10.1016/j.apenergy.2012.09.030]

-
Vetter, J., Novák, P., Wagner, M. R., Veit, C., Möller, K. C., et al., “Ageing Mechanisms in Lithium-Ion Batteries,” Journal of Power Sources, Vol. 147, Nos. 1-2, pp. 269-281, 2005.
[https://doi.org/10.1016/j.jpowsour.2005.01.006]

-
Pastor-Fernández, C., Uddin, K., Chouchelamane, G. H., Widanage, W. D., and Marco, J., “A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-Ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems,” Journal of Power Sources, Vol. 360, pp. 301-318, 2017.
[https://doi.org/10.1016/j.jpowsour.2017.03.042]

-
Xiong, R., Tian, J., Mu, H., and Wang, C., “A Systematic Model-Based Degradation Behavior Recognition and Health Monitoring Method for Lithium-Ion Batteries,” Applied Energy, Vol. 207, pp. 372-383, 2017.
[https://doi.org/10.1016/j.apenergy.2017.05.124]

-
Beelen, H., Raijmakers, L., Donkers, M., Notten, P., and Bergveld, H., “A Comparison and Accuracy Analysis of Impedance-Based Temperature Estimation Methods for Li-Ion Batteries,” Applied Energy, Vol. 175, pp. 128-140, 2016.
[https://doi.org/10.1016/j.apenergy.2016.04.103]

-
Mingant, R., Bernard, J., and Sauvant-Moynot, V., “Novel State-of-Health Diagnostic Method for Li-Ion Battery in Service,” Applied Energy, Vol. 183, pp. 390-398, 2016.
[https://doi.org/10.1016/j.apenergy.2016.08.118]

-
Westerhoff, U., Kurbach, K., Lienesch, F., and Kurrat, M., “Analysis of Lithium-Ion Battery Models based on Electrochemical Impedance Spectroscopy,” Energy Technology, Vol. 4, No. 12, pp. 1620-1630, 2016.
[https://doi.org/10.1002/ente.201600154]

-
Choi, W., Shin, H. C., Kim, J. M., Choi, J. Y., and Yoon, W. S., “Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-Ion Batteries,” Journal of Electrochemical Science and Technology, Vol. 11, No. 1, pp. 1-13, 2020.
[https://doi.org/10.33961/jecst.2019.00528]

-
Gagneur, L., Driemeyer-Franco, A. L., Forgez, C., and Friedrich, G., “Modeling of the Diffusion Phenomenon in a Lithium-Ion Cell Using Frequency or Time Domain Identification,” Microelectronics Reliability, Vol. 53, No. 6, pp. 784-796, 2013.
[https://doi.org/10.1016/j.microrel.2013.03.009]

-
Bard, A. J. and Faulkner, L. R., “Electrochemical Methods Fundamentals and Applications,” Surface Technology, Vol. 20, No. 1, pp. 91-92, 1983.
[https://doi.org/10.1016/0376-4583(83)90080-8]

-
Zhang, Q., Guo, Q., and White, R. E., “A New Kinetic Equation for Intercalation Electrodes,” Journal of the Electrochemical Society, Vol. 153, No. 2, Paper No. A301, 2005.
[https://doi.org/10.1149/1.2142287]

-
Zhu, J., Sun, Z., Wei, X., and Dai, H., “Studies on the Medium-Frequency Impedance Arc for Lithium-Ion Batteries considering Various Alternating Current Amplitudes,” Journal of Applied Electrochemistry, Vol. 46, No. 2, pp. 157-167, 2016.
[https://doi.org/10.1007/s10800-015-0887-z]

-
Cruz-Manzo, S. and Greenwood, P., “An Impedance Model based on a Transmission Line Circuit and a Frequency Dispersion Warburg Component for the Study of EIS in Li-Ion Batteries,” Journal of Electroanalytical Chemistry, Vol. 871, Paper No. 114305, 2020.
[https://doi.org/10.1016/j.jelechem.2020.114305]


M.Sc candidate in the Department of Electrical Engineering, Chungnam National University. Her research interest is battery management system and state control algorithm.
E-mail: yoy0307@naver.com

M.S. in the Department of Electrical Engineering, Chungnam National University. His research interest is battery management system and battery system design.
E-mail: dudrb2691@gmail.com

Ph.D candidate in the Department of Electrical Engineering, Chungnam National University. His research interest is battery management system and state control algorithm.
E-mail: pig25t@naver.com

Professor in the Department of Electrical Engineering, Chungnam National University. His research interest is battery management system, next generation battery, xEV retired battery, energy storage system, fault diagnosis, thermal management, artificial intelligence, power electronics circuits, and fuel cell system.
E-mail: whdgns0422@cnu.ac.kr