코리올리 유량계의 정밀설계를 위한 수치해석적 성능 예측

2.1 코리올리 유량계의 측정원리

Figs. 1(a)에서 직선 파이프 내를 일정한 속도로 움직이는 유체요소는 어떠한 가속도를 갖지 못하게 되는데, 이때 1(b)와 같이 파이프가 Ω의 각속도로 회전할 경우 식(1)과 같은 코리올리 가속도가 발생하게 된다. 이러한 코리올리 가속도는 본 연구에서 다루는 코리올리 유량계의 기본 원리가 된다.⁴

Fig. 1

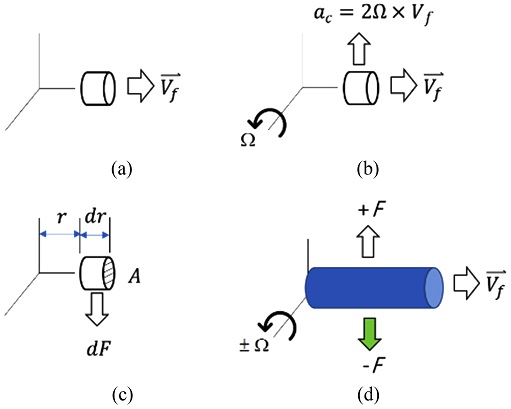
Coriolis mass flowmeter components of (a) Velocity, (b) Acceleration, (c) Elemental force, and (d) Vibration forces

Fig. 1(c)와 같이 미소 거리 dr에 해당되는 미소 질량 dm이 받는 코리올리 가속도에 의해 발생하는 파이프에 작용하는 힘은 뉴턴의 제2법칙에 의해 식(2)와 같이 표현된다.

식(2)에서 힘 dF의 방향은 Fig. 1(d)에서처럼 회전벡터 Ω와 유체요소의 속도벡터 V_f와 수직 방향이다. 따라서 파이프 전체 길이 l에서 발생하는 코리올리 가속도에 의한 총 힘은 식(3)과 같이 표현할 수 있다.

따라서 구하고자 하는 대상인 질량 유량 q_m은 식(4)와 같이 표현한다.

그러나 실제 코리올리 유량계에서는 파이프 튜브를 회전시킬 수 없으므로 Fig. 2와 같이 전자기 가진 코일(Electromagnetic Driving Coil)로 U자형 파이프 튜브 상단 중앙점을 1차 굽힘 주파수(Bending Frequency)로 가진하여 코리올리 가속도를 발생시키게 된다. 이러한 U자 형상의 유량계는 가장 일반적인 코리올리 유량계이며, L은 튜브의 Vertical 방향, d는 폭 방향 길이를 각각 의미한다. 유체요소의 유량에 따라 식(3)의 코리올리 힘이 작용할 경우 힘은 입구 튜브와 출구 튜브 위치에서 반대로 작용하게 되므로 유량계는 비틀림 진동 형태의 운동을 하게 된다. 따라서 이러한 비틀림 운동을 하는 코리올리 유량계는 식(5)와 같은 지배방정식으로 나타낼 수 있다.⁵

Fig. 2

Conventional coriolis mass flowmeter shape and components

식(1)부터 식(5)는 hing일반적으로 알려진 코리올리 가속도 원리와 U자형 코리올리 질량 유량계의 지배방정식이다. 이러한 유량계의 동적 특성을 좀더 정량적으로 파악하기 위해 조화해(Harmonic Solution) 가정을 하고, 식(5)를 다시 표현하면 다시 식(6)과 식(7)로 표현할 수 있다. 여기서 θ₀는 비틀림 최대 변위이고, T_o는 최대 비틀림 토크, Ω_f는 코리올리 힘을 발생시키기 위한 가진주파수로서 튜브의 1차 굽힘 주파수에 해당된다.

식(7)의 최대 토크 T_o는 식(2)의 단위 유체요소에 작용하는 코리올리 힘을 중심거리에 대해 식(8)과 같이 적분하여 구할 수 있다.

식(8)과 식(7)을 결합하면 식(9)와 같이 코리올리 유량계 동작 시의 최대 변위 θ₀를 구할 수 있다.

여기서 비틀림 변위 θ, 시간 τ 그리고 코리올리 가진주파수 Ω_f와의 관계는 식(10)과 같이 나타나며, 이로부터 식(11)과 같이 질량 유량을 도출하는 식을 구할 수 있다.

단순화를 위해 Fig. 2와 같은 U자형 튜브의 1차 비틀림 고유진동수 Ω_s는 식(13)과 같이 비틀림 강성과 질량 관성 모멘트로 표현할 수 있으며, 식(8)부터 식(12)까지 식을 조합하면 구하고자 하는 질량 유량 q_m은 식(13)과 같이 표현할 수 있다.

이론적으로 식(13)에서 Ω_f = Ω_s일 경우 즉, 코리올리 굽힘 가진주파수가 비틀림 주파수와 일치할 경우 실제 발생하는 경우는 없겠지만 질량 유량은 0의 값을 갖게 된다.

Fig. 2의 Inlet과 Outlet Pick-Up 위치에서의 시간위상차(Time Phase Difference) 값인 τ 관점에서 식(13)을 다시 표현하면 식(14)와 같이 표현된다. 이때 마찬가지로 Ω_f≈Ω_s일 경우에는 τ값을 최대로 할 수 있으므로 미소 질량 유량에도 양단 Pick-Up 위치에서의 시간위상차를 크게 함으로서 특히 저 유량에서의 성능 예측을 정교하게 할 수 있는 장점이 있다. 이러한 관점에서 식(14)에서의 시간위상차를 정확히 측정 혹은 예측하는 것은 식(11)에서의 질량 유량 q_m을 직접적으로 구하는 것이므로 매우 중요하다 할 수 있다.

3.1 모드해석법

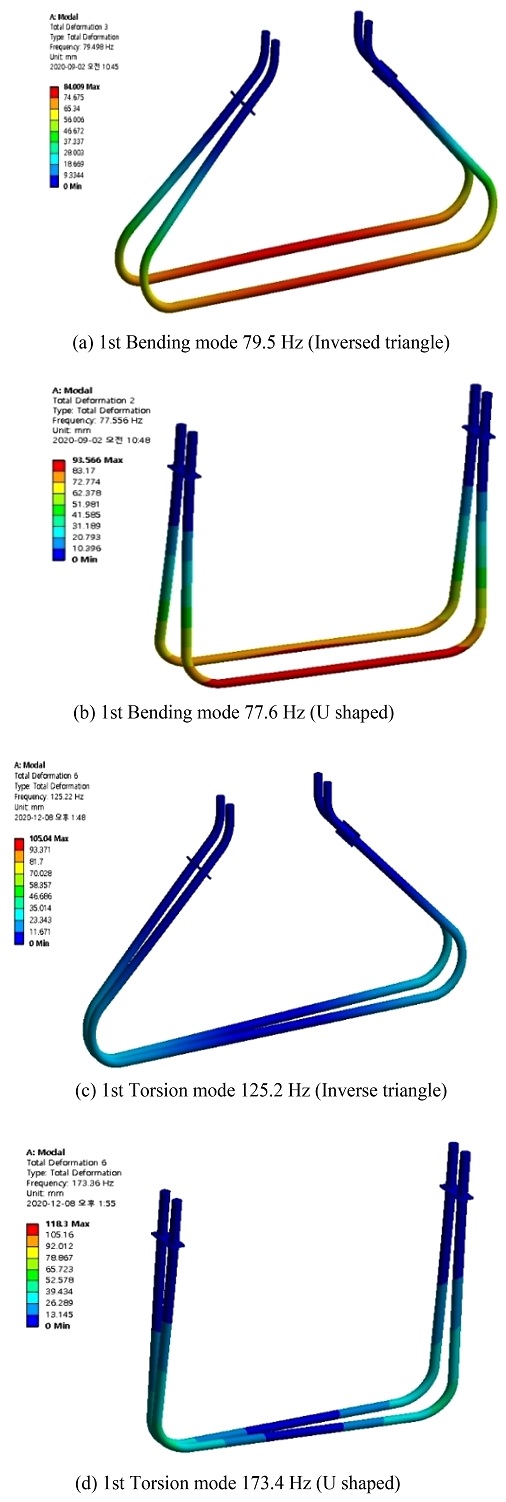
Figs. 3(a)와 3(b)는 각각 역삼각형(Inverse Triangle) 튜브와 U자형 튜브에 대한 1차 굽힘 고유진동수 및 모드 형상을 보여준다. 코리올리 힘을 효과적으로 발생시키기 위해서는 이러한 1차 굽힘 고유진동수 Ω_f에 근접해서 튜브 상단 중심점을 가진하는 것이 필요하다. Figs. 3(c)와 3(d)는 각각의 튜브 형상에 대한 비틀림 주파수와 모드 형상이며, 벤딩주파수 가진에 의해 발생하는 코리올리 힘에 의한 발생하는 비틀림 형상을 의미한다.⁶

Fig. 3

Mode shapes of each shape of CFM

식(14)에서 질량 유량 q_m과 τ는 직접적인 비례관계가 있으므로 동일 질량 유량에 U자형 튜브보다 더 큰 시간위상차 τ와 이를 통한 높은 분해능의 성능을 갖기 위해서는 비틀림 강성 k_s를 낮추는 것이 필요하므로 Fig. 4와 같은 역삼각형 튜브를 제안하였다. 본 연구에서는 이러한 역삼각형 구조와 기존의 일반적 구조인 U자형 튜브 형상에 대한 모드해석 및 고체-유체의 연성해석(Fluid Structure Interaction)⁵을 통해 코리올리 유량계의 핵심 성능인 위상시간 τ을 예측하였고, 실증 실험의 수행과 유량별 측정 결과와의 비교를 통해 본 연구에서 제안하는 코리올리 유량계의 성능 예측 방법에 대한 신뢰성을 확인하였다.

Fig. 4

Overall shape of inverse triangle CFM

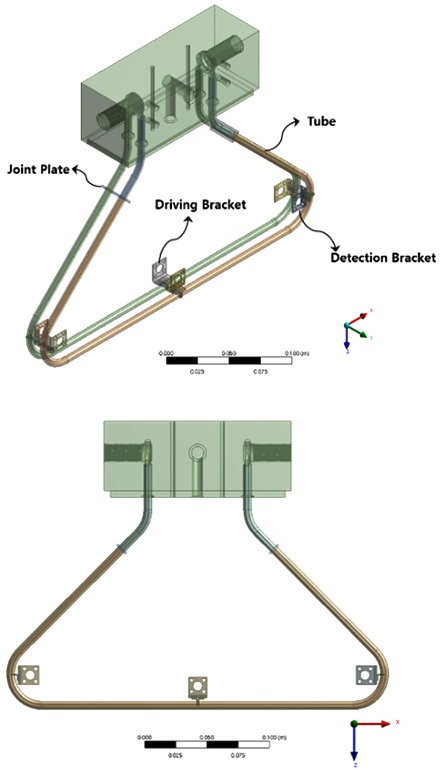
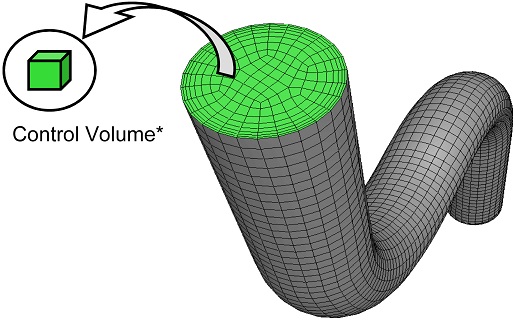
Tables 1과 2는 사용된 튜브의 재질과 주요 부품에 대한 질량 정보이다. Fig. 5는 전산모사해석을 위한 역삼각형 형상과 U자 형상 CFM 튜브의 유한요소 모델을 보여준다. 여기서 1차 벤딩 모드가 중요한 것은 코리올리 힘을 유발하는 가진 주파수가 1차 벤딩 주파수이기 때문이며 실제 임팩트 해머 가진을 통한 모드시험법(Modal Testing)으로 구한 고유 주파수와 두 모델 모두 2% 오차 이내에 있음을 확인하였다.

Table 1

Material properties of tube (SUS 316L) for numerical analysis

Table 2

Mass ratio of each components consisting inverse CFM

Fig. 5

Finite element model of CFM and correlation of modal results

Fig. 6

Finite control volume using fluid element

3.2 고체-유체 연성(FSI)해석

일정 검사 체적 내의 유체의 지배방정식은 식(15)와 같이 불안정항(Unsteady), 대류항(Convection)과 에너지 생성항(Energy Generation)으로 구성된다.

고체-유체 연성(Fluid-Structure Interaction)해석을 위해 튜브와 유체의 경계면에서 발생하는 변형을 해석상에 반영하며, 이때 대변형에도 Mesh Quality가 양호한 Diffusion Smoothing Method를 적용하였다. FLUENT상에서 확산계수(Diffusion Factor)는 1에서 2의 값이 적용되며 실제 변형이 크지 않은 점과 해의 수렴속도를 감안하여 1.0을 적용하였다.

Fig. 7은 FSI 해석을 위한 각 튜브 형상과 유체에 대한 유한요소 모델이다. 해석에 사용된 유체 모델은 물이며 밀도와 점도는 20^oC 기준 각각 998 kg/m³과 1.003 × 10^-3 Nm²/s이다. ANSYS 16.1을 사용하였으며 과도 구조해석(Transient Structural), 유체유동(Fluid Flow)과 시스템 연동(System Coupling) 모듈이 FSI 해석에 사용되었다. 코리올리 힘을 발생시키기 위해서는 Figs. 2에서의 가진 코일을 5에서와 같은 1차 굽힘 드로 가진하게 된다. 이때 발생된 유체의 코리올리 힘에 의해 비틀림 운동이 발생하게 되고, Fig. 2의 양쪽 Pick-Up에서 이로 인한 위상시간차가 발생하게 된다.

Fig. 7

Structure-Fluid interaction model for CFM

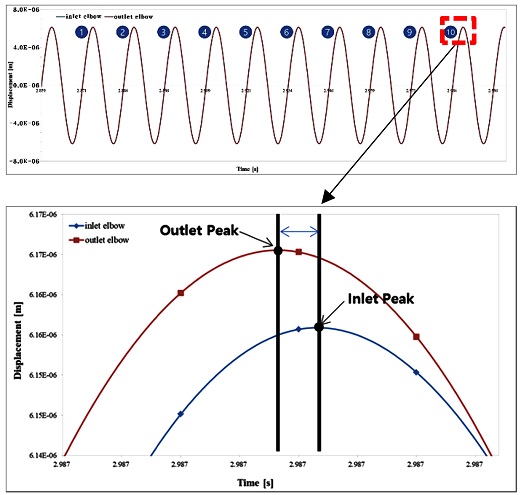
Figs. 8과 10은 FSI 수치해석을 통해 각각 역삼각형과 U자형 튜브의 양쪽 Pick-Up에서의 End Time까지의 과도-정상 변위 응답(Transient-Stationary Displacement Response)과 구하고자 하는 튜브 양단 Pick-Up 위치에서의 시간위상차를 보여준다. Table 3은 본 연구에서 다루는 코리올리 유량계 튜브의 수치해석을 위한 가진 조건이며, 시간 간격(Time Step)과 최종 시간(End Time) 조건은 결과의 충분한 수렴성을 반영하여 선정하였다.

Fig. 8

Time phase difference from FSI analysis for inversed triangle CFM

Table 3

Simulation condition of excitation for driving CFM

이러한 선행적인 수치해석을 하는 가장 큰 목적은 튜브 양단 Pick-Up 위치에서의 위상시간차를 구하는 것이며, 이를 통해 튜브 내를 흐르는 질량 유량을 비교적 정확히 예측하는 것이라고 할 수 있다. 따라서 Fig. 8과 같이 계산된 Pick-Up 양단에서의 과도-정상 상태의 시간응답차를 각 주기별로 계산하고, 이를 평균하여 실증 실험을 통해 구한 실제 질량 유량 측정 결과와 비교하였다. Table 4에서는 역삼각형 형상의 튜브에 대한 10 주기 이내에서의 튜브 양단 Pick-Up 위치에서의 시간위상차를 각 유량 예측 결과와 실증 유량 측정 결과와 비교하였다.

Table 4

Prediction of mass flow rate at each period (Inversed triangle)

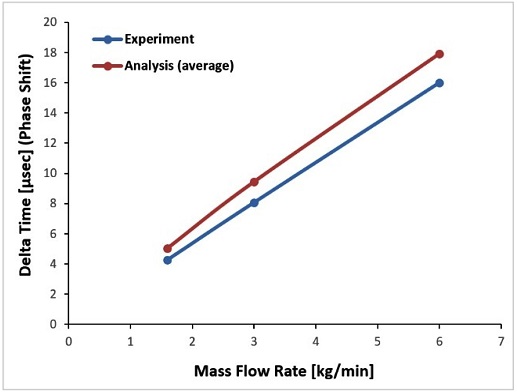
Fig. 9에서는 식(14)에서 언급한 역삼각형 튜브 양단에서의 시간위상차를 수치해석적인 방법과 실증 실험을 통해 구한 결과를 각 유량 조건별로 비교하였다. 튜브 내를 흐르는 질량 유량이 커질수록 동적인 비틀림 변형이 커지게 되며, 이로 인해 시간위상차가 커지는 경향을 보이게 되며, 비교 결과 약 12-17% 오차가 있음을 확인하였다.

Fig. 9

Comparison of mass flow rate for inverse triangle shaped CFM

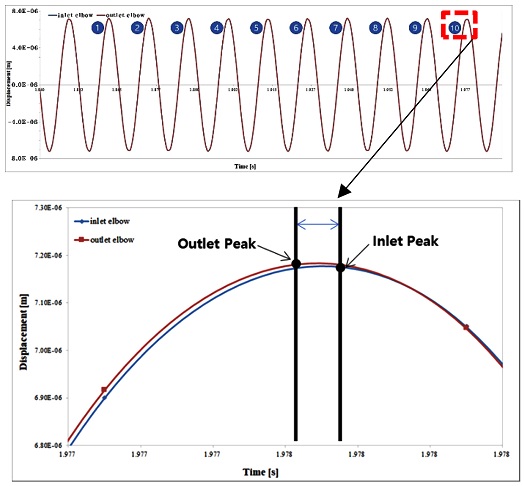
Fig. 10은 U자형 튜브에 대해 1차 굽힘 주파수로 가진하여 양단에서의 코리올리 힘을 발생시키고, 역시 이에 대한 양단 Pick-Up 위치에서 과도-정상 상태의 시간응답차를 수치해석적인 방법으로 예측한 결과이다. 앞서 역삼각형 형상의 튜브에서 위상시간차를 예측하고, 실증 실험 결과와 비교한 동일한 과정을 적용하여 Table 5에서도 각 유량별 조건에 대한 시간위상차를 수치해석적인 방법과 실증 실험 결과를 통해 구한 결과와 비교하였으며 오차는 약 2-14% 수준임을 확인하였다.

Fig. 10

Time phase difference from FSI analysis for U-Shaped CFM

Table 5

Prediction of mass flow rate at each period (U-Shaped)

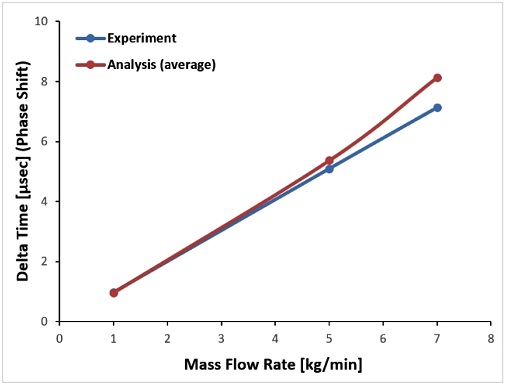
Fig. 11은 U자 형상의 튜브에 대해 수치해석적인 방법과 실증실험을 통해 구한 시간위상차와 질량 유량의 비교 결과치이다. 비교 결과 관심 대역인 저유량대에서는 실증 실험 결과와 수치해석적인 결과가 상당히 근접함을 알 수 있으며 실제 코리올리 유량계의 선형적인 특성을 활용하면 고유량 대역에서도 비교적 쉽게 구하고자 하는 질량 유량을 예측할 수 있을 것으로 판단된다.

Fig. 11

Comparison of mass flow rate for U-Shaped CFM

4.1 실험 Set-Up

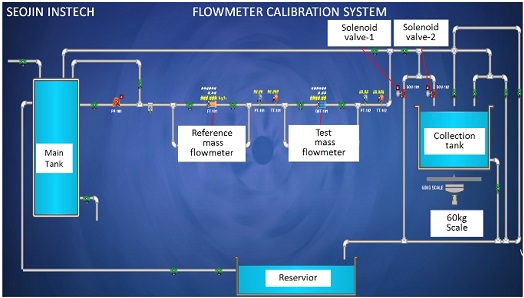
Fig. 12는 코리올리 유량계의 유량 측정을 위한 실험 Set-Up이다. 본 실증 실험을 통해 역삼각형 구조와 일반적인 U자형 튜브 형상의 CFM의 수치해석 모델을 통한 질량 유량 예측 결과의 신뢰성을 검증하였다.

Fig. 12

Experimental set-up for inverse triangle shaped CFM

질량 유량의 측정 범위는 1에서 10 kg/min이며, 측정된 질량 유량은 저수조에 담긴 질량을 전자 저울로 측정하였고, 식(14)에서의 튜브 양단에서의 시간위상차를 통해 구한 질량 유량과 실제 측정한 질량 유량과의 결과를 비교하였다. 실제 계측에 사용된 운영시스템은 Fig. 13과 같은 HMI (Human Machine Interface)로서 튜브 양단에서의 시간위상차와 이를 실제 질량 유량으로 변환하고, 기준 질량 유량과의 결과 차이를 비교할 수 있도록 시스템이 구성되어 있다. 기 언급한 바와 같이 시간위상차 τ와 질량 유량 q_m은 직접적인 비례 관계가 있으며, 이외 변수인 Ω_f, k_s, Ω_s 등은 유량계의 형상이 결정되면 상수로 작용하는 값이다. 따라서 특정 질량 유량에 대해 이러한 상수값을 Calibration하여 결정하면 이후로는 측정된 시간위상차 값을 구하고자 하는 질량 유량으로 바로 환산할 수 있게 된다.

Fig. 13

HMI for signal processing and control set-up

Fig. 12에서는 본 연구에서 Test하려는 개발품과 해외 선진사 제품의 유량을 동시에 비교하였고, 또한 실제 전자 저울이 설치된 간이 저수조 위에서 정해진 시간 동안 질량을 측정하면서 이를 질량 유량의 기준값으로 설정하였다. Fig. 13은 자체 개발한 HMI S/W이다.

4.2 실험 계측 로직

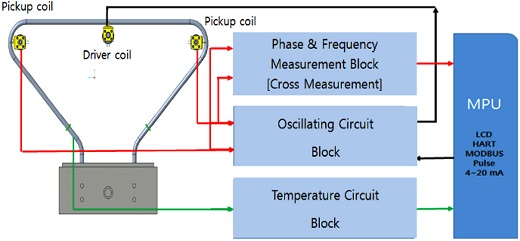
질량 유량 측정을 위한 전체적인 계측 로직은 Fig. 14에 나타낸다. 튜브 양단에서 측정된 두 Pick-Up 신호가 Oscillating Circuit Block에서 신호를 받게 되며 이러한 신호는 두 신호의 교차 신호 분석을 통해 주파수와 위상 시간을 분석하게 된다. 이러한 분석 결과는 MPU (Main Processing Unit)으로 전달되어 측정 대상인 Pick-Up 양단에서의 시간위상차(τ: ΔT)로 질량 유량을 계측하게 되며, 동시에 튜브의 중심에 있는 가진 신호를 Feedback하여 Driving Coil로 전달하게 된다. 이러한 과정을 반복하여 각 유량별 조건에서의 질량 유량을 측정하게 된다.⁷ 일반적으로 측정하고자 하는 시간위상차는 매우 작은 값이며, 아울러 이러한 매우 작은 시간위상차를 정확히 계측하기 위해서는 매우 높은 신호 분해능을 다룰 수 있는 하드웨어가 필요하거나 혹은 동일한 질량 유량 조건에서 최대한 시간위상차를 확보할 수 있는 튜브 형상 설계가 필요하다.⁸

Fig. 14

Block diagram for measuring time phase difference at the pick-up

계측 로직 관점에서 본 연구에서 제안하는 Cross Measurement Method 방법을 활용하면 시간축을 기준으로 상하 일정 높이에 교차된 양단에서 Pick-Up된 시간 길이(Time Length)와 이를 통해 시간위상차(τ: △T)를 비교적 정확하게 측정할 수 있으며, 유량의 정/역방향을 동시에 알 수 있는 장점이 있다.