광변조 기술을 이용한 정밀 형상 측정 센서의 최신 동향
1한국표준과학연구원 물리표준본부2과학기술연합대학원대학교 측정과학전공
2Department of Science of Measurement, University of Science & Technology
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Optical dimensional metrology has playing a long-term key role from high-precision engineering to large-scale industrial manufacturing. Various methods of optical dimensional metrology have been proposed and demonstrated to respond to the ever-growing industrial demands as well as fundamental science demands for the measurement precision and range. However, most of them demonstrated under laboratory conditions have a long way to go outside the laboratory. Here, we present a progress review on optical modulation technique-based dimensional metrology, which has already been used in real applications and has been commercialized. Amplitude modulation (AM) and frequency modulation (FM) based dimensional measurement techniques are described with their operating principles, and recent progresses and applications in 3D imaging are presented in this review.
Keywords:
Optical modulation, Amplitude modulation, Frequency modulation, Length measurement, Distance measurement, 3D imaging키워드:
광 변조, 진폭 변조, 주파수 변조, 길이 측정, 거리 측정, 3차원 이미징1. 서론
길이의 SI(국제단위계) 단위인 ‘미터(Meter)’는 기본 물리 상수 중 하나인 ‘빛의 속도’를 이용해 빛이 진공에서 1/299 792 458초 동안 진행한 경로의 길이로 정의한다. 이러한 빛의 속도에 근거한 미터의 정의에 따라, 빛이 진행한 시간을 측정하면 빛이 진행한 길이를 결정할 수 있다. 빛이 공기 중에서 진행한 시간을 ‘td’라고 할 때, 빛이 진행한 길이 ‘L’은 간단히 식(1)로 표현 가능하다.
| L=td×C0nair | (1) |
여기서, ‘c0’는 진공에서의 빛의 속도이며, ‘nair’은 공기 굴절률이다. 공기 굴절률은 진공 상태에서도 큰 차이가 없기 때문에 나노미터 수준의 매우 정밀한 측정이 아닌 경우에는 일반적으로 1로 가정하여 사용한다.
빛이 진행한 시간(td)은 다양한 방식으로 측정할 수 있다. 그 중에서 매우 정밀하게 빛이 진행한 시간을 측정하는 방법 중 대표적으로 레이저 간섭계(Laser Interferometer)를 들 수 있다. 레이저 간섭계는 잘 정의된 파장의 빛이 기준 경로와 측정 경로를 진행한 뒤 생성된 간섭 신호를 통해 기준 경로와 측정 경로에 의한 위상 지연을 측정하는 방법으로 나노미터 수준의 높은 길이 측정 정밀도를 구현할 수 있다. 하지만 조화파 형태의 간섭 신호 위상은 두 경로 사이의 광경로차가 파장의 배수가 될 때마다 위상이 반복되는 위상 모호성 문제가 발생한다. 예를 들면, 600 nm의 파장을 갖는 레이저 간섭계에서는 광 경로차가 파장의 배수인 600, 1,200, 1800 nm 등등인 경우 간섭 신호가 동일한 위상 정보를 갖기 때문에 같은 간섭 신호를 얻게 된다. 이와 같은 제약으로 인해 레이저 변위 간섭계는 위상 모호성이 생기지 않는 작은 변위들의 측정을 통해 연속적으로 간섭 신호의 위상 정보를 누적하여 길이 정보를 획득해야 한다. 따라서 긴 거리 측정, 고속 측정, 환경 변화가 커서 측정 중 간섭 신호를 잃을 수 있는 조건에서의 측정 등에 쉽게 활용하기에는 현실적으로 어려움이 많다.1,2 이와 같은 문제를 극복하기 위해 최근 새롭게 각광받는 주파수 안정화된 광 빗(Optical Comb)을 이용한 절대 거리 측정법도 다양하게 제안되어 왔지만, 주파수 안정화를 위한 설비의 복잡함과 운용 및 엄격한 환경 제어의 어려움으로 인해 실험실 단위에서 극히 제한적으로 구현되고 있다.3-7
빛이 진행한 시간을 측정할 수 있는 또 다른 방법 중 간단한 구성으로 인해 널리 사용되는 방법이 비행시간법(Time-of-Flight)이다. 이는 빛이 진행한 시간을 직접 측정하기 때문에 레이저 간섭계에서 발생하는 위상 모호성 문제없이 간단하게 긴 길이도 측정할 수 있다. 예를 들면 빛이 진행한 시간이 1 μs일 때, 식(1)에 의해 빛이 진행한 길이는 약 300 m가 된다. 하지만, 아무리 고성능의 시간 검출 회로를 사용하더라도 시간 측정 분해능이 수 ps 수준이기 때문에 길이 측정 정밀도 및 측정 가능한 최소 길이가 수 mm에 불과하다. 예를 들어, 1 mm 수준의 길이에서는 빛이 진행한 시간 자체가 약 3.3 ps로 매우 짧아 시간 검출 회로의 측정 분해능보다 짧기 때문에 일반적인 시간 검출 회로로는 측정 자체가 불가능할 수 있다. 이와 같은 기술적 한계로 비행시간법은 정밀공학분야보다는 수십만 km 수준의 초장거리 측정이 요구되는 우주 분야에서만 아주 제한적으로 사용되고 있다.8,9
본 리뷰 논문에서는 정밀공학분야 대형 산업인 조선, 항공, 자동차 등에서 주로 요구되는 미터 영역의 길이에서 마이크로미터 내외의 정밀도를 구현할 수 있는 길이 측정 방법 중 비교적 간단한 구성으로 안정적으로 사용할 수 있는 광 변조 기반길이 측정 방법의 원리 및 최신 연구 동향에 대해 소개하고자 한다. 광 변조 기반의 길이 측정 방법은 변조 대상에 따라 크게 진폭 변조 방식과 주파수 변조 방식으로 나눌 수 있다. 본 논문의 2장에서는 각 방식에 대한 기본 동작 이론 설명을 다루고, 3장과 4장에서는 각각 진폭 변조 방식과 주파수 변조 방식 기반의 1차원 길이 측정 및 3차원 형상 측정에 대한 최신 연구 동향을 소개하고자 한다.
2. 광 변조 기반 길이 측정
정밀공학분야의 대형 산업계에서 요구되는 측정 영역과 정밀도를 만족하는 길이 측정 기술 중 가장 널리 사용되는 기술은 광변조 기반 측정법이다. 광 변조 기반 길이 측정은 우리가 일상생활에서 많이 접하고 있는 라디오 전송 기법과 같이 크게 진폭변조(Amplitude Modulation) 기법과 주파수 변조(Frequency Modulation) 기법으로 나뉜다. 광 변조 기반 길이 측정은 빛이 진행한 시간 ‘td’를 간접적으로 측정하지만, 서론에서 소개한 단순 비행시간법 방식보다 높은 측정 정밀도를 보여준다.
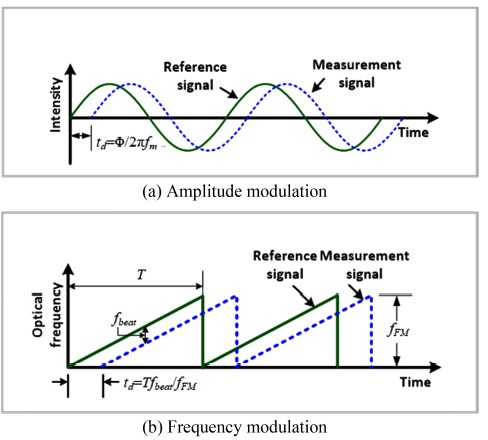
진폭 변조 기반 길이 측정은 Fig. 1(a)에 표현한 바와 같이 시간 축에서 일정한 진폭 변조 주파수(fm)를 갖는 정현파를 생성하여 기준 위치와 측정 위치에서부터 돌아온 정현파 간의 위상 지연(Φ)을 측정하여 빛이 진행한 시간 ‘td’를 구하게 된다. 정현파의 공기 중 파장(Λair = c0/nairfm)을 이용하여 길이 ‘L’을 수식으로 표현하면 식(2)와 같다.
| L=Λair×ϕ2π | (2) |
식(1)과 식(2)는 같은 길이를 표현한 식이므로 앞서 정의한 빛이 진행한 시간 ‘td’는 정현파의 위상 지연과 식(3)과 같은 관계를 갖는다.
| td=ϕ2π⋅fm | (3) |
진폭 변조 기반 길이 측정에서 빛이 진행한 시간의 측정 정밀도는 위상 측정 정밀도에 비례하고, 변조 주파수에 반비례하게 된다. 일반적으로 널리 활용되는 변조 주파수 대역에서 정현파의 위상 지연은 0.1o (또는 1.7 mrad) 이하의 정밀도로 측정이 가능하다. 위상 측정기가 동작하는 범위에서 정현파의 위상 지연의 측정 정밀도는 변조 주파수와 상관없이 일정한 값을 갖기 때문에, 빛이 진행한 시간의 측정 정밀도를 향상시키기 위해서는 높은 변조 주파수를 사용하여 정현파의 파장(Λair)을 짧게 만들어야 한다.10-13 하지만, 높은 변조 주파수에 상응하는 짧은 정현파 파장으로 위상 모호성 없이 측정 가능한 영역 역시 짧아지는 단점이 있으므로, 활용하고자 하는 응용분야에 따라 요구되는 측정 영역 및 정밀도를 고려하여 변조 주파수를 적절히 설정하여야 한다.
한편 주파수 변조 기반 길이 측정은 Fig. 1(b)에 표현한 바와 같이 시간 축에서 레이저 주파수가 일정한 주기 ‘T’ 동안 주파수 변조량 ‘fFM’만큼 선형적으로 변조되는 레이저를 사용한다. 기준 위치와 측정 위치에서부터 되돌아온 레이저는 빛이 진행한 시간만큼 서로 다른 시간 지연 ‘td’를 겪기 때문에 서로 다른 량의 주파수 변조를 겪음으로써 주파수 변조 차이 ‘fbeat’가 결정된다. 이와 같은 ‘fbeat’는 레이저가 측정 위치까지 진행한 경로로 인해 발생한 시간 지연 ‘td’과 단위 시간당 주파수 변조량 ‘fFM/T’의 곱으로 식(4)와 같이 표현할 수 있다.
| fbeat=td×fFMT | (4) |
여기서, ‘fbeat’는 기준 위치와 측정 위치에서부터 되돌아온 빛의 간섭으로 생기는 맥놀이 주파수를 통해 간단히 측정할 수 있고, 식(2)와 식(4)를 사용하여 측정하고자 하는 길이 ‘L’을 식(5)와 같이 결정할 수 있다.
| L=td×c0nair=T⋅fbeatfFM×c0nair | (5) |
주파수 변조 기반 길이 측정에서 최대 측정 영역은 주파수 변조 주기인 ‘T’에 의해 결정되며, 길이 측정 정밀도는 단위 시간당 주파수 변조량 ‘fFM/T’에 반비례하고 맥놀이 주파수 측정 정밀도에 비례한다. 따라서, 측정하고자 하는 용도와 목적에 맞도록 최대 측정 영역과 측정 정밀도를 고려하여 주파수 변조량(fFM)과 주파수 변조 주기(T)를 적절히 설정해야 한다. 또한, 주파수 변조 기반 길이 측정에서 레이저 주파수가 시간에 따라 선형적으로 변조되고 있다는 가정이 만족하도록 이를 정확히 구현하고 검증하는 것이 측정 정밀도 향상에 매우 중요하다.14-16
3. 진폭 변조 기반 길이 측정 동향
3.1 진폭 변조 기반 초정밀 절대 길이 측정
2장에서 소개한 진폭 변조 기반 길이 측정의 기본 이론에 따르면, 높은 정밀도를 얻기 위해서는 높은 변조 주파수를 사용해야 하며, 이 경우 위상 모호성 없이 측정 가능한 영역(Non-Ambiguity Range)이 변조 주파수에 반비례하여 작아진다. 일반적으로 빛이 왕복한 경로를 측정하여 길이를 구하기 때문에 대기 중 파장의 절반에 해당하는 길이가 위상 모호성 없이 측정가능한 영역이 된다. 높은 변조 주파수를 사용하여 높은 거리측정 정밀도를 얻으면서 동시에 긴 거리를 측정하기 위해서는 변조 주파수에 변화를 주어 정밀도는 낮더라도 대략적인 길이를 측정하여 위상 모호성 문제를 해결하는 방법이 널리 활용된다.17 즉, 변조 주파수를 Δfm만큼 변화를 주게 되면, 이에 상응하는 추가적인 파장(Λcoarse = c0/nairΔfm)을 생성할 수 있다. 이와 같이 추가적으로 생성된 파장은 변조 주파수( fm) 자체에 비해 상대적으로 훨씬 작은 변조 주파수 변화량(Δfm)에 의해 생성되기 때문에 위상 모호성 없이 측정 가능한 길이가 아주 큰 값을 갖는다. 이를 활용하여 식(6)과 같이 대략적인 길이(Lcoarse)을 측정하여 일반적인 진폭 변조 기반 길이 측정에서 생기는 위상 모호성 문제를 해결할 수 있다.
| (6) |
예를 들면, 변조 주파수가 3 GHz인 진폭 변조 기반 길이 측정 기술은 위상 모호성 없이 측정할 수 있는 최대 측정 영역이 0.1 m에 불과하지만, 0.1o의 위상 검출 분해능을 갖는 위상 측정기를 활용하면 약 30 μm의 높은 측정 정밀도를 얻을 수 있다. 위상 모호성 없이 측정할 수 있는 최대 측정 영역인 0.1 m 이상의 길이를 측정하기 위해 변조 주파수를 3에서 3.001 GHz로 1 MHz 만큼 변화를 주면서 위상 변화량을 측정하면, 변조 주파수 변화량에 의해 생성되는 파장은 300 m에 이르며, 그 파장 이내에서는 위상 모호성 없이 식(6)에 의해 대략적인 길이를 결정할 수 있다. 물론 300 m 파장으로 측정한 길이의 측정 불확도는 최소한 3 GHz의 변조 주파수로 생성된 파장인 0.1 m를 구별할 수 있어야 한다.
최근에는 진폭 변조 기반 길이 측정에서 더 높은 정밀도를 얻기 위해 10 GHz 이상의 고주파수 대역의 마이크로파를 사용하고 있다. 이런 고주파수 대역의 마이크로파는 너무 빠르기 때문에 위상 지연을 정밀하게 측정하기에 실제로 많은 어려움이 있다. 이를 극복하기 위해 전자적으로 슈퍼헤테로다인 검출기법(Super-Heterodyne Detection Method)을 통해 GHz 대역의 높은 주파수를 정밀한 위상 측정이 보다 용이한 kHz 혹은 MHz 대역으로 낮춰 위상 지연을 측정한다.10-13 하지만 이러한 다양한 주파수 대역의 신호를 처리하는 아날로그 전자 회로들은 입력신호의 세기와 동작 온도 등에 따라 잡음, 비선형성과 같은 다양한 오차가 발생하는 문제점이 보고되었다.18,19
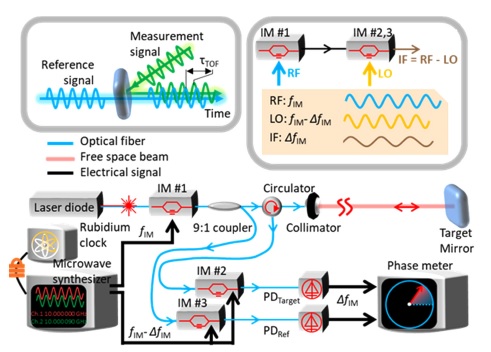
2021년 본 연구팀은 앞서 언급한 전자적인 주파수 낮춤 방식의 단점을 극복하기 위해 광학적 방식 기반의 진폭 변조 기반 길이 측정 기술을 제안하고 구현하였다.20 Fig. 2와 같이 15 GHz의 변조 주파수를 광학적 방법으로 90 kHz로 낮추어 상용 위상 측정기를 통해 진폭 변조된 신호의 위상 지연 값을 측정하였다. 특히, 기존 진폭 변조 기반 길이 측정에서 문제가 되었던 입력 신호의 세기 변화에 따른 위상 왜곡 현상이 크게 개선되었고, 이는 20 dB 이상의 입력 신호의 세기 변화에 따른 위상 왜곡 또는 지연 실험 결과로 충분히 입증되었다. 또한, 측정정밀도 측면에서도 한 점에서 100 nm 미만으로 평가되었고, 이는 현재까지 보고된 진폭 변조 기반 길이 측정 기술 중 가장 정밀한 결과이다. 이 연구에서 주목할 만한 부분은 실리콘 포토닉스 기반 단일 회로에 집적 및 구현할 수 있는 광학 소자들만으로 설계하고 구현하였다는 점이다. 이를 통해 향후 초소형 초정밀 라이다 시스템으로 활용할 수 있을 것으로 기대한다. 최근, 이와 유사하게 CMOS 공정을 통해 집적 회로 형태로 구현된 진폭 변조 기반 길이 측정 시스템이 제안되고 구현되었으며, 이시스템의 성능으로 9 μm의 측정 정밀도와 초당 5백만개의 데이터를 획득할 수 있는 연구 결과가 보고되었다.21
3.2 진폭 변조 기반 3차원 이미징 기술 동향
진폭 변조 기반 길이 측정 연구는 3차원 이미징 분야에서도 활용되고 있다. 레이저를 공간상에 주사하여 여러 점의 길이를 측정하는 종래의 방법은 3차원 이미징을 위해 데이터 획득 시간이 많이 소요되기 때문에 여러 점의 길이를 동시에 측정하기 위한 카메라 센서를 이용한 연구가 활발히 진행되고 있다.22-24 3차원 이미징의 수평 분해능은 피측정물에 맺히는 레이저의 공간상 크기와 카메라 센서의 픽셀 개수에 의해 결정된다. 3.1절의 일차원 길이 측정과는 달리 3차원 공간상에서 변조 주파수를 복조하는 소자와 카메라 센서의 속도 한계로 인해 광원의 주파수 변조는 100 MHz 내외로 제한되고 있다. 이로 인해 수직 분해능은 저하되지만, 넓은 영역에서 한 번의 측정으로 3차원 형상을 획득할 수 있는 3차원 이미징 카메라는 측정 속도 및 효율성에서 장점을 갖는다. 최근 3차원 이미징 카메라 연구는 수평 분해능을 향상하여 Full-HD급 3차원 영상을 얻거나, 카메라 센서의 최적화를 통해 고속으로 대면적 측정이 가능하도록 발전해오고 있다.
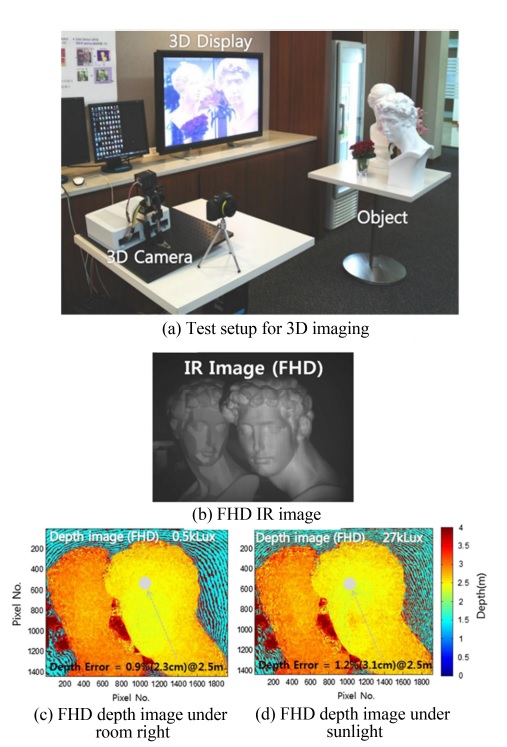
Fig. 3은 진폭 변조 기반 3차원 이미징 연구의 한 사례이다. 20 MHz로 진폭 변조된 레이저를 공간상으로 보내 되돌아온 빛을 광학 셔터(Shutter)로 복조한 뒤 흑백 Full-HD 카메라로 이미징을 하여, 카메라의 각 픽셀에서 특정 위치에 대한 깊이 정보를 획득함으로써 3차원 형상 정보를 복원하게 된다. 이와 함께 컬러 카메라로 얻어진 이차원 이미지와 결합하여 실제 색상 정보가 입혀진 3차원 형상 이미지도 얻을 수 있다. Fig. 3과 같이 3차원 이미징 카메라를 통해 2.5 m 떨어진 물체에 대해 수 cm의 깊이 오차를 갖는 Full-HD급 3차원 이미징을 구현한 연구결과가 보고되었다.23
4. 주파수 변조 기반 길이 측정 동향
4.1 주파수 변조 기반 초정밀 절대 길이 측정
주파수 변조 기반 길이 측정은 주기적으로 레이저의 주파수를 선형으로 변화시키면서 기준광과 측정광 사이의 간섭에 의한 맥놀이 주파수(Beat Frequency)를 측정함으로써 이루어진다.14 주파수 변조 기반 길이 측정은 단순한 구성, 비접촉 측정, 직관적인 동작 원리, 절대 길이 측정과 같은 장점에도 불구하고, 마이크로미터 내외로 측정 정밀도의 한계를 갖고 있다. 2장의 주파수 변조 기반 길이 측정 원리에 따르면, 측정 정밀도는 주파수 변조 선형성(Linearity), 주파수 변조폭(Bandwidth), 주파수 변조속도(Sweep Speed) 등에 의해 결정된다. 그 중에서도 측정 정밀도에 가장 큰 영향을 주는 요소는 주파수 변조 선형성이다. 이상적인 실험 조건에서는 주파수 가변 광원에서 발진하는 빛의 주파수가 동일한 시간 간격에서 일정한 비율로 증가 또는 감소하여야 한다. 하지만, 일반적인 주파수 가변 광원의 경우 주파수 변조를 위한 기계적인 구조 및 구동기의 특성에 따라 변조 함수의 형태, 범위, 속도 등이 달라짐으로 인해 크고 작은 비선형성이 발생하게 된다. 또한, 다이오드 레이저에 인가되는 전류와 발진하는 빛의 파장 사이의 비선형성과 증폭 매질의 온도에 따른 영향 등의 요인으로 인해서도 비선형성이 발생한다.
이와 같은 광원의 주파수 변조 비선형성을 극복하기 위해 2013년 미국 국립표준기술연구소(National Institute of Sciences and Technology, NIST)에서는 펨토초 레이저의 광 빗을 이용하여, 광 빗 기반 주파수 변조 연속 라이다를 제안하였다.15,25 측정 분해능 향상을 위해 주파수 변조 폭이 1 THz 수준으로 매우 넓은 미세전자기계시스템(Microelectromchanical System)으로 제작된 외부 공진기 형태의 주파수 변조 광원을 활용하였다. 이 광원에서 발진하는 주파수 변조 비선형성을 교정하기 위해 200 MHz의 반복률을 갖는 광 빗을 이용하여 약 1016 Hz/s 속도로 주파수 변조 광원의 주파수를 측정하였다. 이 연구에서는 주파수 기준점에 안정화하지 않고, 자유 발진하는 광 빗을 사용했기 때문에 안정화를 위한 비대한 설비와 운용의 어려움 없이 비교적 간단한 형태의 광 빗 기반 주파수 변조 라이다 시스템을 구현하였다. 또한, 높은 측정 정밀도를 구현하기 위해서는 넓은 주파수 변조 광원이 필요하고, 넓은 주파수 대역에서 주파수 변조 비선형성을 교정하기 위해서는 주파수 대역폭이나 안정도 측면에서 광 빗이 매우 유용하다.
Fig. 4는 광 빗 기반 주파수 변조 절대 길이 측정을 위한 라이다 시스템의 구성도를 나타낸다. 외부 공진기 형태의 주파수 변조 광원(External Cavity Diode Laser, ECDL)에서 발진한 빛은 일부가 주파수 변조 비선형성 교정을 위해 광 빗으로 전달되고, 대부분의 빛은 기준 경로(Reference)와 측정 경로로 진행한다. 측정 길이에 따라 기준 경로와 측정 경로의 맥놀이 주파수는 달라지며, 이는 균형 광 검출기(Balanced Detector, BD)에 의해 획득된다. 유리 쐐기(Glass Wedge)로 구성된 약 1 m의 시험 경로 길이를 상대 변위 레이저 간섭계와 비교 측정함으로써 길이 측정 정확도를 검증하였다. 특히, 측정물이 이동하고 있는 경우에는 상대 속도에 의해 도플러 주파수 천이(Doppler Frequency Shift)가 발생하여 맥놀이 주파수에 영향을 줄 수 있으며, 이는 주파수 변조 속도를 높임으로써 최소화할 수 있다. 이를 통해 100 ppb 이하의 측정 정확도와 정밀도를 달성하였다고 보고되었다.
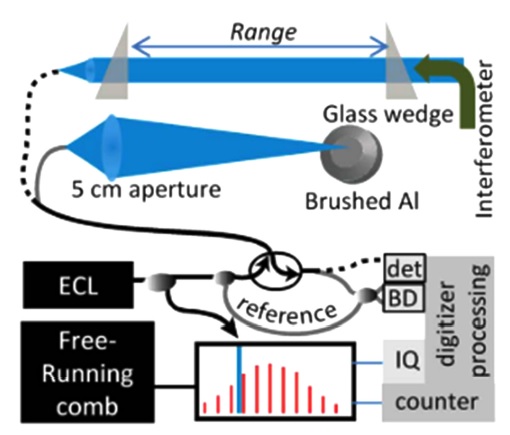
Optical layout of free-running frequency comb calibrated FMCW15 (Adapted from Ref. 15 with permission)
이와 유사하게 주파수 변조 비선형성을 줄이기 위해 마이크로콤(Microcomb)을 이용한 연구가 2021년 텐진대학교와 중국과학원에 의해 수행되었다.26 이 연구는 측정을 위해 변조된 주파수가 광 빗 주파수 모드들과 간섭하여 잘 정의된 첨두 신호를 광 빗의 반복률 간격으로 발생시켜 주파수 교정에 보조적인 수단으로 활용하는 방법이다. 본 연구에서 사용한 마이크로콤은 48.97 GHz의 높은 반복률을 갖고 있어 일반적으로 100 MHz의 반복률을 갖는 광섬유 광 빗보다 적은 수의 간섭 신호를 생성하게 되므로, 넓은 주파수 변조 영역에서도 비교적 적은 수의 첨두 신호를 교정에 활용할 수 있어 빠른 측정이 가능하다는 장점이 있다. 이 연구에서는 2 m의 길이에서 20 μm 이하의 측정 오차가 보고되었다.
앞선 두 연구와 같이 최근 주파수 변조 기반 절대 길이 측정에서는 측정 정밀도 향상을 위해 광 빗에 근거하여 주파수 변조비선형성을 최소화하려는 노력들이 이루어지고 있다. 또한, 4.2절에서 소개하려는 바와 같이 1차원 길이 측정에서 3차원 형상 측정으로 공간적인 차원을 확장하려는 연구도 진행되고 있다.
4.2 주파수 변조 기반 3차원 이미징 기술 동향
주파수 변조 기반 길이 측정은 고민감도, 고분해능, 넓은 다이내믹 레인지(Large Dynamic Range) 등의 장점으로 인해 다양한 반사율을 갖는 원거리 물체의 형상 측정을 위한 3차원 이미징에도 적용되어 왔다.25,27-32 앞서 2장에서 언급한 바와 같이 주파수 변조 기반 길이 측정은 완벽히 선형적인 주파수 변조에 따라 나타나는 기준 위치와 측정 위치 사이의 거리 차에 비례하는 광 주파수 차이를 이용하기 때문에, 거리 측정 정밀도가 주파수 변조 선형성과 직결된다.
2014년 NIST에서는 주파수 변조 비선형성을 보정하기 위해 반복률이 207 MHz인 광 빗을 사용하였으며, Fig. 5(a)와 같이 고속 주사 거울(Fast Steering Mirror)을 통해 원거리에 있는 다양한 물체의 표면 형상을 10 μm 이하의 정밀도로 측정하였다.25 이와 같이 미터 영역에서 밀리미터 이하 정밀도를 가지는 주파수 변조 LADAR (Laser Detection and Ranging)기술은 화재와 같은 극한 환경 하에서도 구조물 변형을 실시간으로 원격 모니터링하는데 적용될 수 있다.27 Fig. 5(b)는 메탄 화염 뒤 2 m 떨어진 위치에 있는 플라스틱 해골의 형상을 측정한 결과이며, 화염을 투과하면서 생긴 빔 편향, 굴절률 변화로 인한 옵셋, 난류 영향에도 불구하고 30 μm 이하의 정밀도 달성이 가능하다고 보고되었다.
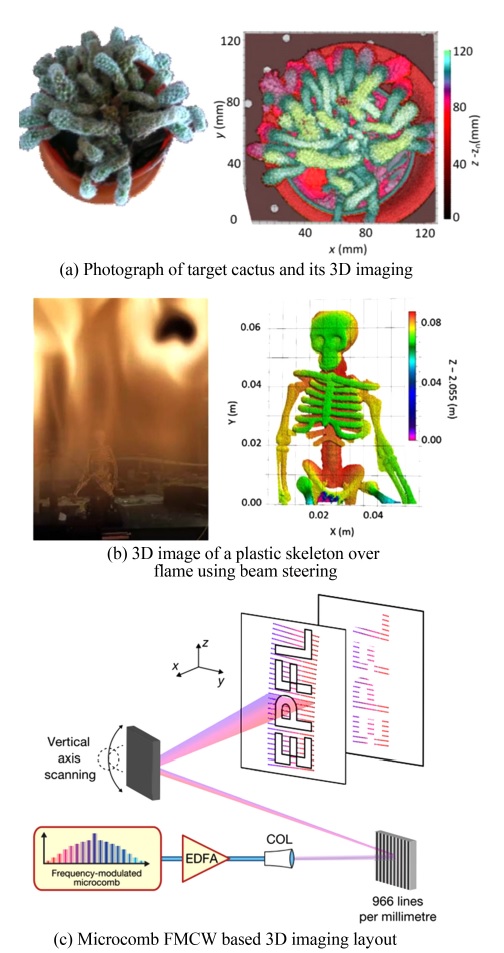
Recent studies on FMCW ladar25,27,31 (Adapted from Refs. 25 on the basis of OA and 27 and 31 with permission)
한편, 앞선 연구들과 달리 3차원 이미징을 위한 기계적인 빔주사 방식을 사용하지 않고, 간단한 시스템 구성을 위해 분산매질(Dispersive Material)을 이용한 비기계적인 주사 방식을 적용한 연구가 수행된 바 있다.30 이 연구에서는 공간적으로 빛을 주사하기 위해 회절 격자가 사용되었으며, 회전 거울을 이용한 1차원 주사 방식과 결합하여 0.5 m 떨어진 위치의 물체의 3차원 형상을 100 Hz의 속도로 측정 가능함을 보였다.
4.1절에서 소개한 앞선 연구에서는 광 빗이 주파수 변조 선형성 보정을 위한 기준 주파수들로서 사용된 반면, 광 빗 자체가 주파수 변조 기반 길이 측정 기술의 광원으로 사용된 연구가 있다. 2020년 EPFL에서는 Fig. 5(c)에 나타낸 바와 같이 99 GHz 반복률을 가지는 마이크로콤(Microcomb)에서 발진하는 각각의 광 빗 모드를 회절 격자를 이용하여 공간상에 30개의 채널로 분산시키고, 각 채널에서 2.9 GHz 수준의 주파수 변조를 수행함으로써 3 megapixels/s의 샘플링 속도로 11.5 cm 떨어진 위치의 물체에 대한 3차원 형상 이미징을 수행한 바 있다. 이를 통해 광 빗 광원을 이용한 동시다발적 주파수 변조는 3차원 형상 측정 업데이트 속도를 획기적으로 향상시킬 수 있음을 보였다.31
5. 결론
본 특집 논문에서는 산업 현장에서 많이 활용되고 있는 진폭 변조 및 주파수 변조 기반 길이 측정의 기본 원리부터 1차원 길이 측정 및 3차원 이미징의 최신 연구 동향을 소개하였다. 광 변조 기반 길이 측정의 대표적인 두 가지 기술은 정밀공학 분야 산업계에서 요구하는 측정 정밀도와 측정 영역을 만족시키면서도 간단하게 구성할 수 있어 지속적으로 활용되고 있다.
진폭 변조 기반 길이 측정의 경우에는 기준 신호와 측정 신호 사이의 위상 지연을 측정하여 길이를 측정한다. 높은 변조 주파수일수록 높은 정밀도를 구현할 수 있지만, 위상 모호성이 없는 최대 측정 거리가 짧아지는 단점이 있었다. 이를 극복하기 위해 변조 주파수를 변화시키는 연구가 수행되었다. 또한, 위상 측정 정밀도를 높이기 위해 고주파수를 저주파수로 전자적으로 변환하는 슈퍼헤테로다인 방법을 통해 위상을 측정하는 방법들이 제안되었지만, 아날로그 회로의 입력 신호 크기와 동작 온도에 따른 왜곡으로 정밀도의 한계가 있었다. 이를 극복하기 위해광학적 방식의 주파수 변환 기법을 이용한 진폭 변조 기반 길이 측정법을 통해 100 nm 미만의 정밀도를 달성한 연구가 소개되었다.
주파수 변조 기반 길이 측정의 경우에는 기준 신호와 측정 신호를 간섭시켜 발생하는 맥놀이 주파수를 검출하여 길이를 측정한다. 이를 위해서는 광원의 주파수가 시간에 따라 선형적으로 변조되어야 하며, 이를 유지하는 것이 정밀도에 가장 큰 영향을 주게 된다. 이를 위해 주파수가 안정화된 광 빗을 이용한 연구가 수행되었다. 광 빗은 주파수의 비선형성을 교정하기 위한 수단으로 활용되었다.
이러한 진폭 변조 및 주파수 변조 기반 길이 측정 방법들은 공간상 주사를 통해 3차원 형상 측정 분야에도 활용되었고, 다양한 물체에 대한 3차원 형상 이미징에 대한 연구를 소개하였다.
향후에는 위상 측정 정밀도 및 주파수 변조 비선형성 개선을 통해 길이 측정 정밀도가 더욱 향상되며, 산업적으로 쉽게 활용 가능한 소형 칩(Chip) 형태로 제작될 것으로 예측된다. 이를 통해 전통적인 정밀공학 분야인 항공, 조선, 자동차, 로봇에서 활용되는 비전 센서 및 레이더 센서를 대체함은 물론 자율 주행, 원격 탐색, 스마트 팩토리 등의 새로운 측정 수요에도 대응할 수 있을 것으로 기대한다.
NOMENCLATURE
| L : | Length |
| td : | Travelling Time of Light |
| co : | Velocity of Light in Vacuum |
| nair : | Refractive Index of Air |
| fm : | Modulation Frequency |
| Λair : | Wavelength in Air |
| Φ : | Phase Delay |
| T : | Period of Frequency Modulation |
| fFM : | Modulation Depth |
| fbeat : | Beat Frequency |
| ΔΦ : | Change of Phase Delay |
| ΔfFM : | Change of Modulation Frequency |
| Λcoarse : | Wavelength for Coarse Length Measurement |
| Lcoarse : | Coarse Length Measurement |
Acknowledgments
본 연구는 한국표준과학연구원 1-2-06. 멀티스케일길이측정팀 과제(No. 21011040) 및 4-1-13. 스마트 팩토리를 위한 대영역 3차원 형상 측정 모듈 개발 과제(No. 21011279)의 지원으로 수행되었습니다.
REFERENCES
-
Bobroff, N., “Recent Advances in Displacement Measuring Interferometry,” Measurement Science and Technology, Vol. 4, No. 9, pp. 907-926, 1993.
[https://doi.org/10.1088/0957-0233/4/9/001]

-
Eom, T., Choi, T., Lee, K., Choi, H., and Lee, S., “A Simple Method for the Compensation of the Nonlinearity in the Heterodyne Interferometer,” Measurement Science and Technology, Vol. 13, No. 2, pp. 222-225, 2002.
[https://doi.org/10.1088/0957-0233/13/2/313]

-
Coddington, I., Swann, W. C., Nenadovic, L., and Newbury, N. R., “Rapid and Precise Absolute Distance Measurements at Long Range,” Nature Photonics, Vol. 3, No. 6, pp. 351-356, 2009.
[https://doi.org/10.1038/nphoton.2009.94]

-
Lee, J., Kim, Y. -J., Lee, K., Lee, S., and Kim, S. -W., “Time-of-Flight Measurement with Femtosecond Light Pulses,” Nature Photonics, Vol. 4, No. 10, pp. 716-720, 2010.
[https://doi.org/10.1038/nphoton.2010.175]

-
Van Den Berg, S. A., Persijn, S., Kok, G., Zeitouny, M., and Bhattacharya, N., “Many-Wavelength Interferometry with Thousands of Lasers for Absolute Distance Measurement,” Physical Review Letters, Vol. 108, No. 18, Paper No. 183901, 2012.
[https://doi.org/10.1103/PhysRevLett.108.183901]

-
Jang, Y.-S., Wang, G., Hyun, S., Kang, H. J., Chun, B. J., et al., “Comb-Referenced Laser Distance Interferometer for Industrial Nanotechnology,” Scientific Reports, Vol. 6, No. 1, pp. 1-10, 2016.
[https://doi.org/10.1038/srep31770]

-
Jang, Y.-S., Liu, H., Yang, J., Yu, M., Kwong, D.-L., et al., “Nanometric Precision Distance Metrology via Hybrid Spectrally Resolved and Homodyne Interferometry in a Single Soliton Frequency Microcomb,” Physical Review Letters, Vol. 126, No. 2, Paper No. 023903, 2021.
[https://doi.org/10.1103/PhysRevLett.126.023903]

-
Dickey, J. O., Bender, P., Faller, J., Newhall, X., Ricklefs, R., et al., “Lunar Laser Ranging: A Continuing Legacy of the Apollo Program,” Science, Vol. 265, No. 5171, pp. 482-490, 1994.
[https://doi.org/10.1126/science.265.5171.482]

-
Korzh, B., Zhao, Q. -Y., Allmaras, J. P., Frasca, S., Autry, T. M., et al., “Demonstration of Sub-3 ps Temporal Resolution with a Superconducting Nanowire Single-Photon Detector,” Nature Photonics, Vol. 14, No. 4, pp. 250-255, 2020.
[https://doi.org/10.1038/s41566-020-0589-x]

-
Fujima, I., Iwasaki, S., and Seta, K., “High-Resolution Distance Meter Using Optical Intensity Modulation at 28 GHz,” Measurement Science and Technology, Vol. 9, No. 7, pp. 1049-1052, 1998.
[https://doi.org/10.1088/0957-0233/9/7/007]

-
Minoshima, K. and Matsumoto, H., “High-Accuracy Measurement of 240-m Distance in an Optical Tunnel by Use of a Compact Femtosecond Laser,” Applied Optics, Vol. 39, No. 30, pp. 5512-5517, 2000.
[https://doi.org/10.1364/AO.39.005512]

-
Xu, X., Zhang, Z., Zhang, H., Zhao, H., Xia, W., et al., “Long Distance Measurement by Dynamic Optical Frequency Comb,” Optics express, Vol. 28, No. 4, pp. 4398-4411, 2020.
[https://doi.org/10.1364/OE.381504]

-
Jang, Y. S., Kim, W., Jang, H., and Kim, S. W., “Absolute Distance Meter Operating on a Free-Running Mode-Locked Laser for Space Mission,” International Journal of Precision Engineering and Manufacturing, Vol. 19, No. 7, pp. 975-981, 2018.
[https://doi.org/10.1007/s12541-018-0115-y]

-
Zheng, J., “Analysis of Optical Frequency-Modulated Continuous-Wave Interference,” Applied Optics, Vol. 43, No. 21, pp. 4189-4198, 2004.
[https://doi.org/10.1364/AO.43.004189]

-
Baumann, E., Giorgetta, F. R., Coddington, I., Sinclair, L. C., Knabe, K., et al., “Comb-Calibrated Frequency-Modulated Continuous-Wave Ladar for Absolute Distance Measurements,” Optics Letters, Vol. 38, No. 12, pp. 2026-2028, 2013.
[https://doi.org/10.1364/OL.38.002026]

-
Hariyama, T., Sandborn, P. A., Watanabe, M., and Wu, M. C., “High-Accuracy Range-Sensing System based on FMCW Using Low-Cost VCSEL,” Optics Express, Vol. 26, No. 7, pp. 9285-9297, 2018.
[https://doi.org/10.1364/OE.26.009285]

-
Jang, Y. S., Lee, K., Han, S., Lee, J., Kim, Y. J., et al., “Absolute Distance Measurement with Extension of Nonambiguity Range Using the Frequency Comb of a Femtosecond Laser,” Optical Engineering, Vol. 53, No. 12, Paper No. 122403, 2014.
[https://doi.org/10.1117/1.OE.53.12.122403]

-
Doloca, N. R., Meiners-Hagen, K., Wedde, M., Pollinger, F., and Abou-Zeid, A., “Absolute Distance Measurement System Using a Femtosecond Laser as a Modulator,” Measurement Science and Technology, Vol. 21, No. 11, Paper No. 115302, 2010.
[https://doi.org/10.1088/0957-0233/21/11/115302]

-
Kim, W., Fu, H., Lee, K., Han, S., Jang, Y.-S., et al., “Photonic Microwave Distance Interferometry Using a Mode-Locked Laser with Systematic Error Correction,” Applied Sciences, Vol. 10, No. 21, Paper No. 7649, 2020.
[https://doi.org/10.3390/app10217649]

-
Jang, Y. S., Park, J., and Jin, J., “Sub-100-nm Precision Distance Measurement by Means of All-Fiber Photonic Microwave Mixing,” Optics Express, Vol. 29, No. 8, pp. 12229-12239, 2021.
[https://doi.org/10.1364/OE.421719]

-
Chen, L.-Y., Vinod, A. K., McMillan, J., Wong, C. W., and Yang, C.-K. K., “A 9-μm Precision 5-MSa/s Pulsed-Coherent Lidar System with Subsampling Receiver,” IEEE Solid-State Circuits Letters, Vol. 3, pp. 262-265, 2020.
[https://doi.org/10.1109/LSSC.2020.3014957]

-
Dorrington, A. A., Cree, M. J., Payne, A. D., Conroy, R. M., and Carnegie, D. A., “Achieving Sub-Millimetre Precision with a Solid-State Full-Field Heterodyning Range Imaging Camera,” Measurement Science and Technology, Vol. 18, No. 9, pp. 2809-2816, 2007.
[https://doi.org/10.1088/0957-0233/18/9/010]

-
Park, Y.-H., Cho, Y.-C., You, J.-W., Park, C.-Y., Yoon, H.-S., et al., “Three-Dimensional Imaging Using Fast Micromachined Electro-Absorptive Shutter,” Journal of Micro/Nanolithography, MEMS, and MOEMS, Vol. 12, No. 2, Paper No. 023011, 2013.
[https://doi.org/10.1117/1.JMM.12.2.023011]

-
Wheaton, S., Bonakdar, A., Nia, I. H., Tan, C. L., Fathipour, V., et al., “Open Architecture Time of Flight 3D SWIR Camera Operating at 150 MHZ Modulation Frequency,” Optics Express, Vol. 25, No. 16, pp. 19291-19297, 2017.
[https://doi.org/10.1364/OE.25.019291]

-
Baumann, E., Giorgetta, F. R., Deschênes, J.-D., Swann, W. C., Coddington, I., et al., “Comb-Calibrated Laser Ranging for Three-Dimensional Surface Profiling with Micrometer-Level Precision at a Distance,” Optics Express, Vol. 22, No. 21, pp. 24914-24928, 2014.
[https://doi.org/10.1364/OE.22.024914]

-
Jia, L., Wang, Y., Wang, X., Zhang, F., Wang, W., et al., “Nonlinear Calibration of Frequency Modulated Continuous Wave Lidar based on a Microresonator Soliton Comb,” Optics Letters, Vol. 46, No. 5, pp. 1025-1028, 2021.
[https://doi.org/10.1364/OL.415524]

-
Mitchell, E. W., Hoehler, M. S., Giorgetta, F. R., Hayden, T., Rieker, G. B., et al., “Coherent Laser Ranging for Precision Imaging through Flames,” Optica, Vol. 5, No. 8, pp. 988-995, 2018.
[https://doi.org/10.1364/OPTICA.5.000988]

-
Ula, R. K., Noguchi, Y., and Iiyama, K., “Three-Dimensional Object Profiling Using Highly Accurate FMCW Optical Ranging System,” Journal of Lightwave Technology, Vol. 37, No. 15, pp. 3826-3833, 2019.
[https://doi.org/10.1109/JLT.2019.2921353]

-
Dong, Y., Zhu, Z., Tian, X., Qiu, L., and Ba, D., “Frequency-Modulated Continuous-Wave LIDAR and 3D Imaging by Using Linear Frequency Modulation based on Injection Locking,” Journal of Lightwave Technology, Vol. 39, No. 8, pp. 2275-2280, 2021.
[https://doi.org/10.1109/JLT.2021.3050772]

-
Okano, M. and Chong, C., “Swept Source Lidar: Simultaneous FMCW Ranging and Nonmechanical Beam Steering with a Wideband Swept Source,” Optics Express, Vol. 28, No. 16, pp. 23898-23915, 2020.
[https://doi.org/10.1364/OE.396707]

-
Riemensberger, J., Lukashchuk, A., Karpov, M., Weng, W., Lucas, E., et al., “Massively Parallel Coherent Laser Ranging Using a Soliton Microcomb,” Nature, Vol. 581, No. 7807, pp. 164-170, 2020.
[https://doi.org/10.1038/s41586-020-2239-3]

-
Li, Z., Zang, Z., Fu, H., Luo, Y., and Han, Y., “Virtually Imaged Phased-Array-Based 2D Nonmechanical Beam-Steering Device for FMCW LiDAR,” Applied Optics, Vol. 60, No. 8, pp. 2177-2189, 2021.
[https://doi.org/10.1364/AO.414128]


Senior research scientist in Korea Research Institute of Standards and Science. His research interests include optical metrology, ultrafast photonics, mode-locked laser, frequency comb, silicon photonics and laser interferometry.
E-mail: ysj@kriss.re.kr

Principal research scientist in division of physical metrology at Korea Research Institute of Standards and Science and a professor in the department of science of measurement at University of Science and Technology. His research interest is optical metrology.
E-mail: jungjae.park@kriss.re.kr

Principal research scientist in division of physical metrology at Korea Research Institute of Standards and Science and a chief major professor in the department of science of measurement at University of Science and Technology. His research interest is optical metrology.
E-mail: jonghan@kriss.re.kr