역강성법을 이용한 다중 입력 시스템의 가진력 규명에 관한 연구

1. 서론

일반적으로 기계 시스템의 진동/소음 문제를 체계적으로 해결하기 위해서는 소음/진동원-전달계-응답계로 구분하여 해석을 진행한다. 본 연구에서는 진동/소음원, 즉 가진력에 대한 규명 방법에 관한 연구를 수행하였다. 가진력은 일반적으로 전달 경로상에 힘 센서를 삽입하여 직접적으로 측정한다. 하지만 이 경우 전달계의 특성이 변하거나 힘센서를 설치하기 적합하지 않은 경우가 있다. 그래서 가진력을 간접적으로 도출하는 방법은 충격 응답 함수(Impulse Response Function, IRF)를 이용하는 시간 대역의 방법과 진동 응답 함수(Frequency Response Function, FRF)을 이용한 주파수 영역에서의 방법으로 나눌 수 있다.¹ 단일 하중의 경우 응답함수를 이용하여 정확한 가진력을 추정할 수 있지만, 다수의 하중이 복합적으로 작용하는 경우에는 가진력을 명확하게 규명하는 것은 어려움이 있다.

가진력을 규명하기 위해서 여러 방법이 이용되었다. Markov Parameter Matrix의 조건수 혹은 상관 분석을 활용하여 최적의 센서 위치를 도출하고, 입력신호 복원을 수행하거나,² 비선형 시스템의 입력을 복원하기 위해서 칼만 필터를 적용하기도 하였다.³ 매우 작은 특이값을 가지는 비최소 위상 시스템(Non-Minimum Phase System)이 아닌 경우에 IRF와 특이값 분해(Singular Value Decomposition, SVD)를 이용하여, 시간 영역에서 신호 복원을 수행하였다.⁴ FRF와 복소 캡스트럼(Complex Cepstrum)을 이용하기도 한다.⁵

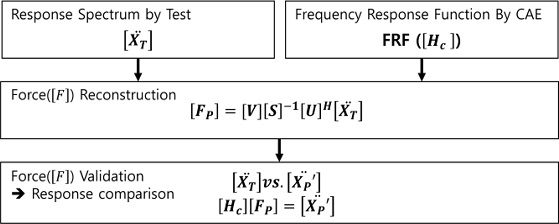
본 논문에서는 상용화를 목표로 개발 중인 철도 감속기 케이스에 12개의 가진력이 작용하는 것으로 가정하여 동등한 진동을 만들어내는 가진력을 구하고자 하였다. Fig. 1과 같이 응답 신호는 무부하 조건에서 측정된 27자유도의 가속도 측정 결과($$ {\ddot{X}}_t$$)를 사용하였다. 실험으로 감속기 조립체에서 가진점과 응답점 사이의 FRF 측정이 어려움이 있어서, 등가 해석 모델을 이용하여 FRF(H_c)를 도출하였다. FRF는 SVD를 수행하여 과도하게 작은 특이값은 연산에서 제외하고 가진력(F_p)을 복원하였다. 복원된 가진력은 임의 지점에서 응답을 비교하여 정확성을 확인하였다. 또한, 신호 복원에 사용되는 응답점의 개수에 따른 차이를 확인하였고, 작은 특이값도 포함되는 경우 복원된 가진력을 비교하였다.

Fig. 1

The flow chart of excitation force identification study

2. 가진력 복원 방법

3. 가진력 추정 방법

3.1 대상 시스템

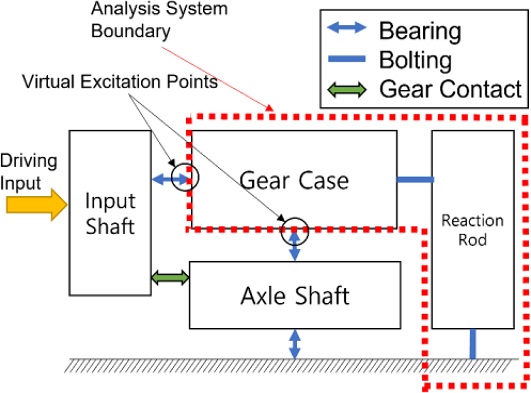
철도 차량용 감속기는 차량의 입력축과 모터 사이의 구동 토크의 증배 기능을 하는 장치로서 차축에는 차륜 기어, 입력축에는 피니언 기어가 연결되어 있다. 대상 감속기는 250 km/h 급의 철도차량의 감속기이며, 감속비는 2.15 : 1로 차륜 기어 86개, 피니언 기어 40개로 구성되어 있다. 감속 기어는 차축에 베어링으로 고정되며, 리액션 로드는 같이 회전하는 것을 방지한다. 감속기 시험기의 전체 시스템의 구성은 Fig. 2와 같으며 여기서 가진력 복원을 위해 사용된 시스템의 범위는 기어 케이스와 리액션 로드이다.

Fig. 2

Configuration of the railway reduction gear and analysis boundary

3.1.1 가상의 가진점 설정

입력축과 차축은 2개의 베어링으로 케이스와 연결된다. 가진력은 다음과 같이 가정하였다. (1) 모든 가진력은 베어링을 통하여 전달된다. (2) 가진력은 X, Y, Z 방향으로 분해하여 나타낼 수 있다. (3) 모든 가진력은 베어링의 중앙에 작용한다. Fig. 3에 가정한 가진력을 나타내었다.

Fig. 3

The virtual points of action of load

3.2 가속도 측정

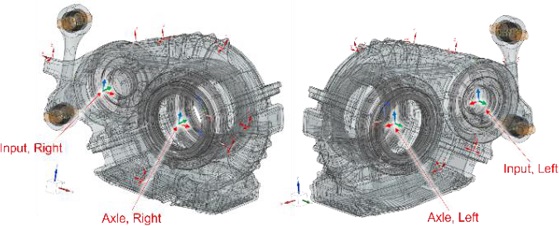
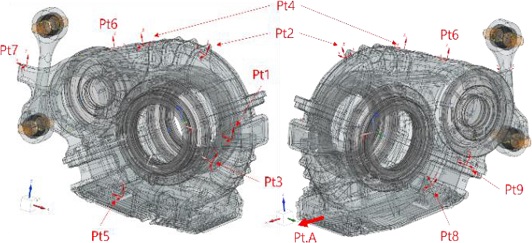
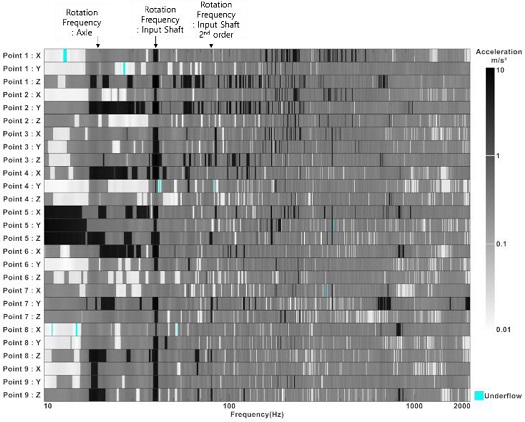
진동 응답은 Fig. 4와 같이 무부하 시험기 조건에서 180 km/h(1,116 RPM)로 동작할 때 케이스 표면의 가속도를 측정하였다. Fig. 5와 같이 9지점에서 3축 가속도계를 이용하여 측정하였다. 또한 임의 1지점(Point A)에 단축 가속도계를 이용하여 가속도를 측정하였다.

Fig. 4

Experimental setup for driving test

Fig. 5

The measurement points of acceleration at driving test

Fig. 6

The measured acceleration at 1,116 RPM

표면의 진동은 차축의 회전 주파수 대역(18.6 Hz)와 입력의 회전 주파수와 그 2배수 성분(40, 80 Hz)에서 큰 진동이 나타난다. 하지만, 무부하 조건이기 때문에 기어 물림 주파수 대역(1,600 Hz)에서는 두드러진 진동이 나타나지 않았다.

3.3 FRF 작성

가상의 가진점과 감속기 케이스의 진동 측정점 사이의 FRF는 실험적인 방법으로 측정하기에는 어려움이 있다. 그래서 등가 해석 모델을 이용하여 구하였다.

3.3.1 등가 해석 모델 구축

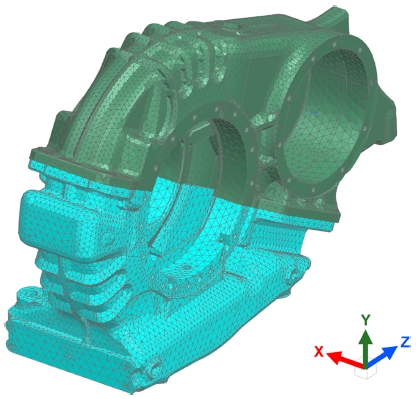
해석 모델은 Siemens사의 Simcenter 3D 2021.1을 이용하여 작성하였다. Fig. 7에서처럼 상하부 케이스 조립품을 331,418개의 Tetra 10 요소로 모델링을 수행하였다. 이때 내부의 유로 형상 및 곡면들을 모사하고, 두께 방향으론 최소 2겹의 요소가 있도록 형상에 따라 2-32 mm 크기의 요소를 사용하였고, 기본적인 Simcenter Nastran의 요소 품질 검토 조건을 만족하는지 확인하였다.

Fig. 7

CAE model of reduction gear

3.3.2 등가 해석 모델 검토

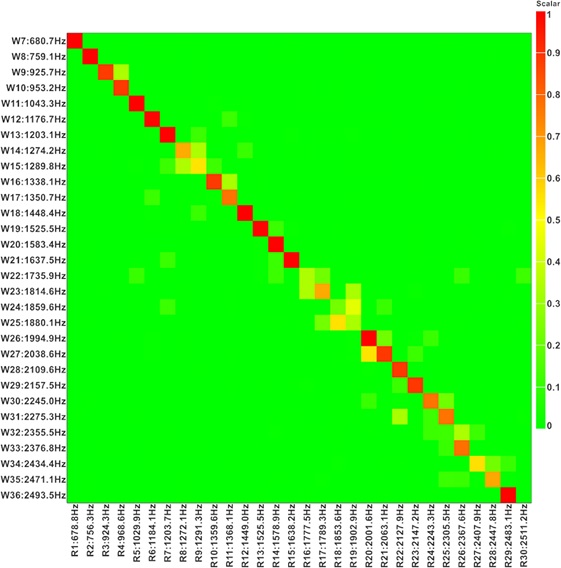
해석 모델을 실험적 모드해석(Experimental Modal Analysis, EMA) 결과와 Cross MAC (Modal Assurance Criterion)을 도출하여 동일한 모드를 확인하고, 공진 주파수를 비교하였다. 또한 FRF 결과가 실험 결과와 유사한지 확인하였다.

Table 1

Comparison of modal frequency

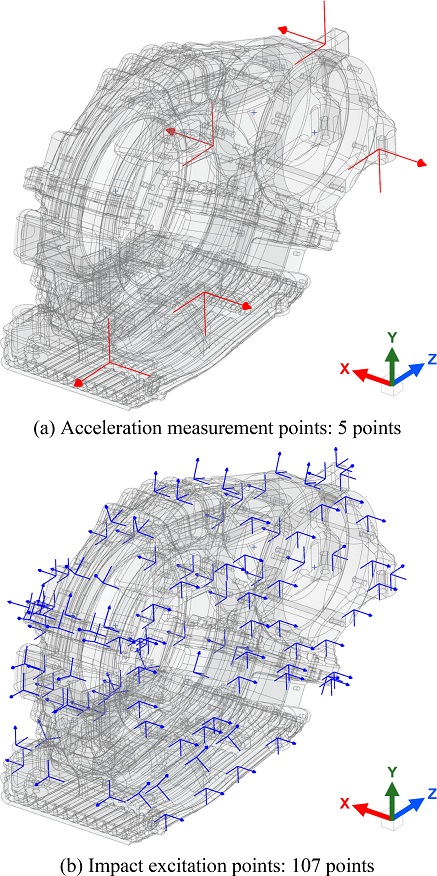
EMA는 Fig. 8과 같이 우레탄 패드 위에 감속기 케이스를 거치하고 대상 표면에 수직 방향으로 5지점의 가속도를 측정하며, 107지점을 임팩트 해머로 충격 가진할 때 계산되는 535개의 FRF 세트를 이용하여 수행하였다. EMA에서는 2 kHz 이하 주파수 대역에서 19개의 고유 진동 특성을 확인하였다.

Fig. 8

Cross MAC results between Test mode-set and CAE mode-set

Fig. 9

Cross MAC results between test mode-set and CAE mode-set

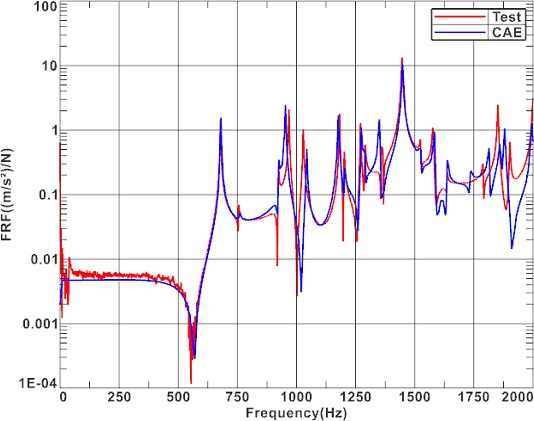
감속기 케이스 해석 모델의 FRF를 비교하여 모델을 검증하였다. 하지만 실험에서는 20 Hz 이하에서 우레탄 패드의 강성에 의한 강체 모드가 나타났다. 하지만 그 이상의 1 kHz 이하 주파수 대역에서는 모델이 실제 동특성을 충분하게 반영하는 것으로 보인다. 1.5 kHz 이상의 대역에서는 다소 피크 주파수 차이가 나타난다. 이는 국부적인 형상 차이들을 해석 모델이 반영하지 못하였기 때문으로 생각된다.

Fig. 10

Comparison Test FRF with CAE of gear case assembly

3.3.3 등가 해석 모델 구축

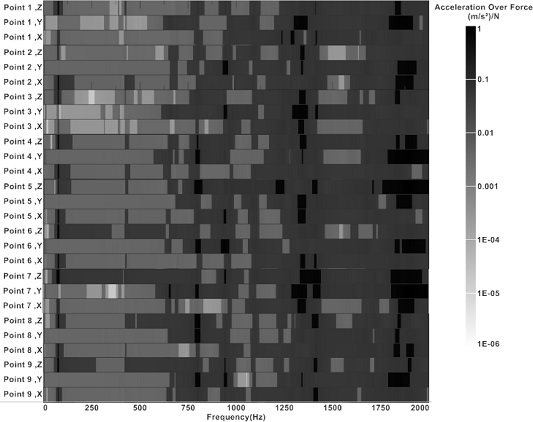
동특성 검증을 수행한 케이스 모델에 리액션 로드와 베어링 시트 등의 연결 부품을 추가하여 FRF 해석 모델을 구성하였다. 이때 FRF는 12개의 가상 가진력과 27개의 응답으로 이루어져 있다. 총 324개의 FRF 세트로 구성하였다. 차축의 우측의 Z 방향 단위 하중에 의한 주파수 응답 함수는 Fig. 11과 같다. 동일 지점에서도 방향에 따라 차이를 보인다. 주요 모드가 있는 주파수 대역에서는 거의 모든 지점과 방향에서 큰 응답 특성을 보인다.

Fig. 11

FRF results by CAE of reduction gear by right axle bearing force Z

3.4 가진력 복원

실험에서 측정된 가속도와 해석에서 도출된 FRF 세트를 이용하여, 역강성법으로 하중을 도출하였다. 각 주파수별로 12개의 특이값 중에서 가장 큰 특이값(s₁) 대비 2%보다 작은 특이값은 계산에서 제거하고 나머지를 이용하여 계산을 수행하였다. 그리고 계산에 사용된 응답의 자유도 숫자에 따라 계산된 가진력을 비교하였다.

3.4.1 진동 가진력 결과

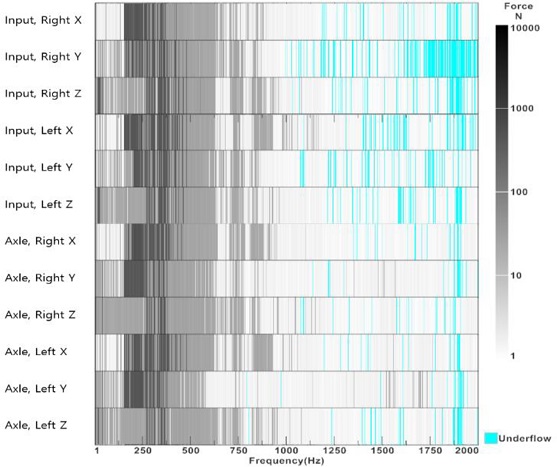
27개의 응답을 이용하여, 가진력을 복원하였을 때, 결과는 Fig. 12와 같다. 125 Hz 이하 대역에서는 X 방향으로는 작은 가진력을 나타내며, Y, Z 방향으로는 상대적으로 큰힘이 나타난다. 125-250 Hz 대역에서는 X, Y 방향으로 큰 힘이 계산된다. 625 Hz 이상 대역에서는 상대적으로 힘들이 작아지는 경향을 보이게 된다.

Fig. 12

Reconstructed force by 27 DOF

3.4.2 응답 자유도에 따른 결과 차이

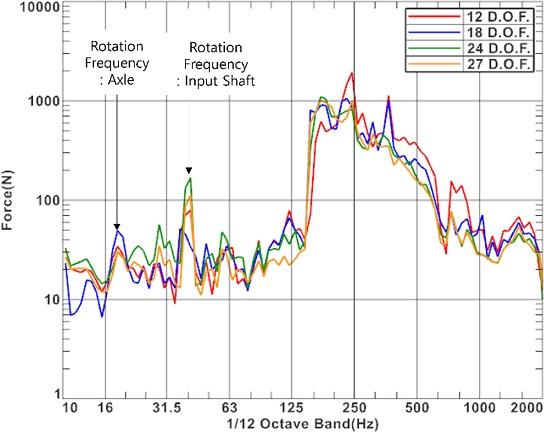
Fig. 13은 가진력은 사용된 응답의 숫자에 따른 우측 차륜의 Y 방향 힘의 결과이다. 모든 경우에 힘은 유사한 개형을 보인다. 하지만 세부적으로 입력 자유도에 따라 크기의 차이가 나타난다. 41 Hz 밴드 입력축의 회전 주파수(40 Hz)이고, 18.3 Hz 밴드는 차축의 회전 주파수(18.6 Hz) 대역이다. 해당 주파수 대역에서 진동 가진력이 다소 크게 나타나는 것을 알 수 있다. 기어 물림 주파수인 1,500 Hz 대역에도 가진력이 발생되는 것을 알 수 있다.

Fig. 13

Reconstructed force for right axle force by Y direction

3.4.3 진동 가진력 검증

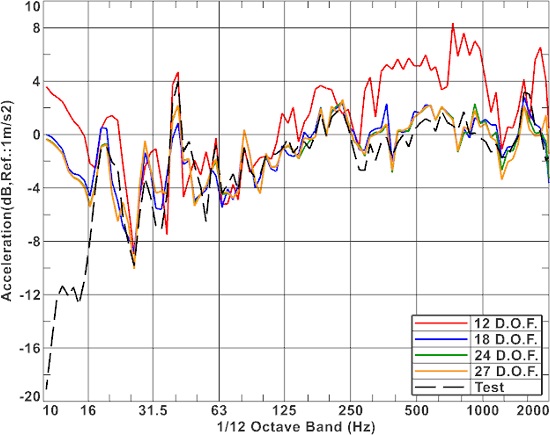
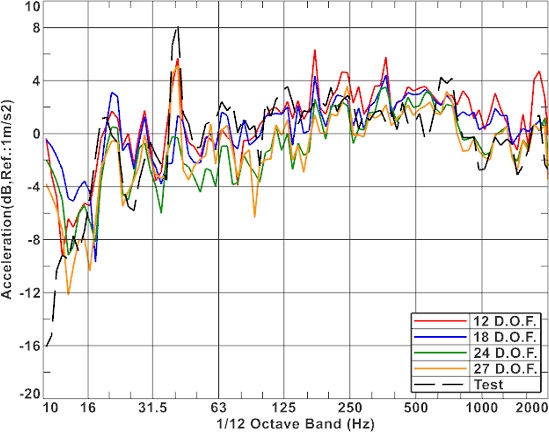
복원한 가진력을 검증하기 위해서 해석 모델에 복원된 가진력을 적용하여 계산한 응답($$ {\ddot{X}}_p^{\text{'}}$$)을 실험 결과($$ {\ddot{X}}_T$$)와 비교하였다. Fig. 14는 10번 지점의 응답을 비교하였다. 18, 24, 27자유도에서는 가진력 도출 시 사용된 측정값($$ {\ddot{X}}_T$$)으로 이러한 경우에는 실험 결과와 매우 유사한 결과를 보여준다. 하지만 12자유도의 경우는 특정 주파수 대역에서는 다소 오차가 발생하는 것을 확인할 수 있다. Fig. 15는 가진력을 도출할 때 사용하지 않은 임의의 측정점(Point A)에서 가속도 결과로서 이러한 경우 계산 시 사용된 지점보다 차이는 두드러지게 나타나지만, 대체적으로 유사한 결과를 얻을 수 있다. 특히 자유도가 충분한 경우 125 Hz 이상 주파수 대역에서는 상대적으로 실험에 근접한 결과를 얻을 수 있었다.

Fig. 14

Comparison of acceleration results at Y-direction of point 9

Fig. 15

Comparison of acceleration results at X-direction of point A

3.4.4 SVD 결과

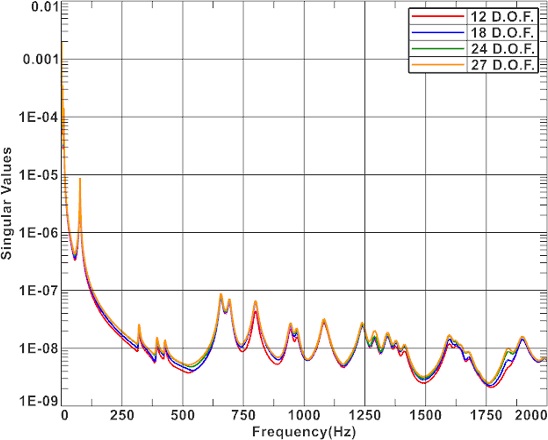
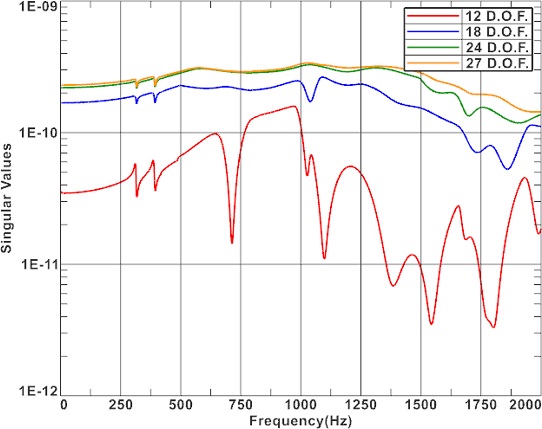
FRF의 SVD 시 주파수별 가장 큰 특이값 결과(s₁)는 Fig. 16에서 보듯이 자유도에 따라 큰 차이가 나타나지 않는다. 하지만 Fig. 17에 표시한 가장 작은 특이값(s₁₂)은 사용된 응답의 크기에 차이가 있고, 12 DOF인 경우에는 상대적으로 매우 작게 나타난다. 작은 특이값은 작은 오차에도 역산된 결과에 과도한 차이를 발생시킨다.

Fig. 16

Largest singlular value (s1) results by input accerelation D.O.F

Fig. 17

Smallist singlular value (s12) results by input accerelation DOF

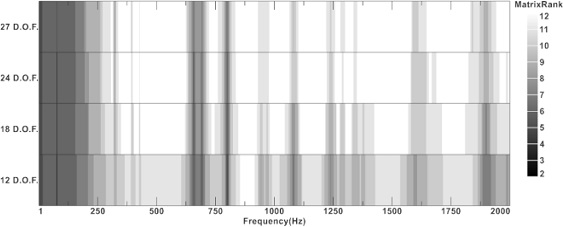
각 주파수별로 s₁ 대비 2% 이하인 과도하게 작은 특이값을 삭제하고 가진력을 복원하였다. 이때 각 주파수별로 사용된 특이값 행렬의 크기는 Fig. 18에 랭크로 표현된다. 특정 주파수 대역에서는 12개의 특이값 중 크기가 큰 2개의 특이값만을 이용하여 가진력이 복원하였다. 충분히 많은 응답(27 DOF, 24 DOF)의 경우에는 버려지는 행렬이 작은 것을 알 수 있다. 하지만 입력된 자유도가 작아질수록 버려진 특이값이 많아져 랭크 부족 현상이 두드러지게 나타난다. 165 Hz 이하 대역에서는 케이스의 강체 모드의 영향이 매우 크기 때문에 낮은 랭크를 보인다. 또한 659, 693, 800 Hz에서는 케이스 조립체의 공진 모드들이 있는 주파수 대역에서도 낮은 랭크를 보이며, 이러한 공진 주파수 대역에서는 주파수의 분해능, 비선형성에 의한 FRF 오차와 악조건성(Ill-Condition)이 두드러지게 나타난다.⁵

Fig. 18

Rank of matrix results by input accerelation DOF

3.4.5 특이값의 임계 범위에 따른 가진력 복원 결과

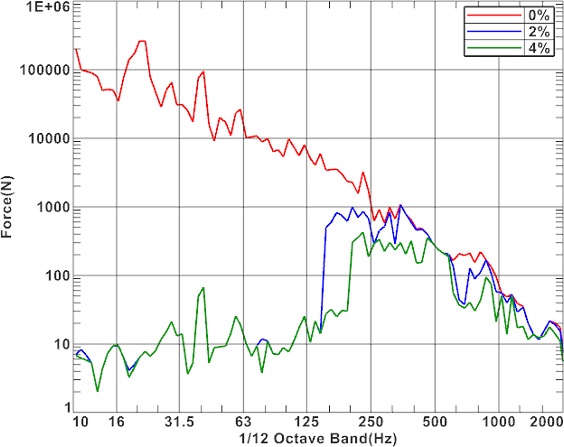
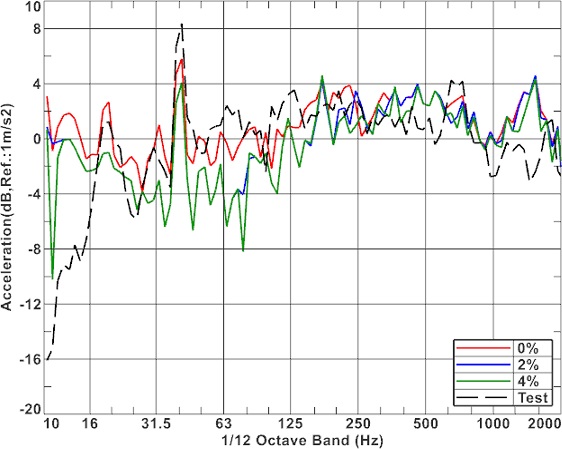
특이값의 임계 범위(Threshold)는 주파수 대역별로 연산에 포함되는 특이값의 경계로서 가장 큰 특이값(s₁) 대비 비율로 표현하였다. 4%는 s₁의 4% 이하의 특이값을 제하고 가진력을 복원하는 것을 말한다. 이 임계 범위가 0, 2, 4%일 때, 오른쪽 차축의 X 방향 결과는 Fig. 19와 같다. 이때 0%는 모든 특이값을 포함한 경우를 말하며, 저주파수에서 매우 큰 가진력 결과를 보인다. 이는 s₁ 이 낮은 주파수 대역에서 매우 큰 값이고, 상대적으로 작은 특이값이 역산되면서 잡음에 큰 영향을 받는 것으로 보인다. 하지만 너무 높은 특이값까지 버려지면 시스템의 동특성이 반영되지 않으므로 적절한 임계 범위를 선정이 필요하다. 대상의 경우 2-4%의 임계 범위는 거의 유사한 특성을 보이지만, 160-400 Hz 대역에서는 다소 차이가 있다. 0%의 경우 저주파수 대역에서 매우 큰 가진력이 도출된다. 임계 범위에 따라 복원된 가진력들을 검증하기 위해서 Fig. 20에 Point A에서 진동 응답을 비교하였다. 응답에서는 Fig. 19의 가진력에 비하여 차이가 두드러지게 나타나진 않는다. 하지만 100,000 N의 가진력은 비현실적이므로 적절한 임계 범위 설정이 필요해 보인다.

Fig. 19

Reconstructed force by relative threshold for singular value (Right axle force, X deration)

Fig. 20

Comparison of acceleration results at X-direction of point A by relative threshold

4. 결론

감속기가 구동 시 발생하는 케이스 표면의 진동과 동등한 진동을 발생시키는 가진력을 역강성법을 이용하여 도출하였다. 철도차량용 감속기의 지지 구조상 실험적 방법을 이용하여 FRF를 도출하는데 어려움이 있기 때문에 동등한 동특성을 보이는 CAE 모델을 구성하였으며, EMA와 비교하여 동등한 특성을 보이는 것을 확인하였다. 또한 FRF의 결과 비교하였다.

해석에서 구해진 FRF와 무부하 구동 시험 시 측정된 진동 결과를 이용하여 가진력을 추정하였다. 추정된 가진력을 이용하여 진동 결과를 도출하였을 때 실제 실험에서 측정된 가속도 결과와 비교하여 가진력의 정합성을 검증하였다.

철도 차량용 감속기와 같은 다중 가진 시스템에서는 단순히 진동 응답 함수의 역행렬만으로는 정확한 가진력을 도출하기 어렵기 12개의 가상의 가진력을 도출하기 위해서는 24개 이상의 응답을 이용하여야 실제 응답과 유사한 특성을 얻을 수 있었다.

주파수 대역별로 큰 특이값보다 특정 임계 범위(0, 2, 4%) 이하의 너무 작은 특이값들 행렬에서 제거할 때 도출된 가진력을 비교하였다. 너무 작은 특이값을 포함하여 역강성법을 수행하는 경우 가진력이 과도하게 커지는 것을 확인하였다. 적정 수준의 특이값 정하기 위한 방안이 필요해 보인다.

본문에서는 베어링에서 전달되는 하중을 3개의 병진 방향으로만 모델링을 수행하였지만, 차후 베어링 하중을 모사하기 위한 가상의 하중에 모델링 방법에 관한 추가적인 연구가 필요하여 보인다.

Acknowledgments

본 연구는 2021학년도 홍익대학교 학술연구진흥비(No. 2021S134101) 및 국토교통부 철도기술연구사업의 연구비 지원(No. 21RTRP-B148870-04)에 의해 수행되었습니다.

REFERENCES

• Patil, R. A. and Gombi, S., “Review on Determination of Forces Using Inverse Techniques,” International Journal of Emerging Technology and Advanced Engineering, Vol. 7, No. 6, pp. 120-125, 2017.
• Wang, J., Law, S., and Yang, Q., “Sensor Placement Methods for an Improved Force Identification in State Space,” Mechanical Systems and Signal Processing, Vol. 41, Nos. 1-2, pp. 254-267, 2013. [https://doi.org/10.1016/j.ymssp.2013.07.004]
• Ma, C.-K. and Ho, C.-C., “An Inverse Method for the Estimation of Input Forces Acting on Non-Linear Structural Systems,” Journal of Sound and Vibration, Vol. 275, Nos. 3-5, pp. 953-971, 2004. [https://doi.org/10.1016/S0022-460X(03)00797-1]
• Kim, S.-J. and Lee, S.-K., “Experimental Identification for Inverse Problem of a Mechanical System with a Non-Minimum Phase based on Singular Value Decomposition,” Journal of Mechanical Science and Technology, Vol. 22, No. 8, pp. 1504-1509, 2008. [https://doi.org/10.1007/s12206-008-0312-1]
• Kim, K. and Choi, S., “Source Waveform Recovery by Using Transfer Function,” Proc. of the KSNVE Annual Spring Conference, pp. 275-280, 1999.
• Lee, J. K., “A Study on Indirect Force Measurement in Structure,” Ph.D. Thesis, Korea Advanced Institute of Science & Technology, 1993.
• Thite, A. and Thompson, D., “The Quantification of Structure-Borne Transmission Paths by Inverse Methods. Part 1: Improved Singular Value Rejection Methods,” Journal of Sound and Vibration, Vol. 264, No. 2, pp. 411-431, 2003. [https://doi.org/10.1016/S0022-460X(02)01202-6]
• Schneider, H. and Barker, G. P., “Matrices and Linear Algebra,” Courier Corporation, 2nd Ed., pp. 360-362, 2012.