무급유 터보 냉동기의 압축기를 지지하는 자기베어링 제어기의 효율적 최적화에 관한 연구

2.1 Plant 전달함수

자기베어링 시스템에서 제어기의 제어대상인 Plant는 회전축, 베어링 액츄에이터, 전류증폭기, 센서 등으로 구성된다. 자기베어링에 의해 지지된 회전축의 동역학을 전달함수 형태로 표현하면 식(1)과 같다.

회전축의 유연모드를 고려하는 경우 N_flex개의 유연모드에 대해 모드강도 A_r, 모드댐핑 ζ_r, 모드주파수 ω_r 등으로 유연모드를 모델링할 수 있다. 유연모드에 대한 파라미터는 유한요소 모델로부터 구하거나 실험을 통한 시스템 식별과정(System Identification)으로부터 구할 수 있다. 회전축의 강체 운동은 음의 부호를 가지는 개루프(Open-Loop) 스프링 상수 K_s 와 질량 m 으로 모델링된다. 코일에 전류를 공급하는 증폭기는 대부분 2차 시스템의 특성을 가지며 전달함수는 다음 식(2)와 같이 표현할 수 있다.

여기서 ω_amp. 는 증폭기의 주파수 대역을 의미하며, ζ_amp. 는 댐핑이다. 센서의 주파수 대역은 제어범위보다 매우 크므로 고정된 이득 K_sensor로 모델링할 수 있다. 따라서, Plant 전달함수는 식(3)으로 같이 구할 수 있다.

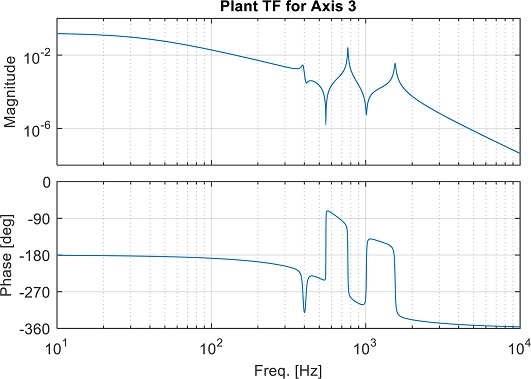
Fig. 1은 Plant 전달함수의 한 예로서 유한요소해석을 통해 구한 결과이다. 회전축은 총 3개의 유연모드를 가지는 유연축으로 모델링되었으며, 전류증폭기의 주파수 대역은 680 Hz, 댐핑은 0.7이다.

Fig. 1

An example of a plant transfer function which includes the dynamics of rotor, amplifier, and sensor

2.2 제어기

자기베어링의 내재적 불안정성을 극복하기 위해 다양한 형태의 제어기가 제시되었으나, 상업용 제품에서 가장 널리 사용되는 제어기는 비례-적분-미분(Proportional-Integral-Derivative, PID) 형태이다. 미분기의 고주파 이득을 제한하고 구현이 가능하도록 비례-미분기를 변형하면 식(4)와 같이 제어기를 표현할 수 있다.

식(4)의 첫 항은 위상선행(Phase Lead) 필터라고도 하며, α = τ_z/τ_p 가 위상선행과 고주파 이득을 결정한다. 위상선행은 진동 관점에서 댐핑과 관련이 있으며, 위상선행을 증가하기 위해 2차 위상선행 필터를 사용하기도 한다.^9,10

일반적으로 PID 제어기와 함께, 센서의 고주파 잡음을 저감하는 저역 통과(Lowpass) 필터, 유연모드를 제어하기 위한 노치 필터가 제어기에 사용된다.

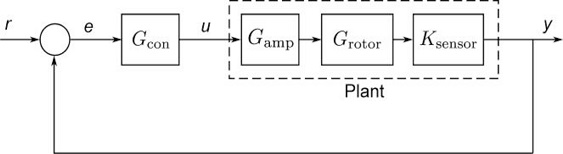
Fig. 2는 자기베어링 제어 시스템을 블록 선도로 보여준다.

Fig. 2

Block diagram of magnetic bearing control. The plant consists of bearing actuator (Including amplifier), rotor and sensor

3.1 강체모드 제어기 설계 과정

회전축의 운전속도가 유연모드에 비해 현저하게 낮거나 초기 부상을 위한 제어기 설계의 경우 회전축의 강체 운동만을 고려할 수 있다. 또한 유연모드 제어기 설계의 초기값으로도 강체 모드 제어기가 활용될 수 있다. 제어기 설계의 목표는 ISO 14839-3에서 제시하는 출력민감도의 최소화인데,¹¹ 단일입력-단일출력(SISO)인 경우 위상여유도(Phase Margin)가 출력민감도와 직접적 관계가 있으므로, 위상여유도를 최대한 확보하도록 설계한다. 위상여유도는 Gain Cross-Over 주파수, 즉 시스템 개루프 전달함수의 크기가 1이 되는 주파수에서 개루프 전달함수의 위상과 180^o 간의 차이를 의미한다.

Plant 전달함수의 전체 이득을 K_f = K_actK_ampK_sensor 로 정의하고, 시상수 형태로 표현하면 식(7)과 같다.

강체 운동의 시상수와 증폭기의 시상수는 다음 식(8)과 같이 정의된다.

Gain Cross-Over 주파수는 식(9)를 만족하는 주파수이다.

수치적 방법으로 식(9)의 해를 구할 수 있겠으나, 분수함수 및 제곱근 형태이므로 보다 수월하게 해를 구하기 위해 식(9) 좌변의 분모와 분자를 각각 D(jω_gc), N(jω_gc) 라고 하면 식(10)이 되어, 다항식 형태로 정리할 수 있다.

제어기에서 위상선행 필터만을 고려한다면 이 식은 $$ {\mathrm{\Omega }}_{gc}={\omega }_{gc}^2$$ 에 대해 6차 방정식이며, Newton-Raphson 방법과 같은 과정을 통해 해를 구할 수 있다. 만일 증폭기의 주파수 대역이 매우 높고 (ω_amp ≫ ω_gc), 위상선행 필터에서 극점이 영점에 비해 매우 크다면 (τ_p ≪ τ_z), 식(10)은 다음 식(11)과 같이 2차 방정식으로 근사화할 수 있다.

식(11)에서 κ_f = K_f/|K_s| 이며, 대문자변수는 소문자변수의 제곱을 의미한다. 즉, $$ T_m={\tau }_m^2, T_z={\tau }_z^2, Z_z={\zeta }_z^2$$ 이다.

Gain Cross-Over 주파수를 구하면, 다음 식(12)로 위상여유도를 구할 수 있다.

만일 위상여유도가 0보다 작으면 시스템의 불안정성을 의미하며, 최적화의 구속 조건으로 활용할 수 있다.

3.2 강체모드 제어기 설계 결과

3.1절의 과정을 통해 강체모드 제어기의 설계를 수행하였다. 대상은 50마력 압축기의 반경 방향 베어링이며 회전축의 질량은 7.3 kg, 개루프 스프링 상수 -871 N/m, 액츄에이터 상수 126 N/A이다. 전류증폭기의 주파수 대역은 800 Hz로 가정하였다. 비례이득은 12이며, 적분기는 사용하지 않았다. 초기 제어기는 시행착오를 거쳐 결정하였다.

Table 1과 Fig. 3은 제어기 설계의 결과이다. 제어기 설계의 목표는 위상여유도를 최대화하여 안정성을 높이는 것이지만, 이와 함께 외란에 대한 강인성을 향상하는 것이다. 안정성과 강인성을 동시에 평가하는 도구로 출력민감도를 사용한다. 출력민감도함수는 식(13)으로 정의되며, SO14839-3은 출력민감도 함수의 최댓값인 ∥S(jω)∥_∞가 3을 넘지 않도록 권고하고 있다.

Table 1

Design result for rigid-body controller

Fig. 3

Output sensitivity function of phase-margin optimized control compared with initial control

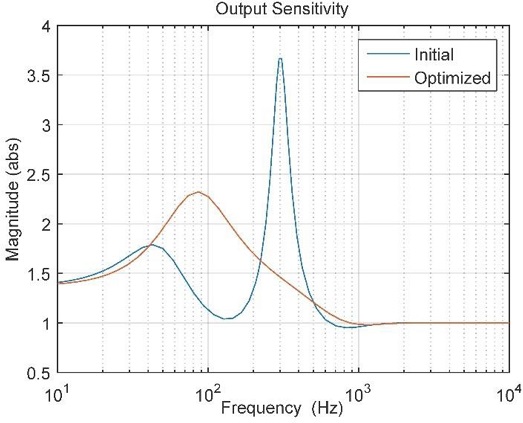
Fig. 3은 초기 제어기와 최적화된 제어기의 출력민감도를 비교하고 있으며, 최댓값은 3.67에서 2.32로 감소하여 기준을 만족한다.

4.1 유연모드 제어기 최적화 과정

많은 경우 회전축의 유연모드는 자기베어링 제어기 설계에 지대한 영향을 미친다. 운전 속도가 유연모드보다 낮더라도 제어 주파수 범위 내에 있는 유연모드는 센서 잡음, 운전속도의 배수 성분 등에 의해 진동을 유발하며, 제어 안정성을 저하한다. 유연모드에 대응하는 가장 일반적인 방법은 노치 필터의 사용이다. 노치 필터는 식(14)와 같은 전달함수로 표현된다.

노치 주파수는 유연모드 주파수에 따라 결정되며, 노치 필터의 설계는 노치의 폭을 결정하는 ζ_np 와 노치의 깊이를 결정하는 ζ_nz 를 정하는 과정이라고 할 수 있다.

위상선행 필터와 노치 필터를 동시에 사용하면 강체모드 제어기에서와 같은 위상여유도 최적화 방법을 사용할 수 없다. 유연모드에 의해 다수의 Gain Cross-Over 주파수가 있을 수 있으며, 노치 필터로 인한 차수의 증가로 수치적 불안정성이 증가한다. 또한 출력민감도 최소화는 여러 개의 지역 최소점(Local Minima)을 가질 수 있어, 전역 최소화(Global Minimization)가 필요하다.

흔히 사용되는 전역 최소화 방법으로 유전자 알고리즘이 있다. 일정 크기의 인구에 대해 비용함수에 해당하는 적합성(Fitness)을 계산하고, 진화와 돌연변이를 거쳐 세대를 반복함으로써 최적을 찾는 방법이다. 유전자 알고리즘의 가장 큰 문제점은 전역 최적치를 찾기 위해 인구가 크거나 세대 수가 많아야 하기 때문에 수렴하기 위해 많은 계산 시간의 필요하다는 것이다. 다음의 사례 연구를 통해 최적화 과정의 문제점을 파악한다.

대상은 340 kW 냉매압축기용 자기베어링으로서 회전축 질량 72 kg, 개루프 스프링 상수 -1,958 N/mm, 액츄에이터 상수103 N/A, 전류증폭기 주파수 대역 680 Hz의 특성을 가진다. Plant 전달함수는 Fig. 1과 같으며 3개의 유연모드를 확인할 수 있다. 유연모드의 주파수는 각각 393, 766, 1,550 Hz이다. 자기베어링 제어기는 식(6)과 같이 PID 기반 위상선행 필터, 노치 필터, 저역 통과 필터로 구성되어 있으며, 저역 통과 필터의 주파수는 1,500 Hz로 설정되었다. 제어기 변수는 위상선행 필터의 4개, 각 유연모드별 노치 필터당 2개로 총 10개이다.

이를 유전자 알고리즘을 이용해 최적화할 때 걸리는 계산 시간을 인구수에 대비해 구한 결과가 Fig. 4에 나와 있다. 계산 시간은 거의 인구수에 비례한다. 인구수가 50일 때 46.5초인거에 비해 인구수가 25,600일 때 거의 10,000초의 시간이 걸려 최적값을 찾아낸다. 계산은 i9-7920X (2.96 GHz) CPU, 64 GB RAM, 64 bit Win-10 컴퓨터에서 MATLAB Global Optimization Toolbox의 유전자 알고리즘을 사용하였다.

Fig. 4

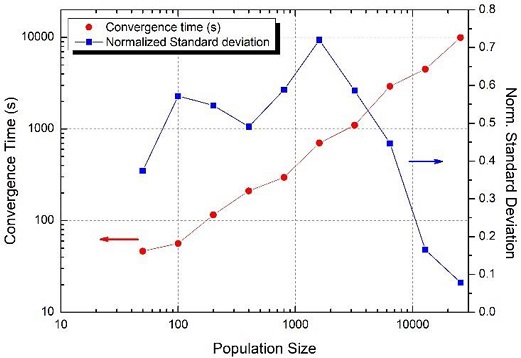
Convergence time with respect to the size of population (Red). Normalized standard deviation of solutions with respect to the population size

유전자 알고리즘의 특성상 인구수가 작을 때는 지역 최솟값으로 수렴할 가능성이 존재한다. 유전자 알고리즘을 여러 번 수행하여 각 파라미터의 평균과 표준편차를 구하면 정규화된 표준편차의 최댓값을 다음 식(15)로 구할 수 있다.

여기서, p_k,i는 k 번째의 제어 파라미터의 i 번째 최적해이다. 즉, $$ {\overline{\sigma }}_{\text{max}}$$는 유전자 알고리즘의 해가 얼마나 퍼져 있는지를 나타낸다. Fig. 4의 파란색 그래프는 유전자 알고리즘을 10회 수행하여 얻은 $$ {\overline{\sigma }}_{\text{max}}$$로 인구수가 작을 때는 최적화 결과값이 40% 이상 다를 수 있다. 수렴 시간의 증가에도 불구하고 인구수가 10,000을 넘어야 최적값의 표준편차가 20% 이하로 줄어들어 전역 최솟값에 수렴하는 경향을 보인다.

제어의 강인성 측면에서 제어 파라미터의 변화에 대한 최적점의 변화가 크지 않아야 한다. 파라미터의 섭동(Perturbation)에 따라 비용함수가 크게 바뀐다면, 제한 조건 근처에 있거나 지역 최소점을 둘러싸는 영역이 매우 작음을 의미하며 파라미터 변화에 따라 제어 결과가 크게 바뀔 수 있다. 이를 확인하기 위해 유전자 알고리즘을 수행하여 얻은 최적점에서 무작위로 10% 이내 만큼 파라미터를 변화시켜 초기값을 설정하고, 기울기 기반 최소화 방법인 Sequential Quadratic Programming (SQP)를 사용하여 최적화를 수행하였다. 만일 SQP에 의해 도달한 최소점이 유전자 알고리즘 결과와 유사하면, 최소점을 둘러싸는 파라미터 영역이 10% 정도의 파라미터 변화를 감당할 수 있음을 의미한다.

Table 2는 인구수 50으로 유전자 알고리즘을 10회 수행하여, 각 최적점의 강인성을 확인한 결과이다. 유전자 알고리즘으로 구한 출력민감도의 최솟값이 두 번째 열에 나와 있다. 유전자 알고리즘을 통해 얻은 파라미터값을 10% 이내로 무작위 변화시켜 초기값으로 설정한 후, SQP를 통해 최소화를 진행하였다. Table 2의 세 번째 열은 SQP에 의해 구한 파라미터와 유전자 알고리즘에서 얻은 파라미터 간의 차이를 비로 나타낸 것이며 다음 식(16)으로 정의된다.

Table 2

Robustness of local optima found by GA

여기서 p_k,GA 는 유전자 알고리즘에 의해 구한 k 번째 제어 파라미터이며, p_k,SQP 는 SQP로 구한 k 번째 제어 파라미터이다. 1번 해의 경우 파라미터가 46% 이상 변하였으며 출력민감도는 거의 불안정성에 가까운 18.5의 결과를 얻었다. 유전자 알고리즘 해가 강인성을 보인 경우는 2, 4, 10번으로 모두 파라미터의 변화가 10% 이내이며, SQP로 구한 출력민감도가 유전자 알고리즘의 출력민감도와 크게 다르지 않았다.

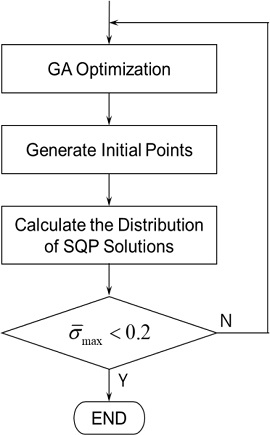
이상의 결과에 근거하여, 본 논문에서는 유전자 알고리즘과 기울기 기반 최적화 방법을 혼합한 효율적 최적화 과정을 제안한다. Fig. 5는 혼합 최적화 방법의 개략적인 순서도로서, 시작 단계에서 최소한의 인구수로 유전자 알고리즘을 수행하여 최적 파라미터를 구한다. 최적 파라미터로부터 일정범위(예를 들어 10%) 내에 무작위로 파라미터를 변화시켜 다수의 초기값을 구하고, SQP를 통해 해를 구한다. 식(15)를 이용해 정규화된 표준편차의 최댓값을 구하여 0.2 이하가 되는지 판단하여, 만족하지 않는 경우 다시 유전자 알고리즘으로 새로운 최적해를 찾아 반복한다. Fig. 4에서 확인할 수 있는 바와 같이 정규화된 표준편차의 최댓값이 0.2 이하로 되려면 인구수가 최소 10,000을 넘어야 하고, 수렴에 필요한 계산 시간은 4,495초이다. 본 논문에서 제안하는 혼합 최적화 과정을 통해 동일한 수렴 결과를 얻는데 걸리는 계산 시간은 평균 126초로 유전 알고리즘만을 사용하였때에 비해 35.7배 빠르게 결과를 얻을 수 있었다.

Fig. 5

Flow chart of mixed optimization algorithm

4.2 유연모드 제어기 최적화 결과

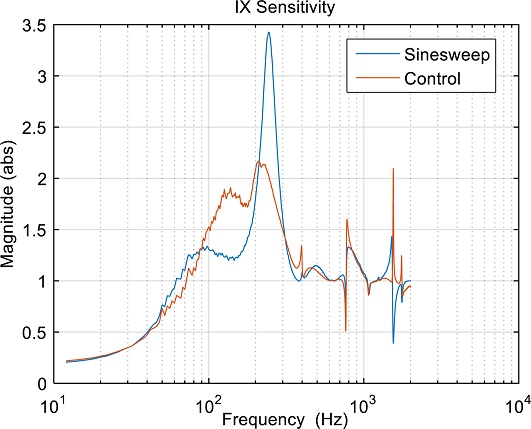
앞서 제시한 혼합 최적화 과정을 냉매압축기 자기베어링 제어기에 적용하였다. 자기베어링이 장착된 압축기는 Fig. 6에 나와 있다. 시스템 식별을 위해 Sine Sweep 방법이 사용되었다. 제어기에서 특정한 주파수의 입력을 인가하고, 출력에서 해당 주파수 성분을 DFT를 이용해 추출하여 주파수 응답을 구하는 방식이다.

Fig. 6

Prototype compressor for 340 kW chiller. The cooling capacity is 500RT

제어기는 위상선행 필터, 노치 필터, 저역 통과 필터로 구성되어 있다. Table 3은 시행착오 과정을 거쳐 수동으로 설정한 제어 파라미터와 최적화 과정을 통해 얻은 제어 파라미터를 비교한다. Fig. 7은 시제품에서 Sine Sweep 방법을 이용하여 측정한 출력민감도이다. 경험에 근거하여 수동으로 설정한 제어기의 경우 출력민감도의 최댓값이 3.43로 ISO 14839-3의 기준을 초과하는데 반해 혼합 최적화 과정으로 얻은 제어기를 적용한 결과 최댓값이 2.13로 기준을 만족하였다.

Table 3

Optimization result for flexible-mode control

Fig. 7

Output sensitivity measured from a prototype compressor test rig using sinesweep tests. Manually tuned control (Blue) vs. Optimized control (red)