무인항공기 이동 목표물 추적 비행 및 착륙 성능 개선을 위한 입력 신호 변형 기반의 제어 보조 시스템

2.1 쿼드콥터 제어 플랫폼

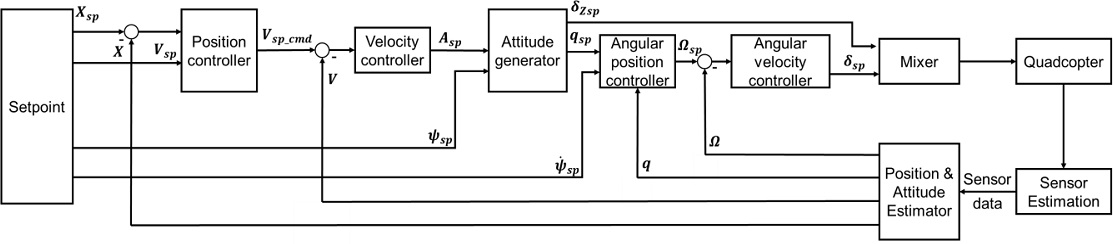
쿼드콥터가 사용자로부터 받은 비행 혹은 착륙 명령대로 동작하게 하기 위해서는 사용자의 명령을 출력 신호로 만들어줄 제어기가 필요하다. 본 연구에서는 위와 같은 역할을 해줄 제어 플랫폼으로 PX4를 사용하였다. PX4는 다수의 PID 제어기로 구성되어 있고, 쿼드콥터의 센서 데이터를 바탕으로 기체의 자세와 위치를 인지할 수 있는 상용 제어 플랫폼이다. PX4의 쿼드콥터 제어 방식은 Fig. 1과 같다.⁴

Fig. 1

PX4 quadcopter control block diagram4 (Adapted from Ref. 4 on the basis of OA)

쿼드콥터가 사용자로부터 명령을 받아 이를 수행하기 위해서는 자기 자신의 위치를 인지하기 위한 계측기가 필요하다. PX4는 쿼드콥터에 장착되어 있는 여러 센서로부터 데이터를 획득한 뒤 Fig. 1의 ‘Position & Attitude Estimator’에서 EKF (Extended Kalman Filter)를 이용하여 쿼드콥터의 현재 위치와 자세를 추정한다. X, X, q, Ω는 위치 및 자세 추정의 결과로, 각각 쿼드콥터의 위치, 속도, 쿼터니언 형태의 각도, 각속도를 의미한다.

PX4 사용자는 목표 위치, 목표 속도, 목표 Yaw축의 각도, 목표 Yaw축의 각속도를 의미하는 X_sp, V_sp, ψ_sp, $$ {\dot{\psi }}_{sp}$$ 등의 파라미터를 이용하여 쿼드콥터에게 명령을 내릴 수 있다. 사용자가 X_sp 를 입력하여 위치 명령을 내리면, X_sp 와 X 의 차이는 P 제어기 형태로 구성되어 있는 위치 제어기를 통해 목표 속도를 의미하는 V_{sp_cmd} 가 만들어진다. V_{sp_cmd} 와 V 의 차이는 PID 제어기 형태의 속도 제어기를 거쳐 목표 가속도인 A_sp 를 생성한다. 단, V_sp 입력이 존재할 경우 위치 제어기로부터 생성된 V_{sp_cmd} 을 V_sp 로 대체시킨다. 입력 받은 ψ_sp 와 속도 제어기로부터 형성된 A_sp 는 자세 생성기를 통해 목표로 하는 쿼드콥터의 자세인 q_sp 와 수직 방향 추력인 ζ_Zsp 를 생성한다. 이후 q_sp 와 q 그리고 $$ {\dot{\psi }}_{sp}$$ 은 P 제어기 형태인 각도 제어기의 입력으로 사용되어 목표 각속도인 Ω_sp 가 출력되고, Ω_sp 와 Ω의 차이를 PID 제어로 구성된 각속도 제어기를 통해 목표 추력인 δ_sp 를 생성시킨다. 최종적으로 자세 생성기로부터 생성된 δ_Zsp 와 각속도 제어기로부터 만들어진 δ_sp 는 ‘Mixer’를 통해 쿼드콥터의 모터 구동 명령으로 변환되어 쿼드콥터에 전달된다. 상용 무인항공기 제어 플랫폼인 PX4는 위와 같이 각각 2개의 P 제어기와 PID 제어기를 통해 쿼드콥터를 동작하게 한다. 쿼드콥터가 안정적으로 비행하기 위해서는 각 제어기로부터의 적절한 출력값이 필요하며, 이를 가능하게 하기 위해서는 총 8개의 제어 이득을 조절해야 한다.

2.2 쿼드콥터의 이동 목표물 인식 방법

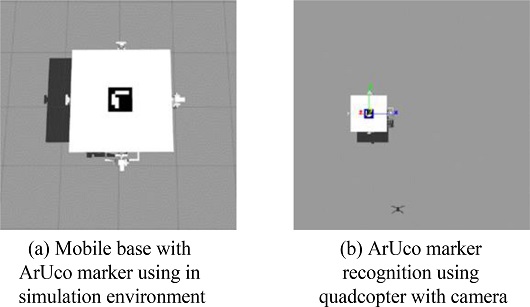
쿼드콥터가 움직이는 목표물을 쫓아 착륙하기 위해서는 목표물을 인식할 수 있어야 하고, 인식한 목표물로부터 높은 정밀도의 위치 정보를 획득해야 한다. 본 연구에서 목표물로부터 고정밀 위치 정보를 얻기 위해 쿼드콥터에는 카메라를, 목표물에는 기준 마커(Fiducial Marker)를 장착하여 쿼드콥터가 목표물을 인식할 수 있게 제작하였다. 기준 마커의 종류로는 ArUco Marker, Apriltag, ARTag, Stag 등이 있으며, 이들 중 Apriltag가 다양한 거리 및 각도에서 가장 인식률이 좋지만, CPU와 메모리 사용량이 가장 많았다. 무인항공기가 이동 목표물을 추적하고 착륙하는 동안에 지속적으로 Marker를 이용한 위치 추정이 이루어지기 때문에 CPU와 메모리 사용량을 무시할 수 없다. 따라서 준수한 인식률을 가지고 CPU와 메모리 사용량이 적은 ArUco Marker를 사용하였다.⁵

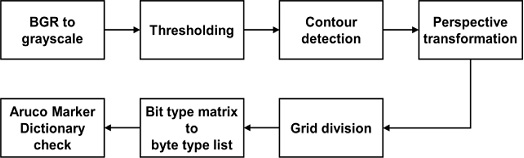
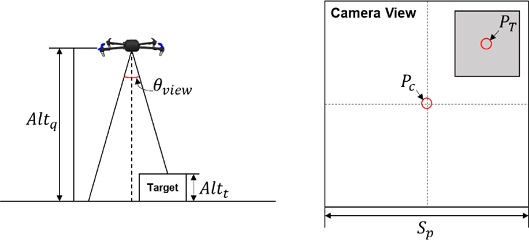
ArUco Marker는 각각 다른 ID를 가지고 있는 이진 매트릭스 Marker로, 이를 인식하기 위해서는 ArUco Marker의 회전각에 따른 바이트 리스트가 ID별로 저장되어 있는 ArUco Dictionary를 필요로 한다.⁶ Fig. 2는 본 연구에서 사용한 Marker의 형태이고 이것을 인식하는 과정은 Fig. 3과 같다.⁷ 먼저 카메라의 BGR 이미지 처리에 용이하도록 회색조로 변환한 이후 이미지에서 Marker의 경계를 뚜렷하게 하기 위하여 이진화시킨다. 이진화 작업으로 경계가 선명해진 이미지에서 외곽선을 추출한 후 추출한 외곽선의 꼭지점을 바탕으로 기울어진 Marker 이미지에 투영 변환을 적용하여 이미지 왜곡을 제거한다. 왜곡이 제거된 Marker를 격자 형식으로 나누어 Marker의 흰 부분을 1로, 검정 부분을 0으로 하는 비트 매트릭스를 만든다. 그 후, 비트 형식의 매트릭스를 바이트 형태의 리스트로 변경한 뒤, ArUco Dictionary에서 해당 ID의 Marker 바이트 리스트와 비교하여 어떤 방향에서도 인식할 수 있도록 하였다. 카메라 이미지에서의 인식한 Marker의 중앙값을 픽셀 형식으로 얻어, 획득한 픽셀 데이터를 바탕으로 쿼드콥터에서 목표물까지의 거리를 측정하였다. Fig. 4는 쿼드콥터와 목표물 사이의 거리 계산에 사용한 파라미터를 시각화한 것이다. θ_View 는 카메라의 화각, P_T 와 P_c 는 목표물 중앙의 픽셀 데이터와 이미지 중앙의 픽셀 데이터이다. Alt_q 와 Alt_t 는 각각 쿼드콥터와 목표물의 고도를 나타내고, S_p 는 이미지의 전체 픽셀 사이즈를 의미한다. 이러한 파라미터들을 이용하여 쿼드콥터와 목표물 사이의 거리 계산 및 픽셀 단위에서 미터 단위의 거리 변환을 적용하여 쿼드콥터와 목표물의 상대 거리를 계산하였다.⁸

Fig. 2

ArUco marker used in this research

Fig. 3

ArUco marker recognize process

Fig. 4

Parameters used for ArUco marker recognition

본 연구에서의 무인항공기는 이동 목표물에 착륙하기 위해 10 m 상공까지 이륙한 뒤 목표물을 따라서 추적하고 영상인식 기반으로 착륙한다. 따라서 시뮬레이션 상황에서 무인항공기의 최대 고도는 10 m이다. ArUco Marker를 이용하여 거리를 측정할 때는 카메라와 Marker 사이의 거리가 측정 결과에 큰 영향을 미치고, 그 거리가 작을수록 측정 결과의 오차 또한 작아진다. 무인항공기가 Marker를 인식할 때의 최대 거리는 10 m 미만이므로, 시뮬레이션 환경에서 무인항공기와 Marker 사이의 X, Y축 거리는 일치시키고, Z축 거리를 10 m만큼 띄워 영상 처리 결과의 오차를 측정하였다. 총 X축, Y축에 대해 각각 2,000개의 데이터를 획득하여 오차를 측정하였으며, Table 1과 같이 최솟값, 최댓값, 평균값으로 나누어 확인하였다. 평균적으로 0.04-0.08 m로 오차가 측정되었으며, 최댓값은 0.2265, 최솟값은 0.001 m 이하였다. 위 수치들을 로우 패스 필터를 통해 평균치와 근사한 값으로 필터링 될 것이기 때문에 무인항공기의 착륙 지점의 크기가 1.5 m × 1.5 m이고, ArUco Marker가 항상 수평을 유지하며, 이동 목표물에 착륙할 때 무인항공기와 ArUco Marker 사이의 거리가 작아지면서 오차 또한 점점 작아질 것이라 가정하였을 때, 측정된 오차값은 실험 결과에 영향을 미치지 못할 것으로 판단한다.

Table 1

The error of position estimation using ArUco marker

2.3 입력 신호 변형 기반 쿼드콥터 제어 보조 시스템

2.2절의 영상인식 방법을 적용하여 쿼드콥터가 목표물을 인식할 수 있도록 한 후 PX4의 쿼드콥터 제어 시스템을 이용하여 무인항공기 이동 목표물 추적 및 착륙을 실시하였다. 이 경우 제어 초기에는 오버슈트로 인해 무인항공기가 목표물을 지나치는 상황이 발생하여 쿼드콥터가 안정적으로 비행하지 못하였고, 제어 후기에는 정상상태 오차를 줄이지 못해서 이동하는 목표물에 착륙하지 못하였다. 원인 분석 결과, PX4는 사용자가 직접 쿼드콥터를 조종하거나 고정된 지점을 향해 자율적으로 비행하도록 명령하는 상황에 적합하게 설계되었기 때문에 이동 목표물 추적이라는 특수한 상황에 대응할 수 없다. 이를 해결하기 위해 본 연구에서는 입력 신호의 형태를 변형시킬 수 있는 제어 보조 시스템인 IST (Input Signal Transformer)를 제작하여 오버슈트와 정상상태 오차를 제거하였다.

앞서 언급된 문제를 해결하기 위해 시간에 따라 변하는 제어 이득인 IST를 고안하였다.⁹ IST는 주 제어기의 기능을 보조하는 전처리기 역할을 하며, 제어 초반부의 입력 신호를 감소시켜 오버슈트를 제거하고 제어 후반부의 입력 신호를 증폭시켜 정상 상태 오차를 제거할 수 있도록 설계되었다. 이러한 기능을 효과적으로 수행하기 위해 IST는 시그모이드 함수의 형태를 도입하였으며, 아래 식(1)과 같이 제어 이득 K_IST로 표현되었다.

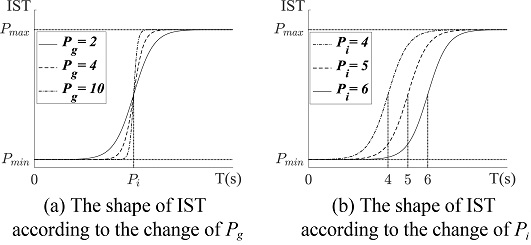
K_IST는 시간에 따라 그 값이 변화하며, P_min, P_max, P_g, P_i 등의 4가지 파라미터를 설정하여 입력 신호의 감쇠 한계점 및 증폭 한계점, 증가율과 증가 시점을 결정할 수 있다. P_min은 K_IST의 최솟값을 지정해주는 파라미터로, 입력 신호를 감소시켜 제어 초반부의 쿼드콥터가 목표물을 추적할 때 발생하는 오버슈트를 줄이는 역할을 한다. P_max는 K_IST의 최댓값을 정하는 파라미터이고, 제어 후반부에 쿼드콥터와 목표물 사이의 오차를 줄여 정밀하게 착륙할 수 있도록 하는 파라미터이다. P_g는 증가 기울기 파라미터, P_i는 중심점 이동 파라미터이다. P_g를 조정하여 K_IST가 P_min부터 P_max까지 증가하는 기울기를 조절할 수 있고, P_i를 변경하여 K_IST의 중심점을 시간 축으로 이동시켜 입력 신호를 증폭시키는 시점을 결정할 수 있다. Fig. 5는 P_g와 P_i의 변화에 따른 IST의 형태를 나타낸다. 4가지 파라미터를 조절하여 만들어진 K_IST는 기존의 입력 신호와 곱해져 S-Curve 형태의 변형된 입력 신호를 만들어낸다. P_min, P_max, P_g, P_i는 아래 사항들을 고려하여 실험적 방법으로 결정하였다.

Fig. 5

The shape of IST according to parameter conditions

(1) 오버슈트를 제거하는데 가장 큰 영향을 끼치는 파라미터는 P_min이다. 따라서 P_min을 충분히 작은 값을 주어 오버슈트를 제거하되, 상승 시간이 너무 길어지지 않게끔 정해야 한다.

(2) 정상상태 오차를 제거하는데 가장 큰 영향을 끼치는 파라미터는 P_max이다. 따라서 P_max는 1보다 크거나 같은 적당한 값으로 결정하여야 한다.

(3) P_i는 증폭 시점을 결정하는 파라미터로, 필요한 증폭 시점에 맞추어 결정하여야 한다.

(4) P_g는 오버슈트 제거와 상승 시간, 증폭 시작 시간, 최대 증폭까지 걸리는 시간 등에 모두 관련이 있기 때문에 P_g를 결정할 때는 위와 같은 사항들을 고려하여 결정하여야 한다.

K_IST는 위 사항들을 고려하여 4가지 파라미터를 결정한 이후 이들을 적용한 시그모이드 함수의 형태를 시각적 확인하여 제어 상황을 유추할 수 있기 때문에 PID 제어기의 실험적 제어 이득 튜닝보다 직관적이라는 장점이 있다.

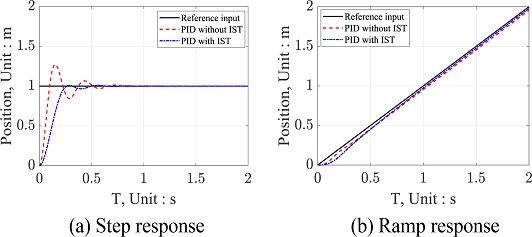
단위 계단 입력과 단위 경사 입력에 대한 IST의 성능을 확인하기 위해 시뮬링크를 이용하여 2차 시스템에 대한 시뮬레이션을 진행하였다. 단위 계단 입력과 단위 경사 입력 때의 PID 제어 이득은 모두 동일하며, 각 입력에 대한 IST 제어 파라미터값은 Table 2와 같이 설정하였다. 단위 계단 입력의 경우 Table 3과 같이 PID 제어기만 사용하였을 때의 상승 시간은 0.065초, 오버슈트는 27.18%, 정착 시간은 0.621초의 성능을 보이는 반면 IST와 PID 제어기를 함께 사용하였을 경우 상승 시간은 0.161초, 오버슈트는 1.04%, 정착 시간은 0.460초의 성능을 보인다. IST를 사용하였을 때가 사용하지 않았을 경우보다 오버슈트와 정착 시간이 감소되는 것을 확인할 수 있지만 상승 시간이 커진 것을 확인할 수 있다. PID 제어기를 사용한 경우, 오버슈트는 제어 초반부의 에러를 줄이기 위해 필요한 제어기 출력보다 더 큰 출력을 발생시켰을 때 생기게 된다. IST는 제어 초반부의 입력 신호를 감소시킨 상태에서 조금씩 증폭시키기 때문에 제어기의 불필요한 출력을 줄여 오버슈트를 제거하는 효과를 가지고 있다. 하지만 제어기의 입력 신호를 감소시킨 후 조금씩 증폭시키는 과정으로 인해 상승 시간이 길어지는 현상이 발생한다. 단위 경사 입력에서는 Table 3과 같이 PID 제어기만 사용한 경우 정상상태 오차가 0.0455였고, IST와 PID 제어기를 함께 사용한 경우에는 0.0227이었다. 경사 신호를 입력하는 경우에는 제어하는 도중에도 입력 신호가 지속적으로 변하기 때문에, 고정된 신호를 추종하는 계단 입력의 경우와 달리 정상상태 오차가 발생하게 된다. IST는 변화하는 입력 신호를 추종하기 위해 제어 후반부의 오차 성분을 증폭시킴으로써 주 제어기의 출력도 함께 증폭시키기 때문에 PID 제어기만 사용한 경우보다 정상상태 오차를 줄일 수 있다. 본 연구에서는 무인항공기의 안정적인 추적과 착륙을 목표로 하기 때문에 상승 시간보다 오버슈트와 정상상태 오차를 더욱 중요한 성능 지표로 판단한다. Figs. 6(a)와 6(b)는 PID 제어기와 IST를 함께 사용한 경우와 그렇지 않은 경우에서의 단위 계단 입력, 단위 경사 입력에 대한 명령 추종 성능을 나타낸다.

Table 2

The parameters used in simulation of step and ramp response

Table 3

Step and ramp responses of PID controller without IST and PID controller with IST

Fig. 6

Step and Ramp response of PID controller without IST and PID controller with IST

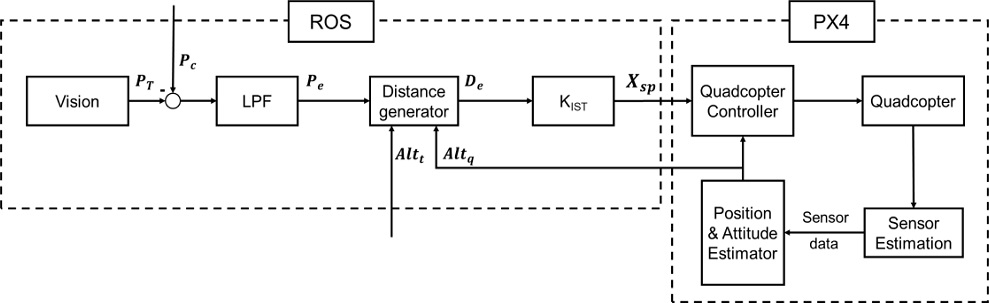
IST를 사용한 영상인식 기반의 쿼드콥터 이동 목표물 추적 및 착륙 제어 시스템은 Fig. 7과 같이 구성하였다. 카메라 이미지상에서 목표물의 위치를 나타내는 픽셀 정보인 P_T 와 이미지 정중앙을 나타내는 픽셀 정보인 P_c 의 차이인 P_e 를 쿼드콥터와 목표물 사이의 거리 D_e 로 변환시킨다. 이때, 픽셀 정보의 노이즈 제거를 위해 LPF (Low Pass Filter)를 사용하였다. D_e 를 쿼드콥터 제어의 입력 신호로 사용할 경우, 오버슈트와 정상상태 오차가 발생하기 때문에 ‘K_IST’를 사용하여 변형된 위치 명령인 X_sp 를 만든다. 만들어진 X_sp 를 이용하여 쿼드콥터 제어기를 거쳐 쿼드콥터에게 이동 명령을 내린다. 쿼드콥터의 제어와 위치 및 자세 추정은 PX4에서 수행 한다.

Fig. 7

Quadcopter moving target tracking control block diagram

3.1 ROS를 활용한 메시지 통신 구조

ROS는 오픈 소스 메타 운영체제로써 일반적인 운영체제에 설치하여 하드웨어 추상화, 저수준 제어, 프로세스 간의 메시지 전달, 패키지 관리 등의 기능을 제공한다.¹⁰ 본 연구에서는 ROS를 활용하여 무인항공기 이동 목표물 추적 및 착륙 시스템을 구축하고, 통신 구조를 구성하였다. PC를 사용하여 쿼드콥터에 이동 명령을 내리기 위해서는 둘 사이의 통신을 위한 프로토콜이 필요하다. 이러한 통신 프로토콜로 MAVLink (Micro Air Vehicle Link)를 사용하여 PC와 쿼드콥터의 통신 체계를 구축하였다. MAVLink는 Marshaling 라이브러리 형태로 만들어진 통신 프로토콜로, 리소스 혹은 통신 대역의 제약을 가지는 시스템에 사용하기 적합한 통신 방법이다.¹¹ ROS와 PX4를 연결해줄 통신 프로토콜로 MAVLink를 사용하기 위해서는 별도의 통신 노드가 필요하다. MAVROS는 ROS와 PX4 사이의 메시지 통신을 연결해줄 통신 노드 역할을 수행한다.

ROS는 시스템 간의 데이터 송수신에 메시지 통신을 이용하며, 메시지 통신 방법에는 Topic, Service, Action이 있다. Topic은 퍼블리셔가 서브스크라이버에게 지속적으로 데이터를 전송하는 단방향 비동기식 통신 방법이며, Service는 클라이언트가 서버에게 데이터 송신 요청을 할 때만 서버가 클라이언트에게 데이터를 전송하는 양방향 동기식 통신이다. Action은 클라이언트가 서버에게 작업을 요청하였을 때, 서버가 클라이언트에게 작업에 대한 피드백과 작업 결과를 보내주는 양방향 비동기식 통신이다.¹²

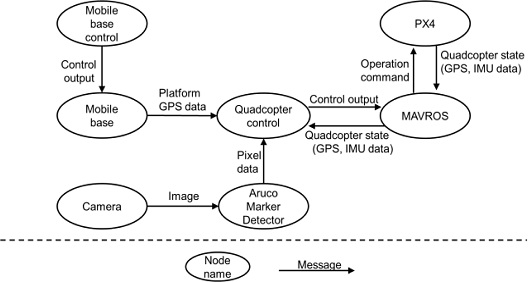
본 연구에서는 각종 센서 데이터 및 제어 명령들을 지속적으로 송신 및 수신하는 것이 가능한 Topic을 활용하여 시스템 간의 통신 체계를 구축하였다. Fig. 8은 본 연구를 위해 제작된 제어 시스템의 메시지 통신 흐름을 나타낸다. ‘Mobile Base’는 쿼드콥터가 추적하고자 하는 이동 목표물을 의미하며, ‘Mobile Base Control’ 노드의 제어 출력에 따라 동작한다. 쿼드콥터와 목표물의 거리를 계산하는데 필요한 정보는 ‘Mobile Base’와 ‘ArUco Marker Detecter’ 그리고 ‘MAVROS’ 노드로부터 얻는다. ‘Mobile Base’ 노드에서 목표물의 고도 정보를 얻고, ‘MAVROS’ 노드로부터 쿼드콥터의 고도 정보 및 상태 정보를 얻는다. ‘Camera’ 노드는 쿼드콥터에 부착된 카메라로 찍은 이미지를 ‘ArUco Marker Detecter’ 노드로 전송하고, 전송받은 이미지를 2.2절의 ArUco Marker 인식 과정을 거쳐 목표물의 픽셀 정보를 얻은 후 ‘Quadcopter Control’ 노드로 보낸다. 상대 거리 계산에 필요한 정보를 모두 얻은 ‘Quadcopter Control’ 노드는 2.4절의 제어 시스템을 거쳐 출력되는 명령을 ‘MAVROS’ 노드로 전송하고, ‘MAVROS’ 노드는 전송받은 위치 명령을 ‘PX4’로 전송하여 쿼드콥터를 움직이게 한다.

Fig. 8

ROS message flow chart for quadcopter moving target tracking and landing system

3.2 Gazebo 시뮬레이션 환경 구성

본 연구에서는 Gazebo 시뮬레이터를 사용하여 쿼드콥터의 이동 목표물 추적 및 착륙 제어 시스템의 성능 검증을 진행하였다.¹³ Gazebo 시뮬레이터는 물리엔진을 탑재하고 있기 때문에 실제와 유사한 환경을 구성할 수 있고, 플러그인을 활용하여 센서와 모터의 동작을 구현할 수 있다. 또한 Gazebo 시뮬레이터는 ROS와 연동하여 사용하기에 용이하다.

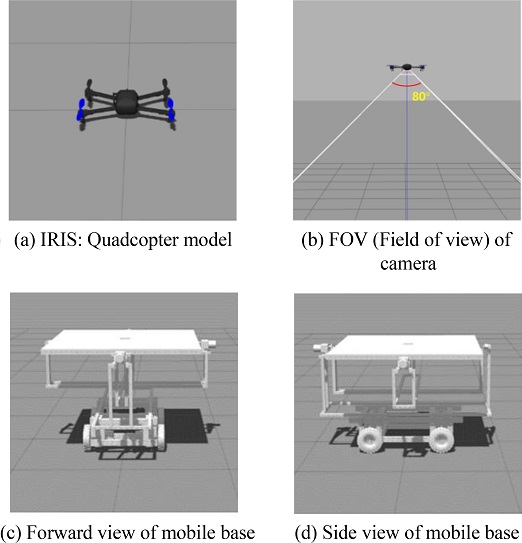
Fig. 9는 성능 검증 시뮬레이션에 사용한 쿼드콥터와 목표물이다. 쿼드콥터는 IRIS 모델을 사용하였으며, ArUco Marker를 인식할 수 있도록 카메라 플러그인을 적용하였다. 적용한 카메라의 화각은 80^o이며, 800 × 800 화소의 이미지를 얻을 수 있다. 그 외 GPS (Global Positioning System), IMU (Inertial Measurement Unit), Barometer 센서 플러그인이 적용되어 있기 때문에 쿼드콥터의 상태를 확인할 수 있다.

Fig. 9

Models used in simulation

목표물로는 착륙 패드가 장착된 모바일 베이스를 사용하였고,¹⁴ 로봇의 물리적인 특성을 표현할 수 있게끔 URDF (Unified Robot Description Format) 형식으로 제작하였다. 본 시뮬레이션에서는 모바일 베이스의 이동 기능을 구현하기 위해 Skid-Steer 플러그인을 사용하였고, GPS 플러그인을 적용하여 수평 유지 플랫폼의 위도와 경도 그리고 고도 정보를 얻을 수 있도록 제작하였다. 또한 Fig. 10과 같이 수평 유지 플랫폼의 상부에 ArUco Marker를 부착하여 쿼드콥터가 모바일 베이스를 목표물로 인식할 수 있도록 하였다.

Fig. 10

Mobile base with ArUco marker in simulation environment

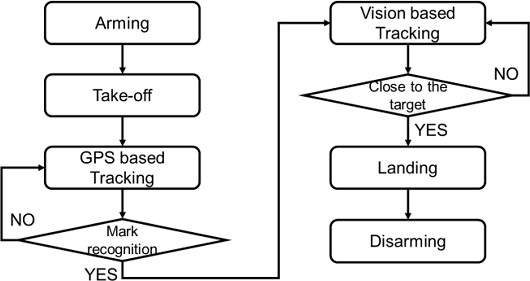
4.1 쿼드콥터 동작 시나리오

Fig. 11은 시뮬레이션에서의 쿼드콥터의 동작 시나리오를 정리한 것이다. 시뮬레이션은 쿼드콥터와 목표물을 10 m 떨어뜨린 상태에서 시작한다. 먼저 쿼드콥터에 시동을 건 이후 이륙 명령을 내린다. 그리고 쿼드콥터가 목표물을 인식할 때까지 GPS 정보를 기반으로 목표물을 쫓아 추적 비행을 진행한다. GPS 기반의 추적 비행 중 목표물에 부착한 ArUco Marker를 인식하였을 때, 영상인식 기반 추적 비행으로 전환한다. 그리고 목표물과 일정 거리만큼 가까워진 경우 목표물에 착륙하도록 명령을 내린다. 착륙이 완료되었다면, 쿼드콥터의 시동을 끈 후 시뮬레이션을 종료한다. 위와 같은 순서로 IST를 사용하였을 경우와 사용하지 않았을 경우를 비교하였다. PX4의 제어 이득은 IST를 사용하였을 때와 사용하지 않았을 때 모두 같은 값으로 진행하고, 목표물의 이동거리가 45 m가 넘어갈 때까지 쿼드콥터가 착륙하지 못하였을 경우 착륙에 실패했다고 판단하여 시뮬레이션을 종료하였다.

Fig. 11

Quadcopter operating scenario

4.2 고정 목표물 추적 및 착륙 시뮬레이션

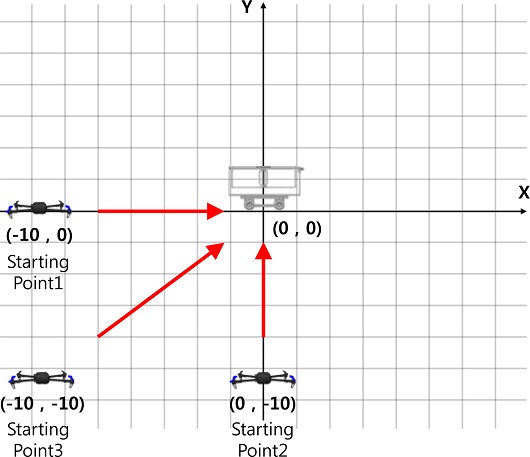
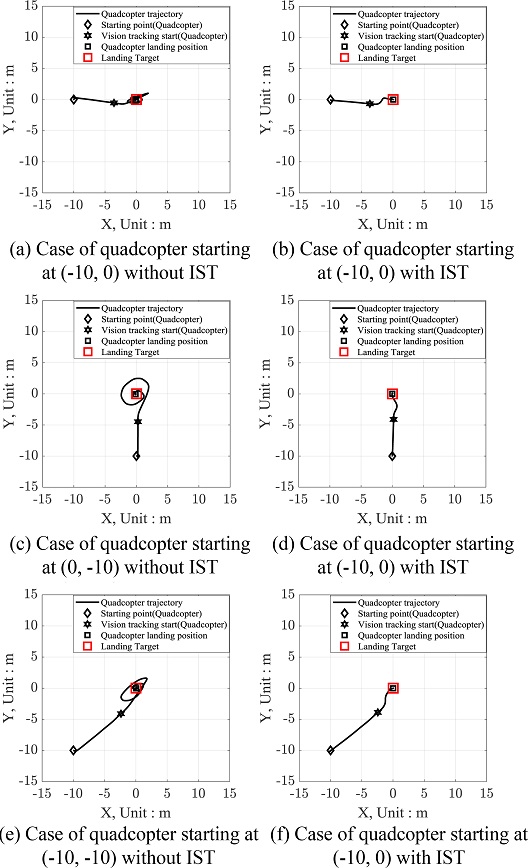
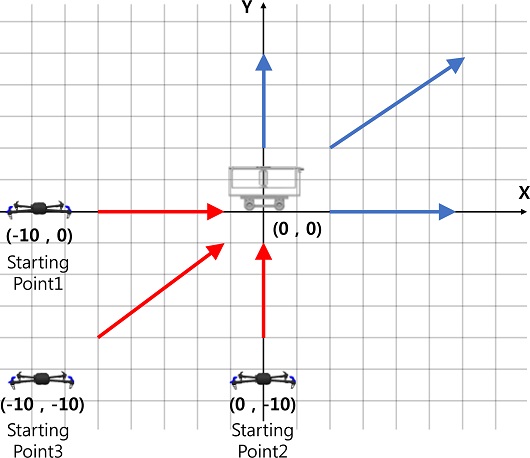
이동 목표물 추적 및 착륙 시뮬레이션을 진행하기 이전에 고정 목표물 추적 및 착륙 시뮬레이션에서 IST를 사용하였을 때 오버슈트의 제거 양상을 확인하였다. 이때, 쿼드콥터의 동작 순서는 4.1절의 시나리오를 바탕으로 진행하였다. Fig. 12는 고정 목표물 추적 및 착륙 시뮬레이션을 진행할 때에 쿼드콥터와 목표물의 시작 위치를 나타낸다. 목표물은 항상 (0, 0)의 자리에 위치하며, 쿼드콥터는 (-10, 0), (0, -10), (-10, -10) 등의 3가지 좌표에서 이륙하여 추적을 시작한다. Fig. 13은 쿼드콥터의 고정 목표물 추적 및 착륙 시뮬레이션의 결과이다. Figs. 13(a), 13(c) 그리고 13(e)는 IST를 사용하지 않았을 경우이고, 13(b), 13(d) 그리고 13(f)는 IST를 사용한 경우이다.

Fig. 12

Starting point of quadcopter in fixed target tracking and landing simulation

Fig. 13

Simulation results of fixed target tracking

IST를 사용한 경우 사용하지 않은 경우 모두 ArUco Marker를 인식한 이후 목표물에 착륙을 성공하였다. 하지만 IST를 사용하지 않은 경우는 오버슈트가 발생하여 ArUco Marker를 인식한 이후부터 착륙까지 안정적이지 않게 비행하는 반면에, IST를 사용한 경우는 IST를 사용하지 않은 경우에 발생했던 오버슈트를 제거하여 안정적으로 비행했음을 확인할 수 있다.

4.3 이동 목표물 추적 및 착륙 시뮬레이션

쿼드콥터가 이동 목표물을 추적하고 착륙할 때에 IST의 오버슈트 및 정상상태 오차 제거 효과를 확인하기 위해 시뮬레이션을 진행하였다. 쿼드콥터의 동작은 4.1절의 시나리오와 동일하게 진행하였고, Fig. 14와 같이 쿼드콥터와 목표물을 배치하였다. 시뮬레이션은 쿼드콥터가 (-10, 0), (0, -10), (-10, -10)의 좌표에서 출발하여 (0, 0) 좌표로부터 +X축, +Y축, 대각선 방향으로 이동하는 목표물을 쫓아 비행하고 일정 거리까지 가까워지면 착륙하는 방식으로 실험을 진행하였다. 목표물의 이동 속력에 따라 쿼드콥터의 이동 목표물 추적 및 착륙 성능의 차이가 생길 수 있기 때문에 이동 목표물의 속력이 0.4 m/s일 때를 저속으로, 0.8 m/s일 때를 고속으로 이동하는 것이라 상정하여 두 가지 경우를 나누어 시뮬레이션을 진행하였다.

Fig. 14

Starting points of quadcopter and direction of moving target in tracking and landing simulation

4.3.1 저속으로 이동하는 목표물 추적 및 착륙

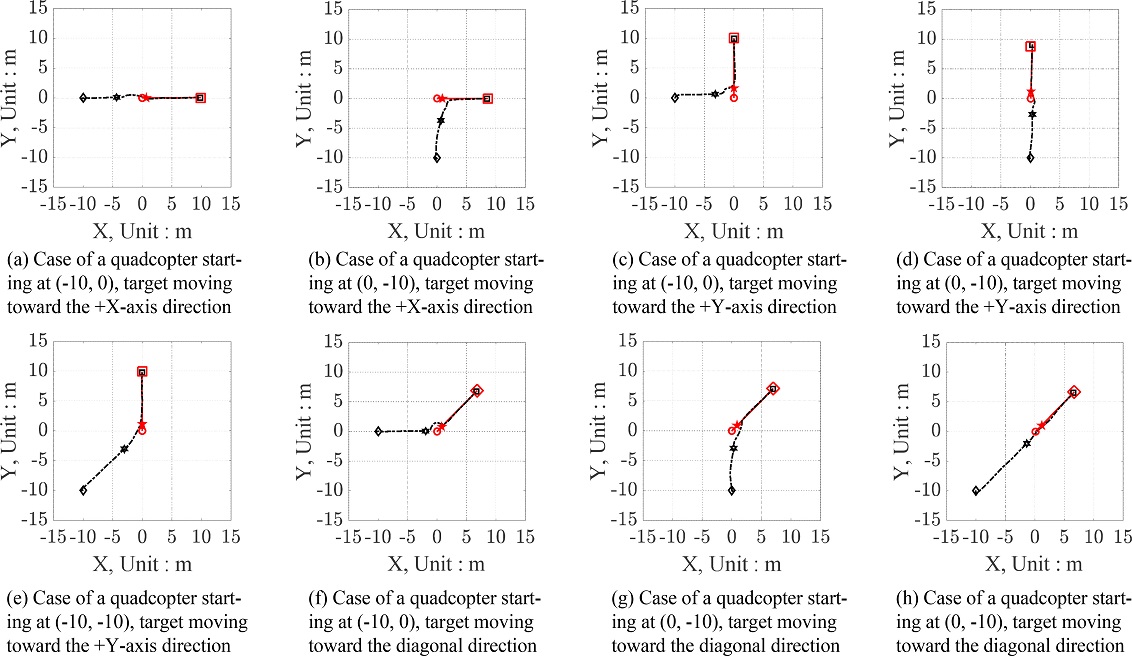
Fig. 15는 쿼드콥터가 (-10, -10)의 좌표에서 이륙하여 +X축 방향으로 저속 이동하는 목표물을 추적하고 착륙할 때에 IST를 사용하지 않았을 경우와 IST를 사용하였을 경우를 나타내는 그림이다. IST를 사용하지 않았을 경우 쿼드콥터가 ArUco Marker를 인식하여 영상인식 기반으로 목표물을 추적할 때에 오버슈트가 발생하여 불안정하게 추적하고 정상상태 오차를 줄이지 못하여 목표물이 45 m까지 이동할 때까지 착륙에 성공하지 못하는 것을 확인할 수 있다. 그에 반해 IST를 사용하였을 경우는 목표물을 추적하는 상황에서 오버슈트가 발생하지 않았고, 빠른 시간 내에 정상상태 오차를 줄여 목표물이 10 m가량 움직였을 때 착륙을 성공하였다. Figs. 16은 15의 경우를 제외한 IST를 사용한 저속 이동 목표물 추적 및 착륙 시뮬레이션 결과이다. Fig. 15(b)와 같이 8가지 상황 모두 이동하는 목표물을 추적할 때 오버슈트 없이 안정적으로 쫓고, 정상상태 오차를 줄여 착륙에 성공하는 모습을 볼 수 있다.

Fig. 15

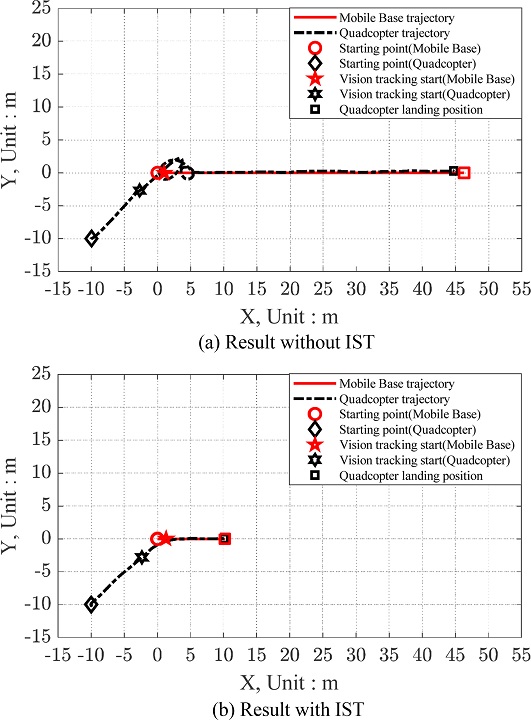
Simulation results of low-speed target tracking and landing with a quadcopter starting at (-10, -10) and target moving toward the +X-axis direction

Fig. 16

Simulation results of low-speed target tracking and landing using IST

4.3.2 고속으로 이동하는 목표물 추적 및 착륙

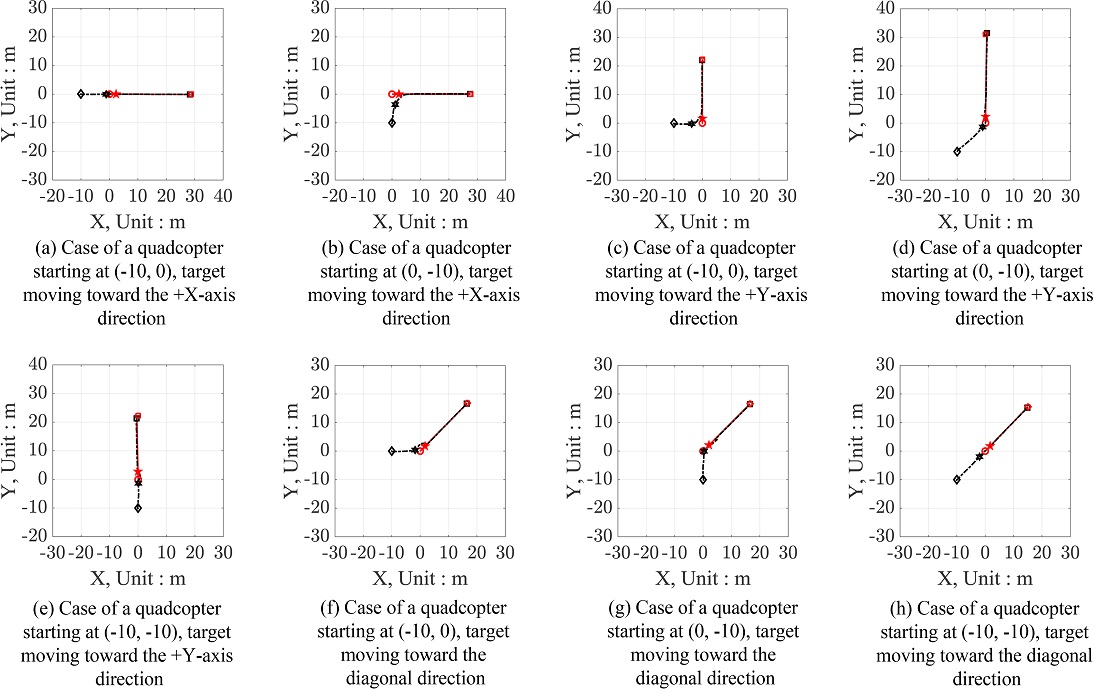
Fig. 17은 +X 방향으로 고속 이동하는 목표물을 (-10, -10) 좌표에 위치한 쿼드콥터가 추적하여 착륙한 결과를 나타낸다. 저속으로 이동하는 경우와 동일하게 IST를 사용하지 않은 경우에서는 오버슈트가 발생하여 기체가 안정적으로 추적할 때까지 시간이 걸리는 반면에, IST를 사용한 경우에는 오버슈트가 발생하지 않아 ArUco Marker를 인식한 이후에 안정적으로 목표물을 쫓아가는 모습을 볼 수 있다. 그리고 IST를 사용하지 않은 경우는 목표물이 45 m까지 이동할 때까지 정상상태 오차를 줄이지 못하여 착륙에 성공하지 못하는 반면에, IST를 사용한 경우는 목표물이 25 m만큼 움직였을 때까지 정상상태 오차를 충분히 줄여 착륙에 성공하였다. Figs. 18은 17(b)의 상황을 제외한 IST를 사용한 경우의 고속 이동 목표물 추적 및 착륙 시뮬레이션의 결과이다. 8가지 모든 경우 영상인식 기반으로 쿼드콥터가 이동 목표물을 추적할 때 발생했던 오버슈트가 사라진 것과 정상상태 오차를 제거하여 착륙에 상공한 결과를 확인할 수 있다.

Fig. 17

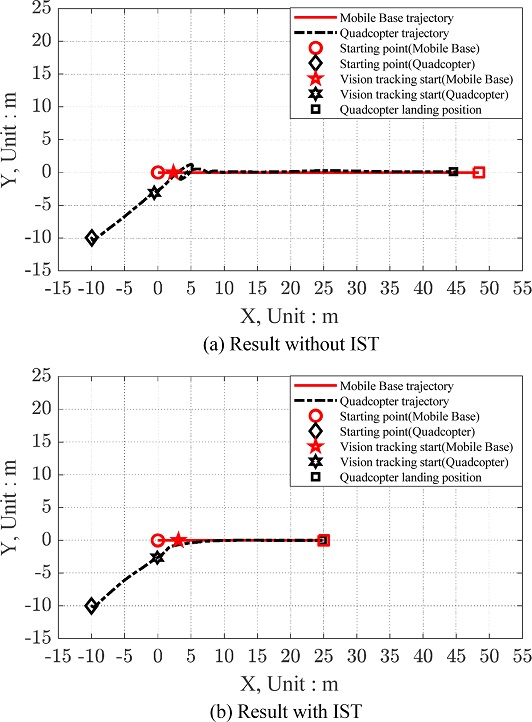
Simulation results in case of high-speed target tracking and landing, quadcopter starting at (-10, -10), target moving on the +X-axis direction

Fig. 18

Simulation result of high speed target tracking and landing using IST