50톤급 유압 브레이커 하우징 최적설계

1. 서론

굴착기의 암(Arm)의 끝부분에 장착되어 시설물의 해체, 암반과 도로 파쇄 등 주로 토목 및 건설공사 현장에서 사용하는 어태치먼트(Attachment)의 한 종류인 유압 브레이커는 굴착기로부터 공급받는 고압의 유압과 질소가스에서 전달되는 힘으로 작동된다. 유압 브레이커는 크게 메인바디(Main Body)와 하우징(Housing)으로 구성되며, 유압과 질소가스로부터의 힘은 피스톤의 운동에너지로 그리고 치즐의 타격에너지로 전달된다.

Lee, et al. [1]은 유압 브레이커 하우징을 대상으로 피로수명시험을 진행하였다. 충격 부하로 인한 피로누적에 의한 크랙이 주요 고장 모드임을 확인하였고, 이를 근거로 하우징의 수명을 추정하였다. 피로수명시험 설계를 위해 1차적으로 응력 취약 부위 선정을 위해 12개소에 해당하는 임의의 부위에 스트레인 게이지를 부착하여 실차시험을 진행하였으며, 그 결과 벌크캡과 체결되는 플레이트부와 U형 리브사이 용접 부위가 타 지점보다 응력에 취약한 걸로 나타났다. 이 결과를 토대로 리브의 두께또는 형상 그리고 강도를 개선할 필요성을 도출했다.

Shin, et al. [2]은 실험계획법을 이용하여 범용 유압 브레이커의 타격에너지와 타격수를 최적화하였다. 브레이커 타격수 극대화를 목적함수로 설정하고, 타격에너지 10% 증가와 설계인자 기준치수를 약 10% 정도 변경을 구속조건으로 하여 최적화를 수행한 결과 피스톤의 행정거리를 10% 증가함으로써 약 8.6%의 타격에너지 증대효과를 기대할 수 있었으나 타격수는 약 10% 정도 감소하였다.

Hur, et al. [3]은 유압 브레이커의 충격흡수를 위한 4가지 구조의 사이드 댐퍼를 제시하고, 유한요소해석 프로그램인 ANSYS를 이용한 응력 해석과 함께 변위 전달율을 계산하였다.

Jung [4]은 36톤급 유압 브레이커 사이드 하우징 브라켓으로 최적설계를 수행한 결과, 초기모델에 비해 중량은 14.7 증가하였지만 최대응력은 41.6% 감소시킬 수 있었다.

Park [5]은 근사 모델(Metamodel)을 이용하여 유압 브레이커 하우징의 최대 응력이 거의 변화되지 않으면서 철판과 Rib 두께 등을 달리하여 무게를 33 kg(4.96%)까지 감소시킬 수 있었다.

Park, et al. [6]은 유압 브레이커의 설계 요구사항을 만족시키면서 초기 중량 664에서 최적 중량 632 kg으로 약 4.8% 감소하는 결과를 얻을 수 있었다.

Cho, et al. [7]은 유압 브레이커의 충격과 소음 저감을 위하여 우레탄 및 사이드 댐퍼에 판 스프링 등을 추가로 적용한 후 유한요소 모델링 및 구조해석을 수행한 결과, 개발품 메인바디의 등가응력이 시제품보다 약 50% 수준으로 감소한 것을 확인하였다.

Lim, et al. [8]은 열-구조 연성해석을 통한 유압 브레이커의 주요 부품인 실린더와 피스톤의 안정성을 평가하였다. 유압 브레이커 외에도 건설기계에 실험계획법을 적용한 최적설계 논문으로는 Yoo, et al. [9] 등의 휠 로더 차축의 최적형상에 관한 연구, Lee, et al. [10]의 크레인 붐의 형상 최적화, Hong, et al. [11]의 저상형 고소작업차량 붐 조인트의 최적설계, Song, et al [12]의 너클크레인 링크의 형상 최적화, Lee, et al. [13]의 텔레스코픽 붐형 지게차의 붐 최적설계 등이 있으며, 주요 내용으로는 FEM 결과를 토대로 안정성을 판단하고 파손이 예측되는 부분을 확인 후 응력을 최소화시키기 위해 실험계획법을 이용하여 최적설계를 실시하였다.

건설기계 이외에도 Helmet Liner [14] 혹은 Metal Bellow [15] 등에 실험계획법을 이용한 논문을 찾아 볼 수 있으며, 다구찌 기법을 이용한 논문[16]과 위상 최적설계[17,18] 등 다양한 최적설계 논문들이 있다.

유압 브레이커는 작동 시 치즐의 반복적인 타격으로 인한 소음과 진동을 줄이기 위한 저소음형 유압 브레이커에 관한 연구[19,20]와 함께 타격 에너지 및 타격 수 등 타격성능 향상에 관한 연구가 주를 이루어 왔으나 굴착기의 동력소모와 피로하중 등에 크게 영향을 미치는 중량에 대한 연구는 상대적으로 미미한 편이다. 본 연구에서는 유압 브레이커 하우징의 중량을 최소화함으로써, 유압 브레이커의 원가 절감과 함께 굴착기의 동력과 피로하중의 영향을 최소화시키는 것을 목표로 하였다. 유압 브레이커의 구조해석을 위해서 상용 FEM 프로그램인 ANSYS Workbench를 사용하였으며, Minitab을 이용하여 최적화 모델을 구하였다.

2. 유한요소해석

2.1 유압 브레이커 모델링

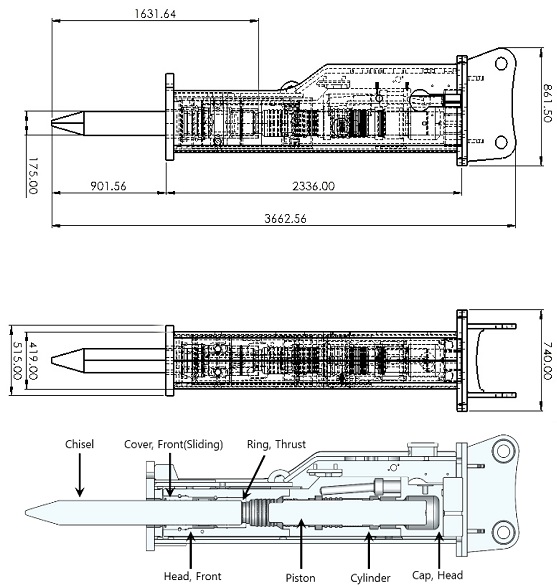
구조해석을 위한 유압 브레이커 외부 프레임의 3D 모델은 Fig. 1과 같다. 프레임의 재질은 SM490A이고, 기타 부품은 Table 1과 같다.

Fig. 1

Hydraulic breaker frame

Table 1

List of materials used in structural analysis

2.2 메쉬 및 경계 조건

ANSYS Workbench를 이용하여 구조해석을 실시하였다. Fig. 2와 같이 브레이커의 볼트 조립부에 Fixed Support 조건을 부가하였다.

Fig. 2

Boundary conditions

하중 조건은 제작사 설계하중과 동등하게 유압 브레이커 내부에 200 Bar를 주었고, 가속도 100 G를 적용시켰다. Mesh는 요소의 크기를 15 mm로 설정하여 적용하였다. 그 결과는 Fig. 3과 같으며 요소 1,340,926개와 절점 2,267,269개로 분할되었다.

Fig. 3

Mesh

2.3 해석 결과 및 요인 선정

Fig. 4는 해석 결과이며 최소 안전율은 2.33이다. 이는 제작사의 안전율 목표치인 2.00을 초과하는 수준으로서 최적화의 필요성이 있다고 할 수 있다. 유압 브레이커의 모델 내부 부품에 대해서는 변경이 될 수 없으므로 외부 프레임에 대해서 중량을 감소시키기 위한 부품 4가지를 Fig. 5와 같이 선정했다.

Fig. 4

Analysis for initial modeling

Fig. 5

Factors

3. 실험계획법

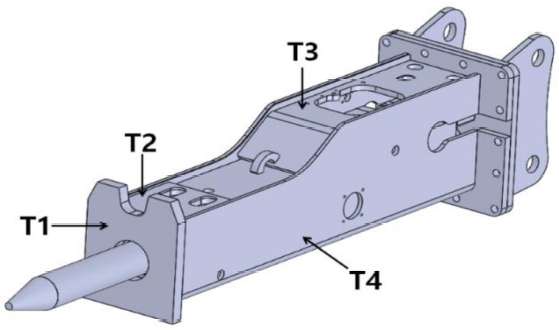
상기한 내용과 같이 프레임의 부품으로 4가지 인자를 선정하였다. 실험계획법을 진행하면서 무게도 고려해야 하기 때문에 중량도 반응값으로 설정했다. 인자의 수준은 Table 2에서 보는 바와 같이 최솟값(Minimum)은 기존값(Initial) 대비 약 75%의 치수로 설정하였고, 4인자 2 수준의 완전요인배치법을 실시하였다. 여기서 기존값이란 최댓값을 의미한다.

Table 2

Set of factors

3.1 완전요인배치법

4인자 2 수준으로 실험한 결과는 Table 3과 같으며, Y1과 Y2는 각 Run에서 구조해석을 실시한 반응값이다. 곡면성을 확인하기 위해 중앙점을 포함하여 진행하였다.

Table 3

Results of experiments

3.1.1 안전율에 대한 분산분석

Table 3에 대한 안전율의 분산분석 결과는 Table 4와 같다. 여기서 DF는 자유도, Adj SS는 제곱합(Sum of Square)으로서 인자 수준에 따른 변동성을 의미하며, Adj MS는 평균 제곱(Mean Square)으로서 각 항의 제곱합을 자유도로 나눈 것이다. Error는 인자들의 효과만으로 설명할 수 없는 변동성을 의미한다. F-Value는 각 항 평균 제곱을 Error 평균 제곱으로 나눈 값이다. F-Value 값이 클수록 P-Value 값이 작아지며 P-Value 값이 유의 수준인 0.05를 넘으면 그 인자는 반응값에 영향을 미치지 않는 것으로 판단한다.

Table 4

Analysis of variance for safety factor

상기한 표는 신뢰도 95% 기준으로 P-Value 값이 0.05를 초과하는 항을 오차항에 포함시킨 후 결정하는 풀링(Pooling) 작업을 수행한 결과다. 목적함수인 안전율과 설계변수들 간의 관계를 나타내는 회귀방정식은 식(1)과 같다.

$\[ \mathrm{Y}1\mathrm{ }=\mathrm{ }-0.479+0.00031T_1+0.00375T_2+0.00063T_3+0.09500T_4 \]$

(1)

회귀방정식이 모형을 나타내는 정도를 결정계수 R²이라 하며, 100%에 근접할수록 모형을 잘 설명한다. 식(1)에 대한 R²값은 98.20%이다.

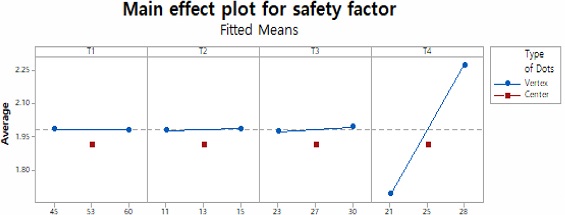
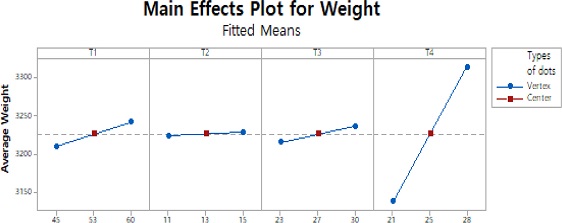
반응값 Y1에 대한 주효과도는 Fig. 6과 같다. x축은 각 인자의 수준이며, y축은 각 인자의 수준에 따른 안전율이다. 주효과도의 기울기를 통해서 T4가 반응값에 가장 큰 영향을 미치고 있다고 할 수 있다. 또한 중앙점이 주효과도의 직선상에서 벗어나 있다는 것을 알 수 있다. 이는 반응값이 비선형적이라고 판단할 수 있으며 더 높은 차수의 실험을 계획할 필요가 있다. 따라서 반응표면분석법의 추가적인 실험이 필요하다.

Fig. 6

Main effect plot for safety factor

3.1.2 중량에 대한 분산분석

Table 3에 대한 중량의 분산분석 결과는 Table 5와 같으며, 신뢰도 95% 기준으로 P-Value 값 0.05를 초과하는 항을 오차항에 포함시킨 후 결정하는 풀링 작업을 수행한 결과다. 목적함수인 중량과 설계변수들 간의 관계를 나타내는 회귀방정식은 식(2)와 같다.

$\[ \mathrm{Y}2\mathrm{ }=\mathrm{ }2398.28+2.11875T_1+1.16875T_2+2.92188T_3+25.3833T_4 \]$

(2)

Table 5

Analysis of variance for weight

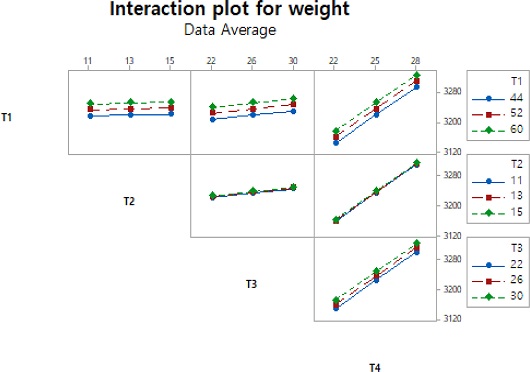
식(2)에 대한 R²값은 100%이며 모형과 일치하고 있다. 반응값 Y2에 대한 주효과도와 교호작용도는 각각 Figs. 7과 8과 같다. x축은 각 인자의 수준이며, y축은 각 인자의 수준에 따른 중량이다. 주효과도의 기울기를 통해서 T4, T1, T3, T2 순으로 반응값에 큰 영향을 미친다고 해석할 수 있다. 또한 중앙점이 주효과도의 직선상에 있으므로 선형적이라 판단할 수 있다. 따라서 이는 추가적인 설계가 필요하지 않다.

Fig. 7

Main effect plot for weight

Fig. 8

Interaction plot for weight

3.2 반응표면분석법

완전요인배치법을 통해 곡면성을 확인하였으므로 고차의 실험인 반응표면분석법을 실시하였다. 반응표면분석법 생성을 위하여 면중심의 중심합성법을 이용한 실험을 계획하였다. 면중심 중심합성법으로 실험한 이유는 수준 범위를 벗어나지 않고 실험할 수 있기 때문이다. 실험 수행 결과는 Table 6과 같다. Y1은 각 Run에서 구조해석을 실시한 반응값이다. Minitab을 이용한 Tables 6의 안전율에 관한 분산분석 수행한 결과 7과 같다.

Table 6

Design of central composite

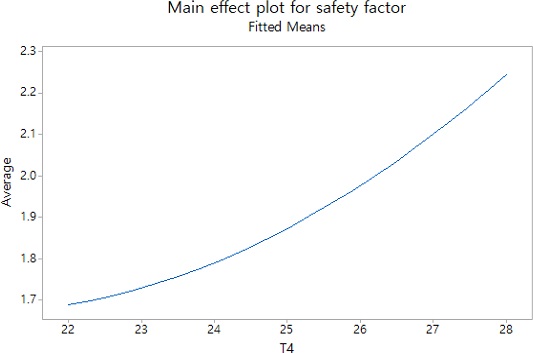
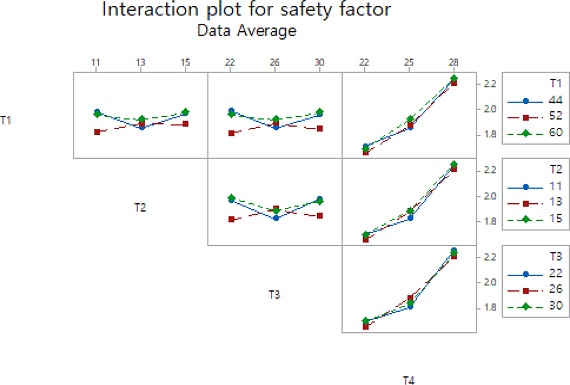
풀링 작업을 할 때 완전요인배치법과는 다르게 반응표면분석법에서는 한 번에 하나씩 유의하지 않은 인자를 제외해야 한다. 한 번에 2개 이상의 인자를 제외하면 그 인자 간에 종속되는 효과가 있을 수 있기 때문에 하나씩 제외하는 절차의 값과 다를 수 있다. 따라서 블록, 교호작용, 제곱항 순으로 차례대로 하나씩 제외시키며 그 결과는 상기한 표는 Table 7과 같다. 인자가 반응값 Y1에 미치는 영향을 나타내는 주효과도는 Figs. 9, 교호작용도는 10과 같다. 분산분석을 통해 확인한 유의한 인자는 T4이고 이를 통해 도출한 반응값 Y1의 회귀방정식은 식(3)과 같다.

$\[ \mathrm{Y}1\mathrm{ }=\mathrm{ }4.18-0.2765T_4+0.00743T_4\mathrm{*}{T}_4 \]$

(3)

Table 7

Analysis of variance for safety factor

Fig. 9

Main effect plot for safety factor

Fig. 10

Interaction plot for safety factor

식(3)에 대한 R²값은 95.67%로써 모형을 잘 설명하고 있다고 할 수 있다.

3.3 반응 최적화

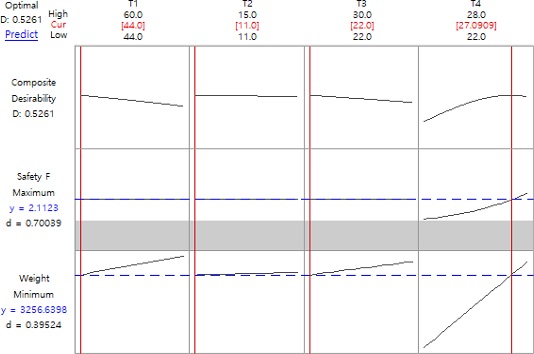
각각의 회귀방정식 식(2)와 식(3)을 통해서 안전율과 중량을 모두 최적화할 수 있는 다중 반응 최적화를 실시하였다. 안전율의 목표치는 2.00을 기준으로 설정하였고, 중량의 목표치는 최소화로 설정하였으며 결과는 Fig. 11과 같다.

Fig. 11

Response optimization plot

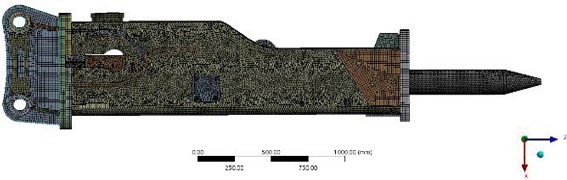
Minitab상에서 최적화된 부품의 치수를 모델링하여 ANSYS Workbench로 돌려본 결과는 Fig. 12와 같다. Fig. 12는 유압 브레이커에서 안전율이 낮게 나왔던 하단 부위의 그림이다. Minitab에서 최적화된 T4의 치수는 실제 철판 규격표와 맞추기 위해서 26으로 설정하였다. 이로 인해 중량에 대한 오차와 안전율의 오차가 발생하였다. Minitab에서 예측한 결과 값과 실제 해석한 결과값의 비교는 Table 8과 같다.

Fig. 12

Safety factors at optimal case

Table 8

Results of optimization

4. 결론

본 논문은 50톤급 유압 브레이커의 하우징을 대상으로 최적 설계를 진행하였다. 완전요인 배치법으로 4인자 2 수준의 설계를 진행하였으며, 반응값인 안전율이 곡면성을 띄는 것을 확인하였다. 완전요인배치법을 통해 곡면성이 확인됨에 따라 고차의 실험인 반응표면분석법을 실시하였으며, 아래와 같은 결과를 얻을 수 있었다.

(1) 안전율과 중량의 최적화된 Minitab의 예측을 토대로 ANSYS Workbench를 이용하여 실제 해석을 진행한 결과, 안전율은 2.03, 중량은 3,222.2 kg이 나왔으며 Minitab 예측과 거의 일치하였다.

(2) 최종 결과는 기존 최초 모델에 비해 안전율은 2.33에서 2.03으로 감소했지만, 안전율은 2.00을 목표로 했기 때문에 최적화 모델 역시 안전하다고 판단할 수 있다.

(3) 중량은 3,341.3에서 3,222.2 kg으로 119.1 kg 감소하는 결과를 얻었다.

Acknowledgments

본 연구는 중소벤처기업부 “50톤급 대형브레이커 장착용 고객지향형 Smart Monitoring System 개발(No. S2613485)” 과제를 통해 수행되었음.

REFERENCES

• Lee, S., Kim, S., Park, J., Choi, B., (2017), An experimental study on the stress distribution of hydraulic breaker housing, Proceedings of the Spring Conference on the Korean Society of Mechanical Engineers Spring Conference, 156.
• Shin, D., Kwon, K., Yang, H., Nam, K., (2009), A study for the performance optimization of the hydraulic breaker, Proceedings of the Korean Society of Mechanical Engineers Conference, 1325-1330.
• Hur, J., Lee, B., Kim, K., (2008), Design of side damper structure for shock absorbing of hydraulic breaker, Proceedings of the Korean Society for Precision Engineering Conference, 169-170.
• Jung, K. I., (2016), Structural design of a side housing bracket of a hydraulic breaker, M.Sc. Thesis, Hanyang University.
• Park, Y. S., (2009). Optimal design of a hydraulic breaker housing for minimizing weight, M.Sc. Thesis, Hanyang University.
• Park, G.-B., Park, C.-H., Park, Y.-S., Choi, D.-H., (2011), Optimal design for minimizing weight of housing of hydraulic breaker, Transactions of the Korean Society of Mechanical Engineers A, 35(2), 207-212. [https://doi.org/10.3795/KSME-A.2011.35.2.207]
• Cho, B. J., Han, H. H., Koo, J. S., (2018), Damping Device for hydraulic breaker: impact and noise reduction, Journal of the Korean Society of Manufacturing Process Engineers, 17(4), 113-122. [https://doi.org/10.14775/ksmpe.2018.17.4.113]
• Lim, D.-W., Park, Y.-S., Shin, B.-C., (2018), Assessment of stability of hydraulic breaker cylinder and piston through thermal-structural coupled field analysis by finite element method, Journal of the Korea Society of Die & Mold Engineering, 12(1), 41-46.
• Yoo, D.-W., Lee, J.-H., (2012), A study on the optimal shape design of front axle of wheel loader using the design of experiments, Journal of the Korean Society for Precision Engineering, 29(2), 193-200. [https://doi.org/10.7736/KSPE.2012.29.2.193]
• Lee, J. H., Song, T. H., Lee, J. H., (2018), Shape optimization of a hydraulic crane boom, Journal of the Korean Society for Precision Engineering, 35(4), 427-432. [https://doi.org/10.7736/KSPE.2018.35.4.427]
• Hong, J. M., Lee, J. H., (2018), Optimal design of boom joint for 2.5 ton class aerial lift truck, Journal of the Korean Society for Precision Engineering, 35(8), 769-775. [https://doi.org/10.7736/KSPE.2018.35.8.769]
• Song, T. H., Lee, J. H., (2019), Shape optimization of a link of the knuckle crane, Journal of the Korean Society for Precision Engineering, 36(1), 59-65. [https://doi.org/10.7736/KSPE.2019.36.1.59]
• Lee, J. H., Kim, K. S., (2020), Optimal design of boom for telescopic boom type forklift truck, Journal of the Korean Society for Precision Engineering, 37(6), 457-464. [https://doi.org/10.7736/JKSPE.020.004]
• Shuaeib, F., Hamouda, A., Wong, S., Umar, R. R., Ahmed, M. M., (2007), A new motorcycle helmet liner material: The finite element simulation and design of experiment optimization, Materials & design, 28(1), 182-195. [https://doi.org/10.1016/j.matdes.2005.04.015]
• Prasanna Naveen Kumar, J., Johns Kumar, S., Sarathi Jeyathilak, R., Venkatesh, M., Simon Christopher, A., Ganesh, K., (2017), Effect of design parameters on the static mechanical behaviour of metal bellows using design of experiment and finite element analysis, International Journal on Interactive Design and Manufacturing, 11(3), 535-545. [https://doi.org/10.1007/s12008-016-0306-7]
• Ahn, T., Heo, J., Lee, S., Jung, H., Kim, J., Yi, H., (2017), Fatigue life analysis of a railway bearing using Taguchi method, International Journal of Computational Methods and Experimental Measurements, 5(5), 733-740. [https://doi.org/10.2495/CMEM-V5-N5-733-740]
• Azevedo, F., Moura, M., Vicente, W., Picelli, R., Pavanello, R., (2018), Topology optimization of reactive acoustic mufflers using a bi-directional evolutionary optimization method, Structural and Multidisciplinary Optimization, 58(5), 2239-2252.
• Panagant, N., Bureerat, S., (2018), Truss topology, shape and sizing optimization by fully stressed design based on hybrid grey wolf optimization and adaptive differential evolution, Engineering Optimization, 50(10), 1645-1661. [https://doi.org/10.1080/0305215X.2017.1417400]
• Kim, B.-S., Kim, M.-G., Byun, D.-W., Lee, S.-M., Lee, S.-H., (2006), A study on the structure improvement of bracket housing for structural noise and vibration reduction in hydraulic breaker, Journal of the Korean Society for Precision Engineering, 23(11), 108-115.
• Alphin, M., Sankaranarayanasamy, K., Sivapirakasam, S., (2010), Experimental evaluation of whole body vibration exposure from tracked excavators with hydraulic breaker attachment in rock breaking operations, Journal of Low Frequency Noise, Vibration and Active Control, 29(2), 101-110. [https://doi.org/10.1260/0263-0923.29.2.101]