2차원 자속밀도 정보를 이용한 선형 모터의 이동자 위치 측정
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A linear motor is an actuator that has strong thrust and high controllability, and can perform linear motion without the use of a motion converter. In this study, we propose a new method to measure the position of the mover of a permanent magnet linear synchronous motor by measuring the magnetic flux density. To resolve the problem that existing methods have to spatially arrange multiple sensors, the proposed method uses a two-dimensional magnetic flux density measurement value at one point. In accordance with this, the estimation method was modified, the convergence condition of the estimation method was obtained, and the time required for the calculation was estimated. The validity of the proposed method was verified through comparative experiments with existing methods. As a result of the test, the proposed method had a small maximum absolute error compared to the existing methods, and was robust against sensor gain changes.
Keywords:
Permanent magnet linear synchronous motor, Mover position, Two-dimensional magnetic flux density, Convergence condition, Gain changes키워드:
영구자석 선형 동기 모터, 이동자 위치, 2차원 자속밀도, 수렴 조건, 이득 변화1. 서론
선형 모터는 운동 변환 장치 없이 바로 직선 운동을 얻을 수 있는 액추에이터이며, 강한 추력이나 높은 정밀도가 필요한 장치에 사용된다. 선형 모터는 영구자석 동기형, 유도형 등 여러 방식이 있으며, 운동 원리가 다른 압전체를 사용하는 선형 모터도 있다. 이 중 영구자석 동기형 선형 모터(Permanent Magnet Linear Synchronous Motor, PMLSM)는 제어성이 우수하여 직선 운동이 필요한 장치에서 폭넓게 사용된다. PMLSM은 이동자가 영구자석인 구조도 있고, 고정자가 영구자석으로 이루어진 구조도 있는데, PMLSM의 이동자를 제어하기 위해 선형 광학식 또는 자기식 엔코더를 부착하여 이동자의 위치를 검출하는 방법을 사용한다.
일부 응용에서는 강한 추력과 직선 운동만 필요하고 높은 정밀도가 필요하지는 않은 경우가 있다. 이런 장치에서는 기구적 단순함을 위해 선형 모터를 사용하는데, 수백 μm 정도의 정밀도를 요구한다[1]. 고정자가 영구자석인 PMLSM에 대해 영구자석의 자속밀도를 측정하여 이동자의 위치를 측정하려는 연구가 오래전부터 이루어져 왔다[1-4]. 이 방법은 선형 자기식 엔코더를 사용하는 것과 원리적으로는 동일하나 영구자석의 자속밀도를 바로 측정함으로써 별도의 엔코더를 사용하는데 필요한 비용을 절감할 수 있다. 자속밀도는 선형 홀 센서(Hall Effect Sensor)를 사용하여 측정하는데, 회전형 모터에서는 이미 확립된 방법이다[5]. 이동자의 진행 방향에 대해 검출되는 자속밀도의 변화 파형은 자석과 센서 사이의 거리에 따라 다르게 나타나는데, 충분한 검출 거리를 확보하면 코사인 형태의 파형을 얻을 수 있다[6]. Wegener [1]는 자석 N-S극 한 사이클의 90o 간격으로 이동자에 2개의 홀 센서를 배치하고 센서 정보를 필터를 통과시킨 후 현재의 위상을 아크탄젠트 함수를 사용하여 구함으로써 이동자의 위치를 측정하였다. Paul [2]은 120o 간격으로 세 개의 홀 센서를 배치하고 세 정보를 α\-β 변환하여 90o 위상차의 두 정보로 변환한 후 다시 아크탄젠트를 통하여 이동자의 위치를 추정하였다. 이 방법은 Wegener [1]의 연구에 비해 각 센서의 동일한 오프셋을 제거할 수 있으며 센서 정보에 포함되는 3고조파의 영향도 제거할 수 있다. 자속밀도 파형에는 기본파 이외에 많은 저조파(Sub-Harmonics)와 고조파(Harmonics)가 포함되어 있다. 이 저/고조파는 필터로는 제거가 되지 않으며, 이 성분을 고려하지 않으면 측정 정밀도에 한계가 있을 수 밖에 없다. 이 저/고조파 성분을 제거하려는 연구도 수행되었는데, Ahn [3]은 n개의 고조파 성분에 대해 2n개의 센서를 장착하여 고조파 성분이 소거되도록 하는 연구를 수행하였고, Kim [4]은 자속밀도 파형을 저/고조파가 포함된 푸리에 급수(Fourier Series)로 표현하고, 센서 정보와 고정점 반복법(Fixed Point Iteration)을 사용하여 이동자의 위치를 추정하였다.
선형 모터 자체를 제작하는 경우는 이동자에 홀 센서가 장착될 위치까지 감안하여 설계할 수 있지만, 상용 선형 모터에 기존의 선형 엔코더를 대치하여 사용하는 경우에는 센서를 장착할 위치를 확보하기가 어려운 문제점이 있다. 이러한 점은 장착할 센서의 수가 많아질수록 어려움이 더 가중되며 센서 때문에 이동 행정의 제한 등이 일어날 수 있다. 또한 센서 시스템의 제작을 자동화하는 경우는 센서 간의 간격을 일정 정밀도 이상으로 유지할 수 있으나 소량 수작업을 하면 센서 간의 간격도 공차를 갖게 되며 이것은 바로 측정 오차로 연결되게 된다. 이런 문제점을 해결하기 위해 본 논문에서는 Kim [4]의 연구로부터 개선된 형태의 이동자 위치 추정 방법을 제안한다. Kim [4]의 연구에서는 120o 간격으로 홀 센서 3개를 배치하고 이 중 데이터의 변화가 가장 큰 정보를 선택하여 이동자의 위치를 추정하였는데, 센서를 장착하는 문제뿐만 아니라 코사인 함수 형태로 표현되는 현재 위치에서의 하나의 자속밀도 신호를 사용하기 때문에 센서 게인의 변화에 대해 민감한 문제점이 있었다. 홀센서는 특히 주변 온도의 변화에 대해 게인의 변화가 민감하게 나타나는 것으로 알려져 있다[4].
본 논문에서는 기존 연구의 문제점을 해결하기 위해 센서를 한 지점에 장착하고, 그 지점에서의 직교 좌표상의 2축 자속밀도 정보를 이용하여 이동자의 위치를 추정한다. 이에 맞게 추정식을 개선하고, 새 추정식의 수렴 조건을 규명한다. 본 논문의 구성은 다음과 같다. 2장에서는 제안하는 추정 방법에 대해 서술하고, 3장에서는 실험 및 성능 비교 결과를 제시한다. 그리고 마지막 4장은 결론이다.
2. 2차원 정보를 이용한 이동자 위치 추정
2.1 선형 모터 표면의 2차원 자속밀도 검출
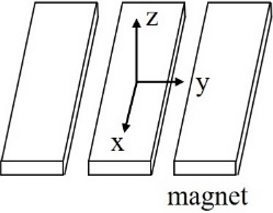
이 논문에서는 센서를 이동자의 한 지점에 설치하고, 2차원 자속밀도값을 측정하여 위치를 검출한다. 센서의 좌표축은 Fig. 1과 같이 설정하였다. 센서의 방향은 이 중 y와 z 방향으로 설정한다. z와 y의 기본파는 90o 위상차를 가진다[6,7]. 그러면 검출된 z, y 방향 자속밀도는 식(1)과 식(2)처럼 푸리에 급수로 표현할 수 있다.
| (1) |
| (2) |
전압 레벨 이동과 기본파의 진폭을 1로 정규화하는 과정을 통해 식(3)과 식(4)와 같이 변형할 수 있다. 여기서 k는 기본파를 제외한 모든 성분이다.
| (3) |
| (4) |
2.2 위치 추정식의 구성
고정점 반복법은 임의의 함수 f에 대하여 식(5)의 해를 식(6)과 같이 반복 계산에 의해 찾는 방법이다.
| (5) |
| (6) |
고정점 반복법은 실수 L < 1에 대해 해를 구하는 영역에서 다음의 Lipschitz 연속 조건을 만족하면 초기값 x0로부터 시작하여 해에 수렴하게 된다[8].
| (7) |
Kim [4]에서는 식(3)의 z(θ)를 사용하여 추정식을 구하였으나 여기서는 식(8)과 같이 z(θ), y(θ)비의 아크탄젠트값으로 추정한다.
| (8) |
| (9) |
이제 추정식 식(8)이 수렴하는 구간을 구해야 한다. 를 θ에 대해 미분하면 식(10)과 같다.
| (10) |
한 주기 내에서 다음 식(11)의 조건이 만족하면 식(10)의 미분값이 항상 0 이상이 되어 증가 함수가 된다. 식(11)은 식(10)의 직접 미분을 통해 구한 식이다.
| (11) |
가 θ에 대해 미분 가능하므로 식(11)에서 증가함수이면 Bi-Lipschitz가 되므로 양수 β에 대해 양수 d가 존재해 식(12)의 관계가 성립한다.
| (12) |
여기서 이다.
| (13) |
따라서 식(9)와 식(13)에서 식(7)의 조건을 만족한다. 즉 식(11)을 만족하면 한 주기 내에서 어떤 양수인 게인 상수 β에 대해 식(8)의 추정식이 수렴하게 된다. 그리고 이 수렴 속도를 결정하는 값이 된다.
제안한 방법에서는 아크탄젠트 함수만을 사용하는 기존의 추정 방법뿐만 아니라 모터의 저/고조파를 고려하여 고정점 반복법의 위치를 추정하는 방법[4]과 비교해서도 계산량이 많은 문제가 있다. 삼각함수는 비교적 계산 시간이 많이 소요되는 함수이지만, 최근 저가의 고성능 마이크로 프로세서의 출현으로 고속 연산이 가능해졌다. STM32 계열 마이크로 컨트롤러에서는 삼각함수의 계산에 Table 1과 같은 계산 시간이 소요된다[9].
3. 실험 결과
3.1 실험 장치
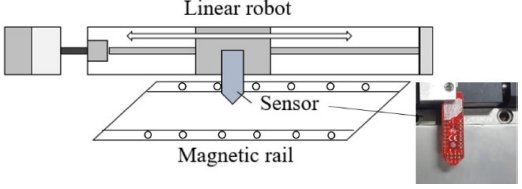
테스트에 사용한 영구자석 레일은 Yaskawa SGLFM-1Z 405 선형 모터 레일로 8개의 N-S극 쌍을 가지고 있고 전체 길이는 450, N-S 자석 한 주기의 길이는 약 56 mm이다[10]. 측정은 공간적으로 여러 위치에 센서를 달아야 하는 기존 방법과 비교를 위해 센서 검출 범위를 고려하여 전체 길이 중 337.5 mm에 대해 실시하였다. 홀 센서는 인피니온의 다차원 홀 센서인 TLE493D-W2B6을 사용하였고[11], A/D 분해능은 12 bit, 최대 측정 범위 200 mT이다. 자석 레일과 홀 센서는 Figs. 2와 3에 나타나 있다. 특정 센서가 제안하는 방법에서 핵심적인 역할을 하는 것은 아니고, 1차원 센서를 서로 수직으로 장착하여 제작할 수도 있다. 홀 센서는 측정 신호의 최대치가 170 mT가 되는 위치에 설치하였다. 측정은 Fig. 4와 같이 외부에 정속 제어가 가능한 1축 선형 로봇에 센서와 데이터 처리장치를 장착하고 실시하였다.
3.2 실험 결과
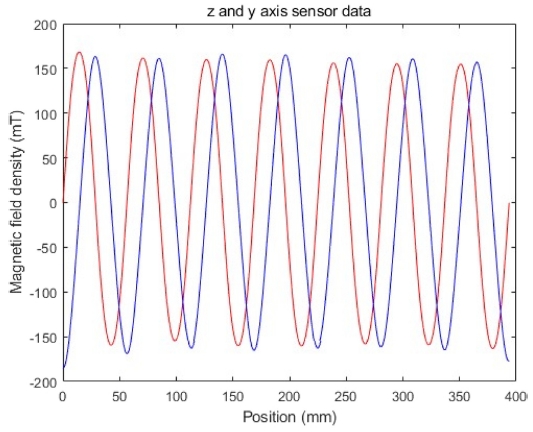
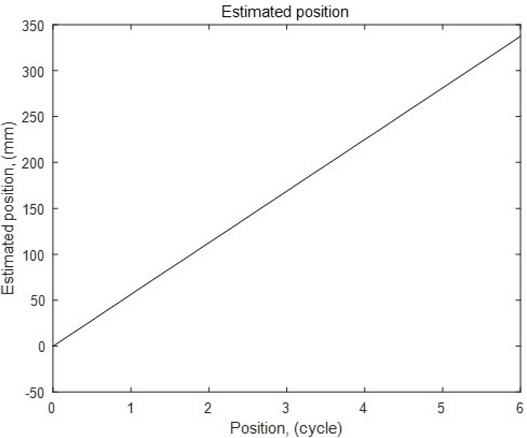
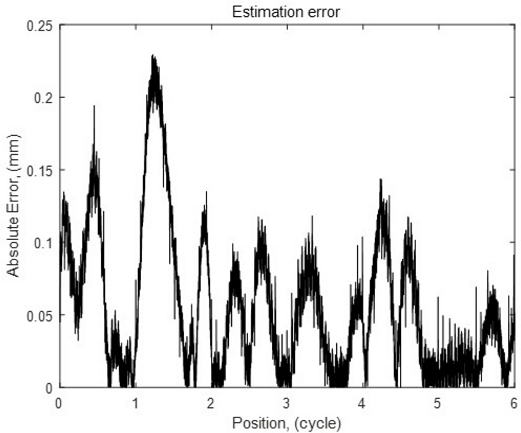
측정된 z 및 y축 방향 자속밀도는 Fig. 5와 같고 그림에서 90o 앞선 신호가 z축 신호이다. 두 신호를 이산 푸리에 변환(Discrete Fourier Transform)을 하여 저/고조파의 크기와 위상을 구하였고, 이 중에 기본파 대비 진폭이 1% 이상 되는 고조파와 저조파 성분은 Table 2와 같다. 실험에서는 이 성분들만 고려하였으며, 이 고조파 성분들의 값은 식(11)의 전 구간 수렴을 위한 충분조건을 만족한다. 또한 수치 계산을 통해 식(13)의 d = 1.074이다. 이 값은 게인 β를 선정하는데 사용된다. Table 3은 테스트 결과를 나타낸 것으로 성능 비교 대상 방법은 ① 90o 간격으로 배치된 두 센서값과 아크탄젠트 함수를 사용하는 방법[1], ② 120o 간격으로 배치된 세 센서값을 α-β 변환하는 방법[2], ③ 120o 간격으로 배치된 세 센서값 중에 하나를 선택하여 고정점 반복법으로 추정하는 방법[4]이다. 방법 ③과 제안하는 방법에서는 위치 갱신 1주기당 10회의 고정점 반복 계산을 수행하였다. 센서의 정보가 정확한 경우에는 저/고조파 성분을 보상하는 방법 ③과 제안하는 방법이 모두 200 μm대의 최대 오차를 보였다. 추정 오차는 선형 로봇의 위치를 기준으로 이동자 위치 추정치와의 차이를 절댓값으로 구하였으며, 자석 한 주기 간의 간격 및 A/D 변환기의 분해능에 따라 달라진다. 사용한 홀 센서의 게인이 모두 10%씩 커지는 경우 신호들의 상대 비율을 사용하는 방법 ①, ②와 제안 방법에서는 최대 오차의 변화가 없지만 방법 ③에서는 예측했던 대로 게인의 오차가 그대로 최대 오차에 그대로 반영된다. 홀센서들의 게인이 불균등하게 변화하는 경우는 모든 방법에서 성능에 영향을 받지만, 홀 센서 게인이 주로 주변 온도에 의해 변동되므로 동일하게 변화하는 경우가 많을 것으로 예상한다. Table 3의 마지막 행은 수행되는 삼각함수 계산 횟수이다. Fig. 6은 제안하는 방법의 위치 추정 그래프이며 가로축은 자석의 위치를 사이클 단위, 세로축은 추정 위치를 나타낸다. 전구역에서 동일한 게인 β를 사용하여 추정이 가능함을 보여준다. Fig. 7은 위치에 대한 추정 오차의 절댓값을 나타낸 그림이다.
4. 결론
본 논문에서는 PMLSM을 대상으로 홀 센서를 사용하여 고정자 자석 레일의 자속밀도를 측정함으로써 이동자의 위치를 추정하는 방법을 제시하였다.
기존의 홀 센서를 이동자에 공간적으로 90이나 120o 간격으로 여러 개 배치하는 방법에서는 센서를 장착할 위치를 확보하는 것이 어렵고, 센서 사이의 공차가 바로 측정 오차로 이어지는 문제점이 있었다. 한 지점에서 2차원 자속밀도를 검출하고 Kim [4]의 방법을 개선하여 기존 연구에서 코사인 함수 형태로 표현되는 현재 위치의 자속밀도값 대신 두 자속밀도 측정값을 사용하는 아크탄젠트 함수를 사용하여 고정점 반복법으로 이동자의 위치를 추정하였다. 실험 결과 56 mm의 자석 주기를 갖는 선형 모터에서 12비트 A/D 변환기를 사용하여 200 μm대의 최대 오차를 얻었으며, 이때 자속밀도 파형의 저/고조파를 보상하는 경우가 보상하지 않는 방법에 대해 대체적으로 우수한 성능을 나타냈다. 또한 2차원 정보를 사용함으로써 기존의 하나의 센서 정보를 사용하는 연구에 비해 센서 게인 변화에 대해 강인한 특성을 보였다. 기존 연구에서는 이루어지지 않은 반복 추정 알고리즘의 수렴 조건을 규명하였고, 이 조건에서 선형 모터의 전체 행정에 대해 추정 방법이 수렴함을 보였다.
기존의 홀 센서를 사용하는 일반적인 방법에 비해 고조파 보상을 통해 정밀도를 높일 수는 있으나 선형 엔코더와 같은 별도의 위치 검출 센서를 사용하는 것과는 비교하기 어렵다. 또한 본 논문의 방법은 연산 시간 부담이 다른 방법에 비해 크다고 볼 수 있다. 저가의 고성능 마이크로 프로세서가 일반화됨에 따라 연산 부담은 해소되고 있지만, 필요한 제어정밀도 등 대상 시스템의 요구사항에 맞춰 기존의 방법과 제안하는 방법 중 선택하여 사용할 수 있을 것으로 생각된다. 본 논문에서는 센서 정보를 처리할 수 있는 서보드라이버의 개발은 연구 범위로 포함하지 않았기 때문에 되먹임 제어시스템은 구현하지 않았으나, 향후 연구에서는 이를 구현하여 전체 되먹임 성능을 평가할 계획이다.
NOMENCLATURE
| Azrk, Ayrk : | (z and y axis) kth Harmonic Magnitude, T |
| Azro, Ayro : | (z and y axis) Measured Offset, T |
| Azk, Ayk : | (z and y axis) Normalized kth Harmonic Magnitude |
| Hk : | Harmonic Number |
| Bzk, Byk : | (z and y axis) kth Harmonic Phase, Radian |
| Bzo, Byo : | (z and y axis) Fundamental Wave Phase, Radian |
| β : | Estimator Gain |
| d : | Lipschitz Constant |
| zr, yr : | (z and y axis) Measured Magnetic Flux, T |
| zs, ys : | (z and y axis) measured and Normalized Magnetic Flux |
| θ : | Mover Position, Radian |
REFERENCES
-
Wegener, R., Senicar, F., Junge, C., Soter, S., (2007), Low cost position sensor for permanent magnet linear drive, Proceedings of the 2007 7th International Conference on Power Electronics and Drive Systems, 1367-1371.
[https://doi.org/10.1109/PEDS.2007.4487882]

-
Paul, S., Chang, J., (2015), A new approach to detect mover position in linear motors using magnetic sensors, Sensors, 15(10), 26694-26708.
[https://doi.org/10.3390/s151026694]

-
Ahn, H. J., Kim, K. R., (2014), 2D Hall sensor array for measuring the position of a magnet matrix, International Journal of Precision Engineering and Manufacturing-Green Technology, 1(2), 125-129.
[https://doi.org/10.1007/s40684-014-0017-0]

-
Kim, J., Choi, S., Cho, K., Nam, K., (2016), Position estimation using linear hall sensors for permanent magnet linear motor systems, IEEE Transactions on Industrial Electronics, 63(12), 7644-7652.
[https://doi.org/10.1109/TIE.2016.2591899]

-
Zhu, Z., Shi, Y., Howe, D., (2006), Rotor position sensing in brushless ac motors with self-shielding magnets using linear hall sensors, Journal of Applied Physics, 99(8), 08R313.
[https://doi.org/10.1063/1.2172178]

-
Huang, L., Huang, X., Jiang, H., Zhou, G., (2010), Comparative study of magnetic fields due to types of planar permanent magnet array, Proceedings of the 2010 International Conference on Electrical and Control Engineering, 3470-3473.
[https://doi.org/10.1109/iCECE.2010.844]

-
Jansen, J., Smeets, J., Overboom, T., Rovers, J., Lomonova, E., (2014), Overview of analytical models for the design of linear and planar motors, IEEE Transactions on Magnetics, 50(11), 1-7.
[https://doi.org/10.1109/TMAG.2014.2328556]

- Wikipedia, Fixed-point iteration. https://en.wikipedia.org/wiki/Fixed-point_iteration
- STMicroelectronic, AN5355. https://www.st.com/resource/en/application_note/dm00614795-getting-started-with-the-cordic-accelerator-using-stm32cubeg4-mcu-package-stmicroelectronics.pdf
- Yaskawa, (2019), Linear Servomotor S-7-Series AC Servo Drive Product Manual.
- Infineon Technologies AG, (2019), TLE493D-W2B6 datasheet.

Professor in the School of Electrical Engineering, Kookmin University, Seoul, Korea. His research interest is robotics, and motor control.
E-mail: mcwnt@kookmin.ac.kr

Ph.D., Research Fellow at Ninebell Co., Ltd.. His research interest is health care robot and semiconductor manufacturing equipment.
E-mail: ydlee@ninebell.co.kr