나노 가공을 위한 듀얼 서보 시스템에 관한 연구

1. 서론

오늘날 일반 기계산업은 4차 산업혁명에 맞추어 IOT 융복합기술이 매우 발전하고 있다. 하지만 발전에 따른 반도체, 자동차 부품, 로봇 부품, 농기계, 건설기계, 광학기기, 공작기계 등 기계산업과 기계부품 산업에서 매우 높은 가공정밀도를 요구하고 있다. 높은 가공정밀도를 충족하기 위하여 고가의 장비를 활용해야 하나 가격을 고려하면 장비를 도입하는 것은 매우 어려운 일이다. 정밀가공기계는 독일과 일본이 가장 앞서가며 연구가 활발히 진행되고 있으며 다양한 정밀가공기를 생산하고 있다. 하지만 국제 무역 환경에 따라 이러한 선진국의 장비와 부품을 수급하기 어려움이 발생하며. 이러한 문제를 해결하고 높은 가공기술을 구현하기 위하여 많은 연구기관에서 연구하고 있으나 절삭공구에 연구가 집중되고 있는 현실이다[1-4].

본 연구에서는 절삭공구가 아닌 가공기계에 서보 제어기를 추가하여 에러를 보상하고 가공정밀도를 높일 수 있도록 Fine Servo System을 제작하여 Dual Servo System을 구현하여 10의 위치정밀도와 40 nm의 표면 거칠기를 확보하는 것을 목표로 연구하고자 한다.

Dual Servo System은 Flexure Hinge 구조에 압전구동기를 활용한 미동제어시스템인 Fine Servo System과 일반 CNC 가공기인 Global Servo System으로 구성되며 Global Servo System 위치 에러를 실시간 보상하며 nm급 위치결정을 한다.

2. Fine Servo System

2.1 Optimum Design of Flexure Hinge

Flexure Hinge는 탄성 변형 형태가 간단하고 동작이 편리하며, 마찰이나 백래쉬가 없고, 응답 속도가 비교적 빠르다는 장점이 있다. 이에 미세 구동 장치에 많이 응용되고 있다. Flexure Hinge는 어느 한 방향의 입력에 대해서는 견고한 성질을 가지고 있다. 따라서 원하는 방향의 운동만 발생시켜주고 나머지 방향에 대해서는 운동을 유발하지 않아 운동의 간섭을 줄일 수 있다.

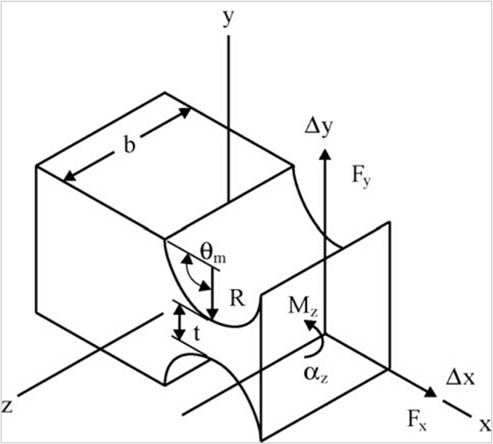
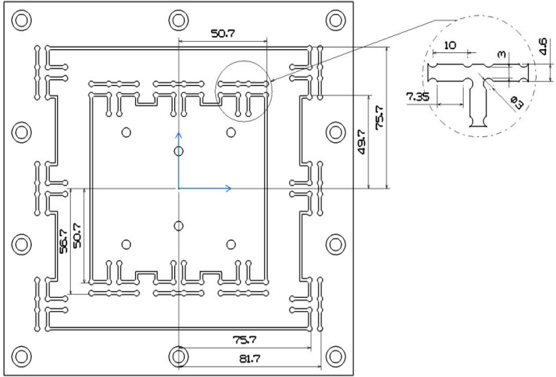
본 논문에서는 탄성 가이드에 10개의 원형 노치를 사용하여 T형 Flexure Hinge를 설계하였으며 굽힘강성은 식(1), 축강성은 식(2)와 식(3), 전단강성은 식(4)와 같다. Fig. 1은 기본적인 Flexure Hinge를 나타내고 있으며, Fig. 2는 설계한 T형 힌지이다. Table 1은 Flexure Hinge 재질과 Stiffness를 표기하였다[4-13].

$\[ \begin{array}{c}\frac{{\alpha }_z}{M_z}=\frac{3}{2Eb{R}^2}\left[\frac{1}{2\beta +{\beta }^2}\right]\left\{\left[\frac{1+\beta }{\gamma }+\frac{3+2\beta +{\beta }^2}{\gamma \left(2\beta +{\beta }^2\right)}\right]\times \left[\sqrt{1-\left(1+\text{β}-{\text{γ}}^{\text{2}}\right)}\right]+\right.\hfill \\ \left. \left[\frac{6\left(1+\beta \right)}{{\left(2\beta +{\beta }^2\right)}^{3/2}}\right]\times \left[{\text{tan}}^{-1}\left(\sqrt{\frac{2+\beta }{\beta }}\times \frac{\left(\gamma -\beta \right)}{\sqrt{1-\left(1+\beta -{\gamma }^2\right)}}\right)\right]\right\}\hfill \end{array} \]$

(1)

$\[ \begin{array}{c}\frac{{∆}_y}{F_y}=R^2{\mathit{sin}}^2{\text{θ}}_m\left(\frac{{\alpha }_z}{M_z}\right)-\frac{3}{2Eb}\left\{\left[\frac{1-\beta }{{\left(1+\beta -cos{\theta }_m\right)}^2}-\frac{2+\frac{{\left(1+\beta \right)}^2}{2\beta +{\beta }^2}}{\left(1+\beta -cos{\theta }_m\right)}\right]\times \right.\hfill \\ \left. \sin {\theta }_m+\left[\frac{4\left(1+\beta \right)}{\sqrt{2\beta +{\beta }^2}}-\frac{2\left(1+\beta \right)}{{\left(2\beta +{\beta }^2\right)}^{3/2}}\right]\times {\text{tan}}^{-1}\sqrt{\frac{2+\beta }{\beta }}\tan \frac{{\theta }_m}{2}-\left({20}_m\right)\right\}\hfill \end{array} \]$

(2)

$\[ \begin{array}{c}\frac{{∆}_x}{F_x}=\frac{1}{Eb}\left[-2{\text{tan}}^{-1}\frac{\gamma -\beta }{\sqrt{1-{\left(1+\beta -\gamma \right)}^2}}+\frac{2\left(1+\beta \right)}{\sqrt{2}}\right.{\text{tan}}^{-1}\hfill \\ \left. \left(\sqrt{\frac{2+\beta }{\beta }}\times \frac{\gamma -\beta }{\sqrt{1-{\left(1+\beta -\gamma \right)}^2}}\right)\right]\hfill \end{array} \]$

(3)

Shear compliance: Ahear modulus, G = E/[2(1+ν)]

$\[ {\left[\frac{{∆}_y}{F_y}\right]}_s=\frac{1}{Gb}\left[-{\theta }_m+\frac{2\left(1+\beta \right)}{\sqrt{2\beta +{\beta }^2}}\times {\text{tan}}^{-1}\sqrt{\frac{2+\beta }{\beta }}\tan \frac{{\theta }_m}{2}\right] \]$

(4)

Fig. 1

Flexure hinge

Fig. 2

Type T flexure hinge

Table 1

Material properties of flexure hinge

2.2 Fine Servo System Finite Element Analysis

Fine Servo System의 유한요소해석은 압전구동기에 가한 전압입력과 그에 대한 압전구동기의 출력 변위의 관계를 규명하는 것이 필요하며, 백터 U_P, MU_P를 다음 식(5)와 식(6)과 같이 정의한다.

$\[ U_P=\left[u_{p1 }{u}_{p2 }{u}_{p3 }{u}_{p4 }{u}_{p5}\right]\text{T} \]$

(5)

$\[ \text{M}{U}_P=\left[x_{p }{y}_{p1 }{y}_{p2 }{z}_{p1 }{z}_{p2}\right]\text{T} \]$

(6)

식(5)와 식(6)에서 U_Pi, MU_Pi는 각각 I번째의 입력전압과 압전구동기의 출력 변위를 나타낸다. 일반적으로 입력전압 U_P와 압전구동기 출력 변위 U_P는 동적으로 결합되어 상호 영향을 주게 되며, 그 관계식은 식(7)과 같이 기술될 수 있다.

$\[ \begin{array}{c}\text{M}{U}_P\left(\text{s}\right)=A\left(s\right)U_P\left(s\right)\\ \text{M}{U}_{P,i}\left(\text{s}\right)={\sum }_{j=1}^5{a}_{ij}\left(s\right)u_{pj}\left(s\right)\left(\text{i}=1, 2, 3, 4, 5\right)\end{array} \]$

(7)

식(7)에서 a_ij(s)는 j번째 압전구동기에 인가한 전압과 I번째 압전구동기의 출력 변위를 연결시켜주는 계수로 식(8)과 같이 표현된다.

$\[ a_{ij}\left(s\right)=b_{ij}{g}_{ij}\left(s\right) \]$

(8)

b_ij는 인가전압에 대한 압전구동기 변위의 정적이득을 나타내고, g_ij(s)는 동특성을 나타낸다. 또한 압전구동기의 변위(x_p, y_p1, y_p2, z_p1, z_p2)와 툴 홀더의 상대변위의 관계는 기하학적으로 식(9)와 같이 나타낼 수 있다.

$\[ \begin{array}{c}M=\left[\begin{array}{c}x\\ y\\ z\\ {\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& \frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& 0& 0& \frac{1}{2}& \frac{1}{2}\\ 0& -\frac{1}{d}& \frac{1}{d}& 0& 0\\ 0& 0& 0& -\frac{1}{d}& \frac{1}{d}\end{array}\right]\left[\begin{array}{c}{x}_p\\ y_{p1}\\ y_{p2}\\ z_{p1}\\ z_{p2}\end{array}\right]\\ {}^{\text{M}}{p}_0={}_P{}^M{J}^{\text{M}}{p}_p\end{array} \]$

(9)

식(7)부터 식(9)까지 입력전합과 ECTS 툴 홀더의 상대변위와의 관계는 식(10)과 같이 정의된다.

$\[ {MP}_O\left(s\right)={}_P{}^{M}JA\left(s\right)U_P\left(s\right)={}_P{}^{M}JBG\left(S\right)U_P\left(s\right) \]$

(10)

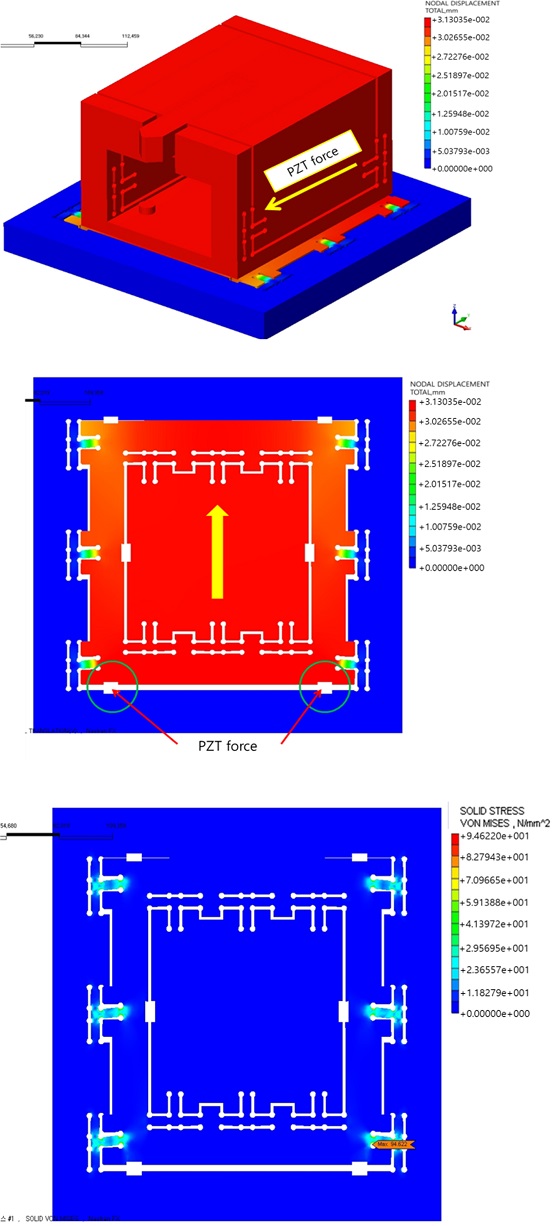
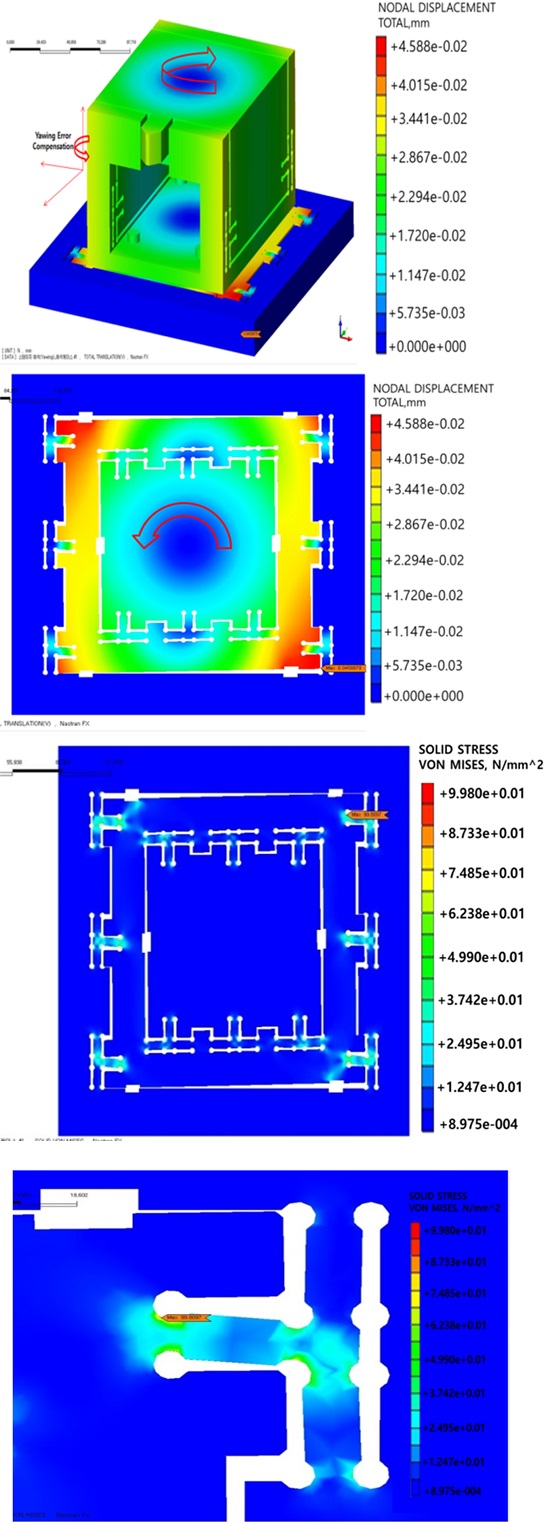
유한요소해석은 PZT의 변위하중에 대한 Hinge의 변위와 안전성을 고려하며 가공 시 발생되는 힘에 대한 스테이지 제어성능을 고려한 설계를 위함이다. Table 1의 Fine Servo System의 재질을 바탕으로 해석한 결과 Fig. 3과 같이 X-Axis의 PZT의 변위에 따른 Hinge의 변위는 31.303 μm이며, 가공 시 발생되는 Yawing 제어 특성은 Fig. 4와 같이 최대 변위 45.88 μm, 등가응력은 99.8097 N/ μm²으로 안전율은 4.8이다. 유한요소 해석 결과 PZT의 최대 변위 40 μm가 발생할 때 모두 안정적인 결과값을 나타내었다. Table 2에 응력집중에 따른 변위와 등가응력을 정리하였다.

Fig. 3

Fine servo system X-Axis FEM

Fig. 4

Fine servo system yawing FEM

Table 2

Fine servo system analysis result

3. Dual Servo System

3.1 Dual Servo System Controller Design

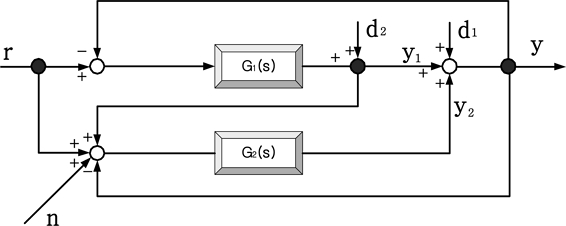
Dual Servo System의 Fine Servo System은 고정좌표계에 대한 센서에 의하여 귀환 제어하며 Global Servo System은 마이크로 서보의 상태 변위를 추정하여 궤환 제어하였으며 Fig. 5에 나타내었다.

$\[ \begin{array}{c}y\left(s\right)=\frac{G_1\left(s\right)+G_2\left(s\right)+G_1\left(s\right)G_2\left(s\right)}{1+G_1\left(s\right)+G_2\left(s\right)+G_1\left(s\right)G_2\left(s\right)}r\left(s\right)\\ y\left(s\right)=\frac{1}{1+G_1\left(s\right)+G_2\left(s\right)+G_1\left(s\right)G_2\left(s\right)}{d}_1\left(s\right)\\ y\left(s\right)=\frac{1+G_2\left(s\right)}{1+G_1\left(s\right)+G_2\left(s\right)+G_1\left(s\right)G_2\left(s\right)}{d}_2\left(s\right)\\ y\left(s\right)=\frac{G_2\left(s\right)}{1+G_1\left(s\right)+G_2\left(s\right)+{e\left(s\right)G}_1\left(s\right)G_2\left(s\right)}n\left(s\right)\end{array} \]$

(11)

Fig. 5

Configuration of dual servo system

Dual Servo System의 X-Y의 2입력 1출력 상태방정식은 Fig. 5의 제어기를 기본으로 하여 Global Servo System과 Fine Servo System을 바탕으로 유도하였다[14-24]. Dual Servo System의 상태방정식은 식(12)과 같다.

$\[ \begin{array}{c}{\dot{X}}_s=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}& 0\\ 0& 0& a_{33}& 0& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& a_{55}& a_{56}\\ 0& 0& 0& 0& a_{65}& a_{66}\end{array}\right]x_s+\left[\begin{array}{cc}0& 0\\ b_{21}& 0\\ b_{31}& 0\\ 0& 0\\ 0& 0\\ 0& b_{62}\end{array}\right]\left[\begin{array}{c}{V}_p\\ V_m\end{array}\right]\\ X_s={\left[x \dot{x} \text{ν} x_c {\dot{x}}_c i_m\right]}^T\\ y=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0\end{array}\right]x_s\\ y=\left[\begin{array}{cc}1& 0\end{array}\right]\dot{y}\end{array} \]$

(12)

식(12)에 사용된 인자들은 아래와 같다.

$\[ \begin{array}{c}{a}_{21}=-\frac{k_p}{m}, a_{22}=-\frac{C_p}{m}, a_{23}=\frac{k_p{k}_p}{m}-\frac{C_p{k}_p}{R{C}_m}, a_{24}=\frac{k_p}{m}, a_{25}=\frac{C_p}{m},\\ a_{33}=-\frac{1}{R_c}, a_{55}=-\frac{C_s}{J+K^{2}M}, a_{56}=-\frac{k{k}_2}{J+k^{2}M}, a_{65}=-\frac{K_1}{L_{m}k},\end{array} \]$

이와 같이 2개의 기구를 1개의 상태방정식으로 표현할 수 있으며 Global Servo System과 Fine Servo System 일체로 설계하는 것이 가능하다.

3.2 Dual Servo System Performance Evaluation

Dual Servo System의 제어 실험은 Fig. 6과 같이 구성하여 진행하였으며, Global Servo System의 제어 분해능과 Dual Servo System의 제어 분해능을 측정하였다.

Fig. 6

Dual servo system configuration

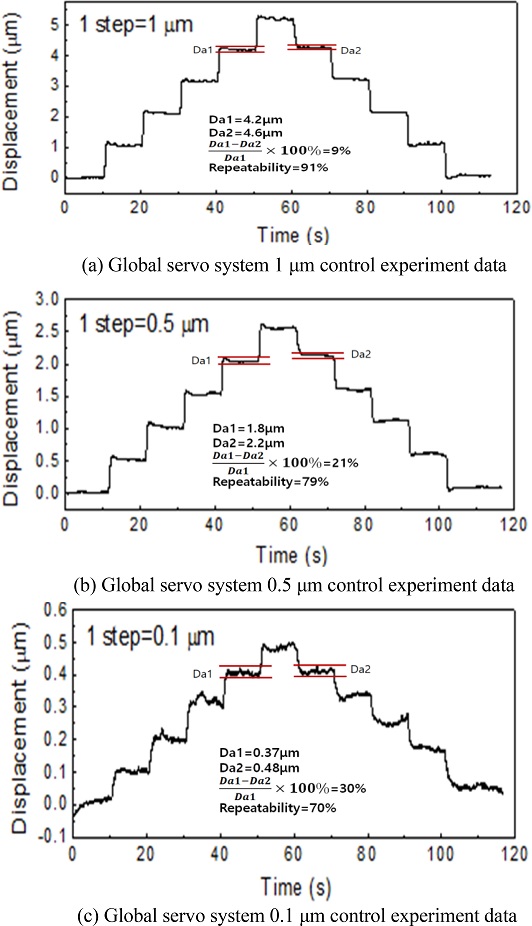
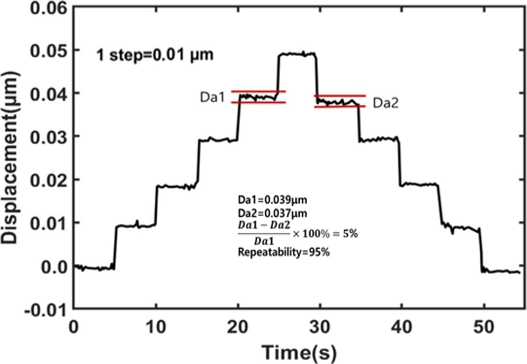
실험은 Fig. 7과 같이 Laser Interferometer를 활용하여 Step당 위치 이송정밀도를 확인하였으며, Global Servo System은 Fig. 8과 같이 1, 0.5, 0.1 μm의 입력을 하였으며, Dual Servo System은 0.01 μm를 입력하여 이송 거리를 측정하였다.

Fig. 7

Dual servo system control experiment

Fig. 8

Global servo system control experiment data

제어 실험 결과 Global Servo System의 위치정밀도는 1 μm 시 반복정밀도 91%를 보였으며, 0.5 μm 시 79%, 0.1 μm 시 70%로 측정되었다. Global Servo System의 이송 위치정밀도의 안정성은 0.5 μm를 최고로 확인되었으며, Dual Servo System은 10 nm의 이송 시 반복정밀도 95%로 확인되었다.

Fig. 9

Dual servo system control experiment data

3.3 Dual Servo System

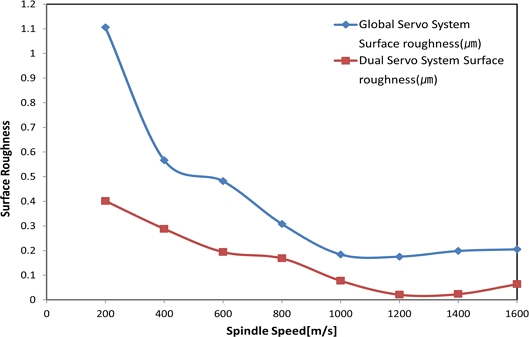
시스템의 성능을 확인하기 위하여 본 연구에서 조도측정기를 활용하여 가공된 알루미늄 공작물의 평균 표면 거칠기를 측정하였다. 측정은 Global Servo System 가공 시편과 Dual Servo System 가공 시편을 각 8개씩 총 16개의 시편을 주축회전속도를 변경하며 가공하여 측정하였으며 실험 조건은 Table 3에 나타내었다.

Table 3

Spindle speed control experiment condition

주축회전속도를 변경하며 실험한 결과는 Table 4에 정리하였으며, Root Mean Square를 계산한 결과 Dual Servo System 0.200394 μm, Global Servo System 0.502164 μm로 확인되었다. 실험 결과 Dual Servo System이 Global Servo System보다 0.35716 μm만큼 표면조도가 향상되는 것을 확인할 수 있다. Fig. 10은 Dual Servo System 가공 실험 결과와 Global Servo System 가공 실험 결과를 나타내었으며, Fig. 11은 가공시편이다.

Table 4

Spindle speed control experiment results

Fig. 10

Comparison of surface roughness

Fig. 11

Processing test piece

4. Conclusion

본 연구에서는 범용 CNC 장비(Global Servo System)에 Fine Servo System을 적용하여 Dual Servo System을 구축하였다.

설계된 Fine Servo System의 변위는 0.04 mm이며, Fine Servo System 힌지 부분의 등가응력이 99.8 N/mm²으로 나타나 안전율은 4.8로 나타나 안전성은 확보되었다. Dual Servo System의 제어 분해능은 Laser Interferometer를 활용하여 측정한 결과 10 nm로 확인되었다.

가공을 통한 Dual Servo System 표면조도 실험은 Table 4와 Fig. 10과 같으며, 최대 표면조도는 0.021 μm로 확인되었으며, Root Mean Square를 통하여 Global Servo System과 Dual Servo System을 비교한 결과 Dual Servo System 0.200394, Global Servo System 0.502164 μm으로 Dual Servo System이 Global Servo System보다 0.35716 μm만큼 표면조도가 향상되는 것을 확인할 수 있다.

Acknowledgments

이 논문은 2021년도 송원대학교 학술연구비 지원을 받아 연구되었음(No. C2021-02).

REFERENCES

• Kim, J., Lee, H.-N., Kwac, L., Han, J., Cho, Y.-T., Jun, C.-G., (2000), Control performance evaluation of ultra precision positioning apparatus, Proceedings of the International Society of Internal Medicine Conference, 252-255.
• Park, D.-K., Lee, G.-I., Gao, J.-C., Kim, J.-Y., (2016), Research on the design of the ultra-high-precision positioning control error compensation, International Journal of Precision Engineering and Manufacturing, 17(10), 1351-1358. [https://doi.org/10.1007/s12541-016-0160-3]
• Kim, J., Han, J., Kim, H., You, S., Kwac, L., Song, I., (1997), A study on the optimal structural design and ultra precision position control using FEM for micro stage, Proceedings of the Korean Society of Precision Engineering Conference, 336-340.
• Sze-Wei, G., Han-Seok, L., Rahman, M., Watt, F., (2007), A fine tool servo system for global position error compensation for a miniature ultra-precision lathe, International Journal of Machine Tools and Manufacture, 47(7-8), 1302-1310. [https://doi.org/10.1016/j.ijmachtools.2006.08.023]
• Yong, Y. K., Lu, T.-F., Handley, D. C., (2008), Review of circular flexure hinge design equations and derivation of empirical formulations, Precision Engineering, 32(2), 63-70. [https://doi.org/10.1016/j.precisioneng.2007.05.002]
• Henning, S., Linß, S., Zentner, L., (2018), DetasFLEX-A computational design tool for the analysis of various notch flexure hinges based on non-linear modeling, Mechanical Sciences, 9(2), 389-404. [https://doi.org/10.5194/ms-9-389-2018]
• Ding, B., Yang, Z.-X., Zhang, G., Xiao, X., (2017), Optimum design and analysis of flexure-based mechanism for non-circular diamond turning operation, Advances in Mechanical Engineering, 9(12), 1-10. [https://doi.org/10.1177/1687814017743353]
• Linß, S., Schorr, P., Zentner, L., (2017), General design equations for the rotational stiffness, maximal angular deflection and rotational precision of various notch flexure hinges, Mechanical Sciences, 8(1), 29-49. [https://doi.org/10.5194/ms-8-29-2017]
• Torres Melgarejo, M. A., Darnieder, M., Linß, S., Zentner, L., Fröhlich, T., Theska, R., (2018), On modeling the bending stiffness of thin semi-circular flexure hinges for precision applications, Actuators, 7, 86-106. [https://doi.org/10.3390/act7040086]
• Darnieder, M., Pabst, M., Wenig, R., Zentner, L., Theska, R., Fröhlich, T., (2018), Static behavior of weighing cells, Journal of Sensors and Sensor Systems, 7(2), 587-600. [https://doi.org/10.5194/jsss-7-587-2018]
• Smith, S., Chetwynd, D., Bowen, D., (1987), Design and assessment of monolithic high precision translation mechanisms, Journal of Physics E: Scientific Instruments, 20(8), 977-983. [https://doi.org/10.1088/0022-3735/20/8/005]
• Quinn, T., Speake, C., Davis, R., (1986), A 1 kg mass comparator using flexure-strip suspensions: Preliminary results, Metrologia, 23(2), 87-100. [https://doi.org/10.1088/0026-1394/23/2/002]
• Doebelin, E. O., Manik, D. N., (1990), Measurement systems: Application and design, McGraw-Hill.
• Gu, Y., Clark, R., Fuller, C., Zander, A., (1994), Experiments on active control of plate vibration using piezoelectric actuators and polyvinylidene fluoride (PVDF) modal sensors, Journal of Vibration and Acoustics, 116(3), 303-308. [https://doi.org/10.1115/1.2930429]
• Inniss, C., Williams, T., (2000), Sensitivity of the zeros of flexible structures to sensor and actuator location, IEEE Transactions on Automatic Control, 45(1), 157-160. [https://doi.org/10.1109/9.827375]
• Dosch, J. J., Inman, D. J., Garcia, E., (1992), A self-sensing piezoelectric actuator for collocated control, Journal of Intelligent Material Systems and Structures, 3(1), 166-185. [https://doi.org/10.1177/1045389X9200300109]
• Lee, C.-K., Moon, F. C., (1990), Modal sensors/actuators, Journal of Applied Mechanics, 57(2), 434-441. [https://doi.org/10.1115/1.2892008]
• Sim, E., Lee, S. W., (1993), Active vibration control of flexible structures with acceleration feedback, Journal of Guidance, Control, and Dynamics, 16(2), 413-415. [https://doi.org/10.2514/3.21025]
• Fanson, J., Caughey, T., (1990), Positive position feedback control for large space structures, AIAA Journal, 28(4), 717-724. [https://doi.org/10.2514/3.10451]
• Patnaik, B., Heppler, G., Wang, D., (1993), Stability analysis of a piezoelectric vibration controller for an Euler-Bernoulli beam, Proceedings of the American Control Conference, 197-201. [https://doi.org/10.23919/ACC.1993.4792836]
• Johnson, C. T., Lorenz, R. D., (1992), Experimental identification of friction and its compensation in precise, position controlled mechanisms, IEEE Transactions on Industry Applications, 28(6), 1392-1398. [https://doi.org/10.1109/28.175293]
• Iwasaki, M., Matsui, N., (1996), Observer-Based nonlinear friction compensation in servo drive system, Proceedings of 4th IEEE International Workshop on Advanced Motion Control, 344-348.
• Ledesma, R., Ma, Z.-D., Hulbert, G., Wineman, A., (1996), A nonlinear viscoelastic bushing element in multibody dynamics, Computational Mechanics, 17(5), 287-296. [https://doi.org/10.1007/BF00368551]
• Bohn, G., Steinmetz, G., (1984), The electromagnetic levitation and guidance technology of the ‘Transrapid’ test facility Emsland, IEEE Transactions on Magnetics, 20(5), 1666-1671. [https://doi.org/10.1109/TMAG.1984.1063246]