Solenoid Coil and Capacitor Design to Improve the Performance of Multi-Stage Coil Guns
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The purpose of this study was to design capacitors and a coil, which are components of an electric circuit, for improved performance of multi-stage electromagnetic coil guns. The electromagnetic force generated in the solenoid coil is determined by the magnitude of the current, supplied from the capacitor to the solenoid coil. Since the current flowing in the solenoid coil is not constant, the variability of electromagnetic force becomes larger. Design variables such as the capacitor capacity, coil winding, and firing distance are complicatedly related and determine the coil gun firing rate together. This study sets the number of turns of the solenoid coil, capacitor capacity, and firing distance as design variables for a five-stage coil gun. The electric circuit configuration of the coil gun with the highest velocity in each firing stage, was derived through the design of experiments. The coil gun’s finite element analysis model was constructed using ANSYS Maxwell, an electromagnetic analysis program, and implemented through a transient simulation to calculate the projectile’s velocity. Additionally, a prototype was manufactured based on the derived results to conduct launch experiments, and the experimental and simulation results were compared.
Keywords:
Capacitor, Electromagnetic launcher (EML), Finite elements method, Multi-Stage coil gun, Solenoid coil1. Introduction
A coil gun is a device that accelerates a projectile with the electromagnetic force generated when current is supplied to a solenoid coil in the device. The operation of the coil gun is based on the conversion of electric energy into magnetic energy and then into kinetic energy. Since there is a limit to the velocity increase in a single coil gun system due to the magnetic saturation point of the solenoid coil, the coil gun system should be configured using multiple coil gun circuits [1,2]. A capacitor applied with a high voltage is generally used in a coil gun system to result in a high current instantaneously flowing into the solenoid coil. The solenoid coil and capacitor are the coil gun’s parts that directly generate electromagnetic force. Hence, studies on the solenoid coil and capacitor have been conducted to improve the firing velocity of the coil gun. Designs that maximize the electromagnetic force in a single solenoid coil were proposed in the previous studies. But, although the projectile is accelerated as it receives an electromagnetic force in a direction same as the direction of progress of the projectile until it passes the center of the solenoid coil, it is decelerated after passing through the center. This phenomenon is due to the structural characteristics of the coil gun that uses the solenoid coil. The projectile receives a force in a direction opposite to the direction of progress of the projectile after passing through the center. The force received in the reverse direction also increases when the electromagnetic force is maximized, leading to poor efficiency [3].
The number of turns of the solenoid coil should be adjusted to overcome the issue of a projectile decelerating after passing through the center of the solenoid coil in a single-coil gun. This adjustment ensures that the electromagnetic force is maximally delivered when the projectile proceeds in the firing direction rather than making the coil gun generate the maximum electromagnetic force. In addition, the waveform of the electromagnetic force can be adjusted by adjusting the capacitance of the coil gun along with the shape of the solenoid coil. This relationship has also been proven by the preliminary studies [4].
The previous researches had studied the solenoid coil turns in case of single coil gun or the discharge position in case of multi coil gun. However, no case to study the turns and discharge position of coils at the same time have not been reported yet. The multi coil gun system in the previous research had poor accelerating performance. In this study, both the solenoid coil turns and the discharge position of multi coil gun were designed in mind simultaneously.
It is also important to effectively deliver the electromagnetic force generated in the coil gun circuit to the projectile. Hence, the capacitor and coil winding, which are the design variables of the electric circuit, should be designed so that the electromagnetic force can be maximally received in the firing direction by the projectile. Therefore, for the distribution of the electromagnetic force, the magnitude of the electromagnetic force generated in the solenoid coil over time, i.e., the waveform of the current flowing in the solenoid coil, should be studied. The electric circuit of the coil gun is a typical RLC (Resistor Inductor Capacitor) circuit, and the shape of the derived current is an underdamped sine curve [5].
This study designed the capacitors and coil windings of the electric circuits at individual stages of the multi-stage coil gun based on finite element analysis. In effect, this study aimed to efficiently distribute the electromagnetic force generated in the coil gun circuit when designing a coil gun. The shapes of acceleration of the projectile and the winding of the solenoid coil, and the capacitor capacity and the shape of the current derived in the coil gun circuit were compared to identify the conditions for deriving the optimum velocity. This identification was performed to present the directions for the solenoid coil and capacitor designs according to the initial velocity at each stage in a multi-stage coil gun.
The firing distance, the distance between the projectile and the solenoid coil, was also set as one of the design variables [6,7] in the present analysis. This additional variable is used because even if the same capacitor and solenoid coil are used in the coil gun circuit, the electromagnetic force received by the projectile varies depending on the location of the projectile. Therefore, the location of the projectile should be designed according to the components of the coil gun. Operating the coil gun when the projectile moving at a high velocity reaches the firing distance set as a design variable for the coil gun at each stage also affected the overall performance of the coil gun in a multi-stage coil gun prototype experiment. This observation was confirmed by comparing the method that used the physical contact of the projectile to detect its position with the method that used a sensor [8]. Therefore, a method with little error in operability should be used. The SCR thyristor element, MOSFET electronic switch, and Arduino were used to control the coil gun at each stage with electronic signals in the multi-stage coil gun system studied using a prototype. These three elements minimized the error of the coil gun operation timing depending on the projectile’s position. The velocity increments of the projectile by stage were recorded using the Ballistic Chronograph, a device that measures the velocity of the projectile. The errors of the multi-stage coil gun control circuit were measured, and the measurement results of the simulations and experiments were compared. In addition, the direction for achieving additional improvement in the velocity of the coil gun manufactured in this study was presented.
Therefore, this paper analyzes the shape of the electromagnetic force generated by the coil gun circuit and suggests a method of designing a coil gun circuit suitable for the acceleration shape of the projectile.
2. Coil Gun System
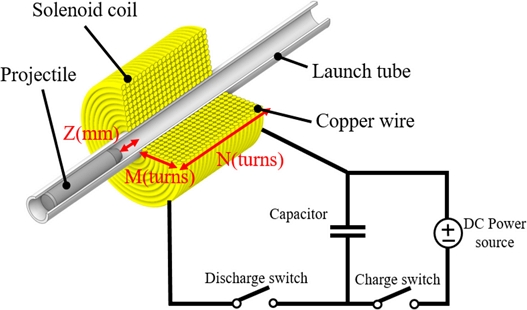
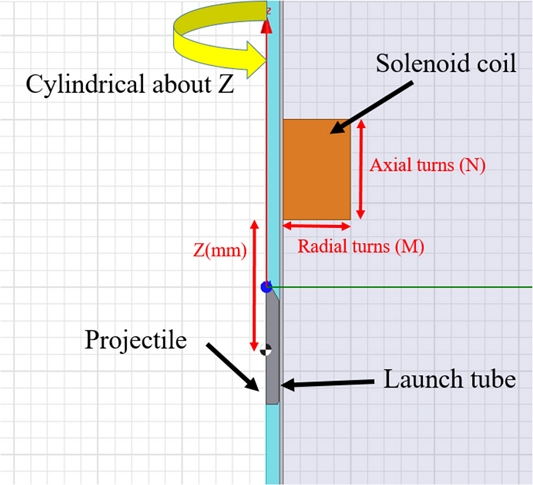
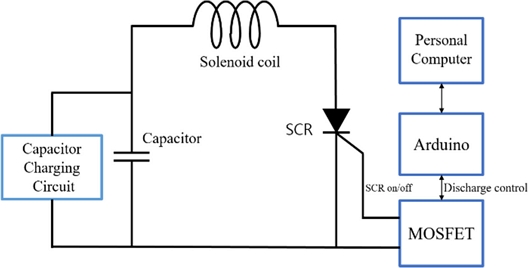
A coil gun system consists of a projectile, coil winding, and an electric circuit, as shown in Fig. 1. A high voltage is charged in the capacitor and discharged instantaneously to result in a high current flowing through the solenoid coil to generate electromagnetic force in the coil. The initial electromagnetic force from the coil acting on the projectile varies according to the initial position of the projectile and affects the inductance as the projectile moves. Hence, the initial electromagnetic force causes changes in the current and eventually affects the electromagnetic force and the projectile’s velocity.
The shape of the solenoid coil winding is determined in the radial (M) and axial (N) directions, as shown in Fig. 2. The allowable current varies according to the diameter when copper wires are used in a solenoid. This study used a copper wire of diameter of 2 mm to which an allowable current of 1,000 Ampere can be supplied. This copper wire was chosen because a current of up to 1,000 Ampere or more is formed in the coil.
Launch tubes made of a metal with at least a certain hardness level, such as stainless steel, are sometimes used in the coil gun. But, when a coil gun is constructed using a metal launch tube, the performance of the coil gun may be degraded due to the eddy currents generated by the metal launch tube. Therefore, the present system was configured using a nonmetallic carbon launch tube.
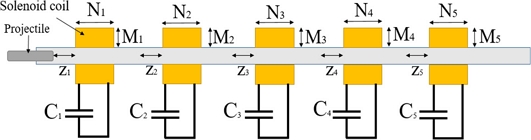
This study designed a 5-stage coil gun based on the above system configuration. The capacitance of several coil windings in each stage was designed, and the Z value for each stage was also derived to achieve the best performance in each stage. The schematic diagram of the 5-stage coil gun is shown in Fig. 2.
3. Establishment of Design Problems
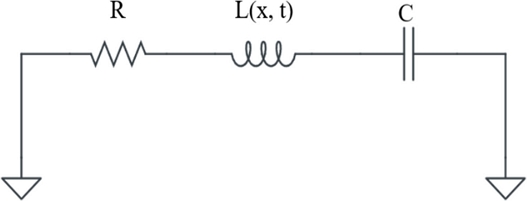
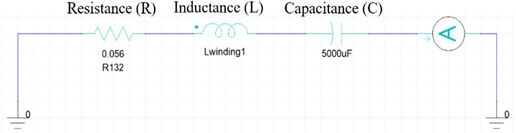
The earlier discussions mentioned that the projectile accelerates towards the center of the solenoid and starts to receive electromagnetic force in the direction opposite to the firing direction when it passes through the center of the solenoid in a coil gun circuit. Therefore, the capacitor, coil, and firing position should be designed so that the electromagnetic force generated until the capacitor is completely discharged is maximally distributed in the direction of progress of the projectile. Fig. 3 shows the RLC circuit of a coil gun that is designed.
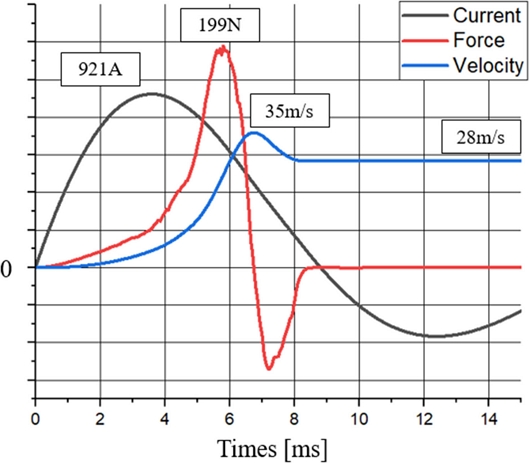
The design should compare the shape of acceleration of the projectile and the electromagnetic force induced in the solenoid coil. The electromagnetic force generated in the solenoid coil is proportional to the magnitude of the current flowing through the solenoid coil. Since the shape of the current is not constant in this case, it should be handled first. The shape of the current flowing through the solenoid coil appears as a function of the RLC underdamped system. Fig. 4 shows the magnetic force, projectile velocity, and coil current of a single-coil gun (Capacitor Charging Voltage 400 V, Charging Capacity 10 mF, Numbers of Turns in the Solenoid Coil: N = 25, M = 11, Resistance = 0.154 Ω, and Firing Distance: Z = 18 mm). The electromagnetic force received by the projectile increases when the current flowing through the solenoid coil increases. Moreover, a part of the projectile passes through the center of the solenoid coil at 5.7 ms and receives a force in a direction opposite to the firing direction. Hence, the net force received by the projectile in the firing direction decreases. Subsequently, the projectile’s center of gravity passes through the center of the solenoid coil at 6.5 ms, and the projectile receives the force completely in the reverse direction reducing the velocity.
The projectile cannot sufficiently accelerate while proceeding in the firing direction if the cycle of the RLC function is shorter than the acceleration time of the projectile. On the other hand, the electromagnetic force acting in a direction opposite to the firing direction of the projectile increases leading to a decrease in the firing efficiency if the cycle of the RLC function is longer than necessary. Therefore, the design should consider the shapes of the projectile’s acceleration and the current and the electromagnetic force induced in the solenoid coil simultaneously.
The cycle T of the solenoid coil current is determined by the inductance, resistance, and capacitance of the coil, and the amplitude of the solenoid coil current is determined by the charging voltage and charging capacity of the capacitor. The two elements, solenoid coil and capacitor, determine the cycle in the RLC function. Therefore, the capacitor capacity should be designed along with the turns of the solenoid coil. Since the charging voltage of the capacitor does not affect the cycle, this study didn’t set the charging voltage of the capacitor as a design variable. Instead, the charging voltage of the capacitor was fixed at 400 V because a capacitor with a charging voltage of 400 V was used for the production of the prototype.
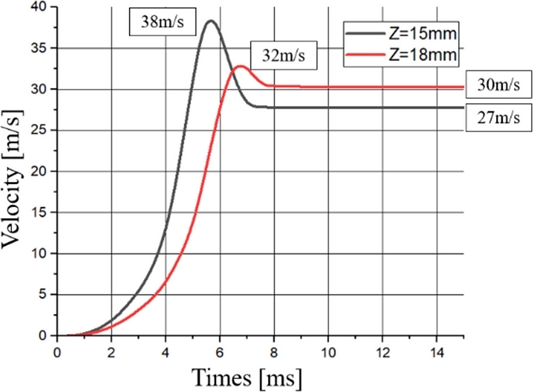
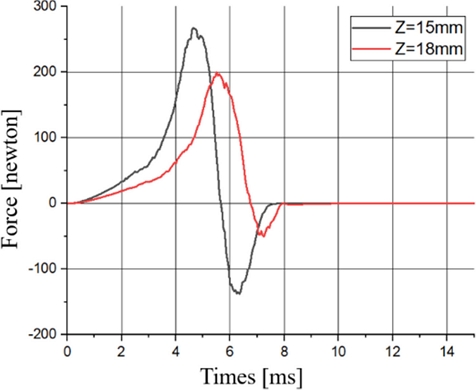
Figs. 5 and 6 show the projectile’s velocity according to the firing distance and the magnetic force acting on the projectile, respectively. The firing distances shown in Figs. 5 and 6 are 15 and 18 mm, respectively. The maximum velocity of the projectile with a firing distance of 15 mm is 38 m/s, as shown in Fig. 5. But, the projectile decelerates after passing through the center of the solenoid coil, and the final velocity is 27 m/s. As a result, the projectile of the coil gun with a firing distance of 15 mm receives a relatively larger electromagnetic force, as shown in Fig. 6. Hence, a higher maximum velocity is derived, but the electromagnetic force the projectile receives in the reverse direction is also larger. Therefore, the decrement of the velocity becomes larger than that of the projectile with a firing distance of 18 mm. As a result, the projectile with a firing distance of 18 mm that shows a smaller decrement of velocity has a higher projectile velocity, as shown in Fig. 5. In other words, the firing distance affects the electromagnetic force leading to differences in the projectile’s acceleration.
In conclusion, when a coil gun is designed, the design of the electric circuit considering the shape of the electromagnetic force generated in the coil gun system and the design of the physical location of the projectile considering the distribution of the electromagnetic force generated should be carried out simultaneously. In other words, the designs of the capacitor, coil winding, and firing distance of the electric circuit of the coil gun should be carried out in combination. This combined design ensures that the cycle of the RLC function in the coil gun circuit can be derived considering the acceleration time of the projectile to derive maximum velocity for the projectile.
4. Analysis of Finite Elements of the Coil Gun
Three sub-systems, namely mechanical, magnetic, and electrical systems, are coupled in a coil gun system. This coupled system can be expressed using the following governing equation.
| (1) |
In addition, the magnetic force received by the projectile from the coil gun is affected by the magnetic flux density, magnetic permeability, etc. The magnetic flux density continuously changes according to the projectile’s position, and the force received by the projectile at position z is expressed as follows.
| (2) |
where u is the magnetic field energy in a certain space and expressed as the product of volume (V) and magnetic flux density (B). The variation of energy Δu is expressed as,
| (3) |
where μ0 and μm are the magnetic permeabilities of air and the material occupying the space. The force F received by the projectile can be obtained by using Eqs. (2) and (3). The magnetic flux density (B) can be expressed as an integral value with respect to the distance as follows, with r as the radius of the projectile and L as the length of the solenoid coil.
| (4) |
where magnetic field B also changes according to the distance z of the projectile. Therefore, it is difficult to simulate the coil gun system expressed above using analytical methods. Therefore, the ANSYS Maxwell finite element analysis program, which is a numerical method for combined mechanical, electrical, and magnetic analysis, is used in this study. The capacitor charging voltage is 400 V, and the capacitor capacity and the distance between the solenoid coil and the projectile were set as design variables. Table 1 shows the design variables of the coil gun finite element model.
The coil gun system was implemented as a two-dimensional (2D) symmetric model shown in Fig. 7 in the coil gun simulation. This 2D symmetric model shortens the analysis time. The state was set to transient in the analysis. The shape of the projectile’s acceleration by the solenoid coil and the shape of the current flowing through the solenoid coil were calculated over time. The results of these analyses were obtained in the form of a graph.
The material of the launch tube was set as nonmetallic, and the material of the solenoid coil was set as copper to complete the analysis model.
The RLC circuit of the coil gun was implemented through the Maxwell Circuit Editor to generate the electromagnetic force in the coil gun circuit and set the capacitor capacity, which is a design variable. Fig. 8 shows the RLC circuit of the coil gun on Maxwell. First, the self-resistance of the solenoid coil was calculated using Eq. (5) below. Subsequently, the circuit of each stage was implemented according to the calculated resistance and the capacitor capacity specified as a variable. In addition, the inductance of the solenoid coil was calculated in the Maxwell program.
| (5) |
Five stages of projectile systems were modeled in the present study. The projectile is stationary in the initial state of a single-stage projectile system. Whereas the final velocity of the projectile accelerated in the previous stage was applied as the initial velocity of the following stage in a multi-stage coil gun with two or more stages.
5. Design of Experiment
Since the solenoid coil, capacitor, and firing distance are independent, the design of experiments was adopted as a design methodology for a sufficient design.
Table 3 shows the experimental points created in an orthogonal arrangement for the design of the first stage of the coil gun and the projectile velocity at each experimental point.
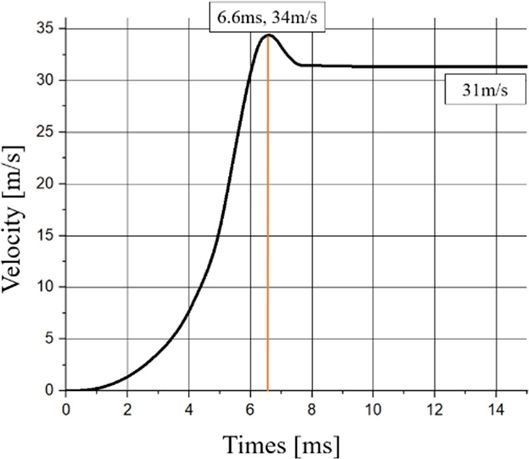
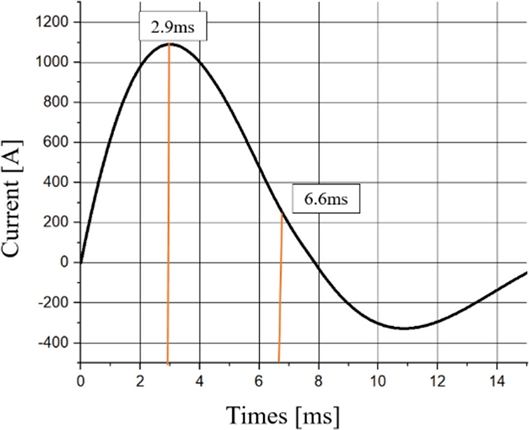
Two velocities, namely the maximum and the final velocities, are indicated in the table. These two velocities represent the maximum velocity of the projectile recorded when the projectile passed through the solenoid coil and the final velocity of the projectile that went out of the solenoid coil, respectively. The reason why two velocities are used separately is to compare the amounts of deceleration. In particular, this comparison is made when the projectile is decelerated as the electromagnetic force is applied in a direction opposite to the firing direction after the projectile passes the center of the solenoid coil. This deceleration phenomenon can be seen in the projectile velocity graph of Fig. 5. The maximum and final velocities were derived for a capacitor capacity of 10,000 uF, numbers of turns of the solenoid coil of 24*11, and the distance between the solenoid coil and the projectile set at 20 mm. Figs. 9 and 10 show the maximum and final velocities of the projectile among the experimental points of the single-stage coil gun and the currents supplied to the solenoid coil in such cases, respectively.
The projectile passes through the center point of the solenoid coil at 6.6 ms, as shown in Figs. 9 and 10, and after that receives the electromagnetic force in the reverse direction. Seventy-two percent of the electromagnetic force applied on the projectile is delivered to the projectile while the projectile progresses in the firing direction.
6. Design of Multi-Stage Coil Guns
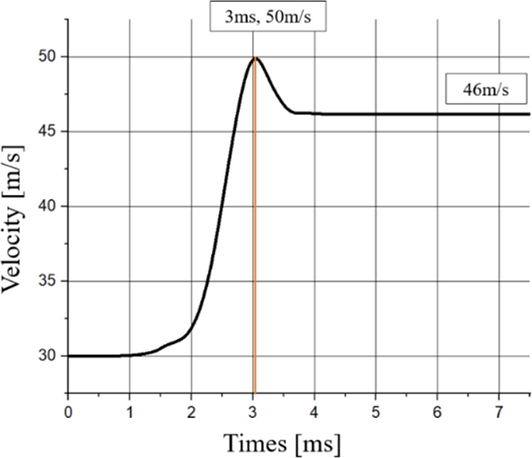
A two-stage coil gun was designed with 31 m/s, the muzzle velocity in the single-stage coil gun, as the initial velocity in the second stage. The ranges of design variables of the two-stage coil gun were set as shown in Table 4 to lower the inductance and resistance considering the initial velocity. On the other hand, in the two-stage coil gun, the distance between the solenoid coil and the projectile should be set higher than the range of the design variable of the single-stage coil gun due to a non-zero initial velocity of the projectile in the two-stage coil gun. The optimum distance for the two-stage coil gun with an initial velocity of 31 m/s was derived from the experimental point where the capacitor capacity is 7,000 uF and the numbers of turns of the solenoid coil are 14*9. This experimental point is taken from the 64 experimental points created with the design variables summarized in Table 3. The distance between the solenoid coil and the projectile was calculated as 71 mm.
Figs. 11 and 12 show the experimental points with the projectile’s maximum and final velocities among the experimental points of the two-stage coil gun and the currents supplied to the solenoid coil at the experimental points, respectively.
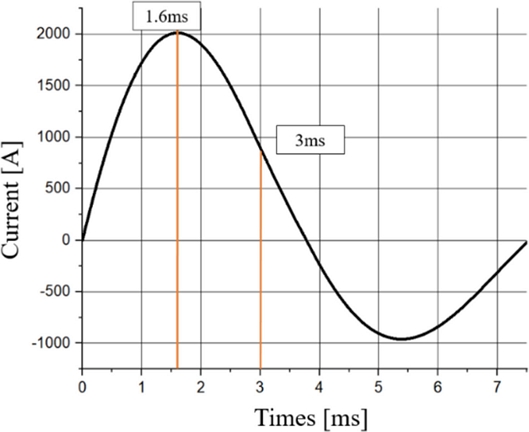
The projectile passes through the center of the coil at 3 ms in a two-stage coil gun with optimum values. In addition, the current flowing through the solenoid coil reaches a peak at 1.6 ms and decreases at 3 ms when the projectile passes through the center. However, despite a non-zero initial velocity, the RLC cycle at the optimum values becomes 3.7 ms, shorter than that of the single-coil gun accelerating from a stationary state. Therefore, the components of the multi-stage coil guns must be designed to shorten the RLC cycle, considering the acceleration time shortened as the number of stages increases.
Optimal designs of 5 stages of coils were carried out based on the above design method. The ranges of design variables in three to five-stage coil guns were set identically to create orthogonal arrangement tables, and Maxwell analysis of the experimental points was conducted after that. In addition, the distance between the solenoid coil and the projectile must be set considering the projectile’s initial velocity.
Table 8 shows the initial and exit velocities and the velocity increase value for each stage. The shape of acceleration of the projectile shows that the velocity increment decreases as the number of stages increases.
Tables 9 and 10 show the optimal values of variables derived from each stage of the five-stage coil gun and the RLC values and function cycles of the entire coil guns, respectively.
The optimum value of the distance between the solenoid coil and the projectile also increases as the projectile’s initial velocity increases. Since it takes time for the current of the solenoid coil to reach the maximum value, the distance between the solenoid coil and the projectile should be adjusted considering the projectile’s initial velocity. This consideration ensures that the projectile passes through the solenoid coil when the solenoid coil generates the maximum electromagnetic force. In effect, there is the effective delivery of the electromagnetic force generated by the solenoid coil. Since the projectile in a stationary state is accelerated in a single-stage coil gun, the RLC function with the longest cycle of 8.8 ms was derived. In comparison, the cycle of the RLC function is shortened as the number of stages increases in the analysis model of two or higher-stage coil guns used to derive the optimum value. The distance between the solenoid coil from which the maximum velocity was derived and the projectile also increases when the number of stages increases.
7. Configuration of a Prototype of Multi-Stage Coil Guns and Velocity Measurement
The discharge time is an important design variable in a coil gun system. Hence, a method with less error in operability should be used to produce a prototype of a multi-stage coil gun system. Choosing methods with less operability error is also important as the method of operating the coil gun at each stage affects the overall performance of the coil gun. The methods of detecting the position of the projectile through a sensor and by physical contact between the projectile and the switch were used in the existing studies of coil guns. But, since the discharge position needs to be physically adjusted, errors will become large when many discharge control devices are used. Typically, a large number of discharge control devices are used when the velocity of the projectile is high and the number of stages of the coil is large. In addition, the higher the velocity of the projectile, the longer the distance between the solenoid coil and the projectile at the time of discharge. Hence, the overall size of the coil gun increases in a multi-stage coil gun system, which is inefficient for the configuration of the experimental device.
This study used an SCR thyristor element to control the voltage over 400 V. A MOSFET electronic switch and Arduino were used to control the coil gun of each stage with electronic signals controlling the SCR element.
The operation method is like as follows. The Arduino outputs the SCR operating signal. And then MOSFET, which received the signal, supplies operating power to the SCR because the Arduino output voltage is insufficient to operate the SCR. When the SCR is operated, it does not turn off until all the capacitors are discharged. The Arduino program output the ON signal simply.
The control method controlled the voltage by adding a delay between each coil gun discharge. The delay was determined by considering the projectile’s position and velocity based on the results of the Maxwell analysis. Figs. 13 shows the diagram and 14 shows the prototype of the discharge control circuit used in the experiment.
Configuring the discharge control circuit using Arduino is advantageous in multi-stage coil guns in which the velocity of the projectile is high, and many stages need to be controlled. This advantage stems from the Arduino enabling the adjustment of the discharge delay even in 1 us units. In effect, the use of Arduino results in more precise discharge control than controlling the time of discharge using a distance sensor in which the position should be physically adjusted. However, using a delay between discharges is inconvenient in that the maximum velocity is derived only in cases where the delay is directly adjusted by conducting an experiment when an error occurs between the simulation and the actual discharge. In addition, errors are accumulated in the acceleration in the next stage when an error occurs. Subsequently, a difference in the amount of change in the velocity occurs. These errors can be reduced with the position of the solenoid coil firmly fixed and the charging device configured so that each capacitor can be uniformly charged in all experiments.
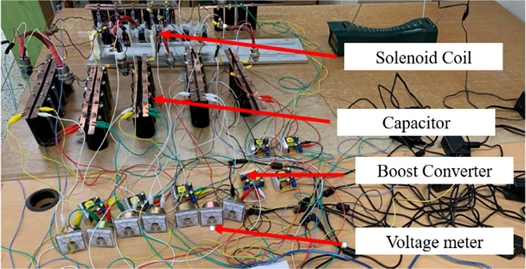
A prototype was manufactured according to the design derived from the design of experiments, and the velocity was measured. The manufactured coil gun circuit consists of a charging device for charging the capacitor, a discharge circuit that operates the coil gun circuit, and a discharge control circuit for controlling the discharge circuit. Figs. 15 shows the overall appearance of the coil gun and the experimental environment, and 16 shows the charging device used to charge the capacitor.
The charging device charged the capacitor by boosting the 12 V power output from the DC power adapter to 400 V, the capacitor charging capacity, using a booster converter boosting circuit. Corrective procedures were followed to prevent errors caused by the differences in the charge amount of each capacitor. In particular, the experimental environment was configured so that when charging the capacitors, the capacitors of individual stages are connected with the device marked by the red circle in Fig. 16 to charge them as one capacitor. The capacitors are separated when the charging has been completed to act as capacitors of individual stages. The entire coil gun experiment environment, including the speed measuring device, is shown in Fig. 17.
The velocity of the projectile was recorded using a speed measuring device. The errors between the velocity of the projectile and the simulation values by stage from stage 1 to stage 8 were recorded and shown in Table 11. The velocity measurement values by stage shown in the table are the average velocities recorded ten times considering the errors.
Errors of at least 3.2% were incurred in the experimental values compared to the simulation values, and the errors increased as additional acceleration progressed. The reason for the errors between the experimental and simulation values is found to be the projectile in the experiment not located at the center of the launch tube, unlike the simulation. So, the projectile is subjected to frictional force by the launch tube and air resistance, which results in the difference between the initial velocity of simulation and experiment. The error accumulates as the number of stages increases.
8. Conclusion
The capacitor, coil gun winding, and firing distance were designed through finite element simulation and the design of experiments to improve the firing speed of the coil gun projectile. The design ensured that the electromagnetic force from the coil is maximally delivered to the projectile until the projectile passes through the center of the coil. The cycle of the RLC function must be set so that the entire electromagnetic force can be distributed to the projectile. Delivering the entire electromagnetic force ensures that the projectile maximally receives the force, according to its movement, while it progresses in the firing direction. Also, since the acceleration time shortens as the number of stages increases according to the projectile’s initial velocity in a multi-stage coil gun system, the cycle of the RLC circuit in the coil gun circuit should be shortened. Therefore, the capacitor and the number of turns of the coil should be designed to be smaller, and the firing distance should be increased.
A solenoid coil using a large diameter copper wire would be capable of generating electromagnetic force sufficient for acceleration as the number of stages increases. This solenoid coil could achieve sufficient electromagnetic force by reducing the inductance and resistance. However, in a single-stage coil gun that accelerates the projectile in a stationary state and the two-stage stage coil with a relatively low initial velocity, a capacitor with a capacity of 7 to 10 mF was used to match the RLC cycle according to the shape of acceleration. But, this design had a poor energy conversion efficiency.
In essence, if the coil diameter is designed differently by stage, high energy conversion efficiency and more effective performance improvement can be achieved.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) and funded by the Ministry of Education (No. 2020R1I1A3A04036862).
REFERENCES
-
Kim, S.-W., Jung, H.-K., Hahn, S.-Y., (1994), An optimal design of capacitor-driven coil-gun, IEEE Transactions on Magnetics, 30(2), 207-211.
[https://doi.org/10.1109/20.312259]

-
Yadong, Z., Ying, W., Jiangjun, R., (2010), Capacitor-driven coilgun scaling relationships, IEEE Transactions on Plasma Science, 39(1), 220-224.
[https://doi.org/10.1109/TPS.2010.2052266]

-
Lee, S. J., Kim, J. H., (2014), Design and experiment of coil gun to apply electomagnetic launcher system, Journal of the Korea Academia-Industrial Cooperation Society, 15(6), 3455-3459.
[https://doi.org/10.5762/KAIS.2014.15.6.3455]

-
He, J., Levi, E., Zabar, Z., Birenbaum, L., (1989), Concerning the design of capacitively driven induction coil guns, IEEE Transactions on Plasma Science, 17(3), 429-438.
[https://doi.org/10.1109/27.32251]

- Guo, L., Guo, N., Wang, S., Qiu, J., Zhu, J. G., Guo, Y., Wang, Y., (2009), Optimization for capacitor-driven coilgun based on equivalent circuit model and genetic algorithm, Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, 234-239.
- Vaneghi, M. M., Khatibzadeh, A. A., Khanbeigi, G. A., Besmi, M. R., (2011), Design and switching position optimization of multi-stage coilgun, Proceedings of the 2011 International Conference on Business, Engineering and Industrial Applications, 130-134.
-
Citak, H., Ege, Y., Coramik, M., (2019), Design and optimization of delphi-based electromagnetic coilgun, IEEE Transactions on Plasma Science, 47(5), 2186-2196.
[https://doi.org/10.1109/TPS.2019.2904515]

-
Kim, S., Kim, J., (2019), Control of discharge time using physical contact in a two-stage coil gun, Advances in Mechanical Engineering, 11(9), 1-8.
[https://doi.org/10.1177/1687814019877082]


Student in the Department of Mechanical Engineering, Yeungnam University. His research interests are electric motor and actuator.
E-mail: ksm090296@ynu.ac.kr

Received Ph.D. degree in Mechanical Engineering from University of California, Berkeley, USA, in 2005. Now he works as the Professor at School of Mechanical Engineering, Yeungnam University, Korea. His research interests include electric machine, vibration, and design.
E-mail: jinho@ynu.ac.kr