3D 변형 공정 지도 기반 AISI 4340 소재의 열간 단조 온도 및 변형률 속도 제어
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper investigated the hot deformation behavior of an AISI 4340 material through high-temperature compression experiments. The compression tests were performed to obtain stress-strain curves at processing temperatures of 900, 1,000, 1,100, and 1,200oϹ, and the strain rates of 0.01, 0.1, 1, and 10 s-1 up to a true strain of 1.0 in the high-temperature compression mode of Gleeble® 3,500. A novel 3D processing map, constructed through power dissipation efficiency and Ziegler's instability criterion, is proposed. The deformation behavior was analyzed by observing changes in the microstructure from the high-temperature compression tests. Electron back scatters diffraction (EBSD) was used to characterize the microstructures for various processing parameters. The process workability of finite element analysis (FEA) was examined in the deformation flow instability map in the three-dimensional space for each strain. As a result, each particle's strain rate and temperature of FEA data can be observed in a three-dimensional flow instability map to control the temperature and process speed to avoid unstable zones.
Keywords:
Processing map, Hot forging, 3D processing map, Hot deformation, AISI 4340, Finite element analysis키워드:
공정 지도, 열간 단조, 3차원 공정 지도, 열간 변형, 유한요소해석1. 서론
열간 단조는 빌렛 또는 예비 성형체를 미리 결정된 형상으로 가공하는 금속 성형 공정이다. 열간 단조 시 소재는 용융 온도의 75%까지 가열되며 용융 온도에 가까워짐에 따라 소성변형에 필요한 응력과 에너지가 감소하여 생산율을 높일 수 있다. 그러나 부적절한 온도에서의 열간 단조 공정은 재료의 소성변형에 따른 결함을 발생시킬 수 있다. 따라서 공정에 따른 결함을 줄이는 것은 매우 중요한 요소 중 하나이다. 그러나 열간 단조 공정에서 결함은 예측이 어려우며, 외부에서 육안으로 관찰할 수 없는 경우가 많다. 이러한 열간 성형 공정에서 형성될 수 있는 성형 결함으로는 Adiabatic Shear Bands, Flow Localization, Dynamic Strain Ageing (DSA), Kink Band 등이 있다. 특히 이러한 성형 결함들은 난성형 소재들에서 흔히 발생하므로, 난성형 소재를 가공하려면 성형 결함을 사전에 예측 및 평가하여 결함을 최소화할 수 있는 방법론의 구축이 선행되어야 한다. 이러한 결함의 발생 원인 중 하나는 금형과 소재의 마찰 및 소재 표면과 중심 간 온도의 불균일인 것으로 알려져 있다[1,2]. 전통적으로 산업의 생산 공정은 작업자의 경험과 시행착오 방식에 의존하여 달라지므로, Trial-and-Error에 따른 비용이 많이 소비된다[3]. 따라서 금속 성형 공정을 설계하는데 보다 효율적인 접근 방식을 사용하여 생산 비용을 줄이기 위한 방법이 필요하다.
일반적으로 고강도 고온 소재의 부품 제조는 고온에서의 변형 공정을 포함하고 있으며, 고온 성형 시 온도와 변형률 속도 등의 변수를 선택하기 위하여 인장, 압축, 굽힘 등의 축소 시뮬레이션 시험 방법이 자주 사용된다[4]. 최초의 변형 공정 지도는 Frost와 Ashby 등이 1982년에 공정 중 결함 발생 여부를 공정 매개변수(변형률, 변형률 속도, 온도)의 관점에서 판정하기 위하여 개발하였다[5]. 변형 공정 지도를 구축하기 위해 열간 변형의 유동응력 값이 사용된다. 이후 Prasad는 동적 재료 모델(Dynamic Material Model, DMM)의 원칙에 따라 구성된 변형 공정 지도를 개발하였다[6]. 이전 변형 공정 지도 연구에서 AZ31 소재는 280-450oϹ 및 0.005-0.05 s-1에서 안정적인 영역을 나타내며 최대 동력 소산 효율은 30.5%로 나타났다[7]. HR3C 소재의 변형 공정 지도 연구에서는 3차원 변형 공정 지도를 제시하며 두 번의 압축 중 두 번째 압축 시 0.6의 변형률에서 가장 큰 동력 소산 효율을 보인다[8].
본 연구에서는 AISI 4340의 온도, 변형률, 변형률 속도 등의 조건에 따른 변형 거동을 연구하기 위해 900-1,200oϹ 온도 범위와 0.01-10 s-1의 변형률 속도에서 압축 시험을 각각 진행하였다. 압축 시험 결과를 활용하여, 고온 변형 시 최적의 성형조건을 제시하며 성형결함을 피할 수 있도록 변형률 속도, 온도를 파악할 수 있는 3차원 변형 공정 지도를 제작하였다. 기존 변형 공정 지도는 특정 변형률에서 변형률 속도와 온도의 평면상에 동력 소산 효율 등고선과 불안정 조건에 따른 불안정 영역을 작도한다. 하지만, 실제 공정에서는 변형률이 연속적으로 변화하기 때문에 변형 공정 지도상 소재의 특정 부분의 공정 상태를 한번에 파악하는 데에 어려움이 존재한다. 본 연구에서 제작한 변형 공정 지도는 연속적으로 변화하는 변형률까지 포함하여 동력 소산 효율과 소성 불안정 영역을 3차원 공간상에 표현한다. 유한요소해석을 통하여 열간 단조 공정 동안 단조품 질점의 변형률에 따른 공정 온도 및 속도를 파악하고, 질점의 변형 이력을 3차원 변형 공정 지도에 도식하였다. 이로부터 결함 발생 방지를 위한 열간 단조 공정변수의 제어 방법을 제시하였다.
2. 재료 및 실험
2.1 고온 압축 시험
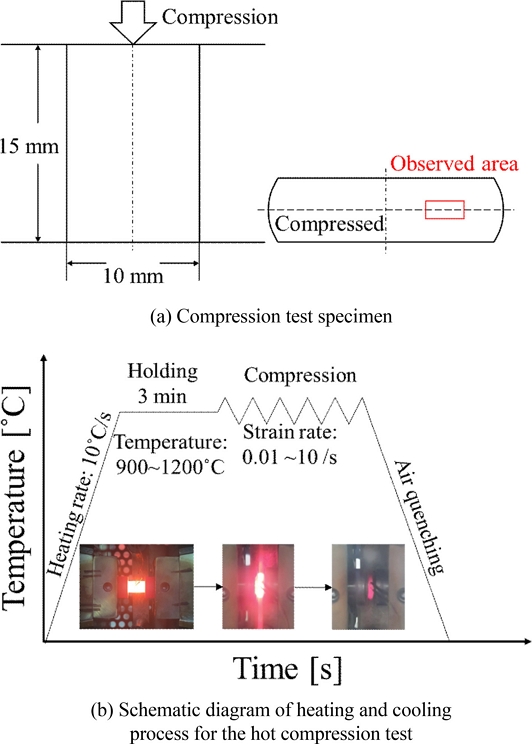
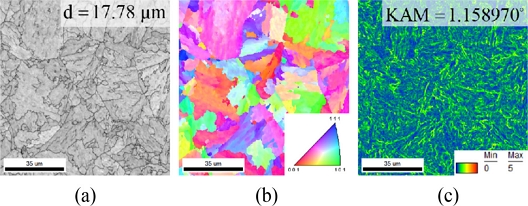
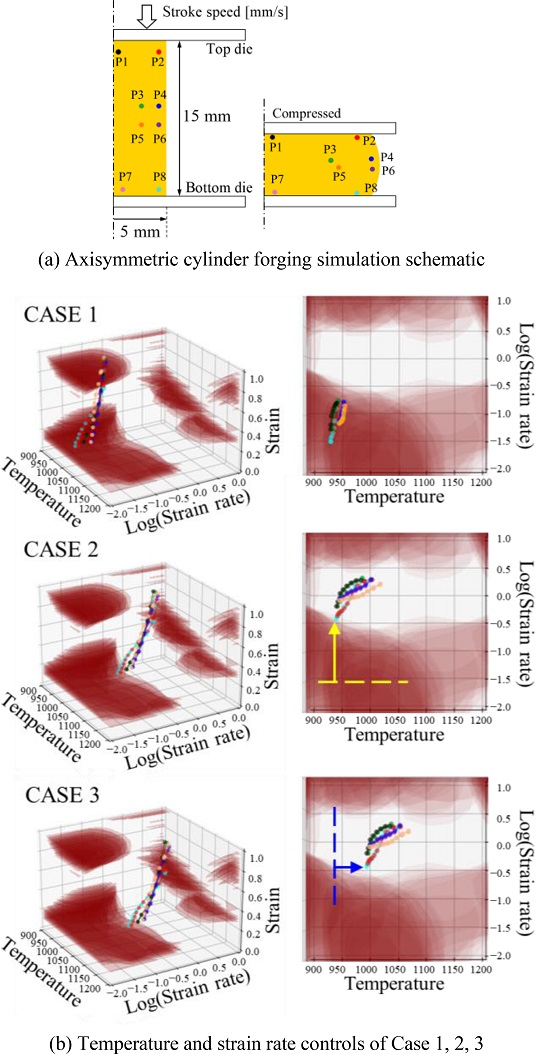
본 연구에서 사용한 AISI 4340의 압축 시험 시 시편은 Fig. 1(a)와 같이 직경 10, 높이 15 mm의 원기둥 시편을 사용하였으며 Gleeble® 3,500 Simulator의 고온 압축모드에서 0.01, 0.1, 1, 10 s-1의 변형률 속도와 900, 1,000, 1,100, 1,200oϹ의 가공 온도 조건에서 응력 및 변형률 곡선을 얻기 위하여 진변형률이 1.0이 될 때까지 압축하였다. 고온으로 가열 시 Fig. 1(b)와 같이 가공온도까지 10oϹ/s의 속도로 가열한 후 180초 동안 해당 온도를 유지하여 시편의 온도가 균일하게 분포하도록 하였으며, 압축 완료 후 상온까지 공냉하였다. AISI 4340을 Fig. 1(a)의 단면 붉은 영역을 전자 후방 산란 회절(EBSD) 분석을 수행하여 결정립 형태 및 결정학적 방향의 미세 구조를 특성화 하였다. Fig. 1(b)와 같이 초기 시편의 100 × 100 μm 영역을 0.1 μm의 일정한 크기로 스캔한 EBSD 결과를 Fig. 2에 나타냈다.
2.2 고온 변형 특성 평가
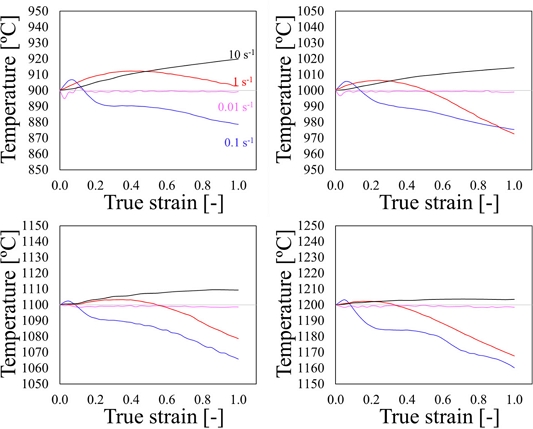
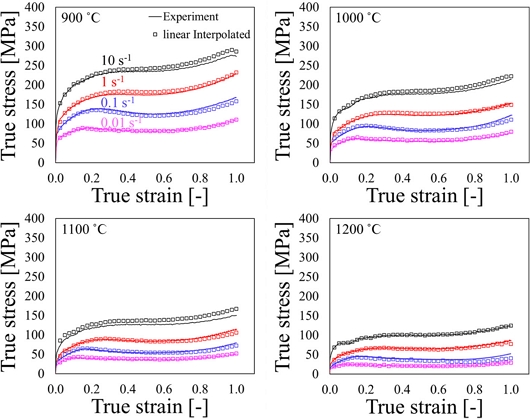
Gleeble 시험 시 높은 변형률 속도에서의 가공열 및 대기 온도에 의해 변화하는 소재의 온도를 Fig. 3에 나타냈다. 유동응력은 특정 온도에서 변형률 속도가 느릴수록 감소하였으며, 특정 변형률 속도에서 온도가 감소할수록 증가하였다. Fig. 4는 각각의 온도 및 변형률 속도 범위에서 고온 압축 시험을 통해 얻은 AISI 4340의 진응력-진변형률 곡선이며, 온도 변화에 따른 응력의 보간 값과 단열 조건을 가정한 응력 간의 비교를 보여준다. 보정 값은 등온 압축 시험 설정 온도에 맞도록 온도와 응력 사이의 관계를 보간한 것이다[9,10]. 두 곡선 사이의 차이는 더 높은 변형률에서 나타났으며, 이는 변형률이 증가함에 따라 초기 온도에 비해 온도 변화가 크기 때문이다.
3. AISI 4340의 변형 공정 지도
3.1 변형 공정 지도 이론
변형 공정 지도를 구성하기 위해 Dynamic Material Model (DMM) 이론을 기반으로, 소재가 받는 총 에너지 P는 온도 상승과 변형 속도 증가에 따른 에너지 G content, 그리고 미세구조의 변화에 의해 소산되는 에너지 J co-content의 합으로 전제하였다[11-14]. 금속의 열간 변형 시 유동응력은 일정한 온도에서 변형률 속도의 함수인 식(1)과 같이 표현 가능하다.
| (1) |
여기서 m은 변형률 속도 민감 지수이고, K는 변형률, 온도 등에 의존하는 강도 계수이다. 소재가 받는 총 에너지 P는 Fig. 5와 같이 두 가지 에너지로 구분된다[15]. 총 에너지 P는 G와 J의 합으로, 식(2)와 같이 나타낼 수 있다.
| (2) |
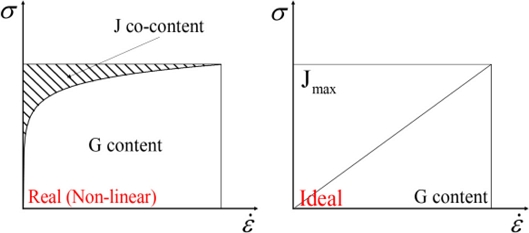
Schematic diagram of the constitutive equation in a non-linear power dissipator and ideal linear dissipator
Fig. 5에 나타낸 바와 같이 소성변형으로 소산되는 에너지와 미세구조의 변화에 소산되는 에너지가 같은 이상적인 (m = 1) 경우, J는 최댓값을 가지며, 로 표현된다.
식(1)에서의 변형률 속도 민감 지수는 식(3)과 같이 나타낼 수 있으며 G와 J를 변형률 속도 민감 지수로 표기가 가능하다[6,16].
| (3) |
식(1)에 식(3)을 대입하면 다음과 같이 식(4)를 얻을 수 있다.
| (4) |
동력 소산 효율(Efficiency of Power Dissipation, η)은 소재가 내부의 미세조직 변화에 의한 에너지를 소산하는 상대적인 효율을 나타내며 식(5)와 같이 정의된다[17].
| (5) |
동력 소산 효율은 소성변형 과정을 비가역 반응으로 간주한 열역학적인 고려와 미세구조 변화 등을 통해 특정 조건에서 일어나는 소성변형의 안정성 여부를 파악하는데 활용할 수 있다[18-21]. 미세 구조적 변화는 동력 소산 효율의 고효율 영역에서 일어나며, 동적 재결정(Dynamic Recrystallisation, DRX), 동적 회복(Dynamic Recovery, DRV)과 같은 특정 미세 구조적 변화가 일어나는 영역이다. 일반적으로 η가 클수록 미세 구조적 변화에 소비되는 에너지 비율이 증가한다. 그러나 균열 및 기공 형성과 같은 일부 내부의 결함 발생 또한 같은 동력 소산 효율을 가질 수 있다[22]. 따라서 변형 시 불안정한 영역을 확인하기 위해 또 다른 기준이 필요하다[23].
Kumar [24]와 Prasad [25]는 소성 불안정성의 영역을 평가하기 위한 기준을 식(6)과 같이 정의하였다. 해당 기준은 Ziegler가 제안한 Large Plastic Flow에 적용되는 연속체 원리를 기반으로 한다[26].
| (6) |
소성 불안정 인자 x는 Instability Map을 통해 주어진 온도와 변형률 속도에 따른 소성 불안정 조건을 판정하는 기준이다. 소성 불안정 인자 값이 음수인 구역에 해당하는 영역에서는 소성 가공 시 불안정한 소성 거동이 일어날 수 있음을 의미한다[27]. 즉, 소성 불안정 영역에서 Adiabatic Shear Bands, Flow Localization, Dynamic Strain Ageing, Kink Bands 등의 결함이 관찰될 수 있다[28].
3.2 AISI 4340 열간 압축 실험 결과
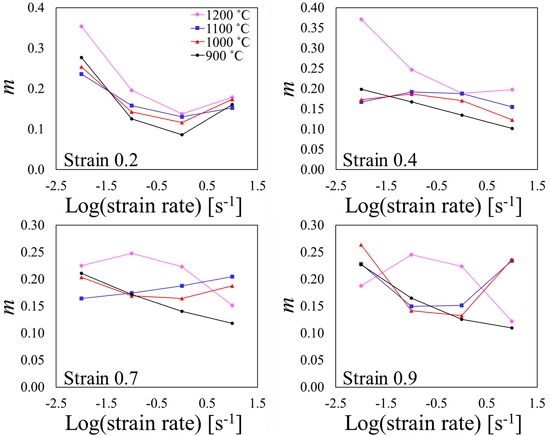
압축 시험 결과에 따른 유동응력에서의 Log (Strain Rate)-Log (s)의 그래프를 Fig. 6에 나타냈다. 변형 공정 지도는 동력 소산 효율(η) 및 소성 불안정 인자(x)로 이루어지며 모두 변형률 속도 민감 지수 m을 포함하는 표현으로 변형률 속도 민감지수가 중요한 요소 중 하나임을 나타낸다. Fig. 7은 변형률에 따른 m 값을 나타낸다. 변형률 속도 0.1, 1.0 s-1 구간에서 온도가 높을수록 m 값이 크며 변형률 0.7부터 1,200oϹ의 경향이 역전되는 경향을 보인다. 900oϹ의 경우 변형률 속도가 높아질수록 m값이 낮아지는 경향을 보인다.
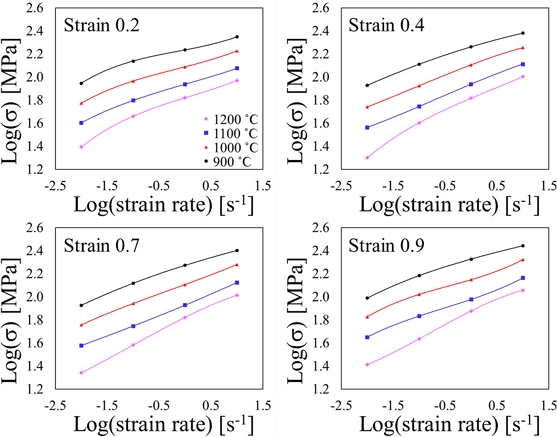
Interpolated curves to describe the relationship between log (σ) and log (ε˙) with respect to strains
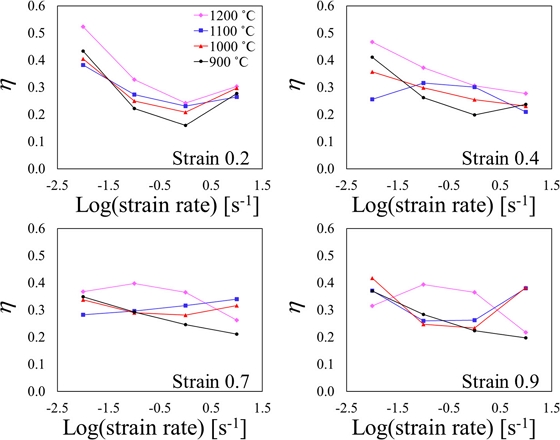
Fig. 8은 각각의 온도와 변형률 속도 변화에 따른 동력 소산 효율을 나타내며, 동력 소산 효율은 온도와 변형률 속도에 큰 영향을 받는다. 또한 Fig. 7의 변형률 속도 민감 지수와 유사한 패턴을 보여준다. 변형률 0.4 이상에서 900oϹ의 동력 소산 효율이 변형률 속도가 증가함에 따라 낮아진다. 전체적으로 변형률 속도가 0.01-0.1 s-1 구간에서 1,200oϹ의 η 값이 가장 큰 것을 알 수 있다. 또한 변형률 0.2에서 온도 1,200oϹ, 변형률 속도 0.01s-1에서 가장 큰 η 값을 보였으며 이는 해당 영역에서 재료의 열간 가공성이 더 우수함을 나타낸다.
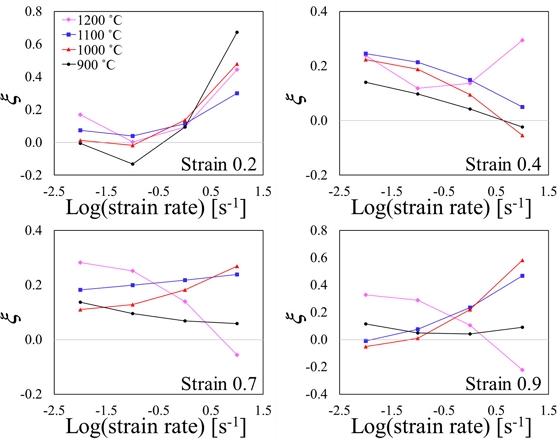
Fig. 9는 변형률, 온도 그리고 변형률 속도 조건에서 AISI 4340의 소성 불안정 인자 x의 변화를 나타낸다. 변형률 0.2, 0.4에서 900, 1,000oϹ, 변형률 0.7에서 1,200oϹ와 변형률 0.9에서는 900oϹ를 제외한 나머지 온도에서 음수의 소성 불안정 인자 값을 갖는다. 변형률 0.6 이전에는 낮은 온도(900, 1,000oϹ)에서 불안정함을 보이며, 변형률 0.7 이후에는 높은 온도(1,100, 1,200oϹ)에서 불안정함을 보인다. 또한, 변형률 0.4이후부터 1,200oϹ에서 다른 온도에 비하여 변형률 속도 변화에 따라 소성 불안정 인자의 값이 급변함을 알 수 있다.
4. 변형 공정 지도를 활용한 단조 공정 설계
4.1 변형 공정 지도 분석
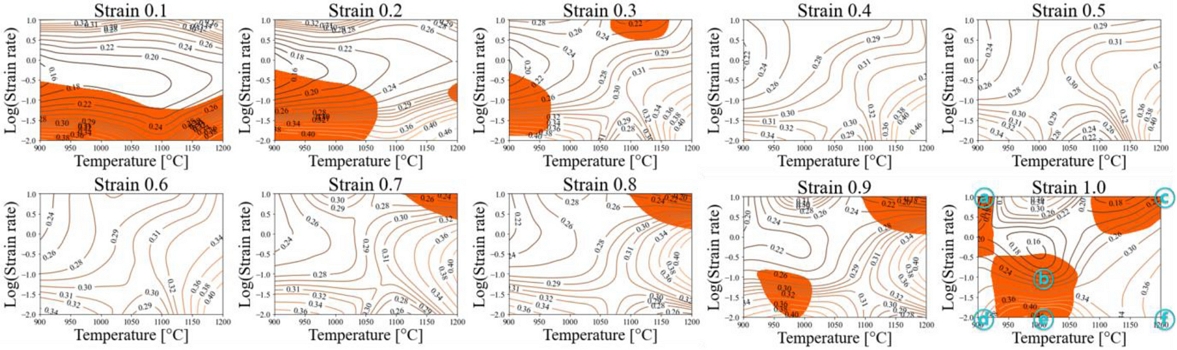
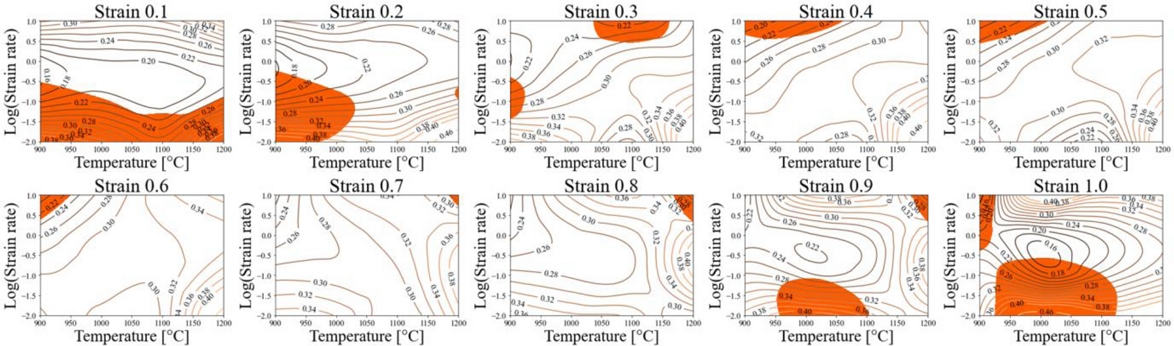
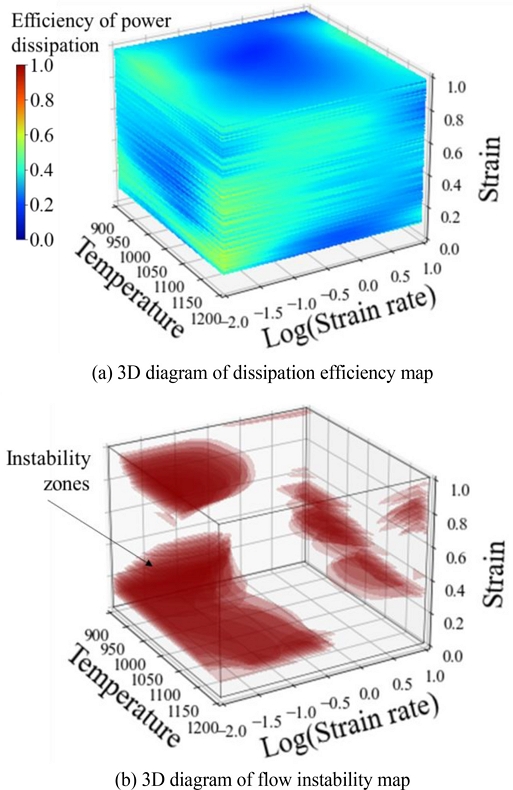
Figs. 10과 11은 고온 압축 실험의 단열 조건을 가정한 유동응력 데이터와 압축 실험 시 변화하는 온도를 반영하여 보간한 유동응력 데이터를 통한 변형 공정 지도의 차이를 볼 수 있다. 변형 공정 지도는 동력 소산 효율의 등고선 위에 소성 불안정 인자가 음수의 값을 가지는 소성 불안정 영역을 붉은색으로 도시하였다. 일반적으로 공정의 온도가 낮고, 변형률 속도가 빠른 구간에서 소성 불안정 영역이 나타난다[29-32]. AISI 4340은 변형률 0.5-0.8 범위에서 변형 온도 1,100oϹ, 변형률 속도 0.1 s-1의 구간에서 다른 온도와 변형률 속도 구간에 비하여 높은 동력 소산 효율을 보여주었다. 본 연구에서는 각각의 변형률에 대한 변형 공정 지도를 3차원 공간 상에 Fig. 12와 같이 제시하였다.
개발된 3차원 소성 불안정 지도는 변형률 0.01 간격으로 2차원 평면상에 나타낸 변형 공정 지도를 Stacking하여 도식하였으며 동력 소산 효율 영역은 동일한 방법으로 변형률 0.1 간격으로 도식하였다. 3차원상에 도시한 변형 공정 지도의 주요 장점은 붉은색으로 표시된 소성 불안정 영역을 한 번에 확인 가능하다는 것이다. 3차원 변형 공정 지도로부터 변형률에 따라 불안정 영역 동력 소산 효율이 어떠한 양상으로 변화하는지 확인 가능하다. AISI 4340의 변형 공정 지도에서 변형률 0.0-1.0 범위에서 변형률 속도 0.316-3.162 s-1, 온도 950-1,150°C 구간에서 안정 영역임을 확인할 수 있다.
따라서, 소재의 변형 이력을 확인하여 안정 영역을 지나도록 공정변수를 결정하면 성형 후 결함을 방지 가능하다. Fig. 13은 EBSD를 이용하여 압축 시험 후의 시편을 촬영한 것이다. Fig. 13에 나타난 바와 같이, 같은 변형률 속도에서 온도 상승에 따라 평균 결정립 크기가 조대화 되며 동일한 온도에서 변형률 속도가 빨라짐에 따라 평균 결정립 크기가 작아지는 경향을 보인다.
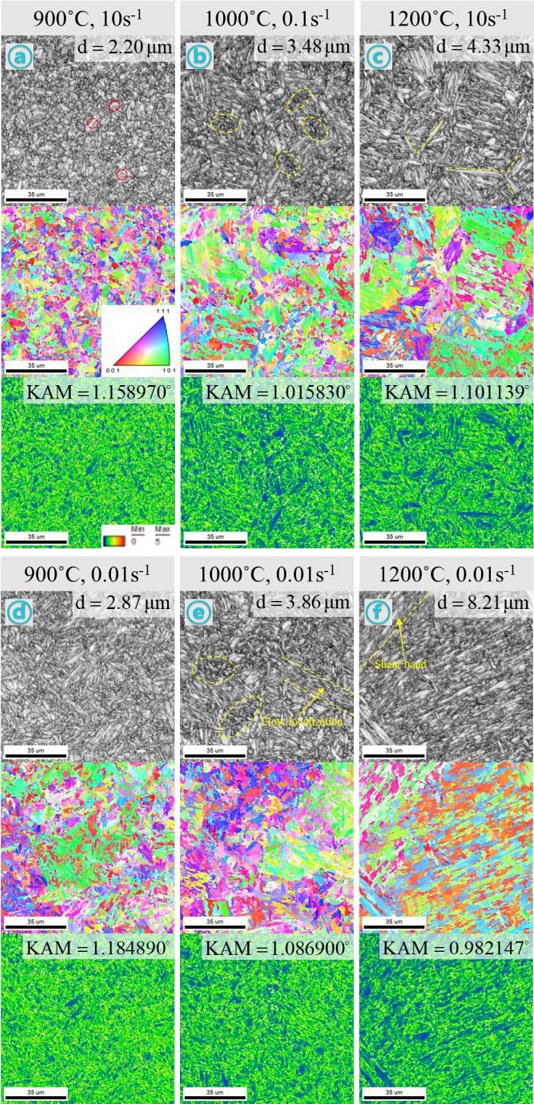
The image quality map of the compression samples of AISI 4340 after the compression tests. The symbols on the upper-right corners of the optical images indicate the locations marked on the processing maps in Fig. 10, Strain 1.0, here, d denotes the average grain size (a) Stroke speed of case 1, 2, 3, and (b) Stroke speed of case 4, 5, 6
Kernel Average Misorientation (KAM) Map의 평균값이 클수록 전위밀도가 높음을 의미하며, 온도 상승에 따라 전위 밀도가 감소함을 알 수 있다. 불안정 영역에 해당하는 Fig. 13의 ⓐ, ⓑ, ⓒ, ⓔ에서 ⓐ의 빨간색 표시에서 볼 수 있듯이 재결정이 다소 활발하지 않음을 알 수 있다. ⓑ, ⓔ의 노란색으로 표시한 영역에서 작은 결정립들이 밀집되어 있는 경향을 보이며 ⓔ에서는 Flow Localization이 관찰된다. ⓒ, ⓕ의 결정립은 1,000oC 이하의 압축 시험을 통한 결정립과 다르게 노란색 쇄선으로 표시한 바와 같이 결정립이 길게 형성되어 있으며 이는 1,200oC의 고온에서 압축으로 인한 것으로 보인다. ⓕ에서는 고온 압축으로 인하여 압축 방향 기준으로 45o의 Shear Band가 발견되었다.
4.2 변형 공정 지도 활용
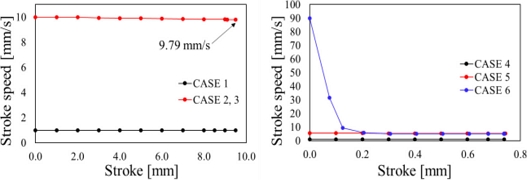
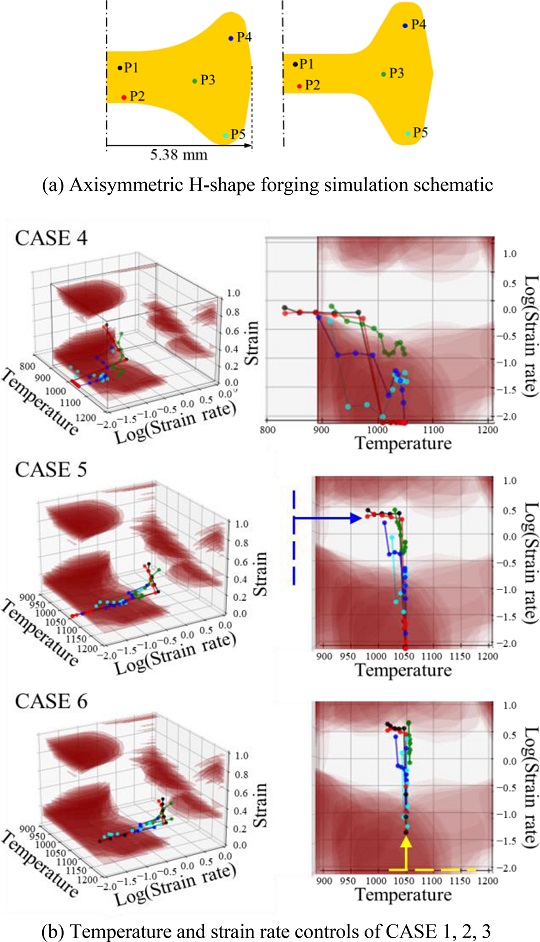
제안된 3차원 변형 공정 지도 활용을 위해 열간 압축 시험과 동일하도록 시뮬레이션 상에서 진변형률 1.0까지 압축하였다. Figs. 15(a)는 압축 전후 형상과 변형률, 변형률 속도, 온도를 추적할 점들을 도시하였고, 15(b)는 해당 점들이 변형 공정 지도상에서 움직인 궤적을 나타낸 것이다. 단조 공정은 탄성 변형량이 소성변형량에 비해 무시할 수 있을 만큼 작기 때문에, 상용 유한요소해석 소프트웨어인 DEFORM 2D Version 11.0 (Scientific Forming Technologies Corporation, USA)을 통해 강소성 유한요소해석을 진행하였다. 압축 속도는 Fig. 14와 같이 총 6개의 Case들로 각각 진행하였으며 시뮬레이션 상 업셋팅 공정에서 Cases 1과 2의 소재 및 다이의 온도는 각각 950, 900oC이다. Cases 3부터 6은 업셋팅 공정의 소재 및 다이의 온도는 각각 1,050, 400oC이다. 모든 Case들의 열전달 계수는 5 W/m·K, 금형과 소재 사이의 마찰 모델은 일정전단 마찰인자 모델을 사용하였고, 마찰인자는 0.1이다. Figs. 10과 12 그리고 13에서의 2D, 3D 변형 공정 지도는 NSMMat 1.1 소프트웨어를 활용하였으며 업셋팅 공정이 진행됨에 따라 변형률이 증가하게 된다.
Fig. 15(b)의 Case 1에서 각각의 절점들이 소성 불안정 영역에 겹쳐 있음을 알 수 있다. 소성 불안정 영역을 피하기 위해서는 공정 시 소재의 변형률 속도를 빠르게 해야 한다는 점과 공정 초기 소재의 온도를 더 높여야 한다는 것을 알 수 있다. Stroke Speed를 달리해주는 것만으로도 Flow Instability 영역을 피할 수 있음을 Case 2를 통해 알 수 있다. Case 3에서는 소재 및 다이의 온도를 50oC 올려 압축을 진행하였을 때 각 8개의 절점이 불안정 영역을 완전히 벗어남을 알 수 있다.
Fig. 16에서 3차원 불안정 지도에 H-Shape 축 대칭 형상의 총 5개 절점의 업셋팅 공정 간 변형 이력을 도식하였다. Case 4에서 각각의 절점들이 소성 불안정 영역에 겹쳐 있거나 3차원 불안정 지도 밖에 도시되어 있음을 알 수 있다. 이는 Stroke Speed가 1 mm/s로 다소 느리기 때문에 변형률이 증가함에 따라 소재가 냉각되며 900oC 이하의 절점이 나타난다. 따라서 Case 5와 같이 Stroke Speed를 5 mm/s로 증가하여 3차원 불안정 지도 공간 내에 도시 되도록 유도하였지만 변형률 초기 절점들은 불안정 영역에 겹쳐 있음을 알 수 있다. Case 6과 같이 초기 Stroke Speed를 90 mm/s으로 시작하여 5 mm/s로 끝내 Cases 4와 5에 비하여 더 많은 절점들이 불안정 영역을 회피했음을 알 수 있다.
5. 결론
시험 결과를 이용하여 3차원 변형 공정 지도를 작성하고, 변형 공정 지도를 활용하여 이로부터 얻은 결론은 다음과 같다.
AISI 4340의 유동응력은 변형 온도와 변형률 속도에 큰 영향을 받으며, 유동응력은 변형률 속도가 증가할수록, 온도가 낮아질수록 높아진다. AISI 4340은 온도가 증가할수록, 변형률 속도가 낮아질수록 동력 소산 효율이 증가하는 경향을 보이며, 변형률 0.5-0.8 범위에서 온도 1,100°C 이상, 변형률 속도 0.3 s-1 이하의 구간에서 높은 동력 소산 효율을 보인다. 3차원 불안정 지도를 통하여 변형률 초기(0.1-0.36), 변형률 속도 0.01-0.3162 s-1, 온도 900-1,200oϹ영역과 변형률 중기(0.25-0.58), 변형률 속도 3.1622 s-1 이상에서 온도가 감소하는 방향으로 불안정하며 변형률 후기(0.85-1.00), 변형률 속도 0.3162 s-1, 온도 920-1,130oϹ 영역에서 뚜렷하게 나타났다.
3차원 변형 공정 지도를 업셋팅 공정에 적용하여 공정설계를 진행하였으며, 이를 통하여 온도 및 변형률 속도를 0.31622-3.1622 s-1 구간으로 유도하여 소성 불안정 영역을 회피 가능하다. 3차원 불안정 지도와 유한요소해석을 활용하여 불안정 영역을 벗어나도록 공정 온도 및 공정 속도를 조절하여 소성 가공 시 결함이 발생할 수 있는 소성 불안정 영역을 회피할 수 있으며 전제적으로 안정 영역인 변형률 속도 0.31622-3.1622 s-1 구간으로 유도되어야 한다. Fig. 15의 원기둥 형상은 각 절점에서 변형률, 변형률 속도, 온도가 비교적 균일한 분포를 형성하는 반면 H-Shape은 각 절점의 변형 시간 별 변형률이 다르기 때문에 모든 절점을 불안정 영역 밖으로 유도하는 것은 제한적이다.
추가적인 연구로 다양한 소재의 열간 압축 시험에 따른 유동응력을 통하여 3차원 변형 공정 지도를 제작할 수 있다. 본 연구에서 명시한 동적 재결정 영역에서 추가적인 미세구조 관찰이 이루어질 수 있다. 본 연구에서는 유한요소해석을 통해 작업자의 경험에 의하여 온도 및 공정 속도를 조절하였지만 불안정 영역을 회피할 수 있는 정량적 방법이 필요하다.
NOMENCLATURE
| σ : | Flow Stress |
| K : | Strength Constant |
| m : | Strain Rate Sensitivity Exponent |
| ε : | Strain |
| : | Strain Rate |
| P : | Dissipated Power |
| G : | Power Generated by Temperature Rises |
| J : | Power Dissipated by Microstructure Evolution |
| η : | Efficiency of Power Dissipation |
| ξ : | Flow Instability Parameter |
Acknowledgments
이 논문은 2021년도 산업통상자원부 소재부품기술개발-패키지형사업 지원(No. 20017503)과 2020년도 산업통상자원부 소재부품기술개발사업 지원(No. 20013060)에 의한 연구임.
REFERENCES
- Semiatin, S. L., Jonas, J. J., (1984), Formability and workability of metals: Plastic instability and flow localization, American Society for Metals, 1984, 299.
-
Sun, S. L., Zhang, M. G., He, W. W., (2010), Hot deformation behavior and hot processing map of P92 steel, Advanced Materials Research, 290-295.
[https://doi.org/10.4028/www.scientific.net/AMR.97-101.290]

-
Maarefdoust, M., (2012), Simulation of finite volume of hot forging process of industrial gear, International Proceedings of the Computer Science and Information Technology, 57, 111.
[https://doi.org/10.1063/1.3623660]

-
Oh, S., Semiatin, S., Jonas, J., (1992), An analysis of the isothermal hot compression test, Metallurgical Transactions A, 23(3), 963-975.
[https://doi.org/10.1007/BF02675571]

- Frost, H. J., Ashby, M. F., (1982), Deformation mechanism maps: The plasticity and creep of metals and ceramics, Elsevier Science Limited.
-
Prasad, Y., Gegel, H., Doraivelu, S., Malas, J., Morgan, J., Lark, K., Barker, D., (1984), Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242, Metallurgical Transactions A, 15(10), 1883-1892.
[https://doi.org/10.1007/BF02664902]

-
Ding, X., Zhao, F., Shuang, Y., Ma, L., Chu, Z., Zhao, C., (2020), Characterization of hot deformation behavior of as-extruded AZ31 alloy through kinetic analysis and processing maps, Journal of Materials Processing Technology, 276, 116325.
[https://doi.org/10.1016/j.jmatprotec.2019.116325]

-
Cheng, Y., Du, H., Wei, Y., Hou, L., Liu, B., (2016), Metadynamic recrystallization behavior and workability characteristics of HR3C austenitic heat-resistant stainless steel with processing map, Journal of Materials Processing Technology, 235, 134-142.
[https://doi.org/10.1016/j.jmatprotec.2016.04.026]

-
Kumar, B., Saxena, K. K., Dey, S. R., Pancholi, V., Bhattacharjee, A., (2017), Processing map-microstructure evolution correlation of hot compressed near alpha titanium alloy (TiHy 600), Journal of Alloys and Compounds, 691, 906-913.
[https://doi.org/10.1016/j.jallcom.2016.08.301]

-
Park, C. H., Cha, D., Kim, M., Reddy, N., Yeom, J.-T., (2019), Neural network approach to construct a processing map from a non-linear stress–temperature relationship, Metals and Materials International, 25(3), 768-778.
[https://doi.org/10.1007/s12540-018-00225-8]

-
Sarkar, J., Prasad, Y., Surappa, M., (1995), Optimization of hot workability of an Al-Mg-Si alloy using processing maps, Journal of Materials Science, 30(11), 2843-2848.
[https://doi.org/10.1007/BF00349653]

-
Lin, Y., Zhao, C.-Y., Chen, M.-S., Chen, D.-D., (2016), A novel constitutive model for hot deformation behaviors of Ti-6Al-4V alloy based on probabilistic method, Applied Physics A, 122(8), 1-9.
[https://doi.org/10.1007/s00339-016-0248-8]

-
Peng, X., Guo, H., Shi, Z., Qin, C., Zhao, Z., Yao, Z., (2014), Study on the hot deformation behavior of TC4-DT alloy with equiaxed α+β starting structure based on processing map, Materials Science and Engineering: A, 605, 80-88.
[https://doi.org/10.1016/j.msea.2014.03.047]

-
Kumar, S., Karmakar, A., Nath, S. K., (2021), Construction of hot deformation processing maps for 9Cr-1Mo steel through conventional and ANN approach, Materials Today Communications, 26, 101903.
[https://doi.org/10.1016/j.mtcomm.2020.101903]

-
Prasad, Y., (2003), Processing maps: A status report, Journal of Materials Engineering and Performance, 12(6), 638-645.
[https://doi.org/10.1361/105994903322692420]

- Prasad, Y., Rao, K., Sasidhar, S., (2015), Hot working guide: A compendium of processing maps, ASM international.
-
Prasad, Y., Seshacharyulu, T., (1998), Modelling of hot deformation for microstructural control, International Materials Reviews, 43(6), 243-258.
[https://doi.org/10.1179/imr.1998.43.6.243]

- Kim, K., Jung, M., Lee, S.-J., (2017), Hot deformation behavior of AISI 4340 using constitutive model and processing map, Journal of the Korean Society for Heat Treatment, 30(5), 187-196.
-
Guo, L., Yang, S., Yang, H., Zhang, J., (2015), Processing map of as-cast 7075 aluminum alloy for hot working, Chinese Journal of Aeronautics, 28(6), 1774-1783.
[https://doi.org/10.1016/j.cja.2015.08.002]

-
Momeni, A., Dehghani, K., Ebrahimi, G., (2011), Modeling the initiation of dynamic recrystallization using a dynamic recovery model, Journal of Alloys and Compounds, 509(39), 9387-9393.
[https://doi.org/10.1016/j.jallcom.2011.07.014]

-
Liao, Q., Jiang, Y., Le, Q., Chen, X., Cheng, C., Hu, K., Li, D., (2021), Hot deformation behavior and processing map development of AZ110 alloy with and without addition of La-rich Mish Metal, Journal of Materials Science & Technology, 61, 1-15.
[https://doi.org/10.1016/j.jmst.2020.04.064]

-
Li, B., Pan, Q., Yin, Z., (2014), Characterization of hot deformation behavior of as-homogenized Al-Cu-Li-Sc-Zr alloy using processing maps, Materials Science and Engineering: A, 614, 199-206.
[https://doi.org/10.1016/j.msea.2014.07.031]

-
Al Omar, A., Prado, J., (2012), Criteria for prediction of plastic instabilities for hot working processes (Part I: Theoretical review), Welding International, 26(12), 921-934.
[https://doi.org/10.1080/09507116.2011.592704]

- Kumar, A. K., (1987), Criteria for predicting metallurgical instabilities in processing, M.Sc. Thesis, Indian Institute of Science.
-
Prasad, M., Inamdar, J., (1990), Effect of cement kiln dust pollution on black gram (Vigna mungo (L.) Hepper), Proceedings of the Plant Sciences, 100(6), 435-443.
[https://doi.org/10.1007/BF03053491]

- Ziegler, H., (1963), Some extremum principles in irreversible thermodynamics, with application to continuum mechanics, Progress in Solid Mechanics, 4, 93-193.
-
Samantaray, D., Mandal, S., Bhaduri, A., (2011), Characterization of deformation instability in modified 9Cr-1Mo steel during thermo-mechanical processing, Materials & Design, 32(2), 716-722.
[https://doi.org/10.1016/j.matdes.2010.07.038]

-
Murty, S. N., Rao, B. N., Kashyap, B., (2005), Identification of flow instabilities in the processing maps of AISI 304 stainless steel, Journal of Materials Processing Technology, 166(2), 268-278.
[https://doi.org/10.1016/j.jmatprotec.2004.09.089]

-
Zhou, G., Ding, H., Cao, F., Zhang, B., (2014), A comparative study of various flow instability criteria in processing map of superalloy GH4742, Journal of Materials Science & Technology, 30(3), 217-222.
[https://doi.org/10.1016/j.jmst.2013.07.008]

-
Chen, L., Ma, X., Liu, X., Wang, L., (2011), Processing map for hot working characteristics of a wrought 2205 duplex stainless steel, Materials & Design, 32(3), 1292-1297.
[https://doi.org/10.1016/j.matdes.2010.09.030]

-
Cai, D., Xiong, L., Liu, W., Sun, G., Yao, M., (2009), Characterization of hot deformation behavior of a Ni-base superalloy using processing map, Materials & Design, 30(3), 921-925.
[https://doi.org/10.1016/j.matdes.2008.05.006]

-
Prasad, Y., Ravichandran, N., (1991), Effect of stacking fault energy on the dynamic recrystallization during hot working of FCC metals: A study using processing maps, Bulletin of Materials Science, 14(5), 1241-1248.
[https://doi.org/10.1007/BF02744618]


MS candidate in the Department of Mechanical Engineering, Sogang University. His research interest is hot forging process based on a processing map.
E-mail: yory11@sogang.ac.kr

Ph.D. candidate in the Department of Mechanical Engineering, Sogang University. His research interest is hot forging process.
E-mail: pdhwi93@sogang.ac.kr

Senior Research Engineer at SBB TECH Co., Ltd. His research is materials science and engineering.
E-mail: syshin@sbb.co.kr

Professor in the Department of Mechanical Engineering, Sogang University. His research interests are manufacturing process and machine learning for various industrial applications.
E-mail: nskim@sogang.ac.kr