스핀들의 가속도 데이터와 이송계의 변위 데이터를 이용한 스핀들의 변위 추정 알고리즘
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the existing machine tool field, the focus was on the displacement of the feed system from the viewpoint of the motion of the machine tool. The displacement of the tool or spindle of a machine tool is useful for developing various functions. In this study, using the acceleration data of the spindle, we proposed an algorithm that tracked the displacement of the spindle with respect to the pseudo-step waveform motion. In order to solve the bandwidth problem of the pseudo-step waveform, the displacement data measured by the motor encoder of the feed system was used. In addition, in order to solve the drift problem due to double integration, a new drift removal filter was proposed and a displacement estimation algorithm was implemented. In order to examine the performance and possibility of the proposed spindle displacement estimation algorithm, it was applied to a gantry-type engraver and its excellent performance was confirmed compared to other algorithms.
Keywords:
Machine tools, Spindle displacement, Acceleration, Motor encoder, Double integration, Drift removal filter키워드:
공작기계, 스핀들 변위, 가속도, 모터 엔코더, 이중 적분, 드리프트 제거 필터1. 서론
기존 공작기계 모션의 관심은 이송계의 변위에 초점이 맞춰져 있다. 예를 들어, 이송계 제어기의 제어 게인 튜닝 시 일반적으로 모터 엔코더 정보에 대해 수행된다. 그러나 공작기계에서 궁극의 관심은 실제 절삭이 수행되는 공구 또는 스핀들 변위에 있다. 이러한 차이는 모터 엔코더 정보에 대한 접근이 용이하고 공구나 스핀들 변위의 측정의 어려움에 기인하는 것으로 보인다.
그러나 공작기계에서 스핀들의 변위를 아는 것은 다양한 기능 개발에 유용하다. 제어적 관점에서는 피치오차 보정 같은 기능을 사용하지 않고도 이송계 차원이 아니라 스핀들 변위 차원에서 제어기 튜닝이 가능해져 가공오차가 줄어들 가능성이 커진다. 공구의 변위를 간접적으로 추정해 볼 수 있기 때문에, 공작기계의 상태를 모니터링한다거나 좀 더 정밀한 가공오차를 추정하는데 사용할 수 있다. 또한 공구에 걸리는 절삭력을 추정하는데 스핀들 변위 정보를 사용할 수도 있다. 보고 되어진 유용한 예로서 가속도 정보에 기반한 이송계의 변위 추정을 이용하여 공작기계의 직진도를 온라인으로 측정한 연구가 있다[1].
이러한 유용성에도 불구하고 기존에 스핀들의 변위를 이송계의 변위와 동일한 것으로 바라보기도 하였다. 모터 엔코더의 변위나 스케일에 의해 측정된 변위를 스핀들 변위로 가정하는 것이다. 추후 실험 결과에서도 보이겠지만 이송계와 스핀들 사이에 다양한 구조물이 존재하기에 동일하지 않다. 정밀도를 요구하지 않는 이전의 공작기계에서는 유효한 가정이지만, 산업이 고도화되고 고정밀도의 요구에는 유효한 가정이 아닐 수 있다.
이와 같은 이유로 공구 또는 스핀들의 변위를 추정 또는 측정하고자 하는 몇몇 연구들이 보고되고 있으나 스핀들의 변위를 측정 또는 추정하는 데는 어려움이 있는 것으로 보인다. A. Ranmon 등은 스핀들의 변위를 온라인으로 측정하고 보상기에 활용하기 위해 레이저 추정 시스템을 설계하였다[2]. 이는 부가적인 공간 및 장비들을 필요로 하며 비용적 측면에서 효율적이지 못하다. H. Mostaghimi 등은 절삭력의 추정하는데 있어 가속도 데이터 및 이중 적분을 이용한 변위 추정을 일부 사용하였다[3]. 일부 연구들에서는 갭 센서를 이용하여 공구의 변위를 측정함으로써 절삭력을 추정하고자 하였다[4,5].
이렇듯 기존의 변위 측정 시스템인 레이저 변위기, 레이저 인터 페로미터, 갭 센서, 레이저 트랙커 등이 스핀들의 변위 측정이 가능하나 여러 단점이 있다. 레이저 인터 페로미터나 레이저 트랙커는 매우 고가이다. 또한 갭 센서는 긴 스트로크의 모션을 측정하기 어렵다.
더욱이 이들 모두는 모션 방향 이외의 방향에 대한 동시 동특성 측정이 어렵다. 예를 들어, x축 방향의 모션 시 x축 변위는 측정이 가능하나 동시에 y축 또는 z축 변위 측정이 어렵다. 이에 더해, 다양한 지점에서 측정하기 위해서는 레이저 트랙커 이외에 재설치가 필요하다. 레이저 트랙커는 시야가 가려지는 경우 측정의 어려움이 있고 광원부가 물리적 모션으로 측정 목표물의 쫓아야 하기 때문에 추종 대역폭에 한계가 존재한다.
그 대안으로 가속도계를 이용한 변위 추정을 고려해 볼 수 있다. 가속도계는 변위 센서와 달리 기준점을 그라운드나 장비에 고정할 필요가 없다. 또한 3축의 모션이 동시에 측정되며, 비교적 저렴하고 설치 역시 용이하다. 그러나 가속도계로부터 측정한 가속도 데이터를 적분하는 것은 오차를 포함하여, 적분된 데이터가 드리프트 하는 현상이 존재한다.
다양한 분야의 연구들에서 이중 적분 시 발생하는 이러한 문제를 고려해 왔다. J. Abir 등은 가속도 데이터를 이용하여 변위에 대한 실시간 추정기를 설계하기 위해 필터에 대한 최적화를 수행하였다[6]. 토목 분야에서 M. Arraigada 등은 차량에 의한 도로의 변위를 측정하기 위해 2개의 가속도계 및 알고리즘을 이용하였다[7]. M. Z. Sarwar 등은 교량의 변위를 추정하기 위해서 가속도계와 스트레인 센서를 함께 사용하였다[8]. 반면 W.-M. Niu 등은 발생하는 드리프트를 실시간으로 추정하여 제거하는 알고리즘을 제안하였다[9]. H. S. Lee 등은 이 문제를 경계 조건 문제로 간주함으로써, 다른 개념으로 접근하였다[10]. 그러나 Ref. 9를 제외한 연구들은 모션의 스트로크가 크지 않고, 대부분 모션의 속도가 빠르지 않다.
따라서 본 논문에서는 스핀들의 변위를 추정하는 오프라인 알고리즘을 제안하고 그 가능성을 검토한다. 본 연구에서는 스핀들의 가속도 데이터를 이용한 이중 적분 알고리즘을 사용하였다. 그러나 대역폭의 문제를 해결하기 위해 스핀들의 가속도 데이터뿐 아니라 모터 엔코더 변위 정보를 함께 사용하였다. 또한 이중 적분의 문제를 드리프트 문제로 바라보고 드리프트를 추정 및 제거하는 알고리즘을 구축하였다. 이를 갠트리형 조각기의 유사 스텝 모션에 적용하여 그 가능성을 검토하였다.
본 논문의 2장에서는 제안하는 변위 추정 알고리즘을 제시한다. 3장에서는 제안 알고리즘에 적용되는 갠트리형 조각기 및 여러 케이스를 살펴본다. 4장에서는 케이스별 결과와 제안 변위추정 알고리즘의 성능 및 적용 가능성을 고찰하였다.
2. 변위 추정 알고리즘
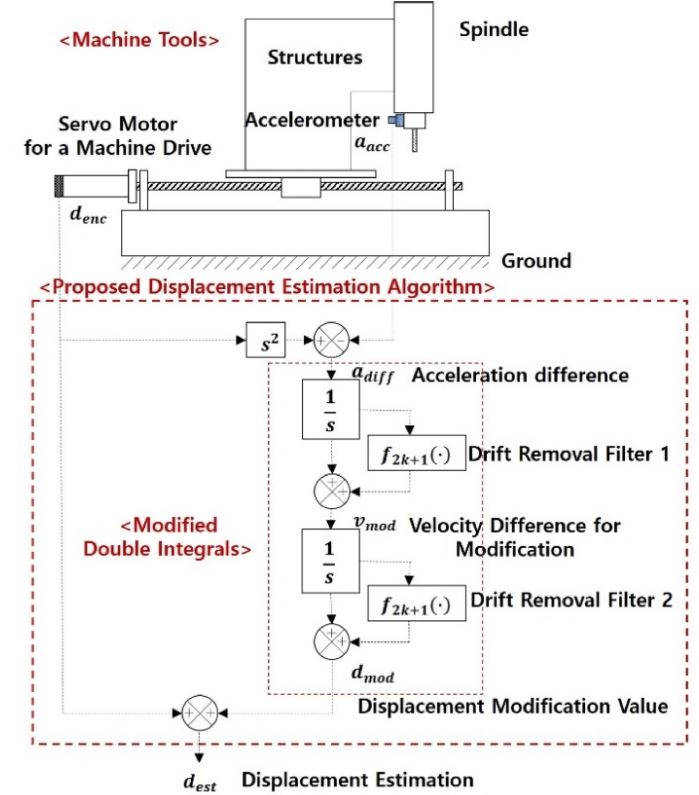
Fig. 1은 계측된 가속도 데이터와 이중 적분을 이용하여 변위를 추정하는 알고리즘이 공작기계에 적용된 모습이다. 그러나 뒤에서 언급하겠지만 가속도 데이터만을 사용하여 스핀들의 변위를 추정하는데 한계가 존재한다. 따라서 본 연구에서는 스핀들의 가속도 데이터와 엔코더 변위 데이터에 기반한 변위 추정 알고리즘을 제안한다. 본 장에서는 먼저 기존 이중 적분을 이용한 변위 추정 알고리즘의 문제점을 고찰하고, 제안된 변위 추정 알고리즘을 제시한다.
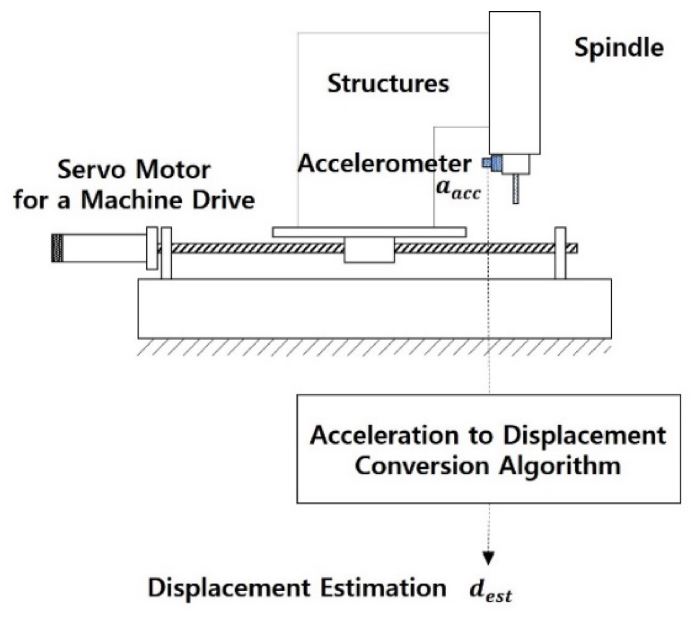
A proposed concept for estimating the displacement of a spindle in a machine tool using acceleration data
2.1 이중 적분을 이용한 변위 추정 알고리즘
전술한 것과 같이, 이중 적분으로 변위를 추정할 경우 측정된 가속도의 오차 성분으로 인해 이중 적분된 변위 데이터는 오차를 갖게 된다. 특히, 변위에서 드리프트 현상으로 발생하는데 이것이 오염 성분에 의한 드리프트인지 실제 신호인지의 구분이 어렵다.
더욱이 본 연구에서는 공작기계의 모션을 고려한다. 스무딩이 적용되지 않은 많은 경우, 직선 운동을 하게 된다. 이는 제어적 관점에서 유사 스텝 모션이다. 유사 스텝 모션은 이론적으로 거의 전 주파수 성분을 갖는다. 이러한 유사 스텝 모션을 추정하기 위해서는 보정 전 데이터 및 추정 알고리즘의 대역폭이 넓어야 한다. 그러나 센서에 의한 취득되는 보정 전 데이터에 실린 정보의 대역폭 한계가 존재하고, 샘플링에 의한 대역폭 한계 역시 존재한다. 더욱이 추정 알고리즘 역시, 알고리즘 자체 기인하는 대역폭 한계를 갖게 된다. 곧, 가속도계 및 적분 알고리즘을 이용한 기존의 방법으로 유사 스텝 모션을 추정하는 것을 어렵다. 따라서 이러한 대역폭 문제를 해결해야 한다
2.2 제안 변위 추정 알고리즘
본 장에서는 제안 변위 추정 알고리즘을 제시한다. 본 연구에서는 스핀들에 부착된 저주파 가속도계로부터 가속도와 모션 제어기 내부의 모터 엔코더 정보를 함께 사용하였다. 먼저, 모터 엔코더 정보를 사용한 배경 및 근거에 대해 논하고, 이후 제안 알고리즘의 상세한 방법을 제시하겠다.
유사 스텝 모션의 이중 적분에 의한 변위 환산에서의 문제를 해결하기 위해, 본 연구에서는 Fig. 2와 같이 스핀들 가속도계의 가속도 데이터 이외에 모터 엔코더 정보를 이용하여 유사 스텝 모션의 기초 정보로 활용하였다. 곧 모터 엔코더의 변위 정보 위에 스핀들의 보정된 변위 정보를 더하여 유사 스텝 모션을 다음과 같이 추정하였다.
| (1) |
여기서 dest(t)는 추정된 스핀들의 변위이고, denc(t)는 모터 엔코더에 의해 측정된 변위이고, dmod(t)는 스핀들 가속도계에 의한 측정 가속도와 모터 엔코더에 의해 측정된 변위를 이용한 보정값이다. 이는 저주파 성분을 갖는 변위 데이터를 기초로 활용하고 이를 가속도 데이터로 보정함을 의미한다.
다음으로 이 보정값 dmod(t)의 도출 방법에 대해 제시한다. 차분 데이터 획득, 적분, 드리프트 추종 필터, 이 과정들의 반복으로 네 가지로 나눠서 설명한다.
첫째, 차분 데이터 adiff의 획득이다. 모터 엔코더에 의해 측정된 변위를 보정하기 위해서는 보정값은 차분값이어야 한다. 이 차분은 모터 엔코더에 의해 측정된 변위와 스핀들의 가속도계에 측정된 가속도이다. 차원을 맞추기 위해 모터 엔코더에서 계측된 변위 데이터 denc(t)를 이중 미분하여 가속도 데이터로 변환한다. 그다음, 이것에서 가속도계에서 계측한 가속도 aacc(t)를 다음과 같이 빼주었다.
| (2) |
여기서, s는 라플라스 연산자이다. 간략한 표현을 위해 앞으로 시간변수는 생략한다.
둘째, 데이터에 대한 이중 적분이다. 위와 같이 도출된 가속도 차분인 adiff를 이중 적분하였다. 그러나 단순하게 이중 적분만을 하게 되면 측정잡음 및 수치 누설에 의한 오염 요소가 드리프트를 발생시킨다. 따라서 매 적분마다 이 드리프트 요소를 추정하고 제거하는 필터를 구현하였다.
셋째, 드리프트 추종 필터 관련 내용이다. 추정된 드리프트 정보를 이용하여 드리프트 요소를 제거하는 식은 다음과 같다.
| (3) |
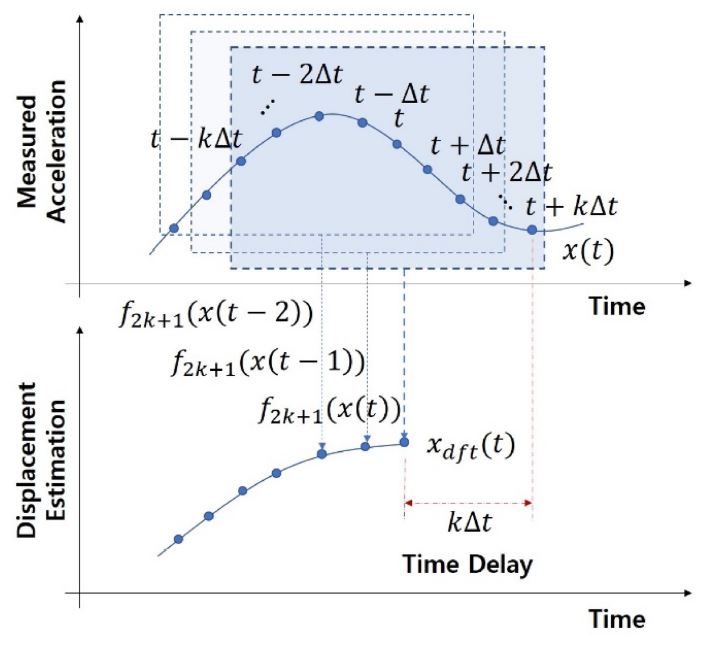
여기서 구현된 드리프트 추종 필터 f2k+1(·)는 다음과 같다.
| (4) |
여기서, Δt는 데이터의 샘플링 시간을, k는 드리프트 추종 필터에 사용되는 데이터 크기와 관련한 변수이다. 참고로, 사용 데이터 크기는 (2k + 1)이다.
Fig. 3은 구현된 드리프트 추종 필터를 나타낸다. (2k + 1)개의 데이터를 평균하는 필터이다. 따라서 일종의 저주파 통과 필터로서, 신호의 드리프트 성분을 추정한다. 데이터를 측정하는 시각은 (t + kΔt)이고, 필터가 필터링된 값을 내보내는 시각은 t이다. 이에 필터링에 의한 시간지연이 kΔt가 발생한다. 따라서 본 연구에서 제안하는 드리프트 제거 필터는 시간지연 kΔt의 수용 여부에 따라 실시간 필터가 될 수도 있고, 오프라인 필터가 될 수도 있다.
제안된 드리프트 제거 필터는 설정해야 하는 파라미터 k를 갖는다. 이는 평균 데이터 수와 관계된 파라미터이다. 실험 결과를 보이겠지만, 파라미터 k에 따라 추정 드리프트의 정확도가 달라진다. 본 연구에서 파라미터 k에 대한 설정에 데이터에 기반한 시행착오법을 적용하였다.
마지막으로, 전술한 과정을 속도 보정값 vmod에 반복하는 것이다. 속도 보정값 vmod에 위와 동일한 과정을 수행하여 차원을 속력에서 변위로 바꾼다.
| (5) |
전체적으로 이중 적분을 수행한 것이 된다. 전술한 것과 같이, 모터 엔코더 변위 데이터에 보정된 변위 데이터 dmod를 더함으로써 최종적으로 스핀들의 변위 추정을 도출한다.
제안된 변위 추정 알고리즘을 요약하면 다음과 같다.
1) 모터 엔코더에서 계측된 변위 데이터 denc를 이중 미분하여 가속도 데이터로 변환한다.
2) 가속도계에서 계측된 가속도 데이터와 변환된 가속도 데이터 s2denc의 차이 adiff를 구한다(식(2)).
3) 이 차이를 적분한다.
4) 이 적분값에 드리프트 추종 필터를 적용한다(식(4)).
5) 3)번에서 4)번 드리프트 추종값을 빼서 속도 보정값 vmod를 얻는다(식(3)).
6) 속도 보정값 vmod에 3)~5)를 다시 적용하여 변위 보정값 dmod를 얻는다(식(5)).
7) 변위 보정값 dmod를 모터 엔코더 변위 denc에 더함으로써, 최종적으로 스핀들 변위 추정 dest을 도출한다(식(1)).
3. 갠트리형 조각기를 이용한 실험
제안 변위 추정 알고리즘을 성능을 검토하기 위해 갠트리형 조각기에 제안 알고리즘을 적용하였다. 본 장에서는 먼저 이 갠트리형 조각기에 대해 기술하고, 제안 알고리즘을 고찰하기 위한 케이스들을 살펴본다.
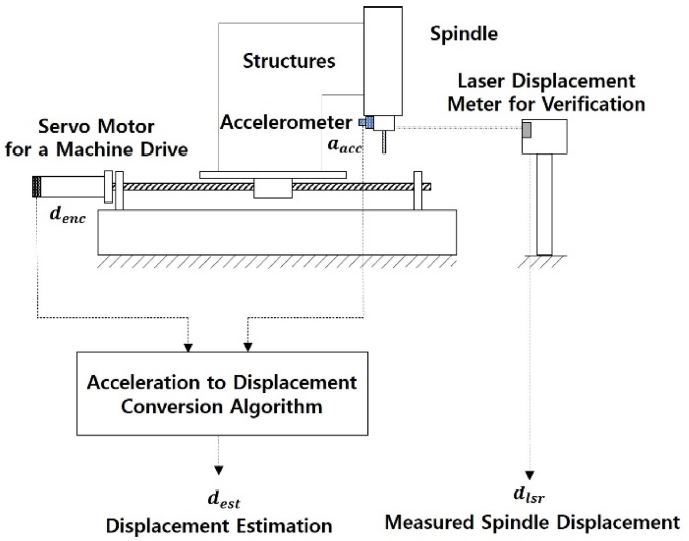
Fig. 4는 제안 알고리즘이 적용한 갠트리형 조각기를 나타낸다. 이 갠트리형 조각기는 자체 제작한 장비로서 상용 제어기에 의해 구동된다. 이 장비는 갠트리형 구조로서 모터 엔코더 변위와 스핀들의 가속도계 사이에 동적 특성을 갖는 구조물이 존재하고, 공작기계들과 같이 스핀들의 변위를 측정하는 장치가 존재하지 않는다. 따라서 본 연구에서 제안하는 스핀들의 가속도 및 이송계 모터 엔코더 정보를 이용한 스핀들의 변위 추정 알고리즘을 테스트하기에 적합하다.
명령 파형은 유사 스텝 파형으로서, 스트로크 19 mm를 피드 300 mm/s로 설정하였다. 가감속 시간은 0.1 s이다. 이는 본 갠트리형 조각기의 구조물의 모션을 발생시키기에 충분하다. 적용 방향은 Fig. 5에서 보이는 것과 같이 y축 한 방향이다.
상용 제어기의 내부 스코프를 이용하여 이송계의 엔코더 변위 데이터를 취득하였다. 샘플링은 2 ms로 하여 25초 데이터를 취득하였다. 가속도계는 Figs. 4, 5와 같이 스핀들 부에 부착되었다. 부착된 가속도계는 Mems 가속도계 타입으로 저주파형 가속도계이다. 대역폭은 0-2 kHz이고, 계측 샘플링 주파수는 1 kHz이다. 검증용 변위 센서로서 Figs. 4, 5와 같이 외부 레이저 변위기가 사용되었다. 계측 샘플링 시간은 2 ms이다. 이 레이저 변위는 갠트리형 조각기가 마운트된 정반 밖의 방진 테이블 위에 설치하여 갠트리형 조각기의 진동 영향을 최소로 하였다. 또한 레이저 변위 단에서 가속도계를 부착하여 진동을 계측함으로써 갠트리형 조각기의 진동이 레이저 변위에 영향을 미치지 않음을 확인하였다.
앞에서 기술한 것과 같이, 모터 엔코더, 가속도계, 레이저 변위기의 샘플링이 일치하지 않는 것을 알 수 있다. 계측 이후 보간을 통해 샘플링에 대한 후처리를 수행하였다. 가장 낮은 샘플링 주파수에 맞춰 보간하여 재 샘플링을 하였다.
본 논문에서는 비교 알고리즘으로서 Ref. 9에서 제안된 알고리즘을 활용하였다. 이 비교 알고리즘은 드리프트를 다항식으로 가정하여 실시간으로 드리프트 추정하고 원신호에서 제거하여 변위 신호를 추정하였다. 기존 다른 문헌들과 달리 10 m 이상의 큰 변위를 추정하였다. 이에 본 연구에선 제안하는 변위 추정 알고리즘과 비교를 위한 알고리즘으로 선정하였다.
제안 변위 추정 알고리즘의 특성 및 성능을 면밀히 분석하기 위해, 단순히 제안 알고리즘의 성능을 제시하기보다 제안 알고리즘의 일부를 분해하는 케이스를 상정하였다.
Case 1 (모터 엔코더 정보 미사용)
본 연구에서 제안하는 변위 추정 알고리즘은 스핀들의 가속도 정보뿐 아니라 모터 엔코더의 변위 정보를 함께 활용한다. 모터 엔코더 정보의 영향을 확인하기 위해 모터 엔코더 정보를 사용하지 않고 오직 스핀들의 가속도 정보만을 사용하여 적분을 수행한다. 곧 스핀들 가속도 정보인 aacc에 대해 적분을 수행하였으며, 제안된 드리프트 제거 필터 및 비교 알고리즘을 이용하여 드리프트를 추정하고 비교하였다. 또한 추정한 드리프트 성분을 원신호에서 제거하여 보정된 신호를 관찰하였다.
Case 2 (드리프트 제거 필터 특성)
이번 경우는 모터 엔코더 정보를 스핀들 가속도 정보를 함께 활용하여 적분 및 드리프트 제거를 수행하였다. 곧, adiff를 적분 및 드리프트를 제거하여 vmod를 얻는 것이다. 이는 제안 변위 추정 알고리즘의 수정된 이중 적분에서 한 번의 적분만을 특성을 살피는 것이다. 이를 통해 본 연구에서 제안한 변위 추정 알고리즘의 특성에 대한 이해를 제공할 것이다.
Case 3 (파라미터 k의 영향)
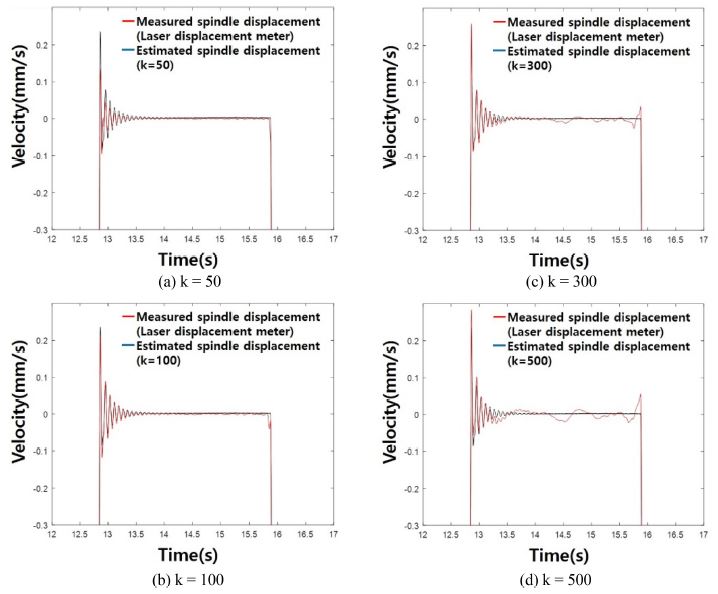
전술한 대로, 드리프트 제거 필터가 적용되는 데이터 수(2k+1)에 따라 제안 추정 변위 알고리즘의 정확도에 영향을 미친다. 파라미터 k에 따라 어떻게 변동하는지 살피기 위해 50, 100, 300, 500으로 설정하여 추정된 변위 특성을 살펴보았다.
Case 4 (제안 알고리즘 성능)
Case 3을 통해 결정된 파라미터 k 값을 이용하여, 제안 변위 추정 알고리즘을 수행하였다. 시간 오차를 살펴보고 주파수 영역에서 측정치와 추정치를 비교하였다.
4. 스핀들 변위 추정 결과
본 장에서는 스핀들의 변위 추정 결과를 보인다. 먼저, Cases 1, 2, 그리고 3을 통해 제안 변위 추정 알고리즘의 특성을 살펴본 후에 그 정확도를 검토한다. 이후 결과에 대해 고찰하고자 한다.
4.1 제안 알고리즘의 변위 추정 결과
Case 1 (모터 엔코더 정보 미사용)
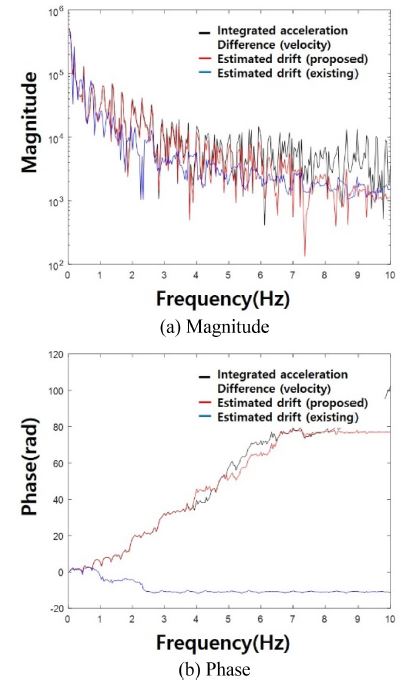
전술한 것과 같이 제안 변위 추정 알고리즘은 계측된 스핀들의 가속도 데이터만을 사용하지 않는다. 타겟 스핀들 변위 파형이 유사 정현파인 경우, 계측된 스핀들의 가속도 데이터만 이용한 변위 추정이 가능하다. 그러나 유사 스텝 파형의 경우, 스핀들의 변위 추정이 되지 않는다. 이는 유사 스텝 파형이 전주파수 요소를 가지기 때문인 것으로 보인다. Fig. 6은 계측된 스핀들의 가속도 데이터만을 사용하여 적분하고 드리프트 성분을 추정하여 제거한 결과이다. Figs. 6(a), 6(b)는 가속도 데이터를 적분한 결과와 드리프트 추정을 나타내고, 6(b), 6(d)는 추정된 드리프트 성분을 제거하여 추정한 결과이다. Fig. 6(a)에서 적분된 가속도가 양의 방향으로 드리프트 하는 것을 확인할 수 있다.
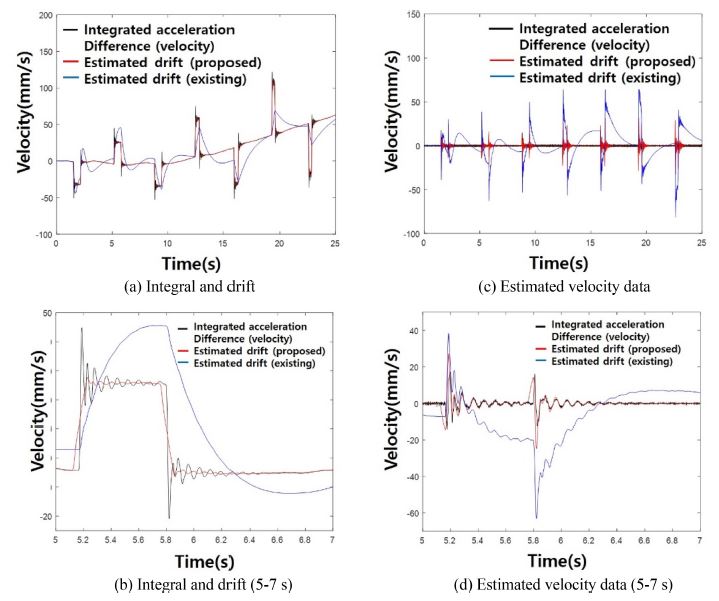
Case 1 Integration of the measured spindle acceleration data and estimated velocity by removing drift
또한 Figs. 6(b), 6(d)에서 비교 알고리즘은 드리프트 성분을 제대로 추정하지 못함을 확인할 수 있다. 그러나 Fig. 6(d)에서와 같이, 제안 알고리즘도 어느 정도 오차 내에서 유사하게 드리프트의 성분을 추정하나 정확히 추정하는 것은 아님을 알 수 있다. 또한 Fig. 6(b)에서 드리프트 성분이 어떤 것인지 불명확하다. 따라서 유사 스텝 파형의 경우 계측된 스핀들의 가속도 데이터만 이용한 변위 추정이 어려움을 알 수 있다.
Case 2 (드리프트 제거 필터 특성)
반면, Fig. 7은 계측 및 이중 미분된 엔코더 데이터와 계측된 스핀들의 가속도 데이터의 차이(차분)에 제안 알고리즘의 일부를 적용한 결과이다. 곧, 두 데이터의 차이에 적분을 수행하고 드리프트 성분을 추정해 보았다. Figs. 7(a), 7(b)는 차분 데이터를 적분한 결과와 드리프트 추정을 나타내고, 7(b), 7(d)는 추정된 드리프트 성분을 제거하여 추정한 결과이다. Fig. 7(c)에서 비교 알고리즘이 추정한 드리프트 성분을 제거했음에도 드리프트 성분이 남아 있음을 확인할 수 있다. 반면, Figs. 7(b), 7(d)에서 제안 알고리즘이 드리프트 성분을 잘 추정함을 알 수 있다. 따라서, 엔코더 변위 데이터의 유용성 및 제안 알고리즘의 드리프트 추정 및 제거 필터의 작동을 확인할 수 있다.
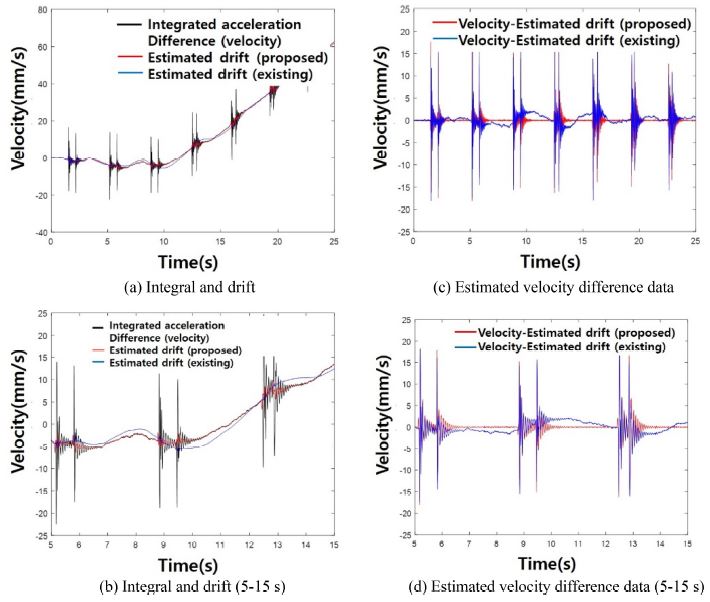
Case 2 Integration of the acceleration difference and estimated velocity difference by removing drift
Case 3 (파라미터 k의 영향)
Fig. 8은 드리프트 추종 필터에 사용하는 데이터 개수의 영향을 나타낸다. 데이터의 개수는 50, 100, 300, 500으로 설정하고 제안 알고리즘을 이용하여 스핀들의 변위를 추정하였다. 먼저, 데이터가 너무 작거나, 너무 크지 않은 특정한 개수(100개)에서 약 13초 전후에 존재하는 진동 성분을 잘 추정함을 확인할 수 있다. 두 번째로 약 14초와 15.9초 사이의 속도가 0인 영역에서는 데이터의 개수가 커질수록 추정 오차가 커짐을 확인할 수 있다. 본 연구에서 최적값을 찾기 위해, 5개의 데이터 간격으로 제안 알고리즘을 수행하고, 오차 RMS를 기준으로 최적 데이터 개수를 75개로 선정하였다.
Case 4 (제안 알고리즘 성능)
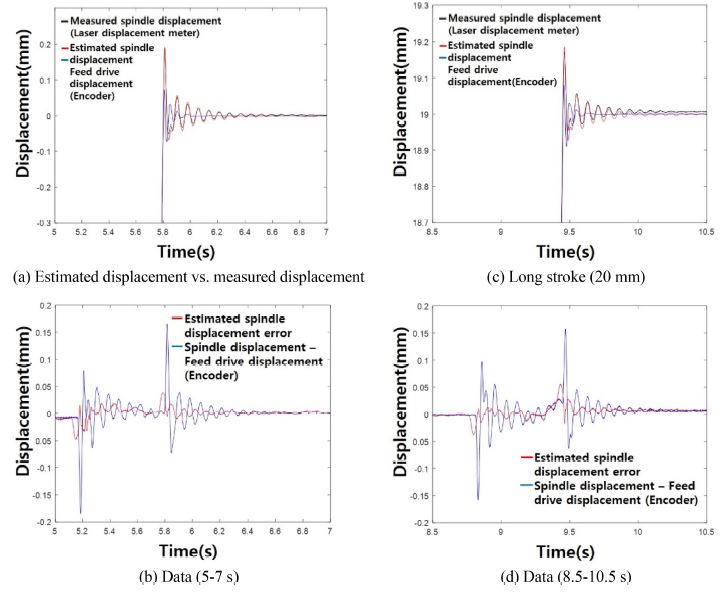
Fig. 9는 제안 변위 추정 알고리즘의 결과를 나타낸다. Fig. 9(a)에서 모터 엔코더의 변위는 레이저 변위로 측정된 스핀들의 변위와 차이가 약 200 μm 정도 존재하는 것을 알 수 있다. 즉, 모터 엔코더 정보로는 스핀들의 모션을 충분히 표현하지 못함을 알 수 있다.
Fig. 9(b)에서 제안 변위 추정 알고리즘의 정확도를 알 수 있다. 등속구간에서 약 20 μm 이하의 오차, 가감속 구간에서 50 μm 이하의 오차를 갖는 것을 확인할 수 있다. 이는 제안 알고리즘이 작동함과 공작기계의 스핀들 변위 추정에 사용될 수 있을 나타낸다. Figs. 9(c), 9(d)는 좀 더 긴 스트로크의 결과로 유사한 결과를 확인할 수 있다.
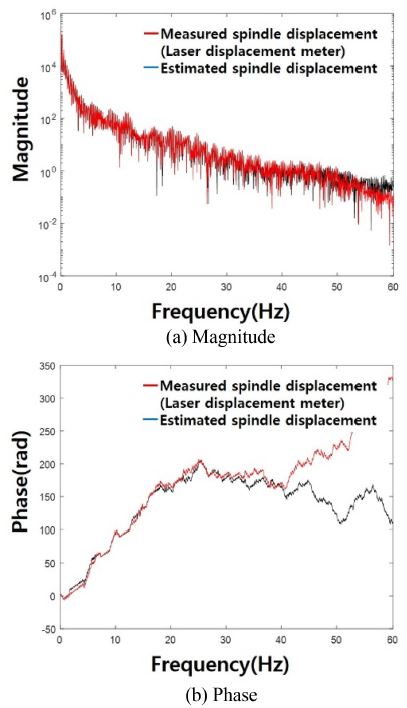
Fig. 10은 제안 알고리즘에 의한 변위 추정 결과와 레이저 변위기에 의해 측정된 스핀들의 변위 주파수 영역에서의 비교이다. 크기 측면에서는 약 50 Hz까지, 각도 측면에서는 약 40 Hz까지 유사한 결과가 나타남을 확인할 수 있다.
4.2 고찰
가속도 데이터를 이용하여 변위 데이터를 추정하는 방법에 있어 본 연구의 가장 큰 특징은 엔코더 변위 정보의 사용과 드리프트 추종 필터에 의한 드리프트의 추종 및 제거이다.
일반적으로 가속도계는 저주파 성분을 잘 측정하지 못하며 전술한 것과 같이 변위 차원에 있어서 대역폭의 문제가 존재한다. 본 연구에서는 이러한 대역폭의 문제를 해결하기 위해 엔코더 변위 정보를 가속도 데이터와 함께 사용하였다. Fig. 11은 Case 1에서 추정된 드리프트의 주파수 분석 그래프이다. 비교 알고리즘에 의한 추정된 드리프트가 갖는 주파수 성분이 저주파 영역에서 적음을 확인할 수 있다. 드리프트 추종 필터의 성능에서 가장 주요한 점은 데이터 개수이다. Fig. 8에서 데이터의 개수에 따라 동특성의 영향이 큰 부분과 작은 부분에서 다른 영향 차이를 확인하고 최적의 데이터 개수를 선정하였다.
그러나 제안 알고리즘을 공작기계 분야에 직접적으로 적용하기에는 성능적 측면에서 부족한 부분이 있는 것으로 판단된다. 먼저 변위 오차의 크기에 대한 성능에 대해 논한다. 범용기인 머시닝센터 3, 5호기에서 피치오차보정 후에 약 5-10 μm 이하의 변위 추종 오차가 요구된다. 따라서, 직접적으로 비교는 어렵지만 간접적으로 최소 1 μm 이하의 변위 오차가 필요할 것으로 판단된다.
제안된 알고리즘은 고정된 데이터 개수를 갖는 알고리즘으로써 임의의 시간대 어디에서나 데이터 개수가 일정하다는 특징이 있다. 이는 특정 시간대의 특성에 따라 데이터 개수를 변경할 수 있다면 제안된 변위 추정 알고리즘의 성능을 더 끌어올릴 수 있음을 나타낸다. 이러한 고찰에 기반하여, 추후 신호 특성에 따라 데이터 개수를 가변하는 알고리즘을 제안하여 요구되는 변위 오차에 만족시킬 수 있는지 후속 연구를 진행하고자 한다.
둘째로, 제안 알고리즘의 대역폭에 대해 고찰하고자 한다. 응용 분야에 따라 필요로 하는 대역폭이 다를 것으로 판단된다. 단순히 공작기계의 이송계 모션에 대한 모사나, 대형 공작기계에 발생하는 약 30-50 Hz의 잔류 진동에 의한 스핀들의 진동을 보기 위해서는 정밀도가 충분히 확보될 수 있다는 가정 하에 현재 대역폭으로도 공작기계 분야에서 사용이 가능할 것으로 판단한다. 그러나 구조 진동을 고려하거나 윤곽 오차에 대한 스핀들의 변위를 살피고, 엔드밀의 동특성을 분석, 모델링하는 영역에 사용하기에는 현재 대역폭을 매우 부족하다 하겠다. 가속도계가 일반적으로 높은 대역폭을 갖는 것을 고려하였을때 변위 추정 알고리즘의 수정이 필요해 보인다. 다만, 이러한 대역폭 문제는 일부 변위 오차와 관련이 있기 때문에, 추후 변위 오차 감소를 달성할 경우 일정 이상의 대역폭이 증가할 것으로 판단된다.
5. 결론
본 논문에서는 스핀들의 변위를 추정하는 방법을 제안하고 그 가능성을 검토하였다. 제안한 방법은 스핀들의 가속도계에서 측정한 가속도 데이터와 이송계의 모터 엔코더에서 측정한 변위 데이터를 함께 사용하여 이중 적분하는 방법이었다. 이중 적분에서 발생하는 드리프트를 제거하기 위해 새로운 드리프트 추종 필터를 제안하였다. 갠트리형 조각기에 제안 알고리즘을 적용하여 제안 알고리즘의 가능성을 검토하였다. 성능 최적화가 이루어지지 않은 알고리즘임에도 불구하고, 약 50 μm 이하의 변위 오차와 약 50 Hz의 대역폭을 갖는 것을 확인하였다. 또한 변위 오차와 대역폭 측면에서 제안 변위 추정 알고리즘의 공작 기계 분야 적용 가능성을 고찰하였다.
Nomenclature
| dest(t) : | Estimated Spindle Displacement |
| denc(t) : | Displacement of Moving System Measured by Motor Encoder |
| dmod(t) : | Modification Value Using Acceleration of Spindle Measured by Accelerometer and Displacement of Moving System Measured by Motor Encoder |
| adiff(t) : | Acceleration Difference between Acceleration of Spindle Measured by Accelerometer and Double Derivative of Displacement of Moving System Measured by Motor Encoder |
| s : | Laplace Operator |
| vmod(t) : | Velocity Difference with Estimated Drift Tracking Removed |
| x(t) : | Arbitrary Signal with No Drift Tracking Filter Applied |
| xdft(t) : | Signal Filtered by Drift Tracking Filter |
| p : | Index for Sigma |
| k : | Parameter related to the Total Number of Filtered Data, (2k+1) |
| f2k+1(·) : | Suggested Drift Tracking Filter |
| Δt : | Sampling Time |
| xdft(t) : | Signal Filtered by Drift Tracking Filter |
Acknowledgments
이 연구는 2021년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원으로 수행됨(Nos. 20012693, 20012834, and 20011271).
REFERENCES
-
Liu, K., Cui, Y., Liu, Z., Wu, J., Wang, Y., (2021), A new method for on-line measurement of the straightness error of machine tools using an acceleration sensor, International Journal of Advanced Manufacturing Technology.
[https://doi.org/10.21203/rs.3.rs-1087483/v1]

-
Ruiz, A. R. J., Rosas, J. G., Granja, F. S., Honorato, J. C. P., Taboada, J. J. E., Serrano, V. M., Jimenez, T. M., (2009), A real-time tool positioning sensor for machine-tools, Sensors, 9(10), 7622-7647.
[https://doi.org/10.3390/s91007622]

-
Mostaghimi, H., Park, C. I., Kang, G., Park, S. S., Lee, D. Y., (2021), Reconstruction of cutting forces through fusion of accelerometer and spindle current signals, Journal of Manufacturing Processes, 68, 990-1003.
[https://doi.org/10.1016/j.jmapro.2021.06.007]

-
Sarhan, A. A. D., Matsubara, A., Sugihara, M., Saraie, H., Ibaraki, S., Kakino, Y., (2006), Monitoring method of cutting force by using additional spindle sensors, JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, 49(2), 307-315.
[https://doi.org/10.1299/jsmec.49.307]

-
Albrecht, A., Park, S. S., Altintas, Y., Pritschow, G., (2005), High frequency bandwidth cutting force measurement in milling using capacitance displacement sensors, International Journal of Machine Tools and Manufacture, 45(9), 993-1008.
[https://doi.org/10.1016/j.ijmachtools.2004.11.028]

-
Abir, J., Longo, S., Morantz, P., Shore, P., (2016), Optimized estimator for real-time dynamic displacement measurement using accelerometers, Mechatronics, 39, 1-11.
[https://doi.org/10.1016/j.mechatronics.2016.07.003]

- Arraigada, M., Partl, M., (2006), Calculation of displacements of measured accelerations, analysis of two accelerometers and application in road engineering, Proceedings of the 6th Swiss Transport Research Conference, 1-31.
-
Sarwar, M. Z., Park, J.-W., (2020), Bridge displacement estimation using a co-located acceleration and strain, Sensors, 20(4), 1109.
[https://doi.org/10.3390/s20041109]

-
Niu, W.-M., Li-Qing, F., Qi, Z.-Y., Guo, D.-Q., (2019), Small displacement measuring system based on MEMS accelerometer, Mathematical Problems in Engineering, 2019, 3470604.
[https://doi.org/10.1155/2019/3470604]

-
Lee, H. S., Hong, Y. H., Park, H. W., (2010), Design of an FIR filter for the displacement reconstruction using measured acceleration in low-frequency dominant structures, International Journal for Numerical Methods in Engineering, 82(4), 403-434.
[https://doi.org/10.1002/nme.2769]

-
Sato, R., Nagaoka, K., (2011), Motion trajectory measurement of NC machine tools using accelerometers, Int. J. Autom. Technol., 5(3), 387-394.
[https://doi.org/10.20965/ijat.2011.p0387]


Senior researcher in the Department of Ultra-Precision Machines and Systems, Advanced Manufacturing Systems Research Division, Korea Institute of Machinery & Materials. His research interest is computerized numerical control (CNC) and modeling/control of dynamic system such as precision machines and robot manipulators.
E-mail: bsg17@kimm.re.kr

Principal researcher in the Department of Ultra-Precision Machines and Systems, Advanced Manufacturing Systems Research Division, Korea Institute of Machinery & Materials. His research interest is machine tool design and analysis.
E-mail: sclee@kimm.re.kr

Principal researcher in the Department of Ultra-Precision Machines and Systems, Advanced Manufacturing Systems Research Division, Korea Institute of Machinery & Materials. His research interest is machine tool dynamics, and precision engineering.
E-mail: changjukim@kimm.re.kr

Principal researcher in the Korea Institute of Machinery & Materials. His research interest is CNC system and machine tool manufacturing.
E-mail: song@kimm.re.kr

Principal researcher in the Korea Institute of Machinery & Materials. His research interests are control system and actuator design for precision machines.
E-mail: cniz@kimm.re.kr