병렬 메커니즘을 이용한 무인 비행체 조종기
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
It is difficult for a human operator to find roll, pitch, yaw (RPY) that indicates the desired direction of unmanned aerial vehicle (UAV) in a three-dimensional space. Herein, a controller for UAV was developed allowing the human operator controlling the direction of UAV without finding RPY information. The algorithm implemented in the controller automatically calculated RPY information of UAV from the normal vector of the end effector. The developed controller was designed using a parallel mechanism. The joint angles of the controller were measured using potentiometers to estimate the normal vector of the end effector. Five subjects participated in an experiment to control a vector in three-dimensional space to follow a randomly generated target vector using the developed controller and the thumb sticks. The performance of the two controllers was evaluated by two methods: measuring the required time to reduce the error between the controlled vector and the target vector to be less than 0.1 cm and calculating a normalized error between the controlled vector and the target vector after manipulating the controlled vector for 10 seconds. When using the developed controller, the difference in control ability between subjects was reduced, and both required time and normalized error were generally reduced.
Keywords:
Unmanned aerial vehicle, Teleoperation, Parallel mechanism키워드:
무인 비행체, 원격조종, 병렬 메커니즘1. 서론
최근 무인 비행체(Unmanned Aerial Vehicle)가 건설, 농업, 에너지, 운송, 공공안전 등의 다양한 산업 분야에서 활용되고 있으며[1] 취미와 여가 활동을 위한 무인 비행체의 수요도 증가하고 있다. 무인 비행체의 활용과 수요가 늘어나면서 무인 비행체의 추락과 충돌로 인한 인적 피해와 물질적 피해도 증가하고 있다[2].
무인 비행체의 운행 방법 중 하나로 조종사가 조종기를 통해 무인 비행체를 원격조종하는 방법이 활용되고 있다. 무인 비행체의 원격조종에는 RC 카나 모형 배 등에서 사용하던 Thumb Controller가 보편적으로 사용되고 있다[3].
무인 비행체의 원격조종에 보편적으로 사용되고 있는 Thumb Controller는 두 개의 Thumb Stick으로 구성된다. 각 Thumb Stick은 무인 비행체의 상하 운동과 수평면에서의 2차원 이동을 조종한다. 두 개의 Thumb Stick이 서로 다른 축에 대한 조종 신호를 생성하므로 Thumb Controller의 조작성과 직관성이 떨어진다. Thumb Controller를 이용한 무인 비행체의 원격조종은 난이도가 높고, 조종사가 조종에 능숙해지기 위해서 많은 시간과 연습이 필요하므로 무인 비행체를 원격조종하는 새로운 방법에 관한 연구가 필요하다[4].
최근에는 무인 비행체를 조종하기 위해 Thumb Controller 이외에 사람의 제스처(Gesture)나 포인팅(Pointing)을 무인 비행체의 움직임과 연결하는 조종 방법도 연구되고 있다[5,6].
사람의 손, 머리 등의 신체를 움직여 생성하는 제스처를 인식해 무인 비행체를 조종하는 방법은 단순한 상황에서는 직관적인 조종이 가능하지만 복잡한 상황에서는 무인 비행체를 조종하기 위한 제스처가 지나치게 복잡해지는 단점이 있다[7]. 사람의 포인팅을 이용한 무인 비행체의 조종 방법은 무인 비행체와 조종사 사이의 거리가 멀어질수록 조종 정확성이 떨어지는 단점이 있다.
본 연구에서는 산업용 매니퓰레이터의 구조에 사용되는 병렬 메커니즘을[8] 활용하여 조종사의 손동작을 실시간으로 측정할 수 있는 3차원 조종기를 개발한다. 3차원 조종기를 통해 획득한 조종사의 손동작을 무인 비행체의 Roll, Pitch, Yaw (RPY) 그리고 스로틀(Throttle)로 변환하여 무인 비행체의 3차원 이동을 제어하는데 사용한다.
2. 병렬 메커니즘을 이용한 3차원 조종기
병렬 메커니즘(Parallel Mechanism)은 두 개 이상의 독립적인 키네마틱 체인이 말단 장치(End Effector)와 바닥 프레임을 연결하여 폐쇄된 키네마틱 체인 구조를 구성한다[9]. 이러한 구조로 인해 병렬 메커니즘은 관절이 구동되는 각도 범위가 작고 링크 간 간섭이 발생하여 작업영역(Workspace)이 제한적이라는 단점이 있다. 그러나 병렬 메커니즘은 일반적으로 직렬 메커니즘(Serial Mechanism)에 비해 낮은 관성(Inertia)과 높은 반복정밀도(Repeatability)를 가지며 소형으로 제작할 수 있다는 장점이 있다. 무인 비행체의 조종을 위해 넓은 작업영역이 필요치는 않으므로 병렬 메커니즘의 장점을 활용하여 무인 비행체를 원격조종하기 위한 3차원 조종기를 개발하였다.
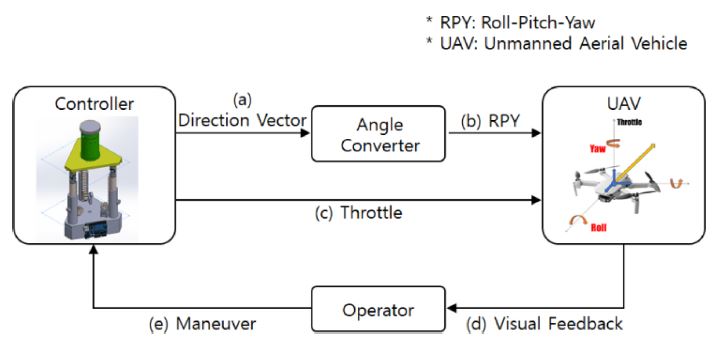
Fig. 1은 병렬 메커니즘을 이용해 개발한 3차원 조종기가 무인 비행체의 제어 신호를 생성하는 과정을 나타낸다. 개발한 3차원 조종기는 무인 비행체를 제어하기 위해 Figs. 1(a)로 표시된 조종사가 무인 비행체를 이동시키고 싶은 방향의 방향 벡터와 1(c)로 표시된 방향 벡터 방향으로의 가속도를 결정하는 스로틀 값을 생성한다. 조종기에서 생성된 방향 벡터는 Fig. 1(b)와 같이 변환 식을 통해 RPY로 변환되어 무인 비행체의 제어에 사용되고, 생성된 스로틀 값은 무인 비행체의 제어에 그대로 사용된다. 조종사는 무인 비행체로부터 Fig. 1(d)로 표시된 시각 피드백을 받아 무인 비행체의 이동 방향과 가속도를 결정하고 개발된 조종기를 조작하여 무인 비행체를 조종사의 의도대로 조종한다.
2.1 병렬 메커니즘을 이용한 3차원 조종기 설계
병렬 메커니즘을 이용한 3차원 조종기를 Fig. 2와 같이 설계하였다. 조종사는 개발한 3차원 조종기를 사용해 Figs. 1(a)와 1(c)로 표시된 무인 비행체가 이동하는 방향 벡터와 스로틀 값을 조종할 수 있다.
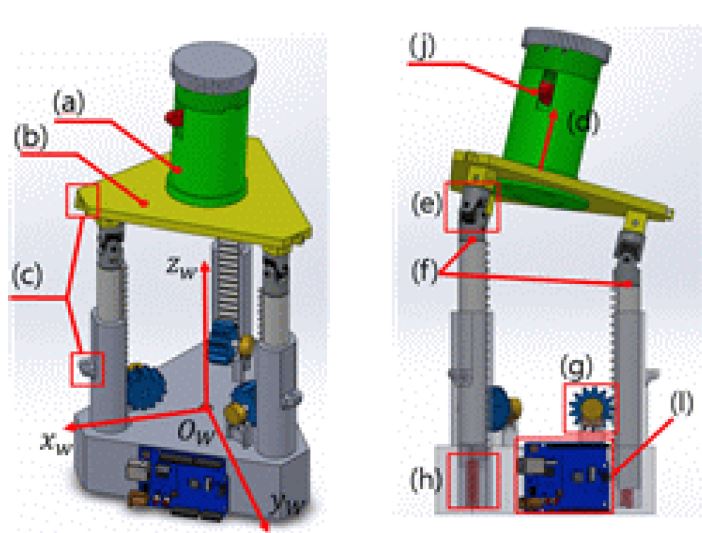
Design of developed controller using parallel mechanism: (a) Handle for grip, (b) Plate for maneuver, (c) Rubber band connector, (d) Normal vector of plate, (e) Universal joint, (f) End point of rack gear, (g) Pinion gear connected to potentiometer, (h) Spring, (i) Microcontroller board (Arduino Uno), and (j) Wheel for throttle control
스로틀 값은 조종사가 Fig. 2(j)로 표시된 회전 가능한 휠을 조작하여 증감한다. 조종사는 Figs. 2(a)로 표시된 손잡이를 잡고 2(b)로 표시된 판을 움직여서 무인 비행체를 이동시키고자 하는 방향의 방향 벡터를 무인 비행체에 전달할 수 있다. 조종사가 Figs. 2(b)로 표시된 판을 조작하면 2(d)로 표시된 판의 법선 벡터가 변화한다. 변화하는 판의 법선 벡터를 계산하여 계산 결과를 Fig. 1(a)로 표시된 무인 비행체가 이동하는 방향 벡터로 사용하였다. 조종사가 조종하는 대로 판이 기구적으로 제한 없이 자유롭게 움직일 수 있도록 판과 랙 기어(Rack Gear)를 Fig. 2(e)로 표시된 유니버설 조인트(Universal Joint)로 연결하였다.
Figs. 2(d)로 표시된 판의 법선 벡터는 2(f)로 표시된 세 개의 랙 기어 끝점을 포함하는 평면의 법선 벡터와 동일하다. 세 개의 랙 기어 끝점을 포함하는 평면의 평면방정식을 계산함으로써 법선 벡터를 결정하였다. 평면방정식을 계산하기 위해 세 개의 랙 기어 끝점 좌표를 Fig. 2에 표시된 절대 좌표축(Ow-xwywzw)을 기준으로 측정하였다. 절대 좌표축을 기준으로 세 개의 랙 기어 끝점 좌표에서 x-와 y-좌표는 기구적으로 고정되어 상수값(Constant Value)을 가지고, z-좌표는 랙 기어의 상하 이동에 의해 결정된다. 판의 움직임에 의해 랙 기어가 상하로 움직이면 Fig. 2(g)로 표시된 피니언 기어가 회전한다. 피니언 기어에는 가변저항을 연결하여 피니언 기어가 회전하는 각도를 가변저항의 전압 값 변화로 측정하였다. 측정된 전압 값을 이용해 세 개의 랙 기어 끝점의 z-좌표를 절대 좌표축 기준으로 각각 측정하였다(상세 측정 방법은 2.2절 참고).
병렬 메커니즘을 이용한 3차원 조종기는 Fig. 2(d)로 표시된 판의 법선 벡터가 절대 좌표축의 축과 평행하게 하는 복원력(Restoring Force)이 작용하도록 설계되었다. 병렬 메커니즘을 이용한 3차원 조종기에는 Figs. 2에 (c)로 표시된 고무줄 걸이 장치에 고무줄이 연결되고, 2(h)로 표시된 9 × 35 mm 크기의 스프링이 장착된다. 복원력은 고무줄과 스프링의 탄성력으로부터 생성된다.
2.2 3차원 조종기의 제어 신호 생성 알고리즘
개발한 3차원 조종기에는 총 네 개의 가변저항(최대 회전각 300o, 10 k ohm)을 사용하여 사용자의 조종 의도를 측정하였다. 네 개의 가변저항은 Fig. 2(i)로 표시된 아두이노 보드(Arduimo Uno R3 SMD)에 연결하여 신호를 측정하였고 측정된 신호는 MATLAB으로 처리하였다. 세 개의 가변저항은 Fig. 2(g)와 같이 세 개의 피니언 기어에 각각 연결하여 사용자가 조종하는 랙기어의 수직 위치를 측정하였다. 다른 하나의 가변저항은 Fig. 2(j)에 표시된 휠에 연결하여 휠의 회전 각도를 측정하는데 사용하였다.
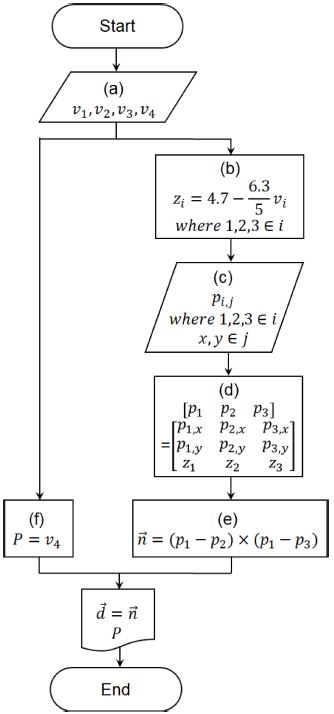
무인 비행체를 제어하기 위한 방향 벡터와 스로틀 값을 계산하는 과정을 Fig. 3에 나타냈다. Fig. 3(a)에서 아두이노 보드를 이용해 네 가변저항의 전압 값(vi where 1, 2, 3, 4 ∈ i)을 측정하였다. Figs. 3(b)에서 2(f)로 표시한 세 개의 랙 기어 끝점 위치의 절대 좌표축 기준 z-좌표(zi where 1, 2, 3 ∈ i)를 세 가변저항의 전압 값(νi where 1, 2, 3 ∈ i), 아두이노 보드의 공급 전압(Vmax), 복원력이 없는 평형 상태를 기준으로 랙 기어의 위쪽 방향 최대 변위(lupward)와 랙 기어의 아래쪽 방향 최대 변위(ldownward)를 이용해 식(1)과 같이 계산하였다.
| (1) |
Fig. 3(c)에서 세 개의 랙 기어 끝점 위치의 절대 좌표축 기준 x-와 y-좌표(pi,j where 1, 2, 3 ∈ i and x, y ∈ j)는 조종사의 조종과 무관하게 설계한 기구부에 의해 상수로 결정되었다. Fig. 3(d)에서 절대 좌표축 기준으로 세 개의 랙 기어 끝점 위치 좌표(pi where 1, 2, 3 ∈ i)를 결정하였다. Fig. 3(e)에서 세 개의 랙 기어 끝점 위치 좌표와 외적을 이용해 조종사가 조종하는 판의 법선 벡터를 계산하였다. Fig. 3(f)에서 손잡이의 휠에 연결한 가변저항 전압 값(v4)을 이용해 무인 비행체의 스로틀 값을 결정하였다.
3. 실험 방법
조종기의 성능 평가를 위한 실험에서는 무인 비행체의 동역학적 성질은 반영하지 않고 조종사가 시각 피드백과 조종기를 통한 조종을 통해 목표로 하는 방향과 크기의 벡터를 생성하여 무인 비행체에 전달할 수 있는지 평가하였다.
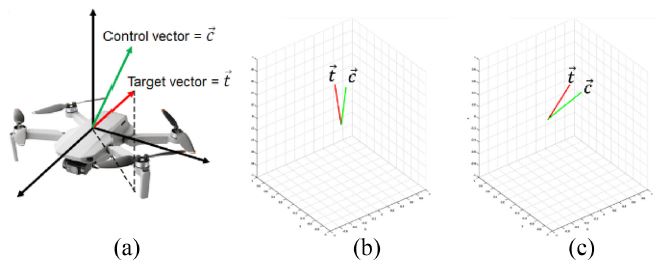
Fig. 4는 조종기의 성능 평가를 위해 구성한 환경을 보여준다. Fig. 4(a)에 무인 비행체가 비행하고자 하는 방향과 스로틀 값의 크기를 나타내는 목표벡터()와 조종사가 조종기로 무인 비행체를 조종하는 방향과 스로틀 값의 크기를 나타내는 조종 벡터()를 표시하였다. 목표 벡터()는 매 실험마다 임의의 크기와 방향을 곱하여 생성하고, 조종 벡터()는 Fig. 3의 알고리즘에서 출력된 방향 벡터()와 스로틀 값(P)의 곱으로 계산하였다. 조종사는 Figs. 4(b), 4(c)와 같은 시각 피드백을 참고하여 두 벡터, 와 ,를 일치시키는 실험을 수행하였다.
조종사가 3차원 공간의 두 벡터를 일치시키기 위해 하나의 시점에서 벡터를 시각적으로 확인하며 조종하기에는 조종사가 확인할 수 있는 위치, 자세 정보가 제한적이므로 실험 과정에서 Figs. 4(b), 4(c)와 같이 동일한 3차원 공간의 벡터를 서로 다른 방향에서 바라보는 두 개의 3차원 그래프를 조종사에게 표시하였다.
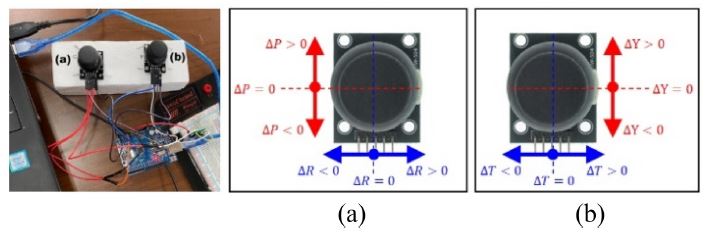
조종사는 Fig. 4의 와 가 일치하도록 조종하기 위해 기존에 무인 비행체 조종을 위해 사용되던 Thumb Controller와 개발된 조종기를 각각 사용하였다. Thumb Controller는 Fig. 5 와 같이 두 개의 Thumb Stick (Arduino PS2 Joystick Module, Wishiot)으로 구성하였다.
Figs. 5(a)에 표시된 Thumb Stick을 통해 조종사는 ΔP와 ΔR값을 조종하여 4에서 의 Pitch와 Roll 값을 결정한다. Figs. 5(b)에 표시된 Thumb Stick을 통해 조종사는 ΔT와 ΔY 값을 조종하여 4에서 의 의 절댓값과 Yaw 값을 결정한다. 시간 t에서의 RPY와 스로틀 값을 Rt, Pt, Yt, Tt라고 했을 때, Thumb Controller는 식(2)를 통해 Fig. 4에서 의 RPY와 스로틀 값을 조종하였다.
| (2) |
조종사가 조종하는 RPY 값을 이용해 Fig. 4에서의 단위 방향 벡터를 계산하고, 스로틀 값을 의 크기로 사용하였다.
개발한 3차원 조종기와 Thumb Controller의 조종 성능을 비교하기 위한 실험에는 총 5명의 24세에서 26세 사이의 건강한 남성이 피험자로 참여하였다. 피험자의 평균 나이는 25세였다.
실험에서 Fig. 4의 가 임의로 생성되면 피험자는 개발한 3차원 조종기와 Thumb Controller를 사용해 를 조종하여 와 일치시키도록 안내하였다. 피험자가 를 조종하여 와 일치시키는 실험에 대해서 두 가지 평가 방법으로 조종기의 성능을 평가하였다. 첫 번째 평가 방법으로 피험자가 와 의 오차 크기를 0.1 cm 이하로 만드는데 걸리는 시간을 측정하고 그 시간이 짧을수록 조종기의 성능이 좋은 것으로 평가하였다. 두 번째 평가 방법으로 피험자에게 10초의 정해진 시간을 부여하고 정해진 시간이 종료됐을 때 피험자가 조종한 와 임의로 설정된 의 오차 크기를 의 크기로 나누어 식(3)과 같이 정규화 오차(errnorm)를 계산함으로써 조종기의 성능 평가 지표로 사용하였다. 정규화 오차의 크기가 작을수록 조종기의 성능이 좋은 것으로 평가하였다.
| (3) |
피험자는 개발한 3차원 조종기와 Thumb Controller를 각각 10회씩 사용하여 두 가지 평가 방법에 대해 를 조종하여 와 일치시키는 실험을 반복하였다.
4. 결과 및 고찰
피험자가 Figs. 4의 와 사이의 오차 크기를 0.1 cm 이하로 만드는데 걸리는 시간을 측정하고, 피험자별 소요 시간의 평균과 표준편차를 6에 나타냈다. 개발한 3차원 조종기를 사용해 각 피험자가 10회씩 실험을 하는 동안 측정된 소요 시간의 평균과 표준편차를 Fig. 6(a) 그래프에 표시하였다. 각 피험자에서 측정된 평균과 표준편차는 6.07±3.02초, 7.12±4.79초, 6.31±2.17초, 6.94±3.29초, 5.71±1.03초였다. 피험자가 Thumb Controller를 사용한 경우에 측정된 소요 시간의 평균과 표준편차는 Fig. 6(b) 그래프에 표시하였다. 각 피험자에서 측정된 소요 시간의 평균과 표준편차는 12.5±8.51초, 6.67±3.60초, 7.18±3.74초, 6.87±2.50초, 10.9±7.48초였다. 피험자 1과 피험자 5는 개발한 3차원 조종기를 사용했을 때의 소요 시간이 Thumb Controller를 사용했을 때의 소요 시간과 비교하여 크게 감소하였다. 하지만 피험자 2, 피험자 3, 그리고 피험자 4의 경우에는 사용한 조종기의 종류에 상관없이 비슷한 평균 소요 시간이 측정되었고 특히 피험자 2와 피험자 4의 경우에는 Thumb Controller를 사용한 경우에 미세하게 더 짧은 평균 소요 시간이 측정되었다. 실험 결과를 통해 각 피험자의 조종 능력이 개발한 3차원 조종기를 사용했을 때 향상되는지에 대해서는 단정하기 어려웠다.
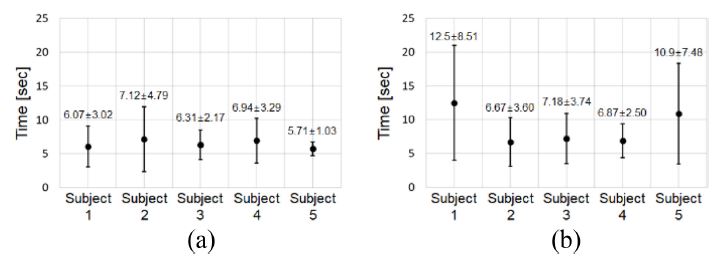
Time measurement results for experiments to reduce the error between target and control vector to less than 0.1 cm: Experimental results using (a) Developed controller, and (b) Thumb controller
그러나 실험 결과를 통해 개발한 3차원 조종기를 사용하는 경우에 피험자에 따른 조종 능력의 개인차가 줄어들고 피험자 모두에게서 우수한 조종 능력이 관찰됨을 확인할 수 있다. Thumb Controller를 사용한 경우에 가장 짧은 평균 소요 시간을 보인 피험자와 가장 긴 평균 소요 시간을 보인 피험자는 각각 6.67초와 12.48초의 평균 소요 시간을 보였다. 개발한 3차원 조종기를 사용한 경우에는 가장 짧은 평균 소요 시간을 보인 피험자와 가장 긴 평균 소요 시간을 보인 피험자가 각각 5.71초와 7.12초로 관찰되었다. Thumb Controller를 사용한 경우에 비해 개발한 3차원 조종기를 사용한 경우에 가장 우수한 결과와 나쁜 결과를 보인 피험자 사이의 차이가 작아지는 것을 확인할 수 있다. 5명의 피험자가 수행한 총 50번의 실험에서 측정된 소요 시간의 평균과 표준편차는 Thumb Controller를 사용한 경우에 8.81±5.96초, 개발한 3차원 조종기를 사용한 경우에 6.43±3.04초로 계산되었다. 개발한 3차원 조종기를 사용한 전체 피험자의 실험 결과에서의 표준편차가 Thumb Controller를 사용한 전체 피험자의 실험 결과에 비해 크게 작음을 확인할 수 있다.
피험자가 10초간 조종한 임의로 생성된 사이의 정규화 오차를 식(3)과 같이 계산하고 피험자별 정규화 오차 크기의 평균과 표준편차를 Fig. 7에 나타냈다.
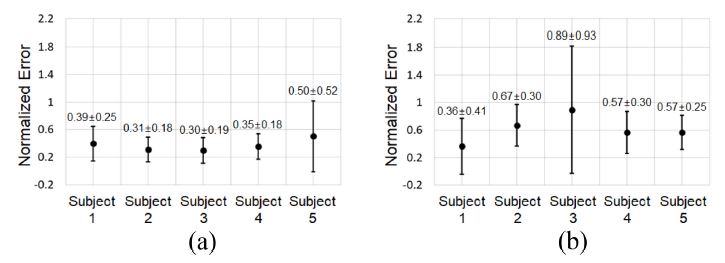
Normalized error for experiments to reduce the error between target and control vector for 10 seconds: Experimental results using (a) Developed controller, and (b) Thumb controller
각 피험자가 개발한 3차원 조종기를 사용해 10회씩 실험을 하는 동안 측정된 정규화 오차의 평균과 표준편차는 0.39±0.25, 0.31±0.18, 0.30±0.19, 0.35±0.18, 0.50±0.52였으며 Fig. 7(a)에 표시하였다. 피험자가 Thumb Controller를 사용한 경우에 측정된 정규화 오차의 평균과 표준편차는 0.36±0.41, 0.67±0.30, 0.89±0.93, 0.57±0.30, 0.57±0.25였으며 Fig. 7(b)에 표시하였다.
피험자 5를 제외한 모든 피험자가 개발한 3차원 조종기를 사용했을 때에 조종 능력이 향상되었다. 피험자 2, 피험자 3, 그리고 피험자 4는 개발한 3차원 조종기를 사용했을 때가 Thumb Controller를 사용했을 때에 비해 정규화 오차의 평균과 표준편차가 모두 감소하여 우수한 조종 능력을 보였다. 피험자 1의 정규화 오차 평균은 조종기의 종류에 상관없이 비슷한 값을 보였으나 개발한 3차원 조종기를 사용했을 때가 Thumb Controller를 사용했을 때에 비해 정규화 오차의 표준편차가 작게 관찰되어 다양한 에 대해 고른 조종 능력을 보였다.
Thumb Controller를 사용한 경우에 각 피험자의 정규화 오차 평균 중 가장 큰 값은 0.89였고 가장 작은 값은 0.36이었다. 개발한 3차원 조종기를 사용한 경우에는 가장 큰 정규화 오차 평균은 0.50이었고 가장 작은 정규화 오차 평균은 0.30이었다. 소요 시간을 측정한 실험과 마찬가지로 정규화 오차를 측정한 실험에서도 개발한 3차원 조종기를 사용한 경우에 가장 우수한 결과를 보인 피험자와 가장 나쁜 결과를 보인 피험자 사이의 차이가 작음을 확인할 수 있다.
5명의 피험자가 수행한 총 50번의 실험에서 측정된 정규화 오차의 평균과 표준편차는 Thumb Controller를 사용한 경우에 0.61±0.51, 개발한 3차원 조종기를 사용한 경우에 0.37±0.29로 계산되었다. 개발한 3차원 조종기를 사용한 전체 피험자의 실험 결과에서 정규화 오차의 표준편차가 Thumb Controller를 사용한 경우에 비해 크게 작음을 확인할 수 있다.
피험자가 와 사이의 오차를 0.1 cm 이하로 만들기 위해 소요한 시간을 측정하는 실험과 피험자가 10초간 조종한 후에 와 사이의 정규화 오차를 측정하는 실험 모두에서 개발한 3차원 조종기를 사용하는 경우에 피험자의 개인차에 의한 조종 능력 차이가 작아지고 모든 피험자가 대체로 우수한 조종 능력을 보였다.
5. 결론
본 논문에서는 무인 비행체의 원격조종을 위한 조종기를 병렬 메커니즘을 활용하여 개발하였다. 개발한 3차원 조종기는 말단 장치의 법선 벡터를 이용하여 무인 비행체의 RPY 신호를 생성하며 말단 장치의 손잡이에 부착된 휠을 이용해 스로틀 신호를 생성한다. 개발한 3차원 조종기의 조종 성능을 기존 무인 비행체의 원격조종에 주로 사용되던 Thumb Controller의 조종 성능과 비교하였다. 조종 성능을 비교하기 위해 조종사가 두 종류의 조종기로 3차원 벡터를 조종하여 임의로 생성된 목표 벡터와 일치시키도록 하였다. 조종사는 3차원 벡터를 조종하기 위해 조종기로 RPY 값과 스로틀 값을 생성하여 3차원 벡터의 방향과 크기를 결정하였다. 실험 과정에서 조종사는 3차원 벡터를 조종하여 임의로 생성된 목표 벡터와 일치시켰다.
조종사가 조종하는 3차원 벡터와 임의로 생성되는 목표 벡터 사이의 오차가 일정 값(0.1 cm) 이하가 될 때까지 소요된 시간을 측정하는 방법과 조종사가 일정 시간(10초) 동안 3차원 벡터를 조종한 결과와 임의로 생성되는 목표 벡터 사이의 정규화 오차를 계산하는 방법으로 조종기의 성능을 평가하였다.
본 논문에서는 조종사가 무인 비행체의 제어 신호를 조종하기 위해 개발한 3차원 조종기를 사용하는 경우가 기존 Thumb Controller를 사용하는 경우에 비해 개인에 따른 조종 능력 편차가 적고 조종 능력도 우수하다는 결과를 통해 무인 비행체를 위한 새로운 3차원 조종기의 연구 가능성을 확인하였다.
실제 무인 비행체에서는 RPY와 스로틀 크기로 결정되는 벡터에 중력 및 항력과 같은 외부의 동역학적 요소가 더해진 결과로 무인 비행체가 움직이는 방향과 가속도가 결정된다. 그러나 본 논문에서는 개발한 조종기의 조종 능력 평가에 집중하기 위해 무인 비행체의 중력 및 항력과 같은 외부의 동역학적 요소는 고려하지 않았다.
본 논문의 결과를 통해 개발한 3차원 조종기를 통한 무인 비행체의 조종 효과를 확인하였으며, 개발한 3차원 조종기를 실제 무인 비행체 또는 중력 및 항력과 같은 동역학적 요소가 반영된 무인 비행체의 시뮬레이션 환경에 적용하고 조종 성능을 평가하는 추가 연구를 진행할 계획이다.
Nomenclature
| vi : | Voltage from ith Potentiometer |
| : | Normal Vector |
| : | Directional Vector |
| : | Controlled Vector |
| : | Target Vector |
| pi : | Coordinates of End Point for ith Rack Gear |
| RPY : | Roll Pitch Yaw |
| P : | Magnitude of Throttle |
Acknowledgments
본 논문은 2022학년도 상명대학교 교내연구비를 지원받아 수행하였음.
REFERENCES
- Jin, J., Kim, H., (2017), Public application of drone technology, Broadcasting and Media Magazine, 22(2), 106-117.
-
Kim, J., (2018), Legal liability and insurance system for unmanned aerial vehicle, Business Law Review, 32(4), 169-201.
[https://doi.org/10.24886/BLR.2018.12.32.4.169]

- Graff, C., (2016), Drone piloting study, University of Italian Switzerland. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.735.3984&rep=rep1&type=pdf
- Cha, M., Kim, B., Lee, J., Ji, Y., (2016), Usability evaluation for user interface of a drone remote controller, Proceedings of the ESK Conference, 417-424.
- Jang, W., Kim, H., (2018), Development of an intuitive drone controller based on hand motions, Proceedings of the HCI Korea Conference, 128-131.
- Kim, Y., Lee, J., Lee, C., Jeon, H., Kim, S., (2021), Implementation and verification of deep learning-based automatic object tracking and handy motion control drone system, IEMEK Journal of Embedded Systems and Applications, 16(5), 163-169.
- Yoo, H.-J., Mok, S.-S., Kim, J.-S., Baek, J.-A., Ko, Y.-S., (2020), Control technology based on the finger recognition of robot cleaners, The Journal of the Korea Institute of Electronic Communication Sciences, 15(1), 139-146.
- Paek, D.-H., Kim, Y.-D., Cho, W., (2020), The current-position cascade pid control of delta-type parallel robot, The Journal of the Korea Institute of Electronic Communication Sciences, 15(2), 273-284.
- Tsai, L.-W., (1999), Robot analysis: The mechanics of serial and parallel manipulators, John Wiley & Sons.

B.Sc. candidate in the Department of Human Intelligence Robot Engineering, Sangmyung University. His research interest is robotics and robot design.
E-mail: vbnm3597@naver.com

B.Sc. candidate in the Department of Human Intelligence Robot Engineering, Sangmyung University. Her research interest is robotics and control.
E-mail: dbsehd1130@naver.com

Professor in the Department of Human Intelligence Robot Engineering, Sangmyung University. His research interest is global navigation satellite system, flight dynamics and control.
E-mail: skjeong@smu.ac.kr

Professor in the Department of Human Intelligence Robot Engineering, Sangmyung University. His research interest is robotics, human-robot interface, data-driven control, machine learning.
E-mail: drbong@smu.ac.kr