Dynamic Analysis and Mathematical Modeling of a Gas Cutting Process

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, the relationship between various physical and chemical dynamics included in a gas cutting process was analyzed and a mathematical model was presented. To express the gas cutting process in a formula that could reflect the physics and chemical reaction dynamics, the entire process was classified into three stages: flame spurt, metal oxidation, and metal oxide melting. Flame spurt is caused by combustion of fuel gas and oxygen. It was modeled through fluid dynamics, chemical species transport, and reaction kinetics. Metal oxidation was modeled as a chemical reaction of surface oxidation and oxide growth based on temperature and concentration of species of the metal surface obtained through flame and cutting oxygen spurt results. Finally, the melting of metal oxide was expressed as a rate equation based on melting conditions, heat flux obtained in the previous two stages, and changed properties of the metal. The presented mathematical model could analyze dynamic relationships for each stage of a gas cutting process and connect them into one process. Results of this study can be used as basic data for future finite element analysis and simulations.
Keywords:
Gas cutting dynamics analysis, Mathematical modeling of a gas cutting, High-temperature oxidation of iron, Oxygen cutting dynamics analysis키워드:
가스절단 역학 분석, 가스절단 수학적 모델링, 철의 고온 산화, 산소절단 역학 분석1. Introduction
The gas cutting is one of the most frequently used cutting methods in the industrial field. After preheating a steel to 700-900oC with a flame, pure high-pressure oxygen is sprayed to oxidize the surface to cut metal oxide with a lower melting point. Since the gas cutting has a low technical difficulty, any special prior research is not required if an operator cuts the steel manually. However, in the case of using a robot or an automatic equipment in a special environment where access is difficult (nuclear decommissioning waste cutting, underwater cutting, etc.), a sufficient review is required in advance. In this stage, a preliminary review is generally performed through a finite element method (FEM) analysis, but the studies necessary for FEM analysis of gas cutting have not yet been sufficiently conducted.
There have been attempts by researchers to study some phenomena during the gas cutting process or to simplify the entire process and analyze it through simulation. Refs. [1,2] analyzed the characteristics of high-temperature oxidation of thin metal films placed in tubes under controlled experimental conditions. In Ref. [3], a numerical modeling was performed on the combustion reaction of oxygen and fuel gas. In addition, Ref. [4] studied on the characteristics of impinging jet flame. Refs. [5-7] tried to numerically analyze similar processes such as laser cutting, plasma cutting, and welding, respectively, but they are different from the gas cutting process. In Refs. [8,9], attempts were made to simulate the entire gas cutting process, but factors such as the heat source model and metal oxidation were simplified. Although these studies are easy to understand and apply to the simulation process, they can only be applied under certain conditions due to the limitations of simplified elements. For the general application of simulation studies, it is important to design more principle-based mathematical models.
This paper presents a mathematical model for the overall process of gas cutting. Modeling targets include heating by fuel gas, cutting oxygen injection, metal oxidation, and metal shape change (melting). Modeling analyzes the relationship between physical mechanics and chemical reaction mechanics for each process of gas cutting and is performed centered on the governing equations expressing the process. We analyzed the relationship between physical mechanics and chemical reaction mechanics for each process of gas cutting, and presented a mathematical model including the entire gas cutting process with a focus on the governing equation.
Prior to the mathematical modeling of the gas cutting process, the gas cutting process was organized and detailed steps were classified. The classified dynamic steps are the spurt of preheating flame and cutting oxygen, the surface oxidation of metal (iron) and the growth of the oxide film (scale), and melting including the change in the properties of metal oxide. For each process, a mathematical modeling was performed by analyzing the physical and chemical dynamics. In addition, in order to connect each process as one process, the correlation between processes was analyzed. The mathematical model presented in this paper can express the entire process of gas cutting. The presented model can be used as basic data for performing a FEM analysis-based simulation in the future.
2. Gas Cutting Process
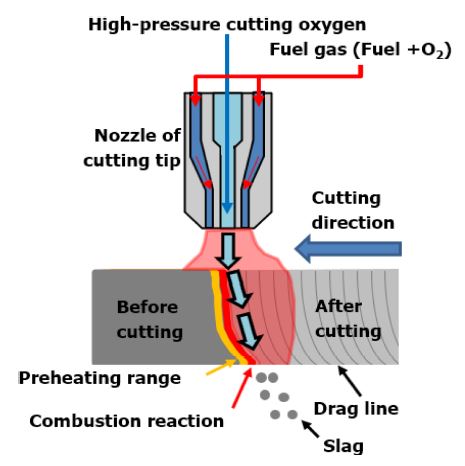
The process of gas cutting was established prior to the analysis of the dynamic relationships. The detail principles and process of a gas cutting are as follows, and it is schematically shown in Fig. 1.
1. Select an object to be cut (base material). The base material that can be cut through the gas cutting should not form a film that inhibits oxidation during oxidation and the melting point of oxide should be lower than that of the base material.
2. The injected fuel (propane, hydrogen, acetylene, etc.) generates a flame to preheat the base material to about 700oC or higher.
3. When the iron is preheated, high-pressure pure oxygen is sprayed to the heated base material from the center of the gas cutting tip.
4. The iron heated above a certain temperature causes various oxidation reactions, which produce iron oxides (FeO, Fe2O3, Fe3O4).
5. Since oxidation is a reaction that releases heat, the base material is heated more and more by the heat of oxidation reaction, and high-temperature conditions promote the reaction.
6. Due to the continuously ejected high-pressure oxygen, the iron melts and flies into the state of FeO and Fe at the same time. At this time, in the case of iron oxide, the lower melting point makes it easier to cut.
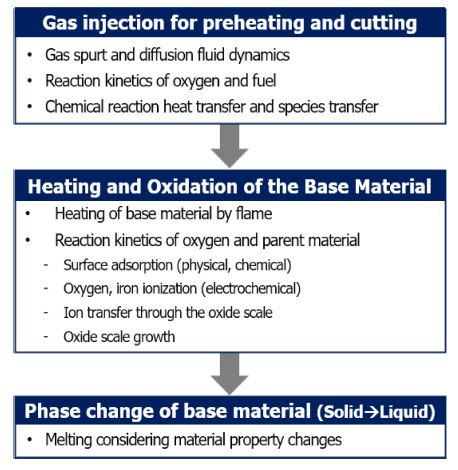
A summary of the dynamics involved in a series of processes for gas cutting is shown in Fig. 2. As shown in Fig. 2, the gas cutting is explained by a very complex dynamic relationships compared to the easy accessibility of industrial fields. In Chapter 3, dynamic analysis and mathematical modeling are performed based on the process of gas cutting summarized and classified in Chapter 2. Chapter 4 organizes the connectivity between the processes described in Chapter 3 and combines them to become a single process.
3. Mathematical Modeling of the Gas Cutting
This paper aims to represent the entire process of gas cutting in one integrated mathematical modeling. As mentioned in the introduction, a gas cutting is easy to handle in the industrial field, whereas in the research area, understanding of various fields such as machinery, chemistry, and materials is required. Therefore, in this paper, according to the process described in Chapter 2, only the most essential contents are covered, and modeling was performed based on the well-known governing equations in the overall process of gas cutting. Accordingly, it expresses the phenomenon and deals only with formulas applicable to numerical analysis. The mathematical model considers only the variables that have a dominant influence on the entire gas cutting process and general factors such as temperature, pressure, concentration, and reactivity. On the other hand, parts such as detailed material properties expressed by specific constants such as iron lattice shape, oxygen solubility, and surface roughness were excluded. Other considerations or limitations on ideal conditions are described in each chapter.
3.1 Preheating Flame and Cutting Oxygen Modeling
When the cutting material is ready, the first step in a gas cutting is the spurt of a preheating flame. The preheating flame spurts the compressed fuel gas and oxygen through a narrow tipped nozzle. This paper deals with a premixed gas that is premixed with oxygen and sprayed together.
The premixed gas spurted in the gaseous state generates heat through a chemical reaction process. The spurted fluid collides with the base material and transfers heat. In general, when creating a mathematical model for combustion, it should be modeled considering six factors: Flow modeling, Turbulence modeling, Turbulence chemistry interaction, Chemical kinetics, Radiant heat transfer, Pollutant formation. In the case of general flame heat transfer, the effect of radiant heat transfer is very large, but in the case of wall collision flames, heat transfer by forced convection has a dominant effect (70-90%) [3]. Therefore, for a gas cutting, reliable results can be obtained without considering the effect of radiant heat transfer. Also, the pollutant formation is excluded because it is a factor that affects radiant heat.
Before creating a mathematical model for the preheating flame and cutting oxygen, the following assumptions were made for the convenience of interpretation. The assumptions below are high-reliability assumptions that have already been verified in relation to the flame combustion modeling [4].
1. All gases behave like ideal gases.
2. In the gaseous state, the binary diffusion coefficient is the same, and it diffuses along Fick’s low.
3. Diffusion preference ratio, Lewis number equals 1.
4. The chemical reaction of combustion is premised on an irreversible reaction.
The dynamic model of the preheating flame starts from the continuity equation of the general fluid. Mathematical modeling of the fluid behavior and heat flux is described with reference to the theorem of Ananth Sharma and Sreenivas Jayanti based on the representative fluid equations and species transport equations [3]. The general conservation equation for a gas mixture consisting of n components that accompanies a chemical reaction is:
| (1) |
where ρ is the density of the fluid (constant in the case of incompressible fluid), t is the time, and ν is the velocity of the fluid. The above equation leads to the Navier-Stokes momentum conservation equation.
| (2) |
where P is the pressure, T is the stress, and f is the volume force. This means that the acceleration of the fluid is determined according to the pressure, stress, and volume force acting on the fluid, and the shear stress is proportional to the shear strain. In this case, the species conservation equation for fluid flow can be written as
| (3) |
where Si [kg/m3] represents the rate of formation of species i by chemical reaction. By applying Fick’s diffusion law to Equation (3), we can derive a more useful form of the species balance equation in terms of mixture properties.
| (4) |
where Γ is the mass diffusion rate, Yi is the mass fraction and –Γ∇Yi is the diffusion flux.
Equation (4) can be used to derive a species balance equation considering the properties of the mixture. Based on the equation, the momentum and energy conservation equations can be expressed as Equations (5) and (6).
| (5) |
| (6) |
where μ and λ are the viscosity and thermal conductivity of the fluid, respectively, and mean the heat release due to the chemical reaction. The total enthalpy H is defined as
| (7) |
where h is the static enthalpy and is calculated as the specific heat as
| (8) |
where Cp is the heat capacity and Tref is the reference temperature at which the static enthalpy becomes zero. The reaction occurring in Equation 4 causes a change in enthalpy. The enthalpy change caused by a chemical reaction is as follows.
| (9) |
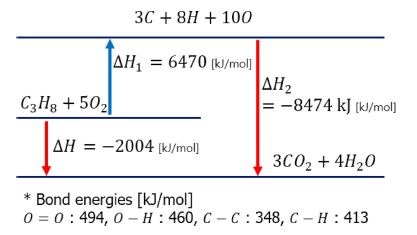
The change in enthalpy due to a chemical reaction can be obtained by calculating the change in standard enthalpy or dissociation and bond energy of molecules. The method of calculating the enthalpy change due to a chemical reaction is to derive the difference by obtaining the dissociation energy and the bond energy in the process of separating all the species participating in the reaction into each element and molecular binding into the final reactants. As a result of the calculation, if the final enthalpy change is negative, it is an exothermic reaction, and if it is positive, it is an endothermic reaction. Fig. 3 shows the enthalpy change for the first order combustion reaction of propane gas and oxygen.
The change in enthalpy obtained through the chemical reaction is organized as follows by Danckwerts boundary condition.
| (10) |
where is the boundary direction vector. The final heat flux Qflame by the flame is
| (11) |
where k is the intrinsic thermal conductivity and the turbulent thermal conductivity kT is defined as
| (12) |
where μT is the fluid viscosity as a function of temperature, and PrT is the Prandti number as a function of temperature.
In this section, the dynamics of the reaction fluid including the preheating flame and cutting oxygen was summarized through Equations (1) to (10). Afterwards, the heat flux transferred to the base material was summarized through Equations (11) and (12). Through the mathematical model, the results of the temperature change of the base material over time and the distribution of each species on the surface of the base material can be obtained.
3.2 Surface Oxidation and Scale Growth of the Metal
We summarized the mathematical model for the temperature change of the base material and the distribution of species through Section 3.1. As in the gas cutting process outlined in Section 2, the temperature rises by the preheating flame, and the surface of the base material forms an oxide film and the oxide film layer (hereafter scale) grows. Oxidation of metals is also carried out at low temperatures, but oxidation carried out at temperatures below 570oC has a very insignificant effect on the cutting process, so the gas cutting mathematical model only considers the effect of high-temperature oxidation [1,10,11].
Oxidation of metals is based on the process in Fig. 4 as described in Wagner’s theory. The key to prior research is that an oxide growth is most affected by oxidation temperature and oxygen pressure. After the publication of Wagner’s theory, studies related to mathematical modeling of the growth rate of the oxide scale continued. These studies can only be applied under specific conditions or have not been fully verified through experiments [12,13]. In this paper, the mathematical modeling of metal oxidation is based on the already verified parabolic equation of Wagner’s theory and assumes the same ideal conditions.
The oxidation stage of metal can be divided into two stages: oxygen adsorption, surface oxidation, and scale growth. The adsorption and ionization processes are described by the chemical formulas presented in Fig. 4.
Oxygen in gaseous state diffuses as the fluid moves, as described in Equations (4) and (5). Physical adsorption occurs when oxygen approaches the surface of the metal. On the surface of the metal, oxygen molecules dissociate, chemically bond with the metal, ionize, and create cation vacancies. In this process, the valence electrons of metals and gases are rearranged to form chemical bonds. In order for oxygen to be chemically adsorbed on the metal surface, the oxygen pressure must be greater than the dissociation pressure of the oxide in equilibrium with the metal [14].
| (13) |
where ΔG is the gibbs energy for oxide formation and R is the gas constant. The reaction rate for the generation of surface species A including adsorption conditions can be expressed as follows.
| (14) |
| (15) |
In Equation (14), ci is the molar concentration of species i, and kf and kr are the ratio constants for forward and reverse reactions, respectively. In Equation (15), is the concentration of all surface species, m is the reaction order, Mi is the molecular weight of the species i, and γA is the sticking coefficient. The chemical adsorption reaction rate of the gas on the metal surface can be summarized through the above equation, and the site volumic concentration (Zi) change and the site surface species concentration (ci) for each surface species i are as follows.
| (16) |
| (17) |
The surface reaction accompanies an enthalpy change of the same value as the bulk reaction, and the heat flux due to the enthalpy change is as follows.
| (18) |
After the oxide layer is formed on the metal surface, the metal and oxygen are separated by the scale and the reaction is carried out through diffusion through the scale. The growth rate of the scale is controlled by the movement of ions or electrons. This process was first outlined by [15]. The growth rate of the scale thickness (X) in the high-temperature oxidation of metal is expressed as a parabolic function in Equation (19).
| (19) |
| (20) |
where kp is the rate constant.
In one-dimension, the rate of diffusion is described by Fick’s law.
| (21) |
| (22) |
In Equation (21), J is the flux through a unit area with respect to a plane orthogonal to the diffusion direction, D is the diffusion coefficient, and Ci is the concentration of the species. The partial differential result of Equation (21) is Equation (22), c1 and c2 are the concentrations of diffusion components at the oxygen-oxide and oxide-metal interfaces, respectively. According to Fick’s law, the diffusion of a species flows from a region of high concentration to a region of low concentration. When the rate is controlled by diffusion, the interface creation process is performed very quickly and it can be assumed that it is in a local thermal equilibrium state. That is, the c1 – c2 is time invariant. As a result, the growth rate coefficient can be summarized as follows.
| (23) |
where Ω is the volume of oxide formed per unit quantity of diffusing species.
3.3 Characteristic Changes and Melting of Metal Oxide
Section 3.3 deals with boundary conditions to be applied to numerical analysis for phase change (melting) of metals. Practically, the metal is in a liquid state after melting and is scattered by high pressure oxygen to become sludge. However, in this paper, in order to focus on the cutting base material itself, only the shape change of the base material is considered, and the molten and scattered metal is not dealt with (assuming it has been removed).
In a metal, the temperature rises and the oxidation proceeds together by the preheating flame and oxidation reaction. Compared to the state before oxidation, the metal oxide changes various material properties, and the melting point also changes. In particular, Wüstite (FeO), which accounts for about 95% of iron oxide in the high-temperature oxidation process, has a melting point that is about 160oC lower than that of conventional iron, and thus melts faster than Fe [16]. The material properties of iron oxide are presented in Table 1.
When the oxidation of the metal is completed and the temperature rises to the melting point, the temperature of the metal does not increase instantaneously. This is a phenomenon in which an object absorbs the latent heat of fusion required before a phase change, and the latent heat of fusion can be expressed as follows.
| (24) |
where m is the mass of the solid and L is the intrinsic latent heat of fusion of the material. Finally, the amount of heat absorbed or released by the material until melting is given as follows:
| (25) |
where Cp is the iron (or iron oxide) heat capacity and ΔT is the temperature change.
The boundary condition for the melting phenomenon of an object can be written as a function of velocity.
| (26) |
where ρm is the density of the metal.
Through the above formula, the melting of the metal is expressed, and the molten metal is scattered by high-pressure oxygen.
4. Interrelationship of the Gas Cutting Mathematical Model
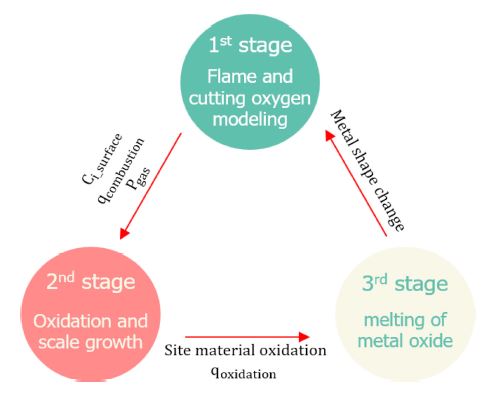
In Chapter 3, the mechanical analysis and mathematical modeling of gas cutting were performed. The mathematical model of each stage is not expressed independently, but mutually influences the mathematical model of the previous or later stage. According to the sequence of the cutting steps, the distribution of species according to the location of the preheating flame and cutting oxygen is calculated by Equations (3) and (4), through Equations (6), (9), (10), (11), and (12), the values for the transfer of heat generated by the combustion reaction and the local oxygen partial pressure can be obtained.
The species distribution, thermal energy (temperature increase of base material), and oxygen partial pressure summarized in Section 3.1 are the main variables in Section 3.2. First, in the case of oxygen partial pressure and temperature, the conditions for the generation of oxides are determined in Equation (13). And the surface concentration, which is the most important variable in Equation (14), is determined based on the distribution of each gas species, and since the other coefficients are functions having temperature as a variable, the temperature also becomes a major variable. In addition, the concentration and temperature (diffusion is a function of temperature) are important variables in determining the growth rate of oxide.
The main results of the process in Section 3.2 are the growth of oxides (oxidation of metal Fe to FexOy) and the heat of reaction arising from the oxidation process. The result also affects the model in Section 3.3. The result of oxide growth determines the material properties of the surface. And the heat of reaction (flame combustion, metal oxidation) calculated in the previous two steps increases the temperature of the metal. After the temperature of the base material reaches the melting point, if the amount of heat accumulates more than the latent heat of fusion, the metal is melted. The melting of the metal causes a shape change, which in turn affects the fluid flow of the 1st stage. Fig. 5 briefly shows what was described above.
5. Conclusion
The gas cutting has been widely used in the existing cutting industry, but unlike the ease of industrial access, analysis from a mechanical point of view has not been performed. In this paper, we organized the gas cutting process based on the relevant dynamics and performed the mathematical modeling for each step. The gas cutting process was divided into three stages: preheating and cutting oxygen spraying, metal oxidation, and metal melting. The thermal energy and partial pressure of metal surface oxygen obtained in the first step affects the growth rate of metal oxides in the second step. In the second step, the oxidation of the metal generates heat of reaction and defines the chemical state of the metal. The temperature increase and property change in the second stage have a decisive effect on the melting phenomenon in the third stage. Finally, the shape of the molten metal affects the first stage flame and oxygen flow. As a result, the antecedent variables occurring in the entire process of gas cutting were summarized so that the coupling between each mathematical model could be finally achieved as a single process. The constructed mathematical model can represent the entire process of a gas cutting. The results of this paper can be used as a basis for building a numerical analysis model in the future.
Acknowledgments
This paper was presented at KSPE Autumn Conference 2022
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korean government (MOTIE) (20201510300320, 방사화된 금속 구조물 해체를 위한 겐트리형 레이저절단-수소연료산소절단을 적용한 하이브리드 고속 절단시스템 개발).
REFERENCES
-
Birks, N., Meier, G. H., Pettit, F. S., (2006), Introduction to the high temperature oxidation of metals, Cambridge University Press.
[https://doi.org/10.1017/CBO9781139163903]

- Khanna, A. S., (2002), Introduction to high temperature oxidation and corrosion, ASM International.
-
Baukal Jr., C. E., (2010), Oxygen-enhanced combustion, CRC Press.
[https://doi.org/10.1201/9781003040781]

- Kim, H. Y., (1994), Study on the characteristics of impinging jet flame. https://scienceon.kisti.re.kr/commons/util/originalView.do?cn=TRKO200200014695&dbt=TRKO&rn=
-
Niziev, V., Nesterov, A., (1999), Influence of beam polarization on laser cutting efficiency, Journal of Physics D: Applied Physics, 32(13), 1455.
[https://doi.org/10.1088/0022-3727/32/13/304]

- Schnick, M., Füssel, U., Zschetzsche, J., (2006), Simulation of plasma and shielding gas flows in welding and cutting arcs with ansys CFX. http://www.modlab.lv/publications/mmp2006/pdfs/143-148.pdf
-
Dal, M., Fabbro, R., (2016), An overview of the state of art in laser welding simulation, Optics & Laser Technology, 78, 2-14.
[https://doi.org/10.1016/j.optlastec.2015.09.015]

-
Arenas, M. J., Hömberg, D., Lasarzik, R., Mikkonen, P., Petzold, T., (2020), Modelling and simulation of flame cutting for steel plates with solid phases and melting, Journal of Mathematics in Industry, 10(1), 1-16.
[https://doi.org/10.1186/s13362-020-00086-0]

-
Thiébaud, R., Drezet, J.-M., Lebet, J.-P., (2014), Experimental and numerical characterisation of heat flow during flame cutting of thick steel plates, Journal of Materials Processing Technology, 214(2), 304-310.
[https://doi.org/10.1016/j.jmatprotec.2013.09.016]

-
Uhlig, H. H., (1956), Initial oxidation rate of metals and the logarithmic equation, Acta Metallurgica, 4(5), 541-554.
[https://doi.org/10.1016/0001-6160(56)90051-7]

-
Chen, R., Yeun, W., (2003), Review of the high-temperature oxidation of iron and carbon steels in air or oxygen, Oxidation of Metals, 59(5), 433-468.
[https://doi.org/10.1023/A:1023685905159]

-
Fontijn, A., Kurzius, S. C., Houghton, J. J., (1973), High-temperature fast-flow reactor studies ofmetal-atom oxidation kinetics, Proceedings of the Symposium (International) on Combustion, 14(1), 167-174.
[https://doi.org/10.1016/S0082-0784(73)80018-9]

-
Lawless, K. R., (1974), The oxidation of metals, Reports on Progress in Physics, 37(2), 231.
[https://doi.org/10.1088/0034-4885/37/2/002]

-
Smentkowski, V., Yates Jr, J., (1990), The adsorption of oxygen on Fe (110) in the temperature range of 90 to 920 K, Surface Science, 232(1-2), 113-128.
[https://doi.org/10.1016/0039-6028(90)90592-V]

-
Wagner, C., (1933), Beitrag zur theorie des anlaufvorgangs, Zeitschrift für physikalische Chemie, 21(1), 25-41.
[https://doi.org/10.1515/zpch-1933-2105]

-
Dieckmann, R., (1982), Defects and cation diffusion in magnetite (IV): Nonstoichiometry and point defect structure of magnetite (Fe3-δO4), Berichte der Bunsengesellschaft für physikalische Chemie, 86(2), 112-118.
[https://doi.org/10.1002/bbpc.19820860205]


Ph.D. candidate in the Department of Electrical Engineering, Changwon National University. His research interest is cutting material engineering.
E-mail: kikigod1039@gmail.com

Ph.D. in the Department of Electrical Engineering, Changwon National University. His research interest is cutting material engineering.
E-mail: iopewq1@gmail.com

Ph.D. course in the Department of Electrical Engineering, Changwon National University. His research interest is cutting material engineering.
E-mail: eell7803@naver.com

Professor in the Department of Electrical Engineering, Changwon National University. His research interest is cutting material engineering.
E-mail: yuik@changwon.ac.kr

CEO of Hanto Cutting System. His research interest is cutting material engineering.
E-mail: hantocut@cnccut.com

Researcher of Hanto Cutting System. His research interest is cutting material engineering.
E-mail: hantocut@cnccut.com

Professor in the Department of Electrical Engineering, Changwon National University. His research interest is cutting material engineering.
E-mail: paku@changwon.ac.kr