십자형 교정체를 이용한 5축 공작기계 회전축의 기하학적 오차 추정에 관한 연구

2.1 회전축 오차와 십자형 교정체 정의

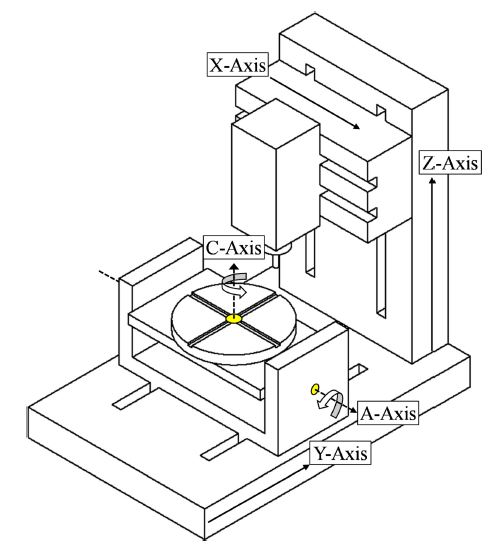
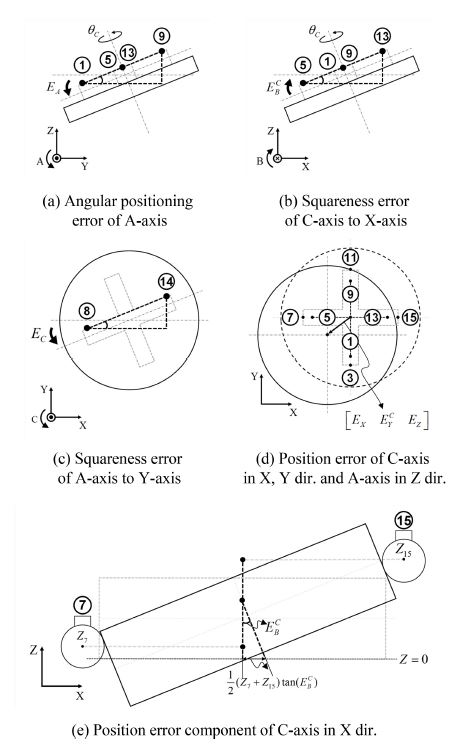
본 논문에서는 Fig. 1에 도시된 것과 같이 A축과 C축 방향으로 회전이 가능한 로터리 테이블이 장착된 TRT (Table-Rotating/Tilting)-CA 타입의 수직형 5축 공작기계를 대상으로 하였다. 5축 공작기계 회전축 오차는 ISO 230-1, 2, 7 [10-12]에 정의되어 있으며, 로터리 및 틸트 각 축 원점의 위치 오차를 나타내는 회전축 중심 오차와 각 직선 이송축 방향으로 회전된 각도 오차를 나타내는 회전축 방향 오차로 구성된다.

Fig. 1

Schematic of a rotating/tilting table of a TRT-CA type machine tool

Ibaraki [3]와 Abbaszadeh-Mir [7]는 5축 공작기계에서 직선 이송축과 회전축, 공작물, 공구에 의하여 발생하는 42개의 오차 중 회전축의 기하학적 오차를 추정하기 위한 8개의 오차를 제안하였다. 본 논문에서는 회전축의 기하학적 오차를 추정하기 위하여 42개의 오차 중 로터리 및 틸트 축의 오프셋 및 직각도 오차 등으로 구성된 8개의 오차를 결정하였으며, 이를 Table 1에 제시하였다. 결정된 오차는 ISO 230-7 [12]에 제시된 축 평균선의 위치오차(Location Errors (Axis Shift) of Axis Average Line)를 의미한다.

Table 1

Errors of associated with a rotating/tilting table

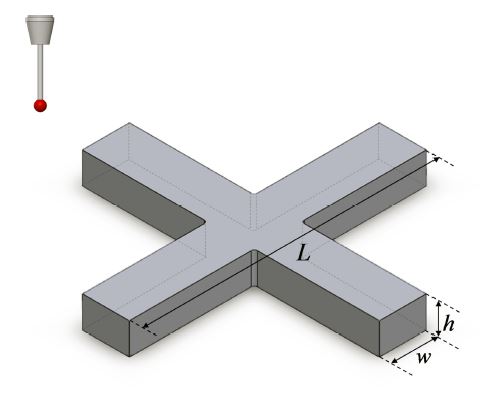
본 논문에서는 Fig. 2와 같은 형상의 십자형 교정체를 활용하여 회전축 오차를 추정하고자 하였다. 교정체의 형상을 활용하여 임의의 회전각에서 회전축 오차 추정이 가능한 일반화된 관계식을 구성함과 동시에 측정점의 개수를 감소시키고자 하였다. 제안된 십자형 교정체는 직육면체 형상의 교정체[3]와 대비하여 단순한 형상은 아니나, 틸트 축의 오차 측정 시 로터리 축을 추가적으로 회전시킬 필요가 없으므로, 측정좌표 사이의 기하학적 관계식을 이용한 회전축 오차를 추정하기에 용이하다. 마지막으로, 단일 교정체를 활용한다는 측면에서 복수개의 교정체를 설치하는 방법[4]과 대비하여 셋업 오차에 따른 회전축 오차 예측 정확도에 대한 영향을 감소시킬 수 있다.

Fig. 2

Schematic of the proposed cross-shaped calibration artifact

2.2 회전축의 기하학적 오차 추정 방법

회전축의 기하학적 오차를 추정하기 위하여 아래와 같이 크게 3단계의 과정으로 측정점들의 위치를 취득하였다.

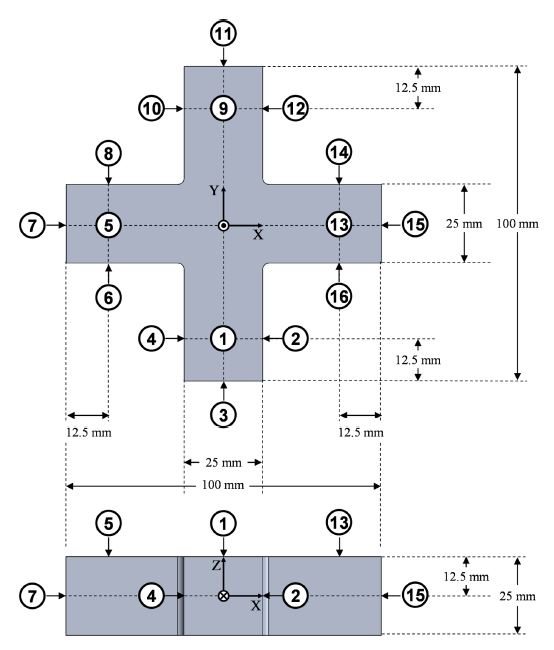
(1) 틸트(A-Axis) 및 로터리 축(C-Axis)의 각도를 모두 0^o로 설정한 상태에서 터치 프로브로 Fig. 3에 제시된 측정점의 위치 좌표들을 취득한다.

Fig. 3

Probing points on the calibration artifact in the first and second probing cycles

(2) 틸트 축을 0^o로 유지한 상태로, 로터리 축의 단위 회전각 φ_C을 고려하여 90^o씩 회전하며 360^o까지 1단계와 동일한 측정점의 위치 좌표를 취득한다.

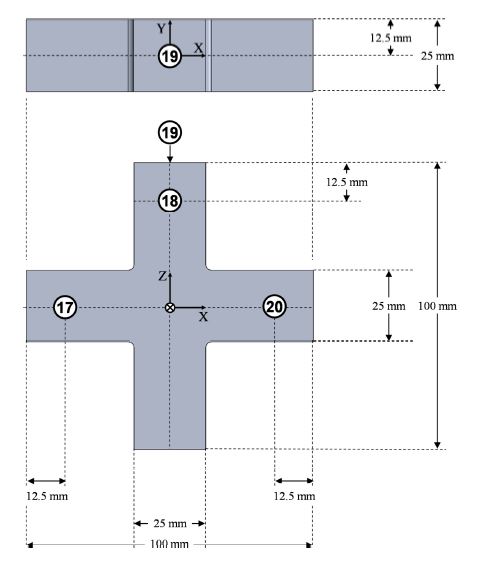
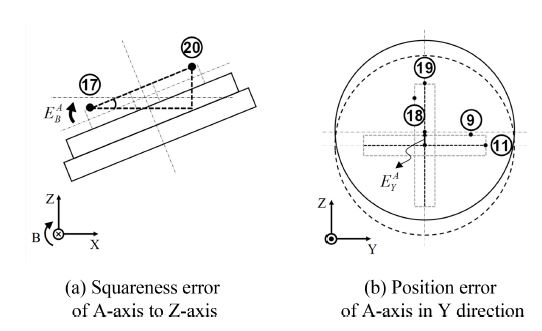
(3) 로터리 축의 각도를 0^o로 유지한 상태로 틸트 축의 단위 회전각 φ_A을 고려하여 틸트 축의 회전각을 +90^o 및 -90^o로 각각 설정하고, Fig. 4에 제시된 4개의 측정점의 위치 좌표들을 추가적으로 취득한다.

Fig. 4

Probing points on the calibration artifact in the third probing cycle

$$ {\mathbf{P}}_n^i$$은 i번째 회전각 n번 측정점에서 취득된 위치 좌표를 의미한다. θ_C, θ_A은 각각 로터리 및 틸트 축의 회전각이며, 식(1)과 식(2)에 의하여 정의된다.

제시된 교정체의 형상과 측정점의 위치 좌표 간의 기하학적 관계를 기반으로 회전축 오차를 추정하기 위한 관계식을 식(3)부터 식(10)과 같이 구성하였다. α축 방향에 대한 오차 성분을 E_α로 표기하며, Table 1에 제시된 회전축의 기하학적 오차 중 B축 및 Y축 방향 오차 성분의 경우 로터리 및 틸트 회전축의 회전각에 따른 측정점 정보가 모두 필요하다. 따라서, B축 및 Y축 방향 오차 성분은 각 회전축에 따라 $$ E_B^C, E_B^A, E_Y^C, E_Y^A$$로 표기한다.

Figs. 3, 4에 제시된 각 측정점의 위치들을 기반으로 Table 1에 제시된 회전축의 기하학적 오차를 추정하였으며, 로터리 및 틸트 축의 회전에 따라 발생할 수 있는 오차 성분들을 추정하기 위한 개념도를 Figs. 5, 6에 제시하였다. 로터리 회전축 회전각 θ_C에서의 A, B축 방향 오차 성분인 $$ E_A,E_B^C$$는 교정체 상면의 측정좌표를 이용하여 구한다. Figs. 5(a)와 5(b)에 나타낸 것과 같이 각각 Y-Z, X-Z 평면상에서 4개의 측정좌표를 통해 정의되는 기울기의 가중 합으로 추정하며, 식(3) 및 식(4)와 같이 구성하였다.

Fig. 5

Schematics for estimating errors by rotating motions

Fig. 6

Schematics for estimating errors by tilting motions

E_C는 틸트 회전축의 Y축 방향 직각도를 추정하기 위한 오차 성분으로, Fig. 5(c)와 같이 18, 20번을 제외한 2n번 측정점들의 위치 좌표들을 이용하여 구한다. 2와 12, 4와 10, 6과 16, 8과 14에 의하여 각각 정의되는 직각 삼각형들의 밑변과 높이의 대소관계를 고려하여 구한 C축 방향 오차의 평균으로 추정하며, 식(5)와 같다.

위치 오차 $$ E_X,E_Y^C$$의 경우 Fig. 5(d)에 제시된 3, 7, 11, 15번 측정점의 X, Y축 방향 평행이동에 의한 오차와 회전 테이블 틸팅으로 인한 오차를 함께 고려하였다. 이를 위하여 해당 측정점들의 X, Y 좌표뿐만 아니라 $$ E_A,E_B^C$$를 반영하였으며, 최종적인 위치 오차는 X, Y축 방향 오차의 가중 합을 활용하여 식(6) 및 식(7)과 같이 표현하였다. 마지막으로 Z축 방향 오프셋 오차 E_Z는 교정체 상면에서 측정한 측정점들의 위치 좌표 중 Z 성분의 평균에서 교정체 높이 h와 터치 프로브의 반경 r을 뺀 값으로 추정할 수 있으며, 식(8)과 같다.

Table 1에 제시된 회전축 오차 중 로터리 회전축과 틸트 회전축 간에서 발생하는 직각도 및 위치 오차를 추정하기 위하여, 틸트 회전축 회전각 θ_A에 따른 오차 성분 $$ E_B^A\mathrm{및}{E}_Y^A$$ 을 추정한다. 터치 프로브와 교정체 간의 간섭이 발생하는 측정점들을 제외하고, 17번, 20번 측정점 사이의 거리와 X축으로부터 두 측정점까지의 거리 차이를 통해 정의된 직각 삼각형 빗변의 기울기를 활용하여 틸트 축의 회전에 따른 B축 방향 오차 성분 $$ E_B^A$$를 추정하기 위한 식(9)를 구성하였다. 틸트 축 회전각에 따른 Y축 방향 위치 오차 $$ E_Y^A$$는 Ibaraki가 제안한 틸트 축의 Y축 방향 위치 오차 추정식[3]을 차용하여 틸트 회전각에 대한 일반식의 형태로 식(10)을 유도하였으며, L은 교정체의 길이를 의미한다.

각 오차 성분들의 평균값을 기반으로 회전축 오차를 추정하는 관계식을 구성하였다. 관계식에서 k_C, k_A는 로터리 및 틸트 회전축에 대한 각각의 회전각 개수를 의미하며 회전축의 구동범위를 고려하여 아래의 식(11)과 식(12)로 정의한다.

추정 대상인 회전축 오차 중에서 회전 축방향 오차 성분들에 의하여 정의되는 회전축 오차는 E_AOA, E_BOA, E_COA, E_BOC가 있으며, 이 중 로터리 회전축과 틸트 회전축 간의 직각도는 E_BOC와 E_BOA의 차로 정의된다. 각 회전축 오차를 추정하기 위한 관계식은 식(13)부터 식(16)과 같다.

회전축 오차 중 위치 오차는 E_XOC, E_YOA, E_ZOA, E_YOC가 있으며, 로터리 회전축과 틸트 회전축 간의 위치오차는 E_YOC–E_YOA로 정의된다. 각각의 위치 오차에 대한 관계식은 식(17)부터 식(20)과 같다.

3.1 측정 시뮬레이션 구성

제시된 회전축 오차 추정 방법의 검증을 위하여 TRT-CA type의 5축 공작기계 구성요소들을 3D CAD S/W를 활용하여 Fig. 7과 같이 모델링하였으며, 다물체 동역학 해석 프로그램인 ADAMS를 이용하여 모델링한 각 구성요소 사이의 구속조건 등을 정의하는 방식으로 5축 공작기계 모델을 구성하였다. 회전축의 구속조건을 이용하여 임의의 회전축 오차를 부여할 수 있도록 하였으며, 직선 이송축의 기하학적 오차는 없는 것으로 가정하였다. 또한, 공작기계에 설정된 공작물 좌표계(Workpiece Coordinates System)의 원점은 로터리 테이블 상면의 중심점에 정의하였다.

Fig. 7

Five-axis machine tool (TRT-CA type) and the proposed cross-shaped calibration artifact

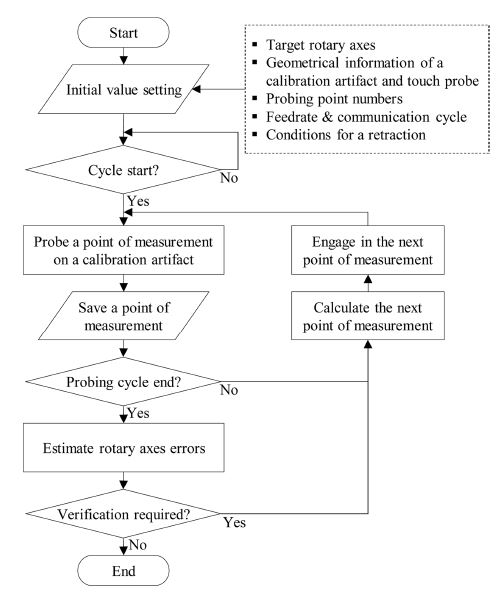
실제 5축 공작기계의 경우 교정체와 터치 프로브 간의 접촉 시 반발력으로 인하여 터치 프로브의 스타일러스가 휘어짐에 따라 측정 오차가 추가적으로 발생할 수 있으나, 본 논문에서는 회전축의 기하학적인 오차를 추정하는 것이 목적이므로 고려하지 않았다. Fig. 8에 제시된 순서도를 기반으로 데이터 통신주기와 이송속도, 십자형 교정체와 터치 프로브의 기하학적 정보 등을 입력변수로 하는 컴퓨터 시뮬레이터를 구성하였다. 구성된 시뮬레이터는 터치 프로브가 십자형 교정체 표면상의 접촉 좌표를 취득할 수 있도록 ADAMS와 MATLAB/Simulink 간의 연동해석을 기반으로 한다.

Fig. 8

Flowchart of the proposed probing cycle process

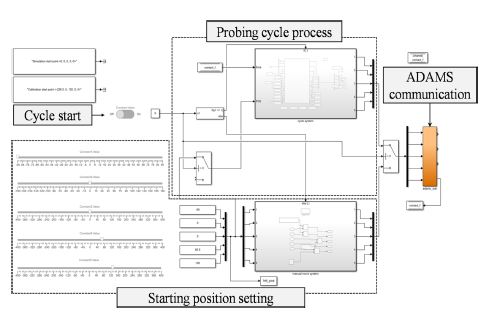
컴퓨터 시뮬레이션 구동 시 각 축의 위치지령은 측정 사이클 과정에서 5축 공작기계 CAD 모델의 회전축 조합을 고려하여 MATLAB 상에 역기구식을 사전에 구성함으로써, 매 통신주기마다 기계좌표계(Machine Coordinates System)로 변환되어 각 직선 이송축 및 회전축 지령이 ADAMS로 전송되는 구조이다(Fig. 9).

Fig. 9

Co-simulation system (MATLAB/Simulink and ADAMS)

터치 프로브를 활용한 접촉 좌표 측정 기능을 구현하기 위하여 ADAMS의 접촉력(Contact Force) 측정 기능을 사용하였다. 입력한 위치지령에서 터치 프로브와 십자형 교정체 사이의 접촉을 판단하고, 접촉이 발생한 좌표를 MATLAB으로 전송하여 저장하는 형태로 측정 과정을 구현하였다.

3.2 회전축 오차 보정을 통한 제시된 방법의 검증

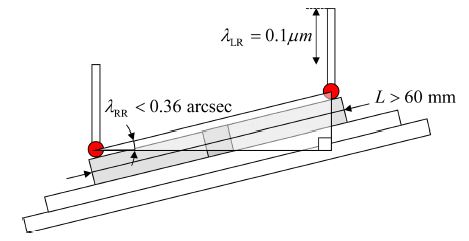
본 논문에서 사용한 컴퓨터 시뮬레이션 환경으로 MATLAB/Simulink에서 생성한 위치지령을 전송하고 ADAMS에서 해석한 터치 프로브와 교정체 간의 접촉 정보를 송수신하는 통신주기는 0.01 msec로 설정하였다. 터치 프로브 선단의 이송속도는 600 mm/min이며, 이송축과 회전축의 분해능은 상용 CNC의 지령단위를 고려하여 각각 0.1 μm, 0.36 arcsec로 설정하였다. 검증에 사용한 십자형 교정체의 길이 L은 Fig. 10에 제시된 것과 같이 이송축의 분해능 λ_LR의 크기가 0.1 μm일 때, 회전축 분해능 λ_RR을 0.36 arcsec 이하 수준으로 확보하기 위해서 식(21)를 만족하여야 한다.

Fig. 10

Schematic for determining the size of a calibration artifact

따라서, 컴퓨터 시뮬레이션에서 활용된 교정체의 길이 L은 100 mm, 높이 h는 25 mm, 너비 w는 25 mm로 설정하였으며, 5축 공작기계 모델링 과정 중에 임의로 부여한 회전축 오차(Random Error)들은 Table 2에 제시된 것과 같다. 전술한 시뮬레이션 조건을 토대로 5축 공작기계에서 회전축 오차를 추정하기 위한 교정체 상의 측정점의 위치 좌표를 도출하였다. 제시된 기하학적 관계식을 적용하여 추정한 회전축 오차와 5축 공작기계 모델링 과정에서 사전에 임의로 부여한 회전축 오차 간의 차이를 비교한 결과를 Table 2에 제시하였으며, 부여된 회전축 오차와 추정된 회전축 오차 간의 차이가 최대 1.7% 이하로 나타나는 것을 확인하였다.

Table 2

Comparison of errors of a rotating/tilting table based on the computer simulation results

제시된 방법으로 추정한 회전축 오차를 기반으로 공작기계 회전축의 보정을 진행하여, 회전축에 대한 유효한 수준의 기하학적 오차 보정 여부를 확인하고자 하였다. 이를 위하여, 추정된 회전축 오차를 기반으로 가공영역 전반에 대한 에러맵(Error Map)을 구성하고 직선 이송축의 이송명령을 지속적으로 보정하는 방법과 CNC 파라미터로 존재하는 각 회전축의 영점 및 각 회전축 중심의 오프셋과 같이 공작기계의 회전축 설정을 보정하는 방법을 각각 수행하였다. 각 직선 이송축의 위치 및 공구 방향 오차로 인하여 발생하는, 이상적인 공구선단과 실제 공구 선단 간의 위치 차이인 공간오차를 계산하기 위하여 가공영역을 300 (가로) × 240 (세로) × 150 (높이) mm의 직육면체 형상으로 가정하였다.

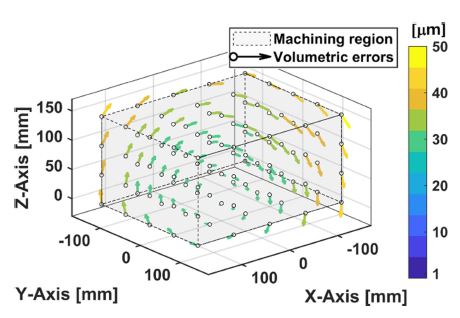
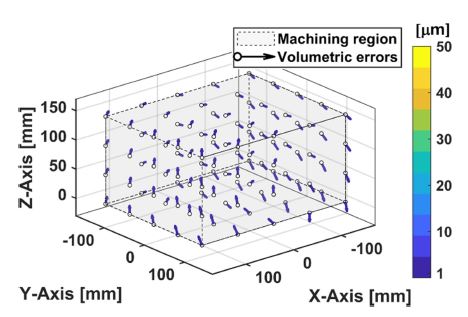
로터리 및 틸트 회전축이 0^o일 때, 보정 전 임의로 부여한 회전축 중심 및 방향 오차로 인하여 가공영역 상에 발생되는 회전축 오차를 도식화한 것을 Fig. 11에 제시하였으며, 가공영역에서의 최대 공간오차의 크기는 50.77 μm로 나타났다. 제시된 방법을 기반으로 추정한 회전축 방향 오차를 이용하여 회전변환 행렬을 구성하고, 회전축 중심 오차만큼 이동하는 동차변환 행렬을 구성하였다. 가공영역 내에서 임의의 위치에 대한 공간오차 계산을 수행하여 에러맵을 구성하였다. 이를 이용하여 직선 이송축의 이송명령을 보정하였을 때, 로터리 및 틸트 회전축 회전각이 0^o에서 예측되는 회전축 오차를 도식화한 것은 Fig. 12와 같다. 구성된 에러맵의 최소 단위는 직선 이송축의 분해능과 같은 수준인 0.1 μm이다. 에러맵을 활용한 회전축의 기하학적 오차 보정 결과 가공영역 상의 최대 공간오차의 크기가 0.08 μm로 감소한다.

Fig. 11

Volumetric errors before compensating errors of rotary axes

Fig. 12

Volumetric errors after compensating errors of rotary axes using the error map

또 다른 보정 방법으로, 상용 CNC에서 파라미터로 제공하는 각 회전축의 영점 및 회전축 중심의 원점 오프셋을 보정하는 방법을 수행하였다. 추정된 회전축 오차들을 기반으로 예측한 교정체 상면의 법선 벡터 n_CRS를 X-Y-Z 오일러 각의 역행렬을 활용하여 식(22)와 같이 추정할 수 있다. ϕ, θ, φ는 각각 순서대로 X, Y, Z 축 회전 시의 회전각 크기를 의미한다. 회전축 오차 보정 시 교정체 셋업 오차를 추가적으로 반영하기 위하여, 관련된 기존의 연구[8,9]에서 활용된 관계식을 참고하여 로터리 테이블의 회전축 방향으로의 셋업 오차인 E_CRS를 식(22)에 추가 반영하였다. 회전축 오차 보정을 위하여 각 회전축의 영점을 식(23)과 식(24)를 활용하여 보정하였다. 원점 오프셋 오차는 회전축 및 교정체 셋업 오차의 원점 오프셋 성분들을 공작물 좌표계에 반영하는 형태로 보정할 수 있다.

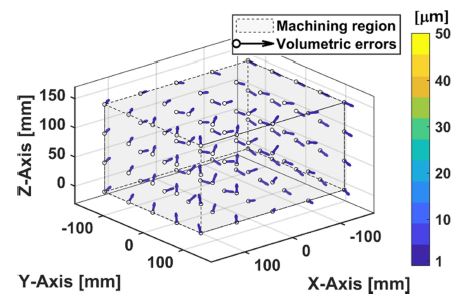
회전축 오차 보정 시 입력 파라미터의 단위는 설정한 CNC의 최소 지령단위와 동일하다. Fig. 13은 로터리 및 틸트 축 회전각의 위치가 각각 0^o일 때 CNC 파라미터만을 보정한 후의 회전축 오차를 추정한 것이며, 가공영역에서의 최대 공간오차의 크기는 0.06 μm로 계산되었다.

Fig. 13

Volumetric errors after parameter compensation of a rotating/tilting table

회전축 오차 보정 전후 및 방식에 따른 최대 공간오차 비교 결과를 Table 3에 제시하였다. 에러맵을 이용한 보정 방법과 CNC 파라미터를 활용한 보정 방법 모두 동등한 수준으로 구현된 것으로 볼 수 있으나, 회전각에 따른 오차 운동(Error Motion)[12]이 회전각의 위치에 따라 비선형적으로 발생한다는 점에서 일반적으로 에러맵 기반의 회전축 오차 보정 방법에 더욱 높은 성능을 기대할 수 있다. 하지만, 본 논문에서 두 보정 방법에 대한 성능 차이가 크지 않게 나타난 이유는 기계장비를 활용한 실험이 아닌 시뮬레이션을 활용한 모의실험 결과를 기반으로 회전축 오차 추정 및 보정을 수행하였기 때문으로 추정된다. 따라서, 제안한 방법을 실제 기계장비에 적용한 결과와 그에 대한 평가는 향후 이어지는 연구에서 다루어질 예정이다. 각각의 보정 방법에 대한 결과와 별개로 5축 CNC 공작기계를 모든 회전축 구동 각도 조합에 따라 독립적인 에러맵을 구성하여 보간하는 방법은 CNC 보간부에 높은 연산부하를 요구할 수 있다는 측면에서 한계가 있다. 이에 반하여 5축 공작기계 회전축에 대한 CNC 파라미터를 활용하여 회전축 오차를 보정하는 방법의 경우, 회전축 오차에 대한 높은 예측 정확도를 확보할 수 있다면 1회의 파라미터 보정으로 에러맵을 활용한 것에 준하는 효과를 기대할 수 있다. 결과적으로, 제안된 방법을 활용하여 두 회전축 오차 보정 시 최대 공간오차의 크기를 모두 99% 이상 감소시켰다는 점에서, 본 논문에 제시된 십자형 교정체를 활용한 5축 공작기계 회전축 오차 추정 방법에 대한 유효성을 확인할 수 있었다.

Table 3

Comparison of maximum volumetric errors