기판에 사전변형률이 인가된 박막의 구조 해석

1. 서론

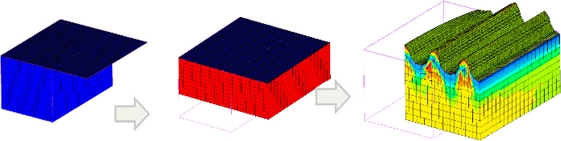
착용형 에너지 소자, 인체 패치형 소자 그리고 디스플레이 소자는 신축성이 있으면 변형이 되더라도 전기적 특성이 유지되어 형태에 제약을 받지 않게 되므로 많은 연구자들의 관심을 받고 있다[1,2]. 신축성을 구현하기 위해서 구조적 방법 또는 재료적 방법의 접근을 하여 개선하는 시도들이 많은 연구자들에 의해서 수행되고 있다[3,4]. 신축성 개선을 위한 구조적 방법으로 웨이브, 주름형 배선, 아일랜드-브리지 구조, 코일, 오리가미 키리가미, 섬유, 균열, 인터락, 사전변형률 등을 이용하는 방법이 있으며, 재료적 방법으로는 나노와이어, 나노파티클, 액체 금속, 전도성 폴리머와 같은 다양한 재료를 도입하고 있다[5,6]. Kim의 연구와 같이 사전변형률의 구조적 방법과 나노와이어의 재료적 방법을 동시에 사용할 수 있다[7]. 신축성 소자의 기판에는 PDMS나 폴리우레탄과 같은 소프트한 재료가 사용된다. 특히 Qi의 연구를 보면 PDMS는 화학적, 열적 안정성, 투명성, 생체적합성이 우수하고 표면 또는 벌크 물성의 개질이 가능하여 신축성 전자소자의 기판 재질로 광범위하게 사용된다[8]. 신축성을 확보하는 대표적 방법으로 Fig. 1과 같이 소프트 기판에 사전변형률 인가 후 하드 박막을 증착하고 기판을 초기상태로 릴리스(Release)시켜 제작하는 방법이 있다[9,10]. 이 방법은 최소한 사전변형률만큼의 신축성을 확보할 수 있는 장점이 있다. 이 방법의 경우 복귀하는 과정에서 주름과 좌굴 현상이 발생하여 이것을 이론적, 수치적으로 분석하는 것이 필요하다. 수치적 분석의 경우 비선형 후좌굴(Post-Buckling) 문제로, 많은 컴퓨팅 자원이 소모되므로 효율적인 전략이 필요하다. Chung과 Cheng의 연구에서는 이론식을 이용하여 단일 박막관점에서 주름현상을 분석하였다[11,12]. Diab은 Ruga Mechanics라는 용어를 도입하였으며 주름의 특성을 예측하였다[13]. Ma는 사전변형률이 인가된 상태에서의 주름의 특성을 이론적으로 분석하였다[14]. 그리고 주름 형성에 관한 연구는 많으나 사전변형률을 확실하게 모사한 사례는 적다. 대부분 Nikaravesh의 연구에서와 같이 사전변형률이 모델링되지 않은 소프트 기판과 하드 박막을 단순 압축만 인가시켜 해석하였다[15]. 그러나 Cao의 연구에서 상용코드인 Abaqus에서 제공하는 Model Change 기능을 이용하여 사전변형률을 모사한 결과를 보여주었으나 다중스텝 및 접촉 등 적용여부와 같은 구체적 정보는 기술되어 있지 않았다[16]. Omairey의 경우 상용코드를 이용하여 전산 균질화 기법을 적용한 사례를 보여주었다[17].

Fig. 1

Procedure for fabricating thin film with pre-strain

본 연구에서는 사전변형률 인가된 박막의 거동을 살펴보고자 한다. 사전변형률의 대표적인 이론적 접근 방법들을 비교 분석하였으며 수치해석적 방법에 있어서 다중 스텝으로 모델링하여 거동을 살펴보고자 한다. 본 연구 대상의 모델은 길이에 비해서 두께가 아주 얇고 변형의 형태가 주기성을 갖기 때문에 주기성을 보이는 부분만 모델링하고 주기경계조건을 인가하는 전산균질화 기법을 이용하였다. 이를 바탕으로 사전변형률 인가 후 박막 거동을 정확히 파악하고 예측하고자 하였다. 또한 사전 변형률 인가에 의한 기계적 거동의 영향을 주는 설계 인자에 대한 영향을 분석하고자 하였다.

2. 이론적 접근

박막에 발생하는 주름의 이론적 접근은 고체역학에 기반을 두고 있으며 20세기 초반에 제시되었다[18,19]. 이론식은 2가지 관점에서 전개할 수 있으며 본 연구에서는 이것들의 특징을 살펴보고자 한다. 그리고 주름도 좌굴 특징을 가지고 있어 용어 정리가 필요하다. 본 논문에서 박막에만 발생하는 사인함수형 변형을 주름이라 하고 기판과 박막에 발생하는 굽힘형 변형은 좌굴이라고 정의하였다. 이론적 검토는 단일 박막의 미분방정식을 이용한 오일러(Euler) 좌굴식이다. 이것은 단일 구조물에 기반을 두는 식이다. 이것은 하부기판을 하부지지하중으로 취급하는 Biot 방법[18]과 하부기판과 박막을 두 개의 박막을 복합재와 같이 등가적으로 취급하는 방법이 있었다[10].

2.1 하부기판을 지지체로 고려한 주름해석(Biot 방법)

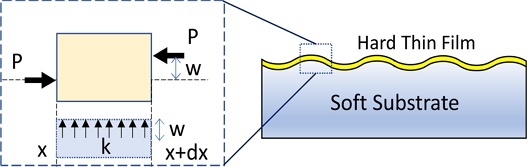
PDMS와 같은 소프트 기판위에 형성된 여러가지 하드 박막에 발생하는 주름을 분석하고자 하였다. 아래와 같은 박막의 미소단위요소에 작용하는 힘들은 Fig. 2와 같으며 이것의 평형식으로부터 식(1)을 얻었다.

$\[ {\overline{E}}_{f}I\frac{d^{4}w}{d{x}^4}+P\frac{d^{2}w}{d{x}^2}+kw=0 \]$

(1)

Fig. 2

Forces of a thin film element on a substrate

식(1)의 첫째 항은 오일러-베르누이 굽힘에 해당하며 둘째 항은 축방향(Axial) 오일러 좌굴하중에 해당한다. 셋째 항은 하부 기판을 탄성 반무한 지지체로 취급한 것인데 하부 기판에 작용하는 힘을 윈클러 모듈러스(Winkler Modulus)를 사용하여 나타냈다. 여기에서 수직변위 w는 x좌표의 함수로서 w(x) = Asin(2πx ⁄ λ)와 같이 진폭 A, 파장 λ를 가지는 사인함수로 가정하였다. 이론식에서 평면변형률 상태로 가정하여 탄성계수는 $$ \overline{E}=\text{E}/\left(1-v^2\right)$$를 사용하였다. $$ {\overline{E}}_f$$는 박막의 탄성계수, $$ {\overline{E}}_s$$는 기판의 탄성계수이다. 그리고 ν는 프와송비(Poisson’s Ratio), I는 I = bh³/12 (h: thickness, b: width)이며 박막의 2차 면적모멘트이다. 넷째항에서 윈클러 모듈러스 k는 $$ k={\overline{E}}_{s}b\text{π}/\lambda $$이다[18]. 식(1)의 해를 구하기 위하여 식(1)의 미분 방정식에 w(x) = Asin(2πx ⁄ λ)를 대입하면 식(2)와 같이 주름현상을 발생시키는 힘 P를 얻을 수 있다.

$\[ P={\overline{E}}_{f}w{\left(\frac{\text{π}}{\text{λ}}\right)}^2+\frac{{\overline{E}}_{s}w}{4}{\left(\frac{\text{π}}{\text{λ}}\right)}^{-1} \]$

(2)

식(2)를 파장(λ)에 관하여 미분(dP/dλ = 0)하면 힘을 최소로 하는 파장(λ)을 식(3)과 같이 구할 수 있다.

$\[ \lambda =2\pi h_f{\left(\frac{{\overline{E}}_f}{\text{3}{\overline{E}}_s}\right)}^{\frac{1}{3}} \]$

(3)

식(3)을 식(2)에 대입하면 주름을 발생시키는 임계하중을 식(4)와 같이 구할 수 있으며 이것으로부터 임계응력과 임계변형률을 식(5)와 식(6)과 같이 얻었다.

$\[ P_c=b{h}_f{\left(\frac{9}{64}{\overline{E}}_f{\overline{E}}_s^2\right)}^{\frac{1}{3}} \]$

(4)

$\[ {\sigma }_c={\left(\frac{9}{64}{\overline{E}}_f{\overline{E}}_s^2\right)}^{\frac{1}{3}} \]$

(5)

$\[ {\epsilon }_c={\frac{1}{4}\left(\frac{{3\overline{E}}_s}{{\overline{E}}_f}\right)}^{\frac{2}{3}} \]$

(6)

그리고 진폭(A)를 얻기 위하여 임계변형률(ε_c)을 제외한 변형률 ε−ε_c를 고려하고 테일러 급수를 적용하면 식(7)을 얻을 수 있어 식(8)과 같이 진폭과 변형률의 관계를 구할 수 있다.

$\[ \epsilon -{\epsilon }_c=\frac{\text{1}}{\text{λ}}{\int }_0^{\lambda }\sqrt{1+{\left(\frac{dw}{dx}\right)}^2}dx-1=\frac{{\pi }^2{A}^2}{{\lambda }^2} \]$

(7)

$\[ A=h_f\sqrt{\frac{\epsilon }{{\epsilon }_c}-1} \]$

(8)

2.2 등가단면계수를 이용한 좌굴 해석

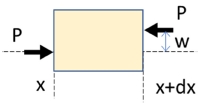
또 다른 방법으로 식(1)에서 첫째항과 둘째항 만을 고려하면 Fig. 3과 같이 된다. 이후 힘의 평형식을 세우고 경계조건을 적용하면 잘 알려진 오일러 좌굴 하중식 식(9)를 얻을 수 있다. 식(9)에 경계조건으로 양끝단의 기울기 0을 적용하면 임계좌굴하중(P_c)은 식(10)이 된다.

$\[ {\overline{E}}_{f}I\frac{d^{4}w}{d{x}^4}+P\frac{d^{2}w}{d{x}^2}=0 \]$

(9)

$\[ P_c=\frac{4{\text{π}}^2\overline{EI}}{L^2} \]$

(10)

Fig. 3

Forces of a thin film (Euler’s approach)

그리고 소프트 기판과 하드 박막의 이중 층으로 구성된 경우 등가굽힘강성을 식(11)과 같이 구할 수 있다.

$\[ \overline{EI}=\frac{{\left({\overline{E}}_f{h}_f^2+{\overline{E}}_s{h}_s^2\right)}^2+4{\overline{E}}_f{h}_f{\overline{E}}_s{h}_s{\left(h_f+h_s\right)}^2}{12\left({\overline{E}}_s{h}_s+{\overline{E}}_f{h}_f\right)}\times \text{b} \]$

(11)

그리고 이 경우 임계변형률은 아래의 식(12)와 같이 전단변형 효과를 포함한 식이 사용되었다[10]. 식(12)의 계수 중에서 1.2는 전단보정계수에 기인한다. 여기서 등가인장강성은 $$ \overline{EA}=\left({\overline{E}}_s{h}_s+{\overline{E}}_f{h}_f\right)\times \text{b}$$이다.

$\[ {\epsilon }_c=\frac{\text{1}}{\text{1+}\frac{1.2P_c}{\overline{G}\left(h_f+h_s\right)}}\frac{P_c}{\overline{EA}} \]$

(12)

하드 박막의 두께가 상대적으로 얇은 경우는 전단효과를 무시할 수 있다. 그러므로 식(12)는 식(13)과 같이 단순화될 수 있다.

$\[ {\epsilon }_c=\frac{P_c}{\overline{EA}}=\frac{4{\text{π}}^2}{L^2}\frac{\overline{EI}}{\overline{EA}} \]$

(13)

3. 기판에 사전변형률이 인가된 박막의 구조해석

3.1 개요 및 경계조건

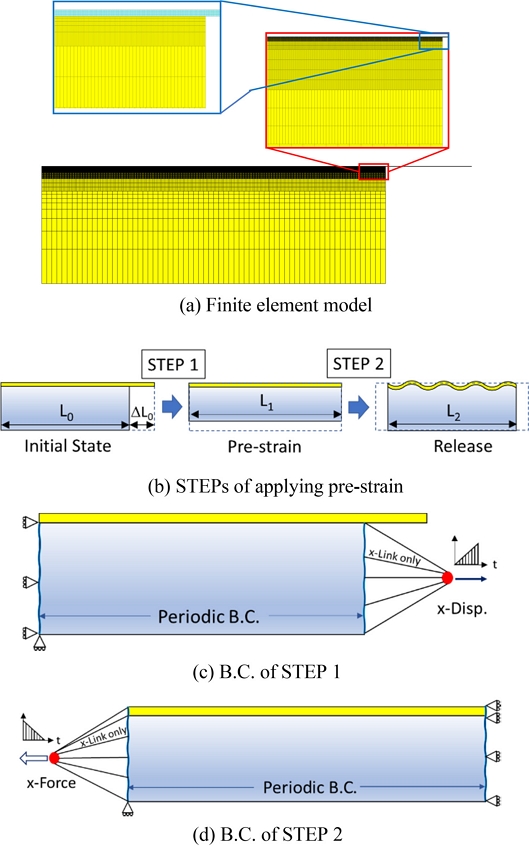
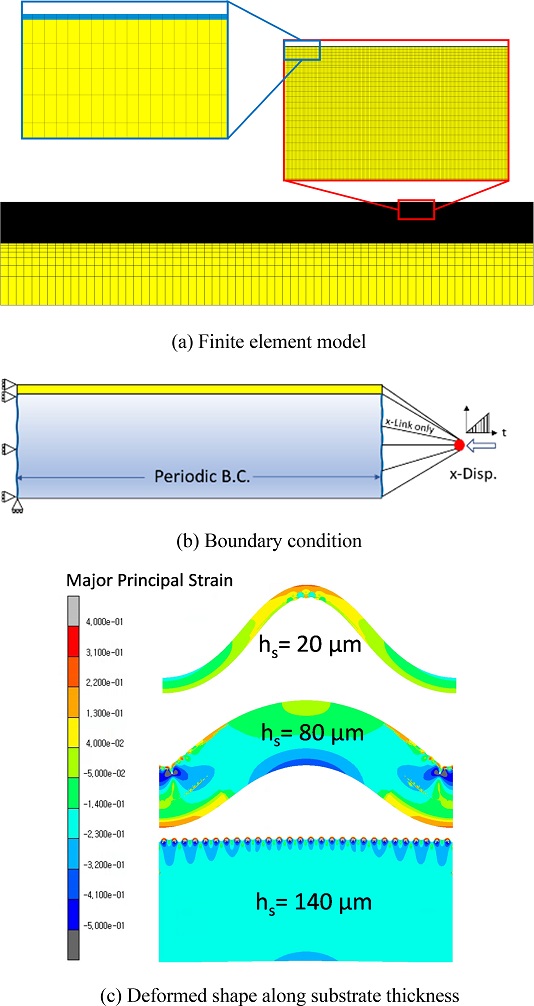
사전변형률이 인가된 소프트 기판 위에 하드 박막을 형성시킨 후 발생하는 후좌굴(Post-Buckling) 거동을 분석하고자 하였다. 후좌굴 거동에서 강성의 크기가 줄어들어 수치적으로 수렴하지 않기 때문에 비선형 전문 해석코드인 MSC/MARC를 활용하였다. 해석모델 요소의 크기는 예상되는 파장의 1/8보다 작게하여야 파장의 형태에 왜곡이 생기지 않는다. 해석모델의 최소 요소 사이즈는 10 nm이며 Fig. 4(a)와 같이 204,049개의 절점과 449,798개의 4절점 평면변형률 요소로 구성되었다. 실제 제작공정과 같게 모사하려고 Fig. 4(b)와 같이 단계 1(사전변형률 단계)과 단계 2(릴리스 단계)를 구분하여 두 개의 단계로 나누어 경계조건을 인가하였다. Fig. 4(c)의 사전변형률 단계에서는 소프트 기판의 왼쪽 면을 구속하고 오른쪽 면을 한 점으로 링크(Link)시킨 후 링크된 한 점에 인장변형을 증가(Ramp-Up)시키며 작용하였다. Fig. 4(d)의 릴리스 단계에서 사전변형률이 인가된 소프트 기판과 하드 박막의 접촉면은 인위적으로 접합되며 이전 단계와는 반대로 오른쪽 면을 구속하고 박막과 기판의 왼쪽 면이 한 점으로 링크되고 링크된 한 점에 하중을 인가하였다. 상세하게는 이전단계에서 인장변형을 인가할 때 얻어지는 반력은 기판과 박막 모두에 작용하며 그 크기는 감소(Ramp Down)되도록 부가하였다. 해석모델은 길이에 비해서 두께가 아주 얇고 변형의 형태가 주기성을 갖기 때문에 주기성을 보이는 부분만 모델링하는 전산 균질화 기법을 적용하였다. 즉, 해석모델의 좌우 끝단에 주기경계조건(Periodic B.C.)을 주어 해석모델이 전체의 거동을 대표할 수 있도록 하였다. 해석과정에서 사전변형률 인가 후 임계하중 이상의 하중이 박막에 작용되면 불안정성(Instability)으로 좌굴이 발생하여 사인함수형 변형이 유발되는데 이것은 해석모델의 불완전성(Imperfection)에 매우 민감한 영향을 받는다. 본 연구에서는 왼쪽 크들 중의 극히 일부를 제거하여 x 방향 구속을 풀어준 부분을 만들어 의도적으로 불완전성을 만들었다. 초기 길이 L₀는 408 μm, 사전변형률 인가 후 길이 L₁은 510 μm이다.

Fig. 4

FE model, STEPs and boundary condition

3.2 박막의 탄성계수에 따른 주름 특성

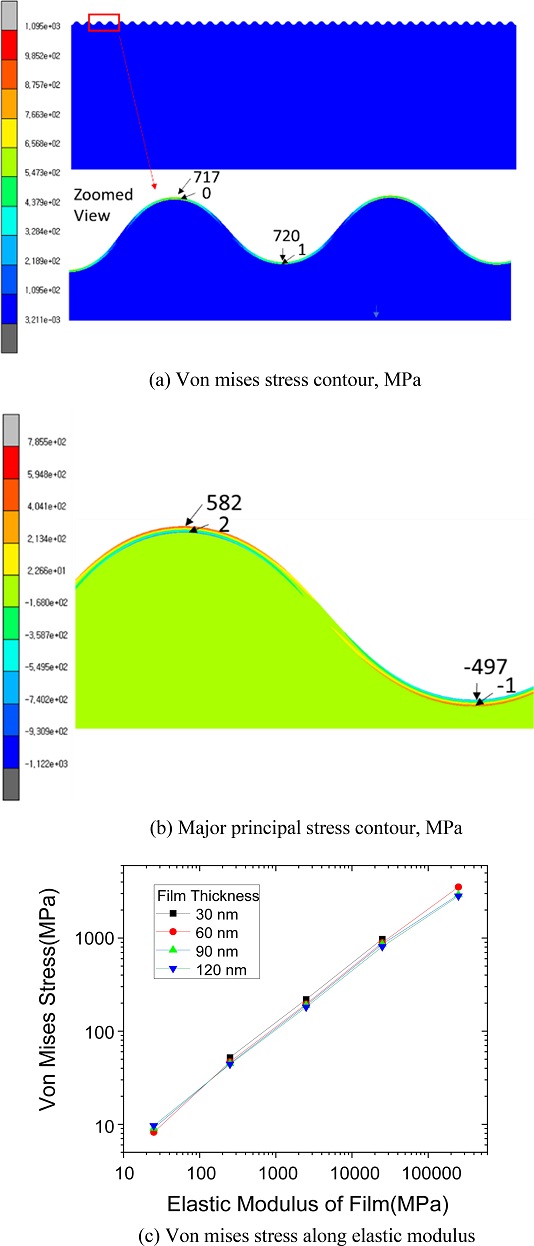
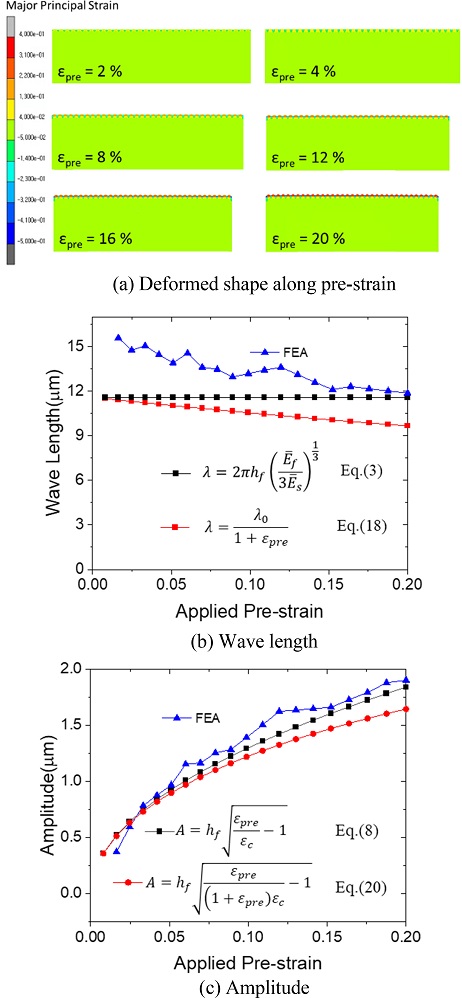
기판의 재료는 흔히 사용되는 PDMS를 채택하였으며 그 탄성계수는 2.5 MPa이다. Figs. 5, 6, 7, 8에서 기판 두께는 140 μm이고 20%의 사전변형률이 인가된 경우의 해석결과이다. Figs. 5(a), 5(b)에서 박막의 두께는 120 nm이고 박막의 탄성계수는 25 GPa이다. 하드 박막은 초기에는 단순 압축 변형을 하다가 하드 박막의 하중이 임계하중을 넘어서면 Fig. 5(a)와 같은 사인함수 형상의 변형이 나타난다. Fig. 5(a)의 미제스 응력 값은 주름의 피크와 밸리 위치에서 거의 같은 값을 형성하고 있으며 두께 방향으로 꼭대기 위치에서만 응력 값이 크고 바닥의 위치에서는 응력이 거의 작용하지 않음을 나타낸다. Fig.5(b)의 주응력을 보면 피크 위치에는 인장 응력이 밸리 위치에는 압축 응력이 작용하고 있다. 마찬가지로 꼭대기 위치에서만 응력이 작용하고 있다. 그리고 탄성계수가 25,000 MPa인 경우 1 GPa 이상의 값을 가질 수 있어 소성변형이 발생할 수 있다. 그렇기 때문에 응력 값을 낮추거나 소성변형이 되더라도 파단되지 않도록 하여야 한다. 그리고 Fig. 5(c)의 미제스 응력을 보면 응력 값에 관계하는 주름의 주요 변수는 박막의 탄성계수이며 박막의 두께의 영향은 매우 작음을 보여준다.

Fig. 5

Stress results of a thin film

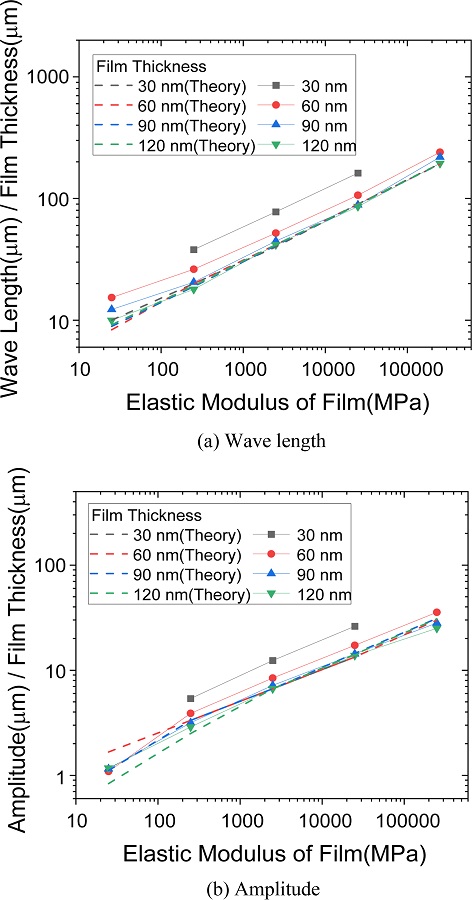
Fig. 6에 사전변형률에 의해 발생한 주름의 파장과 진폭의 이론식 계산결과와 유한요소해석 결과를 박막의 탄성계수에 따라 나타냈다. 그래프에서 파장과 진폭은 박막의 두께로 나누어서 정규화(Normalization)하였다. 박막의 파장과 진폭은 식(3), 식(8)과 같이 박막의 탄성계수 크기에 비례 관계에 있다. 이론식과 해석의 결과는 이러한 관계를 잘 따르고 있다. 박막 두께가 30, 60 nm인 경우 이론식과 해석의 결과 차이가 다소 나고 있다. 그 원인은 유한요소모델의 요소크기로 분석된다. 현재 요소크기는 191 nm이며 이것의 최소 6분할 이상이 필요하나, 모델의 요소 크기 축소는 전체 요소수의 급격한 증가를 가져와 엄청난 컴퓨팅 자원이 필요하므로 이는 후속연구에서 보완하고자 한다. 그리고 박막 두께 30 nm의 경우 탄성계수의 값이 25, 250,000 MPa일 경우에는 주름이 형성된 변형모습이 나오지 않았는데, 그 원인으로 역시 유한요소모델의 요소크기에 기인하는 것으로 분석된다.

Fig. 6

Wave length and amplitude along elastic modulus

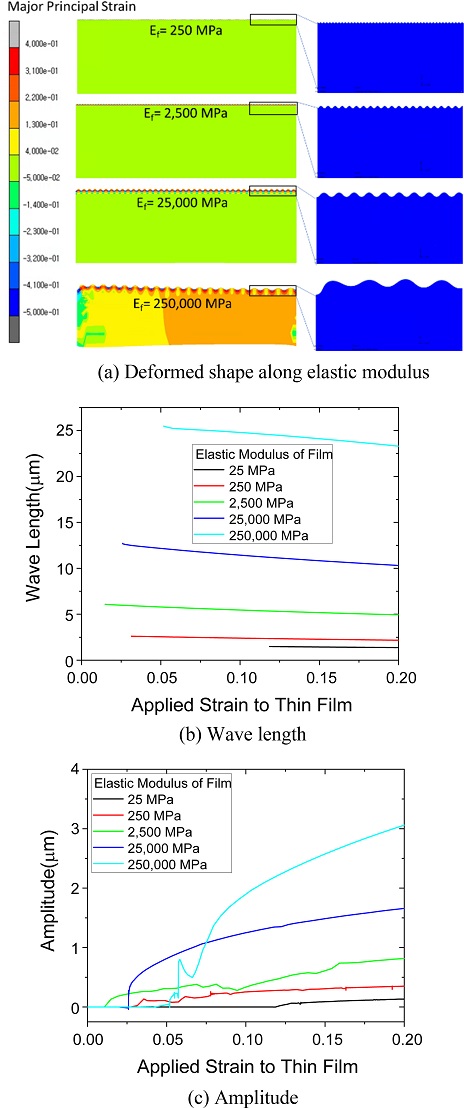
위의 결과 중에서 하드 박막의 두께가 120 nm일 때의 해석 결과를 Fig. 7에 나타냈다. 사전변형률은 20%이며 하드 박막에 인가되는 변형률의 증가에 따라 주름의 파장과 진폭 변화 결과를 보여준다. Fig. 7(a)을 보면 박막의 탄성계수 25,000 MPa까지는 기판이 박막의 거동에 큰 영향을 주지 않는다. 그렇지만 하드 박막의 탄성계수 250,000 MPa에서는 기판의 변형률이 균일하지 않아 기판이 하드 박막에 영향을 주고 있음을 확인할 수 있다. Figs. 7(b), 7(c)의 결과를 보면 하드 박막에 발생하는 주름의 파장과 진폭은 박막의 탄성계수의 크기에 비례하는 결과를 그대로 보여준다. Fig. 7(b)에는 박막에 좌굴이 발생하여 사인함수 형상이 발생한 시점 이후의 결과만을 기록하였다. 파장의 크기는 사전변형률이 증가함에 따라 반비례하여 완만하게 감소하고 있다. 그리고 Fig. 7(c)의 결과를 보면 좌굴 발생 이후 진폭은 사전변형률에 비례하여 증가하고 있다.

Fig. 7

Thin film behavior along elastic modulus

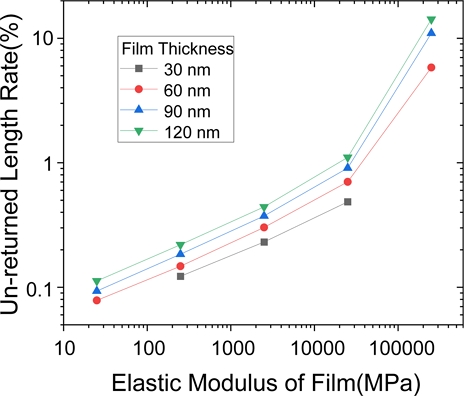
본 연구와 같이 본 연구와 같이 단계 1에서 소프트 기판만의 사전변형률에 의해 발생한 변형에너지가 단계 2의 릴리스 단계에서 소프트 기판에 추가된 하드 박막의 변형에도 사용된다. 그렇기 때문에 최종 변형된 길이는 기판의 초기 상태로 완벽하게 회복하지 못하고 초기 길이보다 약간 크게 되는 잔류 변형이 생기게 된다. 이것의 비회복률(Un-Returned Length Rate, URLR)을 URLR = (L₂-L₀)/L₀×100으로 정의하고 이것의 계산결과를 Fig. 8에 나타냈다. 결과를 보면 박막의 탄성계수가 250,000 MPa인 경우는 10%까지 URLR이 생길 수 있음을 확인하였으며 이것을 줄이기 위해서는 소프트 기판의 두께를 증가시켜 전체적으로 증가된 변형에너지를 확보하는 것이 필요하다.

Fig. 8

Un-returned length rate

3.3 기판 사전변형률과 기판 두께에 따른 주름 특성

Fig. 9에서 하드 박막의 탄성계수는 75,000 MPa, 소프트 기판 두께는 140 μm이다. 단계 1에서 소프트 기판에 1-20%만큼 사전변형률을 각각 인가하면 단계 2에서 이에 따른 하드 박막에 주름이 발생되는데 사전변형률을 20개 구간으로 나누었으며 마지막 최종 릴리스가 완료된 이후의 결과를 이론해와 함께 Fig. 9에 나타냈다. Fig. 9에서 사전변형률이 커지면 하드 박막에 인가되는 변형이 커지며, Fig. 9(a)에서처럼 하드 박막의 변형률이 증가하여 릴리스 이후 최종변형길이 L₂의 크기가 작아진다. 그리고 Figs. 9(b)와 9(c)의 결과를 보면 하드 박막의 파장과 진폭의 해석결과는 이론식과 정량적으로 약간의 차이가 있으나 정성적 경향은 같다. 파장의 해석결과는 식(18)과 같이 변형률의 크기에 반비례하고 있다. 진폭의 해석결과는 파장의 결과와 유사한 경향을 보여준다. 이론식과의 정량적 차이는 요소 크기, 접촉 등 해석적 요인이 원인으로 예상된다.

Fig. 9

Thin film behavior along pre-strain value

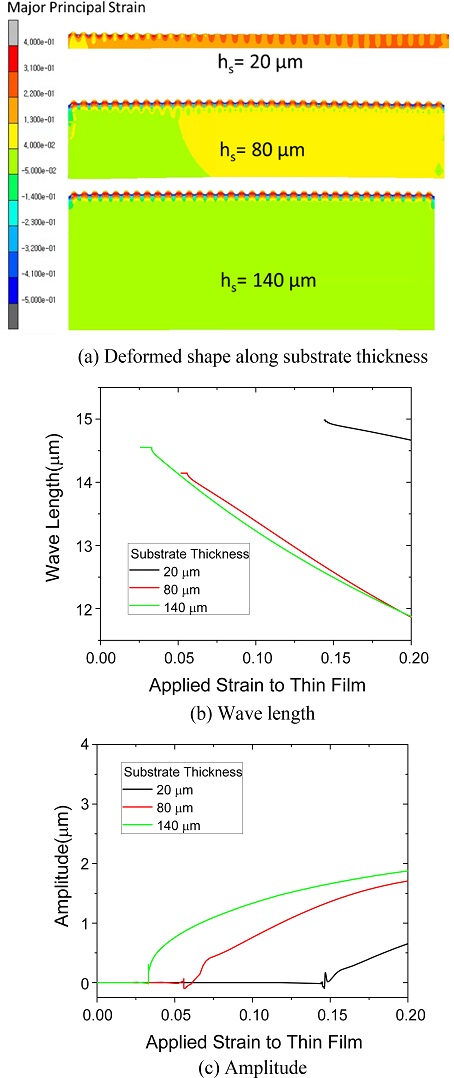
Fig. 10에서 탄성계수 75,000 MPa인 박막에 대하여 기판의 두께를 20, 80, 140 μm으로 변화시키며 기판 두께 효과를 분석하였다. 앞에서와 마찬가지로 사전변형률에 의해 하드 박막의 변형률이 20% 인가되도록 하였으며 하드 박막 변형률 증가에 따라 나타나는 순차적 결과를 Fig. 10에 나타냈다. Fig. 10(a)를 보면 기판의 두께가 감소하면 릴리스 이후 최종변형길이 L₂의 길이가 증가한다. 이는 하드 박막의 변형률이 20%로 동일한 상태에서 소프트 기판의 두께가 감소하면 변형에너지가 그만큼 감소하므로 하드 박막의 변형량도 감소하게 된다. 그리고 주목할 만한 특징으로 소프트 기판의 두께가 20 μm인 경우에도 단계 2에서 좌굴이 발생하지 않았다는 것이다. 이는 기판에 사전변형률이 인가된 경우 최소한 사전변형률이 회복되는 단계에서는 좌굴이 발생하지 않는다고 볼 수 있다. 본 연구의 사례를 벗어나는 경우 좌굴이 발생할 가능성을 배제할 수 없다고 하지만 본 연구의 범위내에서 좌굴이 발생하지 않았음을 확인하였다. 그리고 비교를 위하여 Appendix에 사전변형률이 인가되지 않았을 경우의 거동을 분석하였다. 본 Appendix의 결과를 보면 사전변형률을 인가한 경우 다중스텝으로 나누어 해석한 결과와 변형 모습에서 차이가 있음을 알 수 있었다.

Fig. 10

Thin film behavior along substrate thickness

4. 결론

본 연구에서는 사전변형률이 인가된 기판에 의한 박막 주름과 좌굴의 이론식을 살펴보고 유한요소해석을 이용한 수치해와 비교하였다. 이론적 수식의 경우 기판을 반무한 지지체로 취급하여 박막의 힘의 평형을 고려하는 방법과 소프트 기판과 하드 박막을 하나의 등가박막으로 간주하여 오일러 좌굴로 취급하는 방법이 있다. 오일러 좌굴의 박막이 상대적으로 얇은 경우 전단효과를 무시할 수 있어 이를 반영한 이론식을 제시하였다. 그리고 비선형 유한요소해석을 통하여 실제와 같이 두 개의 단계로 나누어서 모델링하였으며 전산균질화 기법을 적용하였다. 이론식과 수치해석에서 박막의 탄성계수, 기판의 두께, 및 사전변형률 등의 인자에 따른 박막의 파장, 진폭, 응력, 변형률 등의 특성에 관한 결과를 얻었다. 주름의 파장과 진폭의 경우 이론식과 수치해가 어느 정도 잘 일치하는 결과를 보여주고 있다. 해석결과를 보면 사전변형률을 이용하는 경우 파장 및 진폭의 주요 인자는 탄성계수이며 기판의 두께가 20 μm로 얇아지더라도 좌굴이 발생하지 않고 원래의 상태로 복귀하는 특징을 확인할 수 있었다. 기판에 사전변형률이 인가된 경우 최소한 사전변형률이 회복되는 단계에서는 거의 좌굴이 발생하지 않는다고 볼 수 있다. 그리고 기판이 초기 상태로 완벽하게 회복하지 못하는데 이것은 박막의 탄성계수가 틀수록 잔류변형량이 커지므로 이를 방지하기 위해서는 기판의 두께를 증가시키는 것이 필요하다. 이와 같이 본 연구에서 제시한 결과는 사전변형률이 인가된 신축성 소자의 기계적 거동을 정확하게 예측 및 설계할 수 있어 신축성 소자의 개발 및 응용에 있어 설계 가이드를 제공할 수 있다.

Acknowledgments

본 연구는 산업통상자원부 산업기술혁신사업의 일환인 “1 mm 이하 곡률반경을 가지는 신축 디바이스용 50% 이상의 형태 가변이 가능한 점접착소재 개발(No. 20011317)” 사업의 지원과 산업통상자원부 소재부품 기술개발사업의 일환인 “스트레처블 디스플레이용 고전도/초탄성 전극 소재 및 구조체 기술 개발(No. 20017558)” 사업의 지원에 의한 것입니다. 그리고 고려대 홍문표 교수님, 김상일 교수님, 송준호 교수님, 이긍원 교수님의 도움에도 감사드립니다.

REFERENCES

• Ahn, J.-H., Je, J. H., (2012), Stretchable electronics: Materials, architectures and integrations, Journal of Physics D: Applied Physics, 45, 103001. [https://doi.org/10.1088/0022-3727/45/10/103001]
• Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. W., Whitesides, G. M., (1998), Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer, Nature, 393, 146-149. [https://doi.org/10.1038/30193]
• Rogers, J. A., Someya, T., Huang, Y., (2010), Materials and mechanics for stretchable electronics, science, 327(5973), 1603-1607. [https://doi.org/10.1126/science.1182383]
• Kim, D.-H., Lu, N., Huang, Y., Rogers, J. A., (2012), Materials for stretchable electronics in bioinspired and biointegrated devices, MRS Bulletin, 37(3), 226-235. [https://doi.org/10.1557/mrs.2012.36]
• Lang, W., Jakobs, F., Tolstosheeva, E., Sturm, H., Ibragimov, A., Kesel, A., Lehmhus, D., Dicke, U., (2011), From embedded sensors to sensorial materials-The road to function scale integration, Sensors and Actuators A: Physical, 171(1), 3-11. [https://doi.org/10.1016/j.sna.2011.03.061]
• Wu, W., (2019), Stretchable electronics: Functional materials, fabrication strategies and applications, Science and Technology of Advanced Materials, 20(1), 187-224. [https://doi.org/10.1080/14686996.2018.1549460]
• Kim, A., Ahn, J., Hwang, H., Lee, E., Moon, J., (2017), A pre-strain strategy for developing a highly stretchable and foldable one-dimensional conductive cord based on a Ag nanowire network, Nanoscale, 9, 5773-5778. [https://doi.org/10.1039/C7NR02116J]
• Qi, D., Zhang, K., Tian, G., Jiang, B., Huang, Y., (2021), Stretchable electronics based on PDMS substrates, Advanced Materials, 33(6), 2003155. [https://doi.org/10.1002/adma.202003155]
• Khang, D.-Y., Jiang, H., Huang, Y., Rogers, J. A., (2006), A stretchable form of single-crystal silicon for high-performance electronics on rubber substrates, Science, 311(5758), 208-212. [https://doi.org/10.1126/science.1121401]
• Wang, S., Song, J., Kim, D.-H., Huang, Y., Rogers, J. A., (2008), Local versus global buckling of thin films on elastomeric substrates, Applied Physics Letters, 93(2), 023126. [https://doi.org/10.1063/1.2956402]
• Chung, J. Y., Nolte, A. J., Stafford, C. M., (2011), Surface wrinkling: A versatile platform for measuring thin-film properties, Advanced Materials, 23(3), 349-368. [https://doi.org/10.1002/adma.201001759]
• Cheng, H., Song, J., (2014), A simply analytic study of buckled thin films on compliant substrates, Journal of Applied Mechanics, 81(2), 024501. [https://doi.org/10.1115/1.4025306]
• Diab, M., Zhang, T., Zhao, R., Gao, H., Kim, K.-S., (2013), Ruga mechanics of creasing: From instantaneous to setback creases, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 469(2157), 20120753. [https://doi.org/10.1098/rspa.2012.0753]
• Ma, Y., Xue, Y., Jang, K.-I., Feng, X., Rogers, J. A., Huang, Y., (2016), Wrinkling of a stiff thin film bonded to a pre-strained, compliant substrate with finite thickness, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 472(2192), 20160339. [https://doi.org/10.1098/rspa.2016.0339]
• Nikravesh, S., Ryu, D., Shen, Y.-L., (2020), Instabilities of thin films on a compliant substrate: Direct numerical simulations from surface wrinkling to global buckling, Scientific Reports, 10(1), 5728. [https://doi.org/10.1038/s41598-020-62600-z]
• Cao, Y., Hutchinson, J. W., (2012), Wrinkling phenomena in neo-Hookean film/substrate bilayers, Journal of Applied Mechanics, 79(3), 031019. [https://doi.org/10.1115/1.4005960]
• Omairey, S. L., Dunning, P. D., Sriramula, S., (2019), Development of an ABAQUS plugin tool for periodic RVE homogenisation, Engineering with Computers, 35(2), 567-577. [https://doi.org/10.1007/s00366-018-0616-4]
• Biot, M. A., (1937), Bending of an infinite beam on an elastic foundation, 4(1), A1-A7. [https://doi.org/10.1115/1.4008739]
• Bazant, Z. P., Cedolin, L., (2003), Stability of structures: Elastic, inelastic, fracture and damage theories, Dover Publications, Inc..