DED 공정을 이용한 직선형 손상부 보수 시 기저부 끝단 길이와 경사각에 따른 보수부 인근 잔류 응력 및 변형 특성 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The design of a substrate greatly affects the residual stress distribution and the deformation behavior of the repaired region by a directed energy deposition (DED) process. The objective of the present study was to investigate effects of edge length and slope of the substrate on residual stress and deformation characteristics in the vicinity of the repaired region for the repair of the straight damaged region using a DED process. Two-dimensional finite element analysis (FEA) was carried out using SYSWELD. Materials of the substrate and deposited powders were AISI 1045. The maximum residual stress during the deposition decreased when the edge length of the substrate increased, but increased when the slope of the substrate increased. The residual stress after a cooling state increased when the edge length and the slope increased. The displacement of the specimen increased when the slope of the substrate augmented. Finally, the methodology to select a proper edge length and slope of the substrate are discussed in this study.
Keywords:
Directed energy deposition, Edge length, Slope, Residual stress characteristics, Deformation characteristics키워드:
에너지 제어형 용착 공정, 끝단 길이, 경사각, 잔류 응력 특성, 변형 특성1. 서론
21세기 현재 4차 산업 혁명의 기술적 전환기를 맞이하고 있는 가운데 기술의 발전과 함께 환경 문제와 자원 재활용에 대한 관심이 증가하고 있다[1]. 이러한 사회적 경향에 따라 최근 적층제조(Additive Manufacturing, AM) 공정을 이용한 손상된 기계부품의 보수 및 개조를 통하여 원형 제품보다 향상된 제품으로 제작하는 재제조(Remanufacturing)를 위한 연구가 전세계적으로 활발하게 진행되고 있다[2,3]. 재제조 공정을 손상 기계 부품에 적용한 경우 부품의 수명을 향상시킴과 동시에 재료 소모량을 절감시켜 환경 문제 해결과 자원 재활용이 가능하다[4]. 이로 인하여 금속 적층 제조 공정을 이용한 불규칙한 손상이 포함된 노후화된 산업 기계 부품의 재제조를 위한 연구가 시작되고 있다[5].
적층 제조 공정은 선 대 선(Line-by-line) 또는 면 대 면 Layer-by-layer) 적층 기법을 이용하여 3차원의 형상의 제품을 제작하는 공정이다[6,7]. 에너지 제어형 용착(Directed Energy Deposition, DED) 공정은 산업적으로 활용도가 높은 금속 적층 제조 공정 중 하나이다. DED 공정은 고밀도의 에너지원을 사용하여 금속 기저부에 용융지를 생성한 후 금속 분말을 공급하여 금속 기저부위에 적층을 하여 제품을 제작하는 방식이다[5,7,8]. DED 공정은 적층을 위한 기저부 형상의 자유도가 높아 기계 부품의 보수 및 수리에 널리 활용되고 있다[5,7-9]. 그러나 DED 공정에서는 고밀도의 에너지원이 급속 이동함으로써 적층부 인근에 급속 가열과 급속 냉각 현상이 발생한다. 반복되는 급속 가열과 급속 냉각 이력으로 인하여 적층부 인근에 잔류 응력이 발생하며, 이 잔류응력은 DED 공정으로 제작된 제품에 결함을 발생시키는 주된 원인이 된다[6-9]. 그러므로, DED 공정을 이용한 기계부품 손상부 보수를 위해서는 적층 조건, 적층 전략, 기저부 형상 설계 및 적층부 형상 설계 등에 따른 보수부 인근의 잔류 응력 특성 변화에 대한 분석이 필요하다[7,8,10-17].
Kim 등은 DED 공정으로 탄소강인 AISI 1045 기저부 위에 AISI 1045 분말을 적층하여 보수할 때, 기저부 경사각과 적층부 형상이 보수 인근의 잔류 응력 및 변형 특성에 미치는 영향에 대해서 해석적으로 고찰하였다[7]. Hua 등은 유한 요소 해석(Finite Element Analysis, FEA)을 이용하여 레이저 출력, 빔 직경 및 이송 속도가 단일 비드 적층 시 발생하는 잔류 응력에 미치는 영향성을 분석하였다[10]. Lei 등은 FeCrNiCu 합금 분말을 기저부 위에 레이저 클래딩(Cladding)하여 박벽형 블레이드를 보수하기 위해 3차원 FEA로 보수부 인근의 열전달 및 잔류응력 특성 변화를 분석하고, 적층 실험을 통하여 보수 제품의 기계적 특성을 고찰하였다[11]. Oh 등은 그루브 형상의 기저부에 DED 공정을 이용한 시편 보수 시 보수부와 기저부의 경계에 발생하는 기계적/재료적 특성을 실험적으로 분석하였다[12]. Zhang 등은 얇은 두께를 가지는 파이프 형상의 제품을 DED 공정으로 적층 시 발생하는 열전달 및 잔류응력 특성을 열-기계연계 해석으로 고찰하였다[13]. Lee 등은 원형 형상 부품의 키 부분을 보수하기 위한 기저부 형상 설계 및 적층 기법에 대해서 실험적으로 고찰하였다[14]. Kim 등은 DED 공정을 이용하여 기저부 경사각 및 기저부 깊이에 따른 얇은 층 적층 수행 시 발생하는 잔류 응력 특성을 FEA를 통하여 분석하였다[15]. Urbánek 등은 DED 공정을 이용하여 제조된 허니컴(Honeycomb) 형상 제품의 변형 특성 변화를 열-기계 연계 해석을 통하여 예측하였다[16]. Fabian 등은 기저부 경사각 45° 형상의 사다리꼴 홈을 가지는 시편에 DMD (Directed Metal Deposition) 공정을 이용하여 보수하였을 때 결합부 인근의 접합 특성을 실험적으로 고찰하였다[17].
선행 연구들의 고찰을 통해서 기저부 설계에 따른 적층부 인근의 열-기계 특성 변화 고찰에 대한 많은 연구들이 시작되고 있는 것을 알 수 있었다. 기저부 설계의 경우 다양한 형상 변수가 있으며, 이들 형상 변수 조합에 의하여 보수 인근의 잔류 응력과 변형 특성이 현저히 달라진다.
이 연구에서는 DED 공정을 이용한 직선형 손상부 보수 시기저부 끝단 거리와 경사각에 따른 보수부 인근 잔류 응력 및 변형 특성 변화를 2차원 FEA를 통하여 고찰하였다. 4가지 기저부 끝단 길이와 2가지 경사각에 따른 보수 제품의 잔류 응력 및 변형 특성 변화를 분석하였다. 최종적으로 보수 제품의 잔류 응력과 변형 측면에서 적절한 기저부 끝단 길이와 경사각 선정 방법에 대하여 고찰하였다.
2. 2차원 유한 요소 해석
2.1 기저부 형상 설계 및 해석 모델
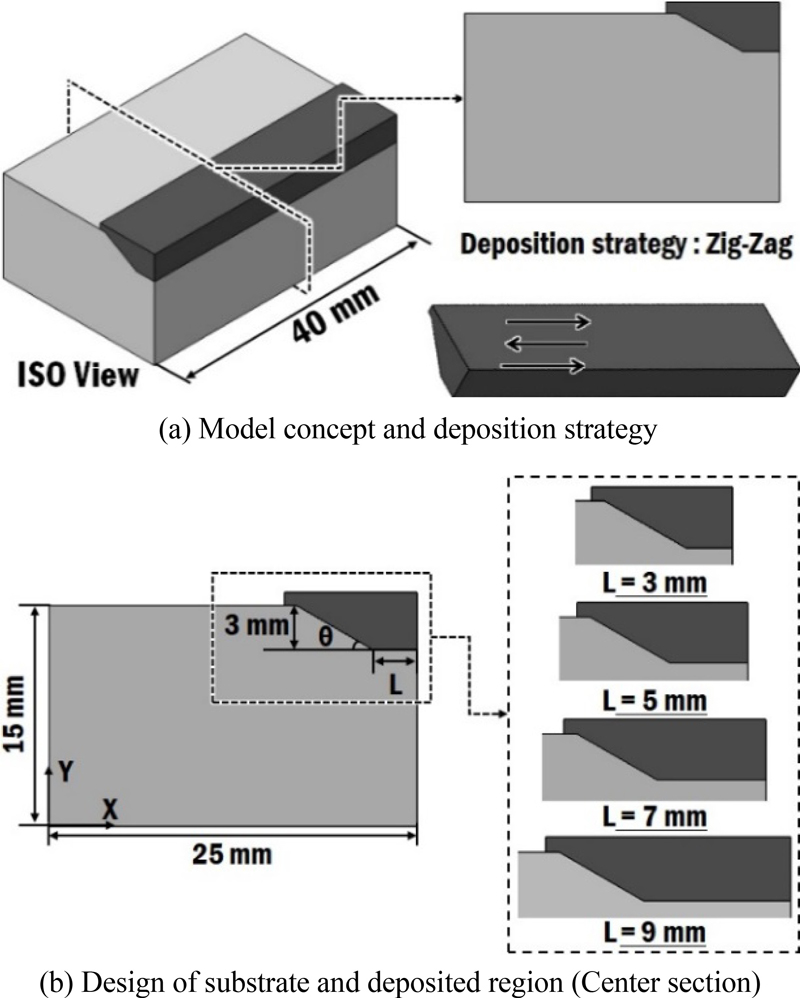
DED 공정으로 직선형 손상부 보수 시 기저부 끝단 길이(L)와 경사각(θ)에 따른 보수 인근의 잔류 응력 특성과 보수 시편의 변형 특성 변화를 분석/고찰하기 위하여 열-기계 연계 해석을 수행하였다. 이 연구에서는 수치 해석 시간과 용량을 감소시키기 위하여 길이 방향 변형이 거의 발생하지 않는 평면 변형 조건으로 가정하여 적층부 중앙 단면만을 해석하는 2차원 FEA 기법을 적용하였다. 이 연구에 적용된 보수 모델의 기저부와 적층부 형상은 Fig. 1과 같다. 기저부 경사각은 30°와 45°로 선정하였다[7,8,14]. Fig. 1의 기저부의 평면부와 경사부 사이 모서리와 기저부 끝단 사이의 거리를 기저부 끝단 길이(L)로 정의하였으며, 기저부 끝단 길이가 증가함에 따라 기저부의 평면부 길이와 적층부의 면적이 증가하도록 설계하였다. 이 연구에서 적용된 기저부 끝단 길이는 Fig. 1과 같이 3-9 mm 범위이며 기저부 끝단 길이와 경사각의 조합에 따라 총 8가지의 기저부 형상이 설계되었다. 이 연구에서 사용된 끝단부 길이와 경사각의 범위는 현업에서 기계부품 직선부 보수 시 사용되는 결함부 제거 후 생성하는 기저부 형상과 크기를 기준으로 선정하였다. Table 1은 기저부 끝단 길이와 경사각의 조합에 따른 적층 면적(Deposited Area)이다. 적층 면적 계산 시 각 기저부 경사각별로 적층 높이는 일정하고 끝단 길이만 변하도록 하였으며, CATIA V5에서 면적을 산출하였다. Table 1에서 기저부 경사각이 30°인 경우가 45° 경우보다 적층 면적이 넓게 형성됨을 알 수 있다. 기저부 형상에 관계없이 적층이 완료된 후 후가공으로 최종 형상을 제작하는 것으로 가정하여 적층부 상단에 과적층 영역을 생성하였다. 과적층을 위한 추가 적층 높이는 약 0.9 mm로 선정하였다.
상용 FEA 프로그램인 SYSWELD V16를 이용하여 열-기계 연계 해석을 수행하였다. 기저부 및 적층부 소재는 모두 AISI 1045이다. 이 연구에서는 JMatPro에서 산출된 AISI 1045 재료의 상변화가 고려된 온도 의존 열-기계 물성 데이터를 사용하였다[7,18]. Table 2는 FE 모델에 적용된 적층부 특성 데이터이다. 해석에 적용된 적층 길이 Fig. 1(a)와 같이 40 mm이며, 정상 상태 열전달 현상이 발생하는 중간 단면에서 2차원 열-기계 연계 해석을 수행하였다. 적층 경로은 Fig. 1(a)와 같이 지그-재그(Zig-Zag) 경로를 선정하였다.
| (1) |
| (2) |
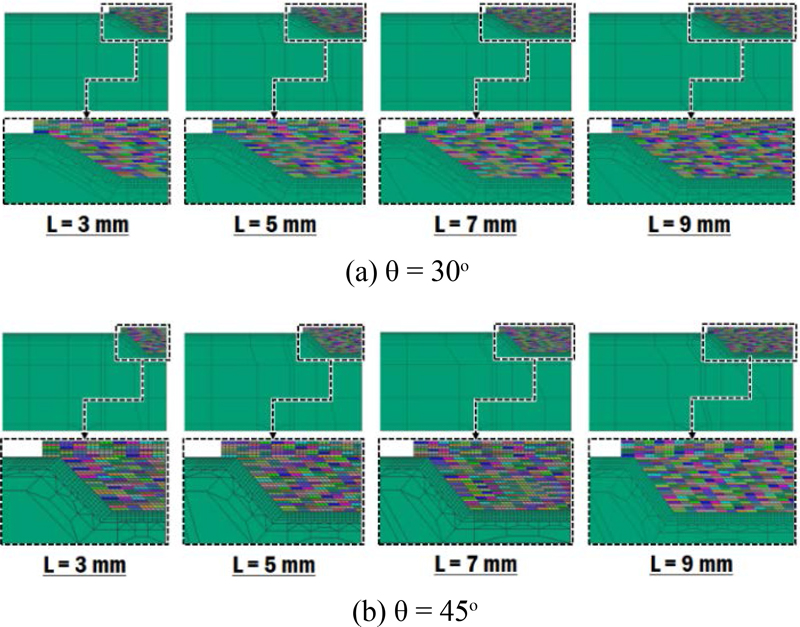
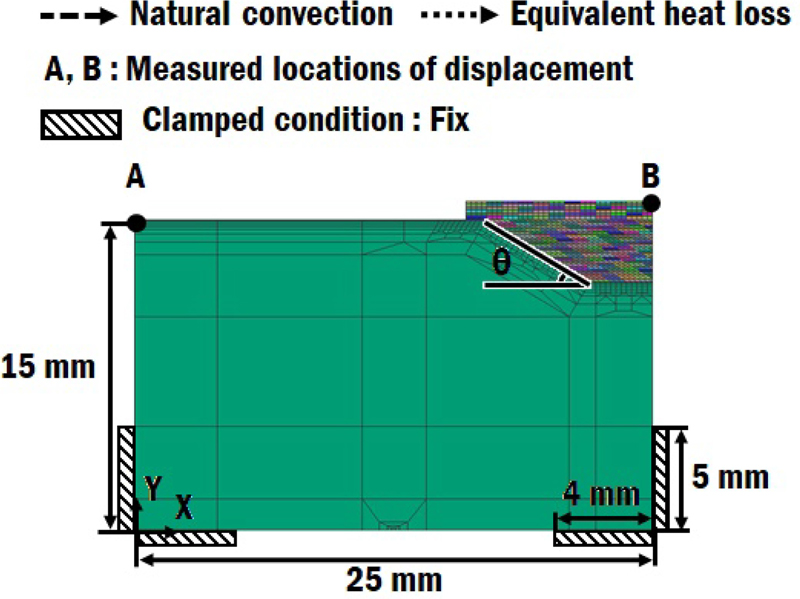
총 8가지의 FE 모델을 생성하였으며, 각 모델에 대한 격자(Mesh) 생성 상태는 Fig. 2와 같다. Table 3은 FEA에 적용된 적층 조건이다. Fig. 3은 적층 공정 중 및 적층 공정이 완료된 후 냉각 공정에 적용되는 적층 경계 조건들이다. FEA에서 레이저빔은 식(1) 및 식(2)와 같이 침투 깊이(Penetration Depth, δ)와 가우시안(Gaussian) 평면 열원 강도 분포를 가지는 3차원 체적 열원(Volumetric Heat Flux)으로 가정하였다[7,14,18,19]. 해석에 적용된 열원의 효율(η)은 0.32이다[7]. 적층 및 탄성 회복(Elastic Recovery)이 고려된 냉각을 포함한 총 공정 시간은 30,000초로 설정하였다. 탄성 회복은 적층이 종료된 후 60초가 지난 시간까지 진행되었다.
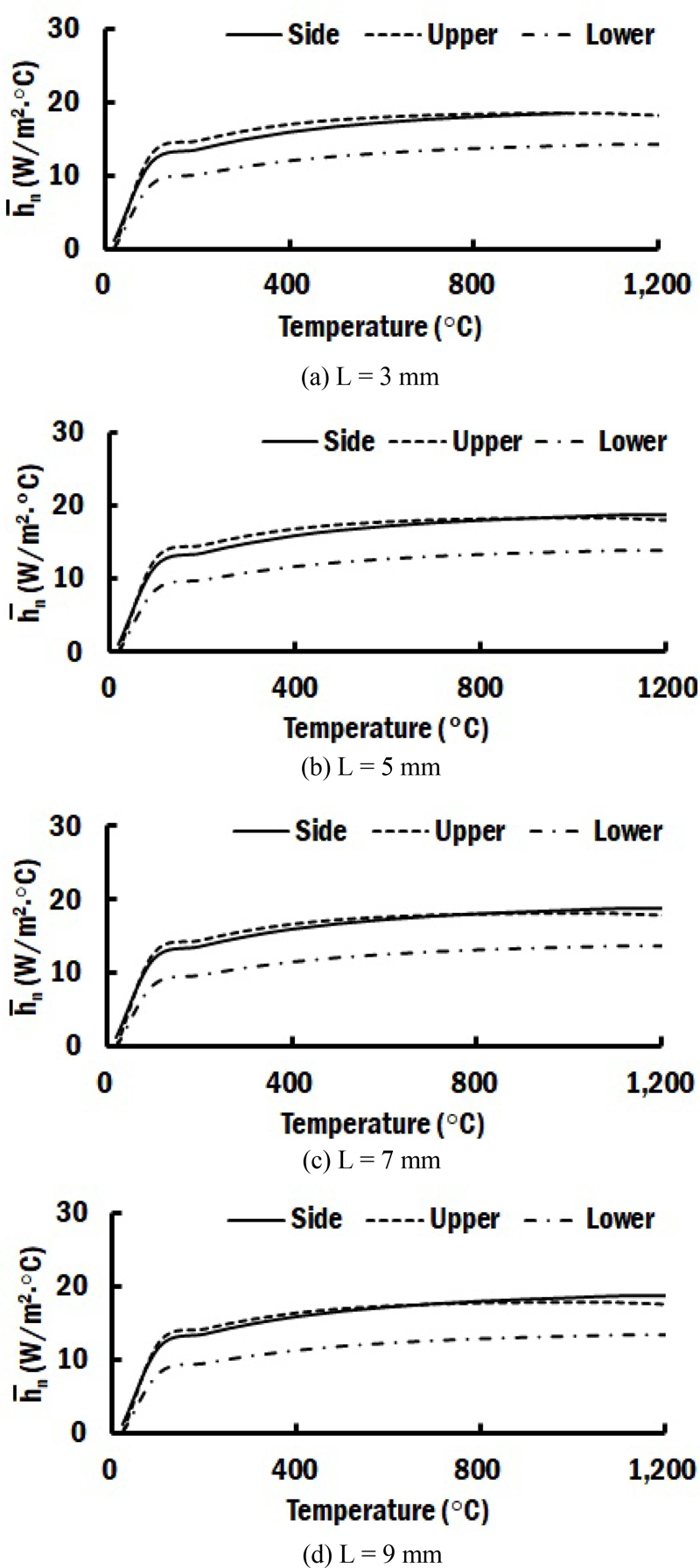
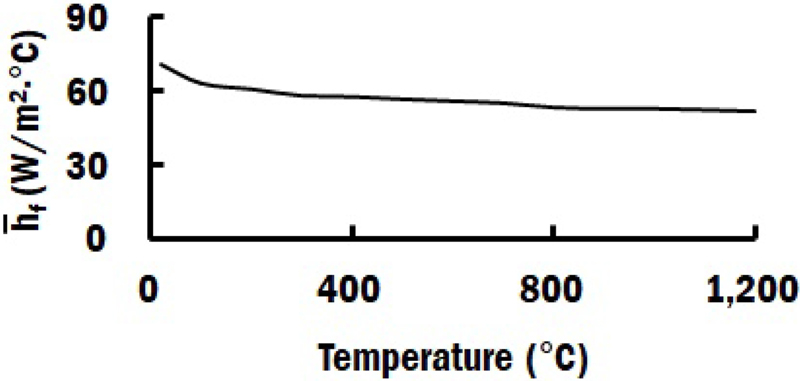
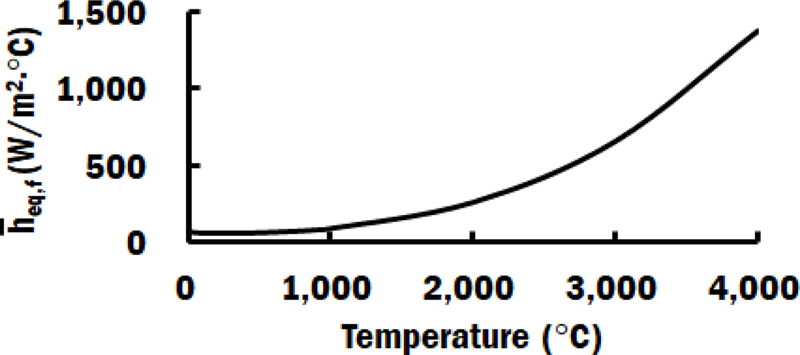
적층이 진행되는 시점에서는 기저부 상면을 제외한 모든 기저부 면에 온도 의존 자연 대류(Natural Convection)가 발생한다고 가정하였으며 적층이 완료된 후 기저부와 적층부의 모든 면에서 온도 의존 자연 대류가 발생하는 것으로 가정하였다. 적층이 진행중인 시점에서의 적층부와 기저부 상면에서는 아르곤 가스에 의한 강제 대류 및 복사에 의한 열손실이 고려되어야 하기 때문에 등가 열손실(Equivalent Heat Loss)이 적용되었다[7,14,18,19]. 해석에 적용된 각 기저부 및 적층부 조건에 맞는 온도 의존 자연 대류 계수는 Fig. 4와 같다. 강제 대류 계수() 및 등가 열손실 계수()는 각각 식(3)과 식(4)에 의하여 산출되었다[18]. 적용된 강제 대류 계수 및 등가 열손실 계수는 각각 Figs. 5 및 6과 같다.
| (3) |
| (4) |
3. 결과 및 고찰
3.1 잔류 응력 분포 특성 분석
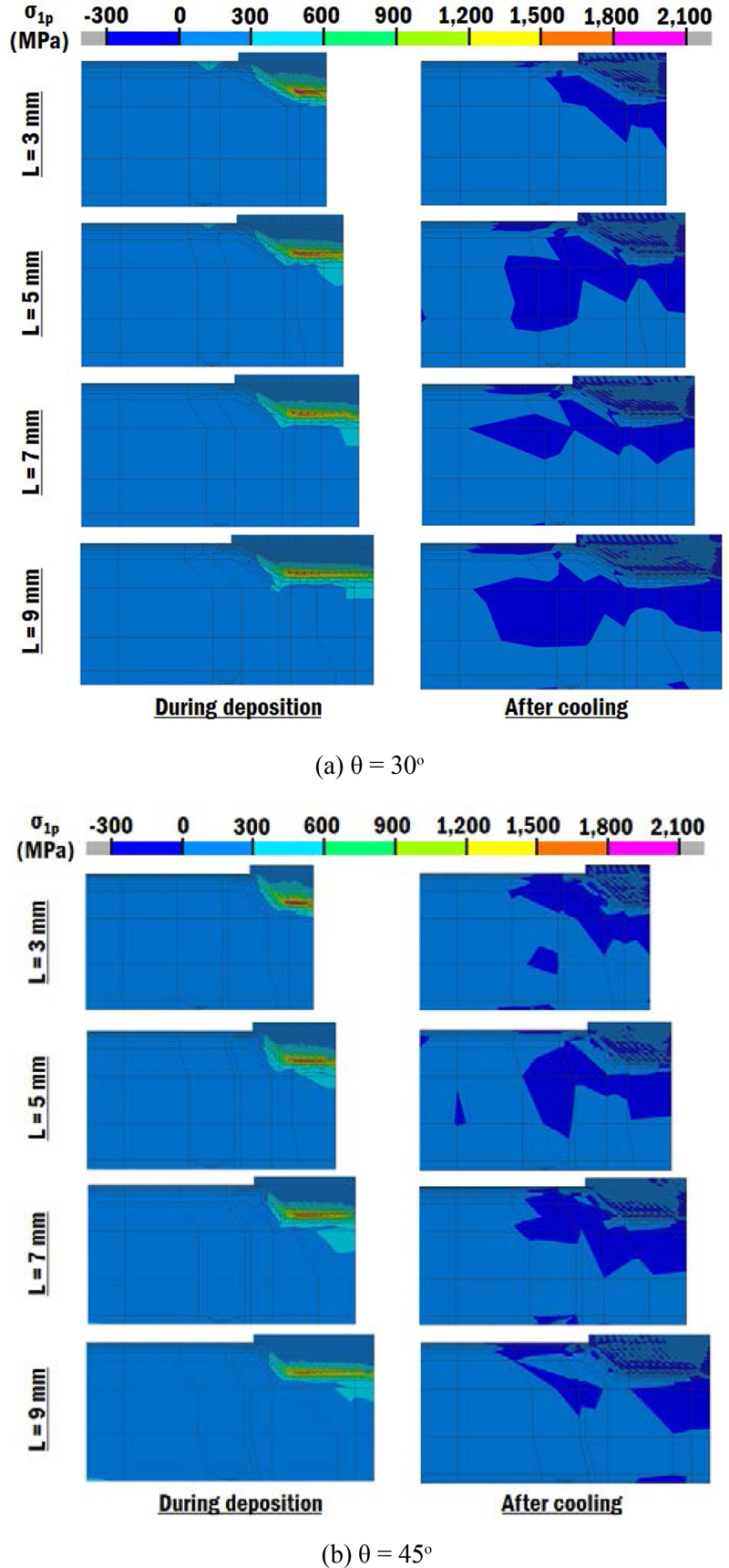
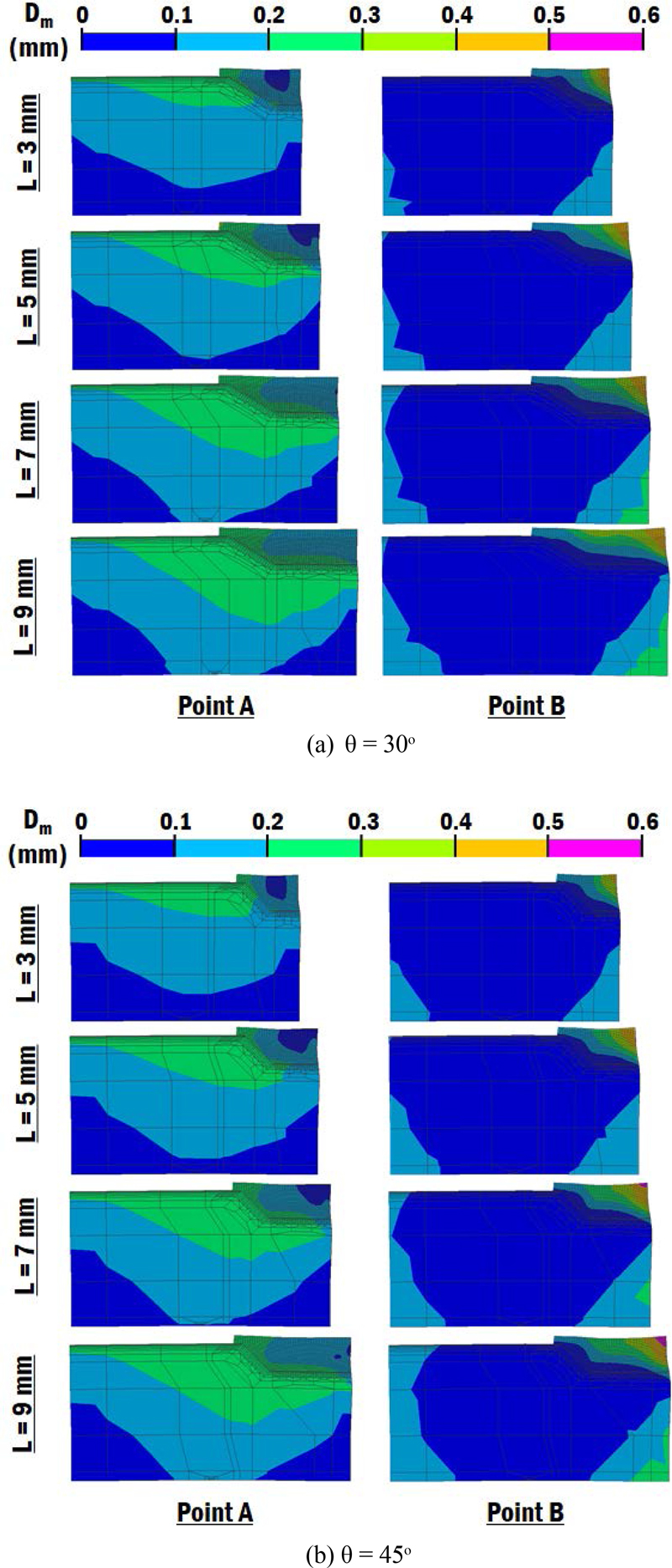
이 연구에서는 잔류 응력 특성 분석을 위하여 척도로 균열 발생의 기준이 되는 최대 주응력(1st Principal Stress, σ1p)을 선정하였다[7]. Fig. 7은 FEA 에서 예측된 기저부 경사각과 끝단 길이에 따른 잔류 응력 분포 변화이다. Fig. 7의 좌측은 적층중 잔류 응력의 최대값이 나타나는 시간의 잔류 응력 분포이고, 우측은 냉각이 완전히 종료된 시간에 대한 잔류 응력 분포를 나타내었다.
Fig. 7에서 기저부 경사각 및 끝단 길이에 관계없이 적층 공정중 발생하는 최대 잔류 응력이 적층 공정이 완료된 후 냉각(Cooling)이 끝난 시점의 잔류 응력보다 매우 높게 발생하는 것을 알 수 있었다. 기저부 경사각과 관계없이 기저부 끝단 길이가 3 mm에서 9 mm로 증가됨에 따라 적층 공정 중 보수부 인근에 발생하는 잔류 응력의 크기가 감소하는 것을 알 수 있었다. 기저부 끝단 길이가 3 mm인 경우 기저부 모서리부와 기저부 평면 영역 인근에 잔류 응력이 집중되어 있는 것을 알 수 있었다. 그러나 기저부 끝단 길이가 증가할수록 집중되는 기저부 평면 영역이 넓어져 잔류 응력이 잔류 응력의 크기는 감소하고 적용 영역은 증가하는 것을 관찰할 수 있었다. 이 결과들로부터 기저부 끝단 길이의 증가시켜 기저부 평면 영역의 면적을 증가시키면, DED 공정을 이용한 보수 공정 중 발생하는 보수부 인근의 잔류 응력 크기 감소 및 잔류 응력 집중 완화가 가능한 것을 알 수 있었다.
3.2 최대 잔류 응력 발생 위치 및 최대값 변화
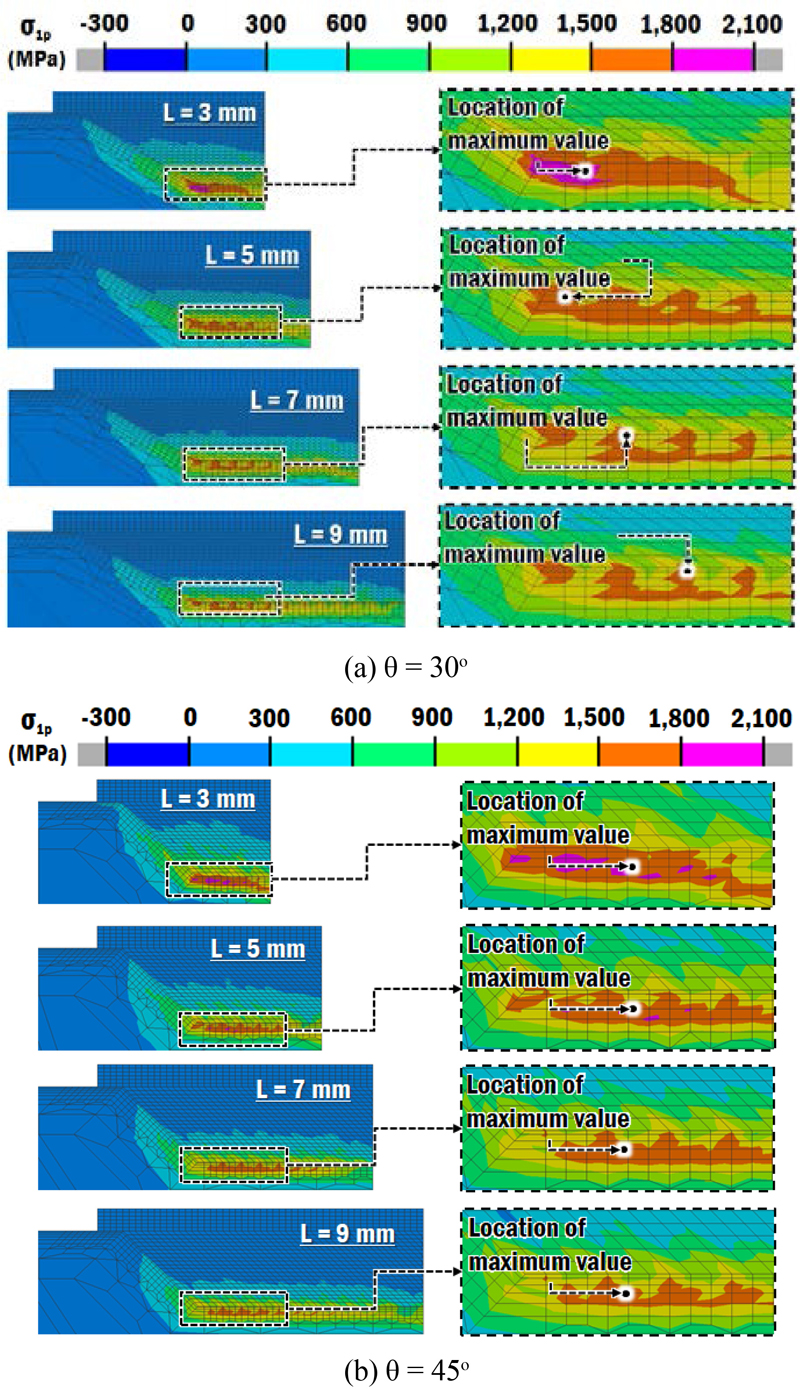
Fig. 8은 적층 공정 중 과도하게 잔류 응력이 집중되는 영역인 ESR (Excessively Stressed Region) 주위의 잔류 응력 분포이다[7,14]. 적층 공정 중 최대 잔류 응력 발생 지점은 Fig. 8과 같이 모서리에 가까운 기저부에서 발생하며, 그 위치는 기저부와 적층부의 경계에서 기저부 두께 방향으로 조금 아래인 것을 알 수 있었다. 최대 잔류 응력이 발생하는 위치는 기저부 경사면과 평면 영역의 교차 지점인 모서리로부터 0.25-1.75 mm 범위였다.
기저부 경사각이 30°인 경우에는 끝단 길이가 증가할수록 최대 잔류응력 발생위치가 기저부 모서리에서 모서리에서 멀어지는 것을 관찰할 수 있었다. 그러나 기저부 경사각이 45°인 경우에는 기저부 끝단 길이에 관계없이 최대 잔류 응력 발생 위치가 모서리로부터 약 1.25 mm로 거의 변하지 않는 것을 알 수 있었다. 기저부 끝단 길이가 증가할수록 과도한 잔류 응력이 발생하는 ESR의 면적이 감소하는 것을 알 수 있었다. 기저부 경사각이 30°에서 45°로 증가할 경우, ESR도 증가하는 것을 알 수 있었다.
Fig. 9는 기저부 끝단 길이와 경사각에 따른 최대 주응력 값 변화이다. Table 1과 같이 끝단 길이가 3 mm에서 9 mm로 증가하면 적층 면적이 증가하게 된다. 그러나, Fig. 9와 같이 기저부 끝단 길이를 3 mm에서 9 mm로 증가시킬 경우, 기저부 경사각 30°와 45°에 대하여 최대 주응력 최대값이 각각 약 22%와 약 17% 감소하는 것을 알 수 있었다. 끝단 길이가 3 mm인 경우를 제외하고 기저부 경사각 30°인 경우가 기저부 경사각 45°인 경우 보다 최대 주응력의 최대값이 조금 낮게 예측되었다. 기저부 끝단 길이가 증가할수록 최대 주응력의 최대값이 감소하는 경향이 나타났다. 특히, 기저부 경사각이 30°인 경우 끝단 길이가 5 mm 이상이 되면 최대 주응력의 최대값이 매우 감소하는 것을 알 수 있었다. 이 현상들은 기저부 끝단 길이가 증가하고 기저부 경사각이 감소할수록 기저부와 적층부의 온도가 증가하여 기저부와 적층부에 적층 중 예열 및 템퍼링(Tempering) 효과가 발생하기 때문으로 사료된다.
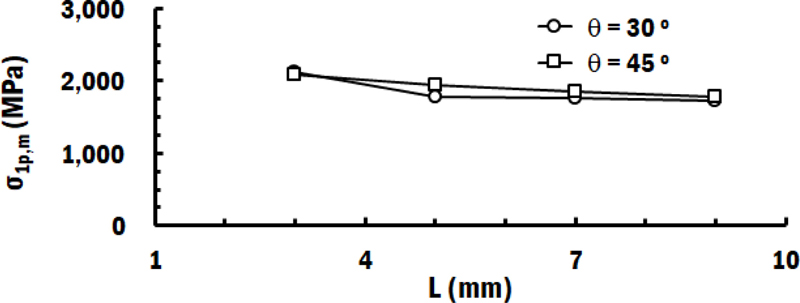
Effects of the edge length and the slope of the substrate on the maximum value of the 1st principal stress
위 결과들로부터 적층 공정 중 적층부 인근에 발생하는 잔류 응력을 감소시키기 위해서는 기저부의 끝단 길이를 증가시키고 경사각은 감소시켜야 함을 알 수 있었다.
3.3 잔류 응력 발생 이력 특성 분석
Fig. 10은 FEA 결과 예측된 최대 잔류 응력 발생 위치에서의 최대 주응력 이력이다. Fig. 10의 수평축은 시간이다. 각 기저부 끝단 길이와 경사각에 대한 최대 잔류 응력 발생 위치들은 Fig. 8과 같다. Fig. 10에서 기저부 끝단 거리와 경사각 관계없이 적층 공정 초기에 잔류 응력이 급격하게 증가하여 최대 잔류 응력이 발생하는 것을 관찰할 수 있었다. 최대 잔류 응력이 발생한 후, 잔류 응력이 감소하여 적층 완료시점에 잔류 응력의 최소값이 발생하였다. 잔류 응력의 최대값이 발생하는 층수는 Table 4와 같다. 기저부 끝단 길이가 증가할수록 최대 잔류 응력이 발생하는 층수가 감소하는 경향이 나타났다.
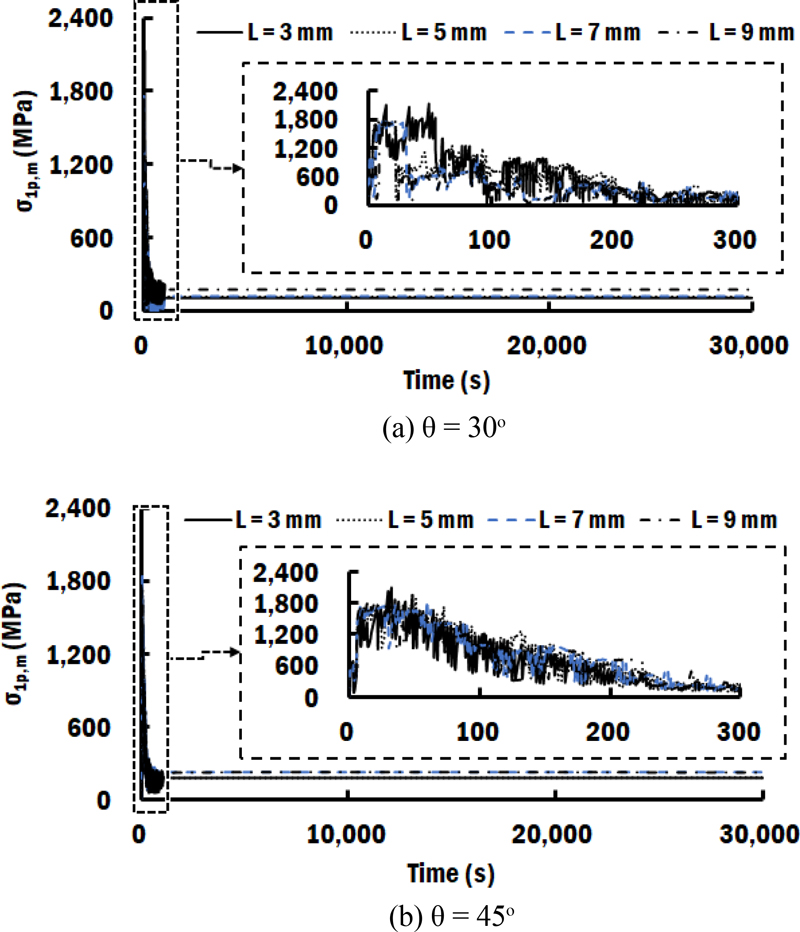
Time histories of 1st principal stress distributions at the occurrence location of the maximum value for different edge lengths and slops of the substrate

Number of layers for s1p,m at the occurrence location of the maximum value and maximum residual stress after cooling stage
Fig. 10에서 탄성 회복이 이루어지고 순수 냉각 공정이 진행되는 과정에서 잔류 응력이 조금씩 증가하여 최종 잔류 응력 분포가 생성되는 것을 알 수 있었다. Fig. 10과 Table 4에서 기저부 끝단 길이와 경사각이 증가할수록 순수 냉각 공정에서의 잔류 응력이 증가하는 것을 알 수 있었다. 적층 공정 중에 발생하는 잔류 응력 최대값과 냉각 완료 후의 잔류 응력을 비교한 결과, 적층 공정중 발생하는 잔류응력 최대값이 냉각 완료 후의 잔류 응력 최대값보다 4.1-5.2배 정도 높은 것을 알 수 있었다. 적층 공정 중 발생하는 잔류 응력 최대값과 냉각 완료 후의 잔류응력 최대값 차이는 기저부 끝단 길이가 증가할수록 감소하는 것을 알 수 있었다.
3.4 변형 특성 분석
Table 5 및 Figs. 11과 12는 FEA로부터 취득된 적층부 인근의 변형 특성 데이터들이다. Fig. 11과 같이 최대 변위는 Fig. 3의 B점에서 발생하였다. B점에서 최대 변위가 발생하는 시간은 Table 5와 냉각이 완료된 시간인 30,000초로 예측되었다. Fig. 3의 A점의 최대 변위는 Table 5와 같이 적층 공정 진행중에 발생하였다. A점의 최대 변위가 발생하는 시점의 변형 형상은 Fig. 11과 같다. Fig. 11에서 보수부 주위에서 적층부과 기저부의 현저한 변형 차이가 발생하는 것을 관찰할 수 있었다. 특히 수평방향으로 기저부의 끝단에서 기저부와 적층부의 수평방향 변위차가 두드러지게 나타나는 것을 알 수 있었다. 또한, B점의 수직 방향 변위가 다른 위치들에 비해서 상대적으로 매우 높게 나타나는 것을 관찰할 수 있었다. 이 결과들로부터 기저부 끝단에서 기저부와 적층부의 변형율 차이가 상당히 발생하는 것을 알 수 있었다.

Times of maximum deformation and finishing times of deposition for different edge lengths and slopes
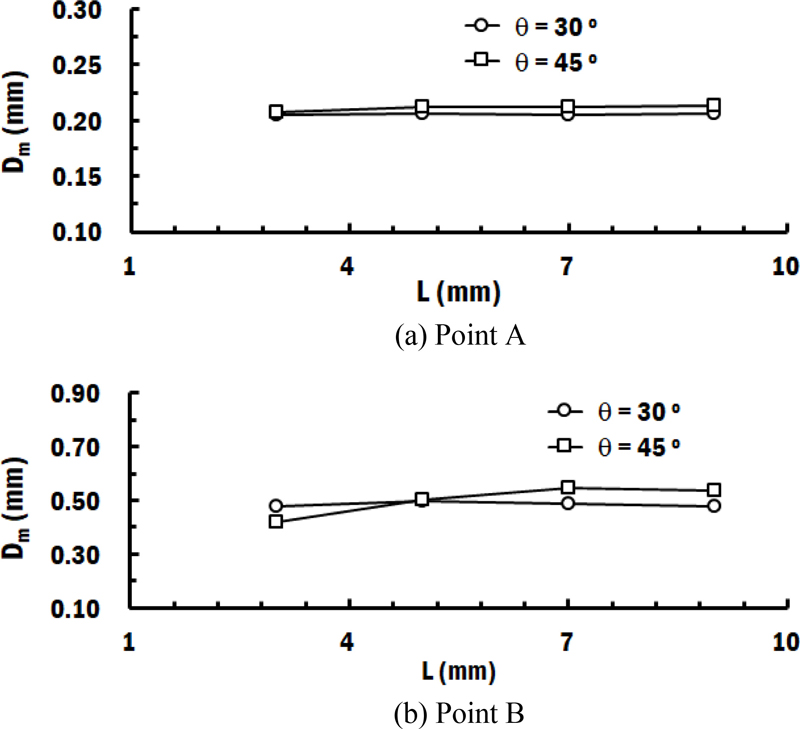
A점의 최대 변위는 Figs. 11과 12(a)와 같이 기저부 경사각이 30°와 45°일 때 각각 약 0.20 mm 및 0.21 mm로 예측되었다. 기저부 끝단 길이는 A점 최대 변위 변화에 거의 영향을 미치지 않는 것을 알 수 있었다. B점의 최대 변위는 Figs. 11과 12(b)와 같이 기저부의 경사각이 30°와 45°일 때 각각 0.48-0.50 mm 및 0.42-0.55 mm 범위로 산출되었다. 기저부 경사각이 30°인 경우에는 기저부 끝단 길이가 5 mm까지는 끝단 길이가 증가할 경우 B점 최대 변위가 증가하였다. 그러나 기저부 끝단 길이가 5 mm를 초과할 경우, 끝단 길이가 증가할수록 B점의 최대 변위는 조금 감소하였다.
기저부 경사각이 45°일 때에는 기저부 끝단 길이 7 mm까지는 끝단 길이가 증가할 경우 B점 최대 변위가 증가하였다. 그러나 기저부 끝단 길이가 7 mm를 초과할 경우, 끝단 길이가 증가할수록 B점의 최대 변위는 조금 감소하였다. 기저부 끝단 길이가 5 mm 이상이 되면, 기저부 경사각이 45°일 때의 최대 변위가 기저부 경사각이 30°일 때의 최대 변위보다 크게 나타나는 것을 알 수 있었다. 이때 기저부 경사각이 45°일 때 A점과 B점의 최대 변위와 기저부 경사각이 30°일 때 A점과 B점의 최대 변위의 차이가 0.06 mm 이하로 매우 작은 것을 알 수 있었다.
4. 결론
이 연구에서는 DED 공정을 이용한 직선형 손상부 보수시 기저부 끝단 거리와 경사각에 따른 보수부 인근 잔류 응력 및 변형 특성 변화를 2차원 FEA로 분석/고찰하여, 다음과 같은 결론을 얻을 수 있었다.
첫째, 기저부 끝단 길이와 경사각에 관계없이 최대 잔류 응력은 적층 공정 초기에 발생하는 것을 알 수 있었다. 적층 공정 중발생하는 잔류 응력 최대값은 냉각 완료 후의 잔류 응력 최대값 보다 4.1-5.2배 정도 크게 예측되는 것을 알 수 있었다. 기저부 끝단 길이가 증가할수록 보수부 인근의 잔류 응력 크기가 감소되고 잔류 응력 집중 정도는 완화되는 것을 알 수 있었다.
둘째, 최대 잔류 응력은 기저부 모서리 인근에서 발생하며, 그 위치는 기저부와 적층부의 경계에서 기저부 두께 방향으로 조금 아래임을 알 수 있었다. 적층 공정 중 적층부 인근에 발생하는 잔류 응력을 감소시키기 위해서는 기저부의 끝단 길이를 증가시키고 경사각은 감소시켜야 하는 것을 알 수 있었다. 또한, 이 연구에 사용된 기저부 설계 조건에서는 기저부 경사각이 30°이고 끝단 길이가 5 mm 이상인 경우가 잔류 응력 측면에서 적절한 기저부 설계로 사료되었다.
셋째, 최대 변위는 냉각 완료 후 Fig. 3의 B점에서 발생하는 것을 알 수 있었다. 수평 방향으로 기저부의 끝단에서 기저부와 적층부의 변위차가 두드러지게 예측되었다. 이 결과로부터 기저부 끝단에서 기저부와 적층부의 변형율 차이가 상당히 발생하는 것으로 사료되었다. 기저부 끝단 길이가 5 mm 이상이고 경사각이 30°인 경우 최대 변위가 거의 유사하게 나타나는 것을 알 수 있었다. 기저부 경사각이 30°인 경우가 45°인 경우보다 잔류 변위가 작게 발생하는 것을 알 수 있었다.
위 결과들로부터 기저부 경사각이 30°이고 끝단 길이가 5 mm 이상인 경우가 이 해석 모델에서의 기저부 적정 설계로 사료되었다.
향후, 추가적인 실험을 통하여 기저부 끝단 길이와 경사각에 따른 적층부 인근의 잔류 응력 변화를 직/간접적으로 측정하고, 이 결과를 FEA에 반영하여 최적 FE 모델을 개발할 예정이다. 또한, 기저부 끝단 길이와 경사각이 적층 인근에 발생하는 변형율 분포 변화에 미치는 영향에 대해서도 추가적으로 연구를 진행하고자 한다.
NOMENCLATURE
| θ : | Slope of Substrate |
| L : | Edge Length of Substrate |
| P : | Power of Laser |
| V : | Scan Speed of Laser |
| r : | Radius of Heat Flux |
| r(z) : | Radius of Heat Flux according to Penetration Depth |
| δ : | Penetration Depth |
| η : | Efficiency of Heat Flux |
| G : | Flowrate of Shielding Gas |
| F : | Flowrate of Powder Feeding Gas |
| : | Linear Intensity of Heat Flux |
| x : | X Coordinate |
| y : | Y Coordinate |
| t : | Scan Time of Laser |
| : | Natural Convection Coefficient |
| : | Forced Convection Coefficient |
| : | Coefficient of Equivalent Heat Loss Model |
| Nu : | Nusselt Number |
| k : | Thermal Conductivity |
| D : | Diameter of Nozzle |
| ε : | Emissivity of AISI 1045 |
| ρ : | Stefan-Boltzmann Constant |
| Ts : | Surface Temperature |
| T∞ : | Environmental Temperature |
| σ1p : | First Principal Stress |
| σ1p, m : | Maximum Value of First Principal Stress |
| Dx : | Displacement in X Direction |
| Dy : | Displacement in Y Direction |
| Dm : | Magnitude of Displacement |
Acknowledgments
“이 논문은 2022년도 조선대학교 학술연구비의 지원을 받아 연구되었음(No.2022-202272-01).”
REFERENCES
- Ko, K.-H., Bae, Y.-J., Moon, J.-Y., Kang, H.-Y., Hwang, Y.-W., (2019), An economic effect analysis on remanufacturing part of automobile, Resources Recycling, 28(4), 37-43.
-
Shamsaei, N., Yadollahi, A., Bian, L., Thompson, S. M., (2015), An overview of direct laser deposition for additive manufacturing; Part II: Mechanical behavior, process parameter optimization and control, Additive Manufacturing, 8, 12-35.
[https://doi.org/10.1016/j.addma.2015.07.002]

-
Ahn, D.-G., (2016), Direct metal additive manufacturing processes and their sustainable applications for green technology: A review, International Journal of Precision Engineering and Manufacturing-Green Technology, 3(4), 381-395.
[https://doi.org/10.1007/s40684-016-0048-9]

-
Rahito, S. W., Wahab, D. A., Azman, A. H., (2019), Additive manufacturing for repair and restoration in remanufacturing: An overview from object design and systems perspectives, Processes, 7(11), 802.
[https://doi.org/10.3390/pr7110802]

-
Ahn, D.-G., (2021), Directed energy deposition (DED) process: State of the art, International Journal of Precision Engineering and Manufacturing-Green Technology, 8(2), 703-742.
[https://doi.org/10.1007/s40684-020-00302-7]

-
Lee, I. H., Kim, H. C., Ahn, D.-G., (2020), Korean Terminologies for Additive Manufacturing according to the ISO/ASTM 52900 Standard, Journal of Korean Society of Precision Engineering, 37(12), 929-936.
[https://doi.org/10.7736/JKSPE.020.093]

-
Yim, S. H., Lee, K. K. and Ahn, D. G., (2022), Effects of deposited shape and substrate slope on residual stress and deformation characteristics for repairing old parts via a DED process, Journal of Korean Society of Manufacturing Process Engineers, 21(12), 77-87.
[https://doi.org/10.14775/ksmpe.2022.21.12.077]

- Kim, D., Lee, K., Ahn, D., (2021), Investigation into the effects of process parameters of DED process on deposition and residual stress characteristics for remanufacturing of mechanical parts, Transactions of Materials Processing, 30(3), 109-118.
-
Yang, Y., Gong, Y., Qu, S., Xin, B., Xu, Y., Qi, Y., (2019), Additive/subtractive hybrid manufacturing of 316L stainless steel powder: Densification, microhardness and residual stress, Journal of Mechanical Science and Technology, 33(12), 5797-5807.
[https://doi.org/10.1007/s12206-019-1126-z]

-
Hua, L., Tian, W., Liao, W., Zeng, C., (2014), Numerical simulation of temperature field and residual stress distribution for laser cladding remanufacturing, Advances in Mechanical Engineering, 6, 291615.
[https://doi.org/10.1155/2014/291615]

-
Lei, X., Huajun, C., Hailong, L., Yubo, Z., (2017), Study on laser cladding remanufacturing process with FeCrNiCu alloy powder for thin-wall impeller blade, The International Journal of Advanced Manufacturing Technology, 90, 1383-1392.
[https://doi.org/10.1007/s00170-016-9445-z]

-
Oh, W. J., Lee, W. J., Kim, M. S., Jeon, J. B., Shim, D. S., (2019), Repairing additive-manufactured 316L stainless steel using direct energy deposition, Optics & Laser Technology, 117, 6-17.
[https://doi.org/10.1016/j.optlastec.2019.04.012]

-
Zhang, Z., Ge, P., Yao, X., Li, T., Liu, W., (2020), Numerical studies of residual states and scaling effects in laser-directed energy deposition additive manufacturing, The International Journal of Advanced Manufacturing Technology, 108, 1233-1247.
[https://doi.org/10.1007/s00170-020-05300-2]

-
Lee, K.-K., Chua, B.-L., Ahn, D.-G., (2022), Remanufacturing strategy of engraved part using directed energy deposition process, International Journal of Precision Engineering and Manufacturing-Green Technology, 9(6), 1575-1582.
[https://doi.org/10.1007/s40684-022-00468-2]

-
Kim, D. A., Lee, K. K., Ahn, D. G., (2022), A study on the influence of the inclined angle and depth of the substrate on thermal and residual stress characteristics in the vicinity of the repaired region by a directed energy deposition process, Journal of Korean Manufacturing Process Engineers, 21(6), 50-59.
[https://doi.org/10.14775/ksmpe.2022.21.06.050]

-
Urbánek, M., Hodek, J., Melzer, D., Koukolíková, M., Prantl, A., Vavřík, J., Brázda, M., Martínek, P., Rzepa, S., Džugan, J., (2022), Prediction of behaviour of thin-walled DED-processed structure: Experimental-numerical approach, Materials, 15(3), 806.
[https://doi.org/10.3390/ma15030806]

-
Soffel, F., Lin, Y., Keller, D., Egorov, S., Wegener, K., (2022), Laser remelting process simulation and optimization for additive manufacturing of nickel-based super alloys, Materials, 15(1), 177.
[https://doi.org/10.3390/ma15010177]

- Kim, D. A., (2022), A study on the influence of deposition and substrate shape on residual stress characteristics in the vicinity of the repaired region of parts for machine tools using a DED process, M.Sc. Thesis, Chosun University.
- Chua, B., Investigation of development of thermo-mechanical analysis method for a wire feeding type directed energy deposition process, Ph.D Thesis, Chosun University.

Master course at the Department of Mechanical Engineering, Chosun University. His research interests are development, application and simulation of metal additive manufacturing technology.
E-mail: socrayim3@naver.com

Ph.D candidate at the Department of Mechanical Engineering, Chosun University. His research interests include development, application and simulation of metal additive manufacturing technology.
E-mail: otq_center@naver.com

Professor at the Department of Mechanical Engineering, Chosun University. He received his M.S. and Ph.D. degrees from KAIST, Korea in 1994 and 2002, respectively. His research interests include development and application of additive manufacturing technology, rapid manufacturing, lightweight sandwich, and mold & die.
E-mail: smart@chosun.ac.kr