UAM 메인 프로펠러 배치에 따른 공력소음 저감 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recently, as UAM has been in the spotlight worldwide, the issue of aerodynamic noise generated from propellers has emerged. Therefore, changes in thrust and aerodynamic noise were compared while changing the propeller lay-out distance. The designed propeller model was analyzed using ANSYS Fluent, a CFD software. Based on steady-state analysis, transient analysis was performed, and SPL was calculated using the FW-H noise model. Based on the standard propeller lay-out distance of 0.1 R (0.12 mm), 5 cases from 0.2 R to 0.6 R were compared with the reference model at equal intervals of 0.1 R. The thrust increased by up to 3.5% as the propeller distance increased. In most listeners positioned to measure SPL, noise was reduced by 0.07-0.7% in the improved model compared to the reference model due to reduction in local vorticity. However, because pressure fluctuation due to the increase in thrust and high SPL in the low-frequency region were measured, noise increased by 0.6% to 3.5% in some listeners. Increasing the propeller distance enhances thrust performance, but inevitably increases noise due to pressure fluctuations and SPL in the low-frequency region. Therefore, strict analysis of noise prediction according to a specific frequency and various design shapes are needed.
Keywords:
Virtual fluid dynamics, Aerodynamic noise, Vertical take-off and landing, Multirotor, UAM propeller, Sound pressure level키워드:
가상 유체역학, 공력소음, 수직이착륙기, 다중로터, UAM 프로펠러, 음압 레벨1. 서론
현재 세계적으로 전기자동차를 대체할 차세대 교통수단으로 도심형 항공 모빌리티(Urban Air Mobility, UAM)가 대두되면서 근 미래의 상용화를 목표로 활발한 연구가 진행되고 있다. 도심의 상공에서 운용되는 UAM은 최근 급격히 늘어나는 교통량에 구애받지 않으며, 특히 전기 모터 및 배터리, 그리고 틸트 로터(Tilt Rotor)를 사용하여 수직 이착륙(Electric Vertical Take-off and Landing, e-VTOL)이 가능한 e-VTOL UAM은 배기가스의 배출이 없어 친환경적이며 수직 이착륙이 가능하여 별도의 활주로를 필요로 하지 않아 도심의 협소한 공간에서 이착륙 및 운행하기에 편리하다는 특징이 있다. 하지만 모터로 프로펠러를 회전시켜 추진력을 얻는 UAM의 특성상 모터의 기계 소음(Mechanical Noise)과 프로펠러의 공력소음(Aerodynamics Noise)이 발생한다. 전기 모터를 사용하는 UAM은 모터에서 발생하는 기계소음에 비해 프로펠러의 공력소음이 지배적이다[1]. 상공에서 비행하는 UAM의 특성상 이러한 소음이 미치는 범위가 광범위할 것이라 예상된다. 따라서 UAM이 상용화되기 위해서는 저소음화가 요구되며 프로펠러에 의하여 발생하는 공력소음을 저감하는 연구가 활발히 진행되고 있다.
최근 UAM은 소음 문제와 추락을 방지하기 위하여 분산 추진(Distributed Propulsion) 방식을 채택하고 있다[2]. 분산 추진 방식은 기존의 단일 추진기에 사용되는 엔진 대신 작은 전기 모터를 사용하므로 엔진 소음으로부터 자유롭고, 프로펠러의 규모가 작아 발생하는 소음 수준이 낮다. 하지만 인접한 프로펠러 간 와류 간섭(Blade Vortex Interaction, BVI)으로 인한 소음이 발생한다. 따라서 이러한 와류 간섭을 방지하기 위하여 덕트(Duct)를 활용한 연구가 진행되었다. Guo 등[3]은 강체 덕트와 다공성(Porous) 덕트를 비교하여 다공성 구조를 가진 덕트가 소음 저감에 있어 효과가 있음을 보여주었으며, Malgoezar 등[4]은 무인항공기(Unmanned Aerial Vehicle, UAV)에 설치하기에 적합한 덕트를 설계하여 소음을 실험적으로 분석하고 정량화하였다.
하지만 이러한 덕트 설계는 소음 저감의 측면에선 효과가 있지만 기체의 중량이 증가한다는 단점이 있다. 이에 프로펠러의 형상을 변경하여 공력 소음을 비교하는 연구가 진행되었다. Ryusuke 등[5]은 프로펠러에 생체 모방형 구조의 추가 설계를 통하여 공력 소음을 줄였지만, 덕트 설계와 마찬가지로 구조의 추가 설계로 인하여 중량 및 비용을 증가시킨다. 이에 본 연구실에서는 프로펠러의 후연(Trailing Edge)에 생체 모방형 커팅(Cutting) 설계를 통하여 공력 소음을 저감하는 연구도 최근에 진행되었다. 하지만 위의 연구들은 단일 프로펠러를 대상으로 진행되었으며, 따라서 분산 추진 방식에서의 공력 특성 및 소음에 대한 연구가 진행되어야 한다.
Choi 등[6]은 고정익(Blade)에 장착된 프로펠러의 위치에 따른 공력 특성에 대한 연구를 진행하였으며, Li 등[7]은 쿼드로터(Quadrotor) 드론의 생체 모방식 프로펠러 배치 설계를 통한 공력 성능 및 특성을 연구하였다. 또한 프로펠러 간 거리에 따른 공력 특성을 연구하며, 무인 항공기의 중량과 프로펠러의 직경, 그리고 피치(Pitch)에 따른 프로펠러 축 사이의 거리를 최적화한 연구[8]가 진행되었지만 프로펠러의 배치에 따른 소음을 분석하는 연구는 거의 수행되지 않았다.
본 연구에서는 분산 추진을 하는 UAM에 적용 가능한 방안으로 정지 비행(Hovering) 상태를 가정하였으며, 다분야에서 활용되고 있는 대표적인 드론 중 하나인 D(社)의 Phantom 3를 연구에 사용하였다. 이웃한 프로펠러 간 간격에 따른 추력(Thrust)의 변화와 공력 소음의 변화를 전산 유체 역학(Computational Fluid Dynamics, CFD) 기법을 활용하여 비교 해석하며 저소음에 기반한 최적의 프로펠러 간격을 설계하는 것에 목표를 두어 연구를 진행하였다.
2. Propeller 모델 및 설계
2.1 Phantom 3
본 연구에서는 D(社)의 Phantom 3 드론을 활용하여 연구를 진행하였으며 Phantom 3 드론은 쿼드로터(Quad-rotor) 방식으로 직경(D)이 240 mm인 9450 프로펠러를 사용한다. Phantom 3와 9450 프로펠러의 상세한 제원은 Table 1에 정리하였으며, 프로펠러의 배치에 따른 공력소음 연구의 목적상 중량은 고려하지 않았다. 프로펠러의 모델링은 CAD SW인 CATIA V5를 활용하였으며 원활한 해석을 위하여 단순화(CAD Repair)하였다. 유동해석을 위하여 가로, 세로의 길이가 10D(2,400 mm), 프로펠러로부터 유체의 입구까지 6D(1,440 mm), 후류의 유동 현상을 관찰하기 위하여 출구까지 16D(3,840 mm)의 충분한 길이를 주어 직육면체의 외부 유동장을 설정하였으며, 유체의 회전 영역은 프로펠러의 직경과 인근 프로펠러와의 거리를 고려하여 유동장과의 간섭이 발생하지 않게 242 mm의 직경으로 유동장을 생성하였다.
2.2 프로펠러 배치 설계
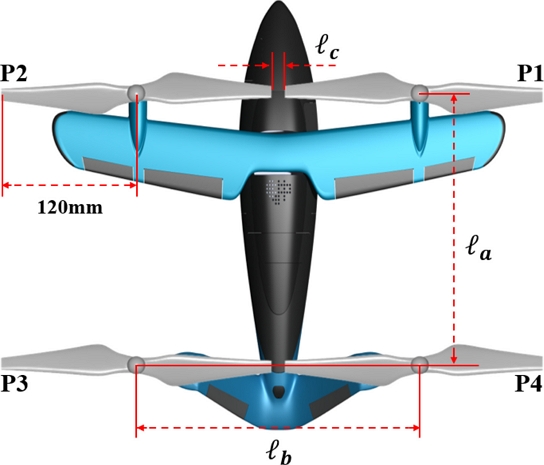
기존 Phantom 3의 프로펠러 배치는 기존 연구[9]를 참고하여 Fig. 1에 나타내었다. 기존 연구[7,8]를 통하여 프로펠러의 간격, 높이 차이 및 기울기 각도에 따라 성능 지수(Figure of Merit, FM)와 양력 및 추력이 변화하는 것을 알 수 있었으며, 특히 프로펠러의 간격이 공기역학적 성능에 현저한 영향을 미친다는 것을 확인했다. 프로펠러의 배치는 유체의 흐름에 영향을 주며, 이에 따른 BVI 소음도 변화할 것으로 예상된다. 하지만 위의 기존 연구들은 각각의 설계 변수들에 대한 공기역학적 성능만을 비교하며 최적 설계를 진행하였지만 소음은 고려하지 않았다. 따라서 본 연구에서는 프로펠러의 간격에 따른 공력 및 소음 특성의 변화를 예측하는 것을 목표로 하여 연구를 진행하였다. 인접한 프로펠러는 서로 영향을 주고받으며 공력 성능 및 소음에 지대한 영향을 끼치기 때문에 작은 간격에서부터 큰 간격으로 조금씩 늘려가며 프로펠러의 공력 성능 및 소음이 어떻게 변화하는지를 확인하여야 하지만 모든 간격에 대해서 연구를 수행하는 것은 비효율적이며, 많은 시간과 비용이 들게 된다. 따라서 기존 연구[10]를 참고하여 프로펠러 간 거리는 기존 Phantom 3의 프로펠러 간격인 12 mm(0.1 R, R = Radius)를 기준으로 정하였다. 또한 유동 현상의 복잡도를 낮추고, 해석 결과의 정밀도를 높이기 위하여 프로펠러의 간격을 12 mm씩 등간격으로 늘리며, 24 mm(0.2R)를 Case 1로 하여 72 mm(0.6R)인 Case 5까지 기존 모델을 포함하여 총 6가지의 모델을 설계하여 연구를 수행하였다. 각 Case별 프로펠러 간격의 자세한 치수는 Table 2에 정리하였다.
3. 수치해석
본 연구에서는 수렴성을 위하여 정상(Steady) 해석 값을 초기값으로 사용하여 과도(Transient) 해석을 진행하였다. 회전체에 대한 해석을 위해서 MRF(Multiple Reference Frame) 기법을 계산에 사용하였다. 정상 해석의 난류 모델은 Reynolds-Averaged Navier-Stokes (RANS)에 기반한 Shear Stress Transport(SST) k-ω 모델을 사용하였다. SST k-ω 모델은 벽면에서의 경계층 유동과 상류층에서의 등방성 자유 난류 예측에 적합하기 때문에 벽면에서의 자유 유동과 박리 현상이 동시에 고려되어야 하는 회전체 해석에 주로 사용되며, 다음과 같은 식으로 나타낼 수 있다[11,12].
| (1) |
| (2) |
| (3) |
여기서 식(1)은 난류 운동 에너지(Turbulence Kinetic Energy, k), 식(2)는 난류 고유 소산율(Turbulence Specific Dissipation Rate, ω), 그리고 식(3)은 난류 점도(Turbulence Viscosity)를 나타낸다.
비정상 해석은 난류를 모사하는 데 사용되는 수치 해석 모델인 Large Eddy Simulation (LES) 모델을 사용하였다. RANS 모델은 물리현상을 시간에 대해 평균화 된 결과에 중점을 둔다면, LES 모델은 실제 물리현상에 중점을 둔다. 따라서 LES 모델은 시간을 평균으로 하지 않으며 유동 현상에서 발생하는 소용돌이(Eddy)를 직접 해석함으로써 보다 정확하게 유동 현상을 해석할 수 있다.
수치적으로 공력 음향해를 해석하기 위하여 본 연구에서는 Lighthill의 음향 상사법(Analogy)에 기반으로 한 Ffowcs Williams and Hawkings (FW-H) 모델을 사용하였다. FW-H 모델은 임의로 움직이는 물체에 의하여 발생하는 소음을 단극자, 쌍극자, 그리고 사중극자의 소음원으로 모델링하여 소음을 예측한다. 따라서 FW-H 모델은 유체의 유동현상으로 인하여 발생하는 소음을 예측하는데 유용하다고 할 수 있다. 본 연구에서는 프로펠러 주변 임의의 수신자를 설정한 후 주파수별 음압 레벨(Sound Pressure Level, SPL)을 계산하여 소음을 예측하였다. SPL [dB]은 물리량의 비를 로그 규모로 표기한 값이며, 계산된 SPL 값은 고속 푸리에 변환(Fast Fourier Transform, FFT)을 통하여 음압 값을 다양한 주파수를 갖는 주기 함수들의 합으로 나타내었다.
3.1 격자 생성 및 의존도 검사
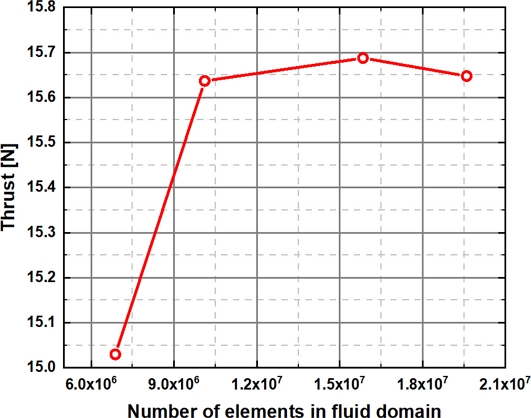
복잡한 프로펠러의 구조를 반영하기 위하여 사면체(Tetrahedron) 형태의 비정렬 격자를 사용하여 생성하였다. 벽면 경계층에서의 박리현상을 고려하여 프로펠러 벽면에 경계층 격자를 생성하였다. 격자에 의한 수치해의 오류와 수렴성을 검증하기 위하여 약 500만 개의 격자로부터 약 2,000만 개의 격자를 생성하여 추력을 비교하였다. 프로펠러의 높은 선속도가 발생하여 유동 현상이 가장 뚜렷하게 나타나리라 예측되는 회전속도인 6,000 RPM을 기준으로 격자 의존도 검사를 진행하였으며, 그 결과를 Fig. 2에 나타내었다. 결과를 바탕으로 해석 시간과 수렴성을 고려하여 약 1,000만 개의 격자를 사용하였다.
3.2 설계 조건
저고도 정지 비행 상태에서의 e-VTOL UAM을 고려하여 입·출구 경계 조건(Boundary Conditions)을 대기압(101,325 Pa)으로 가정하였으며, 각 프로펠러 끝단(Tip)에서의 선속도는 약 0.22 Ma(75 m/s)로 비압축성 유동으로 고려하여 계산하였다. 해당 연구에서 사용된 9450 프로펠러는 6,000 RPM보다 높은 회전 속도에서 운행 시 소음 문제와 구조적 변형으로 인한 문제가 발생할 수 있고, 모터의 효율이 떨어지게 된다. 따라서 회전 유동장의 유체의 속도를 6,000 RPM으로 설정하여 연구를 진행하였다. 상세한 조건은 Table 3에 정리하였다.
4. 결과 및 고찰
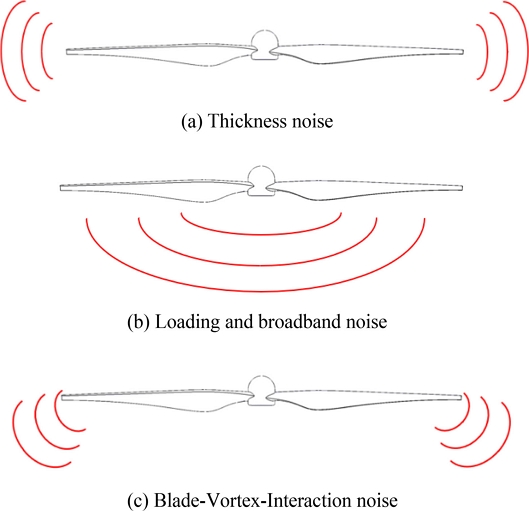
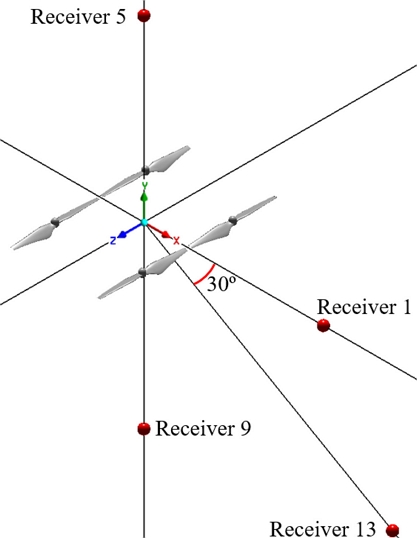
본 연구에서는 Phantom 3 드론에서 사용하는 9450 프로펠러의 형상을 단순화하고 ANSYS Fluent SW를 수치해석에 활용하였다. Fig. 1에서의 거리 변수에 Table 2의 수치를 적용하여 기준 모델과 Cases 1-5를 프로펠러 간격에 따른 추력 및 공력 소음의 변화에 대하여 수치해석을 진행하였다. 총 6가지 모델에 대하여 압력 계수(Pressure Coefficient, Cp)와 와도 분포(Vorticity Contour), 속도 벡터(Velocity Vector), 그리고 주파수(Frequency)에 따른 SPL을 비교하여 공력소음 저감에 기반한 최적의 모델을 설계하기 위하여 유동 소음 해석을 진행하였다. 정지 비행상태에서의 주파수에 따른 SPL 값을 확인하기 위하여 임의의 수신자를 Fig. 3의 소음원에 따른 전파 방향을 고려하여 설정하였으며, 그 위치를 Table 4에 정리하였고, Fig. 4에 나타내었다. 1-4번 수신자는 소음의 전파 방향이 수평인 두께(Thickness) 소음을, 5-12번 수신자는 수직 방향으로 전달되는 로딩(Loading) 및 광대역(Broadband) 소음을, 13-16번 수신자는 수평에서 30º의 각도로 전달되는 BVI 소음을 측정한다. 수신자의 위치를 소음원으로부터 너무 멀리 위치시키면 소음 감소폭의 정도가 미미할 것이라 판단되어 0.5 m의 등간격으로 멀어지게 설정하였다. 해석의 신뢰성을 확보하기 위하여 KISTI의 NURION 수퍼컴퓨터 5호기(Intel Xeon Phi 7250 1.4 GHz, 68 CPU Cores, and 96 GB Memory)를 사용하였다.
4.1 속도 벡터 및 와도 분포
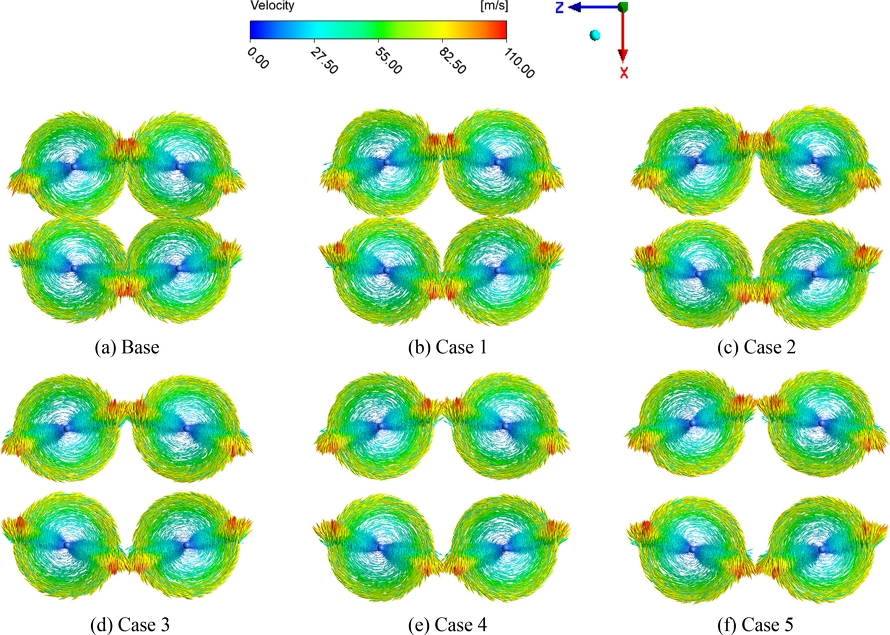
프로펠러의 간격에 따른 속도벡터의 분포를 Fig. 5에 나타내었다. 본 연구에서는 회전영역의 유체를 직접 회전시키는 MRF 기법을 활용하였다. 유체의 최대 속도는 프로펠러의 끝단(Tip)에서 발생하였다. 기준 모델과 Cases 1-5의 속도 벡터의 양상에서 프로펠러의 거리에 따른 눈에 띄는 속도 벡터의 변화는 확인할 수 없었다. 이는 프로펠러의 간격이 프로펠러 및 유체의 속도에는 큰 영향을 끼치지 않으며, 따라서 높은 속도에 의하여 발생하는 고속 충격(High Speed Impulsive, HSI) 소음 및 충격파(Shockwave) 소음의 큰 변화는 없을 것이라 판단된다.
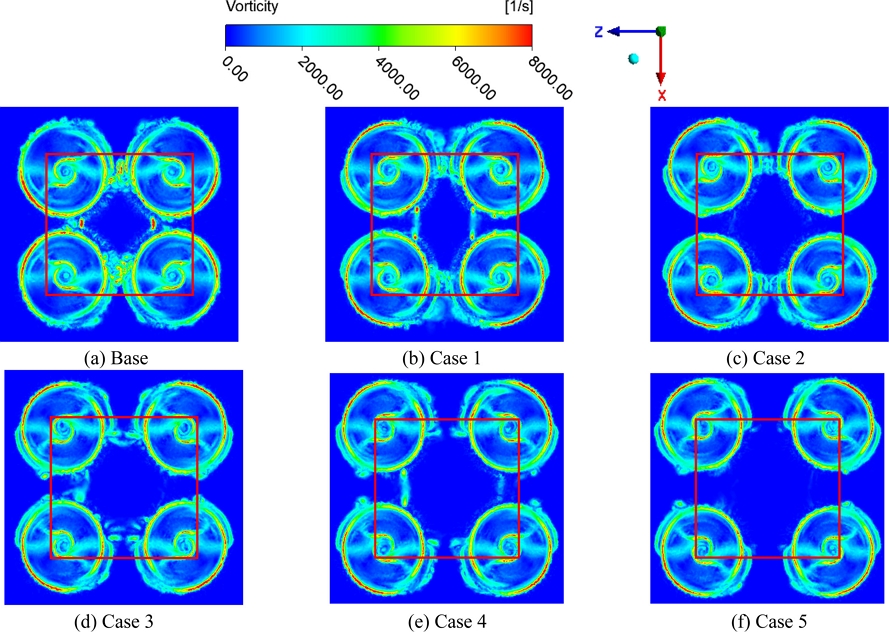
공력소음에 직·간접적으로 영향을 끼치는 와류를 확인하기 위하여 와도 분포에 대한 해석을 진행하였다. 프로펠러의 거리에 따른 와도의 변화를 시각적으로 확인하기 위하여 등고선(Contour)을 사용하여 와도의 변화를 Fig. 6에 나타내었다. 와도는 일부 위치에서만 매우 높게 계산되기 때문에 원활한 비교를 위하여 0-8,000 [s-1]으로 범위를 설정하였다. Fig. 6을 통하여 프로펠러의 선속도가 가장 높은 끝단으로부터 와도가 생성되는 것을 알 수 있으며, 프로펠러의 간격이 짧을수록 각각의 프로펠러로부터 발생하는 와류의 간섭으로 인하여 더 높은 와도가 확인되는 것을 알 수 있었다. 와도가 가장 크게 발생하는 모델은 프로펠러의 거리가 가장 짧은 기준 모델이며, 거리가 가장 먼 Case 5에서 가장 적은 와도가 확인되었다. 특히 4개의 프로펠러의 영향을 모두 받는 중심부에서의 와도가 눈에 띄게 변하였으며, 비교를 위하여 적색 사각형으로 표시하였다. 기준 모델과 Cases 1-5를 비교하면 중심부에서의 와도는 기준 모델에서 가장 크게 확인되며 Case 5에서 가장 적게 확인되었다. 이를 통하여 프로펠러의 거리가 유동의 간섭에 직접적인 영향을 끼치며, 프로펠러의 거리가 멀어질수록 유동의 간섭이 줄어드는 것을 알 수 있다. 따라서 유동의 간섭과 관련된 BVI 소음에 영향을 끼칠 것으로 판단된다.
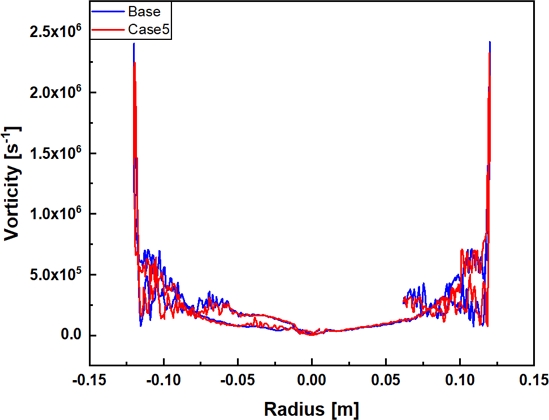
Figs. 7, 8은 각각 프로펠러의 반경에 따른 압력 계수와 와도를 비교한 그래프이다. 명확한 비교를 위하여 압력 계수와 와도의 값 차이가 명확한 기준 모델과 Case 5를 비교에 사용하였다. 압력 계수는 관성력에 대한 압력의 상대적인 비로서, 정압을 동압으로 나눈 값으로 나타낼 수 있다. 따라서 압력 계수의 차가 큰 것은 속도 구배와 압력의 변동이 큰 것을 의미하며, 이는 큰 와류로 인한 소음이 발생한다는 것이다. Fig. 7에서 프로펠러의 끝단으로 갈수록 압력 계수의 차이가 커진다. 이는 프로펠러의 끝단에서 큰 속도 구배와 압력 변동이 발생한다는 것을 알 수 있으며, 때문에 Fig. 8의 와도 그래프에서 프로펠러 끝단에서 가장 큰 와도가 측정되는 것을 확인할 수 있다. Figs. 7과 8을 통하여 기준 모델 대비 프로펠러의 거리가 먼 Case 5에서 압력 계수의 차가 0.934에서 0.883으로 약 5.44% 감소하였고, 와도는 2.401 × 106 1/s에서 2.169 × 106 1/s으로 약 10% 줄어든 것을 확인할 수 있다.
4.2 추력 변화
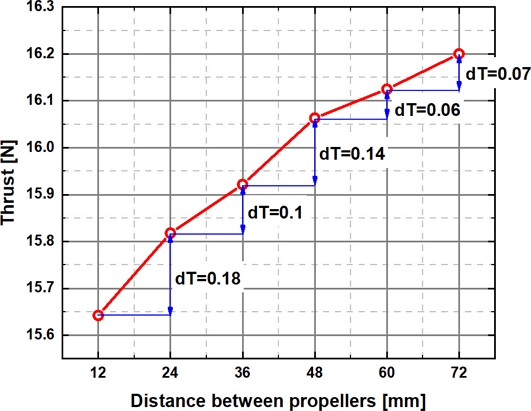
프로펠러의 간격에 따라 유동이 변화하며 와도에 영향을 끼치고 이는 추력의 변화로도 이어질 수 있으므로 거리에 따른 추력 변화를 확인하였다. 추력은 프로펠러의 거리가 멀어질수록 증가하였으며, 기준 모델이 15.64 N, Cases 1-5에서 각각 15.82, 15.92, 16.06, 16.12, 16.2 N으로 나타났다. 해당 결과의 비교를 위하여 Fig. 9에 그래프로 나타내었다. 프로펠러의 거리가 멀어질수록 전체 추력은 증가하는 경향이 있지만, 프로펠러 간 거리가 0.1R(12 mm) 증가할 때마다 추력이 증가하는 비율(Propeller Distance-thrust Ratio, dT)은 감소하며, Fig. 9를 통하여 알 수 있다. 이는 거리에 따른 추력이 무한히 증가하는 것이 아니며 일정 수치에 수렴한다는 것을 예상할 수 있다.
Fig. 10은 프로펠러의 회전으로부터 발생하는 후류(Slipstream)를 속도 분포로 나타낸 것이다. 명확한 비교를 위하여 기준 모델과 Case 5를 비교에 사용하였으며, 프로펠러의 위치를 적색 사각형으로 표시하였다. 기준 모델에서는 후류가 발생하는 초입부에 와류의 영향으로 인하여 후류가 넓게 퍼지는 것을 볼 수 있으며 상대적으로 와류가 적게 발생하는 Case 5에서는 해당 현상이 줄어들었다. 또한 Case 5의 후류의 후반부는 기준 모델에 비해 후류의 폭이 좁아진 것을 알 수 있다.
프로펠러의 거리가 증가함에 따라 후류가 와류로부터 영향을 적게 받으며, 중심으로 집중되는 경향성을 보인다. 이러한 경향성으로 인하여 상대적으로 후류의 흐름폭이 좁은 Case 5에서의 후류의 속도가 기준 모델에 비해 빨라지며 추력이 증가하게 된다.
4.3 공력 소음
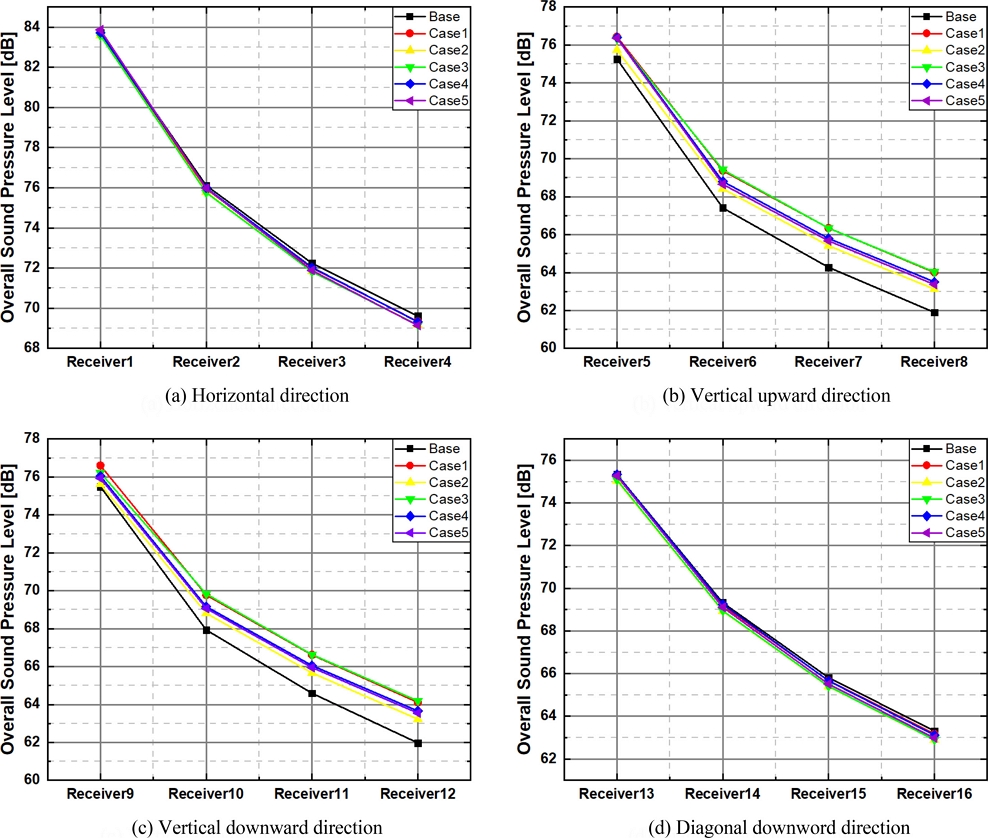
프로펠러의 거리에 따른 공력 소음의 정도를 확인하기 위하여 Table 4의 16가지 수신자에 대한 전체 음압 수준(Overall Sound Pressure Level, OASPL)을 계산하였다. OASPL은 전체 주파수 스펙트럼의 모든 소리 에너지를 고려하며, 일정 시간 동안 측정된 음압의 제곱 평균에 로그를 취한 값에 기준치에 대한 보정 상수를 더한 값으로 나타내고 단위는 데시벨(dB)로 나타낸다. OSAPL은 소음 전파 방향을 고려하여 위치시킨 16가지의 수신자에 대하여 Fig. 11과 같이 계산되었다. 수신자 1-4에서 두께 소음, 5-12에서 로딩 소음과 광대역 소음, 13-16에서 BVI 소음을 측정하였다. 두께 소음 및 BVI 소음을 측정한 수신자 1-4와 13-16에서 프로펠러의 거리가 멀어질수록 소음은 감소하였다. 수신자 1에서 기준 모델(83.72 dB) 대비 Case 1이 83.66 dB로 가장 적게(0.06 dB, 0.07%) 감소하였으며, 수신자 4에서 기준 모델(69.6 dB) 대비 Case 5가 69.1 dB로 가장 많이(0.47 dB, 0.68%) 감소하였다. 이는 프로펠러의 거리가 멀어질수록 유동의 간섭이 줄어든 영향이라 판단된다. 하지만 이러한 변화는 사람이 느끼기 힘들 정도의 미미한 차이이며, 정지 비행 상태에서는 유동의 흐름이 수직 방향으로 이동하기 때문에 소음의 전파 방향이 수평에 가까운 두께, 그리고 BVI 소음은 그 영향을 적게 받아 소음 저감의 차이가 미미한 것이라 판단된다. 반면 수신자 5-8과 9-12에서 측정된 로딩 및 광대역 소음은 프로펠러의 거리가 멀어짐으로 인하여 높게 측정되었다. 수신자 5에서는 기준 모델의 75.257 dB 대비 Case 1에서 76.4349 dB(1.56%), Case 2에서 75.7327 dB(0.63%), Case 3에서 76.3324 dB(1.43%), Case 4에서 76.3967 dB(1.51%), Case 5에서 76.3595 dB(1.46%)로 증가하였다. 수신자 8에서는 기준 모델의 61.8933 dB 대비 Case 1에서 64.0054 dB(3.41%), Case 2에서 63.1227 dB(1.98%), Case 3에서 64.0268 dB(3.44%), Case 4에서 63.5032 dB(2.6%), Case 5에서 63.3674 dB(2.38%)로 증가하였다. 이는 프로펠러의 거리가 멀어짐에 따라 증가하는 추력과 관련이 있다. 프로펠러와 같은 구성 요소가 유체와 상호 작용하면서 압축 및 확장되는 과정에서 압력 변동이 발생하며, 추력이 증가한 것은 압력 변동이 커졌다는 것을 뜻한다. 하지만 이러한 압력 변동은 주파수 성분을 가진 파동을 만들어 내며, 이 파동이 공기나 다른 물체에 부딪히면서 로딩 소음이 발생한다. 따라서 프로펠러의 거리를 멀어지게 함으로써 추력 성능은 증가시켰지만 필연적으로 로딩 소음이 증가하게 된다.
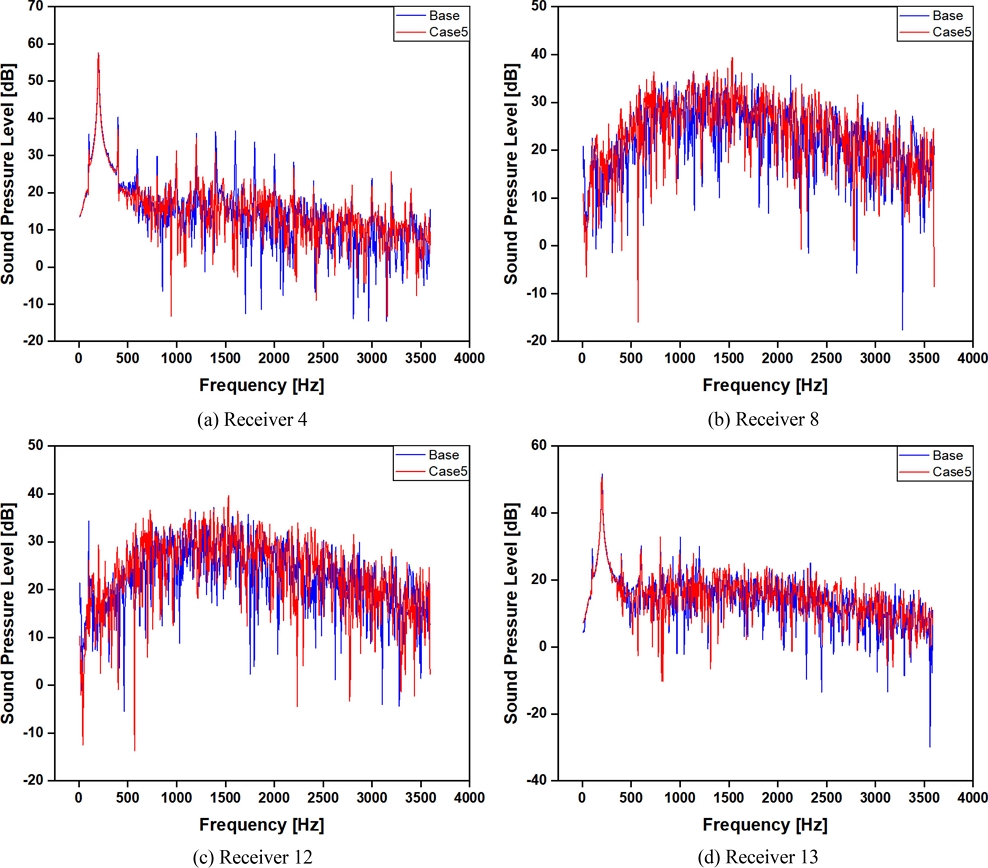
프로펠러의 거리에 따른 소음의 증감을 설명하기 위하여 특정 수신자에서 측정된 주파수에 따른 SPL을 비교하여 Fig. 12에 나타내었다. 비교에 사용된 값은 기준 모델과 OASPL의 증감이 뚜렷하게 나타난 Case 5에서의 수신자 4, 8, 12, 그리고 16에서 측정된 값을 사용하였다. 두께 소음을 비교한 Figs. 12(a)와 BVI 소음을 비교한 12(d)에서는 전체적으로 특정 주파수에서 큰 진폭을 가지는 파장은 줄었지만 OASPL에서의 값에서 알 수 있듯이 저주파 및 고주파 영역에서 값차이가 미미하다. 반면 로딩 및 광대역 소음을 비교한 Figs. 12(b)와 12(c)를 확인해보면 저주파 영역에서 기준 모델보다 Case 5가 평균 SPL이 수신자 8에서 1.27 dB(8.48%), 수신자 12에서 0.26 dB(1.61%) 더 높게 측정된 것을 확인할 수 있었다. 저주파는 공기의 진동이 느리고 큰 파동을 만들어내기 때문에 멀리 전파되어 큰 진동을 만들어 낸다. 이러한 저주파의 특성 때문에 Figs. 10(b)와 10(c)처럼 수신자의 위치가 멀어질수록 소음의 증가폭이 커지게 되었다.
5. 결론
최근 전세계적으로 차세대 교통수단인 e-VTOL UAM이 각광받으며, UAM의 비행 시 발생하는 공력소음 문제가 대두되고 있다. 일반적으로 프로펠러로 인하여 발생하는 공력소음은 덕트를 사용하거나 프로펠러의 형상을 개선하는 경우가 많다. 하지만 덕트의 경우 기체의 중량이 증가하며, 프로펠러의 형상 개선의 경우 생산성 및 실현 가능성의 벽에 부딪히게 된다. 따라서 본 연구에서는 생산성과 소음을 모두 고려하여 프로펠러의 간격에 따른 최적설계에 대하여 연구를 진행하였다. 기준 모델과 다섯 가지 비교 모델에 대한 결론은 다음과 같다.
(1) 수치 해석 값의 수렴성을 향상하기 위하여 정상(Steady) 해석 값을 초기값으로 하여 과도(Transient) 해석을 진행하였다. 정상 해석은 SST k-ω 모델을 사용하였으며, 과도 해석은 LES 모델을 사용하였다. 수치적으로 공력 음향해를 해석하고 FFT를 통하여 주파수에 따른 SPL 값을 확인하기 위하여 FW-H 모델을 사용하였다. 프로펠러의 간격은 0.1R(12 mm)씩 등간격으로 다섯가지 모델을 설계하였다. 프로펠러는 6,000 RPM의 회전속도로 고정하여 연구를 진행하였으며, 해석 시간과 수렴성을 검증하기 위하여 격자 의존도 검사를 진행하였다.
(2) 프로펠러 회전 시 발생하는 주요 소음의 전파 방향을 고려하여 총 16가지의 수신자를 설정하였다. 기준 모델 포함 총 6가지 모델에 대하여 압력 계수, 와도 분포, 속도 벡터, 추력, 그리고 공력 소음을 해석하였다. 압력 계수와 와도의 차이가 분명하게 나타나는 기준 모델과 Case 5를 비교하였을 때 압력 계수의 차는 Case 5에서 5.44% 감소하였고, 최대 와도는 10% 감소된 것을 확인하였다. 속도 벡터는 프로펠러의 거리에 따라 큰 변화를 보이지 않으며, 따라서 유속과 관련된 HSI 소음 및 충격파 소음에는 큰 영향을 끼치지 않을 것이라 판단된다. 와도 분포를 통하여 프로펠러의 거리가 멀어질수록 중심부의 유동 간섭이 줄어드는 것을 확인할 수 있었으며 간섭으로 발생하는 BVI 소음의 저감을 기대할 수 있다.
(3) 프로펠러의 거리가 멀어질수록 추력은 향상되었다. 기준 모델이 15.64 N으로 계산되었으며, Cases 1-5에서 각각 1.15, 1.79, 2.68, 3.07, 3.58%으로 증가된 것으로 나타났다. 해당 현상은 속도 분포도의 후류의 형상을 통하여 확인할 수 있었다. 명확한 비교를 위하여 기준 모델과 Case 5를 비교하였으며, 프로펠러의 거리가 멀어질수록 후류는 중앙으로 집중되는 경향성을 보였다. 이러한 경향성으로 인하여 후류의 흐름폭이 좁은 Case 5에서의 유속이 빨라지게 되며 추력이 증가하게 된다.
(4) 공력소음을 비교하기 위하여 OASPL을 계산하였다. 두께 소음을 측정하기 위한 수신자 1-4와 BVI 소음을 측정하기 위한 수신자 13-16에서는 유동의 간섭이 줄어들어 0.06-0.47 dB(0.07-0.68%) 저감된 소음이 측정되었다. 반면 로딩 및 광대역 소음을 측정하기 위한 수신자 5-12에서는 프로펠러의 거리에 따라 소음이 0.47-2.2 dB(0.6-3.5%) 증가하였다. 이는 추력 성능의 향상으로 인한 압력 변동으로 로딩 소음이 증가하였기 때문이다. 프로펠러의 거리에 따른 소음의 증감을 설명하기 위하여 소음을 FFT를 통하여 주파수에 따른 SPL 값을 비교하였다. 수신자 4와 13에서는 특정 주파수에서의 큰 진폭을 가지는 파장이 줄어들었다. 반면 수신자 8과 12에서는 저주파 영역에서 기준 모델보다 개선 모델에서의 평균 SPL 값이 각각 1.27 dB(8.48%), 0.26 dB(1.61%) 높게 측정되었으며, 저주파의 특성으로 인하여 수신자의 거리가 멀어질수록 소음의 증가폭이 커지는 것을 확인하였다.
본 연구를 통하여 프로펠러의 거리가 멀어질수록 와류가 줄어들어 두께 및 BVI 소음이 줄어들고 추력 성능이 증가하였지만, 추력 성능의 증가로 인한 압력 변동과 특정 주파수 영역에서 소음이 증가하는 것을 알 수 있었다. 따라서 추력의 성능과 비례하는 로딩 소음의 정확한 비교를 위해서는 같은 추력 수치에서의 소음을 비교하여야 하며, 이를 위하여 프로펠러의 간격은 같게 하되 회전 속도를 변경하여 추력을 같게 한 후 소음 측정이 진행되어야 한다. 또한 저주파 및 고주파의 특성을 고려하여 설계 및 소음 측정이 진행되어야 하며, 프로펠러의 거리뿐만 아니라 로터의 틸팅(Tilting) 각, 프로펠러의 형상, 회전 속도 등 다양한 설계 변수를 고려하여 설계가 진행되어야 한다.
Acknowledgments
이 결과물은 2022년도 대구가톨릭대학교 학술연구비 지원에 의한 것임.
REFERENCES
- Chung, K. H., Kim, D. H., Kim, D. K., Song, K. W., Kim, S. H., Hwang, C. J., (2010), Introduction to international research trends and domestic research plans for the noise reduction of helicopter rotor blade, Proceedings of the Korean Society for Noise and Vibration 2010 Autumn Conference, 56-57. https://scienceon.kisti.re.kr/srch/selectPORSrchArticle.do?cn=NPAP10076965
-
Marzouk, O. A., (2022), Urban air mobility and flying cars: Overview, examples, prospects, drawbacks, and solutions, Journal of the Open Engineering, 12(1), 662-679.
[https://doi.org/10.1515/eng-2022-0379]

-
Guo, J., Zhou, T., Fang, Y., Zhang, X., (2021), Experimental study on a compact lined circular duct for small-scale propeller noise reduction, Journal of the Applied Acoustics, 179(108062), 1-10.
[https://doi.org/10.1016/j.apacoust.2021.108062]

-
Malgoezar, A. M., Vieira, A., Snellen, M., Simons, D. G., Veldhuis, L. L., (2019), Experimental characterization of noise radiation from a ducted propeller of an unmanned aerial vehicle, International Journal of Aeroacoustics, 18(4-5), 372-391.
[https://doi.org/10.1177/1475472X19852952]

-
Noda, R., Nakata, T., Ikeda, T., Chen, D., Yoshinaga, Y., Ishibashi, K., Rao, C., Liu, H., (2018), Development of bio-inspired low-noise propeller for a drone, Journal of Robotics and Mechatronics, 30(3), 337-343.
[https://doi.org/10.20965/jrm.2018.p0337]

- Choi, I., S., Han, C. H., (2022), Study on the aerodynamic characteristics of an wing depending on the propeller mounting position, Journal of Aerospace System Engineering, 16(6), 54-63.
-
Li, Y., Yonezawa, K., Xu, R., Liu, H., (2021), A biomimetic rotor-configuration design for optimal aerodynamic performance in quadrotor drone, Journal of Bionic Engineering, 18(4), 824-839.
[https://doi.org/10.1007/s42235-021-0069-0]

-
Penkov, I., Aleksandrov, D., (2017), Analysis and study of the influence of the geometrical parameters of mini unmanned quad-rotor helicopters to optimise energy saving, International Journal of Automotive and Mechanical Engineering, 14(4), 4730-4746.
[https://doi.org/10.15282/ijame.14.4.2017.11.0372]

-
Li, Y., Yonezawa, K., Liu, H., (2021), Effect of ducted multi-propeller configuration on aerodynamic performance in quadrotor drone, Journal of Multidisciplinary Digital Publishing Institute Drones, 5(3), 101.
[https://doi.org/10.3390/drones5030101]

-
Shukla, D., Komerath, N., (2018), Multirotor drone aerodynamic interaction investigation, Journal of Multidisciplinary Digital Publishing Institute Drones, 2(4), 43.
[https://doi.org/10.3390/drones2040043]

-
Menter, F., R., (1993), Zonal two equation k-ω turbulence models for aerodynamic flows, Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, AIAA-93-2906.
[https://doi.org/10.2514/6.1993-2906]

-
Menter, F. R., (1994), Two-equation eddy-viscosity turbulence models for engineering applications, AIAA Journal, 32(8), 1598-1605.
[https://doi.org/10.2514/3.12149]


B.Sc. candidate in the School of Mechanical and Automotive Engineering, Catholic University of Daegu. His research interest is urban air mobility, electric vehicle, and aerodynamics.
E-mail: juu9336@cu.ac.kr

Engineer in the Rotorcraft Flight Dynamics Team, Korea Aerospace Industries (KAI). His research interest is aeroacoustics, aerodynamics, propeller/rotorcraft, optimization, and turbo machinery.
E-mail: jihun.song@koreaaero.com

Professor in the Department of Mechanical Engineering, Catholic University of Daegu. His research interest is heat transfer, fluid engineering, electric vehicle, and advanced air mobility.
E-mail: dlee@cu.ac.kr