미시적 수준에서 인공 고관절 삽입 후 근위 대퇴골의 구조적 거동 분석

1. 서론

대퇴골두 무혈성 괴사는 대퇴골로의 혈류가 줄어듦에 따라 영양분 부족으로 골의 괴사를 일으키는 골격계 질환이다[1]. 이는 고관절의 자유로운 보행과 운동을 불가능하게 할 뿐만 아니라 극심한 통증도 수반한다. 특히 해당 질환의 정확한 원인이 규명되지 않았으며 초기 발병 시 특별한 자각 증상이 없어 더욱 주의가 요구되는 질환이다[2]. 이 질환의 치료법은 골의 괴사 정도에 따라 일반적으로 비수술적 치료와 수술적 치료로 구분된다. 먼저 골두의 괴사가 경미한 경우 자연 경과를 지켜보거나 약물 치료를 통해 증상을 호전시킨다[3]. 하지만 비수술적 치료에도 증상이 호전되지 않거나, 괴사의 정도가 심한 경우 수술적 치료가 시행되며 대표적으로 인공 고관절 전치환술(Total Hip Replacement, THR)이 대표적으로 사용된다[4].

인공 고관절 전치환술은 괴사한 대퇴골두를 제거하고 금속으로 이루어진 인공 고관절을 단단히 끼워 넣어 고정하여 인공 삽입물로 실제 관절을 대신하는 수술이다[5]. 해당 수술 방법은 고관절 통증을 경감하고 관절운동을 증대시켜 일상적인 활동을 가능하게 한다. 특히 골절 질환이 동반된 노인 환자들에게 매우 성공적인 수술법으로 알려져 있다[6]. 이러한 장점에도 불구하고 해당 수술법은 다양한 부작용이 존재한다. 대표적으로 부작용으로 인공 고관절의 탈구(Dislocation), 감염(Infection), 대퇴골 골절(Fracture), 혈전(Blood Clot), 인공 고관절의 해리(Loosening) 등이 존재한다[7]. 특히 인공 고관절의 해리 현상은 수술 후 가장 빈번하게 나타날 뿐만 아니라 다양한 합병증을 야기시켜 임상 분야에서 큰 문제로 대두되고 있다[8].

인공 고관절의 해리 현상은 삽입된 인공물에 의한 응력방패현상(Stress Shielding)으로부터 야기된다[9]. 골격계에서 발생하는 응력방패 현상이란 삽입된 인공 고관절이 삽입 주변부의 정상골 대비 높은 강성으로 인해, 응력이 인공 고관절에서 대부분 발생하고 주변 골에는 거의 발생하지 않는 현상을 말한다[10]. 일반적으로 인체의 골은 자기 최적화 능력을 보유하고 있어 응력이 높은 부위에 골을 생성하고, 반면 응력이 적은 부위는 골을 소실시킨다[11]. 따라서 응력방패 현상이 장기간 지속될 시골 소실로 인한 인공 고관절의 해리가 유발된다. 또한 인공 고관절의 해리는 염증 및 통증 유발, 주변부 골의 파손 등 다양한 합병증을 야기시켜 인공 고관절의 일부 또는 전부를 교체하거나 재배치하는 재치환술을 요구한다[8]. 따라서 고관절 전치환술 전 응력 방패 현상을 미연에 분석하고 예방하는 것이 매우 중요하다.

이러한 중요성과 함께 이전 연구자들은 응력방패 현상을 파악하기 위한 다양한 연구를 진행하였다. 특히, 동일 하중 아래 정상골과 인공 고관절이 삽입된 골의 구조적 거동의 차이를 비교함으로써 응력방패 현상을 파악하는 연구가 대표적이다[12-14]. 비록 위 연구들은 인공 고관절 삽입골과 정상골간 구조적 거동의 상이함을 정량적으로 보였지만, 골 밀도 영상 기반 거시적 수준(Macro Level)의 연구로 대퇴골 미세구조의 특징을 반영하지 못하는 한계점을 가진다. 하지만, 미세구조로 구성된 근위 대퇴골의 해면골은 삽입된 인공 고관절과 직접적인 기계적 상호작용을 한다[15]. 따라서 정확한 응력방패 현상을 분석하기 위해서는 골 미세구조의 특징을 고려한 미시적 수준(Micro Level)에서의 거동 분석이 필수적이다[16,17].

따라서, 본 연구는 미시적 수준에서 인공 고관절 전치환술 이후 인공 고관절이 삽입된 근위 대퇴골의 구조적 거동을 정량적으로 분석하고 응력방패 현상을 파악하는 것을 목적으로 한다. 이를 위해 50 μm 고해상도 근위 대퇴골에 인공 고관절을 삽입 후 일상 하중 조건 아래 발생하는 구조적 거동의 분석을 통해 응력방패 현상을 파악하였다.

2. 본론

2.1 근위 대퇴골과 인공 고관절 모델

본 연구는 대퇴골두 무혈성 괴사의 대표적 환부인 근위 대퇴골을 인공 고관절 삽입 골격계로 선정하였다. 다만, 미시적 수준에서 미세구조의 거동을 분석하기 위해서는, 최소 100 μm의 높은 영상 해상도를 필요로 한다. 하지만, 100 μm의 이상의 해상도는 과도한 방사선량을 요구하여 생체 내(in vivo) 근위 대퇴골 영상의 촬영은 현실적으로 불가능한 상황이다[18]. 반면, 현재 촬영 가능한 근위 대퇴골의 임상 영상은 평균 600 μm의 낮은 해상도를 가져 골 미세구조 표현이 불가하며, 환자맞춤형 하중의 확보가 매우 어렵다. 이에, 본 연구에서는 이전 연구[19]에서 제시된 50 μm 고해상도 인공 근위 대퇴골 영상을 사용하였다.

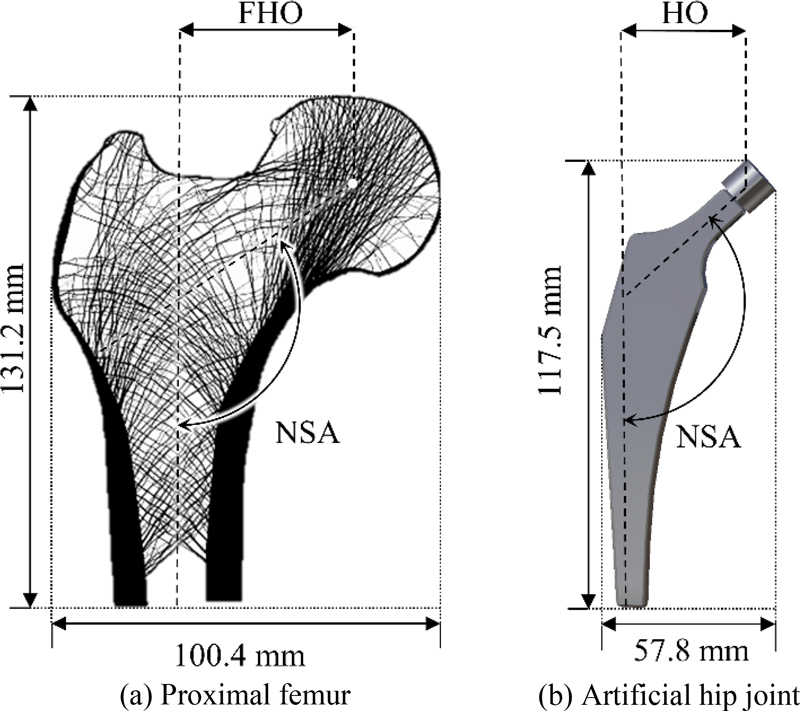
Fig. 1(a)는 본 연구에서 사용한 고해상도 근위 대퇴골 영상을 나타낸다. 해당 근위 대퇴골 영상은 영역별 골 미세구조 고유패턴(Principal and Secondary Compressive Groups, Principal and Secondary Tensile Group) [20,21] 잘 나타낼 뿐만 아니라 해당 미세구조를 생성하는 맞춤형 하중 정보를 포함하고 있다[22]. 이러한 특성으로 인해 해당 근위 대퇴골 영상은 많은 연구에서 활용된 바 있다[17,23]. 근위 대퇴골의 크기는 100.4 × 131.2 mm이며, FHO (Femoral Head Offset)와 NSA (Neck Shaft Angle)는 각각 44.6 mm와 128°이다. 여기서 FHO와 NSA는 임상의 전치환술에서 인공 고관절의 크기를 결정하는데 매우 중요한 변수로 알려져 있다[24].

Fig. 1

High-resolution proximal femur (50 μm resolution) (a) and artificial hip joint (b)

본 연구는 인공 고관절 모델로 구조의 단순성과 뛰어난 치료결과로 인해 임상에서 가장 많이 사용되는 Single Wedge Type을 선정하였다[25]. 인공 고관절의 크기는 57.8 × 117.5 mm이며, HO (Head Offset)와 NSA는 각각 44 mm와 128o로 근위 대퇴골의 치수와 유사하게 선정하였다. 대퇴골과 인공 고관절의 유사한 Head Offset과 Neck Shaft Angle은 기계적 안정성에 기여한다고 보고된 바 있다[24].

2.2 인공 고관절 삽입에 따른 골 미세구조의 구조적 거동 변화 분석

본 연구는 유한요소해석을 통해 정상골과 인공 고관절이 삽입된 근위 대퇴골의 구조적 거동 분석을 수행하였다. 이를 위해 정상 근위 대퇴골과 인공 고관절이 삽입된 근위 대퇴골 영상을 유한요소 모델로 생성하였다. 유한요소 모델은 ANSYS의 PLANE 42를 사용하여 4절점 2차원 사각 요소들로 구성하였다. 각 요소 크기는 영상의 픽셀 해상도와 동일하게 50 × 50 μm로 부여하였다. 따라서 정상골의 유한요소 모델은 2,770,997개의 절점과 2,766,064개의 요소로 구성되었으며, 인공 고관절 삽입골의 유한요소 모델은 2,115,241개의 절점과 2,110,774개의 요소로 구성되었다. 인공 고관절에 해당하는 요소의 물성치는 티타늄 합금(TiAl6v4)의 포아송비(0.32)와 탄성계수(114 GPa)를 부여하였다. 치밀골에 해당하는 모든 요소는 0.3의 포아송비와 22.5 Gpa의 탄성계수 값을 부여하였으며. 해면골에 해당하는 요소는 동일한 0.3의 포아송비와 밀도-탄성계수 변환식(식(1))을 통해 탄성계수를 부여하였다[26].

$\[ \begin{array}{c}{E}_i=0.4567{\left(2{\rho }_i\right)}^{1.49} if {\rho }_i\le 0.84\\ E_i=0.2862{\left(2{\rho }_i\right)}^{2.39} if {\rho }_i>0.84\end{array} \]$

(1)

여기서 E_i는 i번째 요소의 탄성계수이며, ρ_i는 i번째 요소의 상대 밀도값을 말한다.

본 연구는 인공 고관절 삽입골의 응력방패 현상을 분석하기 위해, 먼저 정상골과 인공 고관절이 삽입된 근위 대퇴골의 구조적 거동을 3가지 일상 하중 조건(외발서기, 외전, 내전) 아래 각각 계산하였다. 다만, 해당 근위 대퇴골에 발생하는 일상 하중을 고려하기 위해, 본 연구는 해당 근위 대퇴골의 미세구조를 생성하는 맞춤형 하중을 적용하였다[27-29].

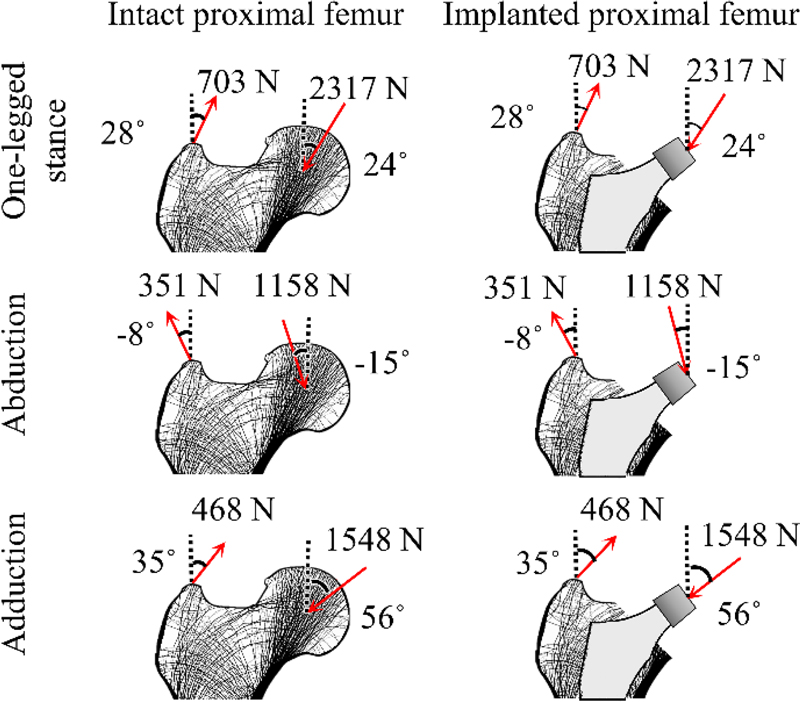
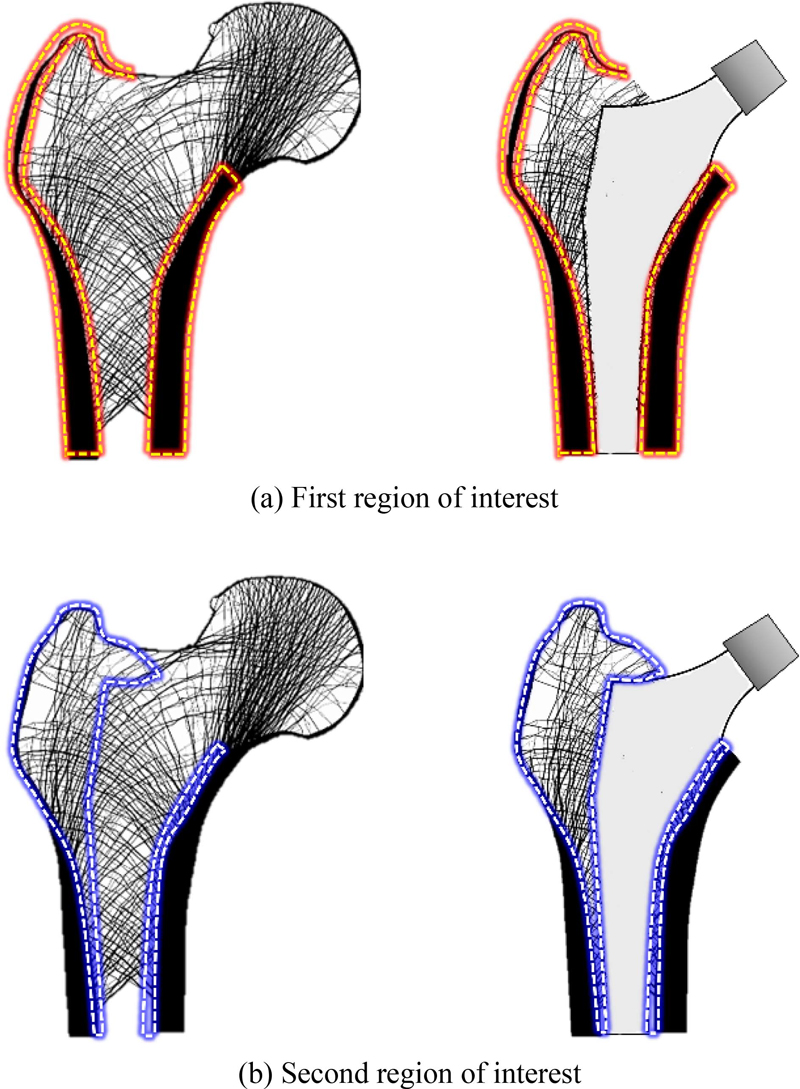
Fig. 2는 본 연구에서 사용한 하중 조건을 나타내며, 본 연구는 각 하중을 대퇴골두와 대퇴전자 부위에 분포 하중의 형태로 부여하였다. 경계조건으로는 3가지 하중 조건 모두 가장 아래 절점을 모든 방향으로 구속했다. 그리고 인공 고관절 삽입골의 치밀골 전체를 첫 번째 관심영역(Region of Interest, ROI)으로 선정하였으며, 두 번째 관심영역으로는 삽입골에서 인공 고관절을 제외한 해면골 전체를 선정하였다(Fig. 3). 그리고 동일한 관심영역에서 정상골과 삽입골의 구조적 거동을 비교 분석하여 응력방패 현상을 파악하였다.

Fig. 2

Three load conditions to consider daily activities

Fig. 3

Two regions of interest: cortical bone (1st row) and cancellous bone (2nd row)

본 연구는 응력방패 현상의 정량적인 비교 분석을 위해 관심 영역에서 발생한 변형률 에너지의 평균값(식(2))과 표준편차(식(3))를 정량적 지표로 사용하였다. 그리고 각 관심영역에서의 하중조건에 따른 응력방패 현상의 발생 가능성은 정상골과 삽입골에서 발생한 변형률 에너지 평균값과 표준편차 값의 상대 변화율로 평가하였다.

$\[ \mathrm{\mu }=\frac{1}{n}\sum _{i=1}^n S{E}_i \]$

(2)

$\[ \sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n {\left(S{E}_i-\mu \right)}^2} \]$

(3)

여기서 SE_i는 각 관심영역의 i번째 요소에서 발생한 변형률 에너지 값이며, n은 각 관심영역의 총 요소 수를 의미한다.

본 연구의 유한요소해석은 ANSYS의 Mechanical APDL 2022 R1과 개인용 데스크탑(CPU: i9-12900K, RAM: 64 GB, GPU: GeForce RTX 3080)을 이용하여 수행되었다.

3. 결과 및 고찰

본 연구는 인공 고관절 삽입에 따른 미시적 수준에서의 골 미세구조 구조적 거동과 응력방패 현상의 파악을 목적으로 한다. 이를 위해 본 연구는 유한요소해석 절차의 타당성을 정상골 구조적 거동 결과와 이전 연구의 결과를 비교 분석하여 검증하였다[16,30,31]. Fig. 4는 3가지 일상 하중 조건 아래 정상골과 인공 고관절이 삽입된 근위 대퇴골의 변형률 에너지 분포를 나타낸다. 먼저 정상골에서 외다리 서기, 외전, 내전 하중에 대해 발생한 최대 변형률 에너지는 치밀골에서 발생하였으며, 각각 에너지는 대퇴경부(Femoral Neck), 골간단(Metaphysis) 내측, 외측에서 발생하였다. 반면 해면골에서는 외다리 서기, 외전, 내전에 대해 각각 대퇴경부, 전자간부, 골간단 외측에서 하중을 담당하며 치밀골로 전달하였다. 이는 이전 연구와 동일한 결과로, 본 연구의 유한요소해석에 대한 절차의 타당성을 입증한다.

Fig. 4

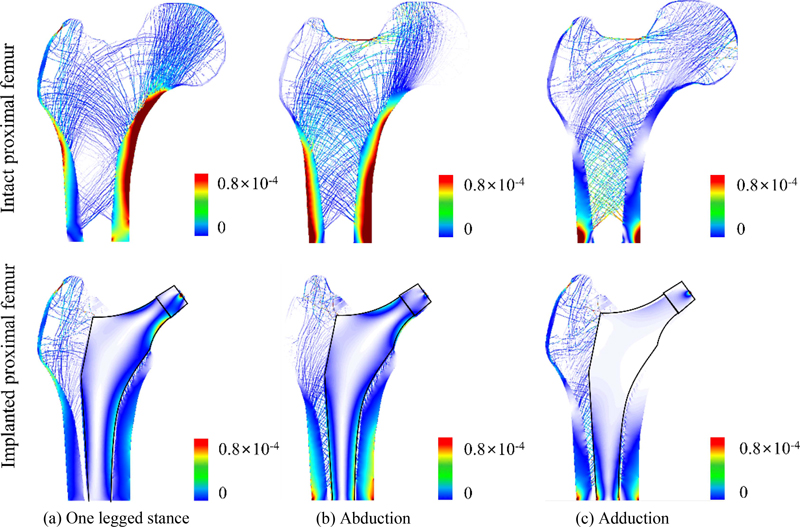
Comparison of strain energy among the implanted proximal femur and intact proximal femur under daily activities (The maximum of the legend was set to 0.8 × 10-4 μJ to visually compare results on the same criteria) [Unit: μJ]

본 연구는 치밀골과 해면골을 각각 관심 영역으로 선정하고, 인공 고관절의 삽입에 따른 관심 영역에서의 구조적 거동을 정상골과 대비하여 비교 분석하였다. Fig. 4에서 확인할 수 있듯, 인공 고관절 삽입에 따른 치밀골(즉, 첫 번째 관심 영역)에서 변형률 에너지는 모든 하중 조건에 대해 감소하였다. 이는 인공 고관절이 정상골의 해면골 대비하여 외부 하중을 더 많이 담당하는 것을 의미한다. 다만, 변형률 에너지의 평균 감소량이 최소 60.8%(외전 하중 조건) 이상으로 상당히 크다는 결과에 주목해야 한다(Table 1). 더욱이 치밀골의 골외막(Periosteum) 대비 골내막(Endosteum) 부분의 변형률 에너지 감소량이 더 많았다. 이는 골내막 부분의 치밀골 소실을 유발하고 최종적으로는 인공 고관절 해리 현상으로 이어질 수 있음을 말한다.

Table 1

Strain energy distribution of normal bone and proximal femur with artificial hip joint implanted at ROI 1[Unit: μJ]

치밀골에서 하중 조건별 변형률 에너지의 평균 감소량을 정량적으로 분석한 결과(Table 1), 외다리 서기 하중 조건이 71.3%로 가장 큰 감소를 보였다. 반면, 외전과 내전은 각각 63.4%, 60.8%의 평균 에너지 감소량을 보였다. 또한 변형률 에너지의 표준 편차 역시 외다리 서기 하중에서 가장 큰 감소(71.5%)가 확인되었으며, 외전과 내전에서 각각 57.7%와 57.8%로 유사한 감소가 확인되었다. 이는 외다리 서기 하중에 의해 발생한 정상 내측 치밀골에서의 변형률 에너지 분포가 인공 고관절의 곡선 형상과 유사하여 발생한 결과로 볼 수 있다. 실제 인공 고관절 형상 설계 시 인체의 하중을 지탱하기 위해 근위 대퇴골 내측 치밀골의 곡선 형상과 유사하게 설계한다고 보고된 바 있다[32]. 다만, 외다리 서기 하중에서 71.3%의 변형률 에너지 감소는 다른 하중 조건 대비 더 많은 응력 방패 현상을 유발할 수 있음을 의미한다.

두 번째 관심 영역인 해면골에서의 변형률 에너지는 치밀골과 동일하게 모든 하중 조건에 대해 감소하였다. 다만, 변형률 에너지의 평균 감소량이 최대 45.1%(외전 하중 조건)로 치밀골 대비 낮은 수치를 보였다. 그럼에도 45.1%의 감소량은 상당히 큰 감소량으로 인공 고관절의 삽입이 치밀골과 더불어 해면골에도 구조적으로 많은 영향을 미침을 의미한다. 감소량으로 인공 고관절의 삽입이 치밀골과 더불어 해면골에도 구조적으로 많은 영향을 미침을 의미한다. 특히 해면골에서 변형률 에너지 감소는 인공 고관절과 직접적인 결합 관계를 가지는 골 미세구조들의 소실을 일으키기 때문에 매우 중요하다.

해면골에서 하중 조건별 변형률 에너지의 평균 감소량을 정량적으로 분석한 결과(Table 2), 치밀골과 달리 외전 하중 조건이 45.1%로 가장 큰 감소를 보였다. 반면, 외다리 서기와 내전은 각각 41.3%, 15.9%의 평균 에너지 감소량을 보였다. 또한 변형률 에너지의 표준 편차는 치밀골과 같이 외다리 서기 하중에서 가장 큰 감소(18.2%)가 확인되었다. 반면, 외전과 내전은 각각 0.25%, 1.1%의 무시할 만한 증가와 감소가 확인되었다.

Table 2

Strain energy distribution of normal bone and proximal femur with artificial hip joint implanted at ROI 2[Unit: μJ]

흥미로운 사실은 외다리 하중 조건에서의 변형률 에너지의 평균 및 표준편차의 감소량이 치밀골과 유사하게 매우 높다는 것이다. 일반적으로 3가지 일상 하중 조건 중 외다리 하중이 차지하는 비율(60%)이 매우 높은데, 이는 다른 하중 조건 대비 외다리 하중 조건에 의해 많은 골 소실이 발생할 수 있음을 말한다. 반면, 내전 하중 조건에서의 매우 적은 에너지 감소도 확인되었다. 이는 내전 하중 시 인공 고관절에 가해지는 하중의 각도가 Neck Shaft Angle(128o)와 유사하여 하중 분산에 불리하여 생긴 현상으로 볼 수 있다. 다시 말해 인공 고관절에 가해지는 하중 각도와 Neck Shaft Angle과 유사할수록 해면골에서 응력방패 현상의 발생 가능성이 낮아짐을 의미한다. 다만, 해당 각도의 하중이 가해질 경우 인공 고관절의 구조적 안전성이 낮아지는 현상도 발생할 수 있음에 주의해야 한다.

미시적 관점에서의 연구를 통해 크게 2가지의 유의미한 결과를 얻을 수 있었다. 첫 번째로 골 미세구조의 이방성 특성을 고려한 연구를 통해 근위 대퇴골과 삽입된 인공 고관절에서 발생하는 기계적 상호작용을 보다 정확히 표현하였다. 특히 이는 인공 고관절과 직접 결합되는 해면골에서의 응력방패 현상을 정확히 분석하는 데 유리하다. 두 번째는 실제와 유사한 골 강성을 적용한 결과를 얻을 수 있었다. 거시적 관점의 연구는 골 밀도 영상을 기반으로 하여 실제보다 높은 골 강성을 가진다. 하지만 본 연구에서는 미시적 관점에서의 연구로 골 미세구조의 특징을 고려하여 실제와 유사한 골 강성을 적용하였다. 이는 마찬가지로 정확한 응력방패 현상을 파악하는 데 유리하다.

본 연구는 다음과 같은 한계점이 존재한다. 첫째, 본 연구는 3가지 일상 하중 조건 아래 구조적 거동 분석을 진행하였다. 하지만 환자의 거동은 다양하고 복잡한 하중에 의해 발생하므로 이후 연구로 다양한 복합 하중 조건 아래 구조적 거동 분석이 필요하다. 둘째, 2차원 인공 근위 대퇴골 모델을 사용하여 구조적 거동을 분석하였다. 정확한 구조적 거동을 분석을 위해서는 3차원 모델을 활용한 연구가 필수적이다. 그럼에도 불구하고 본 연구에서는 환자별 맞춤 하중 아래 정상골과 인공 고관절이 삽입된 근위 대퇴골의 구조적 거동을 비교 분석하였고 이를 토대로 응력방패 현상을 파악하였다. 본 연구의 결과를 바탕으로 위한계점을 극복할 수 있는 추후 연구가 진행되기를 기대한다.

4. 결론

본 연구에서는 미시적 수준에서 인공 고관절 전치환술 이후 인공 고관절이 삽입된 근위 대퇴골의 구조적 거동을 정량적으로 분석하고 응력방패 현상을 파악하였다. 이를 위해 임상에서 가장 많이 사용되고 있는 Single Wedge Type의 인공 고관절을 선정하였으며, 50 μm의 고해상도를 가지는 근위 대퇴골에 삽입하였다. 이어서 인공 고관절이 삽입된 근위 대퇴골의 치밀골, 해면골을 각각 관심 영역으로 정하였다. 이후 3가지 일상 하중 조건 아래 정상골과 인공 고관절이 삽입된 근위 대퇴골에서 발생하는 구조적 거동을 정량적으로 비교 분석하였다. 그리고 변형률 에너지의 평균값, 표준편차를 정량적 지표로 사용해 응력방패 현상을 파악하였다.

정량적인 분석을 통해 관심 영역인 치밀골과 해면골에서 모두 응력방패 현상이 발생할 가능성을 확인하였다. 먼저 치밀골에서는 외다리 서기 하중 시 응력방패 현상의 발생 가능성이 가장 컸다. 이는 인공 고관절의 곡선 형상이 정상 내측 치밀골에 많은 거동이 발생하는 외다리 서기 하중을 받는 데 유리하기 때문이다. 따라서 응력방패 현상을 예방하기 위해서는 내측 치밀골에서 하중이 발생하는 동작에 유의할 필요가 있다는 것을 의미한다. 그리고 해면골에서의 거동 변화는 치밀골에 비해 현저히 낮은 것을 확인하였다. 이러한 결과는 응력방패 현상이 해면골에 비해 치밀골에서 발생할 가능성이 크다는 것을 시사한다. 또한 해면골에서 내전 동작 시 정상골과 인공 고관절이 삽입된 근위 대퇴골의 거동 변화가 크게 나타났다. 이는 내전 동작 시 인공 고관절에 가해지는 하중의 각도가 Neck Shaft Angle과 비슷하기 때문이다. 따라서, 내전 동작 시 응력방패 현상의 발생 가능성은 줄어들지만, 장기적으로 인공 고관절의 안전성과 내구성에 영향을 미치므로 주의할 필요가 있다.

Acknowledgments

본 논문은 2021년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2021R1I1A3043967).

References

• Guerado, E., Caso, E., (2016), The physiopathology of avascular necrosis of the femoral head: An update, Injury, 47, S16-S26. [https://doi.org/10.1016/S0020-1383(16)30835-X]
• Hwang, S. K., (2014), Experience of complications of hip arthroplasty, Hip & Pelvis, 26(4), 207-213. [https://doi.org/10.5371/hp.2014.26.4.207]
• Liu, N., Zheng, C., Wang, Q., Huang, Z., (2022), Treatment of non-traumatic avascular necrosis of the femoral head, Experimental and Therapeutic Medicine, 23(5), 1-15. [https://doi.org/10.3892/etm.2022.11250]
• Savio, D., Bagno, A., (2022), When the total hip replacement fails: A review on the stress-shielding effect, Processes, 10(3), 612. [https://doi.org/10.3390/pr10030612]
• Learmonth, I. D., Young, C., Rorabeck, C., (2007), The operation of the century: Total hip replacement, The Lancet, 370(9597), 1508-1519. [https://doi.org/10.1016/S0140-6736(07)60457-7]
• Monzón, D. G., Iserson, K. V., Jauregui, J., Musso, C., Piccaluga, F., Buttaro, M., (2014), Total hip arthroplasty for hip fractures, Geriatric Orthopaedic Surgery & Rehabilitation, 5(1), 3-8. [https://doi.org/10.1177/2151458514520700]
• Mullins, M. F., Sutton, R. N., Lodwick, G. S., (1974), Complications of total hip replacement, American Journal of Roentgenology, 121(1), 55-60. https://www.ajronline.org/doi/abs/10.2214/ajr.121.1.55 [https://doi.org/10.2214/ajr.121.1.55]
• McGee, M. A., Howie, D. W., Costi, K., Haynes, D. R., Wildenauer, C. I., Pearcy, M. J., McLean, J. D., (2000), Implant retrieval studies of the wear and loosening of prosthetic joints: A review, Wear, 241(2), 158-165. [https://doi.org/10.1016/S0043-1648(00)00370-7]
• Sumner, D., (2015), Long-term implant fixation and stress-shielding in total hip replacement, Journal of Biomechanics, 48(5), 797-800. [https://doi.org/10.1016/j.jbiomech.2014.12.021]
• Be'ery-Lipperman, M., Gefen, A., (2006), A method of quantification of stress shielding in the proximal femur using hierarchical computational modeling, Computer Methods in Biomechanics and Biomedical Engineering, 9(1), 35-44. [https://doi.org/10.1080/10255840600564959]
• Cowin, S. C., (1986), Wolff’s law of trabecular architecture at remodeling equilibrium, 108(1), 83-88. [https://doi.org/10.1115/1.3138584]
• Joshi, M. G., Advani, S. G., Miller, F., Santare, M. H., (2000), Analysis of a femoral hip prosthesis designed to reduce stress shielding, Journal of Biomechanics, 33(12), 1655-1662. [https://doi.org/10.1016/S0021-9290(00)00110-X]
• Fukuoka, K., Todo, M., (2018), Analysis of principal stress projection in femur with total hip arthroplasty using CT-image based finite element method, International Archives of Orthopedic Surgery, 1(1), 1-10. [https://doi.org/10.23937/iaos-2017/1710003]
• Behrens, B.-A., Wirth, C., Windhagen, H., Nolte, I., Meyer-Lindenberg, A., Bouguecha, A., (2008), Numerical investigations of stress shielding in total hip prostheses, Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 222(5), 593-600. [https://doi.org/10.1243/09544119JEIM139]
• Noyama, Y., Miura, T., Ishimoto, T., Itaya, T., Niinomi, M., Nakano, T., (2012), Bone Loss and Reduced Bone Quality of the Human Femur after Total Hip Arthroplasty under Stress-Shielding Effects by Titanium-Based Implant, MATERIALS TRANSACTIONS, 53(3), 565–570. [https://doi.org/10.2320/matertrans.M2011358]
• Yamako, G., Chosa, E., Zhao, X., Totoribe, K., Watanabe, S., Sakamoto, T., Nakane, N., (2014), Load-transfer analysis after insertion of cementless anatomical femoral stem using pre-and post-operative CT images based patient-specific finite element analysis, Medical Engineering & Physics, 36(6), 694-700. [https://doi.org/10.1016/j.medengphy.2014.02.018]
• Kim, J. J., Jang, I. G., (2016), Image resolution enhancement for healthy weight-bearing bones based on topology optimization, Journal of Biomechanics, 49(13), 3035-3040. [https://doi.org/10.1016/j.jbiomech.2016.06.012]
• Krug, R., Burghardt, A. J., Majumdar, S., Link, T. M., (2010), High-resolution imaging techniques for the assessment of osteoporosis, Radiologic Clinics, 48(3), 601-621. [https://doi.org/10.1016/j.rcl.2010.02.015]
• Jang, I. G., Kim, I. Y., (2008), Computational study of Wolff's law with trabecular architecture in the human proximal femur using topology optimization, Journal of Biomechanics, 41(11), 2353-2361. [https://doi.org/10.1016/j.jbiomech.2008.05.037]
• Dyson, E., Jackson, C., Whitehouse, W., (1970), Scanning electron microscope studies of human trabecular bone, Nature, 225(5236), 957-959. [https://doi.org/10.1038/225957a0]
• Whitehouse, W., Dyson, E., (1974), Scanning electron microscope studies of trabecular bone in the proximal end of the human femur, Journal of Anatomy, 118(3), 417-444.
• Jang, I. G., Kim, I. Y., (2010), Computational simulation of simultaneous cortical and trabecular bone change in human proximal femur during bone remodeling, Journal of Biomechanics, 43(2), 294-301. [https://doi.org/10.1016/j.jbiomech.2009.08.012]
• Yoon, S., Schiffer, A., Kim, J. J., Jang, I. G., Lee, S., Kim, T.-Y., (2020), Numerical predictions of the interaction between highly nonlinear solitary waves and the microstructure of trabecular bone in the femoral head, Journal of the Mechanical Behavior of Biomedical Materials, 109, 103805. [https://doi.org/10.1016/j.jmbbm.2020.103805]
• Kim, H.-J., Kim, J.-S., Han, S.-M., You, J.-H., Choi, K.-W., Youn, I.-C., (2009), Evaluation of mechanical stability in development of customized hip implant, Journal of the Korean Society for Precision Engineering, 26(7), 31-37.
• Khanuja, H. S., Vakil, J. J., Goddard, M. S., Mont, M. A., (2011), Cementless femoral fixation in total hip arthroplasty, Journal of Bone and Joint Surgery, 93(5), 500-509. [https://doi.org/10.2106/JBJS.J.00774]
• Kim, J. J., Nam, J., Jang, I. G., (2018), Computational study of estimating 3D trabecular bone microstructure for the volume of interest from CT scan data, International Journal for Numerical Methods in Biomedical Engineering, 34(4), e2950. [https://doi.org/10.1002/cnm.2950]
• Beaupré, G., Orr, T., Carter, D., (1990), An approach for time‐dependent bone modeling and remodeling—application: A preliminary remodeling simulation, Journal of Orthopaedic Research, 8(5), 662-670. [https://doi.org/10.1002/jor.1100080507]
• Beaupré, G., Orr, T., Carter, D., (1990), An approach for time‐dependent bone modeling and remodeling—theoretical development, Journal of Orthopaedic Research, 8(5), 651-661. [https://doi.org/10.1002/jor.1100080506]
• Tsubota, K.-I., Adachi, T., Tomita, Y., (2002), Functional adaptation of cancellous bone in human proximal femur predicted by trabecular surface remodeling simulation toward uniform stress state, Journal of Biomechanics, 35(12), 1541-1551. [https://doi.org/10.1016/S0021-9290(02)00173-2]
• Monzón, D.G., Iserson, K. V., Jauregui, J., Musso, C., Piccaluga, F., Buttaro, M., (2014), Total hip arthroplasty for hip fractures, Geriatric Orthopaedic Surgery & Rehabilitation, 5(1), 3-8. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3962050/ [https://doi.org/10.1177/2151458514520700]
• Naghavi, S. A., Lin, C., Sun, C., Tamaddon, M., Basiouny, M., Garcia-Souto, P., Taylor, S., Hua, J., Li, D., Wang, L., (2022), Stress shielding and bone resorption of press-fit polyether–ether– ketone (PEEK) hip prosthesis: A sawbone model study, Polymers, 14(21), 4600. [https://doi.org/10.3390/polym14214600]
• Abdelaal, O., Darwish, S., El-Hofy, H., Saito, Y., (2019), Patient-specific design process and evaluation of a hip prosthesis femoral stem, The International Journal of Artificial Organs, 42(6), 271-290. [https://doi.org/10.1177/0391398818815479]