볼 조인트형 메카니컬 씰 구조의 회전 용접토치 설계 및 동특성 해석

2.1 기구부 설계사양

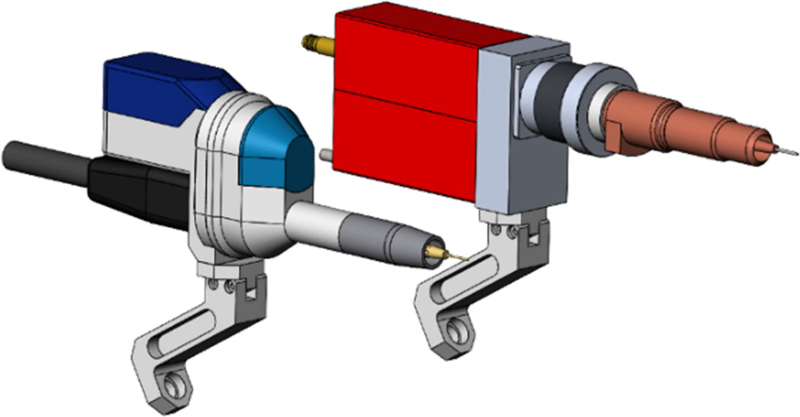
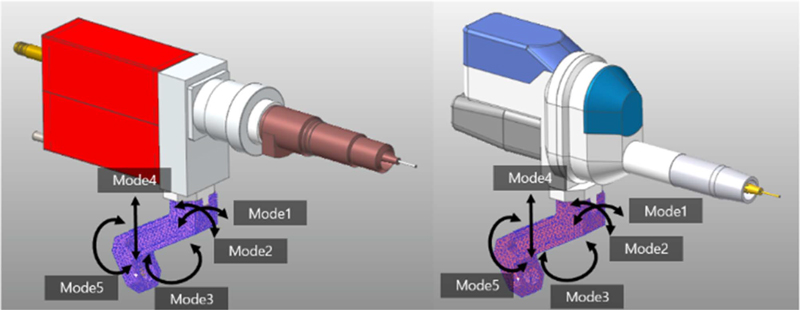
본 논문에서 비교 분석하고자 하는 두 가지 설계 모델을 Fig. 1에 나타냈다. 좌측의 모델이 볼 조인트형 메카니컬 씰 구조의 회전토치이며, 우측은 볼 조인트형 메커니즘과 동일한 자유도를 가지나, 좌측에 비해 더 많은 기계요소부품과 복잡한 구조로 설계된 회전 용접토치이다.

Fig. 1

The proposed rotating welding torch (left) and conventional rotating welding torch (right)

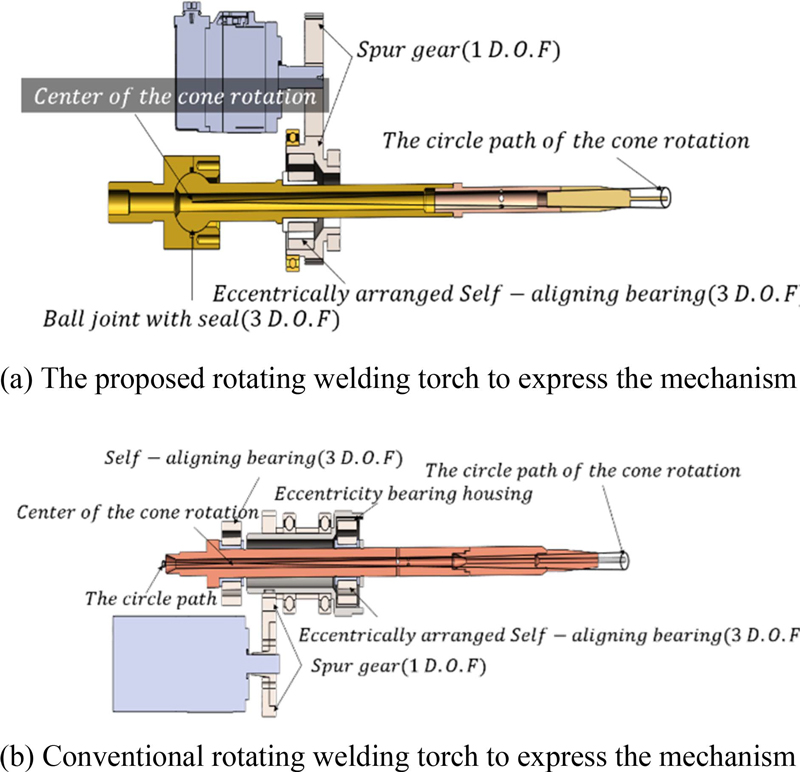
두 설계 모델의 메커니즘을 비교하기 위해 Fig. 2와 같이 단순화하여 나타내었다. Fig. 2(b)의 모델이 Fig. 1의 우측 설계 모델의 단면도로서, 편심운동을 만들기 위하여 2개의 자동조심 베어링이 적용되었으며 편심하우징에 설치된 자동조심 베어링은 평기어로 연결된 모터에 의해 회전을 하면서 토치 몸체를 원뿔회전 운동을 하도록 한다. 하지만 원뿔 회전중심점을 기준으로 뒤쪽으로도 토치 몸체가 돌출이 되어 회전하기 때문에 고정 지지부와 연결하기 위해 유연한 재질의 고무튜브와 같은 부품이 적용된다. 용접을 위해서는 용접 전류가 흘러야 하는데, 고무튜브와 같은 절연구조물로 인해 별도의 통전 라인을 구성 해야한다. 이는 기구적으로 매우 복잡하고, 동특성이 떨어지는 단점이 있다.

Fig. 2

Cross section view of two rotating welding torchs

Fig. 2(a)의 모델은 본 논문에서 제안하는 볼 조인트형 메카니컬 씰이 적용된 구조로서, 구현하고자 하는 메커니즘을 단순화하여 기존 2개의 자동조심 베어링을 1개로 줄였고, CO₂ 가스의 봉입을 위한 메카니컬 씰 구조와 볼 조인트형 기구 구조를 통해서 용접 전류가 흐를 수 있도록 함과 동시에 원뿔 회전 메커니즘이 작동하도록 설계하였다.

두 설계 모델의 수치적인 사양을 Table 1과 같이 정리하였다. 두 모델은 약 직경 3 mm 수준의 원뿔 회전 운동을 하며, 20 Hz의 속도로 고속 회전한다.

Table 1

Specification of mechanical and dynamics properties

기어물림주파수는 모터 회전수와 기어잇수의 곱으로 계산되며, 설계 모델 별로 동특성 분석을 위한 가진주파수 중 하나로 사용된다. 두 모델은 기어물림주파수와 모터용량 그리고 무게에서 큰 수치적인 차이를 보이며, 이러한 설계 요소들이 동 특성에 어떤 영향을 미치는지 3장에서 해석하였다.

2.2 메커니즘의 도식화

메커니즘의 도식화를 통해 다양한 입출력 운동으로 동작하는 복잡한 기계장치의 움직임을 직관적으로 이해하는데 도움을 준다. 메커니즘의 도식화는 Chiou와 Kota [7]에 의해 제안되었으며 이를 응용하여 Lee [8]에 의해 메커니즘의 합성을 도식화하는 형태로도 제안되었다. 상기 2가지 메커니즘의 도식화 방법은 복잡한 링크 구조의 메카니즘을 도식화 하는데는 유용하지만, 현존하는 모든 메커니즘의 운동 상태를 표현하기에는 추가적인 운동의 정의가 필요하다. 이에 본 논문에서는 기존 회전 용접토치와 제안하는 회전 용접토치의 서보 시스템의 구성을 직관적으로 도식화하고 운동 상태와 메커니즘의 표기를 추가하여 두 회전 용접 토치의 운동 메커니즘을 표현하는 도식도를 비교 분석해보고자 한다. Kirschman and Fadel [9]의 운동 분류법에서는 메커니즘이 전달하는 운동을 4가지 형태로 분류하였는데, 이에 회전 원뿔 운동을 추가하여 다음의 Table 2의 5가지로 정의하고자 한다.

Table 2

Mechanism motion definition

상기 5가지 운동의 머리글자 R, O, L, C, CR이 도식적 메커니즘 요소의 입출력 운동상태를 나타내주는 문자이고, 이 문자의 오른쪽 밑에 첨자로서 i, j, k 방향 벡터를 표기하여 운동의 방향을 나타낸다.

메커니즘의 도식화를 위해 원 모양 도형에는 입출력 운동이 명확한 단순 기계요소부품명을 표기하고, 사각박스에는 메커니즘의 약어와 조립상태 그리고, 주요 기계요소부품명을 기입하는 방식으로 표기하였다.

Lee [8]는 메커니즘 요소의 조인트를 P, S, H, C, T와 조인트의 개수를 숫자로 기입하여 표현하였는데, 여기에 3자유도 볼조인트의 조립상태 혹은 구속상태를 나타내는 약어를 하기의 Table 3와 같이 추가로 정의하였다.

Table 3

Joint mechanism definition

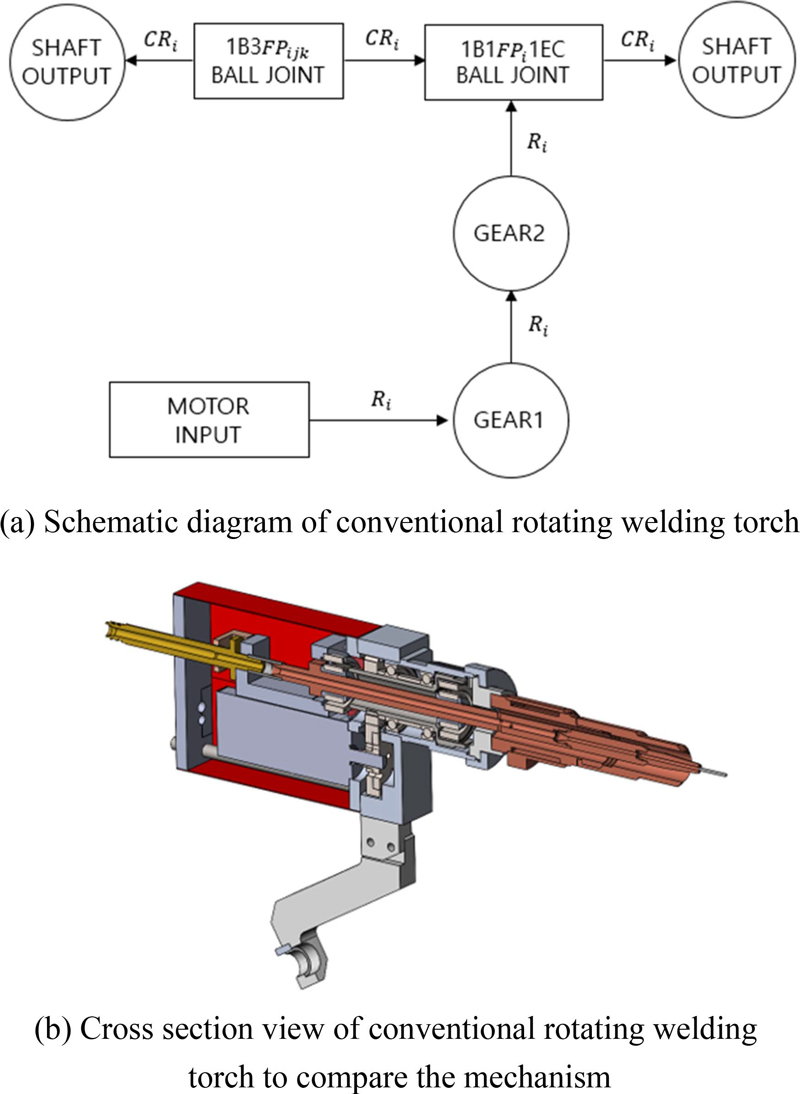
상기 조인트의 구속 자유도 상태를 표기하는 FP_ijk, FO_ijk, EC를 통해 직관적인 조인트의 운동 가능 상태를 이해할 수 있다. Fig. 3은 기존 회전 용접 토치 모델의 도식화를 나타내었다. Fig. 3(a)의 도식도는 기존 회전 용접토치의 도식도로서 2개의 Shaft Output을 가진다. Shaft Output은 CR_i로 표현된 원뿔 회전 운동이며, FP_ijk로 표현된 3자유도 위치가 고정된 볼 조인트의 중심을 기준으로 i 벡터 방향으로 전후로 원뿔 회전운동함을 확인할 수 있다. Fig. 3(b)는 기존 회전 용접토치의 단면도로서, 기계요소부품의 구성상태를 Fig. 3(a)와 비교해 볼 수 있다.

Fig. 3

Mechanism schematic diagram and cross section view of conventional rotating welding torch

Fig. 4는 볼 조인트형 메카니컬 씰이 적용된 회전토치로서 어떠한 기계요소부품의 조합과 조인트 메커니즘으로 구성되어 있는지 도식화되어 있다. Fig. 4(a)는 제안하는 회전 용접토치의 도식도로서 Fig. 3(a)와 달리 Shaft Output이 하나이며, 볼 조인트와 메커니컬 씰로 구성된 원점기준으로 전진 방향으로만 용접토치가 원뿔 회전 운동함을 알 수 있다.

Fig. 4

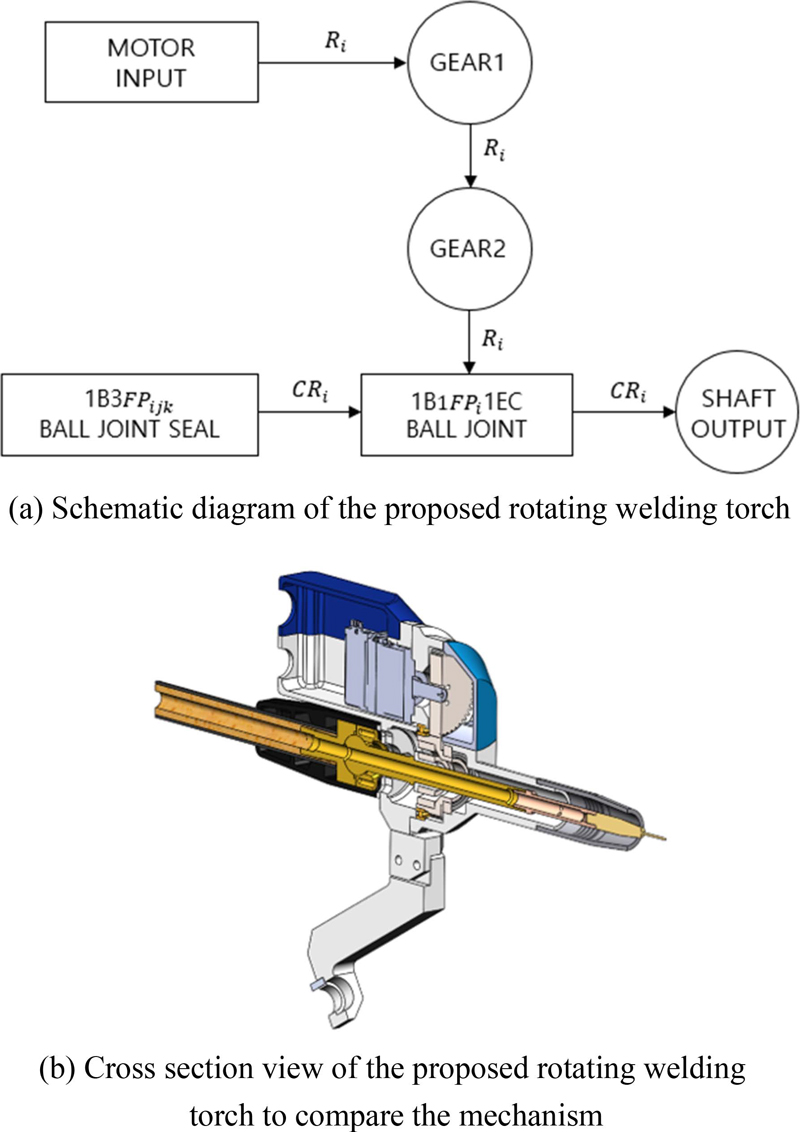
Mechanism schematic diagram and cross section view of the proposed rotating welding torch and the existing rotating welding torch

메커니즘의 도식화를 통해, 두 설계 모델의 메커니즘 차이를 쉽게 구분하여 표현할 수 있고, 출력 운동의 결과를 도식도를 통해 이해할 수 있다.

3.1 구동토크 해석

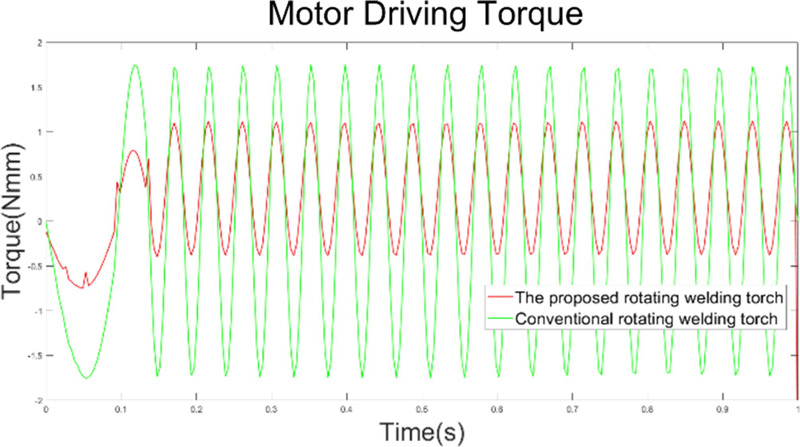
두 가지 설계 모델의 구동토크 해석은 Recurdyn (FunctionBay, 한국)을 이용하여 해석하였다. 모터의 구동토크는 정적인 상태에서 동적인 상태로 변하는 초기 짧은 시간 이후에는 정현파 형태의 토크 변화량을 가지는데, 이것은 회전 토치의 회전운동에 따라 질점의 위치가 변하기 때문이다.

회전 중심 기준으로 회전 용접토치의 자세가 지면과 수평하게 있고, 시계방향으로 회전한다고 가정할 시 토치의 위치가 12시에서 6시로 이동 시 중력 부하가 줄어드는 만큼 부하 토크가 줄어 들게 되고, 6시에서 12시로 이동 시 중력 부하를 받는 만큼 토크 부하가 커지게 된다. 작용하는 관성부하가 더 큰 기존 회전 용접토치의 구동토크가 제안하는 회전 토치 대비 약 2배 이상 큰 것을 Fig. 5를 통해 확인할 수가 있다. 편심 회전운동에 따른 질점의 위치변화로 인하여 구동토크 또한 반복적인 정현파 형태의 출력을 가진다. 정현파 출력은 회전 용접토치의 질점의 진동을 야기하며, 이는 곧 기구부 지지부에 반복적인 동하중이 생길 수 있음을 생각해 볼 수 있다.

Fig. 5

Comparison of driving torque between the proposed rotating torch and conventional rotating torch

3.2 진동에 의한 동 하중 반력 해석

회전 용접토치는 로봇의 End-effector에 장착되며 구동 시 20 Hz(1,200 RPM)의 빠른 속도로 편심 회전하는 토치 몸체의 질점의 진동으로 인해 회전 토치를 지지하는 부위에 반복적인 동 하중 반력이 발생하게 된다. 동 하중은 소음 및 피로 파괴를 유발하기도 하며, 동 하중이 클 경우 안정적인 로봇 제어를 위해서 더 큰 가반하중을 요구하기도 한다. 이에 두 가지 모델의 모터 구동 시에 지지부에 발생하는 진동반력을 Recurdyn을 활용하여 해석하였다.

진동반력 해석을 위하여 Fig. 6에 보이는 두 회전토치의 기구부 몸체는 강체로 정의되었다. 토치 몸체의 변형에 의한 영향은 미비하고 진동에 의한 질점의 떨림이 반력에 가장 큰 영향을 주기 때문이다. 변형까지 고려할 수 있지만, 해석시간 대비 결과에 주는 유의미한 영향이 크지 않기 때문에 기구 변형에 의한 영향은 배제하기로 한다.

Fig. 6

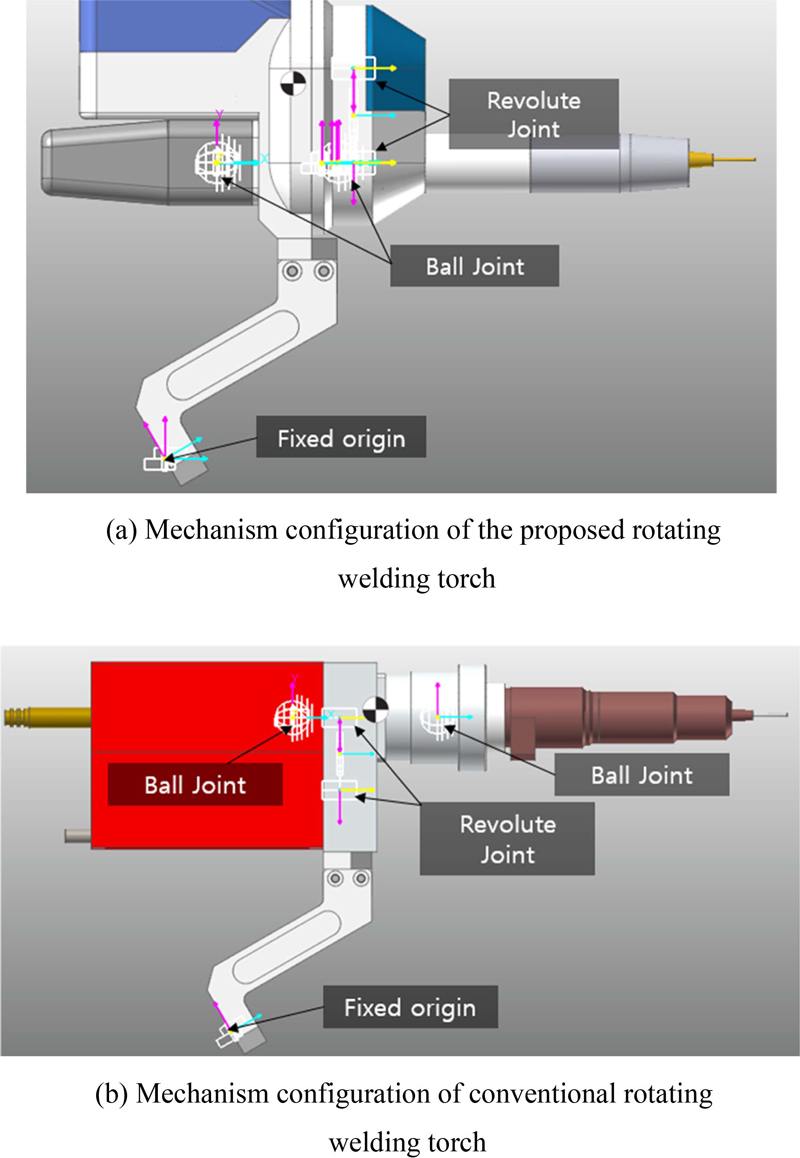
Comparison of the mechanism configuration of conventional rotating welding torch and the newly proposed rotating welding torch

진동반력은 Fig. 6에 보이는 Fixed Origin에서 각 방향 별로 발생하는 힘의 합성을 계산하였다. 진동 반력 역시 원뿔 회전 운동하는 토치 몸체의 위치에 따라 정현파 형태의 반력 변화를 보여준다. 기본적인 반력의 크기는 토치 몸체의 중력에 의한 부하 하중이며, 진동에 의해 질점이 떨리기 때문에 동 하중이 발생한다. 구형과 신형 회전 용접토치의 무게가 각각 2.87 kg과 1.85 kg임을 감안할 시 진동에 의한 반력의 최소치가 회전 토치의 무게임을 Fig. 7을 통해 알 수 있다.

Fig. 7

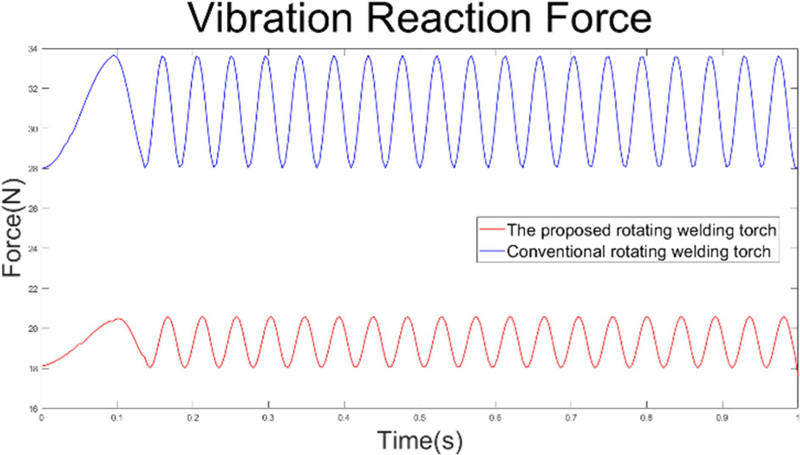
Vibration reaction force magnitude for each rotating welding torch at a fixed origin of a mounting bracket

또한 구형과 신형의 기구부 진동에 의한 반력 변화량 평균이 각각 31.1 N과 19.2 N으로 구형 대비 신형 회전 용접토치가 동일한 메커니즘을 구현함에도 로봇 End-effector에 주는 영향은 구형 대비 62% 수준임을 확인하였다.

3.3 고유진동수 해석

회전 용접토치는 20 Hz의 빠른 회전속도로 토치 몸체가 회전하면서 기구부 진동을 야기한다. 이때 회전토치 기구의 고유진동수가 기어물림주파수 및 구동에 따른 진동수와 일치하게 되면 공진이 발생하게 되고 시스템에 치명적인 파손을 야기할 수 있기 때문에 고유진동수 해석이 필요하다.

고유진동수는 회전 용접토치의 전체 몸체에 대한 것이 아닌 회전 용접토치와 로봇의 End-effector를 연결하는 브라켓 부품을 기준으로 평가하였다. 왜냐하면 회전 용접토치의 전체 무게를 지지하는 브라켓의 고유진동수와 가진주파수가 일치하는 경우가 가장 위험한 경우이며, 강성과 강도 또한 회전 용접토치의 몸체 대비 브라켓이 더 낮다.

고유진동수의 모드 형상별 운동 방향은 Fig. 8의 화살표로 방향을 도식화하였다. 고유진동수의 모드해석은 5단계 모드 형상까지 수행하였으며, 모드 형상별 고유진동수와 가진 주파수를 Table 4에 정리하였다.

Fig. 8

Natural frequency direction for each mode

Table 4

Natural frequency for each mode

두 설계 모델 모두 마운팅 브라켓 부품의 5가지 고유진동수 모드 형상별로 가진주파수와 겹치지는 않았다. 기어물림주파수의 경우 모드 4에서 두 모델의 고유진동수와 가장 근접하였으나, 신형 모델이 구형 모델에 비해 기어물림주파수와의 차이가 더 크게 계산되었다. 이 차이가 클수록 공진주파수 범위에서 멀어지는 것이기 때문에 상대적으로 안정적이라 할 수 있다.

3.4 관성 불일치 해석

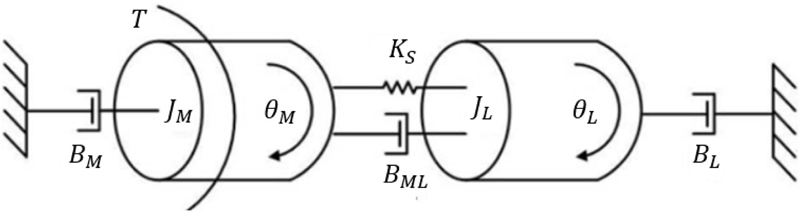
관성 불일치 해석은 부하측 관성과 커플링 강성이 결합하여 서보 축 작동 시 야기될 수 있는 불안정성을 평가하는 해석이다[10]. 부하와 모터 사이의 높은 관성비는 커플링, 축 및 벨트의 상당한 컴플라이언스로 인해 기계요소부품의 기계적 특성이 불량한 경우 기계적 공진으로 인해 모션 제어가 불안정해질 수 있다[11]. 회전 용접토치의 서보모터와 토치 몸체는 평기어로 연결되며, 평기어의 치강성 뿐만 아니라 모터관성 및 부하관성 간의 관성비가 관성불일치 해석에 큰 영향을 끼친다. 또한, 관성 불일치는 식(1)의 관성비와 밀접한 연관이 있는데, 관성비가 높을수록 제어가 어렵고 민감한 시스템이 된다.

Fig. 9는 모터와 연결된 부하 하중 간의 관계를 도식화한 것으로서, 중간에 연결된 커플러들의 강성 인자와 점성 댐핑계수, 관성모멘트, 토크 등을 나타내고 있다. 관성비와 커플링 강성 간의 상호작용에 의한 기계적인 공진의 관계를 정의하기 위하여 모터와 부하 간의 각가속도에 대한 정의가 필요하다. 이에 대한 정의는 식(2)와 식(3)과 같다.

Fig. 9

Relationship factors between mechanical motor actuation system and load

식(2)와 식(3)을 Laplace Transform을 이용하여 하기 식과 같이 주파수 영역의 해석으로 변환한다.

이를 전달함수인 식(7)과 식(8)의 형태로 수식을 정리한다.

D(s)는 두 전달함수의 공통분모로서 식(9)와 같다.

B_M과 B_L이 공진에 미치는 영향은 거의 없기 때문에 0으로 설정하여 식을 정리하면 식(10), 식(11)과 같다.

식(10)과 식(11)을 식(12)로 그룹화하여 정리하면 최종적인 관성비와 커플링 강성 간의 전달함수 형태인 식(13)과 식(14)를 도출할 수 있다.

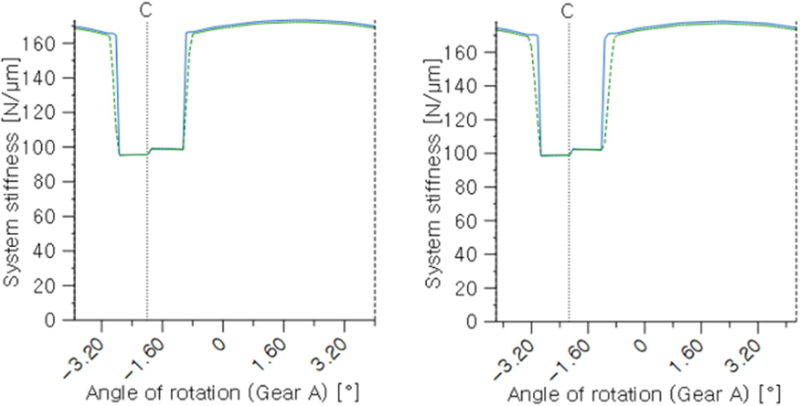
전달함수의 핵심인자는 J_M, J_L, B_ML, K_s 의 4가지로 기어치의 강성인 K_s는 실험 혹은 해석적인 기법을 이용하여 구할 수 있는데, 본 논문에서는 Recurdyn의 Meta 모델을 활용하여 기어치의 강성 값을 Fig. 10과 같이 해석하였다[12].

Fig. 10

A gear teeth rotation compliance of the old (left) and new (right) rotating welding torch

기어의 회전에 따른 맞물림 위치 별로 강성이 변화하게 되고 그에 대한 기어 강성 평균값이 K_s이다. 기어의 점성 댐핑계수 B_ML 또한 실험적으로 구해야 하는 수치이지만 실제 값은 0에 가까울 정도로 매우 미소하며, 수치의 정밀성이 떨어지더라도 2가지 설계 모델에 동일한 기준이 적용되기 때문에 그 차이를 구분하기에는 충분하다고 판단된다. 기어치 강성 K_s의 1/1000로 두 가지 모델에 각각 적용하였다. 그리하여, 관성 불일치 해석을 위한 인자들을 Table 5에 정리하였다.

Table 5

Parameters for inertia mismatch analysis

Fig. 11은 관성 불일치 해석결과로서 Bode Plot은 공진 영역에 대해 두 설계 모델의 Resonancs 및 Anti-resonance 주파수 크기와 위상값 결과를 나타내준다. Anti-resonance와 Resonance Magnitude는 공진 주파수와 일치하는 가진 주파수가 가해질 시 커지는 진폭의 크기이며, Anti-resonance와 Resonance 주파수 사이의 주파수 영역 범위가 공진 주파수 범위이다.

Fig. 11

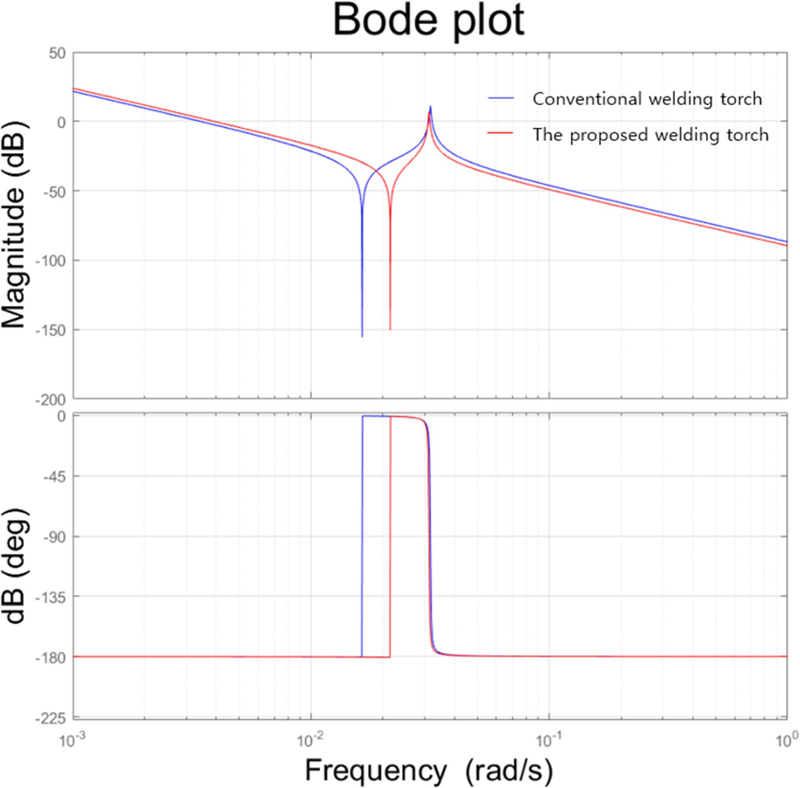
Bode plot of θM/T for the old and new rotating welding torch shows the effects on the position in magnitude of the anti-resonance and resonance peaks

따라서, 주파수 영역에서 Anti-resonance와 Resonance Magnitude가 작고 공진 위상 범위가 작을수록 기계적 동특성이 우수하다고 할 수 있다. 기존의 회전토치 대비 본 논문에서 제안하는 회전 용접토치가 공진 주파수 범위가 작고, Magnitude가 상대적으로 작다는 것을 확인할 수 있다.