압력 추정을 이용한 공압 제진대의 능동 제어

2.1 공압 제진대

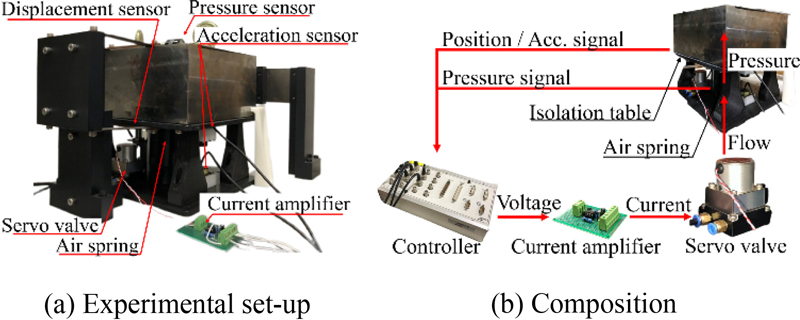
일자유도 능동 공압 제진대는 Fig. 1(a)와 같이 제어부, 공압구동기, 일자유도 진동 모델로 구성된다. 제어부는 제어기(dSPACE, DS1104)와 센서들로 구성된다. 상대 변위 센서(Contrinex, DW-AD), 제진대 상하판 가속도 센서(Tokyo Keiki, TA-25J) 그리고 공기스프링 내압 측정 센서(Sensys, PSC)를 사용했다. 공압 구동기는 노즐-플래퍼 서보밸브(Moog, j814)와 특주 공기스프링으로, 일자유도 진동 모델은 플렉셔 베어링과 부하 중량으로 구성된다.

Fig. 1

One DOF pneumatic vibration isolator apparatus

Fig. 1(b)에 공압 제진대 구성도를 나타냈다. 제어기 출력 전압은 전류증폭기를 거쳐 서보 밸브에 전류를 인가한다. 압축 공기가 서보밸브를 통해 공기스프링으로 유입되면 공기스프링의 내압이 상승하고, 이에 따라 제진대 상판에 구동력이 가해진다. 플렉셔 베어링은 상판의 운동을 수직 방향으로 제한한다.

2.2 공압 제진대의 수학적 모델링

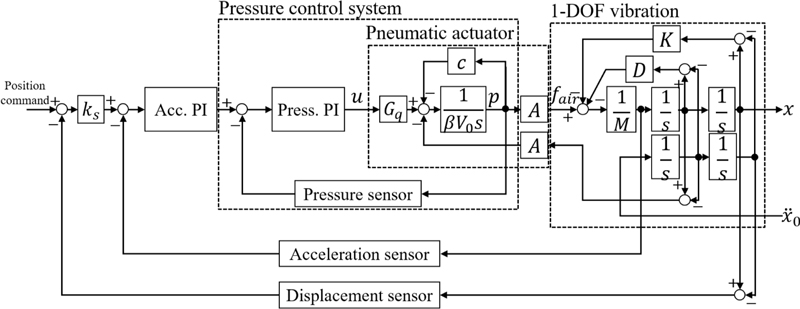
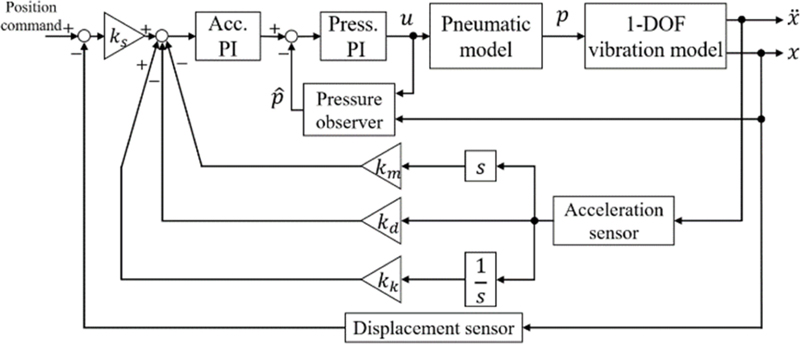
Fig. 2에 공압 제진대의 능동 제어 블록선도를 나타냈으며 공압 구동기, 일자유도 진동 그리고 압력 제어기로 구성된다.

Fig. 2

Control block diagram of pneumatic vibration isolator

2.2.1 공압 구동기 모델

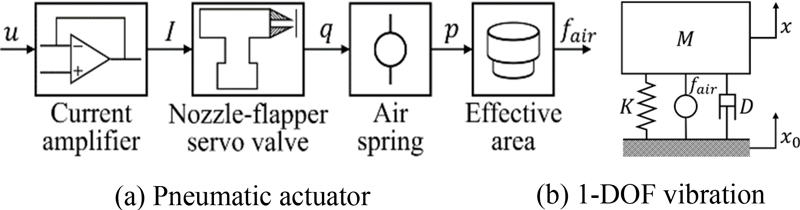
Fig. 3(a)와 같이 공압 구동기는 전류 증폭기, 노즐- 플래퍼 서보밸브, 공기스프링 그리고 유효 면적으로 구성된다. 공압 구동기 수학모델은 평형점 부근에서 선형화하여 1차 지연으로 모델링할 수 있다[5]. 전류 증폭기와 노즐-플래퍼 서보 밸브는 비례요소로, 공기스프링은 이상 기체 상태 방정식에 따라 1차 지연요소로 간략화했다. 여기서 u는 제어 입력, I는 전류, q는 체적유량, p는 압력이다. 공기스프링의 내압에 유효 면적(A)이 곱해져 구동력(f_air)이 발생한다.

Fig. 3

Schematic diagram of the pneumatic vibration isolator

2.3 공압 구동기 동특성 식별

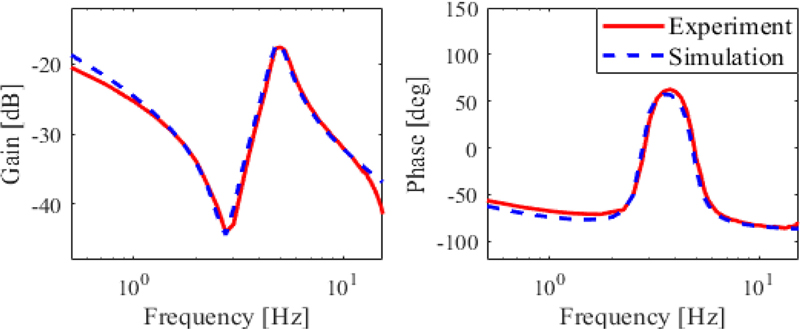
부하 중량의 부상을 위한 일정한 변위 명령과 더불어 정현파가속도 명령을 인가하여 제어 입력(u)에 대한 압력(p)의 주파수응답을 측정하고 Fig. 4에 붉은 실선으로 나타냈다. 실험 수행 중에 부하 중량의 안정적인 부상을 위해 변위, 가속도, 압력 제어을 적용했다. 실험에서 공압 구동기 모델의 공진점 부근의 주파수 응답으로부터 강성(K), 감쇠계수(D)를 계산했다.

Fig. 4

Frequency response from control input u to pressure p

Table 1에 표시한 공기스프링 형상으로부터 체적(V₀), 유효면적(A)을 결정할 수 있다. 압축률(β)은 공기 폴리트로픽 지수(1.4)와 평형점에서 공기스프링 내부 계기 압력의 곱의 역수이다. 서보밸브와 공기스프링을 분리한 후 입력 전압을 점진적으로 증가시키며 서보밸브의 준정적 유량을 측정한 후 유량-전압기울기로부터 서보밸브 유량게인(G_q)의 초기값을 결정했다.

Table 1

Geometric parameters of the air spring

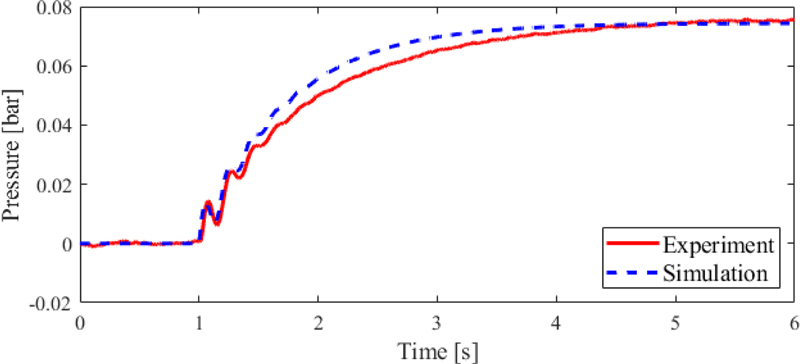
식(1)에 공압 제진대 변수를 대입하고 실험과 이론 주파수응답(Fig. 4의 파란색 점선)을 비교하며 서보밸브 유량게인(G_q)과 체적(V₀)을 추가적으로 조정했다. 또한, 기준 위치(x = 4 mm)가 되도록 전압 입력을 8 V로 조절한 후 0.5 V 계단 입력에 대한 최종 정상상태 압력이 Fig. 5와 같이 일치하도록 유체 컨덕턴스(c)를 결정했다. 이때 부상 평형점에서의 공기스프링 내압을 0으로 설정했다. Table 2에 결정한 변수 값들을 표시하였다.

Fig. 5

Pressure step response from control input u

Table 2

Model parameters of pneumatic vibration isolator

3.1 압력 관측기 설계

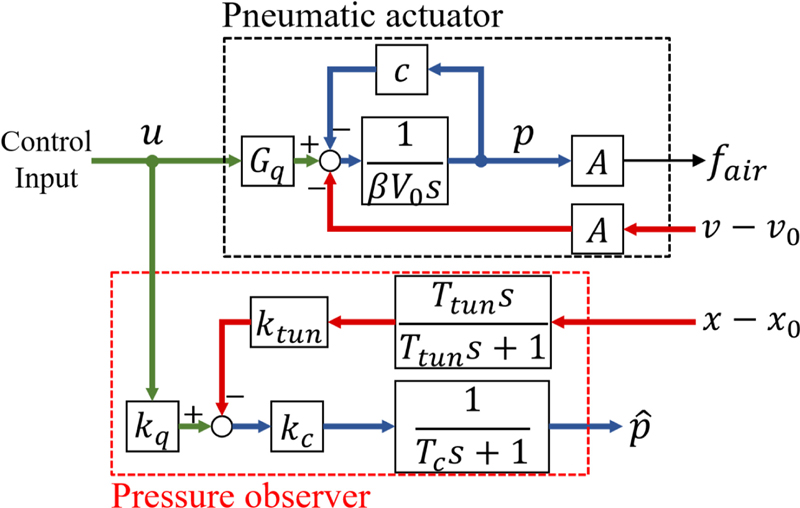
Fig. 6에 이 논문에서 사용할 압력 관측기를 도시하였다. 압력 관측기는 공압 구동기 모델을 기반으로 제어 입력과 상대 변위의 미분을 이용해 압력을 추정한다[4].

Fig. 6

Block diagram of the pressure observer

Fig. 6의 녹색 선과 같이 제어 입력에서 압력을 추정하기 위해 공압 구동기 모델의 1차 지연 시스템을 식(2)의 형태로 근사한다. 여기서 k_c는 공압 구동기 모델의 DC 이득(= G_q/c), T_c는 공압 구동기 모델의 시정수(= V₀/c)이다.

부하 중량의 상대 속도를 유량 게인으로 나누어 Fig. 6의 적색선과 같이 압력 관측기의 입력으로 구현하였다. 정적 이득만을 고려하여 제어 입력단에 궤환되는 항을 유도하면 식(3)과 같다. 여기서, k_tun는 의사-미분기(Pseudo-differentiator)의 이득, T_tun는 의사-미분기의 시정수이다. S_pos는 변위 센서의 민감도(10 × 10³ V/m)이다.

T_tun는 미분을 적용할 주파수를 결정하는 제어 이득으로 T_c 보다 충분히 작은 값을 사용한다. 식(3)을 k_tun에 대해 정리하면 식(4)와 같다.

3.2 압력 추정 성능

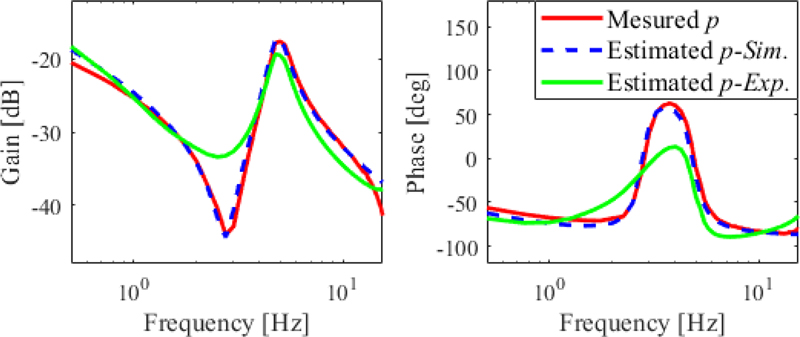
공기스프링의 실제 압력(p)과 압력 관측기의 추정 압력($$ \widehat{p}$$)을 비교하여 압력 관측기의 성능을 검증한다. 제어 입력에 대한 공압 구동기의 측정 및 추정 압력의 주파수 응답을 비교하여 Fig. 7에 나타냈다. 모델로부터 압력 관측기 초기 이득을 계산했고 이를 Table 3에 나타냈다. 반공진점(2-3 Hz)을 제외한 영역에서 평균 오차 21.7%로 실제 압력을 잘 추정하였다.

Fig. 7

Frequency response of the measured and estimated pressure

Table 3

Gains of the pressure observer

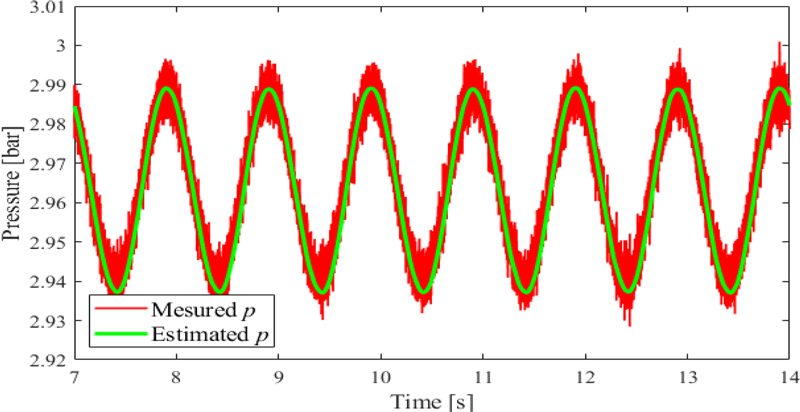
Fig. 8과 같이 정현파 전압 입력에 대한 측정 및 추정 압력을 비교하며 실험을 통해 관측기 이득을 조절하였다. 서보밸브 유량게인(G_q)을 증가시키면 반공진 부근에서의 압력 추정 성능이 향상되고, 압력 추정 이득이 높아진다. 반면, 체적(V₀)을 증가시키면 압력 추정 이득을 낮출 수 있었다. 유량게인(G_q)은 1.6 × 10^-5 m³/s/V에서 2.5 × 10^-5 m³/s/V로, 체적(V₀)은 2.72 × 10^-5 m³에서 4.22 × 10^-5 m³로 변경했다. 관측기로 압력이 잘 추정되었으며 특히 측정 잡음을 효과적으로 제거할 수 있다.

Fig. 8

The measured and estimated pressure of pneumatic actuator

4.1 공압 제진대 제어 기법

Fig. 9는 공압 제진대의 제어 블록선도로 변위 비례, 가속도 PI 그리고 압력 PI 궤환 제어로 구성된다. 특히 가속도 궤환의 이득 k_m, k_d, k_k 은 질량, 감쇠 그리고 강성과 관련되며 이를 통해 1자유도 진동 모델의 고유진동수를 낮출 수 있다[7]. 공압 제진대의 능동 제어에 사용한 제어 이득을 Table 4에 정리하였다.

Fig. 9

Control block diagram of the active pneumatic vibration isolator

Table 4

Control gains for the active pneumatic vibration isolator

압력 PI 제어는 압력 추종 속도를 높여 공압 구동기 동특성을 개선한다. 측정 압력을 이용한 궤환 제어(이하, 직접 압력 궤환)와 추정 압력을 이용한 궤환 제어(이하, 추정 압력 궤환)에 따른 공압 제진기의 진동 절연 성능을 비교하였다.

4.2 압력 관측기의 성능 평가

진동전달률 측정을 위한 실험 장치 구성도를 Fig. 10에 나타냈다. 진동전달률 측정 장치는 가진기를 포함한 가진대와 일자유도 능동 공압 제진기로 구성했다. 바닥 가진에 사용한 가진기의 힘은 최대 196 N, 최대 스트로크 10 mm, 최대 가속도 529 m/s²이다. 정현파 바닥 가진의 주파수와 가속도를 0.5 Hz, 0.23 × 10^-3 m/s²에서 15.5 Hz, 0.18 m/s²까지 증가시키며 하판에 대한 상판 가속도의 전달률을 측정했다.

Fig. 10

Experimental set-up for transmissibility

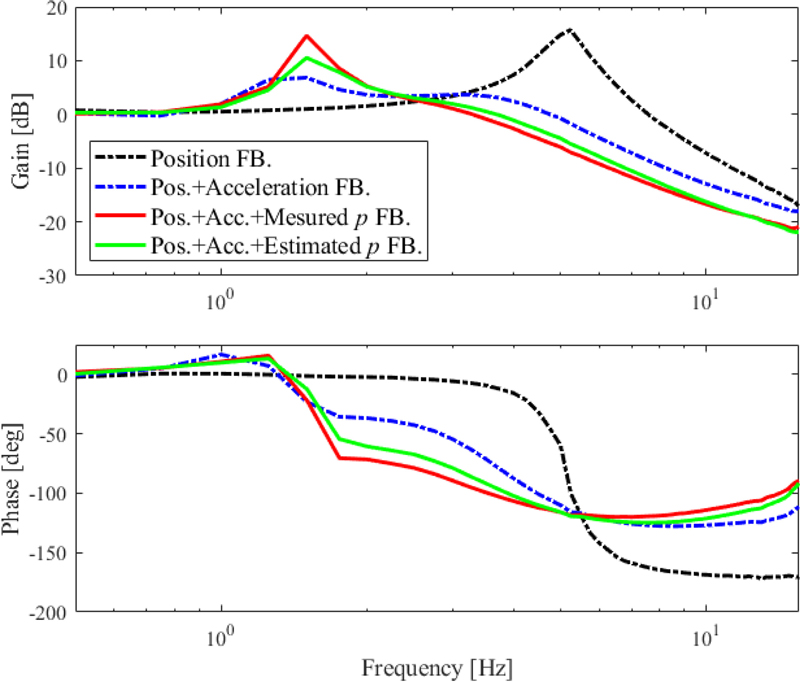
여러가지 능동제어기법과 함께 직접 및 추정 압력 궤환 제어 간의 진동전달률을 비교하여 Fig. 11에 나타냈다. 직접 압력 궤환과 동일하게 추정 압력 궤환도 변위 제어만 적용한 경우의 고유진동수 5.25 Hz를 1.5 Hz까지 낮춰서 진동 절연 대역폭을 넓힐 수 있었다.

Fig. 11

Transmissibility of the active vibration isolator with various control schemes

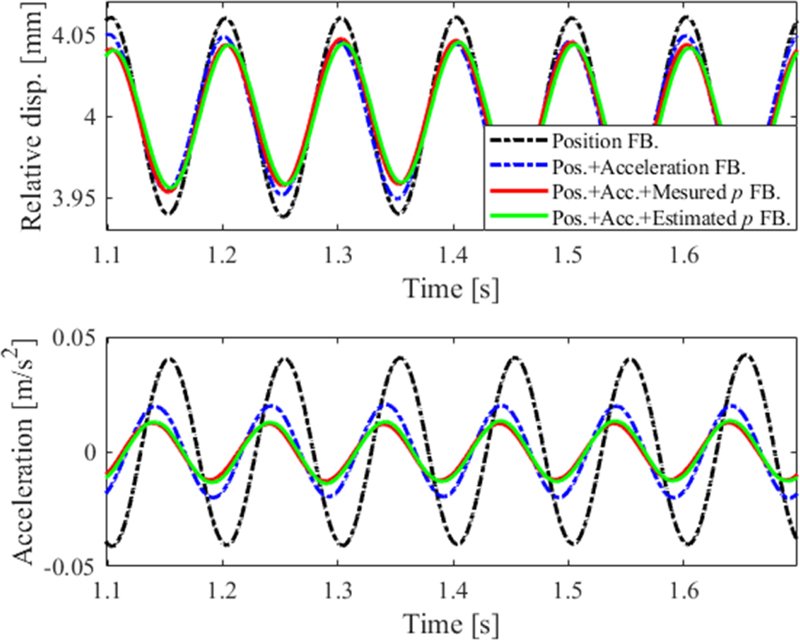
Fig. 12는 10 Hz 바닥 가진에 대한 상하판 상대 변위와 상판가속도이다. 10 Hz 진동전달률은 변위 제어만 적용한 경우를 기준으로 가속도 제어에서 48.3%, 가속도 및 압력 제어에서 64.8%가 감소하였다. 두 압력 궤환에 의한 제진 성능 차이는 거의 발생하지 않았고 압력 추정기의 효과성을 간접적으로 검증하였다.

Fig. 12

Time response of the relative displacement and the isolation table acceleration for 10 Hz floor excitation