에너지소모량 추정용 IMU 신호 기반 신경망 모델의 비교분석

1. 서론

최근 건강관리의 중요성이 대두되면서, 스마트 워치와 같은 웨어러블 기기를 활용하여 건강 상태를 모니터링하고 원격으로 진단하기 위한 유비쿼터스 헬스케어(Ubiquitous Healthcare) 시스템이 각광을 받고 있다. 특히 운동부족에 따른 질병을 예방하기 위하여 운동의 강도와, 시간, 빈도 등을 지속적으로 모니터링하는 기술이 다양한 응용분야에서 활용되고 있다. 이때 에너지 소모량(Energy Expenditure)은 운동 강도와 능력을 평가하는 주요 지표로 활용된다[1-3]. 또한, 근력보조 외골격 시스템에서 보조 성능을 평가하고 개인맞춤형으로 제어 패턴을 최적화하는데 있어 에너지소모량은 필수적으로 사용된다[4-6].

에너지소모량은 호흡가스 대사분석 시스템(Metabolic Gas Analysis System)을 통해 측정된 산소 섭취량(VO₂)과 이산화탄소 배출량(VCO₂)을 바탕으로 산출 가능하다[7]. 호흡가스 대사분석 시스템은 높은 정확도를 갖기 때문에 많은 연구에서 표준장비로 활용되지만, 대부분의 측정 장비가 고가이며, 호흡량을 측정하기 위해서는 마스크를 착용해야 하기 때문에 다양한 사용자가 일상생활 중에 사용하는데 있어서는 한계가 있다. 이러한 한계점을 극복하기 위하여 관성측정장치(Inertial Measurement Unit, IMU) 또는 근전도(Electromyography, EMG) 센서 등의 웨어러블 센서를 통한 에너지소모량 추정 연구가 꾸준히 진행되어왔다[8-14]. IMU와 EMG 등은 소형, 경량, 그리고 비교적 저가이기 때문에 다양한 웨어러블 기기에 쉽게 적용 가능하며, 다양한층의 사용자들이 일상생활에서도 큰 불편함 없이 사용 가능하다는 이점을 지닌다.

가속도계(Accelerometer)와 자이로스코프(Gyroscope)로 구성되는 IMU는 에너지소모량을 직접적으로 측정하지 못하는 대신 신체의 여러 운동학적인 정보를 제공하며[15-17], 이는 에너지 소모량과 상관관계를 갖는 것으로 밝혀진 바 있다[18,19]. 이를 바탕으로, 많은 연구에서 선형회귀(Linear Regression) 또는 기계학습(Machine Learning) 기법 등을 활용하여 에너지소모량을 추정하는 알고리즘을 개발하였다. 이때 일정 시간 내 IMU 신호의 총합 또는 다양한 특징값을 추출하여 모델의 입력으로 사용하는 방식을 많은 알고리즘에서 채택하고 있다. 예를 들어, ActiGraph 사(Pensacola, FL, USA)의 가속도계는 일정 시간동안의 센서 원신호(Raw Signal)를 총합한 수치인 카운트 정보를 제공하는데, 많은 연구에서 이 카운트 정보를 입력으로 사용하거나 카운트로부터 여러 특징값을 추출하여 에너지소모량을 추정하는 회귀 모델을 개발한 바 있다[8-10]. Ellis 등[11]과 Montoye 등[12]은 가속도계의 원신호를 기반으로 일상생활에서의 다양한 신체활동 중 에너지소모량을 추정하는 선형 회귀와 기계학습 모델 등을 새롭게 제시하거나 비교하였으며, 모델의 입력으로 특정 시간 동안의 가속도계 원신호로부터 추출된 평균, 표준편차, 최소, 최대 등 다양한 시간/주파수 영역의 특징값을 사용하였다. Zhu 등[13]은 가속도계 원신호의 시계열을 입력으로 받아 모델이 자체적으로 중요한 특징을 추출할 수 있는 합성곱신경망(Convolutional Neural Network, CNN) 모델을 개발하였다. Paraschiakos 등[14]은 가속도계 신호의 표준편차와 신체 정보를 입력으로 사용하여 에너지소모량을 추정하는 순환신경망(Recurrent Neural Network, RNN) 모델을 개발하였으며, 노인들을 대상으로 데이터 수집 및 모델 검증이 이뤄졌다.

앞서 소개된 연구들은 IMU를 통해 일상생활에서 다양한 신체활동 중의 에너지소모량을 신뢰성 있게 추정 가능함을 검증하였다. 다만, 대부분의 연구는 신체활동의 대략적인 강도를 평가하기 위한 수단으로 에너지소모량을 추정하는 것을 목표로 하였으며, 이는 매우 높은 수준의 정확도를 요구하지 않는다. 그에 반해 외골격 시스템의 보조 성능을 평가하거나 개인별로 최적화가 이뤄지기 위해서는 비교적 높은 성능의 에너지소모량 추정이 필요하며, 이에 최근에는 다양한 보행 조건 또는 외골격의 착용 유무에 따른 에너지소모량을 추정하는 연구가 진행된 바 있다[20-22]. Slade 등[20]은 EMG와 지면반력(Ground Reaction Force)으로부터 다양한 부하 및 경사의 보행과 여러 가지 패턴의 외골격 보조가 이뤄지는 보행 중의 에너지소모량을 추정하는 모델을 제안하였다. 또한 후속연구[21]에서는 다양한 속도의 보행 및 주행 중 에너지소모량을 추정 가능한 IMU 기반의 웨어러블 시스템을 개발하였다. Lopes 등[22]은 IMU와 EMG, 심박수 센서 신호를 기반으로 외골격의 보조가 없는 상태와 있는 상태의 보행 중 각각에 대하여 에너지소모량을 추정하는 CNN과 RNN 모델을 제안하였다. 상기 연구들은 IMU와 EMG를 포함한 웨어러블 센서를 통해 다양한 조건의 보행 중 소모되는 에너지를 추정할 수 있음을 보였다. 하지만 현재까지의 연구 결과에 따르면 IMU 단독으로 다양한 경사와 속도의 보행 및 주행에 대해서 높은 정확도로 에너지소모량을 추정하는 것은 어려움이 있다.

이에 본 논문에서는 IMU를 기반으로 다양한 경사와 속도의 보행 중 에너지소모량을 추정하는 신경망 모델을 구현하고 평지/경사 보행과 평지 주행 중의 추정 성능을 비교 분석하였다. 이때 에너지소모량 추정용 모델은 참고문헌[20]을 바탕으로 구현되었다. 또한 학습/테스트를 위한 데이터셋과 센서 부착위치에 따른 성능 비교가 함께 수행되었다. 신경망 모델의 학습 및 검증은 트레드밀 보행/주행 실험 데이터를 이용하여 이뤄졌다. 본 논문의 목적은 평지 보행/주행과 경사 보행 데이터를 이용하여 모델을 학습시킴으로써 보행조건의 다양성을 보강하고, 기계학습 기법 중 하나인 신경망을 접목하여 정확도 향상을 도모하는 것이다.

2. 방법

2.1 에너지소모량 추정용 신경망 모델

본 연구의 목적은 IMU 신호를 기반으로 여러 조건의 보행 중 정상상태 에너지소모량을 추정하는 신경망 모델을 구현하고 추정 성능을 비교 분석하는 것이다. 본 연구에서는 에너지소모량 추정을 위한 방법으로 참고문헌[20]에서 제시된 두 가지 방식을 채택하였다.

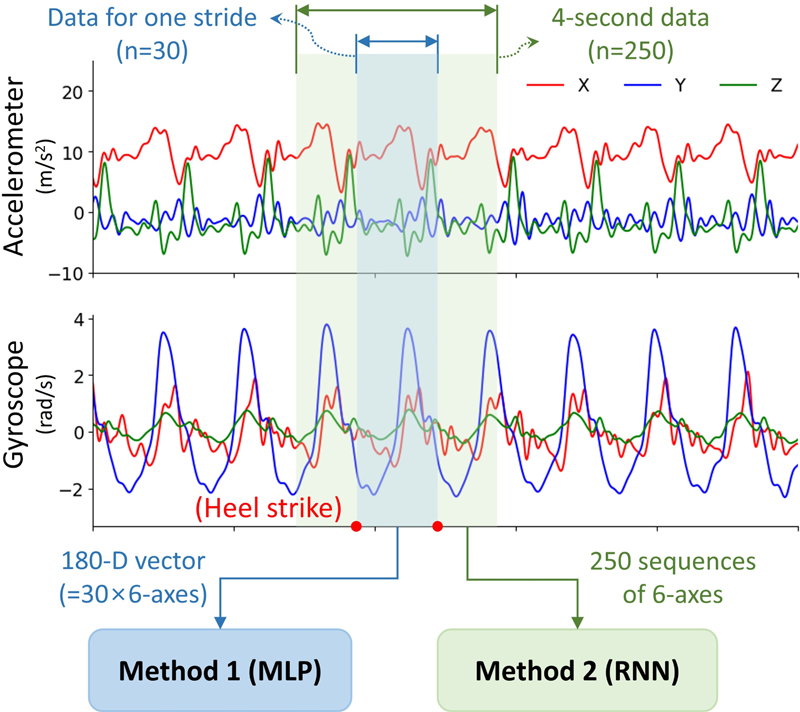
첫 번째 방법(M1)은 센서 데이터를 발꿈치가 닿는 순간(Heel Strike)을 기준으로 분할하여 각 보행 주기 동안의 센서 데이터를 입력으로 사용하는 다층 퍼셉트론(Multi-layer Perceptron, MLP) 모델에 해당한다. 이때 보행 주기마다 소요되는 시간은 서로 상이하므로, 데이터 길이 또한 서로 다르게 나타난다. 이에 각 보행 주기 동안의 데이터를 일정한 길이로 보간하여 사용하며, 본 연구에서는 참고문헌[20]에 따라 보간 크기를 30개로 설정하였다. 또한 피험자의 신체에 따른 영향을 반영할 수 있도록 피험자의 몸무게와 신장을 입력 데이터로 추가하였다. 모델의 구조는 182차원(시계열 길이 30 × IMU 신호 6개+신체 정보 2개)의 입력 신호를 받는 입력층과 400개의 뉴런을 갖는 3개의 은닉층(Hidden Layer), 그리고 400차원의 벡터를 입력으로 받아 최종적으로 1차원의 값을 출력하는 완전연결층(Fully Connected Layer)으로 구성된다. 이때 은닉층에서는 활성화 함수로 ReLU(Rectified Linear Unit) 함수를 사용한다. 두 번째 방법(M2)은 특정 길이의 시계열 데이터를 입력으로 받아 시간의 순서로 연산을 진행하는 RNN 모델에 해당한다. 이때 참고문헌[20]에 따라서 4초 동안의 데이터에 해당하는 250개 시계열 데이터를 입력으로 사용하였다. 이때 피험자의 신체 정보는 가장 마지막의 층에서 이전 층의 출력값과 함께 입력받는 구조로 설계하였다. 모델의 구조는 길이가 250개에 해당하는 6차원 IMU 신호의 시계열 데이터를 입력으로 받는 입력층과 64개의 은닉 유닛을 갖는 2개의 장시간메모리(Long Short-term Memory, LSTM)층, LSTM층에서 출력되는 시계열 데이터를 1차원 배열로 변환하는 평탄화층(Flatten Layer), 그리고 평탄화층의 출력 벡터와 피험자의 몸무게 및 신장을 함께 입력으로 받아 1차원의 값을 출력하는 완전연결층으로 구성된다. Fig. 1은 M1과 M2의 입력 신호의 유형을 보여준다.

Fig. 1

Input type for Method 1 and 2

M1과 M2 모두, 모델 학습 시 입/출력 데이터를 0에서 1 사이의 범위를 갖도록 최소-최대 정규화를 적용하였다. 학습 과정에서 손실함수로 평균 제곱 오차(Mean Squared Error, MSE)를 사용하였으며, 최적화 기법으로는 Adam (Adaptive Moment Estimation)을 적용하였다. 학습 에포크(Epoch) 수는 150번, 배치 크기는 64개로 설정하였으며, 최적의 모델 파라미터를 찾기 위해 학습률을 조정하는 기법 중 하나인 원사이클 스케줄링(One Cycle Scheduling) 기법을 적용하였다. 이때 최대 학습률은 10^-3으로 설정하였다. 모델의 과적합(Overfitting) 문제를 방지하기 위하여 모델의 각 층마다 0.5의 드롭아웃(Dropout)을 적용하고, 모델 학습 시에 L2 정규화를 적용하였다. 신경망 모델의 구현은 딥러닝(Deep Learning)을 위한 Python 기반의 프레임워크 중 하나인 PyTorch를 사용하여 진행되었다.

2.2 검증실험 및 데이터수집

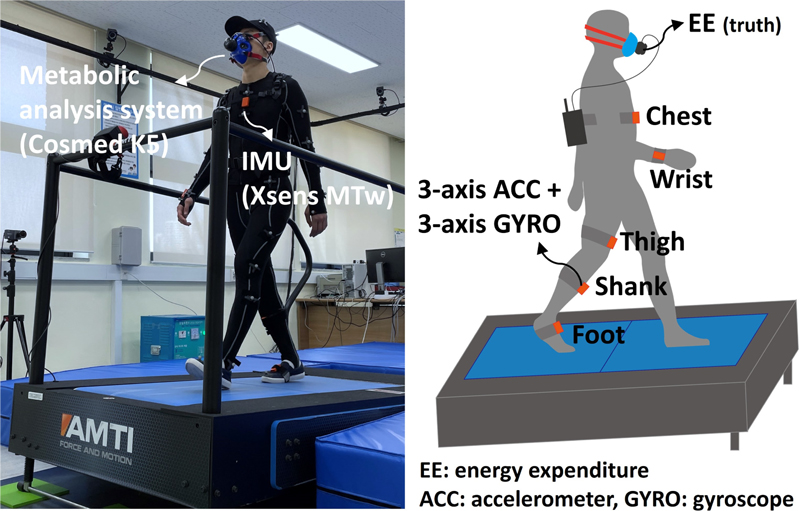
에너지소모량 추정용 모델의 학습과 검증을 위해, 6명의 건강한 남성 피험자(나이: 24.7±1.7세, 키: 1.75±0.05 m, 몸무게: 72.9±6.9 kg)를 대상으로 트레드밀 보행 및 주행 실험을 진행하여 데이터를 수집하였다. 본 연구의 실험은 공용기관 생명윤리위원회로부터 승인을 받아 진행되었다(P01-202110-13-001).

IMU 신호는 가속도계, 자이로스코프 그리고 마그네토미터를 포함하는 9축 IMU 모듈인 MTw (Xsens Technologies B.V, Enschede, Netherlands)를 통해 100 Hz의 샘플링률로 측정되었으며, 차단주파수가 6 Hz인 4차 Butterworth 저주파 통과 필터(Low-pass Filter)에 통과시켰다. 이때 IMU는 가슴, 오른쪽 손목, 오른쪽 다리의 허벅지, 정강이, 그리고 발에 스트랩 밴드를 통해 부착되었다. 에너지소모량의 참조값(Truth Reference) 산출에 필요한 산소 호흡량과 이산화탄소 배출량은 호흡가스 대사분석시스템 K5 (Cosmed, Rome, Italy)를 통해 매호흡(Breath by Breath)마다 측정되었으며, 에너지소모량은 Brockway 방정식[7]을 이용하여 산출되었다. 보행 감지에 필요한 지면반력은 힘판내장형 트레드밀(Advanced Mechanical Technology, Inc., Watertown, MA, USA)을 통해 측정되었다. Fig. 2는 본 실험 환경을 보여준다.

Fig. 2

Experimental setup

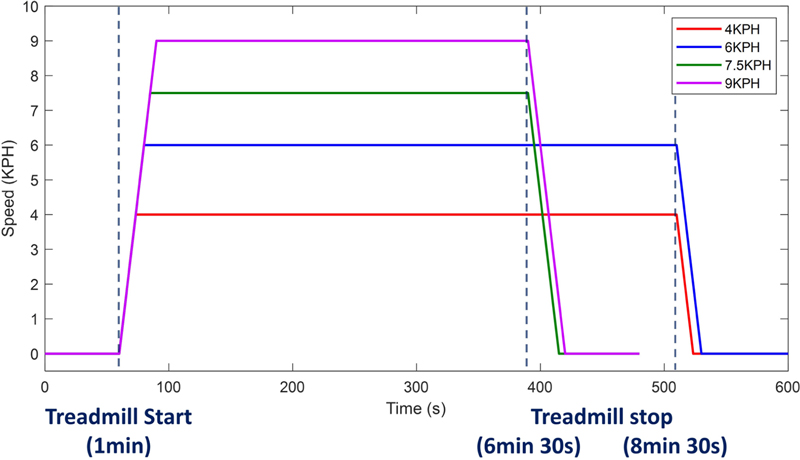
실험에서는 2가지 속도(4, 6 km/hour, KPH)의 평지 보행과 2가지 속도(7.5, 9 KPH)의 평지 주행, 그리고 2가지 속도(4, 6 KPH) 및 2가지 경사(3, 6%)의 경사 보행을 진행하였다. 이때 보행과 주행 실험의 속도는 사람들이 흔히 일상생활 중에 걷거나 뛸 수 있는 속도의 범위를 고려하여 선정되었다. 호흡이 안정된 상태에서 호흡량을 측정하기 위하여 각 실험 이전에 최소 3분 이상의 휴식을 취하도록 하였다. 보행 및 주행 실험 모두 처음 1분 동안 정적상태를 유지한 후에 트레드밀의 구동을 시작하였다. 이후 보행 실험에서는 8분 30초, 주행 실험에서는 6분 30초가 되었을 때 구동 종료 버튼을 누른 후에, 총 실험시간이 각각 10분 및 8분이 될 때까지 정적상태를 유지하도록 하였다. Fig. 3은 각 보행 및 주행 실험에 대한 트레드밀의 속도 그래프를 보여준다. 모든 보행/주행 실험은 각각 2번씩 반복 수행되었다. 각 보행 조건에 대한 정상상태 에너지소모량은 트레드밀 감속 직전 5분 동안의 측정값에 평균을 취함으로써 산출하였다.

Fig. 3

Treadmill speed profile for each walking/running test

모델의 검증 방식으로는 학습 및 검증 데이터를 피험자별로 교차하여 검증하는 방식인 Leave-one-out Subject 교차검증을 채택하였다. 이때 데이터셋으로 (Dataset 1) 평지/경사 보행 실험 데이터, (Dataset 2) 평지 보행/주행 실험 데이터, 그리고 (Dataset 3) 모든 실험 데이터로 나누어 모델의 학습과 테스트를 수행하였다. 모델의 성능은 피험자의 몸무게로 정규화된 평균 제곱근 오차(Normalized Root Mean Squared Error, NRMSE)와 에너지소모량의 참값에 대한 평균 절대 백분율 오차(Mean Absolute Percent Error, MAPE)를 이용하여 평가되었다. 이때 NRMSE와 MAPE 모두 정상상태의 보행(1분 30초-8분 30초)과 주행(1분 30초-6분 30초) 구간의 결과값을 산출하였다.

3. 결과 및 고찰

3.1 결과

Table 1은 Datasets 1-3을 통해 학습된 M1과 2의 추정 NRMSE와 MAPE 결과를 보여준다. 이때 Dataset 3을 학습시킨 모델의 결과에서는, 테스트 데이터로 Datasets 1-3 각각에 대한 결과를 함께 비교하였다.

Table 1

Averaged normalized root mean squared error, i.e., NRMSE in W/kg (with mean absolute percent error, i.e., MAPE in %) of energy expenditure from Method 1 (M1) and 2 (M2) for each training and test sets

Dataset 1을 학습/테스트에 사용한 결과에서, M1과 2 모두 발에 부착된 센서기반 모델이 가장 높은 성능(M1: 0.95 W/kg, M2: 1.02 W/kg, 이하 단위생략)을 보였다. 그 다음으로 우수한 성능을 보인 센서 부착위치로는 M1에서는 정강이(1.09), M2에서는 가슴(1.11)에 해당하였다. 또한 M1과 2를 비교하였을 때, 가슴을 제외한 나머지 위치에서 모두 M1이 우세한 성능을 나타냈다.

Dataset 2를 학습/테스트에 사용한 결과에서, M1의 경우에는 발(0.87), 그 다음으로는 가슴(0.88)에 부착된 센서의 모델이 우수한 성능을 보였으며, M2는 가슴(0.83), 그 다음으로는 손목(1.12) 부착 모델이 우수한 성능을 보였다. 또한 Dataset 1과 마찬가지로 대부분의 부착 위치에 대해서는 M1이 우세하였으나, 가장 높은 성능을 나타낸 모델은 M2의 가슴 부착 모델에 해당하였다.

다음은 Dataset 3을 학습에 사용한 결과이다. Dataset 1의 테스트 결과에서 M1과 2 모두 발 부착 모델(M1, 2: 약 0.86)이, 그 다음으로 M1은 정강이(1.01), M2는 가슴(1.15)의 모델이 우수한 성능을 보였다. 이는 Dataset 1을 학습시킨 모델에 비해 우세한 성능에 해당한다. Dataset 2의 테스트 결과에서는 M1의 경우에 발(0.91)과 정강이(1.04), 그리고 M2의 경우에 가슴(1.28)과 정강이(1.37) 순으로 성능이 우수하였다. 이는 Dataset 2를 학습시킨 모델에 비해 저하된 성능에 해당한다. Dataset 3의 결과에서 NRMSE 기준으로 M1과 2 모두 발(M1: 0.89, M2: 1.14)과 정강이(M1: 1.05, M2: 1.23) 순으로 높은 성능을 보였으나, MAPE 기준으로는 M2의 가슴(14.98%)의 성능이 정강이(16.50%)보다 높게 나타났다. M1과 2를 비교하였을 때, Dataset 1을 제외한 나머지에 대해서는 M1의 성능이 우세하였다.

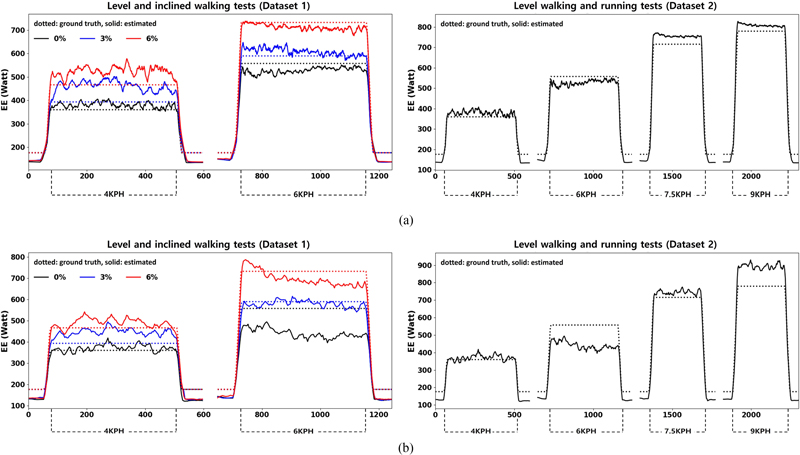
Dataset 3을 학습시킨 결과의 일부 예시로 Figs. 4와 5는 각각 발과 정강이의 센서 기반 M1과 M2의 에너지소모량 추정결과를 보여준다. 이는 평균적으로 우수한 성능을 나타낸 피험자의 결과이다. Fig. 4에서 M1과 M2 모두 여러 보행/주행 조건별 참조 에너지소모량을 높은 성능으로 추종하는 모습을 보였으며, 이 중 M1이 M2 대비 비교적 참조값에 근접한 추정 결과를 보였다. Fig. 5에서 M1은 Fig. 4의 결과와 유사한 추정 성능을 보인 반면에 M2는 6 KPH 보행 구간에서 오차가 비교적 크게 발생하는 모습이 확인되었다.

Fig. 4

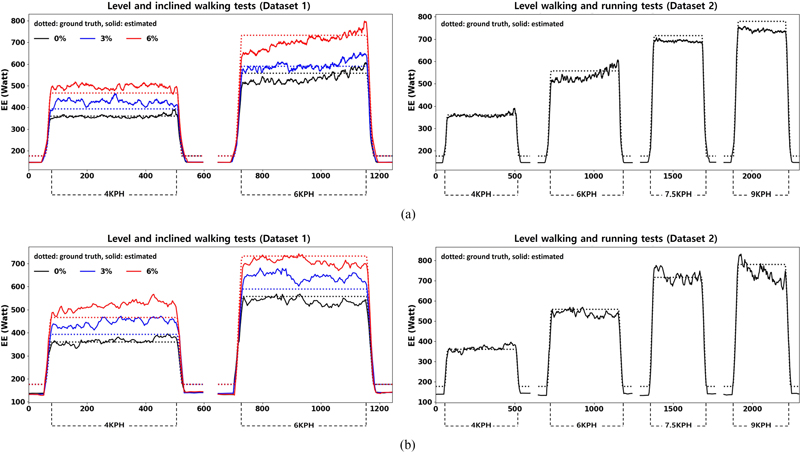
Energy expenditure (EE) estimation results of Datasets 1 and 2 from the (a) M1 and (b) M2 based on the foot-attached IMU

Fig. 5

Energy expenditure (EE) estimation results of Datasets 1 and 2 from the (a) M1 and (b) M2 based on the shank-attached IMU

4. 결론

본 연구에서는 참고문헌[20]의 방법을 바탕으로 에너지소모량 추정용 신경망 모델을 구현하고 IMU의 부착위치별, 추정방법별, 그리고 학습/테스트 데이터셋별로 성능을 비교 분석하였다. 그 결과 센서의 부착위치로는 발에 부착된 센서 기반의 모델이 가장 우수한 성능을 보였으며, 각 보행 주기 동안의 센서신호를 사용하는 MLP 모델이 일정 시간의 시계열 데이터를 사용하는 RNN 모델에 비해서 성능 우세를 나타냈다.

참고문헌[20]에서는 다양한 부하와 경사의 보행, 그리고 외골격보조가 이뤄지는 보행 중의 에너지소모량 추정 성능을 평가한 바 있으나, 다수의 EMG 신호와 지면반력을 입력으로 사용하므로 간단한 센서구성으로 보기 어렵다. 이의 후속연구[21]에서는 두 개의 IMU만으로 구성된 웨어러블 시스템을 개발한 바 있으나, 다양한 경사의 보행에 대해서는 성능 평가가 이뤄지지 않았으며, 각 보행주기 동안의 센서 신호를 입력으로 사용하는 방법(M1)만이 다뤄졌다. 본 연구에서는 간단한 센서구성(단일 IMU)을 활용하여 다양한 경사와 속도의 보행 및 주행에 대해서 추정 및 성능 평가를 하였으며, 두 가지 추정방식을 비교하였다는 점에서 의미가 있다.

추후 연구에서는, 보행 감지의 과정을 요구하지 않는다는 장점을 갖는 M2(즉, 일정 시간의 시계열 데이터를 사용하는 방식)를 대상으로 최적의 딥러닝 기법과 구조를 선정하여 성능을 향상시키기 위한 연구가 진행될 것이다. 또한 본 연구에서는 6명의 남성 피험자만을 대상으로 성능 평가가 이뤄졌기 때문에, 모델의 성능을 일반화하기 어렵다. 향후 다양한 연령과 성별의 피험자를 대상으로 실험 데이터를 수집하여 모델 성능의 일반화 및 평가가 진행될 것이다.

References

• Osgnach, C., Poser, S., Bernardini, R., Rinaldo, R., Di Prampero, P. E., (2010), Energy cost and metabolic power in elite soccer: A new match analysis approach, Medicine & Science in Sports & Exercise, 42(1), 170-178. [https://doi.org/10.1249/MSS.0b013e3181ae5cfd]
• Walker, E. J., McAinch, A. J., Sweeting, A., Aughey, R. J., (2016), Inertial sensors to estimate the energy expenditure of team-sport athletes, Journal of Science and Medicine in Sport, 19(2), 177-181. [https://doi.org/10.1016/j.jsams.2015.01.013]
• Roos, L., Taube, W., Beeler, N., Wyss, T., (2017), Validity of sports watches when estimating energy expenditure during running, BMC Sports Science, Medicine and Rehabilitation, 9(1), 1-8. [https://doi.org/10.1186/s13102-017-0089-6]
• Zhang, J., Fiers, P., Witte, K. A., Jackson, R. W., Poggensee, K. L., Atkeson, C. G., Collins, S. H., (2017), Human-in-the-loop optimization of exoskeleton assistance during walking, Science, 356(6344), 1280-1284. [https://doi.org/10.1126/science.aal5054]
• Kang, J., Kim, H., Kim, K., (2022), Whole-body control based strategy simulation of exo-suit considering singularity, Proceedings of the Korean Society for Precision Engineering Spring Conference, 212. [https://doi.org/10.7736/JKSPE.022.061]
• Jung, D., Kang, D., Lee, J., (2023), Development of passive upper limb exoskeleton device (H-Frame) for augment the load carrying capability of the human, Journal of the Korean Society for Precision Engineering, 40(4), 283-289. [https://doi.org/10.7736/JKSPE.022.113]
• Brockway, J., (1987), Derivation of formulae used to calculate energy expenditure in man, Human Nutrition. Clinical Nutrition, 41(6), 463-471.
• Swartz, A. M., Strath, S. J., Bassett, D. R., O’brien, W. L., King, G. A., Ainsworth, B. E., (2000), Estimation of energy expenditure using CSA accelerometers at hip and wrist sites, Medicine & Science in Sports & Exercise, 32(9), S450-S456. [https://doi.org/10.1097/00005768-200009001-00003]
• Crouter, S. E., Churilla, J. R., Bassett, D. R., (2006), Estimating energy expenditure using accelerometers, European Journal of Applied Physiology, 98, 601-612. [https://doi.org/10.1007/s00421-006-0307-5]
• Staudenmayer, J., Pober, D., Crouter, S., Bassett, D., Freedson, P., (2009), An artificial neural network to estimate physical activity energy expenditure and identify physical activity type from an accelerometer, Journal of Applied Physiology, 107(4), 1300-1307. [https://doi.org/10.1152/japplphysiol.00465.2009]
• Ellis, K., Kerr, J., Godbole, S., Lanckriet, G., Wing, D., Marshall, S., (2014), A random forest classifier for the prediction of energy expenditure and type of physical activity from wrist and hip accelerometers, Physiological Measurement, 35(11), 2191. [https://doi.org/10.1088/0967-3334/35/11/2191]
• Montoye, A. H., Begum, M., Henning, Z., Pfeiffer, K. A., (2017), Comparison of linear and non-linear models for predicting energy expenditure from raw accelerometer data, Physiological Measurement, 38(2), 343. [https://doi.org/10.1088/1361-6579/38/2/343]
• Zhu, J., Pande, A., Mohapatra, P., Han, J. J., (2015), Using deep learning for energy expenditure estimation with wearable sensors, Proceedings of the 2015 17th International Conference on E-health Networking, Application & Services (HealthCom), 501-506. [https://doi.org/10.1109/HealthCom.2015.7454554]
• Paraschiakos, S., de Sá, C. R., Okai, J., Slagboom, P. E., Beekman, M., Knobbe, A., (2022), A recurrent neural network architecture to model physical activity energy expenditure in older people, Data Mining and Knowledge Discovery, 36(1), 477-512. [https://doi.org/10.1007/s10618-021-00817-w]
• Lee, J. K., Park, E. J., Robinovitch, S. N., (2012), Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions, IEEE Transactions on Instrumentation and Measurement, 61(8), 2262-2273. [https://doi.org/10.1109/TIM.2012.2187245]
• Lee, J. K., (2019), A parallel attitude-heading Kalman filter without state-augmentation of model-based disturbance components, IEEE Transactions on Instrumentation and Measurement, 68(7), 2668-2670. [https://doi.org/10.1109/TIM.2019.2906417]
• Weygers, I., Kok, M., De Vroey, H., Verbeerst, T., Versteyhe, M., Hallez, H., Claeys, K., (2020), Drift-free inertial sensor-based joint kinematics for long-term arbitrary movements, IEEE Sensors Journal, 20(14), 7969-7979. [https://doi.org/10.1109/JSEN.2020.2982459]
• Koelewijn, A. D., Heinrich, D., van den Bogert, A. J., (2019), Metabolic cost calculations of gait using musculoskeletal energy models, A comparison study, PloS One, 14(9), e0222037. [https://doi.org/10.1371/journal.pone.0222037]
• Kowalsky, D. B., Rebula, J. R., Ojeda, L. V., Adamczyk, P. G., Kuo, A. D., (2021), Human walking in the real world: Interactions between terrain type, gait parameters, and energy expenditure, PLoS One, 16(1), e0228682. [https://doi.org/10.1371/journal.pone.0228682]
• Slade, P., Troutman, R., Kochenderfer, M. J., Collins, S. H., Delp, S. L., (2019), Rapid energy expenditure estimation for ankle assisted and inclined loaded walking, Journal of Neuroengineering and Rehabilitation, 16(1), 1-10. [https://doi.org/10.1186/s12984-019-0535-7]
• Slade, P., Kochenderfer, M. J., Delp, S. L., Collins, S. H., (2021), Sensing leg movement enhances wearable monitoring of energy expenditure, Nature Communications, 12(1), 4312. [https://doi.org/10.1038/s41467-021-24173-x]
• Lopes, J. M., Figueiredo, J., Fonseca, P., Cerqueira, J. J., Vilas-Boas, J. P., Santos, C. P., (2022), Deep learning-based energy expenditure estimation in assisted and non-assisted gait using inertial, emg, and heart rate wearable sensors, Sensors, 22(20), 7913. [https://doi.org/10.3390/s22207913]
• Zihajehzadeh, S., Park, E. J., (2016), Regression model-based walking speed estimation using wrist-worn inertial sensor, PloS One, 11(10), e0165211. [https://doi.org/10.1371/journal.pone.0165211]
• Paraschiv-Ionescu, A., Soltani, A., Aminian, K., (2020), Real-world speed estimation using single trunk IMU: methodological challenges for impaired gait patterns, Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), 4596-4599. [https://doi.org/10.1109/EMBC44109.2020.9176281]
• Simoni, L., Pancani, S., Vannetti, F., Macchi, C., Pasquini, G., (2020), Relationship between lower limb kinematics and upper trunk acceleration in recreational runners, Journal of Healthcare Engineering, 2020, 2973010. [https://doi.org/10.1155/2020/8973010]
• Lee, J. K., Park, E. J., (2011), Quasi real-time gait event detection using shank-attached gyroscopes, Medical & Biological Engineering & Computing, 49, 707-712. [https://doi.org/10.1007/s11517-011-0736-0]