강화학습을 이용한 능동 현가장치 제어

1. 서론

현가장치는 자동차의 승차감과 주행 안정성 향상에 중요한 역할을 하며, 다양한 제어 방법들을 적용하기 위한 연구가 진행되고 있다. 현가장치는 수동, 반능동, 능동 시스템의 세 가지 유형이 있으며, 각각의 시스템은 장단점을 가지고 있다. 수동 현가 장치는 제한된 주파수 범위 내에서 적절한 성능을 제공하고, 반능동 현가장치는 충격 흡수기의 점도를 조절하여 더 넓은 주파수 대역에서 효율적인 장점이 있다. 하지만 급변하는 도로 및 환경 조건에 대하여 수동 및 반능동 현가장치는 적응성과 반응성이 떨어지는 단점이 존재하여 보다 신속하게 적응할 수 있는 능동 현가장치 기술에 대한 관심이 증가하고 있다. 능동 현가장치에 적용되어 왔던 제어기에는 PID (Proportional, Integral, Derivative), LQR (Linear Quadratic Regulator) 등이 있다[1,2]. 이러한 제어기로도 충분히 좋은 성능을 얻을 수 있지만 시스템의 복잡성이 증가하거나 변화하는 외부 요인에 의해 제어 성능이 감소할 수 있다. 그러한 단점을 해결하기 위해 인공지능과 같은 기계 학습 기법을 이용하여 제어 성능을 향상시키는 연구가 진행되었다. Ghoniem 등은 ANN (Artificial Neural Network)을 사용하여 서스펜션의 피스톤, 밸브 등을 제어하여 성능을 향상시켰다[3]. Vidya 등은 RNN (Recurrent Neural Network) 기반의 MRAC (Model Reference Adaptive Control) 기법으로 능동 서스펜션을 제어하였다[4]. 하지만 신경망과 같은 기계학습은 데이터의 수에 따라 성능이 변화될 수 있고 다양한 환경에 대해 강건한 성능을 확보하는 것은 현재에도 많은 기술적 어려움이 존재한다. 이를 보완하기 위하여 이전에 경험하지 못한 복잡한 상황을 시행착오를 통해 학습하는 강화학습을 적용한 연구가 다양하게 진행되고 있다. Lee 등은 반능동 현가장치 제어를 위해 TRPO (Trust Region Policy Optimization), A2C (Advantage Actor Critic) 그리고 SAC (Soft Actor Critic)와 같은 강화학습 기법들을 비교하고 새로운 접근 방법을 제시하였다[5]. Fares 등은 TD (Temporal Difference) 방법을 사용하여 능동 현가장치를 제어하였다[6]. Han 등은 반능동 현가장치의 진동 제어를 위해 PPO (Proximal Policy Optimization) 알고리즘을 사용하였다[7]. 마찬가지로 Dridi 등도 PPO 알고리즘을 사용하여 능동 현가장치를 제어하며, 다양한 보상함수를 비교하고 설계하여 제어에 적용하였다[8]. 이러한 연구들과 비교하면, DDPG (Deep Deterministic Policy Gradient) 알고리즘을 사용하는 접근 방법은 현가장치 제어에 대하여 몇 가지 이점을 제공한다. DDPG 알고리즘은 심층 신경망 모델을 사용하여 복잡한 비선형 시스템을 모델링함으로써, 정밀하고 향상된 제어 성능을 가질 수 있으며, 정책 기반 학습과 배우-비평가 구조 그리고 경험 리플레이의 활용으로 연속적인 행동 공간에서의 성능이 뛰어나다. 이러한 이점들로 인해 DDPG 알고리즘을 연속적인 행동과 높은 정밀도가 필요한 현가장치 제어와 같은 분야에서 적용하기 위한 연구가 진행되고 있다. Liang 등은 DDPG 알고리즘을 적용하여 랜덤 노면에 대한 반능동 서스펜션의 제어 성능을 평가하였다[9]. 그러나 노면 상태를 랜덤 노면의 레벨 B, C, D로 제한하여 알고리즘의 성능을 평가하였고, 이는 범프(Bump) 노면 또는 정현파 노면 등 다른 노면 상태에서의 성능 평가에 한계를 가지고 있다. 따라서 DDPG 알고리즘을 능동 서스펜션에 적용한 연구 및 다양한 노면 조건에서 DDPG 알고리즘을 적용한 제어 성능을 평가하는 연구가 추가적으로 필요하다.

본 연구에서 DDPG 알고리즘을 활용하여 능동 현가장치를 제어하는 방법을 제안하고 성능을 평가한다. 이를 위해 적절한 보상함수를 설계하고, 조기 종료 조건을 설정하여 학습의 안정성을 확보한다. 랜덤 노면과 범프 노면 데이터를 기반으로 각각 학습된 DDPG 알고리즘의 성능을 랜덤 노면, 범프 노면, 정현파노면에 대하여 비교 분석하고, 학습 데이터 유형에 따른 제어성능의 차이를 확인한다. 또한, 제안된 모델과 기존 PID 제어기법의 성능을 비교하여, 제안된 모델이 다양한 노면 상태에 대하여 강건한 제어 성능을 제공하는 것을 검증하고, 제안된 모델을 적용하여 능동 현가장치를 효과적으로 제어할 수 있음을 확인한다.

2. 실험 구성

2.1 DDPG 알고리즘

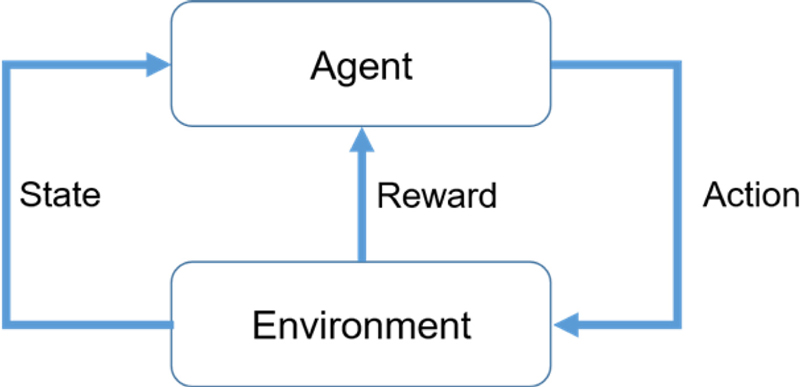
강화 학습은 MDP (Markov Decision Process) 기반의 최적화 개념과 행동 심리학 개념인 시행착오를 결합한 인공지능 기반의 기계학습 알고리즘 중 하나이다. 강화 학습의 기본 구성은 Fig. 1에서 나타낸 것과 같이 크게 환경(Environment)과 에이전트(Agent)로 구성되어 있다. 에이전트는 현재 상태(State)를 관측(Observation)하고 임의의 행동(Action)을 선택한다. 이 때 환경은 에이전트에게 보상(Reward)을 주고 다음 상태를 나타내게 된다. 이 과정에서 에이전트는 지속적인 시행착오를 겪으며 보상을 최대화하는 방향으로 행동을 결정하는 학습 과정이 강화학습이다. DDPG는 강화학습 알고리즘의 종류 중 하나로, DPG (Deterministic Policy Gradient)와 DQN (Deep Q-network)의 개념을 결합한 알고리즘이다. DDPG는 연속적인 행동 공간(Action Space)을 가진 문제를 해결하기 위해 설계된 정책(Policy)에 해당되는 배우(Actor)와 가치 함수(Value Function)에 해당하는 비평가(Critic)에 대해 별도의 모델을 갖는 배우-비평가 기반의 강화학습 알고리즘이다[10]. 이 알고리즘은 DPG의 경사 기반 방법을 사용하여 최적의 정책을 찾는 것을 확률로 나타내어 연속적인 행동 공간에 적합한 장점을 가지고 있다. 그리고 DQN의 딥러닝 구조를 통해 기존 Q-러닝에서의 단점이었던 상태와 행동이 추가될수록 방대해지는 Q-테이블을 비선형 함수인 Q-함수로 근사시켜 모든 상태와 행동에 대한 Q값을 저장하지 않고도 학습이 진행될 수 있게 하면서 복잡한 환경에서도 학습할 수 있는 장점이 있다.

Fig. 1

Basic structure of reinforcement learning

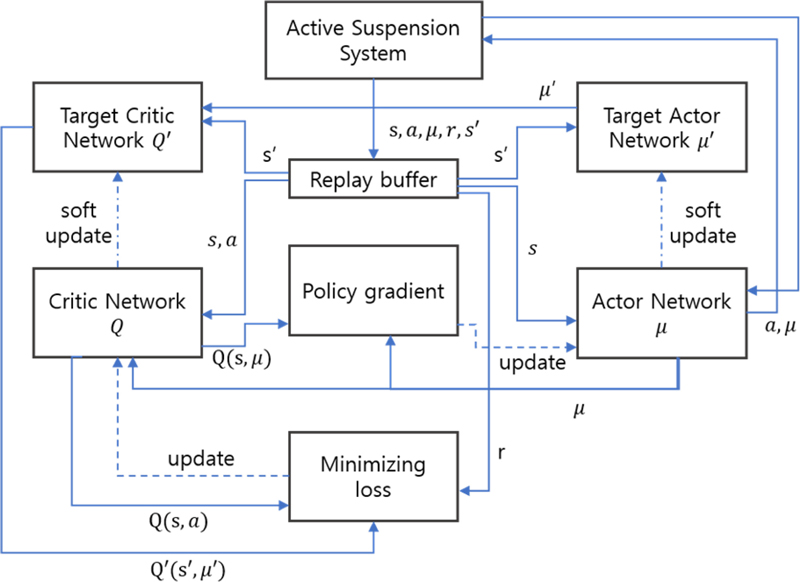
DDPG 알고리즘 구성요소는 Fig. 2에서 나타낸 것과 같이 배우, 비평가, 타겟 네트워크(Target Network) 그리고 경험 리플레이(Experience Replay)가 있다. 배우는 현재 상태를 입력으로 받아 결정론적인 행동을 출력하는 정책 네트워크이다. 비평가는 배우가 출력한 행동과 현재 상태를 입력으로 받아 그 행동을 취했을 때의 보상을 출력한다. 타겟 네트워크는 DQN에서 사용된 방법이며, 배우와 비평가가 훈련됨에 따라 바뀌는 가중치를 주네트워크와 동일한 아키텍처로 구성된 타겟 네트워크를 거쳐 가중치를 일정 비율만큼만 업데이트하는 소프트 업데이트 방식을 적용함으로써 훈련의 안정성을 높이는 방법이다. 경험 리플레이는 에이전트의 상태, 행동, 보상 등과 같은 경험을 저장하고 학습 시 무작위로 추출하여 사용함으로써 샘플들 간의 상관관계를 줄이고 효율적인 학습을 가능하게 하는 역할을 한다. 이와 같은 구성요소를 가진 DDPG는 연속적인 행동 공간에서 진행되는 물리 제어 작업에 주로 사용되고 그에 대한 보상함수의 설계 또한 중요하다. 보상함수는 비평가 네트워크에서 벨만 방정식으로 표현되며, 가장 간단한 형태로 식(1)과 같이 나타낼 수 있다.

Fig. 2

DDPG architecture

$\[ Q\left(s,a\right)=r+\gamma \cdot {max}_{a^{\mathrm{\text{'}}}} Q\left(s^{\mathrm{\text{'}}},a^{\mathrm{\text{'}}}\right) \]$

(1)

여기서 Q(s, a)는 상태 s에서 행동 a를 취했을 때의 Q값이고 r은 보상, γ는 감가율 그리고 max_a’Q(s’, a’)는 다음 상태 s’에서 가능한 모든 행동 a’들 중 가장 큰 Q값을 나타낸다. 보상함수의 경우 정적 목표 상태가 있는 모든 작업에서는 거리를 기반으로 한 보상을 포함하며 본 연구에서 사용된 보상함수는 식(2)와 같이 나타내었다.

$\[ r=-\left[w_1{\left(x_s-x_t\right)}^2+w_2{\ddot{x}}_s^2+w_3{\left(x_t-x_u\right)}^2\right] \]$

(2)

여기서 w는 가중치이며, x_s는 현가 상질량의 변위, x_t는 현가 하질량의 변위, $$ {\ddot{x}}_S$$는 현가 상질량의 가속도 그리고 x_u는 노면의 변위이다. 또한 알고리즘의 안정성과 수렴 속도를 높이기 위해 조기 종료 기능을 사용하였다. 조기 종료 조건은 식(3)과 같은 조건 현가장치의 최대 변위가 10 cm를 넘어갈 시 종료되는 것으로 결정하였다.

$\[ \left|x_s-x_t\right|>0.1 \]$

(3)

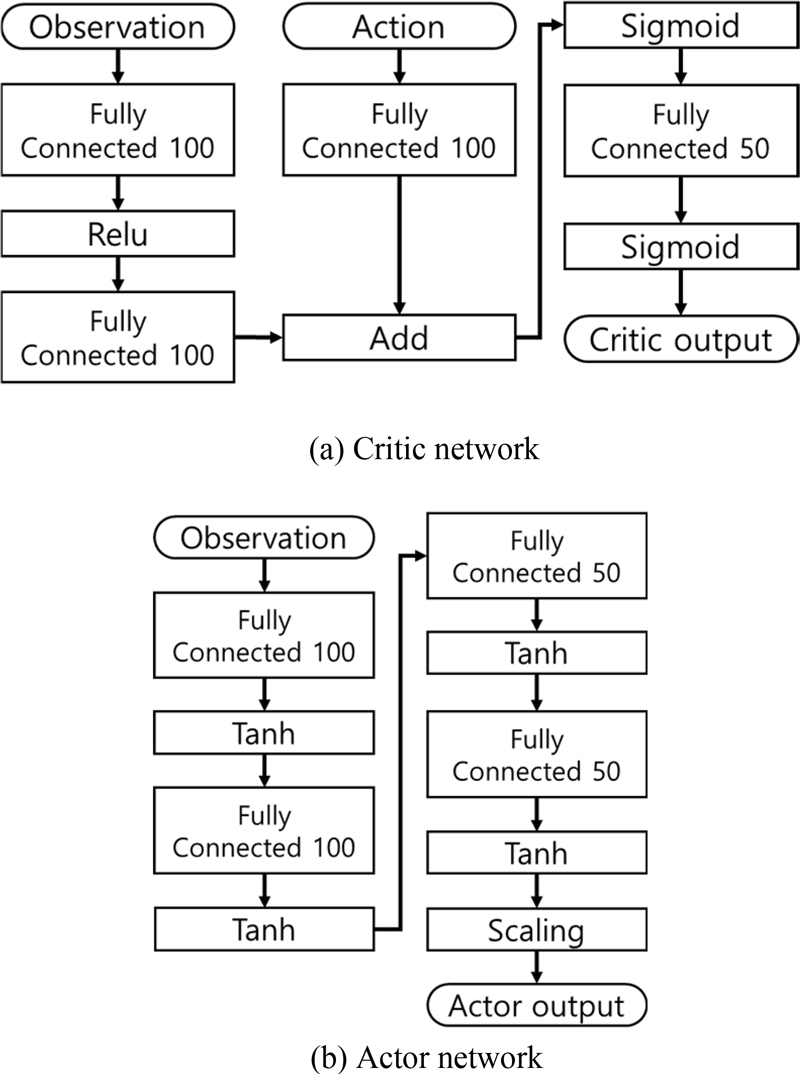
DDPG 알고리즘의 학습에 사용된 하이퍼파라미터는 Table 1에 나타내었으며, 배우-비평가 네트워크의 구성은 Fig. 3에 나타내었다. 현가장치의 힘 제어 범위는 –4,000 N에서 4,000 N으로 설정하였다.

Table 1

Hyperparameters of DDPG

Fig. 3

Critic and actor network

2.2 실험 방법

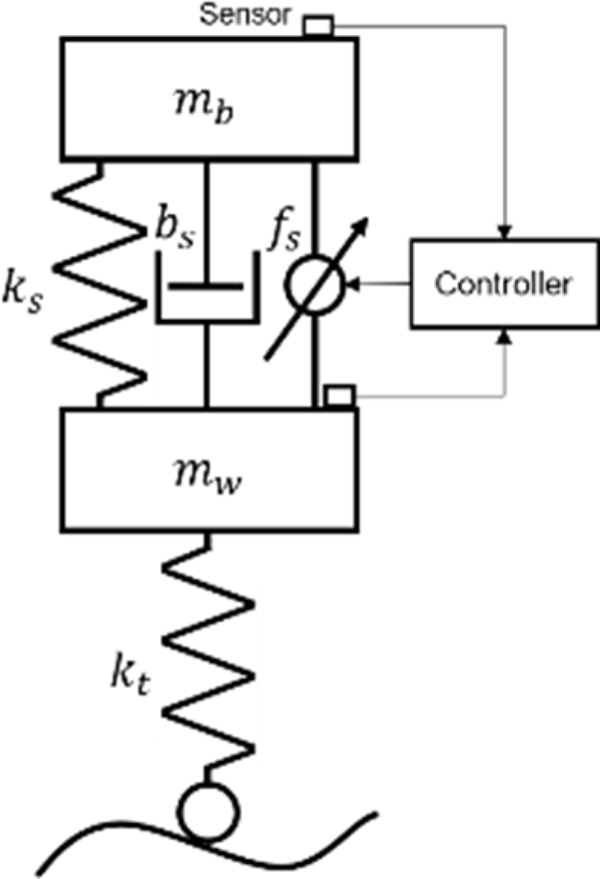
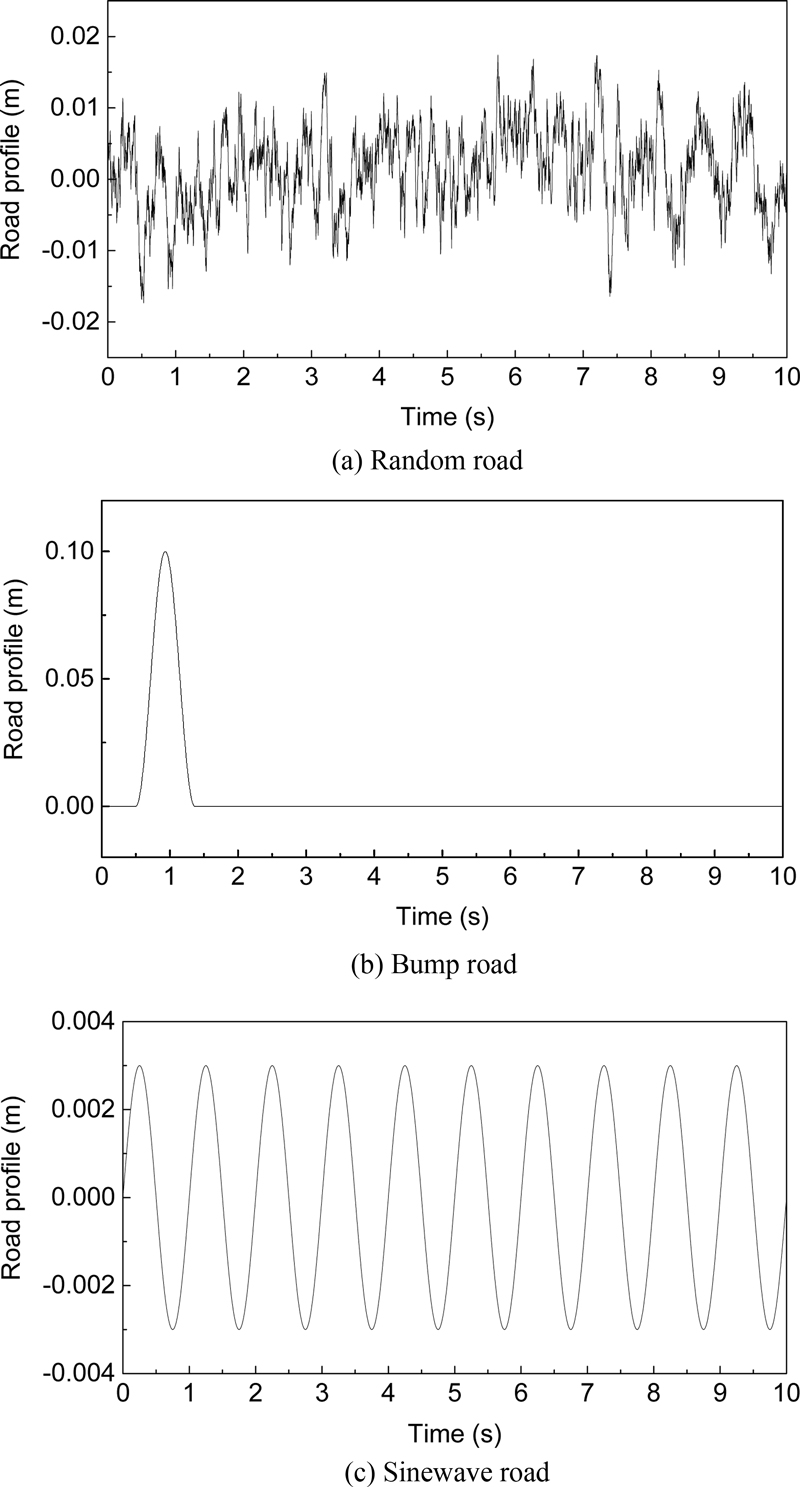
MATLAB의 SIMULINK를 이용하여 1/4 차량 모델을 3가지 종류의 노면 상태에 대해 제어하는 실험을 구현하였다. 사용된 1/4 차량 모델은 Fig. 4와 같으며, 파라미터는 Table 2와 같다. 제어 방법은 PID제어와 DDPG 알고리즘을 랜덤 노면으로 학습한 모델과 범프 노면으로 학습한 모델로 제어하였다. Fig. 5에 본 연구에서 사용된 노면 모델을 나타내었다. 총 3가지의 노면모델을 사용했으며, Fig. 5(a)에서 나타낸 랜덤 노면 모델은 식(4)에서 나타낸 것과 같이 ISO 8608에 기반하여 특정 PSD(Power Spectral Density)를 갖는 백색 잡음 신호가 포함된 시계열 영역의 식을 이용하였다[12].

$\[ \dot{q}\left(t\right)=-2\pi v{n}_{0}q\left(t\right)+2\pi \sqrt{G\left(n_0\right)v}w\left(t\right) \]$

(4)

Fig. 4

Quarter vehicle model

Table 2

Quarter vehicle model parameters

Fig. 5

Road profile model

여기서 v는 차량 속도, n₀는 표준 공간 주파수, G(n₀)는 노면 거칠기 계수 그리고 w(t)는 단위 백색 소음이다. 사용된 파라미터의 값은 Table 3에 나타내었고 G(n₀)는 C-Class의 값을 사용하였다. w(t)는 2σ²ρv의 강도를 가진 단위 백색 소음신호이고 σ²는 노면 랜덤성의 공분산 그리고 ρ는 노면 거칠기 매개변수이며, 포장된 도로 상태를 고려하여 선택되었다[11]. Fig. 5(b)에서 나타낸 범프 노면 모델의 경우 식(5)에 나타내었다.

$\[ x_b\left(t\right)=\left\{\begin{array}{cc}\frac{h}{2}\left(1-cos\left(\frac{2\pi vt}{L}\right)\right)& 0\le t\le \frac{L}{v}\\ 0& Otherwise \end{array}\right. \]$

(5)

Table 3

The value of the random road parameters

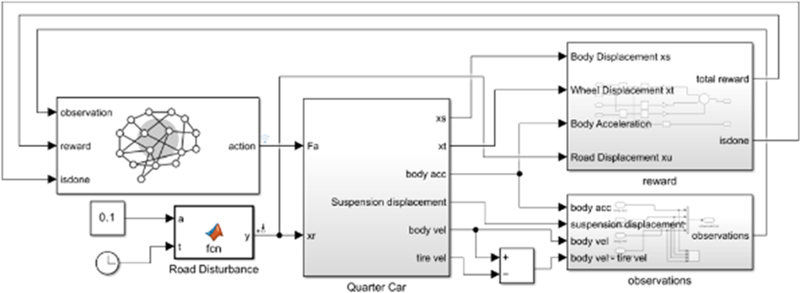
여기서 h는 범프의 높이, v는 차량 속도 그리고 L은 폭 길이이다. 파라미터는 국토교통부가 정한 규격으로 높이는 10 cm 그리고 폭은 3.6 m로 설정되었다. 또한 본 연구에서는 차량 속도가 15 km/h일 때 DDPG 알고리즘의 학습에 사용되었으며, 제어 결과 비교는 각각 15, 30, 60 km/h일 때 진행하였다. Fig. 5(c)에서 나타낸 정현파 노면 모델은 현가장치 성능 평가 방법의 하나인 EUSAMA 테스트를 참고하여 파라미터를 설정하였다. 최종적으로 사용된 시뮬레이션 모델은 Fig. 6에 나타내었다.

Fig. 6

Simulation model

3. 실험 결과 및 분석

3.1 시뮬레이션 결과

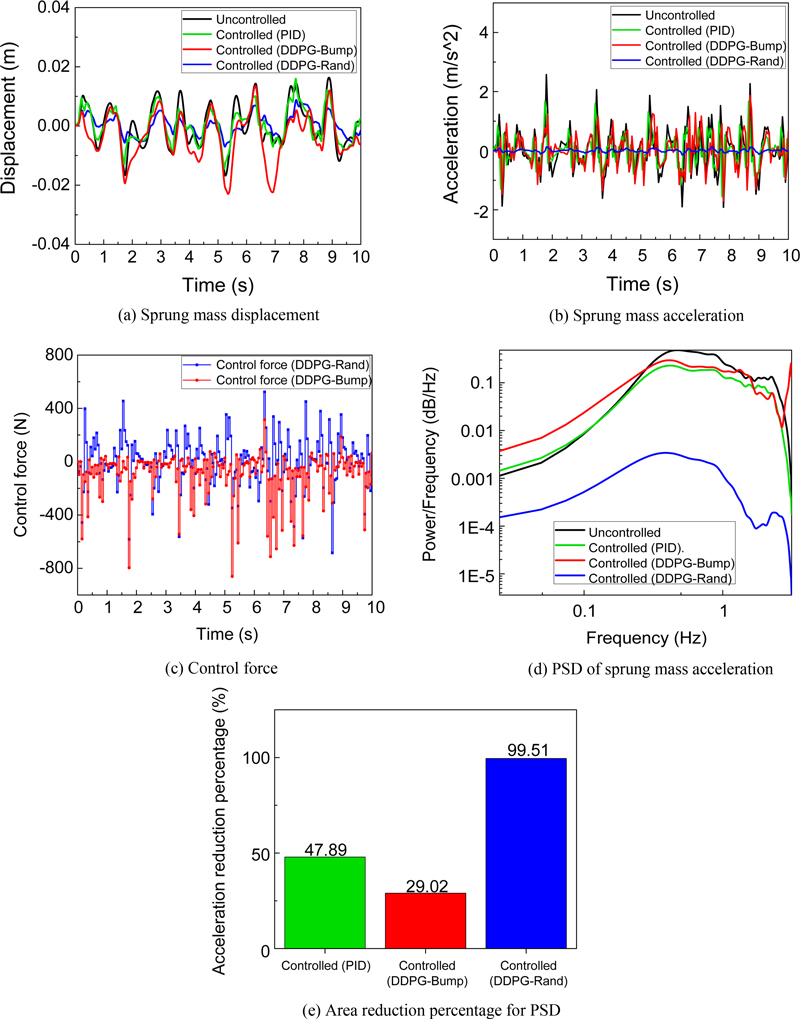
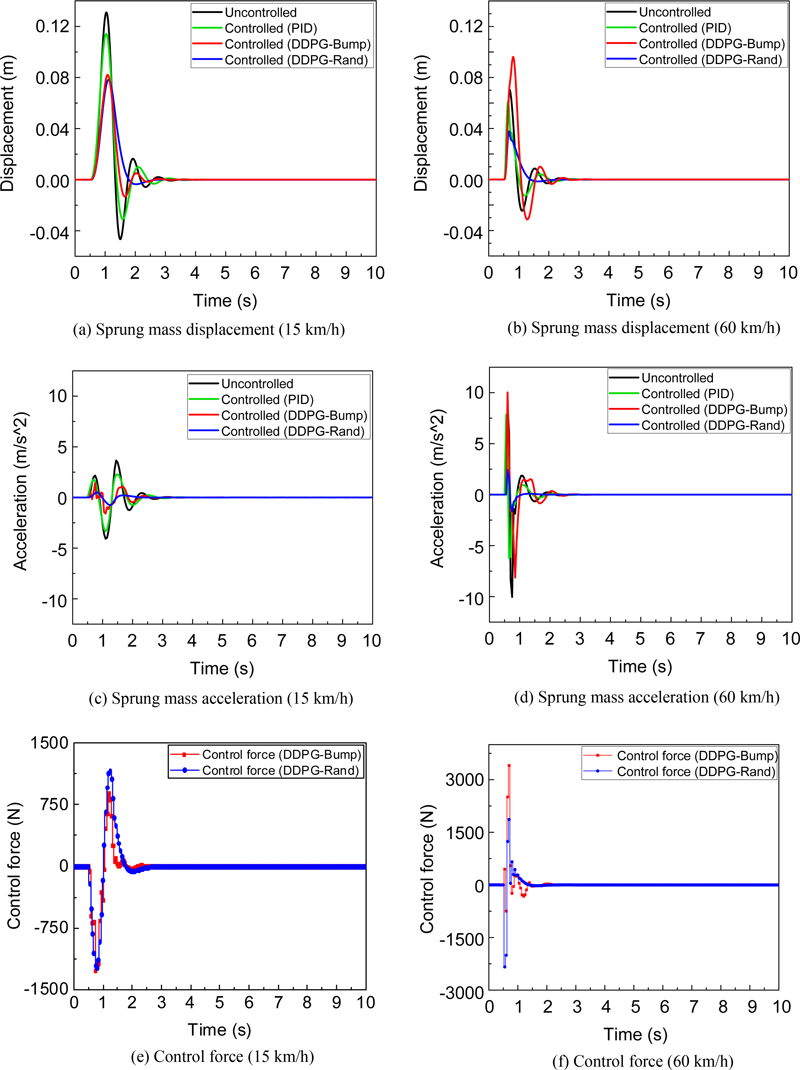
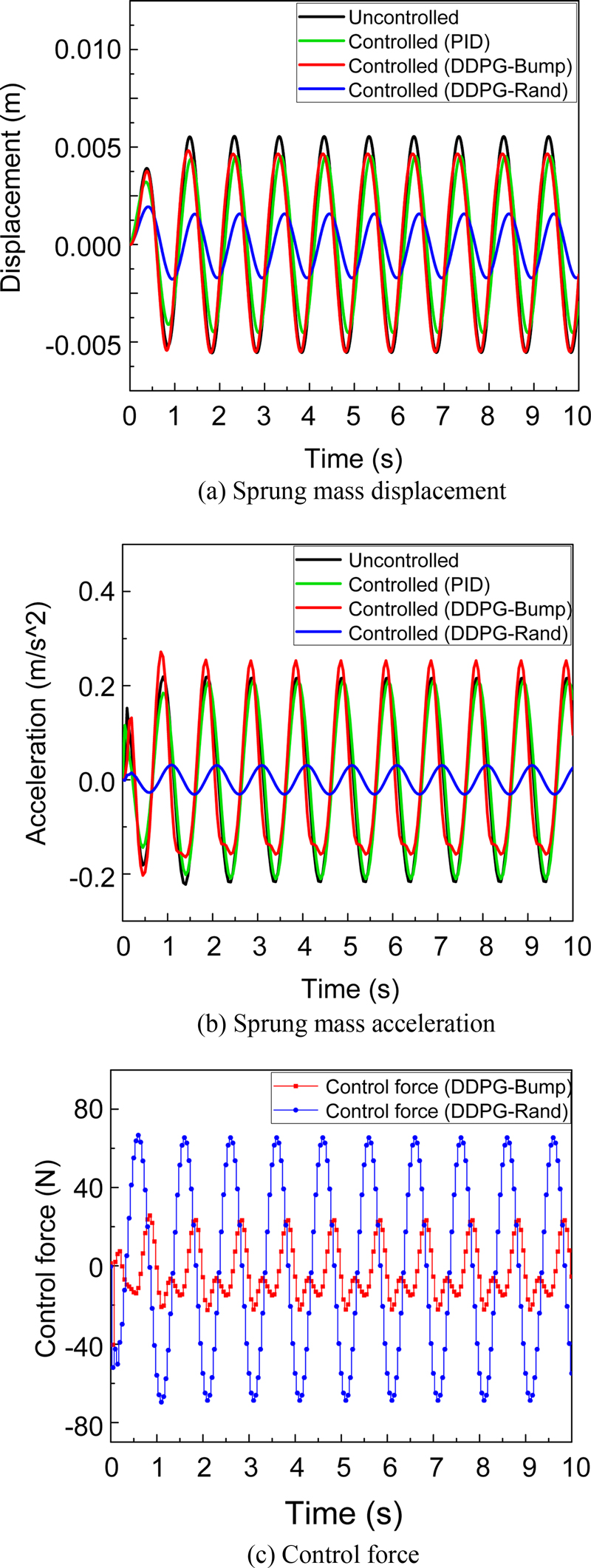
시뮬레이션 결과는 노면 종류에 따라 3가지의 결과로 도출되었다. 첫 번째로 랜덤 노면의 제어 결과는 Fig. 7에서 변위, 가속도, 제어력 그리고 가속도에 대한 PSD 그래프로 나타내었다. 비교의 편의를 위하여 Table 4에서 현가 상질량의 변위와 가속도에 대한 RMS (Root Mean Square) 감소율을 나타내었다. 랜덤 노면에 관한 결과는 범프 노면 모델로 학습한 DDPG 알고리즘의 성능이 PID 제어 결과보다 낮았고 Fig. 7(c)에서 확인할 수 있는 제어력 그래프에서도 불안정한 성능을 나타낸 것을 확인하였다. 하지만 랜덤 노면 모델로 학습한 DDPG 알고리즘의 성능은 변위의 경우 수동 현가장치의 성능보다 약 51%의 변위 감소율을 보였고 가속도의 경우 약 93%의 감소율로 우수한 성능을 가진다. 또한 더 정확한 결과 비교를 위해 가속도에 대한 PSD 그래프를 Fig. 7(d)에서 나타내었다. 가속도에 대한 PSD 그래프에서의 면적을 비교하여 Fig. 7(e)에서 나타내었고 수동 현가장치의 성능보다 약 99%의 가속도 감소율로 매우 뛰어난 성능을 가진 것을 확인하였다. 두 번째로 범프 노면 모델의 제어 결과는 Fig. 8, Tables 5, 6에서 나타내었다. Fig. 8(a)와 Table 5에서 확인할 수 있듯이 15 km/h의 차량 속도에 대한 제어 결과에서 최대 변위의 경우 약 0.08 m로 그리고 RMS 감소율 또한 약 34%로 랜덤 노면과 범프 노면으로 학습한 결과가 거의 비슷한 것을 확인할 수 있었다. 하지만 Table 6에서 가속도에 대한 RMS 감소율에서 약 -20% 정도의 성능 차이를 확인할 수 있었으며, 변위와 가속도 모두 차량 속도가 증가할수록 범프 노면으로 학습한 DDPG 알고리즘의 성능은 떨어지고 랜덤 노면으로 학습한 DDPG 알고리즘의 성능은 변위에서 평균 39.5% 그리고 가속도에서 평균 82.6%를 나타내었다. 세 번째로 정현파 모델의 제어 결과는 Fig. 9와 Table 7에서 나타내었다. Fig. 9에서 육안으로도 성능 차이를 확인할 수 있었으며, Table 7에서 현가상질량의 변위 및 가속도 모두 랜덤 노면 모델로 학습한 결과가 우수한 성능을 가지는 것을 확인하였다.

Fig. 7

Results of random road

Table 4

RMS reduction percentage of sprung mass under random road excitation

Fig. 8

Results of bump road

Table 5

RMS reduction percentage of sprung mass displacement under bump road excitation

Table 6

RMS reduction percentage of sprung mass acceleration under bump road excitation

Fig. 9

Results of sinewave road

Table 7

RMS reduction percentage of sprung mass under sinewave road excitation

3.2 결과 분석

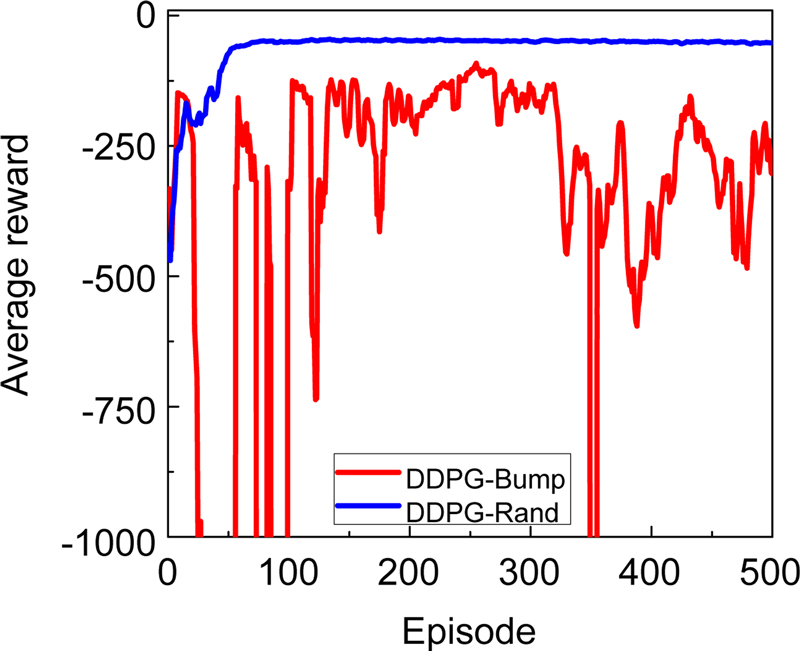
시뮬레이션 결과를 통하여 랜덤 노면에서 학습된 DDPG 알고리즘의 제어 성능이 기존 PID 알고리즘을 적용한 경우보다 우수한 것을 확인하였고, 범프 노면으로 학습한 알고리즘의 성능은 학습 과정에서 사용되었던 동일한 노면 조건 외에서의 성능이 떨어지는 것을 확인하였다. 추가로 Fig. 10에서 학습 과정 중 저장된 평균 보상을 확인한 결과, 랜덤 노면으로 학습한 알고리즘은 평균 보상 약 -40까지 범프 노면 보다 매우 빠르게 수렴한 것을 확인하였다. 최종적으로 사용된 가장 성능이 좋은 DDPG 모델은 랜덤 노면의 경우 에피소드 130번째 그리고 범프 노면의 경우 3913번째에서 훈련이 완료된 모델을 사용하였으며, 랜덤 노면으로 학습된 DDPG 모델이 다양한 노면 상태에 대해 좋은 성능을 나타내는 것을 확인하였다.

Fig. 10

Average rewards per episode

4. 결론

본 연구에서는 강화학습을 이용한 능동 현가장치 제어 기법을 제안하고, 시뮬레이션을 통하여 제안된 시스템을 구현하였다. 1/4차량 모델을 이용하여 랜덤 노면 모델, 범프 노면 모델 그리고 정현파 모델에 대해 PID 그리고 서로 다른 조건에서 학습된 DDPG 알고리즘 모델의 제어 결과를 확인하였다. DDPG 알고리즘을 통하여 학습에 사용되지 않는 다양한 노면 조건에서 현가장치를 효과적으로 제어할 수 있음을 확인하였다. DDPG 알고리즘을 이용한 현가장치와 같은 물리 제어 작업을 위하여 알맞은 보상함수 설계 및 조기 종료 조건이 필요한 것을 확인하였다. 다양한 환경에서 우수한 성능을 나타내는 강화학습을 적용하기 위해 다른 조건의 학습 데이터를 사용한 결과를 비교하였고, 제어 결과에 큰 영향을 미치는 것을 확인하였다. 제안된 기법을 활용하여 강화학습으로 현가장치뿐만 아니라 로봇과 같이 다양한 환경에 직면하게 되는 여러 물리 제어 작업에 대해 확장할 수 있을 것으로 기대된다. 이후에 다양한 강화학습 기법을 이용하거나 최적화된 보상함수의 설계 및 학습 데이터의 선정에 관해 연구를 수행할 예정이다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2023R1A2C1007973). 본 논문은 2023년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학협력기반 지역혁신사업의 결과입니다(No. 22RIS-006). 또한 본 연구는 과학기술정보통신부 및 정보통신기획평가원의 지역지능화혁신인재양성(Grand ICT 연구센터) 사업의 연구결과로 수행되었음(IITP-2024-2020-0-01612).

References

• Ahmed, A. E.-N. S., Ali, A. S., Ghazaly, N. M., Abd el-Jaber, G., (2015), PID controller of active suspension system for a quarter car model, International Journal of Advances in Engineering & Technology, 8(6), 899-909.
• Kumar, M. S., Vijayarangan, S., (2006), Design of LQR controller for active suspension system, International Journal of Engineering & Materials Sciences, 13(3), 173-179.
• Ghoniem, M., Awad, T., Mokhiamar, O., (2020), Control of a new low-cost semi-active vehicle suspension system using artificial neural networks, Alexandria Engineering Journal, 59(5), 4013-4025. [https://doi.org/10.1016/j.aej.2020.07.007]
• Vidya, V., Dharmana, M. M., (2017), Model reference based intelligent control of an active suspension system for vehicles, Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), 1-5. [https://doi.org/10.1109/ICCPCT.2017.8074362]
• Lee, D., Jin, S., Lee, C., (2022), Deep reinforcement learning of semi-active suspension controller for vehicle ride comfort, IEEE Transactions on Vehicular Technology, 72(1), 327-339. [https://doi.org/10.1109/TVT.2022.3207510]
• Fares, A., Bani Younes, A., (2020), Online reinforcement learning-based control of an active suspension system using the actor critic approach, Applied Sciences, 10(22), 8060. [https://doi.org/10.3390/app10228060]
• Han, S.-Y., Liang, T., (2022), Reinforcement-learning-based vibration control for a vehicle semi-active suspension system via the PPO approach, Applied Sciences, 12(6), 3078. [https://doi.org/10.3390/app12063078]
• Dridi, I., Hamza, A., Ben Yahia, N., (2023), A new approach to controlling an active suspension system based on reinforcement learning, Advances in Mechanical Engineering, 15(6). [https://doi.org/10.1177/16878132231180480]
• Liang, G., Zhao, T., Wei, Y., (2021), DDPG based self-learning active and model-constrained semi-active suspension control, Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), 1-6. [https://doi.org/10.1109/CVCI54083.2021.9661158]
• Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., Wierstra, D., (2015), Continuous control with deep reinforcement learning.
• Choi, S., Choi, Y. T., Park, D., (2000), A sliding mode control of a full-car electrorheological suspension system via hardware in-the- loop simulation, Journal of Dynamic Systems, Measurement, and Control, 122(1), 114-121. [https://doi.org/10.1115/1.482435]
• He, L., Qin, G., Zhang, Y., Chen, L., (2008), Non-stationary random vibration analysis of vehicle with fractional damping, Proceedings of the 2008 International Conference on Intelligent Computation Technology and Automation (ICICTA), 150-157. [https://doi.org/10.1109/ICICTA.2008.348]