복합하중을 받는 각접촉 볼베어링을 위한 개선된 피로수명식
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This paper was presented at KSPE Autumn Conference in 2023
Abstract
Rolling bearing fatigue life is an essential criterion in industrial equipment design and manufacturing and requires precise maintenance and replacement predictions. ISO/TS 281:2007 and 16281:2008 are commonly used for angular contact ball bearing (ACBB) fatigue life calculations, but they do not account for the characteristics of individual bearing elements under combined loading conditions. This study proposes an enhanced formula for calculating fatigue life modification factors that considers individual element-specific contact loads and resulting film thickness variations. The proposed fatigue life formula provides longer life predictions than the conventional method of determining modification factors based solely on maximum contact loads. This difference is particularly noticeable in low-speed and/or heavy-loading applications. Analysis conducted using the proposed fatigue life formula on various factors affecting fatigue life revealed that fluid kinetic viscosity coefficients, temperature-associated density changes, and changes in radial loads and rotational speeds could significantly impact the fatigue life of ACBBs. The proposed fatigue life formula is expected to increase the accuracy of ACBB fatigue life predictions.
Keywords:
Angular contact ball bearing, Minimum film thickness, Fatigue life, Life modification factor, Basic rating life, Reference rating life키워드:
각접촉 볼베어링, 최소 유막두께, 피로수명, 수명보정계수, 기본정격수명, 기준정격수명1. 서론
각접촉 볼베어링(Angular Contact Ball Bearing, ACBB)은 내/외륜이 경사진 각을 이루고 있어 축방향과 경방향 하중을 동시에 지지할 수 있는 베어링이다. 비교적 높은 하중지지 능력과 고속회전에 적합한 특성을 가지고 있어 고속 정밀 회전체에 널리 사용된다. 각접촉 볼베어링은 설치 방법과 상태, 운전 시 축방향의 예하중, 경방향 하중, 회전속도, 접촉각의 크기 등 다양한 요인의 영향을 받아 그 특성이 변화한다[1].
구름베어링의 수명은 이를 채택한 기계의 수명을 결정하는 주요 요인이 되므로 매우 중요하게 취급되어 왔으며 오랜 기간동안 많은 연구가 진행되어 왔다. Palmgren [2]에 의해 제시된 구름베어링 피로수명 예측식은 Lundberg-Palmgren (L-P) 피로수명식[3]으로 발전되었으며 현재까지 구름베어링 피로수명 계산의 기본식이 되고 있다. 최초 L-P 피로수명식은 베어링 재료와 제조기술의 발전, 사용조건 등의 변화가 반영되지 않아 점차 실제 베어링 수명과 차이가 발생하였고, 이를 보완하기 위해 미국 ANSI/AFBMA는 L-P 피로수명 공식에 보정계수를 도입하였다[4]. 그리고 이를 International Organization of Standardization (ISO) 에서도 채택하였다[5]. 또한 보정계수에 대한 보다 상세한 내용을 담은 책을 미국 윤활학회(STLE)에서 출판한 바 있다[6]. 그러나 베어링 제조기술의 지속적인 발전에 따라 피로수명식에 의한 예측수명과 실제 베어링 수명이 큰 차이를 보이게 되었으며 이 같은 문제에 대한 연구를 통해 Ioannides 등[7]과 Harris [1]는 내/외륜의 동적 부하용량을 개별적으로 고려하고 구름요소별 접촉하중 차이를 고려한 피로수명식을 제안하였다. ISO에서는 이들의 제안을 바탕으로 기준정격수명식(Reference Rating Life)을 재정의하였고, 보정계수 또한 새롭게 정의한 ISO/TS 281:2007 [8]과 ISO/TS 16281:2008 [9]의 피로수명식을 채택하였다.
ISO에서 채택한 구름베어링의 피로수명식을 이용하기 위해서는 운전조건에서의 베어링 특성을 정확히 예측하기 위한 모델이 필요하다. 각접촉 볼베어링의 특성을 예측하기 위해 많은 연구가 진행되었으며 Jones의 논문[10] 이후 큰 진전을 이루게 된다. 특히 de Mul 등[11]은 구름요소의 원심력, 자이로스코픽모멘트와 같은 동적 요소를 고려하여 모듈화된 방식으로 모델링하고 계산하는 방법을 제안하여 구름베어링 준정적 모델링 및 수치해석에 관한 기반을 제공하였다. 이후 이 같은 구름베어링의 준정적 모델을 이용하여 다양한 주제에 관한 많은 연구가 수행되었다[12]. 구름베어링 피로수명 해석에 관해서도 많은 의미있는 연구성과가 발표되었다. Lee 등[13]은 국내 연구자를 위해 ISO 표준식을 활용한 베어링 피로수명 예측방법에 대해 소개하였다. Zhang 등[14]은 준정적 모델을 이용하여 각접촉 볼베어링에 가해지는 예하중이 베어링 피로수명에 미치는 영향에 대해 조사하였다. Tong과 Hong은 각어긋남이 있는 테이퍼 롤러베어링[15]과 원통 롤러베어링[16]의 수명 변화에 대한 연구결과를 발표하였고, Bae 등[17]은 각어긋남이 있는 각접촉 볼베어링의 수명변화에 대한 연구결과를 발표하였다. 또한 복열 각접촉 볼베어링의 각어긋남, 클리어런스에 따른 접촉하중과 강성, 피로수명 특성도 Tong과 Hong에 의해 연구되었다[18]. 그 밖에도 Oh 등[19]은 공작기계에 장착되는 스핀들에 채용된 베어링의 피로수명 예측을 시도하였으며, Kim 등[20]은 고속 회전에서 발생하는 열적효과를 고려한 테이퍼 롤러베어링의 피로수명을 조사하였다. 최근 Rivera 등[21]은 공간 절약형 베어링인 3점 접촉 볼베어링에 대한 피로수명 특성연구 결과를 발표한 바 있다.
구름베어링의 피로수명에 대한 많은 연구가 진행되어 왔는데, 그 대부분은 ISO/TS에서 제시한 피로수명식을 사용하고 있으며 식에 적용되는 주요 변수들을 준정적 모델을 통해 계산하는 방식을 채택하고 있다. 실제 ISO/TS 표준에서 제공하는 식이 널리 사용되고 있지만 현재 주로 사용하고 있는 ISO/TS 281:2007, 16281:2008에서는 피로수명 보정계수 중 운전조건에 의해 변동되는 보정계수에 대해 복합하중 조건에서의 구름요소별 차이를 반영하지 않고 있다. 즉, 기존방식에 의하면 복합하중조건 하에서 베어링 요소별 접촉하중 차이에 따른 보정계수의 차이를 별도로 고려하지 않고 있으며 베어링 사용조건에 관련된 변수와 동점성 계수비를 사용하거나 최대하중이 걸리는 구름요소에서의 최소유막 관련 매개변수를 이용한 보정계수값을 대표값으로 활용하게 된다[8,9].
본 연구에서는 복합하중이 가해지는 조건에서 베어링 구름요소별 접촉하중 상태를 고려하여 보정계수 차이를 반영하는 새로운 방식을 제안하였으며 이를 기존의 방법과 비교 고찰하였다. 베어링 수명에 대한 계산을 통해 제시된 방법과 기존의 방식에서 베어링 요소별 하중조건에 따른 차이를 확인하였으며 베어링 사이즈 감소 및 온도와 하중이 증가하는 경우 베어링 요소별 보정계수의 변동을 고려할 때 유의미한 차이를 보이는 것을 확인하였다. 제안된 방식은 복합하중 조건에서의 요소별 차이를 고려한 보정계수를 사용하므로 기존방식보다 더 정확한 피로수명을 제공할 수 있을 것으로 기대된다.
2. 구름베어링 피로수명 모델
2.1 기본정격수명
베어링 산업이 발전하면서 베어링 제작사 데이터에 기반을 둔 개별적인 피로수명 예측에서 벗어나 통일된 방법이 필요하게 되었다. 1924년 생존확률을 기반으로 한 Palmgren의 피로수명식[2]이 발표되었고, 1947년에는 Lundberg와 Palmgren에 의해 외부하중에 의해 생성된 내부응력, 응력을 받는 부피, 접촉면적 및 길이를 고려한 피로수명식으로 발전되었으며, 구름요소나 레이스에서 10 [%]가 초기결함이 발생할 때의 회전수[106rev]로 정의되는 기본정격수명(Basic Rating Life of Rolling Bearings, L10)이 제시되었다[3]. ISO는 이러한 접근 방식을 1962년에 채택하였고 현재까지 피로수명식의 기초가 되고 있다[22]. 구름베어링의 기본정격수명은 아래 식(1)과 같이 정의된다[8].
| (1) |
여기서 Cr은 베어링 기본동적부하용량으로 구름요소의 개수, 구름요소의 반경(롤러의 경우 롤러길이와 지름), 접촉각과 같은 내부 형상에 의해 결정된다. 또한 Pr는 베어링에 작용하는 동등 가하중, 지수 p는 볼 베어링은 3, 롤러베어링은 10/3로 정해진다. 동적 부하용량 Cr과 동등가하중 Pr은 식(2)와 같이 주어진다[8].
| (2) |
여기서 bm과 fc는 볼직경(Dw)과 접촉각(αo), 피치직경(Dpw)을 통해 결정할 수 있으며 내륜 곡률반경이 0.52 Dw보다 작고 외륜 곡률반경이 0.53 Dw보다 작은 베어링에 적용할 수 있다[8]. 그리고 Z는 구름요소의 개수, irow는 열수, αo는 초기 접촉각이다. 한편 동등가하중은 식(3)과 같다.
| (3) |
여기서 Fr과 Fa는 구름베어링에 가해지는 축방향, 경방향 하중이고, X와 Y는 하중조건과 접촉각에 따라 결정되는 값이다[8].
2.2 정격수명의 수정
구름베어링 수명에 직접적인 영향을 미치는 다양한 요인에 대해 분석을 기반으로 ISO에서는 기본정격수명 L10에 신뢰성과 재료, 가공, 윤활, 속도 및 각도 오정렬에 대한 보정인자를 적용한 새로운 표준식을 아래의 식(4)와 같이 제안하였다 [5].
| (4) |
여기서 a1은 n%의 베어링 결함 발생을 고려한 신뢰성 보정계수, a2는 베어링 재료 수명을 고려한 보정계수이다[5]. 또, a3는 윤활제에 관한 보정계수로서 구름요소와 내/외륜 사이의 윤활로 인해 형성된 최소유막두께(ho)와 구름요소와 내/외륜의 복합 표면거칠기(σc)간의 비로 정의되는 유막두께 매개변수(Lubricant Film Parameter, λ)를 이용하여 결정할 수 있다[6]. 유막두께 매개변수는 식(5)와 같이 정의된다[5].
| (5) |
타원접촉을 하는 볼베어링의 경우 유막두께 매개변수 결정을 위한 최소유막두께(Minimum Lubricant Film Thickness, ho) 공식으로 Hamrock and Dowson [23]에 의해 제안된 식(6)이 널리 활용된다.
| (6) |
여기서 는 무차원 속도 파라미터, G는 재료 물성에 대한 무차원 파라미터, 는 무차원 접촉하중 파라미터, k는 구름요소와 내/외륜 사이의 타원접촉 시 형성되는 타원의 장/단반경의 비로서 식(7)-식(9)와 같이 정의된다 [1,23].
| (7) |
| (8) |
| (9) |
여기서 Qm은 구름요소와 내/외륜의 접촉하중, βo는 점도의 압력계수(Pressure Coefficient of Viscosity)로 식(10)과 같이 표현된다.
| (10) |
여기서 v는 동점성계수이고, 매개변수 A는 식(11)과 같이 표현된다[24].
| (11) |
이때, ηo는 대기압에서의 윤활유 점도이며 식(12)와 같이 계산할 수 있다.
| (12) |
여기서 voil과 ρoil은 운전 온도에서의 윤활유 점도와 밀도로서 여러 가지 식이 제시되고 있으나 Walther 방정식[25]이 많이 활용되고 있다.
내/외륜과 구름요소의 표면거칠기를 고려한 복합 표면 거칠기(σc)는 식(13)과 같이 표현된다 [1].
| (13) |
여기서 sb, sm는 구름요소와 내/외륜의 표면거칠기 Rq이며 즉 RMS 단위로 정의된 값으로 Rq가 얻어지지 않았을 경우에는 등가적으로 Ra값에 1.25를 곱해 사용한다 [1].
한편 식(1)로 주어진 L-P 정격수명식은 내/외륜의 수명을 개별적으로 고려하지 않았고, 경방향 하중이 작용하는 경우 개별 구름요소의 서로 다른 하중분배 특성을 고려할 수 없다. 이러한 문제점을 보완하기 위해 내/외륜의 수명을 각각 계산하고 개별 구름요소의 하중을 고려한 기준정격수명(Lnr) (ISO/TS 16281:2008)이 채택되었다[9]. Lnr은 식(14)로부터 계산할 수 있다.
| (14) |
여기서 Qci, Qce는 내/외륜의 동적 부하용량을 나타내고 아래의 식(15)와 식(16)으로부터 계산할 수 있다 [9].
| (15) |
| (16) |
여기서 Qei, Qee는 개별 구름요소가 받는 서로 다른 하중을 고려한 구름요소의 동등가하중으로서, 내륜회전/외륜고정 조건에서 식(17) 및 식(18)과 같이 계산할 수 있다[9].
| (17) |
| (18) |
베어링의 설계와 생산기술이 향상되면서 더 나은 재료와 향상된 표면처리 기술로 인해 기존의 식으로 얻어진 예측수명보다 월등히 높은 수명을 가지게 되었다. 이러한 상황을 고려하여 개정된 국제표준(ISO/TS 281:2007)에서는 보정계수를 도입한 보정정격 수명(Modified Rating Life, Lnmr)을 제시하였으며 이후 기준정격수명식에 보정계수를 적용한 보정기준정격수명(Modified Reference Rating Life, Lnmr)을 식(19)와 같이 제시하였다[9].
| (19) |
여기서 aISO는 하중조건, 회전속도, 윤활유의 점성, 오염정도, 재료의 피로하중한계 등을 고려한 수명 보정계수이며 볼베어링의 경우 식(20)과 같이 계산할 수 있다.
| (20) |
여기서 κ는 점성비(Viscosity Ratio)로서 베어링 내 윤활유의 점도와 기준점도의 비로서, 식(21)과 같이 정의된다.
| (21) |
여기서 기준점도 v1은 피치직경과 속도에만 의존하는 단순화된 식(22)이 사용된다[8].
| (22) |
식(21)과 같이 정의된 κ는 하중조건에 따른 효과가 반영되지 않으므로 이를 고려하기 위해서는 새로운 방법을 적용할 필요가 있다. 가공된 내/외륜 표면 거칠기와 운전조건에 부가되어 얻어지는 유막두께 매개변수(λ) 값을 계산하여 점성비 값을 식(23)과 같이 근사적으로 추정할 수 있다[8].
| (23) |
한편, Cu는 피로하중한계(Fatigue Load Limit)로서 식(24)와 같이 계산할 수 있다[8].
| (24) |
여기서 Qu는 단일 접촉 시 피로한도 값으로 식(25)와 같이 계산할 수 있다[8].
| (25) |
여기서 σHu는 헤르츠 접촉응력, E(km)는 2차 완전 타원적분, Σρm은 볼과 레이스의 곡률합(Curvature Sum)을 나타낸다.
그리고,
| (26) |
| (27) |
으로 정의되며, 피로하중한계 Cu를 계산할 때 사용되는 단일 접촉 시 피로한도 값으로는 식(28)과 같이 내/외륜에서 계산된 두 값 중 작은 값을 적용한다.
| (28) |
윤활유가 고체입자로 오염되면 내/외륜의 응력상승에 영향을 미치며 수명감소의 원인이 된다. 오염으로 인한 수명감소를 고려한 인자 ec는 ISO에서 제시한 값을 참조로 결정할 수 있다[8].
2.3 구름요소별 유막두께 변동을 고려한 보정계수 수정
볼베어링에 경방향 하중이 작용하게 되면 개별 구름요소마다 작용하는 하중이 다르기 때문에 볼과 내/외륜 사이에 형성되는 유막두께 또한 볼마다 서로 다른 값을 가진다. 그러나 기존의 수명계산식 ISO/TS 16281:2008에서는 최대 접촉하중에서의 유막두께를 고려한 보정계수를 활용하고 있다. 본 연구에서는 기존 방식의 수명 보정계수를 개선하여 개별 구름요소에 작용되는 접촉하중과 유막두께를 반영한 구름요소별 보정계수를 도입하여 피로수명식을 개선하였다.
식(6)을 활용하여 개별 구름요소의 최소유막두께를 결정하면 복합 표면거칠기로 나누어 개별 구름요소의 유막두께 매개변수(λj)를 결정할 수 있다. 개별적인 구름요소의 유막두께 매개변수를 결정하게 되면 식(23)을 이용하여 요소별 등가의 점성비(κj)를 결정할 수 있으며 이를 식(20)에 적용하면 식(29)와 같이 개별 구름요소의 보정계수 aISO, j를 계산할 수 있다.
| (29) |
본 연구에서는 이렇게 얻어진 개별 구름요소에 대한 보정계수를 고려하여 식(20)을 수정하였다. 즉, 식(20)에 사용된 보정계수 aISO를 Lnr에 포함시켜 재구성한 후 식(17)과 식(18)에서 개별요소에 대한 합산식에서 요소별 차이를 반영한 aISO, j로 대체하는 방식으로 요소별 보정계수 차이를 반영한다. 이 같은 과정을 통해 개선된 보정기준정격수명(Enhanced Modified Reference Rating Life, Lnmre)은 식(30)과 같다.
| (30) |
여기서 는 요소별 수명 보정계수를 고려한 동등가 하중으로, 내륜회전/외륜고정 조건으로 가정하면 식(31)과 식(32)로부터 계산할 수 있다.
| (31) |
| (32) |
내륜이 고정되고 외륜이 회전하는 경우도 동일한 방식으로 유도할 수 있다.
3. 시뮬레이션 및 토의
제안된 피로수명식과 기존 피로수명식을 비교하였다. 먼저, 준정적 모델을 활용하여 개발된 프로그램과 현재 상용 베어링프로그램[26]의 해석 결과를 비교하여 개발된 프로그램의 타당성을 검증하였다. 검증된 프로그램을 사용하여 구름요소별 접촉하중의 변동을 고려한 보정계수를 사용하는 방법과 하나의 대표값으로 설정한 보정계수를 사용하는 방법을 비교하였다. Tables 1과 2는 시뮬레이션을 위해 사용한 서로 다른 크기를 갖는 두 개의 각접촉 볼베어링 주요정보를 나타내고 있다.
3.1 개발 프로그램 검증
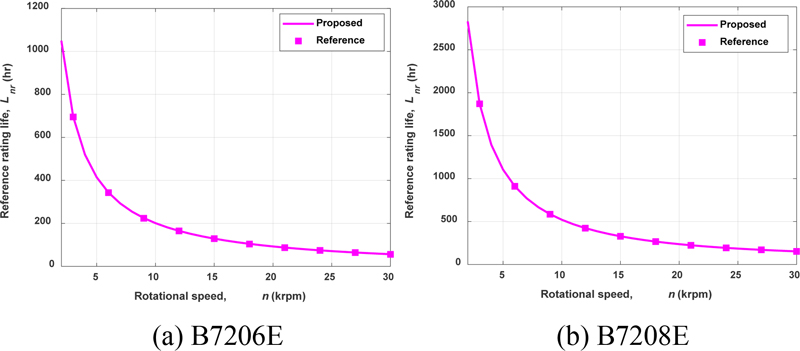
개발된 프로그램의 검증을 위해 베어링 제조업체 프로그램과 비교하였다. Fig. 1은 개발된 프로그램과 상용화된 베어링제조업체 프로그램을 통해 회전속도 변화에 따른 기준정격수명(Lnr)을 계산한 결과를 비교한 것이다. 고려한 두 베어링 모두 축하중(Fz)을 3,000 N, 경방향 하중(Fx)을 4,500 N 인가한 조건으로서 고려한 두 베어링에 대해 결과가 모두 잘 일치하고있다.
기준정격수명의 경우 회전속도가 0에 접근하면 값을 결정할 수 없으므로 저속구간을 제외한 결과를 제시하였다. Fig. 2에서는 기존 방식인 최대 접촉하중을 기준으로 계산된 보정계수를 도입하여 계산한 보정기준정격수명(Lnmr)을 비교하였다. 계산과정에 보정계수 aISO값을 ISO에서 제시하는 50으로 한정하였다[8,9]. 기준정격수명과 달리 기존방식의 보정기준정격수명은 회전속도에 따른 보정계수 aISO의 추세에 따라 속도에 따라 증가하는 추세를 보이나 일정속도에 도달하면 다시 감소하게 된다. 보정기준정격수명이 회전속도에 대해 3번의 추세적인 변화가 발생하게 되는데, 이는 식(20)에서 제시한 바와 같이 보정계수의 구간별 차이에 기인한다. Fig. 2에서도 두 베어링 모두 상용 프로그램의 결과와 매우 잘 일치하고 있다. 이상의 결과로부터 개발된 프로그램의 정확성을 확인할 수 있다.
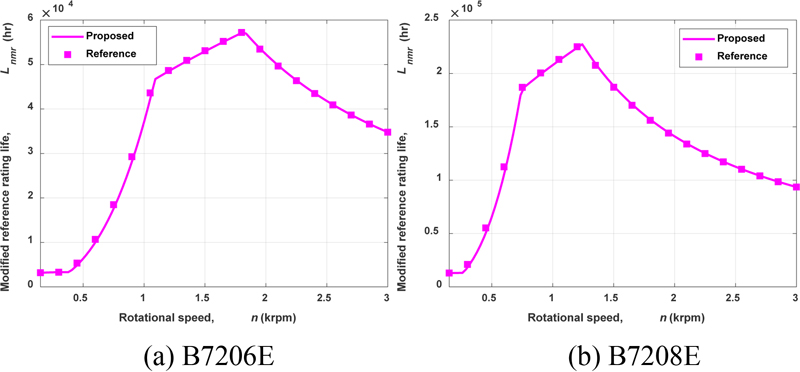
Comparison of modified reference rating life of sample bearings (Fz = 3,000 N, Fx = 4,500 N, T = 40°C)
다음에는 이를 기반으로 개별 구름요소의 보정계수 차이를 반영한 제안된 보정기준정격수명(Lnmre)과 기존 방식에 의한 보정기준정격수명(Lnmr)의 계산결과를 비교하였다.
3.2 제안된 방식과 기존방식 비교
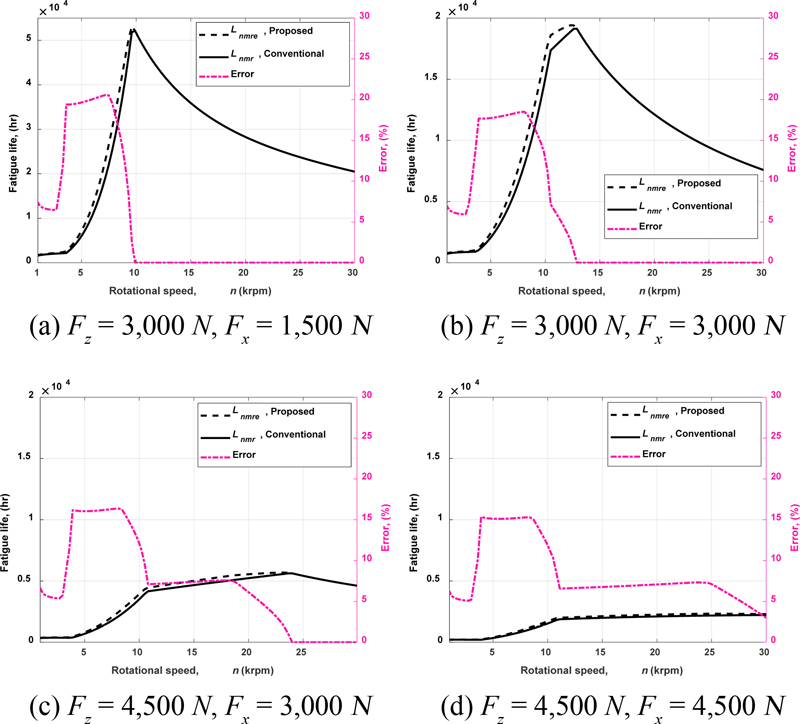
최대 접촉하중에서의 aISO를 이용한 보정기준정격수명(Lnmr)에 대한 식(19)에 의한 계산결과와 요소별 보정계수 차이를 고려한 제안된 보정기준정격수명(Lnmre) 식(30)의 계산결과를 비교하였다. 앞서 프로그램 검증에 사용된 2개의 베어링에 대해 동일한 조건에서 결과를 비교하였다. 두 예측방법 간의 차이를 보다 잘 나타낼 수 있도록 하중과 온도조건을 설정하였다. Fig. 3은 두 방법에 의한 계산 결과와 함께 계산결과의 차이에 대한 백분율([Lnmre - Lnmr] / Lnmr) × 100을 동시에 도시하였다. Fig. 3에서 볼 수 있는 바와 같이 Lnmre-이 Lnmr보다 전반적으로 높은 수명을 나타내고 aISO, j가 모두 50에 도달하는 회전속도에 이르면 같은 값을 가진다. 2개의 베어링 중 작은 크기의 베어링인 B7206E에서 수명예측 결과에 더 큰 차이가 있으며 더 높은 속도영역까지 영향을 받고 있다. 특히 B7206E의 경우 최대 15% 이상의 큰 차이를 보이고 있어 기존 방식이 수명을 크게 저평가하게 된다. 실제로 작은 크기의 베어링에서 두 방법의 차이가 더 크게 나타나게 되는데, 두 방법 간의 차이를 잘 확인할 수 있도록 이와 같이 상대적으로 차이가 크게 나타나는 B7206E 베어링을 중심으로 온도 및 하중 조건에 따른 변화에 대한 시뮬레이션 결과를 제시하였다.
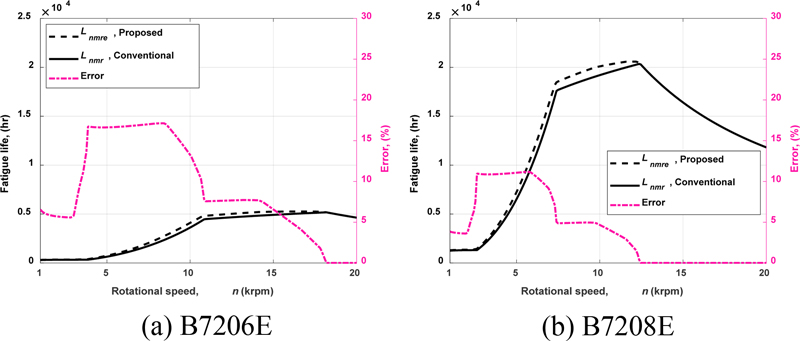
Comparison of fatigue lives by the proposed and conventional methods for two sample bearings (Fz = 3,000 N, Fx = 4,500 N, T = 120°C)
주요 변수들에 대한 변화를 살펴보기 위해 Fig. 4는 회전속도에 따른 구름요소별 유막두께 매개변수와 점성비 변화를 도시하였다. 유막두께 매개변수와 점성 비 모두 구름요소별로 다르게 나타나며 회전속도 증가에 따라 증가한다. Fig. 5는 회전속도에 따른 점성비 계산 결과를 식(29)에 적용하여 구름요소별 aISO, j를 계산한 결과이다. ISO에서 제시하고 있는 바와 같이 aISO, j값의 범위도 0.1 < aISO, j < 50으로 제한한다[8]. 제안된 보정기준정격수명은 기준정격수명에 aISO, j를 고려하므로 aISO, j값이 50에 도달하기 전까지는 수명이 증가한다. 모든 구름요소의 aISO, j가 50에 도달하면 보정계수에 의한 효과가 베어링 요소에 무관한 상수가 되면서 두 수명계산 결과가 기준정격수명의 추세에 따라 감소하는 동일한 곡선을 나타내게 된다.
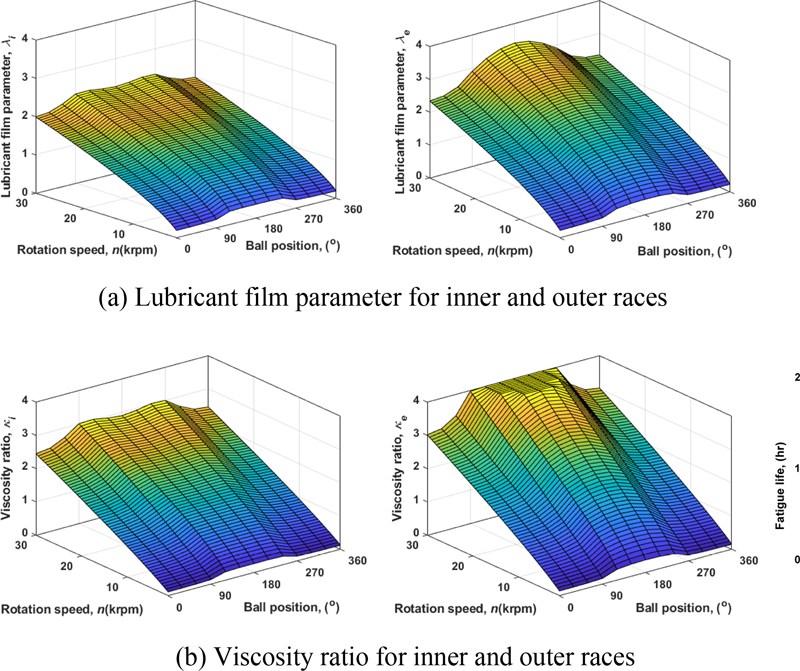
Lubricant film parameter and viscosity ratio with changing ball positions and rotational speeds (B7206E, Fz = 3,000 N, Fx = 4,500 N, T = 120°C)
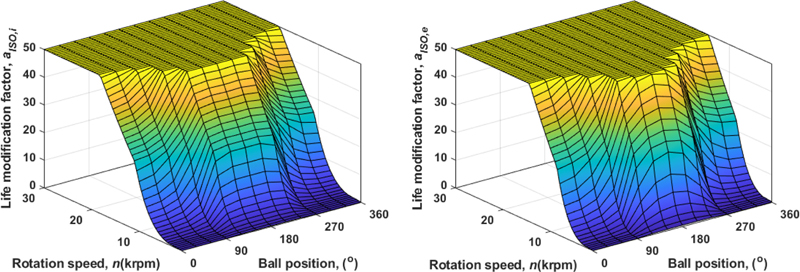
Life modification factor for inner and outer races, based on ISO 281:2007 with changing ball positions and rotational speeds (B7206E, Fz = 3,000 N, Fx = 4,500 N, T = 120°C)
온도변화에 따른 효과를 관찰하기 위해 B7206E 베어링에 대해 온도에 따른 수명예측 결과를 비교하였다. Fig. 6에 온도를 변화시키며 얻어진 결과를 보여준다. 온도의 변화는 유막두께를 결정하는 주요 파라미터인 동점성계수를 변화시키기 때문에 유막두께 매개변수가 달라지며 이로 인해 보정계수도 영향을 받는다. 그림에서 확인할 수 있는 바와 같이 온도가 높아질수록 Lnmre과 Lnmr이 넓은 속도영역에서 오차가 나타난다. 온도가 높아지면 aISO, j값이 모두 50에 도달하는 회전속도가 늦춰지게 되는 것이 주요 요인이다. 온도에 무관하게 요소별 보정계수가 모두 50에 도달하는 조건이 되면 동일한 수명곡선을 나타낸다. 최대 오차는 온도에 무관하게 동일하며, 오차가 나타나는 속도 범위에만 차이가 있을 뿐 그 추세선도 동일한 양상을 보인다.
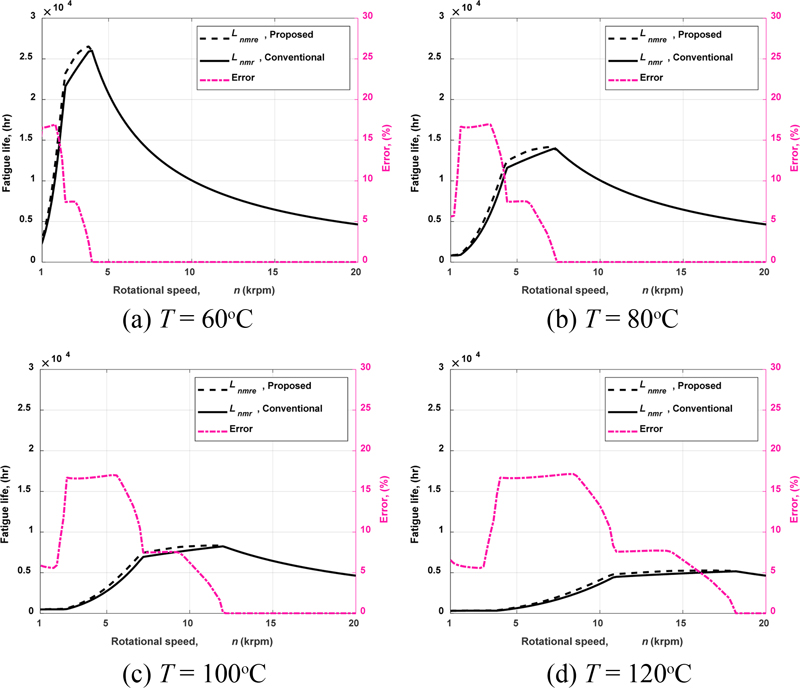
Comparison of fatigue lives by the proposed and conventional methods with changing operating temperature (Fz = 3,000 N, Fx = 4,500 N)
Fig. 7에 하중을 변화시키며 계산한 결과를 비교하였다. 축방향 및 경방향 하중이 증가할수록 접촉하중이 증가하므로 수명은 감소하는 양상을 보이고 aISO, j값이 모두 50에 도달하는 회전속도 즉, Lnmre과 Lnmr이 일치하는 회전속도가 높아지게 된다. 경방향 하중의 증가는 베어링 수명감소에 보다 큰 영향을 미치는 반면, 축방향 하중의 증가는 베어링 수명감소 효과가 있지만 aISO, j 값이 모두 50에 도달하는 회전속도를 늦추는 효과가 있어 넓은 속도범위 영역에서 영향을 미치게 된다.
4. 결론
본 연구에서는 복합하중 작용 시 개별 구름요소의 하중과 이로 인한 유막두께 변동 특성을 고려한 개선된 수명계산 방식을 제안하였다. 제안된 방법을 최대 접촉하중에서의 유막두께를 이용하는 기존의 보정기준정격수명과 비교하였고 여러 조건에서의 시뮬레이션을 통해 그 경향을 분석하였다. 본 연구를 통해 다음과 같은 결론을 얻을 수 있었다.
(1) 유막두께 변동 특성을 고려한 개선된 방법은 구름요소별 하중분배 및 윤활특성을 고려한 보정계수를 사용하므로 복합하중 조건에서의 수명예측 정확성을 향상시킨다.
(2) 개별 구름요소의 하중과 유막두께 변동을 고려한 제안된 방식은 기존 방식과 비교하여 더 긴 수명예측 결과를 제공한다.
(3) 제안된 수명식은 각 구름요소의 보정계수값 변동 효과가 반영되어, 초기에는 기존 수명식 결과보다 큰 값을 나타내다가, 모든 구름요소의 보정계수값이 제한값에 도달하는 구간에서는 기존의 보정기준정격수명과 일치하게 된다.
(4) 베어링 크기가 작을수록, 온도가 높을수록, 그리고 축방향과 경방향 하중이 높을수록 제안된 방법이 기존 방법보다 더 정확한 결과를 제공한다.
NOMENCLATURE
| a1 : | Life Modification Factor for Reliability |
| a2 : | Material Factor |
| a3 : | Lube Life Factor (Calculated Value) |
| aISO : | Life Modification Factor, based on ISO 281:2007 Systems Approach of Life Calculation |
| bm : | Rating Factor for Bearing Type |
| Cr : | Basic Dynamic Load Rating [N] |
| Car : | Basic Dynamic Axial Load Rating [N] |
| Cu : | Fatigue Load Limit [N] |
| d : | Bore Diameter [mm] |
| D : | Outer Diameter [mm] |
| Dpw : | Pitch Diameter of Ball Bearings [mm] |
| Dw : | Nominal Ball Diameter [mm] |
| E : | Modulus of Elasticity [N/mm2] |
| E’ : | Equivalent Modulus of Elasticity, |
| E(km) : | Complete Elliptic Integral of the Second Kind |
| Fr : | Contamination Factor |
| Fa : | Applied Radial Load [N] |
| fc : | Applied Axial Load, [N] |
| fi : | Factor Depending on the Bearing Geometry |
| fe : | Inner Ring Curvature Ratio |
| G : | Outer Ring Curvature Ratio |
| ho : | Dimensionless Material Parameter |
| irow : | Minimum Film Thickness, microns |
| k : | Number of Rows of Rolling Elements |
| Ln : | Ellipticity Ratio, b/a |
| Lna : | Basic Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| Lnm : | Factored Basic Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| Lnr : | Modified Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| Lnmr : | Basic Reference Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| Lnmre : | Modified Reference Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| n : | Enhanced Modified Reference Rating Life, 106 rev (or hr when multiplied by 5000/3n) |
| P : | Shaft and Inner Ring Rotational Speed [RPM] |
| Pr : | Applied Load [N] |
| Pa : | Dynamic Equivalent Radial Load [N] |
| p : | Dynamic Equivalent Axial Load [N] |
| Q : | Exponent; Ball Bearing 3, Roller Bearing 10/3 |
| Qu : | Rolling Element Load [N] |
| Qz : | Fatigue Load Limit [N] |
| Qci : | Dimensionless Contact Load |
| Qce : | Basic Dynamic Load Rating of Inner Ring or Shaft [N] |
| Qei : | Basic Dynamic Load Rating of Outer Ring or Housing [N] |
| Qee : | Dynamic Equivalent Rolling Element Load on Inner Ring [N] |
| Q’ei : | Dynamic Equivalent Rolling Element Load on Outer Ring [N] |
| Q’ee : | Dynamic Equivalent Rolling Element Load on Inner Ring, Considering the Individual Film Thickness Characteristics [N] |
| Ri : | Dynamic Equivalent Rolling Element Load on Outer Ring, Considering the Individual Film Thickness [N] |
| Re : | Equivalent Inner Radius |
| ri : | Equivalent Outer Radius |
| re : | Cross-sectional Raceway Groove Radius of Inner Ring [mm] |
| si, e : | Inner or Outer Ring Surface Roughness [μm] |
| sb : | Rolling Elements Surface Roughness [μm] |
| Ui : | Inner Ring Velocity [m/s] |
| Ue : | Outer Ring Velocity [m/s] |
| : | ηoUi,e/E’Ri,e |
| v : | Kinetic Viscosity [mm2/s] |
| vE : | Poisson’s Ratio |
| v1 : | Reference Kinetic Viscosity, [mm2/s] |
| X : | Dynamic Radial Load Factor |
| Y : | Dynamic Axial Load Factor |
| Z : | Number of Balls |
| α0 : | Unloaded Contact Angle [°] |
| β0 : | Pressure Coefficient Of Viscosity, [mm2/s] |
| γ : | Auxiliary Parameter, Dw cos α0/Dpw |
| ηo : | Fluid Viscosity at Atmospheric Pressure, [Ns/mm2] |
| κ : | iscosity Ratio, v / v1 |
| λ : | Lubricant Film Parameter |
| ρoil : | Oil Density [g/cm3] |
| σc : | composite Roughness [μm] |
| σHu : | Hertzian Contact Stress at which the Fatigue Limit of the Raceway Material Is Reached [N/mm2] |
| m : | i or e |
| i : | Inner Ring |
| e : | Outer Ring |
| j : | Rolling Element Index |
Acknowledgments
이 논문은 2023년 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(KRIT-CT-21-006, 베어링 장수명화 및 온도/발열량 정밀 예측 기술 개발).
References
- Harris, T. A., (2000), Rolling bearing analysis, 4th Edition, Wiley.
- Palmgren, A., (1924), Die lebensdauer von kugellagern, Zeitschrift des Vereines Deutscher Ingenieure, 68(14), 339-341. https://archive.org/details/nasa_techdoc_19710009534/mode/2up
-
Lundberg, G., Palmgren, A., (1949), Dynamic capacity of rolling bearings, The Journal of Applied Mechanics, 16(2), 165-172.
[https://doi.org/10.1115/1.4009930]

- American National Standards Institute, (1990), Load ratings and fatigue life for ball bearings, ANSI/AFBMA Std 9-1990.
- ISO 281:1990, (1990), Rolling bearings–Dynamic load ratings and rating life.
- Zaretsky, E.V., (1992), Life factors for rolling bearings, Society of Tribologists and Lubrication Engineers, Park Ridge, Ill.
- Ioannides, E., Bergling, G., Gabelli, A., (1999), An analytical formulation for the life of rolling bearings, Finnish Academy of Technology.
- ISO 281:2007, (2021), Rolling bearings – Dynamic load ratings and rating life.
- ISO/TS16281:2008, (2008), Rolling bearings–Methods for calculating the modified reference rating life for universally loaded bearings.
-
Jones, A., (1960), A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions, Journal of Basic Engineering, 82(2), 309-320.
[https://doi.org/10.1115/1.3662587]

-
De Mul, J., Vree, J., Maas, D., (1989), Equilibrium and associated load distribution in ball and roller bearings loaded in five degrees of freedom while neglecting friction—Part I: General Theory and Application to Ball Bearings, Journal of Tribology, 111(1), 142-148.
[https://doi.org/10.1115/1.3261864]

-
Hong, S.-W., Tong, V.-C., (2016), Rolling-element bearing modeling: A review, International Journal of Precision Engineering and Manufacturing, 17, 1729-1749.
[https://doi.org/10.1007/s12541-016-0200-z]

- Lee, S., Lee, N., Lee, I., (2012), Bearing life calculation by using the ISO281:2007, Proceedings of the Korean Society of Precision Engineering Conference, 903-904.
-
Zhang, J., Fang, B., Hong, J., Zhu, Y., (2017), Effect of preload on ball-raceway contact state and fatigue life of angular contact ball bearing, Tribology International, 114, 365-372.
[https://doi.org/10.1016/j.triboint.2017.04.029]

-
Tong, V.-C., Hong, S.-W., (2016), Fatigue life of tapered roller bearing subject to angular misalignment, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 230(2), 147-158.
[https://doi.org/10.1177/0954406215578706]

-
Tong, V.-C., Kwon, S.-W., Hong, S.-W., (2017), Fatigue life of cylindrical roller bearings, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 231(5), 623-636.
[https://doi.org/10.1177/1350650116668767]

-
Bae, G.-H., Tong, V.-C., Hong, S.-W., (2016), Fatigue Life Analysis for angular contact ball bearing with angular misalignment, Journal of the Korean Society for Precision Engineering, 33(1), 53-61.
[https://doi.org/10.7736/KSPE.2016.33.1.53]

-
Tong, V.-C., Hong, S.-W., (2017), Analysis of the stiffness and fatigue life of double-row angular contact ball bearings, Journal of the Korean Society for Precision Engineering, 34(11), 813-821.
[https://doi.org/10.7736/KSPE.2017.34.11.813]

-
Oh, H., Kwon, S., Park, W., Hong, S., (2018), Study on the dynamic characteristics and fatigue life of a spindle-bearing system for large machine tools, Journal of Korean Society Manufacturing Technology Engineers, 27(6), 591-599.
[https://doi.org/10.7735/ksmte.2018.27.6.591]

-
Kim, T., Suh, J., Lee, J., Lee, B., Yu, Y., (2023), Fatigue life prediction of double-row tapered roller bearings considering thermal effect, Advances in Mechanical Engineering, 15(2), 16878132231154099.
[https://doi.org/10.1177/16878132231154099]

- Rivera, G., Sa, J., Hong, S., (2022), Study on the fatigue life of three-point contact ball bearings, Proceedings of the Korean Society of Manufacturing Technology Engineers Fall Conference, 20-20.
- ISO 281:1962, (1962), Rolling bearings methods of evaluating dynamic load ratings.
-
Hamrock, B. J., Dowson, D., (1977), Isothermal elastohydrodynamic lubrication of point contacts: Part III—fully flooded results, Journal of Lubrication Technology, 99(2), 264-275.
[https://doi.org/10.1115/1.3453074]

-
Khonsari, M. M., Booser, E. R., (2017), Applied tribology: Bearing design and lubrication, John Wiley & Sons.
[https://doi.org/10.1002/9781118700280]

-
Sánchez-Rubio, M., Chinas-Castillo, F., Ruiz-Aquino, F., Lara-Romero, J., (2006), A new focus on the Walther equation for lubricant viscosity determination, Lubrication Science, 18(2), 95-108.
[https://doi.org/10.1002/ls.9]

- Schaeffler medias, BEARINX Calculation Modules. https://medias.schaeffler.de/en/bearinx

received his B.E. degree in Mechanical Engineering from Kumoh National Institute of Technology (KIT), Korea in 2023. He is currently in graduate school, pursuing M.S. degree in Mechanical Engineering at Kumoh National Institute of Technology (KIT), Korea.
E-mail: 20170552@kumoh.ac.kr

received his M.E. degree in Mechanical Engineering and B.E. degree in Mechanical System Engineering from Kumoh National Institute of Technology (KIT), Korea in 2021 and 2017, respectively, and his B.S. degree in Mechanical Engineering from Mapúa University, the Philippines in 2019. He is currently a postmaster researcher at KIT, Korea.
E-mail: gibsrivera@kumoh.ac.kr

received his B.E. degree in Mechanical Engineering from Yonsei University, Korea, in 1990. Currently, he is a Director of the R&D Center in V&C Tech Co., Ltd. His current research interests include modeling, analysis and test of rolling bearings.
E-mail: cskang@vnc-tech.com

received his M.S. and Ph.D. degrees in Mechanical Engineering from KAIST, Korea, in 1985 and 1989, respectively. Currently, he is a Professor in the Department of Mechanical System Engineering of Kumoh National Institute of Technology. His current research interests include spindle and bearings modeling and analysis, command shaping for positioning systems, vibration control, and structural vibration analysis for mechanical systems.
E-mail: swhong@kumoh.ac.kr