비행하중 조건에서 항공기 외부장착 포드의 비행적합성 검증을 위한 구조안전성 검증
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A pod mounted on an aircraft external must be installed on an aircraft after its structural safety is verified under flight conditions. This paper presents methods of flight load and test load generation. Evaluation of test result data and standards for failure mode are also presented. First of all, to verify the static structural stability, flight loads for the aircraft maneuvering conditions were calculated. Finite element analysis was then performed with flight loads. As a result of the analysis, structures were verified to have a margin of safety for a given design requirement. In addition, it was confirmed that the launcher tube had enough rigidity to support the missile. Thus, the role of stinger such as longeron and hardback was insignificant. Finally, based on results of tests and analysis, the static structural stability of pod was substantiated and the reliability and effectiveness of the analysis model were obtained. These results and dynamic stability verification results suggest that an optimal design is necessary.
Keywords:
Aircraft operating condition, External store, Finite element analysis, Flight compatibility, Static structural test키워드:
항공기 운용조건, 외부장착물, 유한요소해석, 비행적합성, 정적 구조시험1. 서론
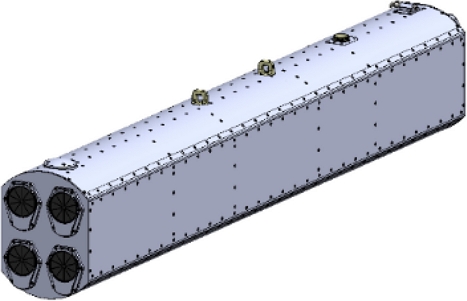
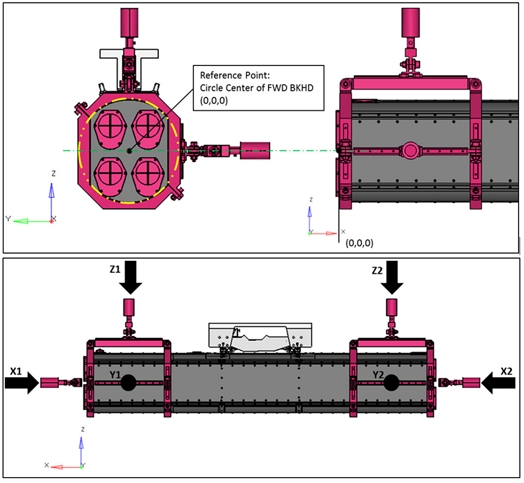
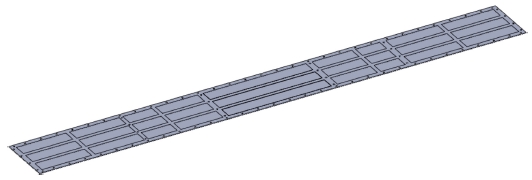
본 연구의 대상 구조물은 Fig. 1과 같이 항공기 외부에 장착된 포드(Pod)로 항공기의 안전을 위하여 감항인증과 같은 비행 적합성을 검증해야 한다[1]. 비행적합성 중 구조안전성 평가는 크게 정적구조안전성과 동적구조안전성으로 나뉘게 되며, 정적 구조안전성은 항공기 기동조건에서 발생하는 비행하중을 MIL-STD-8591 [8] 규격에 따라 분석하고 이를 반영하여 평가한다. 이러한 항공기 주 구조물과 외부 장착물에 작용하는 비행하중을 분석하고 수치해석적방법과 시험적 방법으로 정적구조안전성을 검증하는 연구가 많이 수행되었다[2,3]. 동적구조안전성은 항공기에서 발생하는 엔진진동과 공력에 의한 플러터(Flutter) 같은 진동 환경에서 내구성평가를 MIL-STD-810G [9] 규격에 따라 수행하여 검증한다. 진동 환경에서 구조물의 고유주파수를 분석하고 회피 설계를 수행하거나 구조물의 피로수명을 분석하는 동적구조안전성에 대한 연구 또한 많이 수행되고 있다[4,5]. 본 연구에서는 비행하중이 작용하는 포드의 정적구조안전성을 평가하기 위하여 포드가 장착되는 항공기 기동조건에 따라 발생하는 관성하중(Inertia Load)과 포드표면에 발생하는 공력하중(Aerodynamic Load)을 분석하였다. 정적구조해석은 관성하중과 전산유체역학(Computational Fluid Dynamics, CFD) 분석으로 계산한 공력하중을 맵핑(Mapping) 알고리즘으로 유한요소모델(Finite Element Model)에 적용하여 수행하였다. 포드의 안전성을 검증하기 위해 구조물에서 발생할 수 있는 파손모드에 따라 안전여유(Margin of Safety, M.S)를 분석하였다. 해석결과를 토대로 포드에 작용하는 전단력선도(Shear Force Diagram)와 굽힘하중선도(Bending Moment Diagram)를 이용하여 비행 하중을 시험하중으로 변환하여 정적구조시험을 수행하였다. 분포하중 형태의 시험하중을 최소한의 작동기(Actuator)로 포드에 모사하기 위하여 휘플트리(Whiffle Tree)를 사용하였다[6]. 시험으로 구조물의 파손 여부를 판단하고, 해석의 변형률과 비교/분석하여 구조물의 안전성과 해석기법에 대한 검증을 수행하였다.
2. 항공기 비행하중 분석
항공기의 비행하중 분석은 항공기 기동조건에서 포드와 같은 외부장착물에 작용하는 하중을 분석하고 이를 이용하여 구조적 안전성을 검증하기 위해 우선으로 수행된다. 비행하중은 관성하중과 공력하중으로 이루어져 있으며 MIL-STD-8591 절차에 따라 분석을 수행하였다.
비행하중 분석에 사용되는 기준 좌표는 규격에 따라 Fig. 2와 같이 고정익 항공기의 좌표를 대상항공기인 회전익기에 동일하게 적용하였다.
2.1 관성하중
관성하중은 Table 1의 MIL-STD-8591 Appendix B Table C-II 회전익기의 기동조건에서 하중배수, 각속도, 그리고 각가속도로 항공기 특정 위치에 장착되는 포드 질량중심(Center of Gravity)에 작용하는 하중을 의미한다. 외부 장착물에 작용하는 관성하중은 선형관성하중과 회전관성하중이 있으며, 선형관성 하중은 항공기의 선형가속도와 회전체에서 발생하는 오일러 힘(Euler Force)과 원심력(Centrifugal Force)을 식(1)과 같이 나타낼 수 있다. 식(1)에 포드의 중량을 곱하여 식(2)와 같이 포드 질량중심에 작용하는 선형관성력을 계산한다.
| (1) |
| (2) |
여기서 ΔX = Xstore cg – Xairfraft cg, ΔY = Ystore cg – Yairfraft cg, ΔZ = Zstore cg– Zairfraft cg는 항공기의 롤(Roll), 피치(Pitch), 그리고 요(Yaw) 기동으로 인해 회전체에서 발생하는 힘을 계산하기 위한 항공기 질량중심과 포드의 질량중심의 차이를 나타낸다. 회전관성력은 식(3)과 같이 Transport Theorem에 각 운동량(Iw)를 대입하여 회전관성력을 구한다. 관성하중은 운동의 반대 방향으로 작용하는 가상힘으로 부호는(-)를 적용하였다.
| (3) |
2.2 공력하중
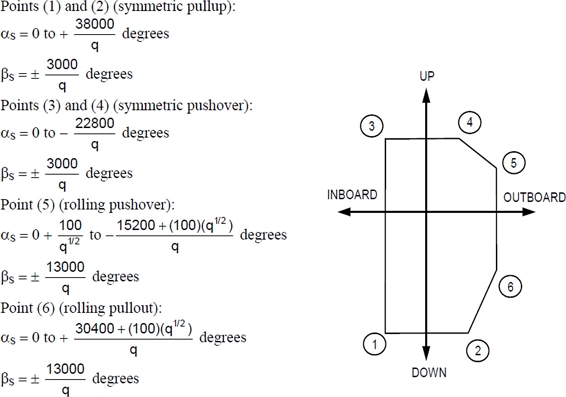
공력하중분석은 일반적으로 전산유체역학분석을 수행하지만 여러 조건에 대하여 전산유체역학분석으로 하중을 분석할 경우 많은 시간이 필요하다. 그래서 본 연구에서는 유도무기의 다양한 형상과 기동조건에 대하여 시험적 데이터를 기반으로 공력계수를 분석하는 Missile DATCOM으로 공력하중을 산출하고 최종적으로 선별된 기동조건에 대하여 전산유체역학분석을 수행하였다. 공력하중은 항공기의 운항고도, 속도에 따른 동압(Dynamic Pressure)과 받음각(Angle of Attack, AOA) α, 옆미끌림각(Side Slip Angle) β 그리고 장착각(Incidence Angle)로 계산된다. 본 연구의 포드는 항공기에 장착되는 장착각은 0o이며, 받음각 α와 옆미끌림각 β는 Fig. 3의 MIL-STD-8591FIGURE B-3과 FAA29-2C의 규격으로 최대/최소 각도를 선정하였다.
2.3 비행하중 선정
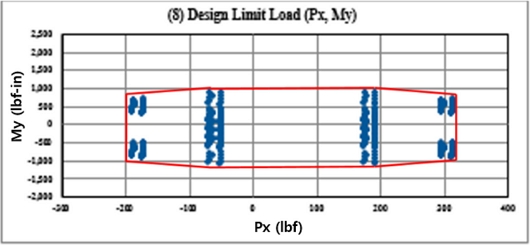
관성하중과 공력하중을 계산하여 포드 질량중심에 작용하는 비행하중 분석을 수행하면 수많은 경우의 비행하중이 계산된다. 모든 경우의 비행하중에 대하여 포드의 구조안전성을 검증하려면 많은 시간과 노력이 필요하므로 비행하중 중에 구조물 파손에 가장 영향을 많이 주는 비행하중을 선정할 필요가 있다. 비행하중을 선정하기 위하여 Fig. 4와 같은 볼록포(Convex Hull) 알고리즘과 Table 2과 같이 6분력의 최대/최소 하중을 이용하는 방법이 있다. 본 연구에서는 6분력에 대한 최대/최소 하중을 선정하여 구조안전성을 검증하는 설계제한하중(Design Limit Load, DLL) 비행조건을 선정하였다.
3. 포드 정적구조해석
3.1 유한요소해석 모델 및 경계조건
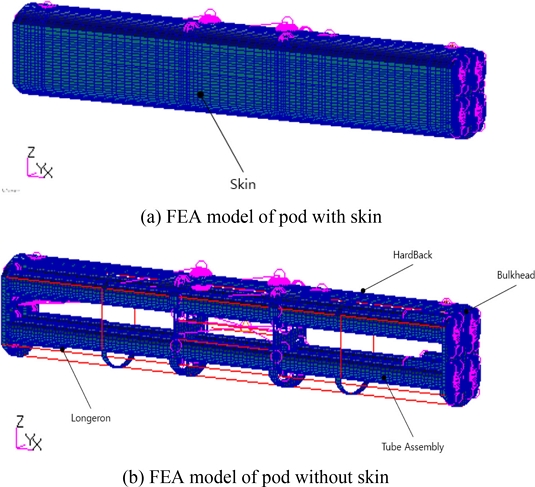
포드의 구성품은 유도탄이 장착되는 4개의 발사관과 유도탄이 장착된 발사관의 하중을 분산하여 지지하기 위한 론저론, 탄장착대(Bomb Rack)와 연결되는 하드백(Hardback), 발사관과 론저론 그리고 하드백을 연결하는 벌크헤드(Bulk Head), 포드 구조체를 덮는 스킨으로 구성되어 있다. 포드의 정적구조 안전성을 유한요소해석으로 검증하고 시험하중으로 변환하기 위하여 상용 유한요소해석 프로그램인 MSC.Patran/Nastran을 사용하여 해석을 수행하였다. 유한요소모델은 Fig. 5와 같이 발사관과 스킨은 2D (Shell) 요소를 벌크헤드와 하드백은 분석을 위하여 3D (Solid) 요소와 2D 요소를 사용하였고 형상이 단순하고 세장비가 큰 론저론은 1D (Beam) 요소를 이용하여 단면형상을 실제 형상과 동일하게 적용하였다. 체결부의 경우 일반적으로 접촉면을 완전접촉 또는 체결부를 강체요소로 연결한다. 체결부를 강체요소로 연결할 경우 전체적으로 구조물의 강성이 떨어지고 완접접촉으로 적용할 경우 강성이 증가한다. 본 연구에서는 충분한 체결수량으로 체결이 강하게 이루어진 스킨 및 하드백 론저론 부분은 해석시간 단축을 위하여 완전접촉과 같은 절점(Node)을 공유하였고, 상대적으로 체결력이 약한 발사관 조립체 부분은 절점을 강체요소로 연결하여 해석을 수행하였다. 유한요소해석모델은 전반적으로 5-10 mm의 요소크기로 해석모델을 구현하였다. 포드의 주구조물인 하드백, 론저론 그리고 벌크헤드의 경우 강도가 상대적으로 높은 알루미늄 70계열을 사용하였고, 발사관은 알루미늄 60계열, 스킨은 알루미늄 50계열을 사용하여 설계하였다. 각 재료의 기계적 물성치는 Table 3과 같이 적용하여 각 구조물의 구조 안전성을 분석하였다.
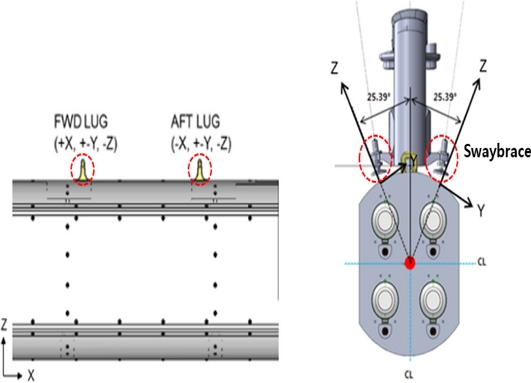
포드가 항공기에 장착되는 탄장착대에는 2개의 훅(Hook)과 4개의 스웨이브레스(Swaybrace)가 있다. 훅은 포드 하드백 상부에 장착된 전방/후방 러그(FWD/AFT Lug)와 연결되고 스웨이브레스는 포드의 하드백에 수직하게 누르며 포드를 고정한다. Fig. 6과 같이 전방러그의 경우 +X, ±Y, -Z 방향의 하중을 지지하고 후방러 그의 경우 -X, ±Y, -Z 방향으로 하중을 지지한다. 스웨이브레스는 포드와 25o기울기로 수직하게 접촉이 되어있어 압축하중(+Z)만 지지한다. 이러한 탄장착대와 포드의 경계조건을 구현하기 위하여 MSC.Patran의 선형간격(Linear Gap) 조건을 사용하였다.
3.2 비행하중 적용
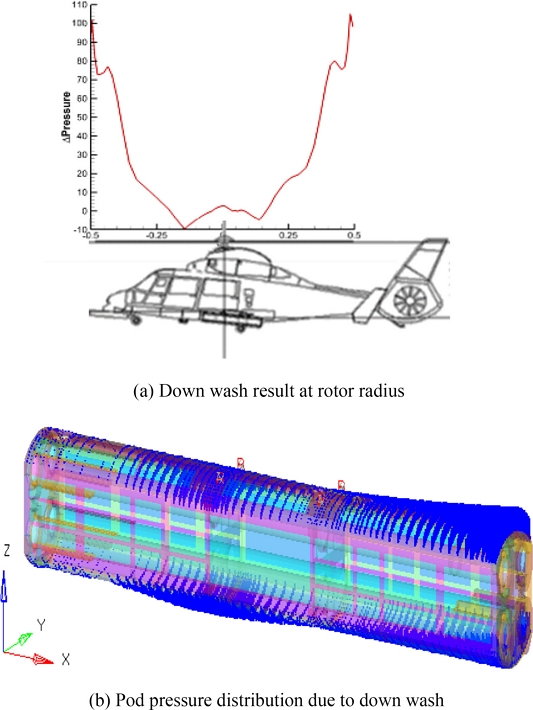
포드의 정적구조 안전성을 유한요소해석으로 검증하기 위하여 앞서 선정한 설계제한하중과 MIL-STD-8591의 5.1.3에 따라 안전계수 1.5를 적용한 설계극한하중(Design Ultimate Load, DUL)을 해석모델에 적용하였다. 관성하중은 가속도와 각속도/각가속도의 성분으로 가속도는 MSC.Nastran의 GRAV CARD를 회전성분은 RFORCE CARD를 사용하였다. 공력하중의 경우 선정된 받음각 α와 옆미끌림각 β 그리고 동압에 대하여 전산유체역학분석을 Fig. 7과 같이 포드표면에 작용하는 압력분포를 산학 연구로 수행하였다. 회전익기의 경우 비행자세에 따른 양력, 항력 등의 공력하중과 회전익기의 로터회전으로 발생하는 내리흐름(Down Wash)이 존재한다. 로터 블레이드 길이에 따른 내리흐름 분석은 Fig. 8(a)와 같이 전산유체역학분석으로 수행하였으며, Fig. 8(b)와 같이 해석모델에 적용하였다. 전산유체역학분석에서 계산된 압력 값을 유한요소해석모델에 적용하기 위하여 MSC.Nastran 필드(Field)의 맵핑 알고리즘을 이용하였다. 맵핑은 해석모델의 각각의 절점에서 가장 근접한 전산유체역할모델의 절점압력을 적용하는 방식이다. 이를 이용하여 Fig. 9(a)와 같이 전산유체역학분석모델의 절점과 동일한 형상으로 만든 유한요소해석모델에 적용된 압력 값을 Fig. 9(b)의 실제 구조물의 유한요소해석모델에 맵핑하여 압력분포가 유사하게 나타나는 것을 확인하였다. 그리고 포드 질량중심에 작용하는 공력하중값을 비교한 결과 유한요소해석모델과 전산유체역학분석모델이 ±7% 이내로 다소 오차가 있지만 전반적으로 일치함을 확인하였다.
3.3 포드 정적구조해석 결과
비행하중조건에서 포드의 정적 구조안전성을 수치해석 기법으로 분석하기 위하여 각 부재에서 발생할 수 있는 파손모드를 식별하고 파손모드에 따른 구조안전성을 분석하였다. 각 구조물의 파손모드는 하드백, 론저론 그리고 벌크헤드의 경우 강도(Strength), 기둥좌굴(Colum Buckling), 크리플링(Crippling), 그리고 체결부에 대한 지압강도(Bearing Strength)에 대하여 분석하였다. 스킨의 경우 강도와 면좌굴(Web Buckling)그리고 체결부 간격과 체결류 크기의 적합성을 분석하기 위하여 인터 리벳 좌굴(Inter Rivet Buckling)을 분석하였다. 각 파손모드에 대한 분석은 Airframe Stress Analysis and Sizing [7]에서 제시한 식(4)부터 식(8)을 이용하였다.
- Inter Rivet Buckling
| (4) |
- s = Fastener Spacing, t = Thickness, E = Young’s Modulus
- Column Buckling
| (5) |
- c = 1.0 (Edge Condition: Hinge), L = Bay Length, E = Young’s Modulus
- Web Buckling
| (6) |
- Kcx_h = 3.62 (Edge Condition: Hinge), ncx = Plastic Reduction Factor, t = Thickness, b = Length
- Crippling
| (7) |
- bn, tn: Length/Thickness of the Individual Segment,
- Fccn = Allowable Crippling Stress of Individual Segment
- Margin of Safety
| (8) |
- FAllowable stress = Material Ultimate Strength,
- FApply stress = Element Stress (DUL)
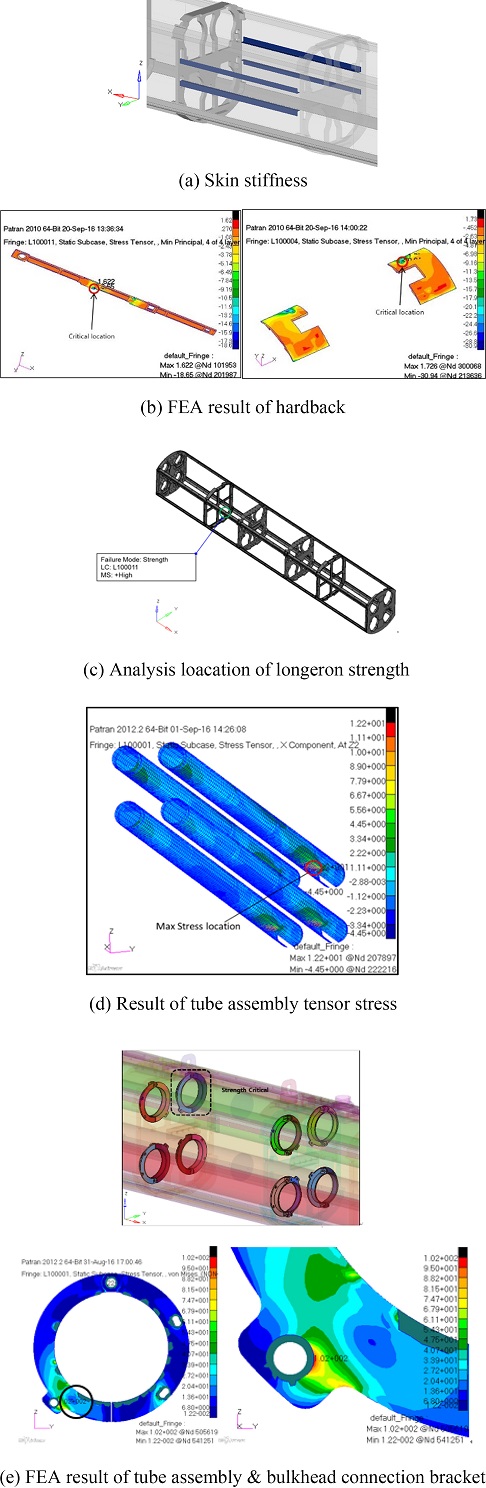
각 포드 구조물의 파손모드에 따른 구조안전성을 분석에서 포드 중심스킨부에서 굽힘하중에 의한 면좌굴이 발생하였다. 이를 보강하기 위해 Fig 10(a)와 같이 L-보강재(Stiffener)를 적용하여 면좌굴에 대한 0.8의 안전여유를 확보하였다. Figs. 10(b)와 10(c)는 하드백과 론저론의 해석결과로 종재 구조물의 안전여유가 매우 많음을 확인하였다. Fig. 10(d) 발사관은 벌크헤드와 연결되는 부분에서 수직응력과 전단응력이 각각 6.6과 0.2 MPa이며, 수직응력과 전단응력에 대한 안전여유는 42.74로 충분한 안전여유가 있었다. Fig. 10(e)의 발사관과 벌크헤드를 연결하는 브래킷의 체결부 주변에서 최대응력 102 MPa 안전여유 1.84로 가장 낮았다. 이는 발사관이 유도탄을 지지할 충분한 강성을 가지고 있으며, 유도탄의 하중을 지지하기 위한 하드백과 론저론 같은 종재의 구조적역할이 발사관만으로 충분하다는 것을 알 수 있었다. 이를 통하여 하드백과 론저론의 크기를 줄여 중량을 감소시킬 수 있을 것으로 판단된다. 추후 동적 구조안정성에 대한 검증결과와 함께 포드의 최적설계를 통한 경량화설계를 수행할 예정이다.
포드의 유한요소해석결과 설계제한하중조건에서 항복강도(Yield Strength) 기준 영구변형이 발생하지 않았고, 설계극한하중에서 극한강도(Ultimate Strength) 기준 구조물이 파손되지 않아 안전여유가 있는 것을 확인하였다. 그리고 발사관과 벌크헤드와 연결되는 부분에서 가장 높은 응력이 발생하였고 나머지 구조물에서 안전여유가 충분한 것을 보았다. 이 결과와 동일한 하중조건의 구조시험결를 비교하여 구조안전성 및 해석기법의 타당성 검증을 수행하였다.
4. 전기체 정적구조시험
4.1 시험하중 분석
수치해석을 통한 포드의 구조안전성을 일차적 확인한 후 포드의 주요하중경로(Load Path) 분석 및 해석기법을 검증하기 위하여 정적구조시험을 수행하였다. 이를 위하여 앞서 선정한 설계제한하중에 대하여 포드에 부가되는 시험하중을 산출하여야 한다. 시험하중 산출은 포드를 파손시킬 수 있는 주하중인 전단력선도와 굽힘하중선도를 분석하여 산출한다. 포드는 하드백과 론저론, 발사관과 같은 종재들이 인장/압축을 지지하는 형태의 구조물로 전단하중과 굽힘하중이 커플링(Coupling)되어 있어 굽힘하중이 크면 이와 비례하여 전단하중도 커진다. 따라서 본 연구에서는 굽힘하중이 구조물의 주요 파손을 일으키는 주요 하중으로 판단하고 굽힘하중을 기준으로 시험하중을 계산하였다.
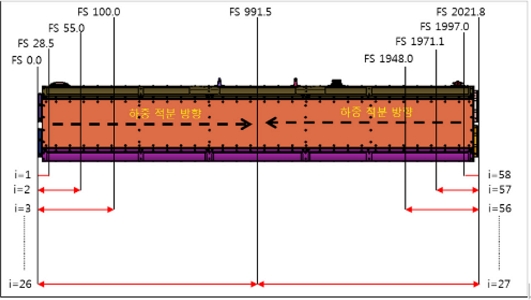
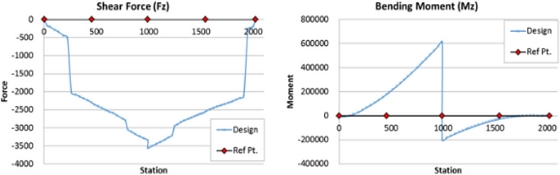
비행하중을 시험하중으로 변환하기 위하여 전단력과 굽힘하중을 Fig. 11과 같이 포드를 길이 방향 58개 영역으로 분할하여 포드중심을 기준으로 전방부와 후방부로 나누어 계산하였다. 시험하중 계산은 각 영역에서 분포하중을 해당 영역 질량중심 위치에 작용하는 하중으로 계산하고, 이를 Fig. 12와 같이 전단력 선도과 굽힘하중선도로 나타내었다.
4.2 하중부가장치
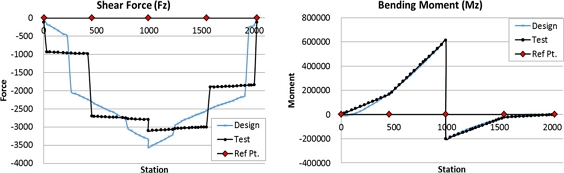
구조시험은 실제 구조물에 분포하중으로 작용하는 하중을 제한된 하중을 인가하는 위치에 집중하중을 부가하여 분포하중의 전단력선도와 굽힘하중선도를 유사하게 모사한다. 포드의 경우 시험하중을 계산하는 과정에서 포드를 58개 영역으로 분할하여 선도를 계산하였지만 하중부가장치로 인한 구조물의 파손이 발생하지 않는 벌크헤드 4개의 영역에 6개의 작동기를 이용하여 6개의 분력을 모사해야 한다. 이를 위하여 항공기 날개 구조시험에 자주 사용되는 휘플트리를 이용하였다. 휘플트리는 중심에 회전이 가능한 바(Bar)의 양끝에 하중부가 위치를 연결하고 중심위치를 변화하면서 양 끝에 작용하는 하중의 비를 조절하여 힘을 분산시키는 메커니즘(Mechanism)이다. Fig. 13과 같이 포드의 벌크헤드가 있는 4개의 영역을 클램프(Clamp)로 고정하고 X, Y, Z축 각 2개씩 작동기를 연결하였다. 이러한 시험 형상에 대하여 휘플트리의 위치와 작동기의 하중을 계산하며 시험하중의 전단력선도와 굽힘하중선도를 Fig. 14와 같이 비교하였다. 선도를 비교한 결과 Y, Z축의 굽힘하중선도는 일치하나, 전단력선도와 X축 굽힘하중선도에 다소 오차가 있다. 하지만 전단력선도의 경우 포드의 주요 파손모드가 아니며, X축 굽힘하중선도의 경우 크기가 작고 파손 영향이 크지 않아 Y, Z축 굽힘하중선도에 더 중점을 두었다.
4.3 정적구조시험
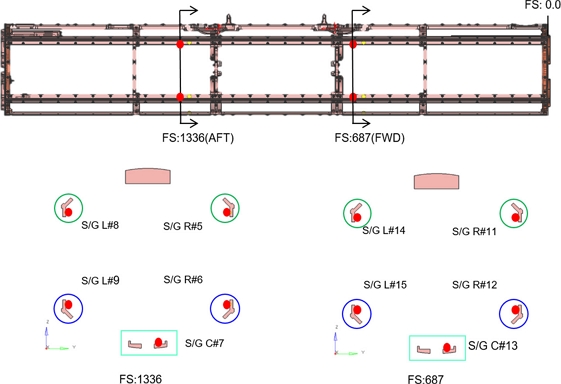
구조시험에 작용하는 시험하중은 로드셀(Load Cell)을 이용하여 측정하였고, 포드의 변형과 파손을 분석하기 위하여 스트레인게이지(Strain Gage)와 변위센서(LVDT)를 사용하여 시험데이터를 측정하였다. 스트레인게이지는 Fig. 15와 같이 수치해석에서 구조적으로 취약하다고 판단되는 16영역에 단축 스트레인게이지 CEA-06-125UW-350 14개와 주응력 방향을 확인하기 위하여 로제트(Rosette)게이지 CEA-06-125UW-350 2개를 설치하였고 포드 전/후방에 변위 센서를 설치하였다. 시험데이터 획득을 위하여 HBM 사의 MX840BR과 MX1615B-R을 사용하였고, 샘플링(Sampling)은 500 Hz로 설정하였다.
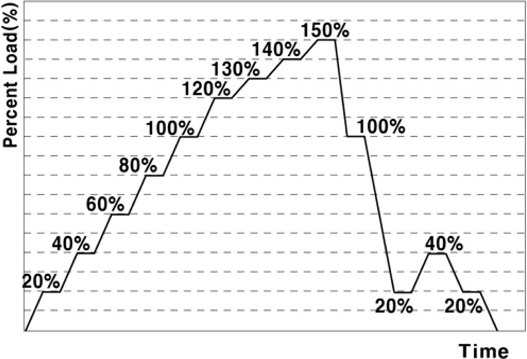
포드의 구조시험은 설계제한하중과 설계극한하중으로 나누어 수행하였다. 설계제한하중의 경우 영구변형이 없는 항복응력 이하의 조건으로 100% 하중까지 20% 단위로 하중을 증가하면서 구조물의 응력이 항복강도 이상 발생하는지 확인하며 시험을 수행하였다. 그리고 구조물이 선형적인 거동을 보이는지 확인하고 구조물에 남아있는 잔여하중(Load Hysteresis)을 제거하기 위하여 100-20-40-20-0% 순서로 하중을 감소시켰다.
설계극한하중도 동일하게 하중의 120%까지는 20% 단위로 하중을 증가시키고 120%에서 150%까지 10% 단위로 하중을 증가시키면서 구조물에 파손이 발생하지는 확인하였다. 그리고 구조물의 선형성과 잔류하중을 제거하기 위하여 설계제한 하중때와 동일하게 하중을 감소시키며 Fig. 16과 같이 수행하였다.
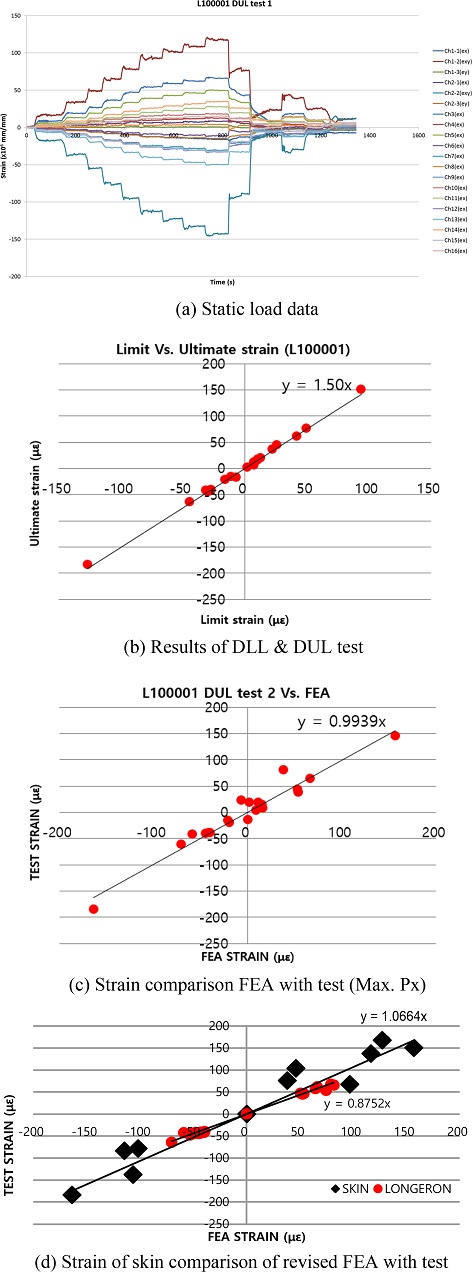
구조시험을 통하여 Fig. 17(a)과 같이 하중부가 장치로 시험을 수행한 후 변형률이 원점으로 돌아가지 않는 것을 볼 수 있다. 이는 시험하중이 인가되면서 각 구조물의 면접촉 압축하중으로 지지되어 있던 부분에 움직임이 발생하여 잔여응력이 남아 있었다. 이러한 구조물의 움직임으로 인한 잔여하중을 없애기 위하여 40%의 하중을 인가하여 잔여응력을 없애주는 사전시험을 수행한 후 본 시험을 수행하였다. 구조물의 영구변형 발생 여부와 선형성을 가지는지 확인하기 위하여 설계제한하중과 설계극한하중의 변형률값을 Fig. 17(b)와 같이 비교한 결과 하중인가 %와 변형률의 증가분의 비가 유사한 것을 확인하였다. 설계극한하중의 최대 변형률과 설계제한하중의 최대 변형률이 약 1.52배, 오차 1.3%[(1.52-1.5)/100]로 구조물이 선형성을 가지며 구조물이 파손되지 않았다. 해석기법을 검증하기 위하여 Figs. 17(c), 17(d)와 같이 정적구조시험과 유한요소해석을 분석한 결과 최대 비틀림(Torsion) Mx 조건에서 해석의 변형률이 시험보다 높았다. 그리고 포드의 론저론 변형률이 시험대비 해석 결과에서 더 크게 계산되었음을 알 수 있다. 이는 해석모델 설계 당시 경량설계되어 있는 판 형태의 스킨을 단순한 형상으로 해석하기 위하여 Fig. 18과 같이 경량설계되어 있는 스킨의 형상을 단순 판 형상의 2D 요소로 설계하는 과정에서 실제 스킨과 강성 차이가 발생하여 론저론으로 일부하중이 전달되었다. 이러한 오차를 줄이기 위하여 스킨의 형상을 실제와 동일하게 하거나 스킨의 탄성계수를 증가시켜 론저론으로 전달되는 일부하중을 스킨이 지지하도록 하는 방법이 있다. 본 논문에서는 스킨을 평판형상의 2D 요소로 유지하면서 해석의 정확도를 높이기 위해 실제 스킨형상에 대하여 굽힘강성(E·I, E: Young’s Modulus)과 비틀림강성(G·J, G: Shear Modulus)을 측정하여 해석모델 단순화로 감소된 단면 이차 모멘트(Area Moment of Inertia, I)와 극관성모멘트(Polar Moment of Inertia, J)만큼 스킨의 재료강성을 30% 증가시켜 각 시험하중조건에서 해석과 시험을 비교하였다. 그 결과 해석과 시험결과 12가지 시험조건에서 잘 일치하고 있음을 알 수 있었다. 이는 해석을 위해 포드를 단순화하는 과정에서 스킨을 제외하고 구조물의 강성에 영향을 주지 않는 선에서 단순화된 해석모델을 생성한 것을 알 수 있었다.
5. 결론
항공기 외부에 장착되어 비행하중을 받는 포드의 비행적합성 검증을 위해 구조안전성검증을 수행하였다. 우선 MIL-STD-8591에 따라 항공기 기동조건에서 관성하중과 전산유체역학으로 공력하중을 계산하여 비행하중을 계산하였다. 비행하중을 적용하여 유한요소해석 수행하였고, 그 결과 파손모드에 따른 포드 구조물의 안전여유가 높음을 확인하였다. 특히 종재의 역할이 발사관만으로 충분함을 알 수 있었다. 그리고 선정한 비행하중을 시험하중으로 변환하여 작동기와 휘플트리로 구조시험을 수행하였다. 시험 결과 설계제한하중과 설계극한하중의 오차가 1.3%로 구조물이 선형성을 가지고 있어 구조물이 파손되지 않음을 확인하였으며, 시험과 해석의 변형률을 비교/분석한 결과로 본 연구에서 적용한 론저론과 프레임을 1D로 단순화한 것과 체결부 체결강도에 따라 절점공유와 절점간에 강체요소로 연결한 유한요소해석모델이 포드의 구조거동을 잘 예측하였음을 보았다.
본 연구를 통하여 항공기에 장착되는 포드의 정적구조 안전성을 검증하기 위한 비행하중 분석, 해석결과로 파손모드를 분석하여 구조안전성 검증하는 기준을 마련하였다. 아울러 시험과 해석을 비교와 보정을 통하여 해석모델의 신뢰성을 확인할 수 있었고 향후 경량설계에 신뢰성 높은 결과를 얻을 수 있는 바탕을 마련하였다.
NOMENCLATURE
| ai : | Acceleration of an Aircraft (I = x, y, z) |
| : | Angular Rate of an Aircraft (I = x, y, z) |
| g : | Gravity Acceleration |
| ws : | Mass of the Pod |
| Ii : | Moment of Inertia of the Pod |
REFERENCES
-
JJun, O.-C., Jun, S.-M., Ryu, G.-H., Kim, J., (2005), Design of instrumented pod for external store flight test, Journal of the Korean Society for Aeronautical & Space Sciences, 33(4), 85-90.
[https://doi.org/10.5139/JKSAS.2005.33.4.085]

- Uhm, W. S., Yoon, J. M., (2015), Static test and analysis of wing support structure for external stores, Journal of Aerospace System Engineering, 9(1), 28-34.
-
Jang, S., Kim, S. Y., Kim, Y., Cho, C., (2013), Flight Loads Analysis of aircraft with high aspect ratio flexible wing by using MSC/NASTRAN, Journal of The Korean Society for Aeronautical and Space Sciences, 41(8), 657-664.
[https://doi.org/10.5139/JKSAS.2013.41.8.657]

- Cho, J. M., Jang, J., Choi, W. C., Bae, J. I., (2019), Fatigue life prediction of sensor pod for aircraft considering aircraft loads, Journal of Aerospace System Engineering, 13(3), 32-39.
-
Jeong, H., Park, J., Son, D., Jang, J., (2019), Study on fatigue life estimation of an aircraft external store under dynamic loads, Transactions of the Korean Society for Noise and Vibration Engineering, 29(4), 462-469.
[https://doi.org/10.5050/KSNVE.2019.29.4.462]

- Kim, H.-G., Kim, S. C., Park, S. H., Ha, B. G., An, S. H., Kim, J. T., (2021), Transformation of flight load to test load for the static load test of external fuel tank for aircraft, Journal of Aerospace System Engineering, 15(1), 80-85.
- Michael, C. Y. N., (1997), Airframe stress analysis and sizing, Hong Kong Conmilit Press Ltd..
- MIL-STD-8591 (W/CHANGE-1), (2012), Department of defense design criteria: Standard airborne stores, Suspension Equipment and Aircraft-Store Interface (Carriage Phase).
- MIL-STD-810G, (2008), Department of defense test method standard: Environmental engineering considerations and laboratory tests.

Research Engineer in LIGNex1. His research interest is Dynamics, Structural Analysis.
E-mail: wooje.cho@lignex1.com

Chief Research Engineer in LIGNex1. His research interest is Dynamics, Structural Analysis.
E-mail: dongseol.choi@lignex1.com

Research Engineer in LIGNex1. His research interest is Dynamics, Structural Analysis.
E-mail: parkjinbo@lignex1.com

Chief Research Engineer in LIGNex1. His research interest is Dynamics, Structural Analysis.
E-mail: kevin71@lignex1.com