자율주행 발렛 주차 시스템을 위한 계층적 주차 경로 계획

1. 서론

자율 발렛 주차 시스템의 경우 제한된 공간에서 승객이 탑승하지 않은 환경이라는 점에서 자율주행 차량의 좋은 서비스 조건으로 부각되며 많은 연구가 이뤄지고 있다[1-3]. 기존의 많은 주차 알고리즘의 경우 발렛 기능을 고려하지 않고, 주차 가능 공간에서 차량을 목표 위치와 방향각으로 주차하기 위한 경로를 생성하는 것에 초점이 맞춰져 있다[4,5]. Qiu[4] 등은 평행 주차 시나리오에서 종횡 방향 위치 오차와 방향 오차를 줄이는 연구를 진행했으며, 궤적 계획과 궤적 추종 제어의 계층구조를 가지는 시스템을 구성하여 모델 예측 제어(MPC) 기반의 알고리즘을 통해 장애물을 제약조건으로 설정하여 이차 프로그래밍 알고리즘으로 주차 연구를 진행했다. 반면, Liu[5] 등은 차량 모델을 사용하지 않고 원호 궤적을 이용하여 장애물을 제약 조건으로 설정하고 비선형 최적화 문제를 통해 주차 연구를 진행했다. 하지만 이와 같은 경로 생성 방법은 주차 공간이 단순하거나 주변에 장애물이 없는 환경에서만 가능하다는 단점이 있다.

실제 자율 발렛 주차 알고리즘을 활용하기 위해서는 입구에서부터 주차 공간까지 협로를 주행하기 위한 방법과 주차 공간에서 주변 차량들을 고려하여 목적지에 원하는 방향각을 만족하며 안전하게 주차할 수 있는 경로를 생성하는 것이 필수적이다. 따라서 두 가지의 서로 다른 방법의 유기적인 연결을 위해 자율주행 발렛 주차 시스템의 경로 계획을 위한 계층구조가 필수적이다. 계층구조의 주요 목적은 자율 발렛 주차 시스템의 도전 과제인 주차 공간까지 이동 단계에서 안전한 협로 주행을 위한 경로 생성과 주차 단계에서 주변 차량 및 장애물을 고려하여 효율적이고 안전하게 주차하는 것이다. 고려해야 할 파라미터와 추구하는 효율이 서로 다른 도전 과제의 유기적인 연결을 위해 계층구조를 가진다.

자율 발렛 주차를 위해 먼저 주차 공간까지 이동하는 단계에서는 장애물을 회피하며 목표 위치까지 도달하는 것이 주요 목표이고 경로의 복잡성이 낮을수록 시간 효율성과 안전성이 높아지기 때문에 최단 거리 경로 계획이 필요하다. 기존의 최단 거리 경로 계획은 주로 그래프 탐색과 샘플링 기반의 방법을 사용해왔다. 그래프 탐색기반은 주변 환경과 자유공간을 그래프를 통해 표현하고 관련 정보들을 비용으로 사용한다. 전통적인 Dijkstra[6], A*[7] 등 탐색 알고리즘을 사용하여 비용을 평가하여 최선의 경로를 계획할 수 있다. 그래프 탐색 기반의 방법은 경로가 존재한다면 반드시 결과를 도출해 낼 수 있지만, 그래프의 차원이 증가할수록 계산 비용이 증가할 수 있다. 샘플링 기반의 방법 또한 먼저 주변 환경들을 표현하고 자유공간에서 무작위의 샘플들을 생성하여 충돌을 평가한 후 샘플을 반복 생성하여 탐색 알고리즘으로 경로를 계획한다. 샘플링 기반의 방법은 고차원의 환경에서도 빠른 성능을 기대할 수 있지만, 반복 횟수 제약에 따라 결과를 제공하지 못할 수도 있다는 단점을 가지고 있다. 이번 연구에서는 2차원 그래프에서 장애물과 충돌하지 않는 최단 거리 경로 생성을 위해 단순하고 수렴성이 보장되는 그래프 탐색 방법을 이용한다. 그래프 탐색을 이용하여 생성된 경로는 차량이 주행하기에 부드럽지 않은 경로로써 기준 경로로 사용하기에 적합하지 않다. 따라서 부드러운 경로 계획을 위해 경로 평활화를 이용하여 기준 경로를 생성한다[8].

그래프 탐색 방법은 위치 정보만 고려하고 방향 정보는 고려하지 않기 때문에 차량이 기준 경로를 따라 주행하며 주차 가능 공간에 위치하면 새로운 기준 경로가 필요하다. 새로운 기준 경로는 주변 차량과 충돌하지 않고 안전하게 주차하기 위해서는 목표 위치에서 목표 방향각으로 주차를 완료해야 한다. 따라서 방향까지 고려된 경로 계획이 필요하며, 이번 연구에서는 3차 다항식을 이용하여 방향각이 고려된 주차 경로 계획을 통해 안전한 경로를 생성하는 목표를 가진다. 3차 다항식 경로 계획은 주로 자율주행 차량의 부드러운 경로 계획을 위해 이용되지만, 출발지와 목적지의 위치 및 방향 관계에 따라 추종 불가능한 곡선이나 목적지에서의 급격한 방향 전환으로 인해 원하는 방향각을 만족하기 어려운 경우가 있다. 이러한 문제들을 해결하기 위해 차량의 방향각에 여유를 두어 후보 경로들을 생성하고 주차에서 고려되는 효율성 들을 비용 함수로 설계하여 여러 조건을 만족하며 목표 방향각 오차를 줄일 수 있는 최적 경로를 생성할 수 있다.

계층구조의 자세한 내용은 섹션 2에 설명되어 있으며 섹션 3에서는 진행한 연구를 검증하기 위한 시뮬레이션과 분석 그리고 섹션 4는 결론으로 구성했다.

2. 자율 발렛 주차 경로 계획

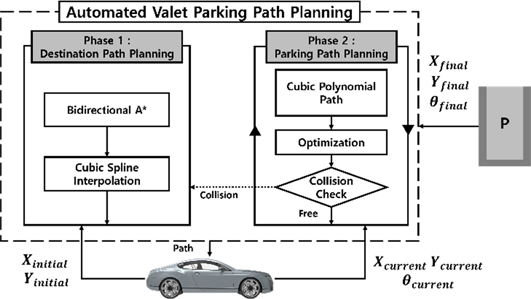
자율주행 발렛 주차 시스템의 경로 계획을 위한 계층 구조도를 Fig. 1에 나타내었다. 앞서 설명한 두 가지 목적에 따른 계층 구조는 주차장 외부에서부터 주차 공간까지 이동하는 목적지 경로 계획과 주차 가능 공간에서 활성 조건을 가지는 주차 경로 계획으로 구성되어 있다. 두 알고리즘 모두 자차량으로부터 좌표 정보를 받고 기준 경로를 생성한다. 주차 경로 계획은 경로에 방향까지 고려돼야 하기 때문에 현재 차량의 방향각 정보와 목표 공간의 위치와 방향각 정보를 추가로 제공받는다. 전체 알고리즘의 작동 순서는 먼저 목적지 경로 계획에서 주행 가능 경로가 생성된 후 기준 경로를 차량이 추종하는 모든 시간 동안 두 번째 알고리즘이 실행되며 충돌 위험 및 제약조건이 만족될 경우 작동조건이 활성화된다. 두 알고리즘은 독립적으로 기능하며 충돌 위험이 없는 경로가 우선순위로 선택되고, 최적 경로 선택 방법에 따라 최종적으로 기준 경로가 생성된다. 계층구조의 첫 번째 알고리즘인 목적지 경로 계획은 2.1에서, 두 번째 알고리즘인 주차 경로 계획은 2.2에서 자세히 설명한다.

Fig. 1

System structure of path planning for automated valet parking

2.1 Phase 1: 목적지 경로 계획

계층구조의 첫 번째 알고리즘인 목적지 경로 계획은 주차장에서 주차 공간까지 장애물과 충돌하지 않는 최단 거리 경로를 생성하는 목표를 가지고 있다. 안전한 최단 거리 경로를 생성하기 위해 목적지 경로 계획은 연속된 두 가지 방법으로 이루어져 있다. 먼저, 자율주행 차량이 주차 가능 공간까지 주행하기 위한 전역 경로를 생성한다. 다음으로 주행 안정성과 경로의 연속성을 보장하기 위해 경로 평활화를 진행한다. 전역 경로 계획은 섹션 2.1.1에 자세히 설명되어 있고, 부드러운 경로를 위한 경로 평활화는 섹션 2.1.2에 자세히 설명되어 있다.

2.1.1 전역 경로 계획

전역 경로는 자율주행 차량이 목적지까지 도달하기 위해 기본이 되는 경로이며, 안전한 최단 거리 경로를 탐색을 위해 A* 알고리즘의 변형인 양방향 A* 알고리즘을 사용한다. 양방향 A* 알고리즘은 복잡한 장애물이 존재하는 넓은 공간에서 최적 효율성을 보장하는 경로를 탐색할 수 있다는 장점이 있다.

양방향 A* 알고리즘은 시작 노드에서 목표 노드로의 탐색과 동시에 목표 노드에서 시작 노드로의 역 탐색을 병행하는 탐색 알고리즘이다. 이 알고리즘은 전체 탐색 공간을 두 부분으로 나누어 각 부분에서 독립적으로 A* 알고리즘을 실행한다. 각각의 탐색은 시작 노드와 목표 노드에서 출발하여 다른 쪽 노드를 향해 진행된다. Fig. 2에 설명된 알고리즘의 흐름은 다음과 같다:

Fig. 2

Pseudo code of bidirectional A* algorithm

1) 각 노드의 열린 집합, 닫힌 집합, 비용 및 부모 노드 등을 초기화한다.

2) 열린 집합이 비어 있지 않는 한 최소 비용을 갖는 노드들을 선택한다.

3) 시작 노드 쪽에서 A* 알고리즘을 수행한다. 시작 노드에서 가장 적절한 다음 노드를 선택하여 탐색을 진행한다. 이 과정에서는 시작 노드의 이웃 노드를 검토하고 각 이웃 노드의 비용 및 부모 노드를 갱신한다.

4) 목표 노드 쪽에서도 3. 과 동일한 방법을 수행한다.

5) 두 탐색이 상호간섭 없이 독립적으로 진행된다. 만약 시작 노드 쪽의 탐색이 목표 노드 쪽의 닫힌 리스트에 있는 노드를 방문하거나, 목표 노드 쪽의 탐색이 시작 노드 쪽의 닫힌 리스트에 있는 노드를 방문하면, 양방향 탐색은 종료된다.

6) 양방향 탐색이 종료되면 최종 경로를 생성하여 반환한다.

양방향 A* 알고리즘은 출발지와 목적지에서 병렬적으로 노드를 탐색하기 때문에 A* 알고리즘의 단점인 넓은 공간에서의 탐색 시간을 줄여 시간 효율성 측면에서 큰 장점을 가지고 있다.

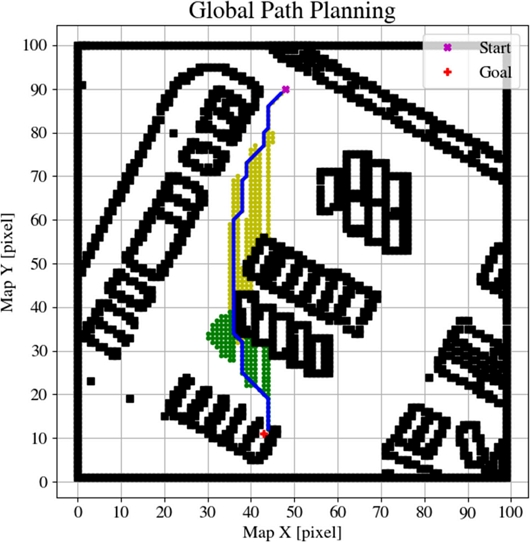
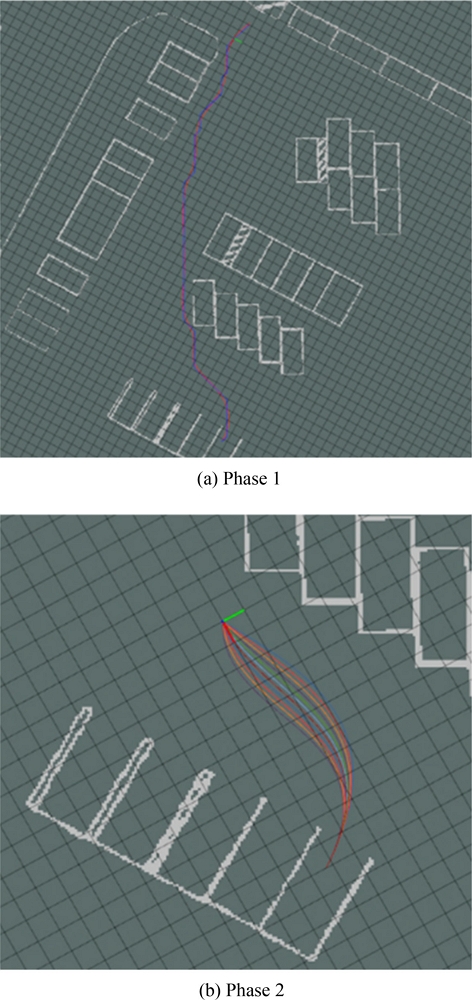
양방향 A* 알고리즘을 사용하기 위해 주차장을 위에서 본 이미지를 그래프화 하여 주차장의 장애물과 차선의 위치 정보를 노드로 나타낸다. 주행 가능 공간에는 일반적인 휴리스틱 함수를, 장애물과 차선에는 매우 큰 비용을 부여하여 경로를 탐색할 때 주행 불가 영역 위로 경로가 생성되는 것을 방지한다. 출발지 노드와 목적지 노드에서 병렬적으로 주변 노드를 탐색을 진행하며 두 탐색 노드가 중복되거나 기존에 탐색을 마친 노드와 중복될 시 탐색을 종료하고 탐색한 노드 중에서 가장 낮은 비용을 가지는 최적 경로를 생성한다. 이렇게 생성된 전역 경로는 최적 효율성을 보장한다. Fig. 3은 주차장 지도를 그래프화 하고 양방향 A* 알고리즘을 이용하여 주차장에서의 전역 경로를 생성한 그래프이다. 연두색 원은 출발지 노드로부터 탐색을 마친 노드이고, 초록색 원은 목적지 노드로부터 탐색을 마친 노드이다. 출발지와 목적지에서 병렬적으로 노트 탐색을 통해 연두색 노드와 초록색 노드가 만나게 되어 탐색이 중단되고, 탐색한 노드들 중 이웃한 노드에서 가장 비용이 적은 노드들의 연속인 파란색 전역 경로로 생성된다.

Fig. 3

Global path planning using bidirectional A* algorithm

2.1.2 전역 경로 평활화

그래프 탐색 기반으로 생성된 전역 경로는 이산화 된 그리드로 인해 차량이 경로를 따라 이동할 수 없는 경우가 있다. 따라서 추종 가능한 경로를 생성하기 위해 꺾여 있는 전역 경로를 부드럽게 펴주는 과정이 필요하다. 경로 평활화를 이용하여 경로를 연속적이고 미분 가능성을 보장하여 차량의 경로 추종 성능을 높이고 주행 가능성이 보장된 경로를 제공한다. 주로, 연속성을 보장하기 위해 보간법을 사용하여 불연속 경로를 연속 경로로 만들고, 미분 가능성을 보장하며 부드러운 경로를 위해 스플라인[9]을 사용한다. 자율주행 차량을 위한 기준 경로로써 연속성과 미분 가능성을 보장하여 부드러운 경로를 필요로 하기 때문에 스플라인과 보간법을 융합한 스플라인-보간법을 사용한다.

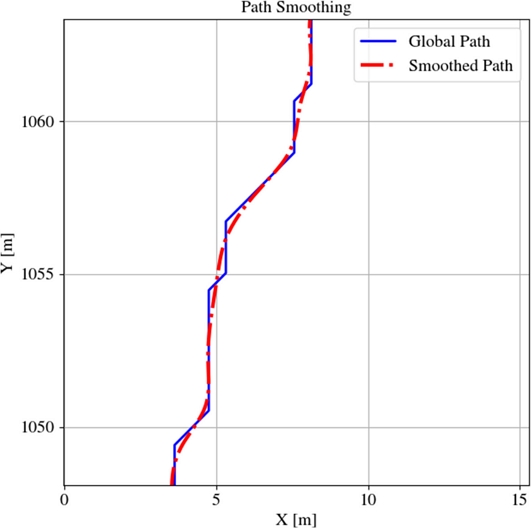
스플라인-보간법이란, 불연속 항들을 보간법을 이용하여 낮은 차수의 다항식으로 만들고 불연속점들을 스플라인의 제어점으로 이용하여 부드러운 곡선을 만들어 불연속이고 비선형을 연속적이고 선형으로 근사하는 방법이다. 식(1)과 같이 먼저 스플라인 집합을 위한 구간을 정의하고 식(2)의 형태인 3차 다항식 스플라인 집합을 정의한다. 이때, 연속성을 보장하기 위해 식(3)과 식(4)의 보간 조건을 만족해야 하며, 미분 가능성을 보장하고 부드러운 경로를 위해 식(5)와 식(6)의 연결 조건을 만족해야 한다. 이러한 조건을 모두 만족시키는 c를 구하여 각 구간에서 3차 다항식으로 연결된 경로를 생성할 수 있다. 스플라인-보간법을 이용해 생성된 경로는 Fig. 4의 그래프이며, 파란색 실선은 전역 경로이고 빨간색 쇄선은 전역 경로를 평활화한 경로이다. 전역 경로는 꺾인 직선의 형태로 차량이 추종하기 어려운 경로이지만, 평활화한 경로는 전역 경로의 모양을 띠며 부드러운 기울기를 보여준다.

$\[ \stackrel{-}{X}=X-X_i, 1\le i\le n-1, i\in N \]$

(1)

$\[ S_i\left(X\right)=c_{3_i}{\stackrel{-}{X}}^3+c_{2_i}{\stackrel{-}{X}}^2+c_{1_i}\stackrel{-}{X}-c_{0_i} \]$

(2)

$\[ S_i\left(X_i\right)=Y_i \]$

(3)

$\[ S_{i+1}\left(X_i\right)=Y_i \]$

(4)

$\[ S_i^{\mathrm{\text{'}}}\left(X_i\right)=S_{i+1}{}^{\mathrm{\text{'}}}\left(X_i\right) \]$

(5)

$\[ S_i^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(X_i\right)=S_{i+1}{}^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(X_i\right) \]$

(6)

Fig. 4

The global path shows a linear variation in slope, while the smoothed path demonstrates a gradual slope change, maintaining the overall shape observed in the global path

2.2 Phase 2: 주차 경로 계획

Phase 2는 계층구조 경로 계획의 두 번째 알고리즘으로 목적지의 위치와 방향을 고정하고 현재 차량의 방향에 여유를 두어 여러 후보 경로들을 제안하고 평가하여 최고의 효율을 가지는 경로를 계획한다. 여러 후보 경로를 제안하는 이유는 현재 차량의 방향에 고정된 하나의 경로만 제시했을 때, 목적지에서 목표 방향을 만족하기 위해 급격하게 기울기가 변하는 경로가 생성되는 경우가 있어 실제 기준 경로는 목표 방향을 만족하지만, 추종 가능성이 보장되지 않아 주차의 안전성이 감소하기 때문이다. 따라서 현재 차량의 방향각에 여유를 두어 경로의 다양성을 증가시켜 더 안전한 경로를 선택할 가능성을 높이고 비용 함수에 따라 최고 효율을 가지는 경로를 선택할 수 있다.

Phase 2의 작동조건은 Phase 1의 경로를 따라 차량이 목적지까지 이동하는 도중 차량의 현재 위치와 방향 그리고 목적지의 위치와 방향을 고려한 경로가 장애물과 충돌하지 않는 경로로 판단될 때이다. 이 경우 Phase 1이 종료되고 실시간으로 Phase 2가 작동하여 지속해서 최적의 경로를 계획한다.

2.2.1 3차 다항식 경로 계획

자율 주차가 진행되는 환경은 주변 장애물이 복잡한 상황으로 충돌이 일어나지 않도록 안전하게 주행해야 한다. Phase 1의 경로 계획과 달리 도착지에 차량이 정렬되어야 하므로 차량의 위치뿐만 아니라 방향까지 고려한 경로 계획이 필수적이다. 차량의 위치와 방향을 고려하기 위해 3차 다항식을 이용하여 경로를 계획한다. 3차 다항식을 구성하기 위해서는 현재 및 목적지의 위치 및 방향 정보가 필요하다. 식(7)과 식(8)은 차량의 현재 위치와 목적지의 위치로 두 개의 식이 정의되고, 차량 좌표계에서 dy/dx는 차량의 방향각으로 근사 될 수 있기 때문에 식(9)와 식(10)은 현재 차량의 방향과 목적지의 목표 방향으로 정의된다. 최종적으로 후보 경로는 식(11)의 형태를 띠게 된다.

$\[ y_{cur}=c_3{x}_{cur}^3+c_2{x}_{cur}^2+c_1{x}_{cur}+c_0 \]$

(7)

$\[ y_{tar }=c_3{x}_{tar }^3+c_2{x}_{tar }^2+c_1{x}_{tar }+c_0 \]$

(8)

$\[ {\theta }_{cur }=3c_3{x}_{cur }^2+2c_2{x}_{cur }+c_1 \]$

(9)

$\[ {\theta }_{tar }=3c_3{x}_{cur }^2+2c_2{x}_{tar }+c_1 \]$

(10)

$\[ C\left(x\right)=c_3{x}^3+c_2{x}^2+c_{1}x+c_0 \]$

(11)

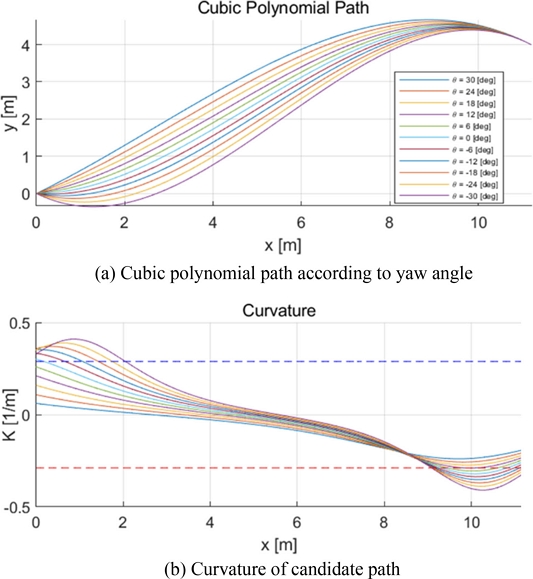
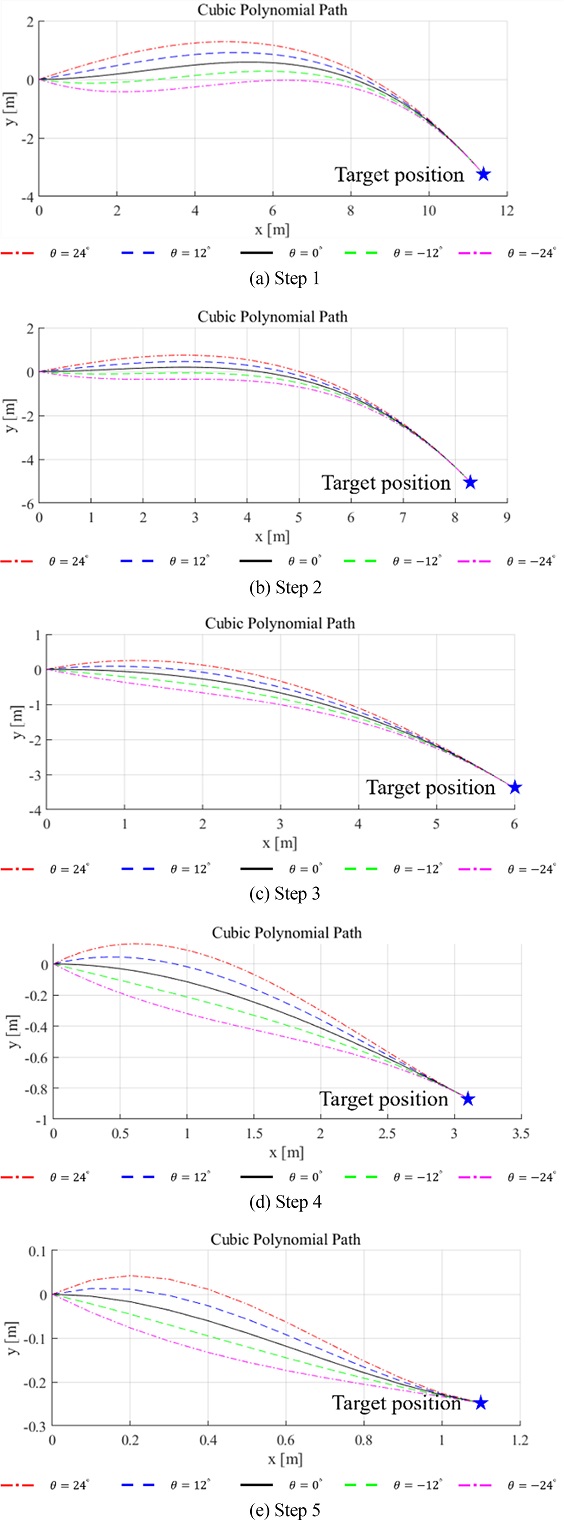
같은 방법으로 현재 차량의 방향각을 실제와 여유를 두어 차량의 방향각을 변경해가며 그린 후보 경로들은 Fig. 5(a)와 같다. 후보 경로는 0도부터 음의 방향과 양의 방향 모두 30도까지 6도씩 증가하여 총 11개의 후보 경로로 이루어져 있다.

Fig. 5

Path planning optimization

2.2.2 경로 최적화

후보 경로에서 안전성 및 추종 가능성을 보장하며 주차의 경로가 단순할수록 얻는 이득을 높이기 위하여 제어 노력과 경로 길이에 대한 항을 비용 함수를 구성하는 데 포함한다.

안전성을 보장하기 위하여 차량을 간단한 기구학적 모델로 나타낸다[10]. 차량 모델은 Fig. 6과 같이 차량의 전장을 이등분하여 두 개의 원을 차량의 길이 중심에 접하도록 하고, 두 개의 원과 접하는 점에서 동일한 반지름을 가지는 원을 그린다. 3개의 원은 장애물과의 충돌 예측에 사용되며, 3차 다항식 경로 위에 식(9)를 이용하여 구한 θ로 3개의 연속된 원을 회전하여 주변 장애물들과 충돌을 비교한다. 충돌이 일어나는 경로는 후보 경로에서 제외되며 충돌이 일어나지 않는 경로는 후보 경로에 추가된다. 실내 주차장과 같이 폐쇄적인 공간에서는 위치와 방향각의 추정 불확실성이 존재하므로 해당 모델에서 사용한 원의 반지름을 증가시켜 사용해야 할 필요가 있다.

Fig. 6

3 circle model to ensure safety

안전성이 보장된 경로 후보들이 결정된 후, 추종 가능성을 판단하기 위해 차륜의 최대 조향 각도를 이용하여 최대 곡률을 구할 수 있다. 대부분의 주차가 저속에서 진행되기 때문에 Ackermann Steering Geometry를 이용하여 차량의 주행 가능한 최대 곡률을 구한다. 다항식의 곡률 공식인 식(12)를 이용하여 경로에서 최대 곡률이 최소 선회 반경을 넘지 않도록 제약조건을 설정하여 추종 가능성을 보장하고 각 후보 경로에서 최대 곡률을 비용 함수의 첫 번째 항으로 구성한다. Fig. 5(b)의 그래프를 보면 최대 곡률 제약조건이 위배된 경로들을 확인할 수 있다.

$\[ K=\frac{C^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(x\right)}{\sqrt{1+C^{\mathrm{\text{'}}}{\left(x\right)}^2}} \]$

(12)

주차 경로에서 제어 노력이 적을수록 부드러운 곡선을 따라 차량이 주행할 수 있으며 이는 에너지 효율성과 주행 안전성 그리고 추종 정확도가 높아진다. 제어 노력의 효율을 높이기 위하여 3차 다항식 경로의 기울기 변화량이 최소가 되는 경로를 선택하기 위해 경로의 2계 도함수의 절댓값의 합을 비용 함수의 두 번째 항으로 구성한다.

마지막으로 경로의 길이를 줄여 시간 효율성을 높이기 위해 후보 경로 길이를 식(13)과 같이 직선 경로 길이로 정규화하여 비용 함수의 세 번째 항으로 구성한다.

$\[ L=\frac{{\int }_{x_{cur }}^{x_{tar }} \sqrt{1+C^{\text{'}}{\left(x\right)}^2}dx}{\sqrt{{\left(x_{cur}-x_{tar}\right)}^2+{\left(y_{cur}-y_{tar}\right)}^2}} \]$

(13)

각각의 서로 다른 의미를 가지는 비용 함수의 항들은 물리적 의미가 서로 다르며 이에 따라 단위 또한 통일되지 않는다. 이를 위해 각 항을 식(14)를 이용해서 정규화한다.

$\[ X_{normalized }=\frac{X}{X_{max}} \]$

(14)

완성된 비용 함수는 식(15)에 표현되어 있으며, 각 항에 대한 가중치인 α, β, γ는 음이 아닌 실수이다. 가중치는 사용자의 효율 추구에 따라 다르게 설정할 수 있으며, 중요한 의미를 가질수록 가중치의 값을 크게 설정한다. 비용 함수의 세 항을 각각 P, Q, R로 나타냈다.

$\[ \begin{array}{c}P,Q,R=argmin\left(P+Q+R\right)\\ P=\alpha K_{{max}_{normalized }}\left( s.t.\left|K_{max }\right|\le \frac{\text{tan}\left|{\delta }_{max }\right|}{l}\right)\\ Q=\beta {\text{Σ}}_{cur }^{x_{goal }}{\left|{\nabla }^{2}C\left(x\right)\right|}_{normalized }\\ R=\gamma L_{normalized }\end{array} \]$

(15)

최종적으로 후보 경로들의 비용 중 가장 작은 비용을 가지는 경로를 최종 선택하여 기준 경로로 사용하며 차량의 변화하는 위치와 방향에 따라 지속적으로 더 적은 비용을 가지는 경로를 선택한다.

3. 시뮬레이션 및 분석

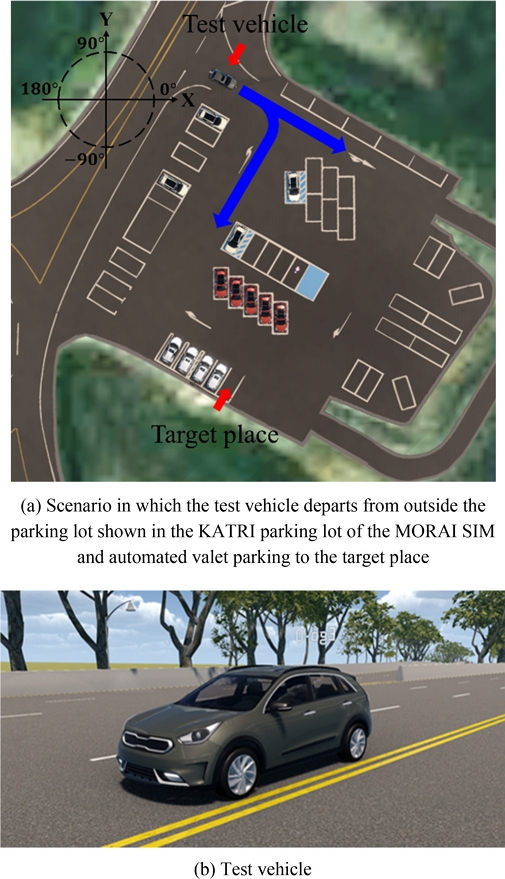
시뮬레이터를 이용하여 자율주행 발렛 시스템의 계층적 주차 경로 계획과 경로 최적화가 적절한지 평가한다. 평가를 위한 주차장 환경은 교통안전공단 자동차안전연구원의 K-city 주차장 환경을 사용하였으며, 동일하게 구현된 MORAI SIM의 K-city 환경에서 시뮬레이션을 진행하였다. 주차장 외부에서부터 주차 완료 구역까지 기준 경로를 따라 주행하며, 주차 구역에는 다른 차량들이 주차 되어있어 안전성 높은 주차를 요구하는 시나리오로 구성하였으며, 주차장 환경은 Fig. 7(a)에 나타내었다. 시뮬레이션에 사용된 차량은 KIA의 Niro 차량을 사용하였으며, Fig. 7(b)에 나타내었다. 실험에 사용된 차량의 파라미터는 Table 1과 같으며, 비용 함수의 가중치는 기본값으로 Table 2에 구성했다. 기준 경로를 추종하기 위한 횡방향 제어기는 모델 예측 제어(MPC)를 이용했다.

Fig. 7

Simulation environment

Table 1

Test vehicle parameters

Table 2

Cost weights

3.1 자율 발렛 주차 경로 계획 평가

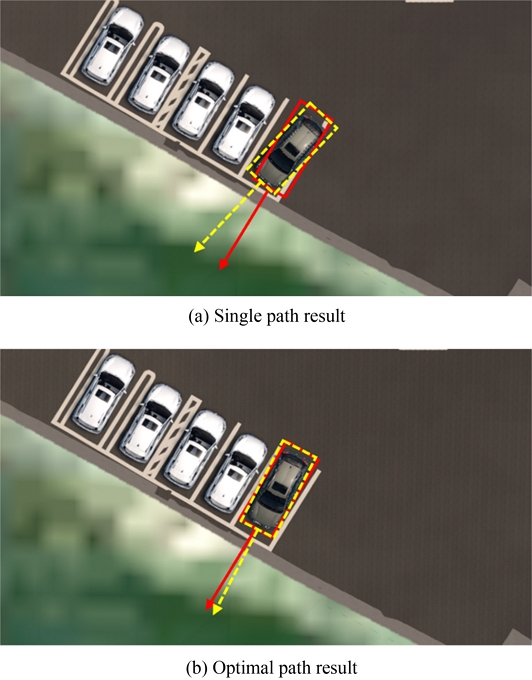
Phase 1에서 양방향 A* 알고리즘을 이용하여 주차장 외부에서부터 목적지까지 전역 경로를 생성하고 경로 평활화를 진행했다. Fig. 8(a)의 그래프가 보여주듯이, 평활화된 경로를 따라 차량이 차선을 밟지 않으며 차량이 경로를 추종하며 주차 완료 장소 주변에 차량이 근접하였을 때 Phase 2에서 계획한 3차 다항식 경로 후보 중 차선과 타 차량과의 충돌 가능성이 없는 경로가 존재하여 Phase 1의 경로 추종을 중단하였다. Fig. 8(b)가 보여주듯이, Phase 2의 후보 경로들이 장애물과 충돌하지 않고 차량의 현재 방향각에 여유를 두어 경로의 최대 곡률이 작아 완만한 곡선을 그리는 경로, 목표 위치 부근에서 기울기 변화율이 작은 경로 그리고 경로의 길이가 가장 짧은 경로 등 여러 효율 특성을 가지는 경로가 생성되었다. 이 중 최적 경로를 따라 주차 완료 후 차량의 목표 위치와 방향각을 고정한 단일 경로와 최적 경로에 따른 비교 값을 Fig. 9와 Table 3에 나타냈다. Fig. 9의 결과에서 최적 경로로 주차를 진행했을 때, 단일 경로 주차보다 방향각 오차가 상당량 줄어듦을 확인할 수 있다. 단일 경로로 주차했을 때와 비교하여 최적 경로로 주차했을 때, 위치 오차는 0.8 m, 74.1% 감소했고 방향 오차는 7.0 deg, 62.4% 감소했다.

Fig. 8

Path generation result

Fig. 9

Result comparison of yaw angle between parking on the single path and the optimal path

Table 3.

Evaluation of pose accuracy

3.2 비용 함수 최적화 평가

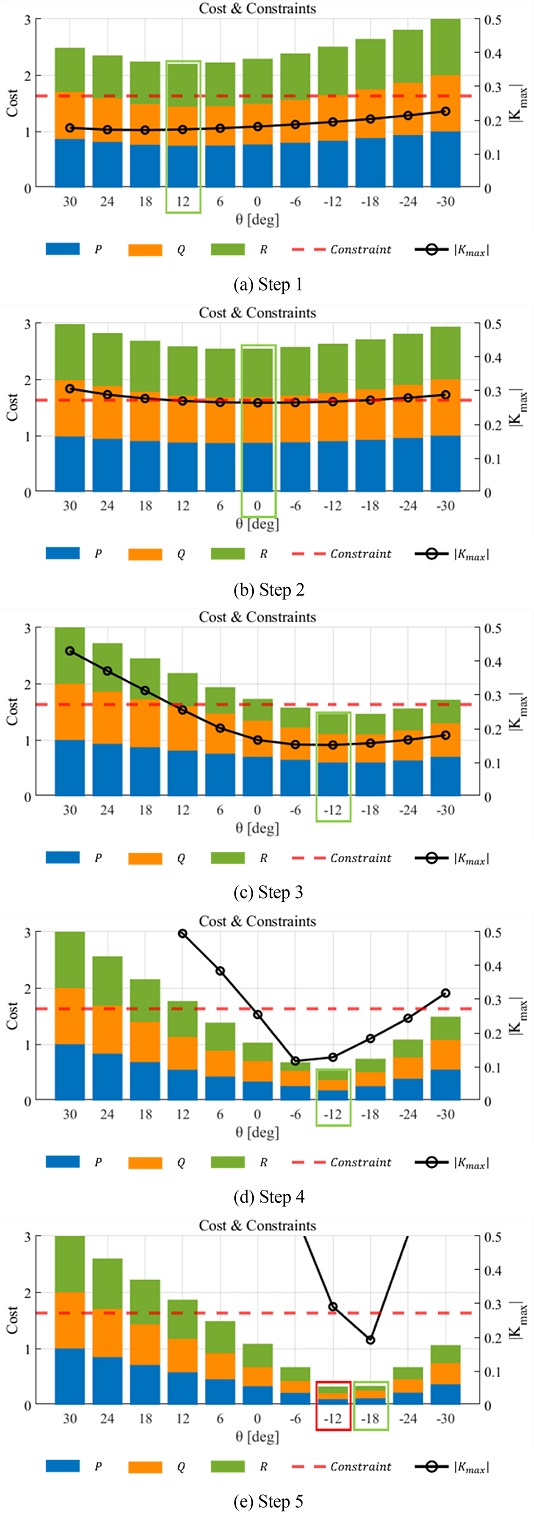
비용 함수가 적절하게 설계되었나 확인하기 위하여 비용 함수 최적화 평가를 진행했다. Phase 2가 작동조건이 활성화된 이후부터 주차 완료까지 최적 경로가 선택되는 과정을 5단계로 나눠 Figs. 10과 11에서 나타냈다. Fig. 10은 11개의 후보 경로들의 비용 함수 합이며, 각 후보 경로들의 제약조건과 함께 나타내어 제약조건을 만족하며 가장 적은 비용을 가지는 최적 경로를 확인할 수 있다. Figs. 11은 10에 대응하는 후보 경로의 모습이며, 경로를 명확히 구별하기 위해 5개의 경로만 시각화하였다. Fig. 10에서 연두색 상자로 둘러 쌓인 막대 그래프가 제약 조건을 만족하는 최적 경로이고 빨간 상자로 둘러싸인 막대그래프는 가장 작은 비용을 가지지만 제약조건을 만족하지 못하는 후보 경로이다. Fig. 10(d)와 같이 후보 경로 중 비용이 최소인 경우에도 제약조건이 위배되어 최적 경로 선택에서 제외되는 경우를 확인할 수 있다.

Fig. 10

Costs and constraint of candidate optimal path

Fig. 11

Phases of candidate optimal path

Figs. 10(a)-10(c)에서 확인할 수 있듯이, 방향각에 여유를 둔 후보 경로들이 최적 경로로 선택되고 있으며 차량이 주행하며 목적지의 방향 오차를 줄이는 최적 경로가 선택되는 것을 확인했다. 따라서 설계한 비용 함수가 주차 경로 계획 목적에 맞게 설계되었음을 확인했다.

4. 결론

본 연구에서는 자율주행 발렛 주차 시스템을 위한 계층적 경로 계획 방법을 제안하였다. 이 방법은 주차장 외부에서부터 목적지까지 경로 계획과 주차 가능 구역에서의 후보 경로 최적화로 나누어져 자율 발렛 주차 시스템의 안전하고 효율적인 주행을 보장할 수 있다. 기존에 문제가 되었던 먼 거리에서의 주차 공간까지의 주행과 연결되는 목적지에서 주차 공간의 목표 방향각과 차량의 주차 방향의 정확도를 높이는 것이 핵심 목표였으며, 시뮬레이션 결과 제안한 방법이 단순하고 효율적인 경로를 계획하고 안전하게 차량의 목표 방향각과 차량의 방향각 오차를 62.4% 향상시켜 주차하는 것을 확인하였다. 경우에 따라 비용 함수의 특정 효율 항이 최솟값 값을 가지지만 총 비용 합이 최소가 아닌 후보 경로들을 확인할 수 있었다. 이는 각 비용 함수의 가중치에 따라 최적 경로가 선택되는 경향을 변경할 수 있다는 것을 의미하고, 다양한 시나리오에 따라 가중치가 변경될 수 있음을 의미한다.

본 연구에서는 차량이 주차함에 있어 후진 주행을 고려하지 않았으나, 후진 주행 알고리즘을 추가할 경우 알고리즘의 활용도가 높아질 것으로 기대한다.

다양한 시나리오에서 비용 함수의 가중치를 변경하며 각 가중치에 따른 경로 선택의 경향성과 특성을 분석하고 직각, 대각, 평행주차 환경에서 정형화될 수 있는 가중치 집합에 대한 추가 연구가 필요하다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2021R1C1C1004154).

REFERENCES

• Hussain, R., Zeadally, S., (2018), Autonomous cars: research results, issues, and future challenges, Institute of Electrical and Electronics Engineers Communications Surveys & Tutorials, 21(2), 1275-1313. [https://doi.org/10.1109/COMST.2018.2869360]
• Jhang, J.-H., Lian, F.-L., (2020), An autonomous parking system of optimally integrating bidirectional rapidly-exploring random trees and parking-oriented model predictive control, Institute of Electrical and Electronics Engineers Access, 8, 163502-163523. [https://doi.org/10.1109/ACCESS.2020.3020859]
• Zips, P., Böck, M., Kugi, A., (2016), Optimisation based path planning for car parking in narrow environments, Robotics and Autonomous Systems, 79, 1-11. [https://doi.org/10.1016/j.robot.2016.02.004]
• Qiu, D., Qiu, D., Wu, B., Gu, M., Zhu, M., (2021), Hierarchical control of trajectory planning and trajectory tracking for autonomous parallel parking, Institute of Electrical and Electronics Engineers Access, 9, 94845-94861. [https://doi.org/10.1109/ACCESS.2021.3093930]
• Liu, S., An, X., Shang, E., He, H., (2012), A path planning method for assistant parallel car-parking, Proceedings of the 2012 Fifth International Symposium on Computational Intelligence and Design, 65-68. [https://doi.org/10.1109/ISCID.2012.168]
• Dijkstra, E. W., (1959), A Note on two problems in connexion with graphs, Numerische Mathematik, 1, 269-271. [https://doi.org/10.1007/BF01386390]
• Hart, P. E., Nilsson, N. J., Raphael, B., (1968), A formal basis for the heuristic determination of minimum cost paths, Institute of Electrical and Electronics Engineers Transactions on Systems Science and Cybernetics, 4(2), 100-107. [https://doi.org/10.1109/TSSC.1968.300136]
• Kim, J., Park, S. H., Shin, D.-G., Kim, M.-G., Chung, S. Y., Hwang, M. J., Kim, M., (2021), 3-D model-based trajectory generation algorithm for robotic shoe sole spray system, Journal of the Korean Society for Precision Engineering, 38(11), 825-832. [https://doi.org/10.7736/JKSPE.021.067]
• Ravankar, A., Ravankar, A. A., Kobayashi, Y., Hoshino, Y., Peng, C.-C., (2018), Path smoothing techniques in robot navigation: State-of-the-art, Current and Future Challenges, Sensors, 18(9), 3170. [https://doi.org/10.3390/s18093170]
• Lin, F., Wang, K., Zhao, Y., Wang, S., (2020), Integrated avoid collision control of autonomous vehicle based on trajectory re-planning and V2V information interaction, Sensors, 20(4), 1079. [https://doi.org/10.3390/s20041079]