자동변속기 스러스트 베어링 동력 손실에 대한 유성기어 세트 설계의 헬릭스 방향과 헬릭스 각의 영향에 관한 연구


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Automatic transmissions, which have the advantages of compact structure and smooth shifting, are installed in various vehicles with engines and hybrid power sources. Research and development are continuously being conducted to improve power and fuel efficiency. In this study, the influence of helix direction and helix angle of the planetary gear set on thrust-bearing power loss in an automatic transmission was analyzed. A sample automatic transmission model was constructed to analyze the axial load and bearing relative rotation speed, which are the main factors in thrust-bearing power loss. The relative rotation speed of the bearing was analyzed using the sample model, and the thrust-bearing load in the axial direction was analyzed according to the helix direction of the planetary gear set constituting the model and the helix angle of the planetary gear set. The power loss occurring in thrust-bearing was derived using the analysis results of relative rotational speed and load, and the influence of the helix direction and helix angle of the planetary gear set was analyzed.
Keywords:
Automatic transmission, Thrust bearing, Planetary gear, Helix angle, Power loss키워드:
자동변속기, 스러스트 베어링, 유성기어, 헬릭스각, 동력 손실1. 서론
컴팩트한 구조와 부드러운 변속의 장점이 있는 자동변속기는 엔진과 하이브리드 동력원을 갖는 다양한 차량에 적용되고 있으며, 동력과 연비 향상을 위하여 많은 연구개발이 지속적으로 추진되고 있다. 성능 개발을 위하여 전기 모터와 제어를 활용하는 전동화 기술이 대거 적용되고 있으나, 자동변속기는 많은 부품이 조립되어 유기적으로 작동하는 만큼 성능 개선을 위하여 연구개발 할 수 있는 요소들이 여전히 존재한다.
자동변속기와 관련하여 구조, 역학, 설계, 시스템 측면 다양한 연구들이 수행되었다. 첫 번째 연구 그룹은 자동변속기에 대한 구조 고안과 분석에 관한 연구를 수행하였다. 자동변속기를 구성하는 유성기어 세트의 주요 회전 요소인 선 기어, 링 기어, 캐리어와 연결 관계를 선과 점으로 구성되는 그래프로 변환하고, 새로운 구조의 고안과 중복 구조, 연결성 분석 등 컨셉 구조에 관한 연구가 수행되었다[1-3]. 유성기어 세트로 구성되는 동력 전달계의 기본적인 성능 분석을 위하여 회전 속도비와 토크비 해석을 위한 레버(Lever) 분석법과 일반화된 행렬 분석법에 관한 연구가 제시되었다[4,5].
역학 관련하여 더블 헬리컬 유성기어 세트에 대한 동적 모델 개발과 기어 전달 오차 가진 응답에 관한 연구[6]가 제시되었으며, 유성기어 세트 적용 동력계에 대한 모드 분석에 관한 연구[7]가 수행되었다. 기어 물림에 의한 기어 치의 변형 관련하여 유한요소법을 활용한 모델링과 경계 조건에 따른 기어 전달 오차 해석 연구 결과가 제시되었다[8].
유성기어 세트로 구성되는 동력 시스템에 관한 설계 연구로는 강도식 기반의 응력 해석을 활용한 유성기어 세트에 대한 설계 연구가 수행되었다[9,10]. 유성기어 시스템의 선 기어, 링 기어, 피니언 기어의 물림 위상과 조립 조건을 고려하고, 기어 물림 단계에서 전달 하중에 의한 응력과 전달 오차 성능을 고려하는 유성기어 세트 설계법에 관한 연구가 제시되었다[11].
시스템 단위의 연구로서 차축에 대한 동력 손실 모델 개발과 검증에 관한 연구[12]와 유성기어 세트로 구성되는 시스템에 대한 동력 효율에 관한 연구[13]가 제시되었다. 본 연구와 관련하여 자동변속기의 스러스트(Thrust) 베어링에 작용하는 축 방향의 하중 해석과 베어링 동력 손실에 관한 연구 결과가 제시되었다[14,15].
자동변속기 혹은 유성기어 세트 적용의 동력계에 관한 다양한 분야의 연구가 수행되었으나 기어의 헬릭스 방향과 헬릭스 각의 기어 설계와 동력 손실의 베어링 성능에 관하여 수행된 연구는 찾기 어렵다. 본 연구는 자동변속기를 구성하는 유성기어 세트의 여러 설계 인자 중에서 기어의 헬릭스 방향과 헬릭스 각의 변화에 따른 스러스트 베어링의 동력 손실을 분석하였다. 본 연구는 연구에 적용되는 스러스트 베어링 동력 손실 모델에 관하여 설명하고, 자동변속기 모델링, 베어링에 작용하는 축 방향 하중 해석, 베어링 동력 손실 해석의 순서로 수행하였다.
2. 스러스트 베어링 동력 손실
유성기어 세트와 유성기어 세트의 주요 회전 요소를 연결하는 샤프트가 단위 부피 당 밀도 높게 배치되는 자동변속기에서 다른 속도로 회전하는 인접 부품의 상대 회전을 가능하게 하고 하중을 지지하는 베어링의 역할은 매우 중요하다. 베어링은 내/외측 레이스와 볼 혹은 니들 형태의 구름체로 구성되며, 레이스와 구름체의 형상과 크기, 재질에 따라 베어링의 성능이 결정된다.
베어링이 회전하는 과정에서 레이스와 구름체 사이의 접촉부에 구름과 미끄러짐의 현상이 발생하며, 이러한 구름과 미끄러짐의 과정에서 발생하는 마찰에 의하여 기계적 동력 손실이 발생한다. 유체역학 측면, 윤활유의 점성과 베어링 구성 요소의 상대 회전 속도에 의한 유체 저항에 따른 유체적 동력 손실도 발생한다. 기계적 및 유체적 동력 손실로 구성되는 베어링의 동력 손실은 작용 하중, 표면 거칠기, 점성, 회전 속도, 온도 등 다양한 인자가 영향을 미치는 복합적인 물리적 현상으로서 시험에 기반한 다양한 연구[16-18]가 수행되었다. 본 연구에서는 실링 등의 상세 조건을 포함하지 않으며 베어링 동력 손실에 대하여 작용 하중과 회전 속도의 주요 인자를 명시적 함수로 고려하는 Harris 모델[18]을 활용하였다.
Harris의 베어링 동력 손실 모델은 하중에 의한 동력 손실(Pl)과 상대 회전에 의한 동력 손실(Ps)로 구성되는 베어링 동력 손실(Pb)의 예측값을 제시한다. 본 연구에 대한 스러스트 베어링의 동력 손실 모델은 다음 식(1)부터 식(3)과 같다.
| (1) |
| (2) |
| (3) |
여기서 Fa, dp, n은 축 방향 하중, 베어링 피치 경(Pitch Diameter), 회전 속도를 의미한다. 윤활 타입과 동점성 계수는 fo와 vo로 표현된다.
3. 자동변속기 모델링
본 연구 목적인 자동변속기 내 스러스트 베어링의 동력 손실에 대한 유성기어 세트 헬릭스 각의 방향과 크기 변화의 영향성 연구 수행을 위하여 베어링 동력 손실의 주요 인자인 베어링에 수직으로 작용하는 하중과 베어링 상대 회전 속도에 대한 해석이 필요하다. 상대 회전 속도는 자동변속기 컨셉 구조에 대한 기구학 해석을 통하여 입력 회전 속도에 대한 주요 회전 요소의 속도와 베어링이 지지하는 상대 회전 요소를 고려하여 계산할 수 있다.
스러스트 베어링에 작용하는 축 방향의 하중은 자동변속기를 구성하는 여러 유성기어 세트 기어 헬릭스 각의 방향과 크기에 따라 주요 회전 요소에서 발생하는 하중 해석을 통하여 확인할 수 있다. 개별 스러스트 베어링은 베어링이 지지하는 회전 요소에 의한 하중뿐만 아니라 인접한 베어링에 작용하는 하중에 의한 영향도 받는다. 따라서, 베어링 스러스트 하중은 전체 동력시스템 모델링을 통하여 해석할 수 있다.
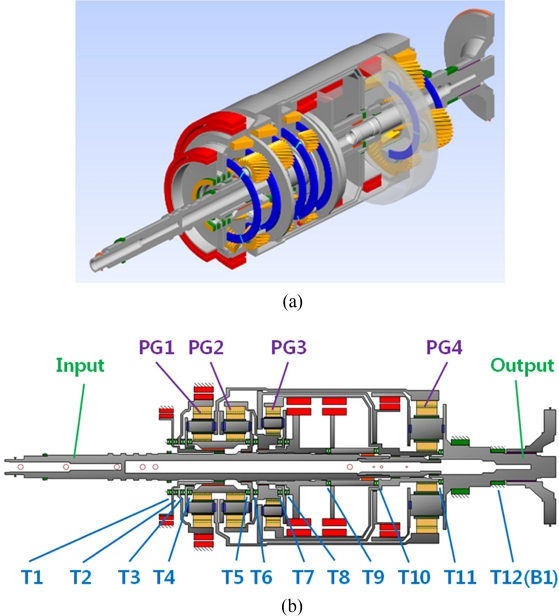
전진 8단과 후진 1단의 변속 성능을 제공하는 유성기어 세트 4개로 구성되는 자동변속기 구조[19]를 본 연구를 위한 샘플 변속기로 선정하였다. 자동변속기를 구성하는 1-3번 유성기어 세트는 Table 1의 제원으로 모델링을 하였으며, 4번 유성기어 세트는 Table 2의 제원 범위를 갖는 5개 유성기어 세트 설계를 적용하여 Fig. 1 과 같이 모델링을 하였다. 각 유성기어 세트의 헬릭스 각 크기 변화가 스러스트 베어링에 작용하는 하중에 영향을 미칠 것이다. 본 연구에서는 출력축과 연결되어 가장 큰 비틀림 토크의 동력을 전달하는 4번 유성기어 세트로 한정하여 모델링과 해석을 수행하였으며, 여러 유성기어 세트 헬릭스 각 변화에 따른 결과는 본 연구를 확장하여 확인할 수 있을 것이다.
동일 혹은 유사한 크기의 4번 유성기어 세트 설계로 한정하여 헬릭스 각 크기 변화에 따른 베어링 동력 손실의 변화를 보기 위하여 기어 잇수(Z), 압력 각(PA), 중심거리(CD)는 동일하나 18-22o 헬릭스 각(HA) 크기로 구성되는 총 5개의 유성기어 세트 설계를 모델링에 적용하였다. 노말(Normal) 모듈(m)의 최대/최소 차이는 0.037 mm이며, 각 기어의 외경(Do)과 루트경(Dr)의 최대/최소 차이는 0.082 mm 이하, 그리고 노말 방향 치 두께(Tooth Thickness, TT)의 최대/최소 차이는 0.001 mm이다. 5개 유성기어 세트는 헬릭스 각을 제외한 나머지 제원이 큰 차이가 없는 거의 동일한 제원이라고 볼 수 있다. 1-4번 유성기어 세트에 포함되는 선 기어, 링 기어, 피니언 기어 치 폭의 크기는 모두 동일하다. TTD (Diameter at Measured Tooth Thickness)는 치 두께가 측정된 위치의 지름을 의미한다.
Fig. 1의 자동변속기 모델에는 축 방향의 하중을 지지하는 스러스트 베어링, 경 방향의 하중을 지지하는 니들 롤러(Needle Roller) 베어링, 축과 경 방향의 하중을 지지하는 볼(Ball) 베어링이 적용된다. 스러스트 베어링에 대하여 축 방향 하중 지지의 컨셉 베어링 모델을 적용하였으며, 니들 롤러 베어링에 대하여 경 방향 하중 지지의 컨셉 베어링 모델을 적용하였다. 축과 경 방향 하중 지지의 볼 베어링은 축과 경 방향에 대한 컨셉 베어링 모델을 적용하였다. Fig. 1(b)에는 축 방향 하중을 받는 베어링만 표시하였으며, 스러스트 베어링은 T1-T11로, 볼 베어링은 B1 혹은 T12로 표시하였다.
유성기어 세트 모델링, 컨셉 베어링 모델 적용, 유성기어 세트의 주요 회전 요소를 연결하는 샤프트 모델링 등을 포함하는 전체 자동변속기에 대한 모델은 구동계 전용의 상용 S/W[20]를 활용하여 구성하였으며, 회전 속도, 하중 등의 시스템 해석을 수행하였다.
4. 해석 결과
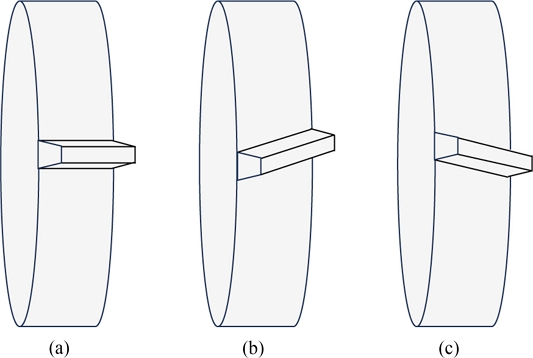
자동변속기를 구성하는 유성기어 세트의 기어 헬릭스 각의 방향과 크기 변화에 따른 스러스트 베어링 동력 손실 해석을 위하여, 헬릭스 각의 방향과 크기 변화에 대한 시스템 해석을 수행해야 한다. Fig. 2(a) 평기어의 물림률 증대 목적으로 기어에 적용하는 헬릭스 각은 Figs. 2(b)와 2(c)와 같이 왼 방향 L (Left) 혹은 오른 방향 R (Right)으로 적용한다. 외접 기어 쌍의 한 기어 헬릭스 각 방향이 L이면 맞물리는 기어의 헬릭스 각은 R 방향이고, 내접 기어 쌍의 내접 기어(링기어) 헬릭스각 방향이 L이면 맞물리는 피니언 기어의 헬릭스 각은 L 방향이다. 유성기어 세트의 선 기어, 링 기어, 피니언 기어는 동시에 맞물려 회전하므로, 한 기어의 헬릭스 방향이 정의되면, 나머지 두 개 기어의 방향은 결정된다. 예를 들어, 선 기어 헬릭스 각 방향이 L이면, 피니언 기어와 링 기어의 방향은 R과 R 방향이 된다. 본 연구에서 유성기어 세트의 헬릭스 방향은 선 기어 기준으로 설명할 것이며, 자동변속기 내 각 유성기어 세트의 헬릭스 방향은 Fig. 1(b)의 유성기어 배치 기준으로 가장 왼쪽부터 오른쪽 순서로 표현한다. 예를 들어, PG1과 PG4의 HA 방향이 R이고 PG2와 PG3의 HA 방향이 L인 배치는 RLLR로 표현한다.
자동변속기 모델의 개별 스러스트 베어링에 가해지는 축 방향의 하중과 베어링 상대 회전 속도 해석을 위하여 입력축에 입력 토크 550 Nm와 회전 속도 2,000 RPM의 동력을 적용하였다. 유성기어 세트 4개 헬릭스 각 방향에 대한 총 16 (= 24) 가지 조합과 4번 유성기어 세트 제원 5개를 고려하여 총 80회 시스템해석을 수행하였다.
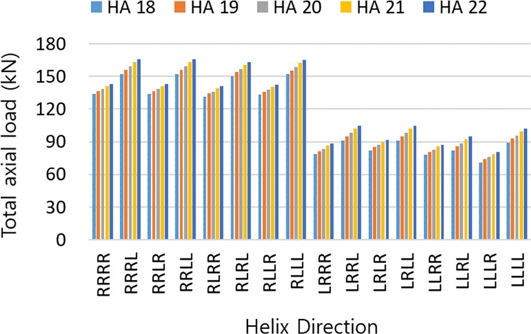
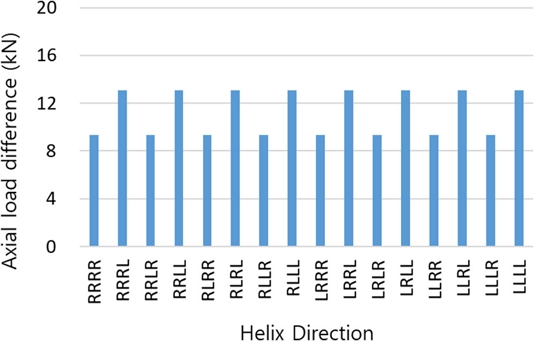
Fig. 3은 기어 헬릭스 각 변화에 따른 전진단에서 개별 스러스트 베어링에 작용하는 최대 수직 하중의 총 합을 보여준다. 구동계 효율에 기여도가 적은 후진단의 결과는 제외하였다. 모든 유성기어 헬릭스 방향 조합에 대하여 헬릭스 각 크기가 증가함에 따라 최대 하중 총합의 크기는 증가한다. PG1이 R 방향으로 시작하는 조합 결과의 평균은 148 kN이며, PG1이 L 방향인 조합 결과의 평균은 89 kN이다. 각 베어링에 작용하는 최대 하중의 총합은 PG1이 R 방향인 조합의 결과가 PG1이 L 방향 조합의 결과보다 큼을 확인할 수 있다. Fig. 4는 HA 18o와 22o에서 발생하는 최대 수직 하중 총합의 차이를 보여준다. 스러스트 베어링 하중 변화에 대하여 본 연구에서 고려하는 PG4의 헬릭스 각 크기의 변화가 PG4의 헬릭스 방향이 R인 경우보다 L일 때 영향성이 더 크게 작용함을 확인할 수 있다. 이는 베어링이 지지하는 회전요소에서 발생하는 수직 하중이 기어 헬릭스 각의 방향에 따라 베어링 혹은 인접 베어링에 작용하는 수직 하중을 증대 혹은 상쇄함에 따른 결과이다. 각 속도단에 대한 베어링 작용하중은 다양한 결과를 보일 것이나, 베어링에 작용하는 최대 수직 하중의 총합 기준으로 본 연구의 샘플 변속기 구조에서는 PG1과 PG4의 헬릭스 각 방향이 베어링 수직 하중에 주요한 영향을 갖는다고 볼 수 있다.
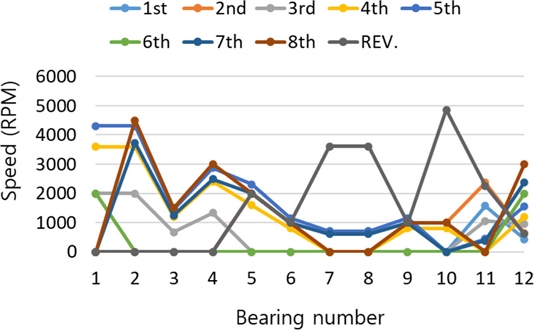
유성기어 세트의 헬릭스 방향과 헬릭스 각 크기 변화에 따른 스러스트 베어링 하중 결과와 Harris의 베어링 동력 손실 모델을 활용하여 해석을 수행하였다. 베어링 지지 부품의 회전에 대한 베어링 상대 회전 속도는 Fig. 5와 같으며, 각 스러스트 베어링의 피치 경 치수는 Table 3과 같다. 베어링 윤활 타입은 윤활유 잠김으로 설정하였으며, 동점성 계수(vo)는 7.1을 적용하였다.
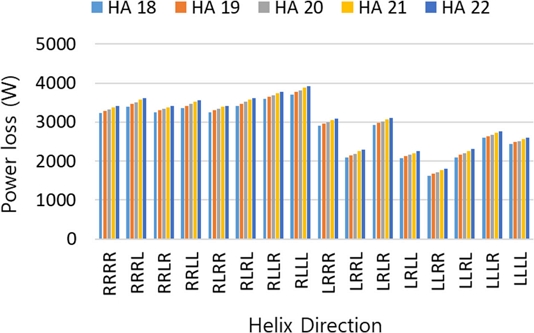
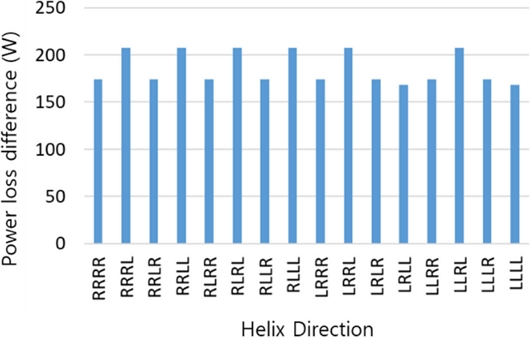
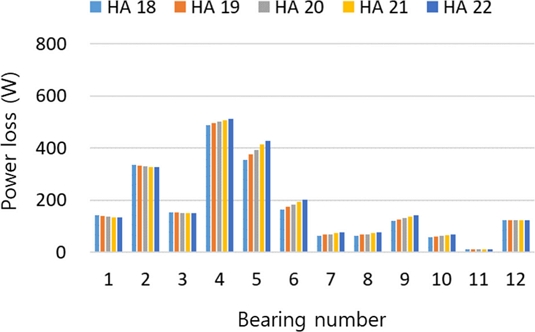
Fig. 6은 헬릭스 각 크기 변화와 헬릭스 방향 조합에 따른 전진단에서 발생하는 스러스트 베어링 동력 손실의 총합 결과를 보여준다. 축 방향 하중 결과의 경향과 두 가지 측면에서 동일한 결과를 확인할 수 있다. 첫 번째는 PG4의 헬릭스 각이 증가함에 따라 스러스트 베어링에서 발생하는 총 동력 손실량의 증가 경향이다. 두 번째는 PG1의 헬릭스가 R 방향인 그룹과 L 방향인 그룹의 결과이다. 스러스트 베어링 총 동력 손실 측면 R 방향 그룹의 결과가 L 방향 그룹의 결과보다 큼을 확인할 수 있다. Fig. 7은 HA 18o와 22o에서 발생하는 동력 손실 총합의 차이를 확인할 수 있다. LRLL과 LLLL 조합을 제외하고, PG4의 헬릭스 방향이 L인 조합의 결과가 R인 조합의 결과 대비 큰 차이를 보여준다. Fig. 6의 다양한 동력 손실 결과는 유성기어 세트의 헬릭스 방향 조합에 따른 각 전진 변속단 별다르게 작용하는 하중과 상대 회전 속도를 고려한 결과이다. 이 결과로부터 스러스트 베어링에 대한 수직 하중이 크게 발생하는 헬릭스 방향 조합에서 동력 손실이 크게 발생하는 경향을 찾을 수 있으며, 스러스트 베어링 동력 손실에 대하여 베어링 수직 하중을 증대 혹은 상쇄하는 기어 헬릭스 방향을 고려해야 함을 확인할 수 있다.
16개의 유성기어 세트 헬릭스 방향 조합 중 LRLL과 LLLL 조합을 제외한 나머지 조합의 결과는 RRLL 조합의 결과(Figs. 8과 9)처럼 PG4 헬릭스 각이 증가함에 따라 영향을 받는 스러스트 베어링 최대 하중은 증가하며 동력 손실량도 증가함을 확인할 수 있다. 헬릭스 각의 크기가 증가할수록 헬리컬 기어의 물림과정에서 발생하는 축 방향의 하중은 증가하고, 이에 따라 베어링에 작용하는 스러스트 하중의 증가와 함께 동력 손실도 증가한다.
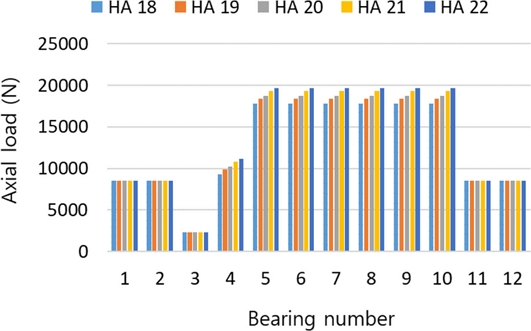
Max. axial loads acting on thrust bearings of RRLL helix angle directions for 18-22 degree of helix angles of PG4
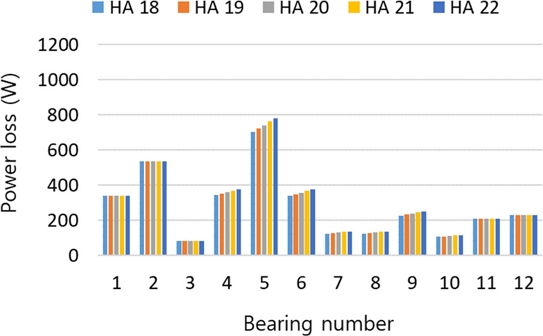
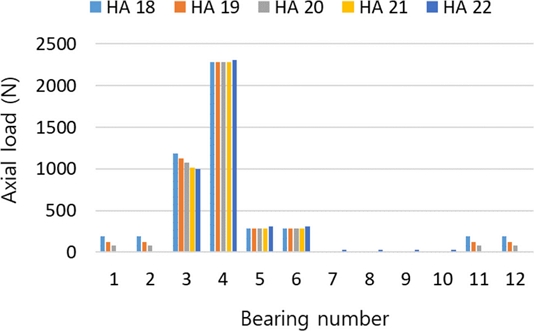
LRLL 조합에 대한 각 속도단 별 베어링 하중과 동력 손실 결과는 Fig. 10과 11과 같다. PG4의 헬릭스 각 증가에 따라 4-10번 베어링의 하중과 동력 손실은 증가하나, 베어링 1-3번의 동력 손실은 감소함을 확인할 수 있다. 베어링 11-12번도 동력 손실량이 감소하나 그 크기는 베어링 1-3번 감소량 대비 절반 이하 수준이다. Fig. 12는 유성기어 헬릭스 방향 조합 LRLL의 HA 22o에서 발생하는 베어링별 전진단 동력 손실 합에서 HA 18o의 동력 손실 합을 뺀 결과를 보여준다. 이러한 결과는 동력 손실의 주요 인자인 각 변속단별 베어링에 작용하는 하중 결과(Fig. 13)를 통하여 분석할 수 있다. Fig. 13의 축 방향 하중 결과를 보면 전진 5단을 제외한 모든 단에서 헬릭스 각이 증가할수록 축 하중도 증가하나, 5단에서는 감소한다. 이러한 경향은 5단의 결과인 Fig. 14에서 베어링 1/2/3/11/12번에 작용하는 하중이 감소함을 확인할 수 있다. 이는 PG4의 헬릭스 각 크기 증가에 따라 증가하는 스러스트 하중이 베어링 인접 부품에서 발생하는 하중을 상쇄하여 나타나는 결과이다. 스러스트 하중 감소의 크기가 비슷한 베어링 1-3번과 11-12번의 동력 손실 차이(Fig. 12)는 베어링 피치 경의 차이에 기인한다.
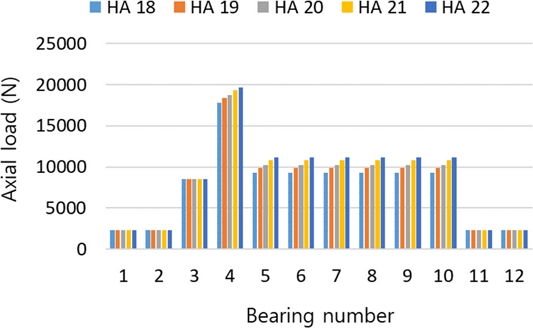
Max. axial loads acting on thrust bearings of LRLL helix angle directions for 18-22 degree of helix angles of PG4
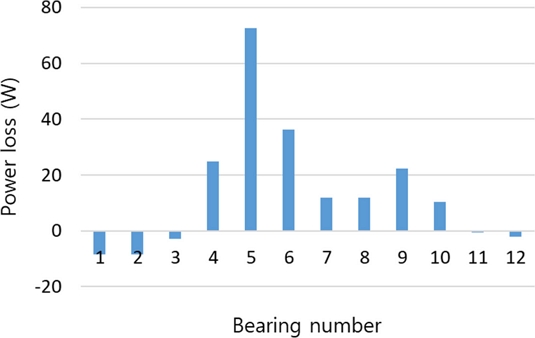
Differences of thrust bearing power losses at 18 and 22 degree of helix angle for forward speed ratios
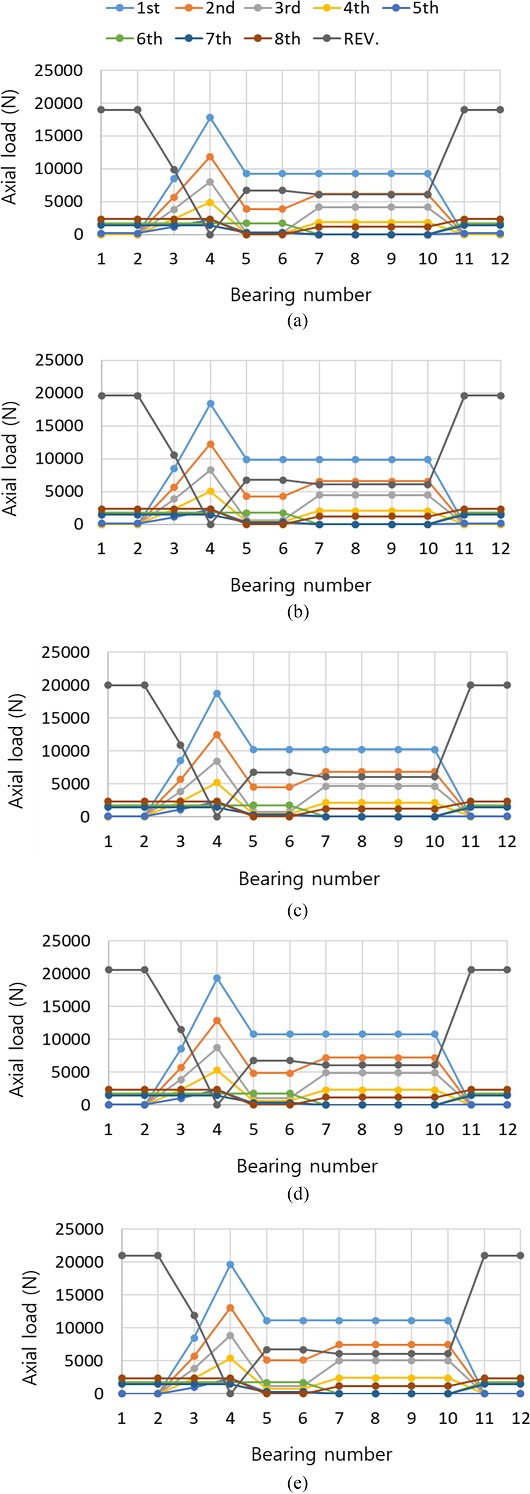
Thrust loads of LRLL helix directions for (a) 18, (b) 19, (c) 20, (d) 21, and (e) 22 degree of helix angles of PG4
5. 결론
본 연구에서는 자동변속기 스러스트 베어링 동력 손실에 대한 유성기어 세트의 헬릭스 방향과 헬릭스 각의 영향성을 분석하였다. 스러스트 베어링 동력 손실의 주요 인자인 축 방향 하중과 베어링 상대 회전 속도 해석을 위하여 샘플 자동변속기 모델링을 구성하였다. 샘플 모델을 활용하여 베어링 상대 회전 속도를 해석하고, 모델을 구성하는 유성기어 세트의 헬릭스 방향과 4번 유성기어 세트의 헬릭스 각 변화에 따른 축 방향의 스러스트 베어링 하중을 해석하였다. 상대 회전 속도와 하중에 대한 해석 결과를 활용하여 스러스트 베어링에서 발생하는 동력 손실 결과를 도출하고 유성기어 세트의 헬릭스 방향과 헬릭스 각의 영향성을 분석하였다.
자동변속기를 구성하는 유성기어 세트의 헬릭스 방향 조합에 따라 주요 회전 요소에서 발생하는 축 방향 하중의 방향은 변화하며, 스러스트 베어링 지지부와 인접하는 부품의 하중 방향의 변화에 따라 베어링에 수직으로 작용하는 하중의 크기는 증가 혹은 상쇄된다. 헬릭스 방향 조합에 따라 변화하는 베어링 수직 하중에 의하여 베어링 동력 손실량도 변화한다. 유성기어 세트의 헬릭스 방향 조합에 대하여 한 유성기어 세트의 헬릭스 각 크기가 증가할수록 베어링 동력 손실의 크기도 증가함을 확인하였다. 일부의 경우에서 헬릭스 각 증가에 따라 스러스트 하중이 상쇄되어 동력 손실이 감소하는 베어링이 발견되었다.
다음의 결과는 본 연구에서 활용한 샘플 자동변속기 구조에 관한 결과로 한정할 수 있으나, 연구의 내용과 결과를 다른 자동변속기 혹은 유성기어 적용 구조의 베어링 동력 손실 분석에 활용할 수 있을 것이다.
1) 모든 유성기어 헬릭스 방향 조합에 대하여 헬릭스 각 크기가 증가함에 따라 스러스트 베어링에 작용하는 최대 하중 총합의 크기는 증가한다.
2) 각 베어링에 작용하는 최대 하중의 총합은 PG1이 R 방향인 조합의 결과가 PG1이 L 방향 조합의 결과보다 크며, PG4의 헬릭스 각 크기의 변화가 PG4의 헬릭스 방향이 R인 경우보다 L일 때 영향성이 더 크게 작용한다.
3) PG4의 헬릭스 각이 증가함에 따라 스러스트 베어링에서 발생하는 동력 손실량은 증가하며, PG1의 헬릭스 방향이 R 방향인 그룹의 결과가 L 방향 그룹의 결과보다 크다.
4) LRLL과 LLLL 조합을 제외하고, PG4의 헬릭스 방향이 L인 조합의 결과가 R인 조합의 결과 대비 큰 차이를 보여준다.
5) LRLL과 LLLL 조합을 제외한 나머지 조합의 결과는 RRLL 조합의 결과처럼 PG4 헬릭스 각이 증가함에 따라 영향을 받는 스러스트 베어링 최대 하중은 증가하며 동력 손실량도 증가한다.
6) LRLL 조합에 대한 각 속도단 별 베어링 하중과 동력 손실 결과는 PG4의 헬릭스 각 증가에 따라 4-10번 베어링의 하중과 동력 손실은 증가하나, 베어링 1-3번의 동력 손실은 감소한다.
REFERENCES
-
Hsu, C. H., Wu, Y. C., (1997), Automatic detection of embedded structure in planetary gear trains, Journal of Mechanical Design, 119(2), 315-318.
[https://doi.org/10.1115/1.2826253]

-
Hsu, C.-H., Lam, K.-T., (1993), Automatic analysis of kinematic structure of planetary gear trains, Journal of Mechanical Design, 115(3), 631-638.
[https://doi.org/10.1115/1.2919237]

-
Kwon, H. S., Kahraman, A., (2016), An assemblability check methodology for the kinematic configurations of automatic transmission planetary gear trains, Journal of Mechanical Science and Technology, 30, 5605-5616.
[https://doi.org/10.1007/s12206-016-1129-y]

-
Raghavan, M., (2010), The analysis of planetary gear trains, Journal of Mechanisms and Robotics, 2(2), 021005.
[https://doi.org/10.1115/1.4001092]

-
Kahraman, A., Ligata, H., Kienzle, K., Zini, D. M., (2005), A kinematics and power flow analysis methodology for automatic transmission planetary gear trains, Journal of Mechanical Design, 126(6), 1071-1081.
[https://doi.org/10.1115/1.1814388]

-
Sondkar, P., Kahraman, A, (2013), A dynamic model of a double-helical planetary gear set, Mechanism and Machine Theory, 70, 157-174.
[https://doi.org/10.1016/j.mechmachtheory.2013.07.005]

-
Kahraman, A., (1994), Natural modes of planetary gear trains, Journal of Sound and Vibration, 173(1), 125-130.
[https://doi.org/10.1006/jsvi.1994.1222]

-
Kim, J., Sohn, J., Kim, M.-G., Lee, G., Kim, S., (2023), Analysis of the transmission error of spur gears depending on the finite element analysis condition, Journal of the Computational Structural Engineering Institute of Korea, 36(2), 121-130.
[https://doi.org/10.7734/COSEIK.2023.36.2.121]

-
Kim, J. G., Park, Y. J., Lee, G. H., Nam, Y. Y., Yang, W. Y., (2014), Optimum design of pitch reducer for wind turbine using genetic algorithm, Transactions of the Korean Society of Mechanical Engineers A, 38(2), 185-192.
[https://doi.org/10.3795/KSME-A.2014.38.2.185]

- Nam, S. J., Bae, M. H., Cho, Y. S., (2022), Strength evaluation of complex planetary gear train of traveling reducer for 1.7-ton grade small excavator, Tribology and Lubricants, 38(1), 22-26.
-
Kwon, H. S., Kahraman, A., Lee, H. K., Suh, H. S., (2014), An automated design search for single and double-planet planetary gear sets, Journal of Mechanical Design, 136(6), 061004.
[https://doi.org/10.1115/1.4026871]

-
Talbot, D., Kahraman, A., Li, S., Singh, A., Xu, H., (2016), Development and validation of an automotive axle power loss model, Tribology Transactions, 59(4), 707-719.
[https://doi.org/10.1080/10402004.2015.1110862]

-
Del Castillo, J. M., (2002), The analytical expression of the efficiency of planetary gear trains, Mechanism and Machine Theory, 37(2), 197-214.
[https://doi.org/10.1016/S0094-114X(01)00077-5]

-
Kwon, H. S., (2021), A study of effects of the helical angle directions of planetary gear sets on the axial forces on thrust bearings in an automatic transmission, Journal of Korean Society of Manufacturing Process Engineers, 20(3), 92-99.
[https://doi.org/10.14775/ksmpe.2021.20.03.092]

-
Kwon, H. S., (2021), Investigation of the influences of thrust loads resulted by helix angle directions of planetary gear sets on bearing power losses in automotive planetary gear trains, Applied Science, 11(19), 8827.
[https://doi.org/10.3390/app11198827]

- ISO 14179-1, (2001), Gear thermal capacity - part 1: rating gears drives with thermal equilibrium at 95oC sump temperature.
- SKF GROUP, Bearing friction, power loss and starting torque. https://www.skf.com/africa/en/products/rolling-bearings/principles-of-rolling-bearing-selection/bearing-selection-process/operating-temperature-and-speed/bearing-friction-power-loss-and-starting-torque
-
Harris, T. A., Kotzalas, M. N., (2007), Rolling bearing analysis: essential concepts of bearing technology, Taylor and Francis Group.
[https://doi.org/10.1201/9781420006582]

-
Dick, A., Greiner, J., Locher, A., Jauch, F., (2013), Optimization potential for a state of the art 8-speed AT, SAE International Journal of Passenger Cars-Mechanical Systems, 6(2), 899-907.
[https://doi.org/10.4271/2013-01-1272]

- MASTA 12, MASTA13. https://www.smartmt.com/software/masta

Assistant professor in the Department of Automotive Engineering, Dong-eui University. His research interest includes gear mechanics/dynamics, transmission modeling/analysis.
E-mail: hskwon@deu.ac.kr