Study on Thermo-mechanical Modeling and Analysis of High-speed Angular Contact Ball Bearings Under Oil-jet Lubrication
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents an integrated thermo-mechanical model for analyzing angular contact ball bearings (ACBBs) operating under oil-jet lubrication. The proposed approach enables a comprehensive analysis of both the mechanical and thermal behavior of the ACBB system. The proposed formulation employs a quasi-static approach to accurately calculate contact loads and heat generation, taking into careful consideration variations in internal clearance resulting from factors such as surface pressure, centrifugal forces, and thermal expansion. For the thermal analysis, a refined thermal network model is utilized. The proposed thermal model incorporates a newly derived correlation for the drag coefficient under oil-jet lubrication, which is obtained through high-fidelity computational fluid dynamics simulations. The validity of the proposed model is confirmed through comparison with experimental data. Furthermore, extensive simulations are conducted to investigate the impact of bearing fit-up and thermal variations on the performance of ACBBs.
Keywords:
Angular contact ball bearings, Quasi-static model, Internal diametral clearance, Thermal network model, Oil-jet lubrication키워드:
각접촉 볼베어링, 준정적모델, 내부직경틈새, 열네트워크 모델, 오일젯 윤활1. Introduction
High-speed rotating machines are versatile components in numerous critical industries, spanning power generation and oil and gas to process plants and aviation [1-3]. Angular contact ball bearings (ACBBs) are found in diverse high-speed rotating machines. In gas turbine engines, high-speed ACBBs and roller bearings are prevalent in the shaft and gearbox pinion shafts. Notably, the axial load-carrying ball bearing plays a critical role within an aircraft gas turbine [4-6]. Due to the combined loadings, each ball in ACBBs has a unique loading and speed. Moreover, it is common for the shaft to rotate at a very high speed where the centrifugal forces and gyroscopic moments are significantly large relative to the loads applied to the balls. The dynamic characteristics of the high-speed machines can also be affected by several important factors, including the fitting between the shaft and inner ring, the fitting between the housing and outer ring, and changes in temperature caused by the heat generated in an ACBB.
Numerous researchers have focused their efforts on shaft-bearing systems, with particular emphasis on the performance of rolling-element bearings [7-10]. Zaretsky [7] investigated the feasibility of ceramic bearings in gas turbines, while Glockner et al. [8] conducted experimental research on hybrid ceramic and actively cooled ball bearings in the same context. Despite the abundance of studies on shaft-bearing systems, the thermo-mechanical performance of ACBBs under oil-jet lubrication remains largely unexplored. Given that ACBBs operating under oil-jet lubrication typically run at high speeds, significant heat generation and elevated temperatures within the system are expected. Consequently, thermal effects emerge as crucial factors influencing bearing characteristics, as temperature fluctuations alter the interaction between balls and races, as well as their material and fluid properties. Thus, operating temperature plays a pivotal role in the overall performance of the entire spindle-bearing system [11-13].
Besides the excessive heat generated in the high-speed region, the adjustment of internal clearance in ACBBs significantly influences the system's performance. When installing bearings, an appropriate level of interference fit should be applied to prevent any relative motion between the inner ring and the shaft, as well as between the outer ring and the housing. However, excessive interference during installation can lead to detrimental side effects. To accurately assess the change in internal clearance in ACBBs, it is essential to analyze the operational fits between the shaft and housing, the effects of temperature changes, the radial expansion induced by ring rotation, and the radial components of the contact loads between the balls and the races [14-19].
This study aims to develop an integrated thermo-mechanical model for predicting the characteristics of ACBBs operating under oil-jet lubrication. A numerical model is introduced to analyze both the mechanical and thermal characteristics inherent in the system. A quasi-static methodology [20,21] computes the contact loads and heat generation. Additionally, a fit-up model improved from the existing models [14-17] is proposed to consider the impact of inner ring to shaft, and outer ring to housing fittings, contact loads, surface pressures of rings, centrifugal expansion of rings, and temperature gradients, thereby calculating changes in diametral clearance of ACBB. The thermal behavior within the system is accurately captured using an advanced thermal network model (TNM) [22].
The proposed model is enhanced by a newly formulated correlation for the drag coefficient, derived from computational fluid dynamics (CFD) simulations. Heat generation is computed using a running torque-based model [21,23-29], which incorporates friction sources from sliding, rolling, and viscous drag. Moreover, one of the essential parameters for thermal analysis, the actual flow rate of the oil injected into the bearing cavity [22,30-32], is also included. Validation of the thermo-mechanical model is achieved by comparing the simulated temperature results with experimental data. In addition, rigorous simulations are conducted to investigate expansions of the bearing components, contact loads, stiffness, and heat generation.
2. Thermo-mechanical Model for ACBB
2.1 The Quasi-static Model of Bearing
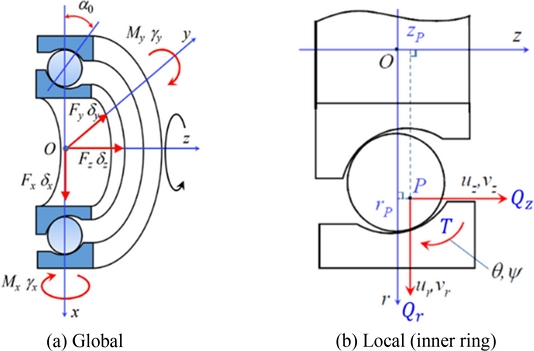
The ACBB model used in this study is based on the quasi-static model of ball bearings [20,21]. The effects of centrifugal forces and gyroscopic moments are included. Fig. 1(a) shows the five-degrees-of-freedom (DOF) model of an ACBB with external loads and corresponding inner ring displacement, respectively.
| (1) |
| (2) |
In the figure, α0 denotes to the nominal contact angle of the ACBB.
Fig. 1(b) shows the cross-section of ACBB with local coordinates. Here, the inner ring and ball displacements are indicated, respectively, by
| (3) |
| (4) |
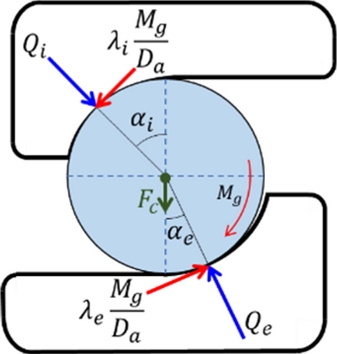
Fig. 2 shows the free-body diagram of a ball where the ball equilibrium equations can be established [20]. αi, αe represent the operating inner and outer contact angles. Da is the ball diameter. λi, λe indicate the traction coefficients for the gyroscopic moment which are set to λi = 0, and λe = 2 for outer raceway control [11]. Fc, Mg are the centrifugal force and gyroscopic moment. ωm, ωR, β denote the ball orbital speed, and ball rotational speed in rad/s, and the pitch angle of the ball [21]. By solving the ball equilibrium equations, the ball displacement vector in Eq. (4) can be estimated. The inner ring force equilibrium can be written as
| (5) |
where the inner ring contact load at the i-th ball is defined as
| (6) |
and [Rϕ] is the transformation matrix from local frame to global frame [15]. The contact loads between the ball and races can be calculated using Herzian contact theory as
| (7) |
| (8) |
where Ki, Ke denote the contact stiffness constants between the ball and inner race, and the ball and outer race, respectively. δi, δe represent the contact compression between the ball and races. If any one of these compressions becomes negative, the contact compression is assumed to be zero.
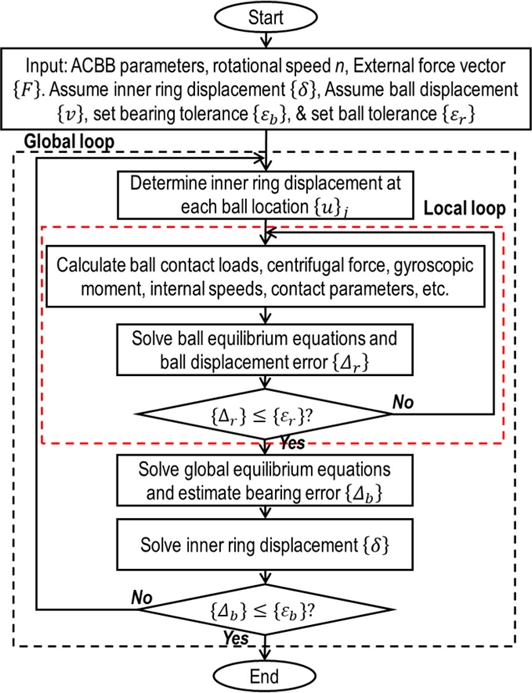
This study implements a constant force preloading condition, which treats the external loads as inputs, while the displacement vector of the inner ring is the unknown variable to be determined. To calculate the displacement vector for an ACBB, it is imperative to consider the force equilibrium between the balls and the inner ring. Due to nonlinearity of these equations, an iterative approach is necessary to solve the equilibrium equations. The calculation methodology for the entire model is depicted in Fig. 3, which relies on the iterative Newton–Raphson method. The calculation procedure encompasses iterative loops for the global equilibrium equations of the inner ring and for the equilibrium equations of each ball. Upon achieving global equilibrium solution, the contact forces and angles between the balls and races are estimated for subsequent calculations of running torque and heat generation.
2.2 The Fit-up Model
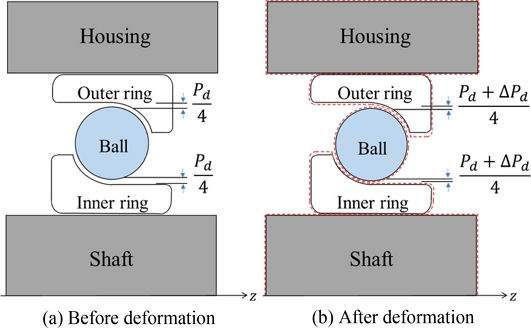
When an ACBB is mounted to a shaft, the internal diametral clearance (Pd) may change due to ball-race contact loads, fit-up condition between the shaft and inner ring and housing and outer ring, centrifugal expansions of rotating rings, and temperature changes [14-17] as shown conceptually in Fig. 4. The estimation of the change of diametral clearance of an ACBB is performed based on the thick-ring theory [16,19].
The estimation of diametral clearance change comes with estimating the total deformation of the bearing inner ring, outer ring, and the balls. The changes in bearing geometry are calculated by combining the diametral displacements from each race and the change of diametral displacement from the ball. The total diametral deformation (uTOT) is the combination of the deformation due to surface pressures (uSP), centrifugal expansions of rotating rings (uCE), and temperature change (uTC) as outlined in Eq. (9):
| (9) |
Therefore, the change in diametral clearance is given by
| (10) |
Here IR, OR denote as the inner ring and outer ring, respectively. With a new diametral clearance, the internal geometry of ACBB will change and causes changes in contact loads and heat generation.
The deformation due to surface pressures (uSP) is observed in cold to hot mounted fittings and from the ball-race contact loads. In a thick-walled cylinder scenario, this deformation manifests when the cylinder with uniform wall thickness is exposed to evenly distributed internal and external pressures. Such deformation is symmetrical along the axis of the cylinder and is presumed not to impact its length [14]. Importantly, this deformation sums up the effect of pressures stemming from ball-race contact loads and the fittings of bearings to shafts and housings.
The deformation due to centrifugal expansion (uCE) is associated with rotating rings originates from the centrifugal expansion effect observed in rotating shaft and ACBB inner ring. This phenomenon is primarily due to the centrifugal force generated as the inner ring and shaft operate at high velocities, which softens some of the compressive stress induced by interference fits. Thus, this reduction in compressive stress leads to a decrease in the inner ring-to-shaft contact stress, with the rate of reduction accelerating as the rotational speed increases [17]. Such a dynamic property can cause the inner ring-to-shaft operating fit to transit from a tight to a loose state, potentially resulting in fretting wear, increased shaft vibration, and rotor eccentricity [15].
The deformation due to temperature variations (uTC) is a result of changes from ambient to operating temperatures within the inner ring, outer ring, and balls. This temperature change induces linear expansion, altering the components’ diameter and affecting the diametral clearance of the ACBB. To accurately predict the operating temperatures within ACBBs, a TNM is utilized, as elaborated in section 2.4. This methodology enables precise estimations of temperature-induced dimensional alterations, critical for evaluating their influence on ACBB performance.
2.3 Heat Generation Model
The heat generation in ACBB is obtained from the ACBBs’ running torque-based model on the friction sources presented by SKF [23], in which the friction torque of ACBB with respect to bearing axis comprises three components: sliding friction torque (Msl), rolling friction torque (Mrr), and viscous drag friction torque (Mν). In this study, the friction coming from any interactions in cage and seal is not considered.
The distribution of heat generation on the inner race and outer race can be calculated as
| (11) |
| (12) |
After calculating the rates of heat due to friction torque, it is possible to determine the bearing temperatures using a TNM. In this analysis, the contact parameters of the most heavily loaded ball are considered, and the heat generations for each race represent the average heat generation of that specific race.
Sliding friction torque (Msl) is characterized by two primary sources: macro sliding and micro-sliding. Macro sliding stems from the conformity of contact influenced by the macro-geometrical features of the components and spinning motion inherent in their operation. Micro-sliding, on the other hand, results from the geometrical distortions that occur due to elastic deformation between the ball and races [23]. The sliding friction torque is defined as the combination of torque from spinning friction [21,25-29] and the differential sliding frictions [25,28,29] that occur within the ball-race contacts of ACBBs. It is noted that under high-speed operational conditions, the sliding friction is prone to increase.
Rolling friction losses are a constant factor in rolling contacts, regardless of whether they are dry or lubricated [23]. The origins of rolling friction torque (Mrr) can be traced back to two main factors: the effects of elastohydrodynamic lubrication (EHL) between the balls and races [21,23,25], and elastic hysteresis losses within the materials [23,29]. These factors contribute to the creation of rolling resistance that acts to resist motion between the balls and races. Rolling friction torque has the unique characteristic of potentially decreasing at higher speeds. This decrease is particularly noticeable at very high rotational speeds, where increased temperatures can alter the behavior of the lubricant within the bearing. These changes may lead to phenomena such as inlet shearing, caused by oil reverse flow, and lubrication starvation [23]. Both conditions can significantly reduce the rolling resistance in ball-race contacts.
This study develops a viscous drag friction torque (Mv) model designed for ACBB under oil-jet lubrication conditions. In such a bearing system, lubricated with a mixture of lubricant and air, balls travel in an orbital path around the bearing's axis, navigating through the lubricant-filled space. This motion necessitates overcoming the viscous drag force (Fν) generated by the lubricant, which becomes significant at very high speeds [25,31]. However, estimating viscous friction for ACBBs under oil-jet lubrication presents analytical challenges, primarily due to the difficulty in precisely determining the lubricant volume within the bearing cavity. Crucial factors such as the oil density and viscous drag coefficient are highly sensitive to variations in this volume. In this study, the effective density of the lubricant is deduced by calculating the lubricant cavity ratio [32], and the viscous drag friction coefficient is derived from a sequence of CFD simulations.
2.4 Thermal Network Model (TNM)
The TNM is a representative method used to analyze the temperature distribution of thermal systems, consisting of a series of nodes and resistances, similar to an electrical circuit network.
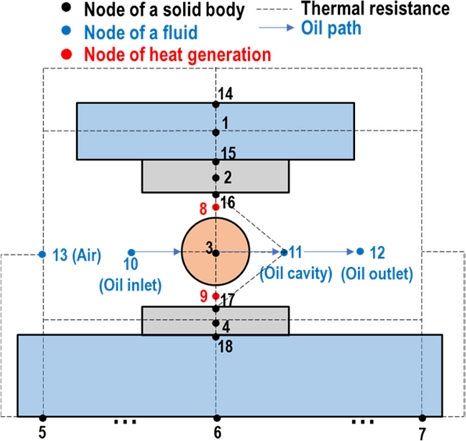
Each node represents a specific component of the system, and a node's temperature represents the temperature associated with its component. Nodes are connected to their neighboring nodes through thermal resistances, and heat transfer occurs in proportion to the temperature difference between two adjacent nodes and in inverse proportion to their thermal resistance (). In this study, the nodes on the surface as well as the center of system components were defined. Fig. 5 and Table 1 show the locations and the detailed information of the nodes, respectively.
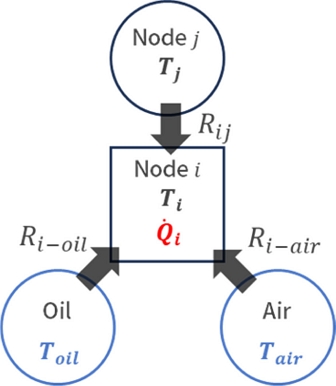
Governing equations need to be established to predict the temperature at each node. This study focuses on the steady-state bearing temperature during normal operation. The governing equation for each node can be determined from the energy balance, as shown in Fig. 6. The following is the energy equation for node i:
| (13) |
| (14) |
Here, the subscripts i and j are node indices, and the subscripts air and oil denote ambient air and lubricant oil, respectively. Nb is the number of neighboring nodes of node i. Rij, Ri−air, and Ri−oil represent the thermal resistances between node i and node j, between node i and air, and between node i and oil, respectively.
Eq. (13) indicates that the sum of all heat transferred to node i and the heat generated at node i becomes zero when steady state is achieved. Each term represents, in order, heat transfer from node j, heat transfer from air, and heat transfer from oil. Eq. (13) can be rewritten as Eq. (14), where the temperatures Ti and Tj are placed on the left-hand side, and the remaining terms corresponding to source terms are on the right-hand side. By solving these equations, the temperatures of the bearing components can be obtained.
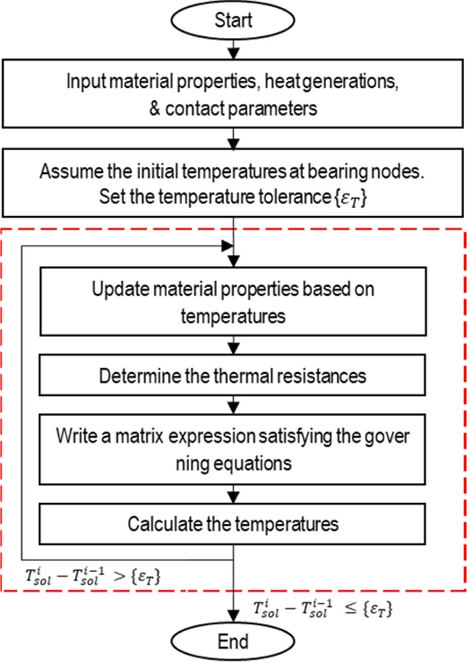
The heat generated in a bearing is transferred to the bearing parts such as ball, inner ring, outer ring, shaft, and housing, and eventually transferred to surrounding air and lubricant oil. During this process, conductive and convective heat transfer occurs, in the solid structure and at fluid-solid interfaces, respectively. The conductive heat transfer rate is affected by contact conditions. Therefore, thermal resistances can be classified into conductive resistance, convective resistance, and contact resistance, based on the heat transfer mechanism. The formulas for calculating thermal resistances can be found in the literature on thermal network [30,32]. The process of predicting the temperature of a bearing system using a TNM is shown in Fig. 7.
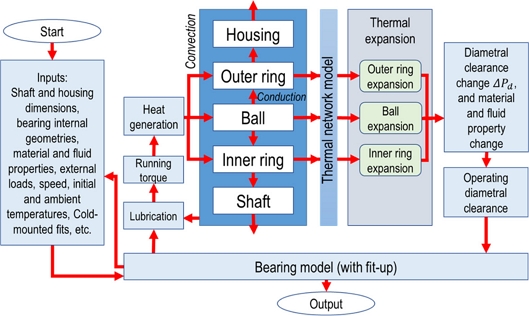
2.5 Calculation Procedure for Integrated Model
The procedure for integrating the quasi-static model with the TNM is delineated in Fig. 8. It commences with gathering requisite inputs, encompassing dimensions of the bearing, shaft, and housing, external loads, rotational speed, oil properties, oil flow rate for oil jet lubrication, initial temperatures of the bearing and oil, and fit conditions between the shaft-inner ring and housing-outer ring. Subsequently, the bearing model, incorporating fit-up conditions, computes the heat generated by the inner and outer races. Following this, the TNM computes the temperature of system components. As bearings expand, alterations in ACBB clearance, material properties, and fluid properties occur, modifying the ACBB’s characteristics. These modifications are then fed-back into the ACBB model and the TNM for subsequent iterations of results. The process iterates until achieving the desired accuracy in calculations.
3. Experiments and Model Validation
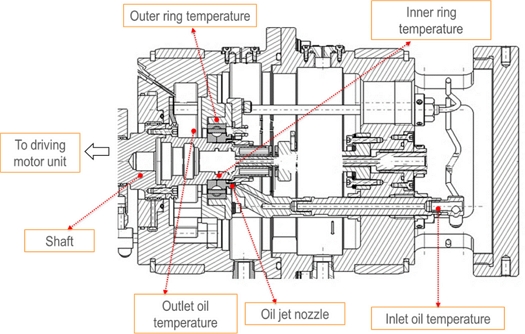
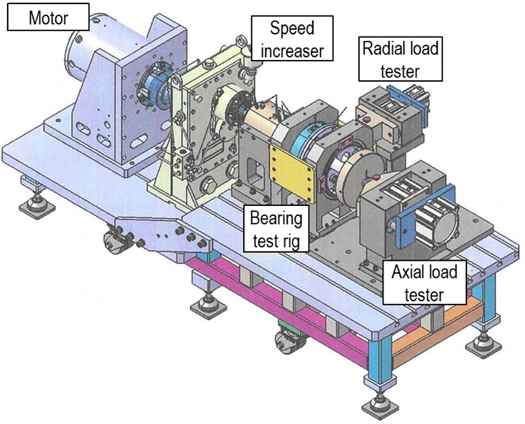
This study considers a rotor-ACBB assembly, comprising a 40-mm bore ACBB with ceramic balls, affixed to a shaft with an outer diameter of 40 mm. The assembly is encased within a housing with an 80-mm inner diameter and a 250-mm outer diameter. The housing, shaft, and bearing ring materials have identical material properties. Lubrication for the ACBB is facilitated through an oil-jet system employing MIL-L-23669 lubricant. The ambient temperature is set at Tamb = 25oC. A diametral interference fit of 0.02 mm is applied between the shaft and ACBB inner ring, while the fit between the housing and ACBB outer ring is set to 0 mm. Fig. 9 shows the schematic drawing of the bearing test rig, in which the sensor locations are also indicated. Fig. 10 depicts the experimental setup along with its peripherals. The outcomes from simulations are compared with experimental results, under the operating conditions as detailed in Table 2.
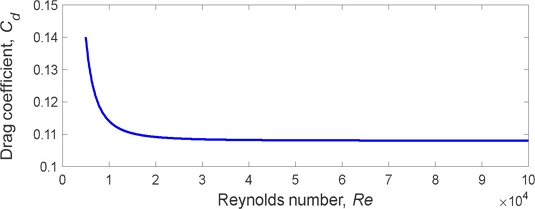
The drag coefficients for the ACBB were determined through CFD simulation. Fig. 11 illustrates the simulated drag coefficient plotted against Reynolds numbers, exhibiting an asymptotic approach to 0.108 at high Reynolds numbers. Notably, this drag coefficient is small compared to the typical value of approximately 0.45 for an isolated sphere [30]. However, it closely aligns with the value of 0.09 proposed by Pouly et al. [32], derived from measurements of drag on in-line multiple spheres. The reduced drag coefficient can be attributed to the periodic arrangement of multiple balls in close proximity. This established drag coefficient was then employed in the heat generation analysis within the ACBB, a critical factor for predicting bearing temperature using the TNM. The findings from the heat generation analysis under the specified experimental conditions are succinctly presented in Table 3.
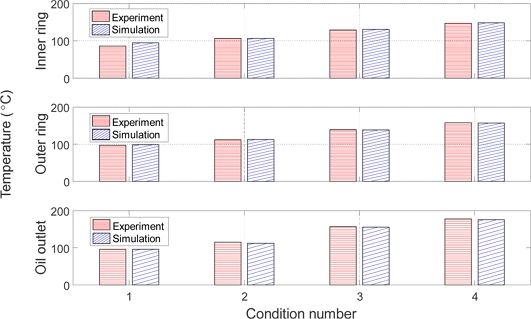
Fig. 12 presents a comparison between bearing temperatures obtained from simulation and experimentation. Notably, the temperatures of the inner ring, outer ring, and outlet oil were specifically chosen for simulation to correspond with the experimental configuration, which employs thermocouples for temperature measurements at the designated locations. Each graph illustrates a temperature increase corresponding to escalating speeds. The simulation data is depicted by blue bars, while the experimental data is represented by red bars. The close agreement between the simulated and experimental data confirms the model's accuracy in predicting behavior at varying speeds. The maximum discrepancy of |ΔT| = 8.72oC is observed in the inner ring temperature at 10,084 RPM in Fig. 11. This discrepancy may be attributed to factors such as the limited accuracy of thermal resistance models and the limitations of obtaining precise measurements at the designated locations.
4. Simulation and Discussion
This section presents simulation results with experimental condition 4 specified in Table 4. The effect of diametral clearance on contact loads, stiffnesses, and heat generation are rigorously discussed below.
4.1 Change of Diametral Clearance in ACBB
Table 4 displays tabulated results on the changes in the components of the investigated ACBB. Three scenarios are examined: a) without fit-up and TNM, focusing solely on a basic ACBB model that ignores all fit-up conditions and temperature changes. b) with fit-up but without TNM, adding the effects of tightly fitting parts together but keeping temperatures of the bearing parts at ambient level, and oil at given conditions. c) with both fit-up and TNM, integrating all models.
The comparison across these scenarios shows significant variations in diametral clearance of ACBB. Without any fit-up or TNM, the clearance remains unchanged. When fit-up is applied, the clearance tends to decrease because the inner ring is more affected by the combined effects of deformation from surface pressures and centrifugal expansion than the outer ring, which is mainly altered by surface pressure alone. The final scenario, which combines fit-up and TNM, results in greater expansion of all bearing components due to heating. This outcome is believed to reflect real-world behavior more precisely, underscoring the importance of accounting for both fit-up adjustments and operating temperature considerations to estimate ACBB characteristics.
4.2 Change of Contact Loads
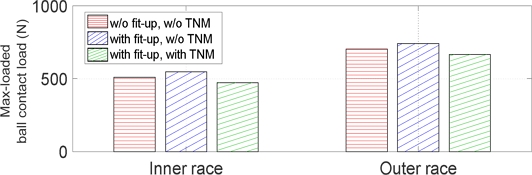
Fig. 13 depicts the contact loads on both races of the most heavily loaded ball across various rotational speeds. These contact loads increase as the operating diametral clearance of the ACBB nears a negative value, indicating an interference fit between the balls and races. This indicates that without incorporating fit-up and TNM, the contact load outcomes (Qi: 510.63 N, Qe: 703.61 N) (red) differ significantly from the scenario where both are applied (Qi: 472.23 N, Qe: 665.14 N) (green), highlighting their critical importance for realistic applications.
4.3 Change of Bearing Stiffness
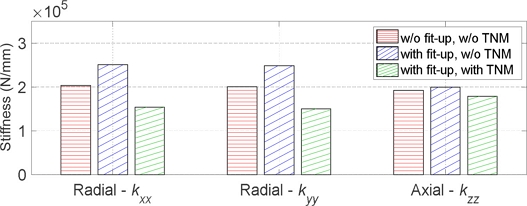
Fig. 14 illustrates how fit-up and thermal changes influence the stiffness of ACBB. When neither fit-up adjustments nor thermal changes from TNM are considered, the results are derived solely from the quasi-static model of ACBB. However, introducing only the fit-up model under cold-mounted conditions leads to a gradual increase in stiffness. This is attributed to the operating clearance of ACBB becoming negative, as discussed in section 4.1, thereby creating higher contact loads. When both fit-up and thermal changes from TNM are considered, an additional notable effect is observed. In this scenario, all factors that deform the ring are considered, resulting in lower stiffness than others.
4.4 Change of Heat Generation
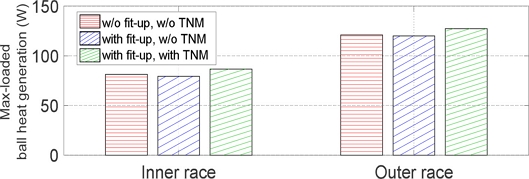
Fig. 15 presents the findings on heat generation at the position of the most heavily loaded ball, showing a pattern different from the discussions in sections 4.2 and 4.3. Upon reviewing the overall results for either the total or the max-loaded ball’s heat generation, it becomes apparent that the outcomes do not vary as substantially as the contact loads and stiffness. Contrary to the behaviors observed in contact loads and stiffness, the findings related to the heat generation of ACBB are completely opposite. When the internal clearance turns negative, its orbital speed drops, leading to a decrease in drag friction. This observation highlights the complex interplay between fit-up adjustments, thermal effects, and rotational speed in influencing ACBB’s heat generation. Detailed results of the total heat generation and the distribution of heat generation across both races are provided in Table 5.
5. Conclusions
This paper introduced an advanced numerical model developed for the thermo-mechanical analysis of high-speed ACBBs under oil-jet lubrication. The proposed model, comprising a quasi-static model, a fit-up model, and a thermal network model, demonstrates a strong correlation with experimental data, accurately representing temperature variations across different rotational speeds. A simulation result is provided to illustrate the thermo-mechanical behavior of ACBBs. Through simulation and analysis, the following conclusions were drawn:
1) The proposed model consistently estimates bearing temperature with a demonstrated error margin maintained within 10%.
2) Incorporating both fit-up adjustments and TNM into the modeling of ACBBs leads to increased expansion and reduction of diametral clearance, offering a more precise depiction of real-world operational behaviors.
3) The influence of fit-up adjustments and TNM significantly impacts contact loads. Their combined consideration results in reduced internal contact loads compared to scenarios where these factors are omitted
4) The initial introduction of fit-up under cold-mounted conditions increases stiffness in ACBBs, primarily due to the elevation of contact loads from negative operating clearance. However, integrating fit-up with TNM subsequently results in a reduction of stiffness.
NOMENCLATURE
| d : | Bearing Bore Diameter, mm |
| dm : | Bearing Pitch Diameter, mm |
| D : | Bearing Outer Diameter, mm |
| Da : | Ball Diameter, mm |
| F : | External/Equivalent Force, N |
| Fc : | Centrifugal Force, N |
| {F} : | External Load Vector, N, Nmm |
| M : | External/Equivalent Moment, Nmm |
| Mg : | Gyroscopic Moment, Nmm |
| Mrr : | Rolling Friction Torque, Nmm |
| Msl : | Sliding Friction Torque, Nmm |
| Mv : | Viscous Drag Friction Torque, Nmm |
| n : | Shaft/Inner Ring Rotational Speed, RPM |
| Pd : | Internal Diametral Clearance, mm |
| Q : | Ball Contact Load, N |
| : | Heat Generation, W |
| {Qi} : | Inner Ring Contact Load Vector, N, Nmm |
| R : | Thermal Resistance |
| [Rϕ] : | Transformation Matrix |
| T : | Temperature, oC |
| Z : | Number of Balls |
| α0 : | Nominal Contact Angle, rad |
| α : | Operating Contact Angle, rad |
| γ : | Misalignment Angle, rad |
| δ : | Bearing Displacement, mm |
| {δ} : | Displacement Vector, mm, rad |
| λ : | Traction Coefficient for Gyroscopic Moment, mm |
| uSP : | Total Displacement due to Surface Pressure, mm |
| uTC : | Total Displacement due to Temperature Change, mm |
| uTOT : | Total Displacement of a Bearing Component, mm |
| uCE : | Total Displacement due to Centrifugal Expansion, mm |
| {u} : | Inner Ring Displacement Vector, mm, rad |
| {v} : | Ball Displacement Vector, mm, rad |
SUBSCRIPTS FOR ACBB QUASI-STATIC MODEL
| e : | Outer Race |
| i : | Inner Race |
| j : | Rolling Element Index |
SUBSCRIPTS FOR THERMAL NETWORK MODEL
| i, j : | Node Location |
| j : | Node Location Adjacent to Node i |
| air : | Node Location for Air |
| oil : | Node Location for Lubricant |
Acknowledgments
This work was supported by Korea Research Institute for Defense Technology Planning and Advancement (KRIT) - Grant funded by Defense Acquisition Program Administration (DAPA) (No. KRIT-CT-21-006).
REFERENCES
-
Schobeiri, M. T., (2019), Gas turbine design, components and system design integration, Springer.
[https://doi.org/10.1007/978-3-030-23973-2]

- Soares, C., (2014), Gas turbines: a handbook of air, land, and sea applications, 2nd Edition, Elsevier-Health Sciences Division.
- Boyce, M., (2011), Gas turbine engineering handbook, 4th Edition, Elsevier.
-
Hong, S.-W., Tong, V.-C., (2016), Rolling-element bearing modeling: a review, International Journal of Precision Engineering and Manufacturing, 17(12), 1729-1749.
[https://doi.org/10.1007/s12541-016-0200-z]

-
Liu, J. Y., (1971), The effect of misalignment on the life of high-speed cylindrical roller bearings, Journal of Lubrication Technology, 93(1), 60-68.
[https://doi.org/10.1115/1.3451535]

-
Ioannides, E., Harris, T. A., Ragen, M., (1990), Endurance of aircraft gas turbine mainshaft ball bearings-analysis using improved fatigue life theory: part 1 – application to a long-life bearing, Journal of Tribology, 112(2), 304-308.
[https://doi.org/10.1115/1.2920257]

-
Zaretsky, E. V., Chiu, Y., Tallian, T., (1989), Ceramic bearings for use in gas turbine engines, Journal of Materials Engineering, 11(3), 237-253.
[https://doi.org/10.1007/BF02834841]

- Glockner, P., Martin, M., Flouros, M., (2016), Experimental investigation results of a hybrid ceramic and actively cooled ball bearing for gas turbines, Proceedings of the Future of Gas Turbine Technology 8th International Gas Turbine Conference, 1-10.
-
Tong, V.-C., Hong, S.-W., (2018), Vibration analysis of flexible rotor with angular contact ball bearings using a general bearing stiffness model, Journal of the Korean Society for Precision Engineering, 35(12), 1179-1189
[https://doi.org/10.7736/KSPE.2018.35.12.1179]

-
Harris, T. A., Barnsby, R. M., (1998), Tribological performance prediction of aircraft gas turbine mainshaft ball bearings, Tribology Transactions, 41(1), 60-68.
[https://doi.org/10.1080/10402009808983722]

- Harris, T. A., (2001), Rolling bearing analysis, 4th Edition, John Wiley & Sons, New York.
-
Pruvot, F. C., Mottu, A., (1980), High speed bearings for machine tool spindles, CIRP Annals, 29(1), 293-297.
[https://doi.org/10.1016/S0007-8506(07)61339-0]

- Tong, V. C., (2017), Study on the modeling and analysis of tapered roller bearings, Ph.D. Thesis, Kumoh National Institute of Technology.
- Crecelius, W. J., Milke, D. R., (1973), Dynamic and thermal analysis of high speed tapered roller bearings under combined loading, (Report No. NASA CR-121207), https://ntrs.nasa.gov/citations/19730017755
- Hadden, G. B., Kleckner, R. J., Ragen, M. A., Sheynin, L., (1981), Steady state and transient thermal analysis of a shaft bearing system including ball, cylindrical and tapered roller bearings, (Report No. 165365), https://ntrs.nasa.gov/citations/19820024093
- Timoshenko, S., (1941), Strength of materials Part II: advanced theory and problems, 2nd Edition, D. Van Nostrand Company.
-
Shang, P., Zhan, Y., Feng, S., Zhou, J., Yu, L., (2013), Exact solution of high-speed couplings for interference fits, Advanced Materials Research, 744, 180-184.
[https://doi.org/10.4028/www.scientific.net/AMR.744.180]

- Rivera, G., Po, P. J., Kang, C. S., Hong, S. W., (2024), Analytical formulation for sliding friction torque in cylindrical Roller bearings, Journal of Mechanical Science and Technology. (under review)
- Rivera, G., Ferrer, M. A., Po, P. J., Hong, S. W., (2024), Effect of the operational diametral clearance change on the characteristics of angular contact ball bearings, Proceedings of the KSPE 2024 Spring Conference.
-
De Mul, J. M., Vree, J. M., Maas, D. A., (1989), Equilibrium and associated load distribution in ball and roller bearings loaded in five degrees of freedom while neglecting friction-Part I: General theory and application to ball bearings, Journal of Tribology, 111(1), 142-148.
[https://doi.org/10.1115/1.3261864]

-
Tong, V.-C., Hong, S.-W., (2018), Study on the running torque of angular contact ball bearings subjected to angular misalignment, Proceedings of the Institution of Mechanical Engineers Part J: Journal out Engineering Tribology, 232(7), 890-909.
[https://doi.org/10.1177/1350650117732921]

- Park, S.-H., (2024), Development of bearing temperature prediction program based on thermal network model and CFD simulation, M.Sc Thesis, Kumoh National Institute of Technology.
- SKF, The SKF model for calculating the frictional moment. https://www.skf.com/binaries/pub12/Images/0901d1968065e9e7-The-SKF-model-for-calculating-the-frictional-moment_tcm_12-299767.pdf
-
Harris, T. A., Kotzalas, M. N., (2006), Rolling bearing analysis: advanced concepts of bearing technology, 5th Edition, CRC Press.
[https://doi.org/10.1201/9781420006582]

-
Tong, V.-C., Hong, S.-W., (2018), Improved formulation for running torque in angular contact ball bearings, International Journal of Precision Engineering and Manufacturing, 19(1), 47-56.
[https://doi.org/10.1007/s12541-018-0006-2]

-
Popescu, A., Houpert, L., Olaru D. N., (2020), Four approaches for calculating power losses in an angular contact ball bearing, Mechanism and Machine Theory, 144, 103669.
[https://doi.org/10.1016/j.mechmachtheory.2019.103669]

-
Rivera, G., Tong, V.-C., Hong, S.-W., (2021), A study on ball-race contact in angular contact ball bearing during rotation, Journal of the Korean Society for Precision Engineering, 38(11), 851-862.
[https://doi.org/10.7736/JKSPE.021.086]

-
Rivera, G., Tong, V.-C., Hong, S.-W., (2022), Improved formulation for sliding friction torque of deep groove ball bearings, Journal of the Korean Society for Precision Engineering, 39(10), 779-789.
[https://doi.org/10.7736/JKSPE.022.045]

-
Kakuta, K., (1961), Friction moment of radial ball bearing under thrust load, Proceedings of Mechanical Engineering Congress, 27(178), 945-956. Japan etc.
[https://doi.org/10.1299/kikai1938.27.945]

-
Brossier, P., Niel, D., Changenet, C., Ville, F., Belmonte, J., (2020), Experimental and numerical investigations on rolling element bearing thermal behaviour, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 235(4), 842-853.
[https://doi.org/10.1177/1350650120932335]

-
Niel, D., Changenet, C., Ville, F., Octrue, M., (2017), Thermomecanical study of high speed rolling element bearing: A simplified approach, Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 234(4), 135065011775080.
[https://doi.org/10.1177/1350650117750806]

-
Pouly, F., Changenet, C., Ville, F., Velex, P., Damiens, B., (2010), Power loss predictions in high-speed rolling element bearings using thermal networks, Tribology Transactions, 53(6), 957-967.
[https://doi.org/10.1080/10402004.2010.512117]


received his M.E. degree in Mechanical Engineering in 2021 from Kumoh National Institute of Technology (KIT), Korea. Currently, he serves as a Postmaster Researcher at KIT. His current research interests include bearing modeling and analysis.
E-mail: gibsrivera@kumoh.ac.kr

received her M.E. degree in Mechanical Engineering from KIT, Korea in 2024. She is currently working as a research engineer at LIG Nex1. Her research interests include computational fluid mechanics and bearing modeling.
E-mail: shinhyang.park@lignex1.com

received his B.S. degree in Mechanical Engineering from Yonsei University, Korea, in 1990. Currently, he is a Director of the R&D Center in V&C Tech Co., Ltd. His current research interests include modeling, analysis, and test of rolling bearings.
E-mail: cskang@vnc-tech.com

received his Ph.D degree in Mechanical Engineering from Seoul National University (SNU), Korea, in 2002. Currently, he is a Professor in the Department of Mechanical Engineering, KIT, Korea. His research interests include computational fluid mechanics, particle dynamics, and bearing modeling and analysis.
E-mail: kdj@kumoh.ac.kr

received his Ph.D. degree in Mechanical Engineering from KAIST, Korea, in 1989. Currently, he is a Professor in the School of Mechanical System Engineering, KIT. His research interests include spindle and bearings modeling and analysis, command shaping for positioning systems, vibration control, and structural vibration analysis for mechanical systems.
E-mail: swhong@kumoh.ac.kr