박판 시편을 사용한 Split-Hopkinson Tensile Bar의 변형 영역에 대한 해석적 연구

1. 서론

최근 자동차, 항공 등의 여러 산업분야에서는 경량화와 내구성 강화를 위해 합금과 고강도 강판의 사용이 확대되고 있다. 알루미늄 합금, 스테인리스 스틸과 같은 소재는 탄성 복원과 낮은 성형성으로 인해 원하는 결과물을 얻기 어려울 수가 있어 액중방전성형(Electro-hydraulic Forming), 전자기성형(Electro-magnetic Forming)과 같은 고속 성형 기법이 연구되고 있다. 고속 성형기법은 매우 짧은 시간 안에 이루어지는 성형으로 의한 관성효과(Inertia Effect)와 높은 변형률 속도에 의한 연신율 증가로 인해 성형성을 증대시킬 수 있다는 이점이 있다[1,2]. 소재의 물성은 준정적 실험을 통해 얻어지는 것이 일반적이지만, 변형률 속도가 증가하면 소재의 항복강도와 인장강도가 증가하는 경향을 보이므로[3,4] 고 변형률 속도에서의 현상을 정확하게 분석하고 예측하기 위해서는 동적 물성의 획득에 관한 연구가 필수적이다.

동적 물성은 고속인장시험기[5]와 Taylor 봉[6,7], 홉킨슨 바(Hopkinson Bar)[8-11]를 이용하여 구할 수 있다. 이 중 홉킨스바는 10²-10⁴ s^-1의 고변형률 속도에서의 물성 획득을 위해 널리 사용되는 장비로 압축 물성을 구하는 SHPB (Split-Hopkinson Pressure Bar)와 인장 물성을 구하는 SHTB (Split-Hopkinson Tensile Bar)가 존재한다. SHPB 실험은 시편을 긴 봉 형상의 입력봉과 출력봉 사이에 위치시키고 입력봉에 충격봉을 충돌시킴으로써 시편을 압축시키게 된다. 이때 봉에서의 응력파를 측정하고 1차원 응력파 전달 이론을 이용하여 시편의 동적 물성을 구한다. SHTB 역시 같은 원리를 기반으로 하나, 입력봉을 인장 시키기 위해 입력봉을 감싸는 튜브(Tube) 형태의 충격봉이 주로 사용된다. 봉과 시편 사이 경계면의 접촉만에 의해 시편이 압축되는 SHPB와는 달리, SHTB는 볼트를 이용하여 결합하거나[12-14] 시편과 봉에 나사산[15,16]을 파서 결합하게 된다. 응력파의 전달을 이용하는 홉킨슨 바의 특성상, 이러한 결합부의 형상에 의한 노이즈가 물성획득에 큰 영향을 줄 수 있다. 하지만 SHTB는 압축이 아닌 인장 물성을 구할 수 있다는 점, 원기둥뿐만 아니라 판재 시편의 실험이 가능하다는 점, 시편의 네킹(Necking)이나 인장 파단을 관찰하기 용이하다는 장점이 있어 지속적인 연구가 필요하다.

본 논문에서는 SHTB의 유한요소해석을 통해 입력 응력-변형률 선도와 홉킨슨 바 이론을 이용하여 구한 선도의 일치도를 향상시킬 수 있는 방법을 연구하였다. 홉킨슨 바 이론에서 응력-변형률 선도를 계산하기 위해서는 시편의 길이(L_S)와 단면적(A_S)을 알아야 한다. SHPB 실험에서 이것은 단순히 원기둥 시편의 길이와 단면적에 해당한다. SHTB에서는 시편에서 변형이 집중되는 부분과 그렇지 않은 부분이 극명하게 차이가 나므로 정확한 응력-변형률 선도를 구하기 위해서는 시편의 변형길이(L_D)와 너비(W_D)를 선택할 수 있는 기준이 필요하다. 이를 위해 두께 1 mm의 박판 SUS430 시편을 다양한 초기 게이지 길이(L_I)와 너비(W_I)에 대하여 모델링하여 해석을 수행하고 변형 영역을 구하였다. 그리고 초기 게이지 길이인 L_I, W_I를 사용한 응력-변형률 선도와 본 연구에서 도출한 L_D와 W_D를 사용하여 계산한 선도를 비교하였다. 홉킨슨 바 이론을 통해 구한 응력-변형률 선도는 어떤 L과 W값을 사용하느냐에 따라 민감하게 변화함을 확인하였고, 입력 응력-변형률 선도와의 일치도를 높일 수 있는 L_D와 W_D의 선정 기준을 제시하였다.

2. SHTB

2.1 SHTB 이론

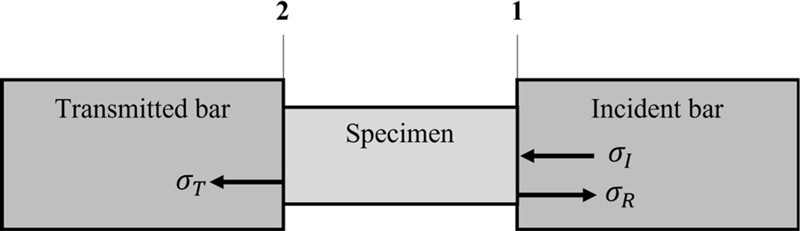
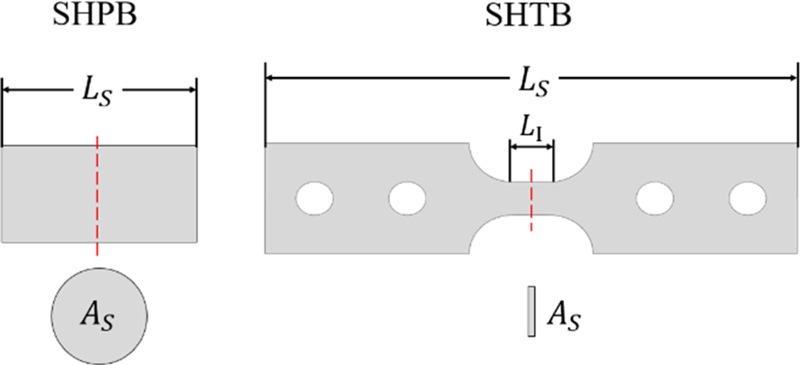
SHTB 장비의 형상은 Fig. 1과 같다. 입력봉(Incident Bar), 출력봉(Transmitted Bar), 시편(Specimen), 충격봉(Striker)은 동일 축상에 정렬되며 출력봉의 끝단은 고정되어 움직이지 않는다. 충격봉은 입력봉을 감싸고 있는 튜브 형태이며 공압 장치에 의해 발사된다. 충격봉이 입력봉에 충돌하면 인장 응력파가 발생하는데, 여기에 1차원 응력파 전달 이론을 적용시켜 각 봉과 시편에서의 응력을 계산할 수 있다[8]. 이 충돌로 인해 입력봉을 따라서 전파하는 응력파를 입사파(Incident Pulse)라고 한다. 각 봉의 재질과 단면적은 모두 동일하게 설계하여 임피던스(Impedance) 차이가 없도록 한다. 임피던스 Z는 식(1)과 같이 표현된다.

Fig. 1

Schematic of SHTB apparatus

$\[ Z=\rho AC=\rho A\sqrt{\frac{E}{\rho }} \]$

(1)

여기서 ρ는 밀도, A는 단면적이며, C는 탄성파 전파 속도, E는 탄성계수이다. 시편의 면적, 밀도, 탄성계수가 봉과 다르므로 임피던스 차이가 발생한다. 이에 입력파는 Fig. 2와 같이 반사파(Reflected Pulse)와 투과파(Transmitted Pulse)로 나누어진다. 입력파, 반사파, 투과파는 입력봉과 출력봉에 부착된 스트레인 게이지(Strain Gauge)에 의해 각각 ε_I, ε_R, ε_T으로 측정된다.

Fig. 2

Reflection and transmission of the stress wave

시편 양단 1, 2면에서의 속도는 식(2) 및 식(3)으로 표현된다. 봉은 탄성 변형만 발생하도록 높은 항복 강도를 가진 소재로 제작하므로 양단에 걸리는 힘은 식(4)와 식(5)로 나타낼 수 있다.

$\[ V_1\left(t\right)=C_B\left\{{\epsilon }_I\left(t\right)-{\epsilon }_R\left(t\right)\right\} \]$

(2)

$\[ V_2\left(t\right)=C_B{\epsilon }_T\left(t\right) \]$

(3)

$\[ P_1\left(t\right)=E_B{A}_B\left\{{\epsilon }_T\left(t\right)+{\epsilon }_R\left(t\right)\right\} \]$

(4)

$\[ P_2\left(t\right)=E_B{A}_B\left\{{\epsilon }_T\left(t\right)\right\} \]$

(5)

여기서 C_B, E_B, A_B 는 봉에서의 탄성파 속도, 봉의 탄성계수, 봉의 단면적이다. 시편 내의 변형률 속도 $$ \dot{\epsilon }\left(t\right)$$는 식(6)처럼 시편 양단의 속도차이를 시편의 길이 L_S로 나눈 것으로 나타낼 수 있다.

$\[ \dot{\epsilon }\left(t\right)=\frac{V_1\left(t\right)-V_2\left(t\right)}{L_S} \]$

(6)

시편 양단의 힘이 같다고 가정하면 식(4)와 식(5) 의해 ε_I+ε_R=ε_T이 성립하고 시편의 응력 σ_S(t)와 변형률 ε_S(t), 변형률 속도 $$ {\dot{\epsilon }}_S\left(t\right)$$를 식(7)부터 식(9)와 같이 계산할 수 있다.

$\[ {\sigma }_S\left(t\right)=\frac{A_B}{A_S}{E}_B{\epsilon }_T\left(t\right) \]$

(7)

$\[ {\epsilon }_S\left(t\right)=-2\frac{C_B}{L_S}{\int }_0^t{\epsilon }_R\left(t\right)dt \]$

(8)

$\[ {\dot{\epsilon }}_S\left(t\right)=-2\frac{C_B}{L_S}{\epsilon }_R\left(t\right) \]$

(9)

여기서 A_S는 시편의 단면적이다. 식(7)부터 식(9)는 공칭응력과 변형률이므로 식(10)부터 식(12)와 같이 진응력, 진변형률, 진변형률 속도로 변환하여 응력-변형률 선도를 구한다.

$\[ {\sigma }_{S,T}\left(t\right)={\sigma }_S\times \left(1+{\epsilon }_S\left(t\right)\right) \]$

(10)

$\[ {\epsilon }_{S,T}\left(t\right)=\mathrm{l}\mathrm{n}\left(1+{\epsilon }_S\left(t\right)\right) \]$

(11)

$\[ {\dot{\epsilon }}_{S,T}\left(t\right)=\frac{{\dot{\epsilon }}_S\left(t\right)}{1+{\epsilon }_S\left(t\right)} \]$

(12)

SHPB와 SHTB 모두 봉과 시편의 접촉에 의해 응력파가 투과또는 반사되며, 이 관계를 이용하여 시편의 물성을 간접적으로 계산한다. 시편 전체가 입력봉과 출력봉에 의해 압축되는 SHPB는 식(7)부터 식(9)의 L_S에 시편의 전체 길이를 사용할 수 있으며, 지름이 일정한 원기둥 시편이 사용되므로 어느 지점의 단면적을 A_S에 사용해도 무방하다. 반면 SHTB 시편 변형은 시편의 중앙 부분에 집중되므로 시편의 전체 길이나 너비를 계산에 사용하는 것은 적절하지 않다. 정확한 응력-변형률 선도를 구하기 위해서는 변형 길이와 너비를 선정하는 기준이 필요하다. 이를 위하여 SHTB의 유한요소모델을 구축하고 시편 형상에 따른 변형 영역을 살펴보았다.

2.2 SHTB 유한요소모델

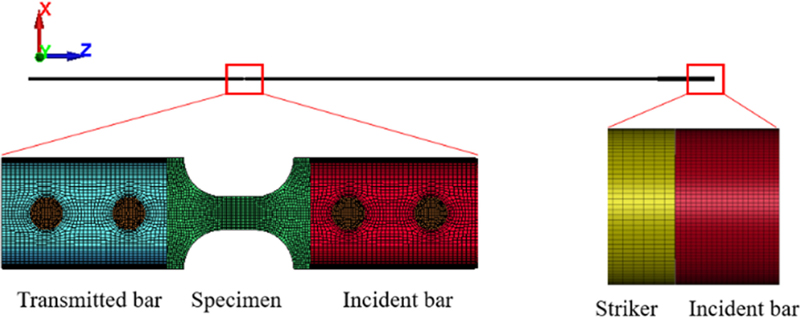
상용 프로그램 LS-DYNA를 이용하여 Fig. 3과 같이 유한요소 모델을 구축하였다. 본 SHTB 장비는 중심을 지나는 X-Z 면에 대하여 대칭이므로 절반의 모델만 해석하여 시간을 단축하였다. 충격봉의 속도는 8 m/s이며 INITIAL_VELOCITY_GENERATION 키워드를 통해 부과하였다. 입력봉, 출력봉, 충격봉의 소재는 SNCM439 고강도강으로 소성변형이 일어나지 않으므로 MAT001_ELASTIC 키워드를 사용하였다. 볼트 역시 봉과 같은 소재를 사용하여 임피던스 차이에 의한 노이즈를 최소화하였다. 봉의 물성과 치수는 Tables 1과 2에서 확인할 수 있다. 식(7)부터 식(9)의 계산에 필요한 ε_I, ε_R, ε_T는 스트레인 게이지 위치에 있는 요소(Element)의 변형률을 사용한다.

Fig. 3

Finite element model of SHTB

Table 1

Specification of the bars

Table 2

Material properties of SNCM439

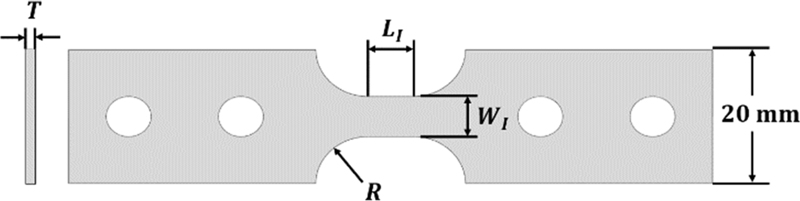
시편의 기본 형상은 Fig. 4와 같다. L_I는 초기 게이지 길이, W_I는 초기 너비이며 두께 T는 1 mm이다. W_I=6 mm로 고정하고 L_I는 4, 6, 8, 10, 12 mm에 대하여 해석한 후, L_I= 6 mm로 고정하고 W_I를 4, 5, 6, 7 mm에 대하여 해석하여 결과를 비교하였다. 시편의 소재는 SUS430이며 식(13)과 같이 Cowper-Symonds 구성 방정식을 이용한 물성을 입력하였다.

Fig. 4

Schematic of the plate specimen for SHTB

$\[ \stackrel{-}{\sigma }={\sigma }_0\left[1+{\left(\frac{\dot{\epsilon }}{C}\right)}^{1/p}\right] \]$

(13)

$$ \stackrel{-}{\sigma }$$는 동적 유동응력, σ₀는 정적 유동응력, $$ \dot{\epsilon }$$는 변형률 속도이며 C와 p는 Cowper-Symonds 재료상수이다. 위 구성 방정식을 이용한 변형률 속도별 응력-변형률 선도를 MAT024_PIECEWISE_LINEAR_PLASTICITY 키워드를 통해 적용하였으며, 이를 본 논문에서는 ‘입력 물성’이라고 지칭할 것이다. SUS430의 물성과 Cowper-Symonds 재료상수는 Table 3에 나타내었다.

Table 3

Material properties and Cowper-Symonds parameters of SUS430

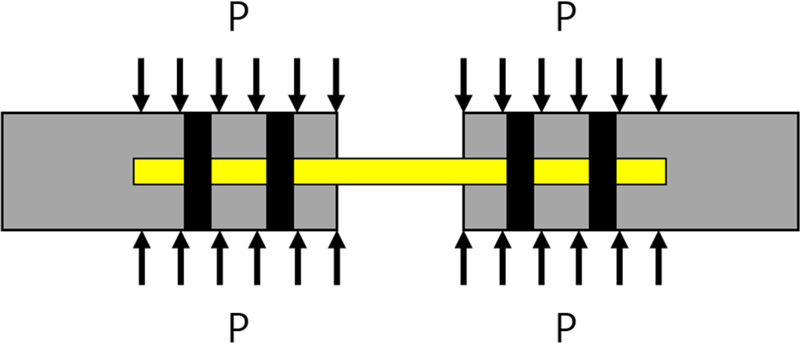
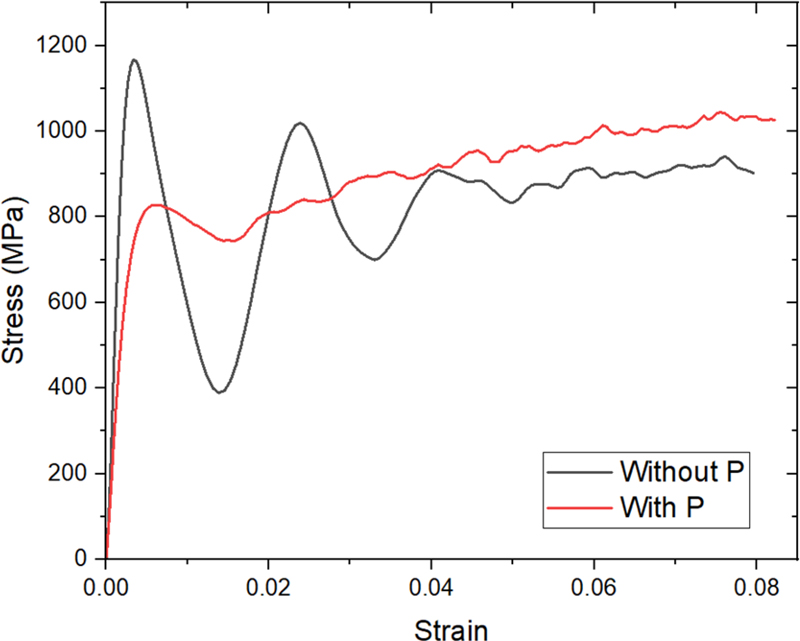
시편은 4개의 볼트를 이용하여 고정하였다[12]. 봉에서 시편으로의 응력파 전파를 용이하게 하기 위하여 볼트를 견고히 체결하여 그립(Grip)과 시편이 서로 밀착되도록 한다. 이를 해석적으로 구현하기 위하여 Fig. 5와 같이 볼트에 의해 그립에 가해지는 클램핑(Clamping) 압력 P=124 MPa를 부과하였다[14]. P의 크기는 별도의 정해석 결과를 바탕으로 추정하였다. Fig. 6에서와 같이 P가 가해질 경우 응력파가 가지고 있는 진동이 줄어드므로 클램핑 압력의 중요성을 확인할 수 있다. 정적 해석으로 시작하여 클램핑 압력을 부과하였고 평형 상태에 이르면 동적 해석으로 전환하여 SHTB의 충돌해석을 수행하였다. 이를 구현하기 위해 CONTROL_IMPLICIT_GENERAL 키워드를 사용하였다.

Fig. 5

Clamping pressure condition on grip of the bars

Fig. 6

Comparison of stress-strain curves; with clamping pressure and without clamping pressure

2.3 유한요소해석결과

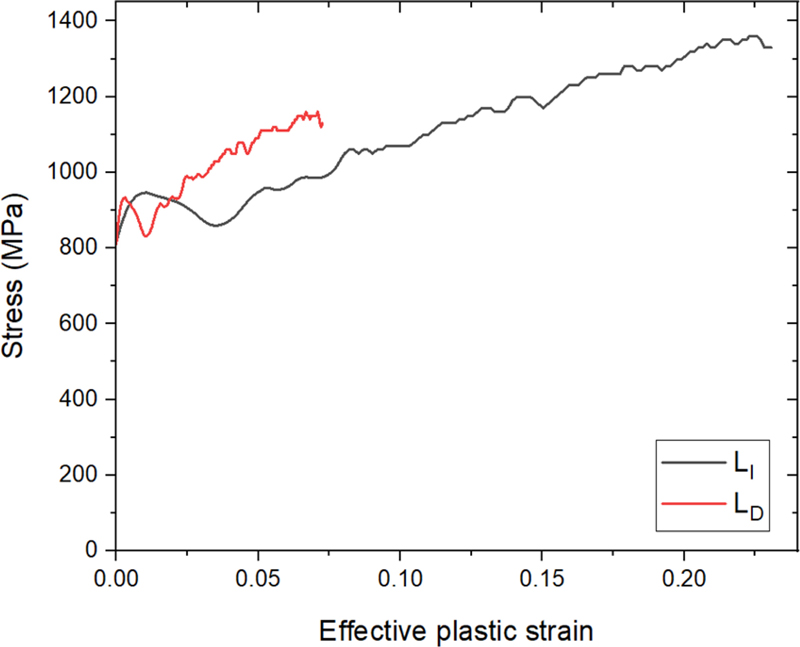
해석 결과로부터 응력-변형률 선도를 계산하기 위해 식(7)부터 식(9)의 L_S에는 초기길이 L_I를, A_S에는 W_I×T를 사용하였다. Figs. 7과 8은 각각 W_I = 6 mm로 고정하고 L_I를 변화시켰을 때와 L_I = 6 mm로 고정하고 W_I를 변화시켰을 때의 응력-변형률 선도이다. 길이 L_I가 짧고 너비 W_I가 좁을수록 변형률과 변형률 속도가 커지는 것을 확인할 수 있다. 충격봉의 속도가 8 m/s으로 동일하므로 시편에 가해지는 에너지도 같다고 볼 수 있다. 시편의 길이와 너비가 작아지면 같은 에너지로 더 작은 영역을 변화시키는 것이므로 변형률과 변형률 속도가 커진다고 볼 수 있다. Figs. 7과 8에서 각 선도의 변형률 속도 차이는 수백 s^-1임에도 항복응력이나 유동응력의 크기에 큰 차이가 없다. 변형률 속도 1,500 s^-1에서의 입력 물성과 L_I = 4 mm, W_I = 6 mm일 때 식(7)부터 식(9)에 의한 선도를 Fig. 9에 나타내었다. 같은 변형률 속도에서의 응력-변형률 선도이므로 서로 일치하는 것이 이상적인 결과이다. 하지만 입력 물성에 비해 유동응력이 확연히 낮은 수준에 머무는 것을 볼 수 있다. 입력 유동응력과의 평균 퍼센트 오차는 8.58%였다.

Fig. 7

Comparison of stress-strain curves for different gauge lengths. LI and WI were used for the calculation

Fig. 8

Comparison of stress-strain curves for different gauge widths. LI and WI were used for the calculation

Fig. 9

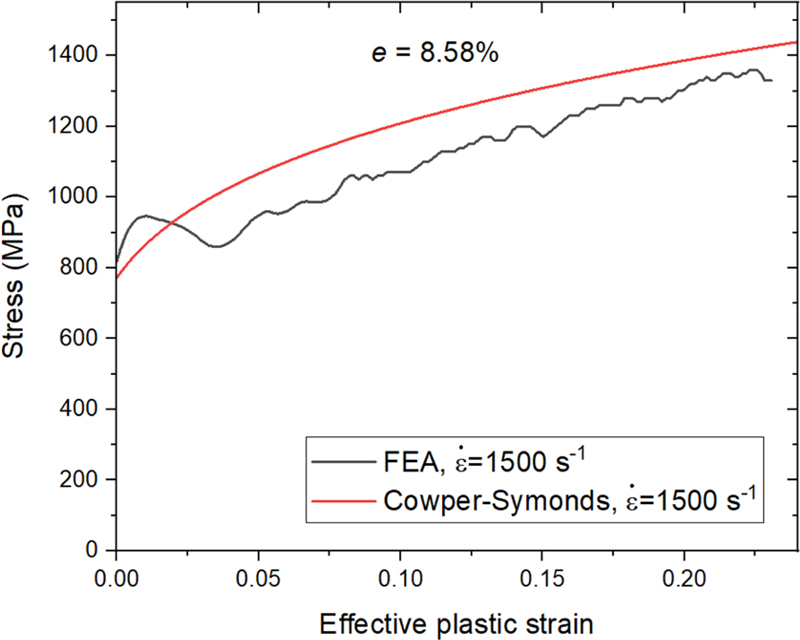
Comparison between the input Cowper-Symonds curve and FEA result. LI and WI were used for the FEA result calculation

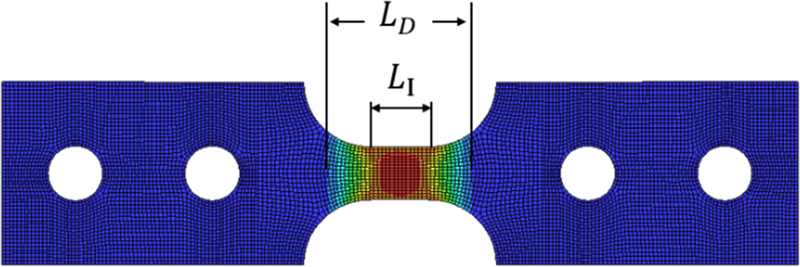
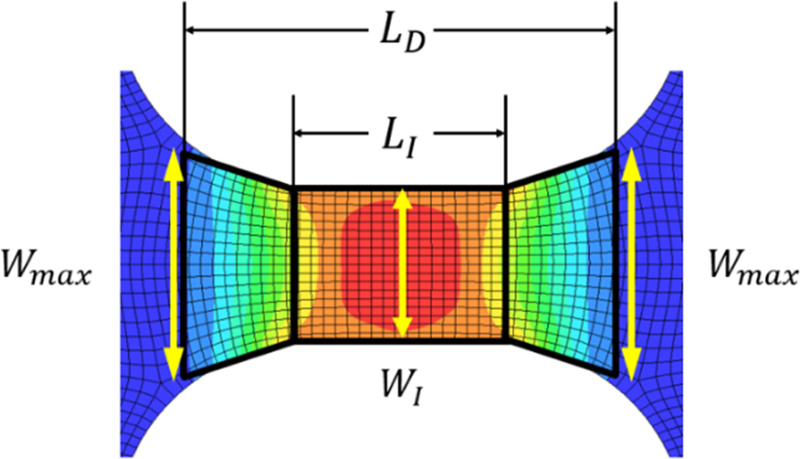
이러한 문제가 발생하는 이유는 SHPB에서 기반한 이론식이 SHTB에서 그대로 사용되고 있기 때문이다. SHPB에서는 Fig. 10에 나타난 시편 전체에서 변형이 발생하므로 L_S와 A_S를 사용하여 응력과 변형률을 계산하여도 무방하다. Fig. 11에서 볼 수 있듯이 SHTB는 시편의 중앙 게이지 부근에서 대부분의 변형이 발생하며 그립과 접하는 인근의 변형은 없거나 매우 작아 무시할 수 있는 수준이다. 그러므로 시편 전체 길이를 식(7)부터 식(9)에 대입할 수 없음은 명백하며, L_I를 사용하였을 때도 Fig. 9와 같이 오차가 발생하므로 적절한 길이를 선택할 수 있는 기준이 필요하다.

Fig. 10

Comparison of LS and AS between SHPB and SHTB

Fig. 11

Effective plastic strain of specimen after the first stress wave passed

Fig. 11에서 확인할 수 있듯이 실제로 변형이 일어나는 길이 L_D는 L_I와 큰 차이를 보인다. 해당 시편의 경우는 L_I = 6 mm, L_D =12.9 mm로 2배 이상 차이가 나며 시편의 형상이나 변형률 속도에 따라 더 큰 차이가 나는 경우도 있다. 이에 따라 식(8)과 식(9)에서 L_I를 사용하면 실제보다 변형률과 변형률 속도가 높게 계산됨을 알 수 있다.

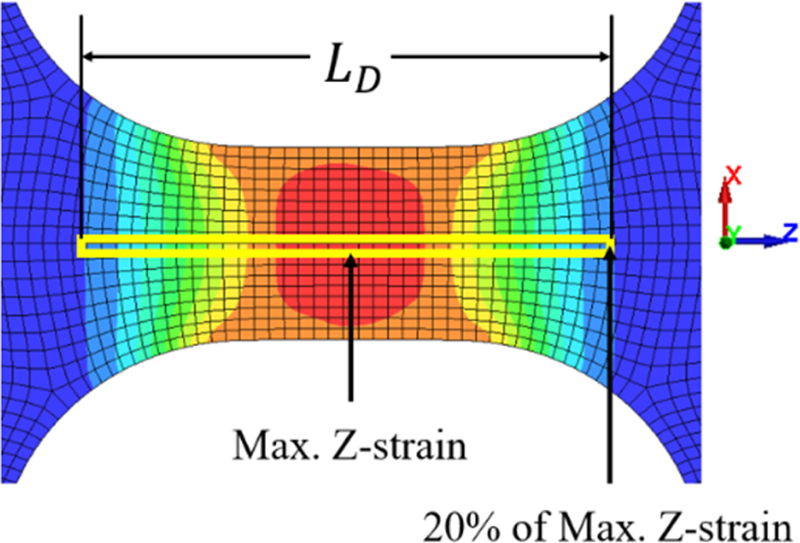
L_I대신 L_D를 이용하여 다시 응력-변형률 선도를 구하였다. L_D의 측정 기준은 Fig. 12와 같다. 시편의 최대 Z-변형률은 시편의 정중앙에서 발생한다. 이 값을 기준으로 하여 시편 Z축을 따라가며 요소의 Z-변형률이 최대 Z-변형률의 20%가 되는 지점까지의 길이를 L_D로 하였다. Fig. 13은 L_I = 4 mm, W_I = 6 mm 시편의 응력-변형률 선도를 L_I 대신 L_D 사용하여 계산한 것이다. Fig. 14는 각각 L_I와 L_D를 사용하였을 때의 응력-변형률 선도를 비교한 것이다. 변형률 속도는 1,500 s^-1에서 530 s^-1으로 60% 이상 감소하였으며, 첫 응력파에 의하여 변형되는 시편의 소성 변형률 역시 0.23에서 0.07로 감소하여 3배 이상의 차이를 보였다. 같은 조건에서 이루어진 해석이지만 후처리 과정에서 L_I 대신 L_D를 사용함으로 인해 차이가 발생하였다. L_S는 응력에도 영향을 주는데, 공칭응력을 구하는 식(7)에는 L_S가 포함되어 있지 않지만 식(10)의 공칭응력을 진응력으로 변환하는 과정에서 변형률이 사용되기 때문이다.

Fig. 12

Calculation of LD for plate specimen of SHTB

Fig. 13

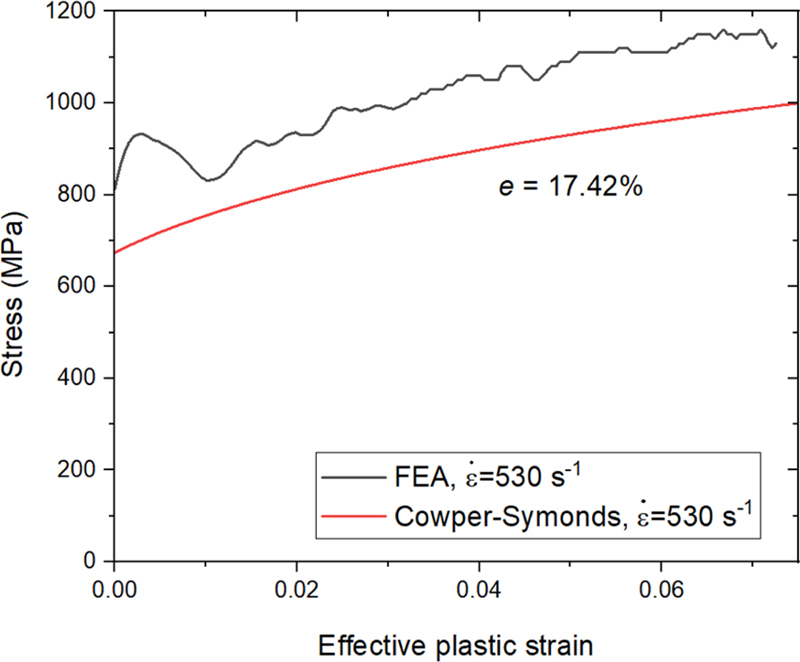
Comparison between the input Cowper-Symonds curve and finite element analysis result. LD and WI were used for the calculation

Fig. 14

Comparison of stress-strain curves calculated using LI and LD

Fig. 13에서는 L_D를 사용하자 응력의 오차가 e = 17.42%로 더 커졌다. 이것은 L_D를 사용하여 변형률과 변형률 속도는 교정되었으나 응력을 일치시키는 데에는 한계가 있기 때문이다. 응력 계산에 L_D보다 큰 영향을 끼치는 것은 시편의 단면적 A_S=T_S×W_S이다. 시편의 두께 T_S는 1 mm로 동일하므로 Fig. 15의 방법으로 실제 변형이 일어나는 시편의 너비 W_D를 구하였다. 길이 L_I구간은 너비 W_I의 직사각형 영역이며 양옆의 (L_D-L_I)영역은 윗변과 아랫변이 W_I, W_max 인 사다리꼴로 간주할 수 있다. 이때 총변형 길이 L_D에 대해 평균 변형 너비 W_D=W_Avg는 식(14)과 같이 구해진다.

Fig. 15

Calculation of WD for plate specimen of SHTB

$\[ W_D=W_{Avg}=\frac{L_I\times W_I+\left(L_D-L_I\right)\times \frac{W_{max}+W_I}{2}}{L_D} \]$

(14)

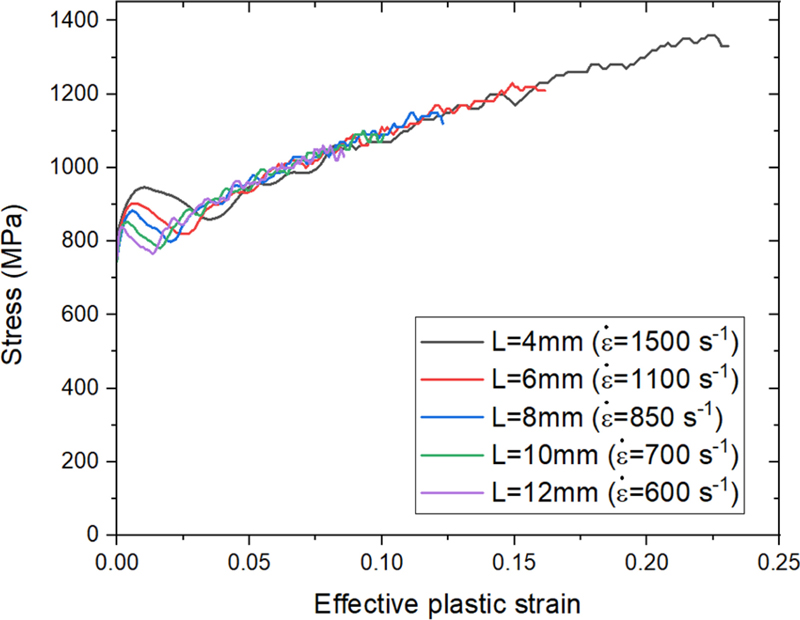
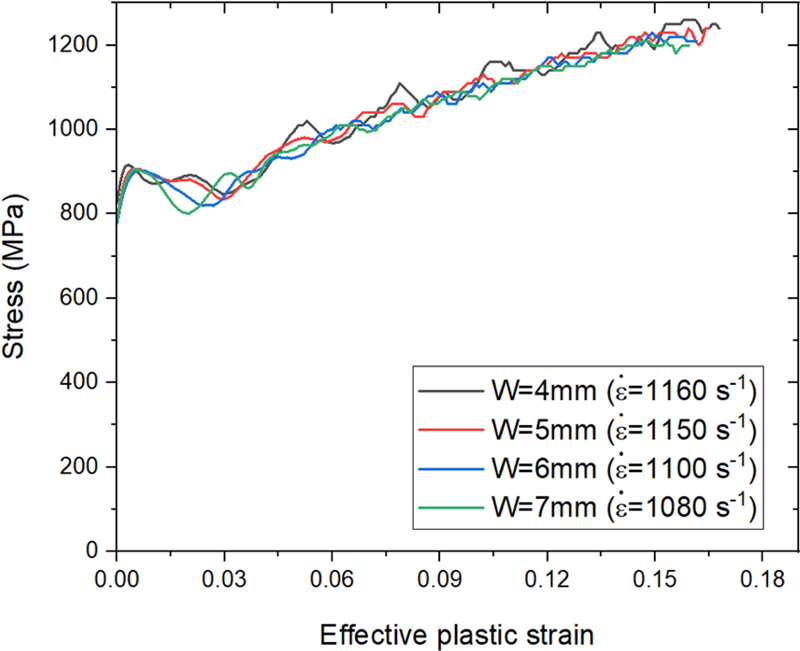
L_D 와 W_D를 사용하여 응력-변형률 선도를 구하고 Figs. 16 및 17에 나타내었다. 충격봉 속도는 V = 8 m/s, 시편 두께는 1 mm로 이전과 동일하다. Table 4와 Fig. 16은 W_I = 6 mm에서 시편의 L_I를 변화시켰을 때를, Table 5와 Fig. 17은 L_I = 6 mm 일 때 시편의 W_I를 변화시킨 결과이다. W_I를 고정하고 L_I를 증가시켰을 때, W_D에는 큰 변화가 없으면서 L_D가 주로 증가하는 모습을 보였다. 이때 L_D의 증가폭이 L_I증가폭과 유사하므로 (L_D-L_I)의 영역은 시편의 길이가 길어져도 크게 변하지 않음을 알 수 있다. e는 시편의 길이가 길수록 커지는 경향을 보였다. L_I = 4 mm일 때 최소로 2.31%였고 10 mm일 때 최대로 5.5%였다. L_I를 고정하고 W_I를 증가시켰을 때는 L_D의 소폭 증가하면서 W_D가 주로 변화하였다. W_D의 증가폭은 W_I의 증가폭과 같았다. e는 4.2에서 3.61% 사이였으며 형상에 따른 뚜렷한 경향성은 없었다.

Fig. 16

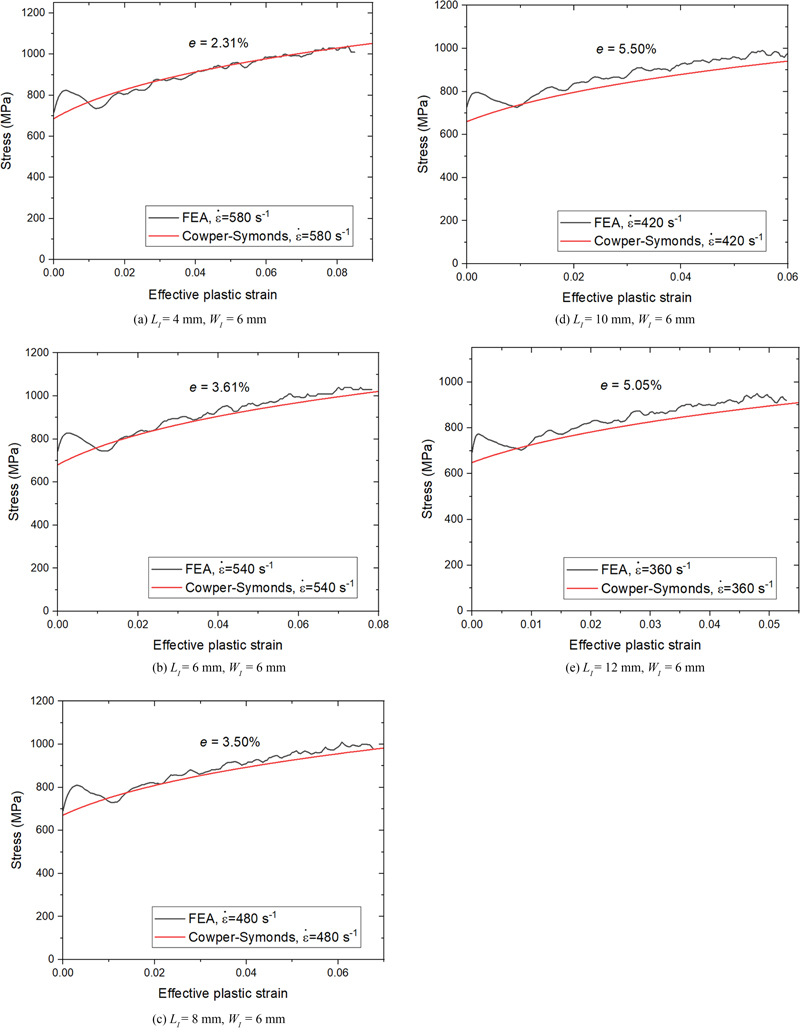
Comparison of the input Cowper-Symonds curves and FEA results for different gauge lengths. LD and WD were used for the FEA results calculation

Fig. 17

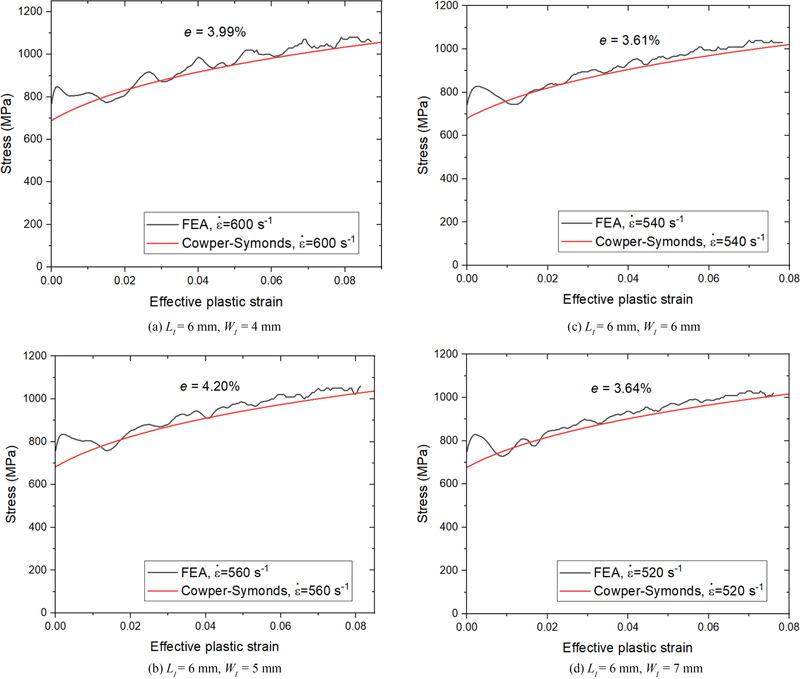
Comparison of the input Cowper-Symonds curves and FEA results for different gauge widths. LD and WD were used for the FEA results calculation

Table 4

Changes in LD, WD and e with variation in specimen’s LI

Table 5

Changes in LD, WD and e with variation in specimen’s WI

시편의 형상뿐만 아니라 변형률 속도의 영향을 알아보기 위해 L_I = 6 mm, W_I = 6 mm의 동일한 시편 형상에서 충격봉의 속도 V만 바꾸어 해석을 수행하였다. V는 현재 보유한 장비에서 주로 사용되는 속도인 4, 6, 8, 10 m/s으로 하였고 결과는 Table 6에 정리하였다. 충격봉의 속도가 빠를수록, 즉 시편이 겪는 변형률 속도가 높을수록 L_D가 증가하였으며 입력 유동응력과의 오차 e는 변형률 속도가 낮을수록 증가했다.

Table 6

Changes in LD, WD and e with variation in strain rate

마지막으로 실제로 시편이 변형한 변형률 속도가 L_D와 W_D를 이용해 구한 변형률 속도와 일치하는지 검증하기 위해 시편의 요소에서 직접 변형률 속도를 구하였다. Fig. 12의 L_D 영역에 해당하는 요소들의 변형률 평균을 구한 뒤 시간에 대하여 미분하여 변형률 속도를 구했다. 이를 식(9)를 이용한 결과와 비교하여 e를 구하고 Tables 7및 8에 정리하였다. e는 최소 0.87에서 최대 21.17%였으며 평균 e는 10.6%로 충분한 신뢰도를 가진다고 판단했다.

Table 7

Percentage error e between the specimen’s actual strain rate and strain rate by SHTB method when WI = 6 mm

Table 8

Percentage error e between the specimen’s actual strain rate and strain rate by SHTB method when LI = 6 mm

3. 결론

본 연구에서는 유한요소해석을 사용하여 SHTB에서 신뢰성 있는 응력, 변형률, 변형률 속도를 구하기 위한 변형 영역 L_D와 W_D 값을 계산하는 방법을 제시하였다. L_D는 시편의 최대 축방향 변형률의 20%가 되는 지점까지의 직선거리로 하였으며, W_D는 식(14)를 이용하여 평균 너비를 계산하였다. 이 기준이 적합한지 확인하기 위하여 두께 1 mm의 SUS430 시편의 초기 게이지 길이와 너비인 L_I와 W_I를 변경하며 유한요소해석을 수행하였다. 제시한 방법대로 L_D와 W_D를 구하여 홉킨슨 바 이론에 따른 응력-변형률 선도를 구하였다. 이를 입력 물성인 Cowper-Symonds 구성 방정식에 의한 응력-변형률 선도와 비교하였다. 잘못된 과 값을 사용하여 계산을 수행할 경우 응력, 변형률, 변형률 속도 모두 민감하게 변하여 입력 물성과 상이한 응력-변형률 선도가 나타나지만, L_D와 W_D를 사용하면 입력 물성과의 일치도를 향상시킬 수 있음을 보였다.

W_I와 충격봉 속도 V는 유지한 채 L_I를 변경하며 해석을 수행한 결과, L_I가 증가하면 L_D도 증가하는 경향을 보였으며 이때 L_D의 증가폭은 L_I의 증가폭과 유사했다. 이에 따라 시편의 길이가 증가하여도 (L_D-L_I)영역은 더 확장되지 않고 유지됨을 알 수 있었다. 그리고 L_I를 유지한 채 W_I를 변경하며 해석을 수행하였을 때는 W_I가 증가함에 따라 L_D는 소폭 증가하였으나 뚜렷한 경향성은 없었다. W_D의 증가량은 W_I 증가량과 유사하였다. 같은 형상의 시편에 대해 충격봉 속도를 달리하여 변형률 속도의 영향도 살펴본 결과, 변형률 속도가 높을수록 L_D가 증가하였다.

홉킨슨 바 이론으로 구한 응력-변형률 선도의 응력을 입력 선도의 응력과 비교한 퍼센트 오차 e는 시편의 길이가 길수록, 변형률 속도가 낮을수록 커졌다. 전체 케이스들에 대해 e는 2.54-6.62% 사이이므로 제시된 방법이 충분히 신뢰성이 있다고 판단했다.

추가 검증을 위해 시편의 요소에서 직접 구한 변형률 속도를 식(9)에 L_D, W_D를 대입하여 구한 변형률 속도와 비교하였다. e는 0.87-21.17% 사이로 L_D과 W_D의 계산방법이 적합했음을 확인하였다.

Acknowledgments

이 논문은 2023년도 중소기업기술정보진흥원의 재원으로 중소기업기술개발지원사업의 구매조건부 신제품개발사업(구매연계형) (No. G21S334512301)과 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 기본연구지원사업(RS2023-00253462182065300001)의 지원을 받아 수행된 연구입니다. 이에 관계자 여러분께 감사드립니다.

REFERENCES

• Golovashchenko, S. F., Gillard, A. J., Mamutov, A. V., (2013), Formability of dual phase steels in electrohydraulic forming, Journal of Materials Processing Technology, 213(7), 1191-121. [https://doi.org/10.1016/j.jmatprotec.2013.01.026]
• Trzepieciński, T., (2020), Recent developments and trends in sheet metal forming, Metals. 10(6), 779. [https://doi.org/10.3390/met10060779]
• Khan, A. S., Baig, M., Choi, S. H., Yang, H. S., Sun, X., (2012), Quasi-static and dynamic responses of advanced high strength steels: Experiments and modeling, International Journal of Plasticity, 30-31, 1-17. [https://doi.org/10.1016/j.ijplas.2011.08.004]
• Cadoni, E., Fenu, L., Forni, D., (2012), Strain rate behavior in tension of austenitic stainless steel used for reinforcing bars, Construction and Building Materials, 35, 399-407. [https://doi.org/10.1016/j.conbuildmat.2012.04.081]
• Huh, H., Lim, J. H., Park, S. H., (2009), High speed tensile test of steel sheets for the stress-strain curve at the intermediate strain rate, International Journal of Automotive Technology, 10, 195-204. [https://doi.org/10.1007/s12239-009-0023-3]
• Taylor, G. I., (1946), Testing of materials at high rates of loading, Journal of the Institution of Civil Engineers, 26(8), 486-519. [https://doi.org/10.1680/ijoti.1946.13699]
• Rakvåg, K. G., Børvik, T., Hopperstad, O. S., (2014), A numerical study on the deformation and fracture modes of steel projectiles during taylor bar impact tests, International Journal of Solids and Structures, 51(3-4), 808-821. [https://doi.org/10.1016/j.ijsolstr.2013.11.008]
• Chen, W., Song, B., (1997), Split hopkinson (kolsky) bar: design, testing and applications, Springer.
• Al-Mousawi, M. M., Reid, S. R., Deans, W. F., (1997), The use of the split hopkinson pressure bar techniques in high strain rate materials testing, Proceedings of the Institution of Mechanical Engineers, 211(4), 273-292. [https://doi.org/10.1243/0954406971522042]
• Li H., Li, F.-H., Zhang, R., Zhi, X.-D., (2023), High strain rate experiments and constitutive model for Q390D steel, Journal of Constructional Steel Research, 206, 107933. [https://doi.org/10.1016/j.jcsr.2023.107933]
• Li, P., Yuan, K., Guo, W., Wang, R., Chen, L., Gao, M., Du, P., (2022), Dynamic compressive behavior of a single crystal nickel-base superalloy at ultra-high temperature: mechanism investigation with a modified electric synchronous SHPB technique, Journal of Materials Research and Technology, 18, 637-657. [https://doi.org/10.1016/j.jmrt.2022.02.121]
• Huh, H., Kang, W. J., Han, S. S., (2002), A tension split hopkinson bar for investigating the dynamic behavior of sheet metals, Experimental Mechanics, 42, 8-17. [https://doi.org/10.1007/BF02411046]
• Ledford, N., Paul, H., Ganzenmüller, G., May, M., Hüfemann, M., Otto, M., Petrinic, N., (2015), Investigations on specimen design and mounting for split hopkinson tension bar (SHTB) experiments, Proceedings of the EPJ Web Conferences, 94, 021049. [https://doi.org/10.1051/epjconf/20159401049]
• Pham, T. N., Choi, H. S., Kim, J. B., (2013), A numerical investigation into the tensile split hopkinson pressure bars test for sheet metals, Applied Mechanics and Materials, 421, 464-467. [https://doi.org/10.4028/www.scientific.net/AMM.421.464]
• Nguyen, K.-H., Kim, H. C., Shin, H., Yoo, Y.-H., Kim, J.-B., (2017), Numerical investigation into the stress wave transmitting characteristics of threads in the split hopkinson tensile bar test, International Journal of Impact Engineering, 109, 253-263. [https://doi.org/10.1016/j.ijimpeng.2017.07.004]
• Moreira, B. S., Nunes, P. D. P., da Silva, C. M., Tenreiro, A. F. G., Lopes, A. M., Carbas, R. J. C., Marques, E. A. S., Parente, M. P. L., da Silva, L. F. M., (2023), Numerical design of a thread-optimized gripping system for lap joint testing in a split hopkinson apparatus, Sensors, 23(4), 2273. [https://doi.org/10.3390/s23042273]