Piezoelectric Actuator 기반 FSM의 동역학 모델

1. 서론

Fast Steering Mirror (FSM)은 레이저 빔의 정밀 제어가 요구되는 많은 응용분야에서 사용되고 있다. 레이저 커팅, 용접 같은 자재 가공 응용분야에서는 정확하고 신속하게 레이저 빔을 요구되는 방향으로 조사하는데 사용된다[1]. 최근에는 항공, 우주, 방위산업 분야가 성장함에 따라 FSM을 이용한 기술들이 연구되고 있다. 우주 분야에서는 인공 위성들 간의 레이저 통신의 안정화와 정렬을 하는 목적으로 사용되고 있으며 항공, 방위산업 분야에서는 레이저를 이용한 조준 장치와 시선 안정화 제어에 사용되고 있다[2-6].

일반적으로 FSM은 Actuator, 반사 거울, 베이스, Hinge Joint로 구성되며 Hinge Joint를 중심으로 2개 또는 4개의 Actuator를 구동하여 반사 거울의 각도를 조정하여 거울에 반사되는 빔의 경로를 제어한다. Actuator의 종류에 따라 Voice Coil Actuator (VCA) 기반의 FSM[7]과 Piezoelectric Actuator(PZT) 기반의 FSM[8]으로 분류된다. VCA기반의 FSM (VFSM)은 넓은 구동 범위를 동작할 수 있는 장점이 있지만 낮은 주파수 대역폭의 한계가 있다. PZT기반의 FSM (PFSM)은 높은 주파수 대역폭의 장점을 가지지만 구동 범위가 제한적인 단점이 있다.

FSM은 2자유도의 미소 변위를 동작시키기 위해 Flexible Hinge 구조로 설계가 된다[9]. 2자유도 회전 메커니즘은 Ball Joint로도 쉽게 구현은 가능하지만 Ball Joint는 높은 마찰 때문에 높은 힘이 요구되며 제한적인 힘을 가진 VCA나 PZT로는 구동의 한계가 많다. Flexible Joint는 이러한 단점들을 보완한 구조로 적은 마찰 특성과 간소한 구조 설계가 가능해지는 장점이 있다.

한편, FSM은 적용되는 응용분야의 특성상 정밀한 제어가 요구되며 그런 기대에 맞춰 제어 방법에 대한 연구도 다양하게 진행되었다. 기존에 흔히 사용되는 방식은 PID기반의 제어이지만[10,11] 동역학 모델 기반의 제어 방식은 기존 PID 제어보다 더 높은 제어 성능을 기대할 수 있는 결과를 보여주었다[12]. 이러한 양상은 FSM뿐만 아니라 모터를 이용한 대부분의 서보 제어시스템에서도 이미 입증이 되었다[13]. 동역학 모델 기반의 제어를 통해 뛰어난 성능을 기대하기 위해서는 정확한 동역학 모델이 필요한데 기존 연구들[14,15]에서는 FSM의 동역학 모델을 단순 질량-스프링-댐퍼 시스템으로 모델링을 하였다. 단순 질량-스프링-댐퍼 모델은 VFSM에서는 적용이 가능하지만 PFSM에서는 PZT 자체의 특성 때문에 적합하지 않다.

PZT는 작고 간단해 보이는 구동기지만 전기적인 특성으로 인해 발생되는 히스테리시스와 내장된 탄성으로 인해 발생되는 공진 때문에 제어적인 관점에서는 매우 복잡한 시스템이다. 비선형 특성이 제어에 미치는 영향이 미비하다면 피드백 제어를 통해 보상되기 때문에 제어 설계에 중요하게 고려할 요소는 아니지만 PZT의 히스테리시스는 제어 성능에 상당한 영향을 미친다. 하지만 비선형, 선형 특성을 통합적으로 고려한다면 제어 설계가 쉽지 않고 안정도와 성능 분석이 어렵다. 그래서 기존 연구에서는 비선형 특성과 선형 특성을 분리하고 선형 특성을 고려한 모델 기반 제어에 비선형 특성을 고려한 피드포워드 제어방법을 적용하였다[16].

본 논문에서는 PZT 특성과 FSM의 Flexible Hinge Joint를 고려한 새로운 동역학 모델을 제안하였다. 제안된 동역학 모델은 기계 시스템과 전자 시스템으로 분류되었으며 모델을 검증하기 위해 주파수 응답을 측정하였으며 제안된 동역학 모델이 타당하다는 것을 입증하였다.

2. PFSM 시스템

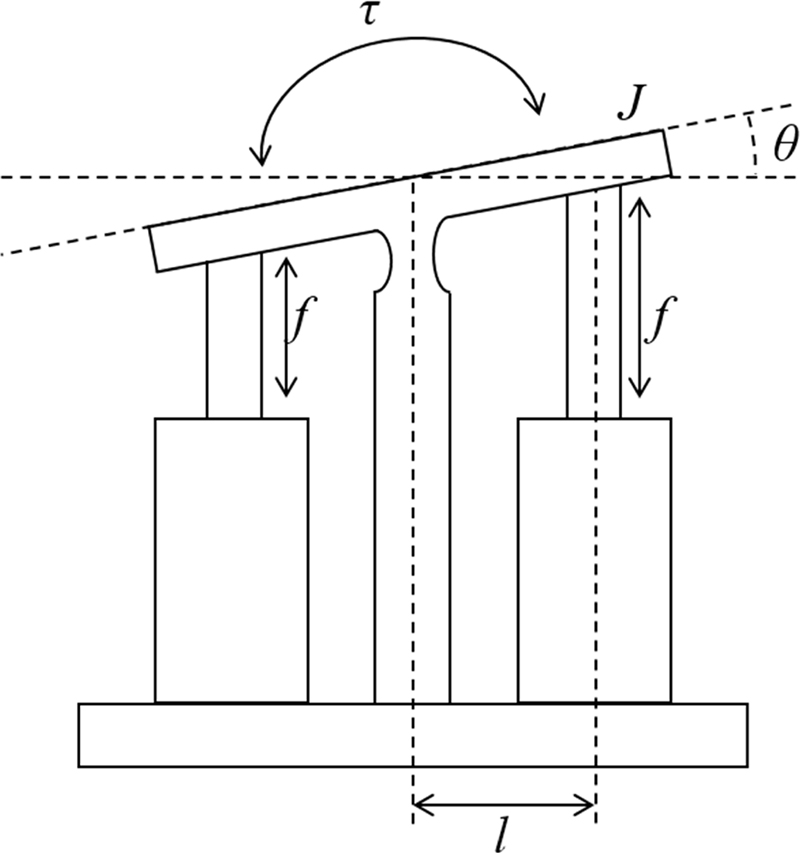
일반적을 PFSM은 각 축에 Hinge Joint를 기준으로 PZT 2개가 거울 양 끝 단에 부착되어 있다. 일반 DC모터처럼 전류를 제어하는 VCA와는 반대로 PZT는 전압을 제어하여 Piezo소자의 길이를 변화시킨다. 양단의 두 PZT의 길이 차이에 의해 Tip/Tilt 모션을 만들며 Fig. 1에 동작 구조가 묘사되어 있다. VFSM에서 위치값은 VCA의 와전류를 측정하는 반면 PFSM은 PZT에 Strain-gauge를 부착하여 위치값을 측정한다.

Fig. 1

General structure of FSM

서론에서 언급한 것 처럼 FSM은 소형화된 구조를 구현하기 위해 Flexible Hinge 구조로 설계된다. Flexible Hinge는 두 회전축의 중심을 동일하게 만들고 두 축을 기구학적으로 분리시켜주므로 FSM의 각도 제어를 간단하게 만들어준다. 이러한 구조는 PFSM에만 국한된 것이 아니며 VFSM 또한 이런 구조로 되어 있다. 이 Flexible Hinge 구조는 작은 구조와 두 축의 기구학적 분리를 만들어주는 장점을 가졌지만 FSM 각도 제어의 한계를 만들어내는 큰 요인이다. Flexible Hinge 구조가 갖고 있는 탄성에 의해 진동이 발생하며 제어의 대역폭은 진동에 의해 발생되는 공진주파수에 제한되기 때문이다.

이러한 특징 때문에 기존 연구에서는 FSM의 제어 설계를 할 때 동역학 모델은 질량-스프링-댐퍼 시스템 모델이 적용되었다. 하지만 질량-스프링-댐퍼 모델은 VFSM에는 적합한 모델이지만 PFSM에는 적합하지 않다. 왜냐하면 PZT가 자체적인 질량-스프링-댐퍼 시스템 특성을 가지기 때문이다. 정확하지 않은 동역학 모델을 고려하여 제어기를 설계했을 경우 예측되지 않은 불안정성을 야기하는 문제가 발생할 수 있다. 그러므로 PFSM은 두 개의 질량-스프링-댐퍼 시스템이 적용된 2 관성계 시스템으로 모델링이 되어야 한다.

3. PFSM 동역학 모델

3.1 기계적 2 관성계 모델링

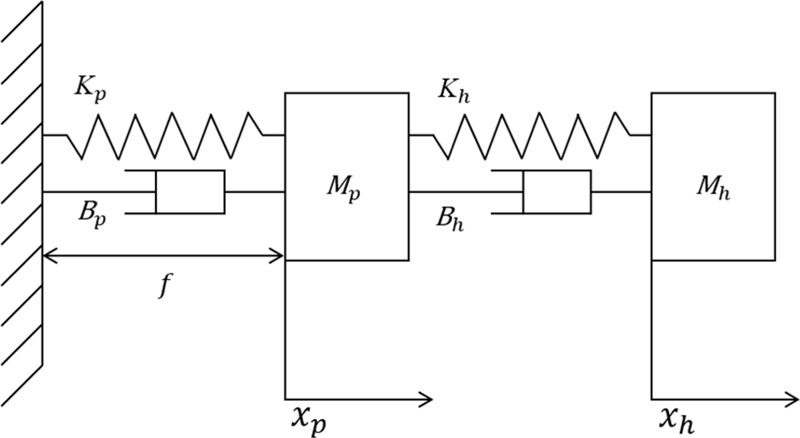
PZT는 전자 시스템과 기계 시스템이 합쳐진 형태이므로 PFSM의 입력 전압부터 Strain-gauge 센서 출력까지 시스템의 전달함수를 구하기 위해서는 기계 시스템과 전자 시스템을 분리하여 계산해야 한다. PFSM의 기계 시스템은 보통 넓은 가동 범위로 동작하기 위해 탄성을 띠는 구조물이 Piezoelectric 소자에 예압을 가한 형태로 제작되며 질량-스프링-댐퍼 시스템으로 모델링할 수 있다. PFSM은 Flexible Hinge 구조에 PZT가 직렬로 결합된 형태이기 때문에 2 관성계 시스템으로 모델링 될 수 있으며 2 관성계 시스템으로 표현한 PFSM의 자유물체도는 Fig. 2와 같이 표현할 수 있다. Flexible Hinge에 회전 동작을 하는 반사 거울의 관성계는 수식을 간단히 하기 위해 병진 운동으로 관성계로 표현하였으며 2 관성계의 동역학 수식은 아래와 같다.

Fig. 2

PFSM System model represented as two inertia system

$\[ M_p{\ddot{x}}_p=\left(B_p+B_h\right){\dot{x}}_p+\left(K_p+K_h\right)x_p-B_h{\dot{x}}_h-K_h{x}_h=f \]$

(1)

$\[ M_h{\ddot{x}}_h+B_h{\dot{x}}_h+K_h{x}_h-B_h{\dot{x}}_p-K_h{x}_p=0 \]$

(2)

식(1)과 식(2)에 라플라스 변환을 적용하여 정리하면 식(3)처럼 표현할 수 있다. 식(3)을 통해 구동힘에서 PZT의 변위까지 전달함수를 식(4)처럼 구할 수 있다.

$\[ A\left[\begin{array}{c}{X}_p\left(s\right)\\ X_h\left(s\right)\end{array}\right]=\left[\begin{array}{c}F\left(s\right)\\ 0\end{array}\right] \]$

(3)

$\[ G_m\left(s\right)=\frac{X_p\left(s\right)}{F\left(s\right)}=\frac{M_h{s}^2+B_{h}s+K_h}{D} \]$

(4)

여기서,

$\[ \begin{array}{c}A=\left[\begin{array}{cc}{M}_p{s}^2+\left(B_p+B_h\right)s+K_p+K_h& -\left(B_{h}s+K_h\right)\\ -\left(B_{h}s+K_h\right)& M_h{s}^2+B_{h}s+K_h\end{array}\right]\\ \left.D=\left(M_p{s}^2+\left(B_p+B_h\right)s+\left(K_p+K_h\right)\right)\right)\left(M_h{s}^2+B_{h}s+K_h\right)\\ -{\left(B_{h}s+K_h\right)}^2\end{array} \]$

3.2 PFSM의 전기적 시스템 모델링

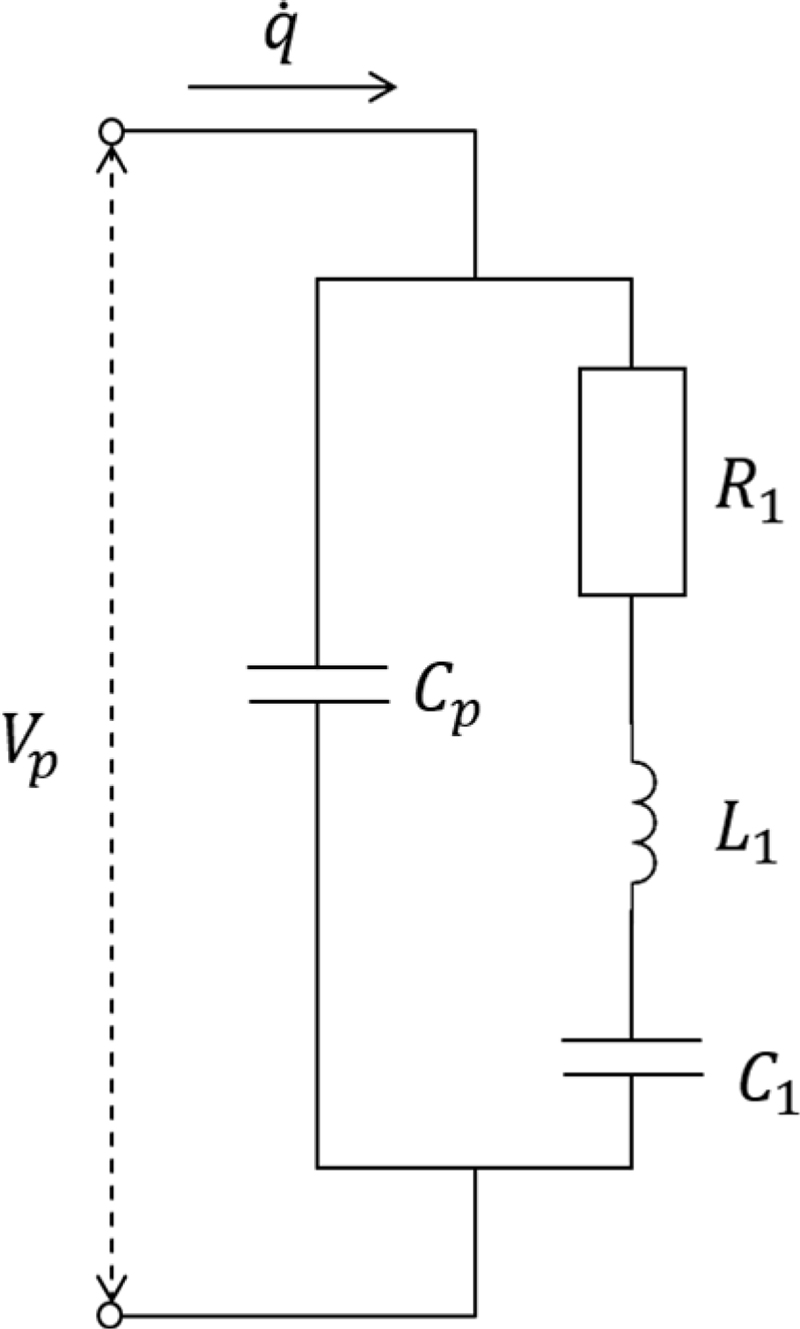
PZT의 전기적 시스템은 Fig. 3과 같이 IEEE 모델[13]을 적용하였다. PZT 양단의 전압에서 전하량까지의 전달함수는 식(5)로 나타낼 수 있다. 식(5)에서 알 수 있듯이 Piezoelectric Actuator의 전기적 시스템은 공진과 반공진이 존재하며 이때 공진주파수와 반공진 주파수는 각각 식(6) 및 식(7)과 같다.

Fig. 3

Electrical part model of piezoelectric actuator using IEEE model

$\[ G_e\left(s\right)=\frac{q}{V_p}=\frac{C_p\left(L_1{C}_1{s}^2+R_1{C}_{1}s+1+C_1/C_p\right)}{L_1{C}_1{s}^2+R_1{C}_{1}s+1} \]$

(5)

$\[ {\omega }_{er}=\frac{1}{\sqrt{L_1{C}_1}} \]$

(6)

$\[ {\omega }_{er}=\sqrt{\frac{1+C_1/C_p}{L_1{C}_1}} \]$

(7)

위의 식을 통해 알 수 있듯이 반공진 주파수는 공진주파수보다 더 높은 주파수에 존재한다.

3.3 동역학 모델 타당성

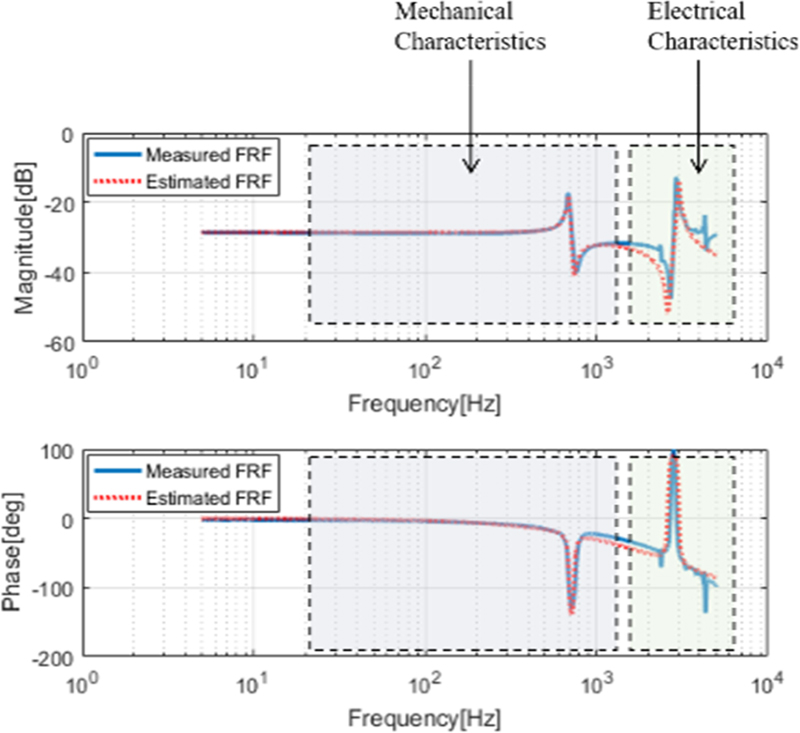
본 연구에서는 PFSM의 동역학 모델을 주파수 응답을 통해 검증하였다. 주파수 응답은 Digital Signal Analyzer (LIQUID INSTRUMENTS, Moku: Lab)을 이용하여 측정하였으며 입력 신호는 FSM의 증폭기 입력 전압, 출력 신호는 Strain-gauge 센서 출력이다. 입력 신호는 Swept Sine 신호를 5 Hz에서 5 kHz까지 주파수를 증가시켜 측정하였다. Fig. 4 측정된 FRF를 보여준다. 1 kHz 미만에서 나타나는 기계적인 특징은 3.1절에서 언급한 것처럼 2 관성계 시스템의 공진과 반공진이 발생하는 특징을 보여준다. 전기적인 특징은 2 kHz 이상에서 나타나며 3.2절에서 언급한 것과 동일하게 반공진과 공진이 연속적으로 나타나는 것을 볼 수 있다. Strain-gauge 센서 출력에는 노이즈 제거를 위한 1차 저주파 통과 필터가 적용되어 있으며 차단 주파수는 2 kHz이다. 이러한 특징들을 종합하여 PFSM의 전달함수를 식(8)과 같이 나타낼 수 있다.

Fig. 4

FRF from piezoelectric input voltage to strain-gauge output

$\[ G_{PFSM}\left(s\right)=G_e\left(s\right)G_m\left(s\right)G_l\left(s\right) \]$

(8)

여기서,

$\[ G_l\left(s\right)=\frac{1}{{\tau }_{l}s+1} \]$

식(4)를 참고하면 기계특성에서 반공진 주파수는 Flexible Hinge Joint설계에 따라 결정되는데 Joint의 강성이 클수록 반공진 주파수는 증가한다. 만약 반공진 주파수만 고주파로 증가시키고 Notch 필터를 적용하여 공진을 상쇄시킬 수 있다면 높은 제어 대역폭이 기대되는 FSM을 설계할 수 있을 것이다.

이 모델은 시스템의 선형 특성만 서술한 것이며 비선형 마찰, 히스테리시스 등의 비선형 요소는 포함되지 않았다. 5 Hz 미만의 저주파 범위에서는 비선형 마찰이나 히스테리시스가 주파수 응답을 통해 측정될 수 있을지 모르나 이 연구에서는 다루지 않았다. 실제 PFSM을 정밀하게 제어하는 데 있어 동역학 모델뿐만 아니라 히스테리시스나 비선형 마찰 또한 중요하게 고려되어야 하는 요소이다. Fig. 5에 PFSM의 통합적인 동역학 모델을 블록선도로 표현하였다.

Fig. 5

Block diagram of the PFSM dynamic model

이전 장에 언급한 것처럼 식(5)에 기술된 PFSM의 전기적 시스템은 공진 주파수는 반공진 주파수보다 더 저주파에 존재해야 하지만 실제 FRF는 반대로 반공진주파수가 더 저주파에 존재하는 형태이다. 이런 응답이 발생한 원인으로는 다음과 같이 추정할 수 있다. 통상적으로 전압을 증폭시키는 증폭기를 이용하여 구동시키는데 여기서 증폭 회로의 구조로 인해 출력이 반전되는 특징을 가질 수 있다. 그래서 이 특징을 적용하면 증폭기 입력에서 Strain-gauge 센서까지 실제 시스템의 주파수 응답을 측정하였을 때 식(5)의 역수의 형태를 띠게 된다.

4. 결론

본 연구에서는 PFSM의 동역학 모델을 도출하고 이를 실험적으로 검증하였다. 동역학 모델은 크게 기계적인 부분과 전기적인 부분으로 나뉜다. 기계적인 시스템 모델은 Flexible Hinge의 탄성과 PZT에 내장된 탄성이 직렬로 연결된 구조를 고려하여 2 관성계 시스템으로 모델링하였다. 전기적인 시스템은 IEEE 모델을 적용하였으며 전달 함수와 주파수 응답이 반전되는 특징은 증폭기 회로에 기반하여 나타나는 특징으로 보이며 제조사의 회로를 알지 못하므로 이는 향후 회로를 설계하여 명확히 해봐야 할 것으로 보인다.

향후 연구에서는 히스테리시스 모델을 포함하여 비선형 부분과 선형 부분을 나누고 히스테리시스를 보상하기 위한 히스테리시스 모델을 연구할 것이다. 기존에 일반적으로 사용되는 히스테리시스 보상 방법은 Bouc-Wen 모델을 적용하여 피드 포워드로 보상하는 것이다[15]. 히스테리시스 모델을 기반으로 피드포워드 보상하는 방법은 온도에 대한 히스테리시스를 보상하지 못하기 때문에 온도 변화가 심한 우주, 항공 분야에 적용되기에 부적합하다. 도출된 동역학 모델을 고려하면 Disturbance Observer (DOB) 같은 강인 제어기가 적용될 수 있으며 DOB는 모델에 포함되지 않은 히스테리시스를 외란으로 추정하여 보상할 것이다.

References

• Hafez, M, (2000), Compact fast-steering tip/tilt laser scanner for high power material processing applications, Ph.D. Thesis, Swiss Federal Institute of Technology in Lausanne.
• Portillo, A. A., Ortiz, G. G., Racho, C., (2001), Fine pointing control for optical communications, Proceedings of the IEEE Aerospace Conference, 3, 3/1541-3/1550. [https://doi.org/10.1109/AERO.2001.931385]
• Pérez Arancibia, N. O., Chen, N., Gibson, J. S., Tsao, T.-C., (2006), Variable-order adaptive control of a microelectromechanical steering mirror for suppression of laser beam jitter, Optical Engineering, 45(10), 104206. [https://doi.org/10.1117/1.2363189]
• Skormin, V. A., Tascillo, M. A., Busch, T. E., (1995), Adaptive jitter rejection technique applicable to airborne laser communication systems, Optical Engineering, 34(5), 1263-1268. [https://doi.org/10.1117/12.201638]
• Wilkerson, B. L., Giggenbach, D., Epple, B., (2006), Concepts for fast acquisition in optical communications systems, Proceedings of the Free-space Laser Communications VI, 6304, 67-78. [https://doi.org/10.1117/12.680487]
• Kim, H. S., Lee, D.-C., Lee, K.-D., Kim, Y.-S., (2014), Performance evaluation of the tip-tilt actuator in fast steering secondary mirror for large telescope, Journal of the Korean Society for Precision Engineering, 31(5), 403-409. [https://doi.org/10.7736/KSPE.2014.31.5.403]
• Hafez, M., Sidler, T. C., Salathé, R. P., Jansen, G. L. M., Compter, J. C., (2000), Design, simulations and experimental investigations of a compact single mirror tip/tilt laser scanner, Mechatronics, 10(7), 741-760. [https://doi.org/10.1016/S0957-4158(99)00093-8]
• Sweeney, M. N., Erdelyi, E., Ketabchi, M., Kent, B, (2003), Design considerations for optical pointing and scanning mechanisms, Proceedings of the Optomechanics, 5176, 135-146. [https://doi.org/10.1117/12.523415]
• Zhou, Q., Ben-Tzvi, P., Fan, D., Goldenberg, A. A., (2008), Design of fast steering mirror systems for precision laser beams steering, Proceedings of the International workshop on robotic and sensors environments, 144-149.
• Tang, T., Ma, J., Ren, G., (2011), PID-I controller of charge coupled device-based tracking loop for fast-steering mirror, Optical Engineering, 50(4), 043002. [https://doi.org/10.1117/1.3567059]
• Yu, Z., Cui, N., Chen, X., Xu, C., Cao, K, (2015), H∞ control for fast steering mirror based on the incremental PI controller, Proceedings of the Conferences of the Photoelectronic Technology Committee of the Chinese Society of Astronautics 2014, 9521, 95-99. [https://doi.org/10.1117/12.2087306]
• Hinnen, K., Verhaegen, M., Doelman, N., (2008), A data-driven H2-optimal control approach for adaptive optics, IEEE Transactions on Control Systems Technology, 16(3), 381-395. [https://doi.org/10.1109/TCST.2007.903374]
• Park, Y., Paine, N., Oh, S., (2017), Development of force observer in series elastic actuator for dynamic control, IEEE Transactions on Industrial Electronics, 65(3), 2398-2407. [https://doi.org/10.1109/TIE.2017.2745457]
• Goldfarb, M., Celanovic, N., (1997), Modeling piezoelectric stack actuators for control of micromanipulation, IEEE Control Systems Magazine, 17(3), 69-79. [https://doi.org/10.1109/37.588158]
• Fujii, F., Tatebatake, K. I., Morita, K., Shiinoki, T., (2018), A bouc-wen model-based compensation of the frequency-dependent hysteresis of a piezoelectric actuator exhibiting odd harmonic oscillation, Actuators, 7(3), 37. [https://doi.org/10.3390/act7030037]
• Jamaludin, Z., Van Brussel, H., Swevers, J., (2009), Friction compensation of an XY feed table using friction-model-based feedforward and an inverse-model-based disturbance observer, IEEE Transactions on Industrial Electronics, 56(10), 3848-3853. [https://doi.org/10.1109/TIE.2009.2017560]