에너지 기반 마모모델을 적용한 압입축 프레팅 마모해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Railway axles are among critical components ensuring safe and efficient train operations. They are particularly susceptible to damage mechanisms such as fretting wear and fatigue. Fretting induced by high contact pressure and microslip between contact surface can significantly deteriorate fatigue strength at the contact edge of the press-fit section. Recent research has been conducted to enhance axle strength and reliability. However, fretting wear or micro-crack formation at the wheel-press-fit zone of axles is still an active area of investigation. Accurately analyzing fretting wear is challenging due to its sensitivity to numerous factors such as changes in friction coefficient, influence of wear particles, and selection of an appropriate wear model. This paper aimed to establish a comprehensive analysis method for fretting wear in interference-fitted axles using finite element analysis (FEA) and numerical analysis techniques. Two wear models were applied in simulations: an Archard wear model and an energy-based wear model. Analysis results were compared with experimental data from rotating bending fatigue press-fit specimens. This comparison will help validate the proposed analysis method and assess the effectiveness and accuracy of different wear models in predicting fretting wear in press-fit axles.
Keywords:
Press-fit axle, Fretting wear, Contact pressure, Slip, Wear model, Finite element analysis키워드:
압입축, 프레팅 마모, 접촉 압력, 미끄럼, 마모모델, 유한요소해석1. 서론
철도차량 차축은 철도차량의 안전을 보장하는 가장 중요한 부품 중 하나이다. 차축이 손상되거나 파손되면 주행 중 탈선이나 심각한 사고를 유발할 수 있기 때문에, 차축의 손상을 예방하고 관리하는 것이 필수적이다[1]. 철도차량 차축은 차륜이 억지 끼워맞춤으로 강제 압입된 구조를 가지고 있으며, 기어 및 베어링 압입부와 같이 차축의 차륜 압입부 접촉 끝단에는 프레팅(Fretting) 손상이 발생한다. 프레팅은 접촉면에 높은 접촉 압력과 미세한 미끄럼(Microslip)으로 인해 발생하는 손상으로, 프레팅이 발생하면 피로강도가 현저히 감소한다[1-3].
초기 연구에서는 압입축의 피로강도 향상 방안에 집중하였다. Nishioka 등[4]은 실물 및 압입 시험편을 이용한 피로시험을 통해 여러 인자가 압입축의 수명에 미치는 영향을 분석하였고, 압입부 형상 변경에 따른 응력집중 완화 방법[5]과 열처리에 의한 피로수명 향상 방안을 제시하였다[6]. 그러나 이들 초기 연구는 프레팅 마모에 의한 단면적의 변화량이 매우 적어 피로강도에 크게 영향을 미치지 않는다는 연구 결과[7]를 기반으로 프레팅 마모에 대한 관심을 갖지 않았다. 그러나 압입축에 프레팅이 발생하면 접촉표면에는 프레팅 마모와 프레팅 피로에 의한 균열이 동시에 발생한다. Kubota 등[8]은 압입축의 피로균열의 발생 및 진전이 프레팅 마모와 밀접하게 관련되어 있으며, 피로균열은 프레팅 마모와 접촉응력이 균형을 이루는 접촉영역에서 발생한다고 하였다. 또한, Lee 등[9]은 압입축의 피로 사이클별 마모형상을 이용하여 유한요소해석을 수행하고, 마모에 따른 피로수명의 변화를 분석하였으며, 프레팅 마모에 의해 응력분포가 급격히 변화하므로 피로수명 예측 시 프레팅 마모가 고려되어야 한다고 하였다.
따라서, 최근에는 압입축의 수명을 정확하게 예측하기 위해 프레팅 마모를 고려한 수명평가가 수행되고 있다. Lee[10] 등과 Zhang등[11]은 압입축의 프레팅 마모를 해석하고, 마모를 고려한 피로균열 발생 수명을 해석하였다. 또한, Zeng 등[12]은 실제 압입 차축의 마모를 고려한 균열 발생 수명을 예측하고, 응력완화 홈(Stress Relief Groove)의 영향을 검토하였다. Dong 등[13]은 실험적으로 측정한 압입축의 프레팅 마모 형상을 반영하여 균열 진전 수명을 해석하였으며, 마모를 고려하였을 때 더 정확하게 균열 진전 수명을 예측할 수 있다고 하였다.
이상과 같이, 압입축의 피로손상 예측에서 프레팅 마모의 고려는 매우 중요하므로, 정확한 피로수명 예측을 위하여 프레팅 마모 예측의 신뢰성을 확보해야 한다. McColl 등[14]은 유한요소해석과 수치해석을 통해 원통 패드와 평판(Cylinder-on-flat)프레팅 시험편의 마모 예측 방법을 제안하고, 효율적인 마모 해석을 위하여 마모 증분 크기 최적화(Cycle Jumping Technique)를 사용하였다. 이후 Madge 등[15], Cruzado 등[16]을 포함한 많은 연구자들이 프레팅 마모 예측에 대한 향상된 방법을 제안하였다. 그러나 수만 혹은 수십만 사이클에 해당되는 마모 해석 시간을 줄이기 위하여 도입한 마모 증분 값에 따라 해석 결과의 불안정성 문제와 길들이기 영역의 마모를 예측할 수 있는 적절한 마모 모델의 선택 등은 여전히 해결이 필요한 부분이다[14,15,17].
Lee 등[18]은 유한요소해석과 영향계수(Influence Coefficient)를 이용한 마모 수치해석 방법을 제안하였으며, 압입 시험편 마모형상 시험 결과와 비교하여 해석 방법의 유효성을 검증하였다. 본 논문에서는 이전 연구를 바탕으로 압입축 프레팅 마모해석 방법의 향상을 위하여 유한요소해석 모델과 수치해석 방법을 개선하고, Archard 마모 모델과 에너지 기반(Energy Based) 마모 모델을 적용하여 마모해석을 수행하였다. 마모모델에 따른 시뮬레이션 결과를 실험결과와 비교하여 마모해석 방법의 타당성을 검토하고, 마모 모델의 적용 타당성을 평가하였다.
2. 유한요소해석 및 마모해석
2.1 유한요소해석
유한요소해석은 시험 결과와 비교를 위해 회전 굽힘 압입 시험편[3]을 대상으로 하였고, 시험편의 축과 보스 압입부 간섭량(Shrinkage Allowance)은 Lamé의 평균 공칭 접촉 압력[19]이 90 MPa일 때를 해석하였다. 유한요소해석은 ABAQUS[20]를 사용하였으며, 유한요소해석 모델링 및 해석 방법은 기존연구[18]와 동일하다. 주요 특징은 다음과 같다.
1) 압입축은 축대칭 형상이지만, 굽힘하중이 작용할 때 비대칭 변형을 나타내므로 비선형, 비대칭 굽힘을 허용하는 축대칭 솔리드 요소(Axisymmetric Solid Element, CAXA4R)[20] 사용
2) 압입축의 길이 방향으로 형상 및 하중 조건이 대칭이므로 1/2 모델 구축
3) 축과 보스의 접촉영역은 미끄럼 접촉 요소(Axisymmetric Slide Line Element)와 Slide Line으로 접촉을 모델링, 마찰해석은 라그랑지 방법(Lagrange Multiplier Friction Formulation)을 사용하고 마찰계수 μ = 0.6 적용[26]
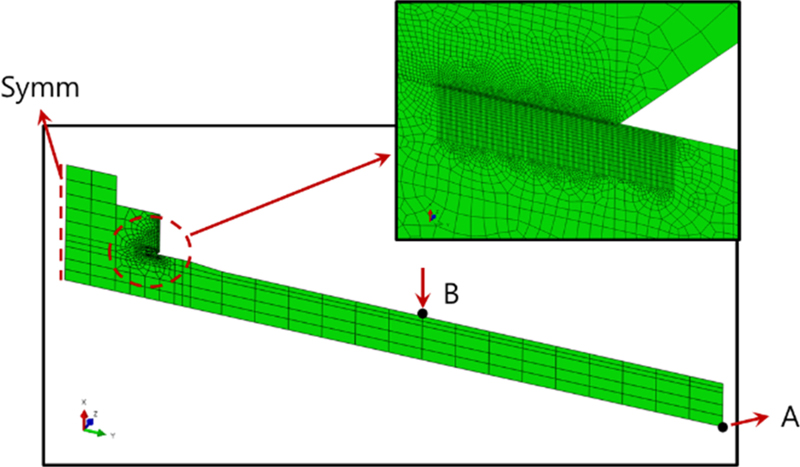
4) 경계 조건으로는 시험편에 굽힘응력이 작용하도록 축 끝단(Fig. 1(A))을 고정하고, 하중은 시험기 그립 끝단에 해당되는 위치(Fig. 1(B))에 집중하중을 주었으며, 축방향 대칭면에 대칭조건(Fig. 1(Symm))을 적용
5) 탄성계수(Young’s Modulus)는 207,000 MPa, 푸아송비(Poisson’s Ratio)는 0.3 적용[18]
구축된 유한요소 해석 모델은 Fig. 1과 같다. 기존 연구와 달리, 압입부 끝단 프레팅 발생영역의 요소 분할 크기는 해석 시간과 최대 접촉 압력의 변화를 검토한 후, 최소 요소를 0.004 mm로 설정하여 응력집중을 최대한 반영할 수 있도록 하였다. 위와 같이 비대칭-축대칭요소를 이용하여 압입축의 굽힘 하중 상태를 해석하는 모델은 3차원 솔리드 요소를 사용하는 모델에 비해 해석 시간을 크게 줄일 수 있어 마모와 같은 반복 해석에 효율적이라는 장점이 있었다.
2.2 마모해석
유한요소해석 및 수치해석을 통한 프레팅 마모 해석에서 해석 결과에 영향을 미치는 가장 중요한 요소는 마모 해석 방법과 적합한 마모 모델의 적용이다.
첫째, 마모 해석 방법에 대해 대부분의 연구는 유한요소해석 결과를 이용하여 수치해석으로 마모를 계산하고 있다. 이러한 마모 시뮬레이션에서는 매 사이클 마다 유한요소해석과 마모 계산을 반복하게 되면 너무 많은 시간이 소요되므로, 이를 최적화하기 위한 방법으로 마모 사이클 증분 기법(Cycle Jumping Technique)을 사용하고 있다[14,15]. 이 접근 방법은 마모가 발생하는 적은 수의 사이클 동안 마모가 일정하게 발생한다는 가정하에 시뮬레이션 속도를 높인다. 구체적으로 한 사이클의 마모량에 사이클 증분 계수 N을 곱하여 N회의 실제 마모량을 계산하는 방식이다. McColl 등[14]은 Archard 마모식을 이용한 마모량 ∆h 계산 방법에 사이클 증분 계수 ∆N을 적용하여 해석 시간을 감소시키고자 다음과 같은 수식을 적용하였다.
| (1) |
여기서 s는 미끄럼 거리, p는 접촉 압력, k는 마모계수(Archard Wear Coefficient)이다. 이 방법은 계산시간을 줄일 수 있지만, 증분계수에 따라 해석 결과가 달라지므로 적절한 값의 선정이 어렵다[14,15]. 또한, 증분계수가 마모해석에서 일정한 값을 유지하므로 마모에 따라 급격하게 변화하는 접촉 압력의 변화에 동일한 값을 적용해야 하는 문제가 발생한다. 이와 같은 문제를 해결하기 위해 Lee 등[21]은 증기발생기 튜브 및 연료봉 등의 접합부에서 발생할 수 있는 프레팅 마모 현상을 예측하기 위해 영향함수(Influence Function)를 이용하여 접촉 압력과 슬립량을 계산하고 마모량을 계산하는 2차원 마모해석 모델을 개발하였다. 또한, Lee 등[18]은 유한요소해석과 영향 함수법을 사용하여 압입축의 프레팅 마모를 해석하였다. 압입축에 굽힘 하중이 작용할 때 접촉 압력과 미소슬립을 계산할 수 있는 유한요소해석 모델을 구축하고, 이를 바탕으로 Archard’s Equation을 기초로 한 마모 깊이 계산과 영향함수법(Influence Function Method)을 이용하여 마모에 따라 변화된 접촉 압력을 해석하여 반복적인 마모량을 계산하였다. 이 방법은 압입축 끝단에 발생하는 응력집중에 따른 마모량을 효율적으로 해석할 수 있어, 본 논문에서도 이 방법을 적용하였고, 해석 방법 및 절차는 다음과 같다.
1) 압입축의 압입상태와 굽힘하중 작용 시 유한요소해석을 수행하고, 인장 및 압축 하중이 작용할 때 접촉끝단의 접촉 압력 p와 미끄럼 거리 s계산
2) 유한요소해석 결과의 접촉 압력을 이용하여 2차원 평면에 접촉 압력이 작용할 경우 다음식과 같은 접촉 압력-변형량 관계[22]에 따라 영향계수(Influence Coefficient)와 각 접촉노드 i 위치의 변형량 δi계산
| (2) |
여기서 E는 탄성계수, n는 푸아송비, Cij는 영향계수이며, 이등변 삼각형 접촉요소가 등간격 a로 분포되어 있을 때 다음과 같이 계산
| (3) |
여기서, k는 접촉 노드의 위치 i와 j 사이의 거리
3) 마모 모델을 이용하여 각 접촉 노드별 마모깊이 ∆hi계산
4) 마모가 n사이클 진행될 경우 변형량 프로파일이 마모량만큼 감소한다고 가정하여 마모가 고려된 새로운 변형량 δi,n+1계산
| (4) |
5) 역행렬 계산(Matrix Inversion Method)으로 마모가 고려된 변형량 δi,n+1으로부터 각 접촉 노드별 새로운 접촉 압력 pi,n+1 계산
| (5) |
6) 다음 수렴 조건(초기 최대 접촉 압력 max(pi,initial)과 n사이클 마모 시 최대 접촉 압력 max(pi,n)의 변화가 10% 이하)이 만족할 때까지 3)-5) 반복
| (6) |
7) 원하는 마모 계산 사이클만큼 1)-6) 반복
프레팅 마모해석에서 두 번째로 중요한 요소는 마모 모델의 선정이다[23]. 현재까지 마모현상을 설명하고 예측하기 위한 많은 모델들이 제안되었으나, 광범위하게 사용되고 있는 모델은 접촉역학에 기초한 현상학적 모델인 Archard and Hirst 모델[24] 과 접촉표면에서 소산되는 에너지를 기반으로 하는 Fouvry등의 에너지 기반 마모모델[25]이다.
Archard 마모 모델에서는 다음식과 같이 마모량 V는 수직하중 P와 미끄럼 거리 S, 마모상수 k에 비례하며, 마모상수는 수직하중과 미끄럼 거리에 따라 달라진다.
| (7) |
Archard 마모 모델은 계산과정이 간단하고 적은 수의 변수만 필요하므로 다양한 프레팅 마모 시뮬레이션에 널리 사용되고 있다.
에너지 기반 마모 모델은 마모량 V가 누적된 소산 에너지(Dissipated Energy) ΣEd와 에너지 마모 상수(Energy Wear Coefficient) a에 비례하며 다음 식과 같다.
| (8) |
여기서 소산 에너지는 전단력 q와 미끄럼 거리 s의 곱으로 계산된다.
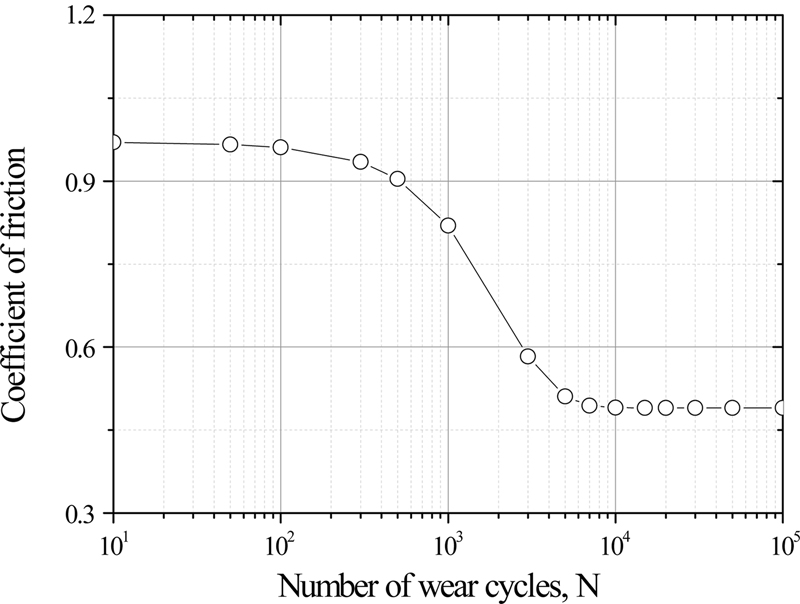
본 연구에서는 압입축의 프레팅 마모해석에서 마모 모델 적용성을 검토하기 위해 위와 같은 대표적인 마모 모델을 이용하여 마모해석을 수행하였다. 해석에 사용된 에너지 마모상수는 참고문헌[26]의 α = 4.17 × 10-8을 적용하였다. 에너지 기반 마모 모델 적용 시 마찰계수 μ는 길들이기 영역의 변화하는 마모량을 예측하기 위해 마모 사이클 N에 따라 변화하는 다음 수식의 값을 적용하였으며[27], 마모 사이클별 마모 계수의 변화는 Fig. 2 와 같다.
| (9) |
3. 해석 결과
3.1 마모형상 예측결과
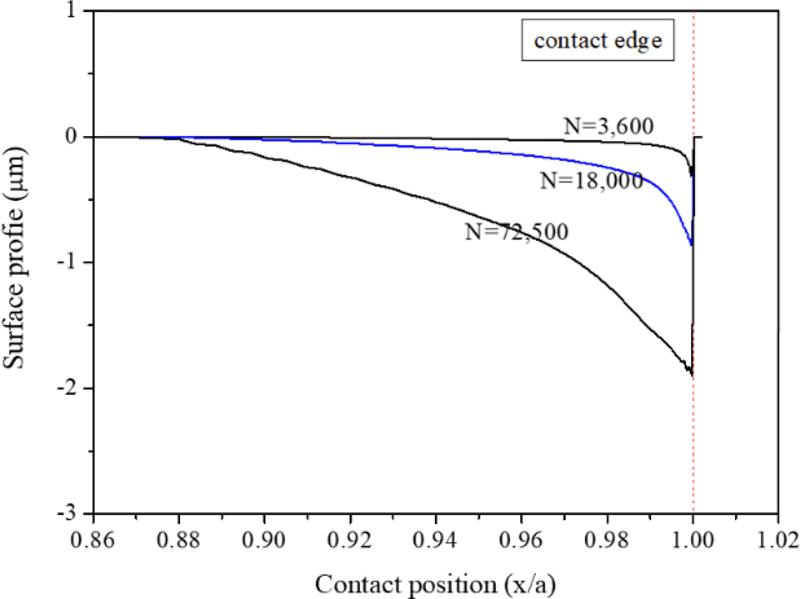
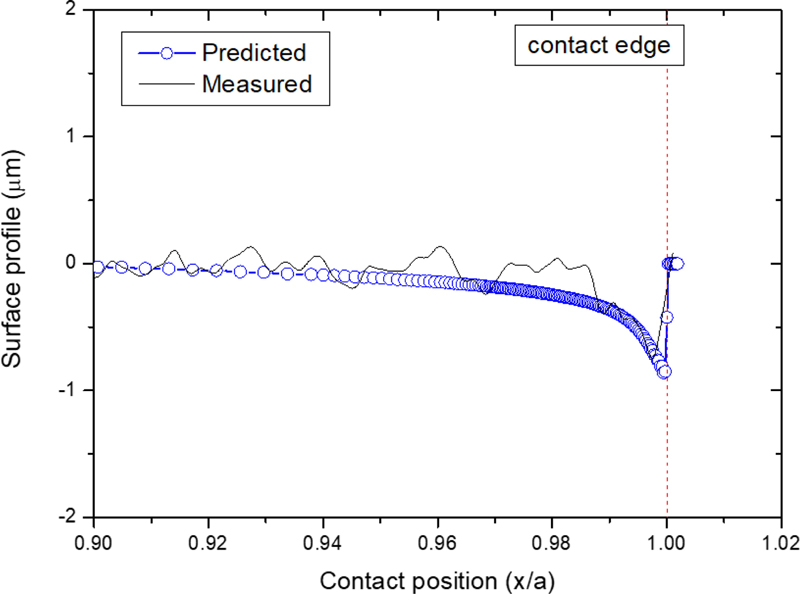
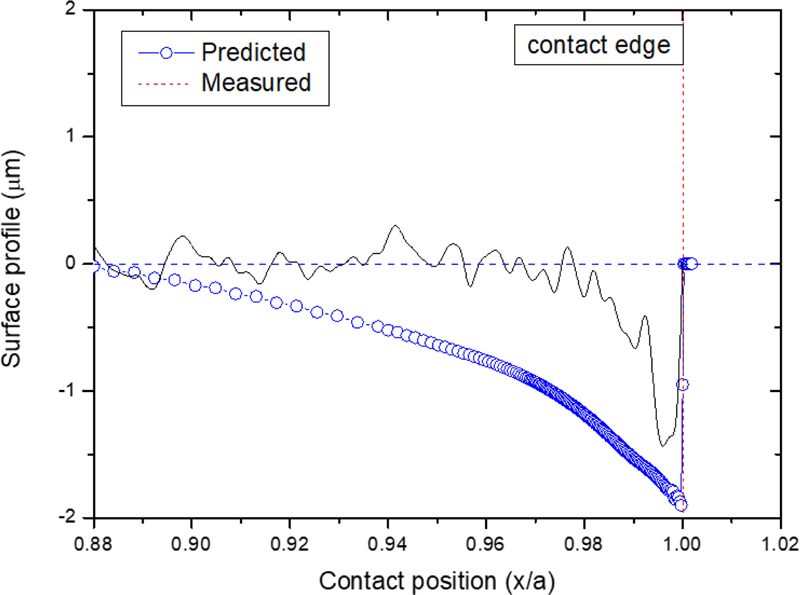
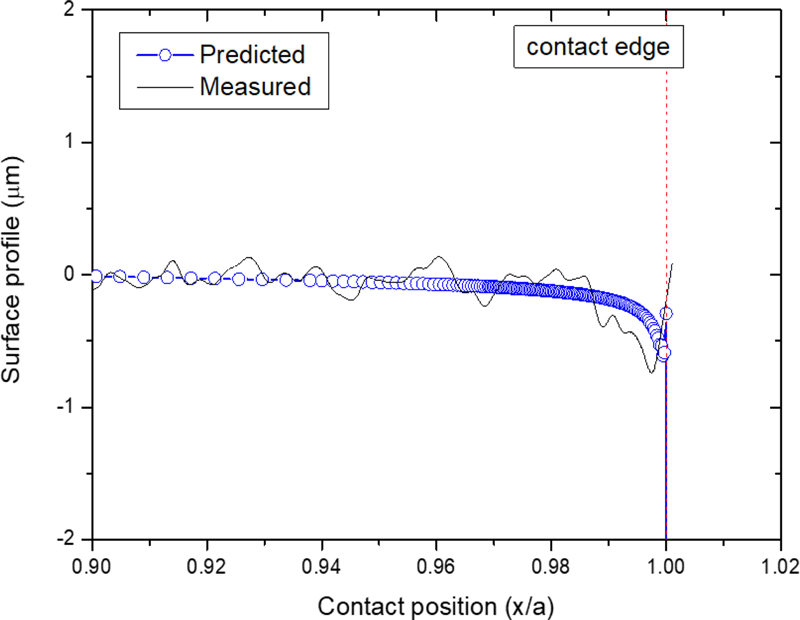
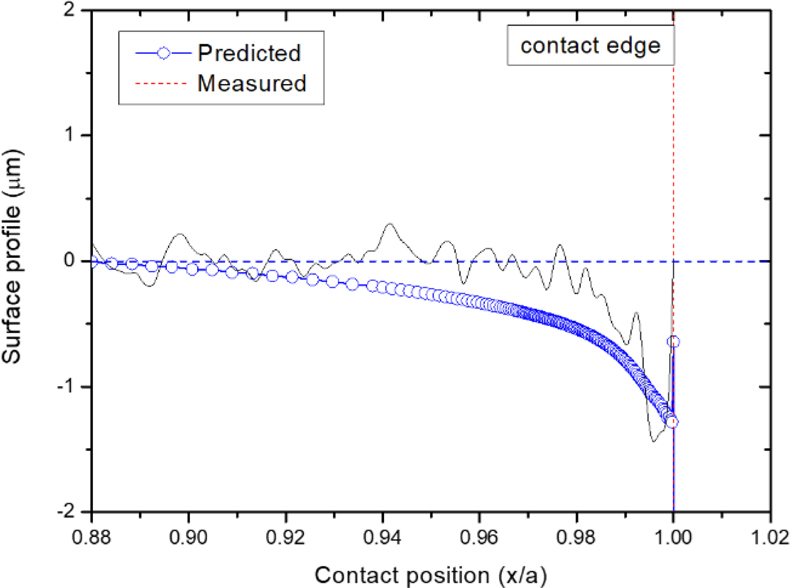
Fig. 3은 공칭 굽힘응력 180 MPa 에서Archard 마모 모델을 적용하여 마모 사이클별 압입축 끝단의 마모 형상을 예측한 결과이다. 마모상수는 에너지 기반 마모 모델에 적용하였던 에너지 마모상수를 동일하게 적용하였다. 그림에서 x축은 접촉면의 길이(a = 14.5 mm)로 나누어 표시하였고, x/a = 1의 위치는 접촉면의 끝단을 의미한다. 마모 초기에는 접촉 끝단에서 마모가 발생되며, 마모 사이클이 증가함에 따라 차츰 안쪽으로 마모가 확대되는 현상을 잘 나타내고 있다. Fig. 4 는 18,000 마모 사이클에서의 시험 결과와 해석 결과를 비교한 것으로, 해석 결과는 시험 결과와 잘 일치하였다. 그러나 Fig. 5 와 같이 마모 사이클이 더 증가했을 때, 접촉 끝단의 마모 깊이뿐만 아니라 접촉 끝단 안쪽의 마모 량도 과도하게 예측되는 경향을 보였다.
Fig. 6은 에너지 기반 마모 모델을 적용하여 18,000 사이클의 압입축 접촉 끝단 마모 형상을 예측 결과를 시험 결과와 비교한 것이다. Fig. 3의 Archard 마모 모델 결과와 비교하면, 마모량이 실험 결과보다 약간 적게 예측되었다. Fig. 7은 72,500 사이클에서 압입축 접촉 끝단 마모형상 예측 결과를 시험 결과와 비교한 그림이다. Fig. 5의 Archard 마모 모델 결과와 비교하면, 에너지 기반 마모 모델의 마모 형상 예측 결과는 실험 결과와 거의 일치한다.
3.2 접촉 압력 분포 및 결과 검토
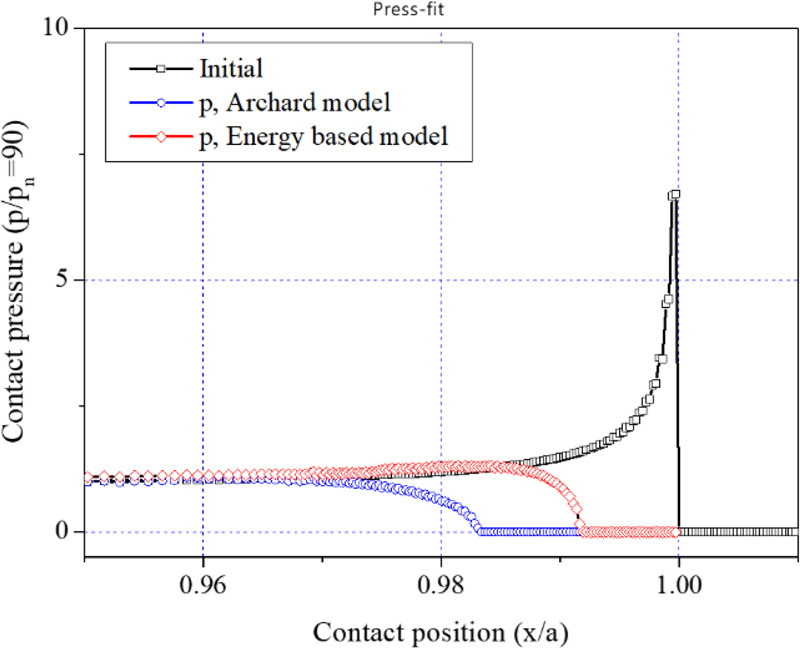
Fig. 8 는 압입 시 마모가 발생하지 않은 상태의 압입축 접촉 압력 해석 결과와 72,500 사이클의 마모 형상 예측 결과를 이용한 압입축의 접촉 압력 해석 결과를 비교한 것이다. 마모가 발생하지 않은 초기 상태에서는 접촉 끝단(x = 1.0 위치)에서 응력 집중이 발생하지만, 두 가지 마모 모델 모두 마모가 발생 후 접촉 압력이 급속히 감소하여 접촉 압력이 0인 영역이 발생한다.
Fig. 5의 Archard 마모 모델 적용 결과는 Fig. 7의 에너지 기반 마모 모델 적용 결과보다 마모 량이 더 크게 예측되었으므로, 접촉이 발생하지 않은 영역이 더 크게 나타났다. 실험 결과[3]에 따르면 압입축 균열발생 위치는 접촉 끝단에서 5-50 mm 위치이고, Fig. 8의 x = 0.996-0.999 위치에 해당된다. 압입축의 피로균열은 프레팅 마모와 접촉 압력이 균형을 이루는 영역에서 발생[8]한다고 할 때, Archard 마모 모델의 경우 고 사이클 영역에서 마모량을 과대하게 예측하는 경향을 보인다. 마모상수를 조정한다면 고 사이클의 마모량을 줄일 수 있지만, 이 경우 Fig. 4와 같이 저 사이클의 마모형상이 적게 예측되는 문제가 발생한다. 결론적으로 Archard 마모 모델은 비선형적으로 증가하는 압입축의 프레팅 마모 형상을 정확하게 예측할 수 없다.
반면, 에너지 기반 마모 모델은 Fig. 6의 저사이클 마모 영역에서 약간 적게 예측되었지만, Fig. 7의 고사이클 마모 영역에서는 실험결과와 거의 일치하는 결과를 보였다. 저사이클 마모 영역에서 마모가 적게 예측된 원인은 해석에 사용된 식(4)의 마모계수 특성 때문으로 판단된다. 식(4)의 마모계수는 1,000-3,000 사이클 사이에서 급격히 감소하고, 약 5,000 사이클 이상에서 약 0.5를 나타낸다. 압입축의 마모량 변화 실험결과를 이용하여 비 선형 마모계수를 산출하여 마모해석을 수행한다면, 에너지기반 마모 모델은 비 선형으로 나타나는 압입축의 프레팅 마모형상을 잘 예측할 것으로 판단되며, 향후 이 모델을 적용하여 압입축의 마모해석 및 수명 평가에 활용할 예정이다.
4. 결론
본 연구에서는 압입축의 프레팅 마모 해석을 위하여 유한요소해석과 수치해석 방법을 구축하고 두 가지 주요 마모 모델, Archard 마모 모델과 에너지 기반 마모 모델을 비교 분석하였다. 공칭 굽힘 응력 180 MPa에서 두 모델을 적용하여 마모 형상과 접촉 압력 분포를 예측하고, 그 결과를 실험 데이터와 비교하였으며 주요한 결론은 다음과 같다.
1) 압입축 유한요소해석 모델 구축에서 비대칭-축대칭요소를 이용하여 압입축의 굽힘 하중 상태를 해석하는 모델은 해석 시간을 크게 줄일 수 있어 마모와 같은 반복 해석에 효율적이다.
2) 유한요소해석 결과와 영향계수를 이용하여 가상 변형량을 계산하고 마모에 따라 변형량을 업데이트하여 접촉 압력을 계산하는 마모해석 방법은 압입축 끝단에 발생하는 응력집중에 따른 마모량을 효율적으로 해석할 수 있다.
3) Archard 마모 모델은 저사이클 영역에서는 예측이 잘 맞지만, 고사이클 영역에서의 마모량이 과도하게 예측되는 문제로 인해 비선형적인 프레팅 마모 형상을 정확히 예측하지 못한다.
4) 에너지 기반 마모 모델은 마모 사이클이 증가함에 따라 실험 결과와의 일치도가 높아지며, 비선형적인 프레팅 마모 형상을 잘 예측할 수 있다. 특히, 마모 계수의 비선형 특성을 반영한 경우 예측의 정확도가 더욱 향상될 것으로 보인다.
Acknowledgments
This research was supported by a grant from R&D Program (A study on the development of derailment prevention technology for high-speed train based on artificial intelligence, PK2303G1) of the Korea Railroad Research Institute, Republic of Korea.
References
-
Hirakawa, K., Toyama, K., Kubota, M., (1998), The analysis and prevention of failure in railway axles, International Journal of Fatigue, 20(2), 135-144.
[https://doi.org/10.1016/S0142-1123(97)00096-0]

-
Smith, R. A., Hillmansen, S., (2004), A brief historical overview of the fatigue of railway axles, Proceedings of the Institution Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 218(4), 267-278.
[https://doi.org/10.1243/0954409043125932]

-
Lee, D.-H., Kwon, S.-J., Choi, J.-B. Kim, Y.-J., (2007), Experimental study on fatigue crack initiation and propagation due to fretting damage in press-fitted shaft, Transactions of the Korean Society of Mechanical Engineers A, 31(6), 701-709.
[https://doi.org/10.3795/KSME-A.2007.31.6.701]

-
Nishioka, K., Komatsu, K., (1967), Researches on increasing the fatigue strength of press-fitted shaft assembly, Bulletin of Japan Society of Mechanical Engineers, 10(42), 880-889.
[https://doi.org/10.1299/jsme1958.10.880]

-
Nishioka, K., Komatsu, H., Morita, Y., (1971), Researches on increasing the fatigue strength of press-fit axle: 2nd report pressfitted shaft assembly two dimensional photoelasticity, Bulletin of Japan Society of Mechanical Engineers, 14(73), 629-635.
[https://doi.org/10.1299/jsme1958.14.629]

-
Nishioka, K., Komatsu, H, (1970), Researches on Increasing the fatigue strength of press-fitted axles: 3rd report, effect of tufftriding, Transactions of the Japan Society of Mechanical Engineers, 36(291), 1805-1811, Japanese.
[https://doi.org/10.1299/kikai1938.36.1805]

-
Nishioka, K., Hirakawa, K., (1969), Fundamental investigations of fretting fatigue (Part 4. The effect of mean stress), Bulletin of Japan Society of Mechanical Engineers, 12(51), 408-414.
[https://doi.org/10.1299/jsme1958.12.408]

-
Kubota, M., Niho, S., Sakae, C., Kondo, Y., (2003), Effect of understress on fretting fatigue crack initiation of press-fitted axle, JSME International Journal Series A Solid Mechanics and Material Engineering, 46(3), 297-302.
[https://doi.org/10.1299/jsmea.46.297]

-
Lee, D.-H., Kwon, S.-J., Choi, J.-B., Kim, Y.-J., (2007), The effect of fretting wear on fatigue life of press-fitted shaft, Transactions of the Korean Society of Mechanical Engineers A, 31(11), 1083-1092.
[https://doi.org/10.3795/KSME-A.2007.31.11.1083]

-
Lee, D.-H., Kwon, S.-J., You, W.-H., Choi, J.-B., Kim, Y.-J., (2009), Evaluation of fatigue crack initiation life in a press-fitted shaft considering the fretting wear, Transactions of the Korean Society of Mechanical Engineers A, 33(10), 1091-1098.
[https://doi.org/10.3795/KSME-A.2009.33.10.1091]

-
Zhang, Y. B., Lu, L. T., Zou, L., Zeng, D. F., Zhang, J. W., (2018), Finite element simulation of the influence of fretting wear on fretting crack initiation in press-fitted shaft under rotating bending, Wear, 400, 177-183.
[https://doi.org/10.1016/j.wear.2018.01.008]

-
Zeng, D., Zhang, Y., Lu, L., Zou, L., Zhu, S., (2019), Fretting wear and fatigue in press-fitted railway axle: A simulation study of the influence of stress relief groove, International Journal of Fatigue, 118, 225-236.
[https://doi.org/10.1016/j.ijfatigue.2018.09.008]

-
Dong, Y., Zeng, D., Wu, P., Lu, L., Zou, L., Xu, T., (2024), Numerical prediction of fretting fatigue crack growth in scaled railway axles considering fretting wear evolution, International Journal of Fatigue, 181, 108150.
[https://doi.org/10.1016/j.ijfatigue.2024.108150]

-
McColl, I. R., Ding, J., Leen, S. B., (2004), Finite element simulation and experimental validation of fretting wear, Wear, 256(11-12), 1114-1127.
[https://doi.org/10.1016/j.wear.2003.07.001]

-
Madge, J. J., Leen, S. B., McColl, I. R., Shipway, P. H., (2007), Contact-evolution based prediction of fretting fatigue life: effect of slip amplitude, Wear, 262(9-10), 1159-1170.
[https://doi.org/10.1016/j.wear.2006.11.004]

-
Cruzado, A., Urchegui, M. A., Gómez, X., (2012), Finite element modeling and experimental validation of fretting wear scars in thin steel wires, Wear, 289, 26-38.
[https://doi.org/10.1016/j.wear.2012.04.018]

-
Fouvry, S., (2023), Friction energy wear approach, in: Fretting wear and fretting fatigue, Liskiewics, T., Dini, D., (Eds.,) Elsevier.
[https://doi.org/10.1016/B978-0-12-824096-0.00006-8]

-
Lee, D.-H., Kwon, S.-J., Choi, J.-B., Kim, Y.-J., (2008), Fretting wear simulation of press-fitted shaft with finite element analysis and influence function method, Transactions of the Korean Society of Mechanical Engineers A, 32(1), 54-62.
[https://doi.org/10.3795/KSME-A.2008.32.1.054]

- Ugural, A. C., Fenster, S. K., (2003), Advanced strength and applied elasticity, Prentice-Hall, Inc.
- ABAQUS Analysis User’s Manual, Version 6.14, Dassault Systemes Simulia, Inc. https://www.3ds.com/products/simulia/abaqus
- Lee, C. Y., Tian, L. S., Bae, J. W., Chai, Y. S., (2006), Application of influence function method to the fretting wear problems, Proceedings of the Korean Society Mechanical Engineers Autumn Conference, 13-18.
- Johnson, K. L., (1987), Contact mechanics, Cambridge University Press.
-
Llavori, I., Esnaola, J. A., Zabala, A., Larrañaga, M., Gomez, X., (2018), Fretting: review on the numerical simulation and modeling of wear, fatigue and fracture, in: Contact and Fracture Mechanics, Darji, P. H., Darji, V. P., (Eds.,), IntechOpen.
[https://doi.org/10.5772/intechopen.72675]

-
Archard, J. F., Hirst, W., (1956), The wear of metals under unlubricated conditions, Proceedings of the Royal Society A, Mathematical, Physical and Engineering Sciences, 236(1206), 397-410.
[https://doi.org/10.1098/rspa.1956.0144]

-
Fouvry, S., Liskiewicz, T., Kapsa, P., Hannel, S., Sauger, E., (2003), An energy description of wear mechanisms and its applications to oscillating sliding contacts, Wear, 255(1-6), 287-298.
[https://doi.org/10.1016/S0043-1648(03)00117-0]

-
Shu, Y., Yang, G., Liu, Z., (2023), Simulation research on fretting wear of train axles with interference fit based on press-fitted specimen, Wear, 523, 204777.
[https://doi.org/10.1016/j.wear.2023.204777]

-
Argatov, I. I., Chai, Y. S., (2021), Fretting wear with variable coefficient of friction in gross sliding conditions, Tribology International, 153, 106555.
[https://doi.org/10.1016/j.triboint.2020.106555]


Principal researcher in the Department of Railroad Accident Research, Korea Railroad Research Institute. His research focuses on fatigue life evaluation of railway components.
E-mail: dhlee@krri.re.kr

Chief researcher in the Railroad Safety Division, Korea Railroad Research Institute. His research focuses on derailment mechanics.
E-mail: ysham@krri.re.kr

Chief Researcher in the Railroad Safety Division, Korea Railroad Research Institute. His research focuses on safety evaluation of railway vehicles and railway systems.
E-mail: cwlee@krri.re.kr