차량 안전성 및 안정성 향상을 위한 유한요소해석 기반 스트럿 바의 굽힘 및 압축 성능 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A strut tower brace is one of the components that can improve the driving stability of a vehicle. This component has received steady attention for a long time due to its affordable price and easy installation. However, strut tower braces sold in the market have different structures. Moreover, most of them do not contain sufficient information related to safety or stability. Thus, this study aimed to analyze and compare structural behaviors of strut tower braces having various body shapes under bending and compressive scenarios. For this purpose, this study selected six representative models in the market and calculated structural behaviors (stress and deformation) using finite element analysis. Results revealed the body shape had a decisive effect not only on the durability of the strut tower brace, but also on the safety and stability of the vehicle. Among the six models tested, the model having a body shape with a single-axis form utilizing a wide rectangular cross-sectional showed the best bending and compressive performances. This study also confirmed that bending and compressive performances could be simultaneously improved depending on body shape.
Keywords:
Strut tower brace, Bending, Compression, Finite element analysis키워드:
스트럿 바, 굽힘, 압축, 유한요소해석1. 서론
스트럿 바(Strut Tower Brace)는 차량의 서스펜션 시스템 중 하나로, 차량의 안정성(Stability)을 향상시키는 부품이다. 굽힘 강성이 충분히 확보된 스트럿 바는 차체의 강성을 증가시켜 비틀림을 줄이는 역할을 한다. 이는 주행 시 발생하는 강한 좌우 흔들림이나 선회 시 발생하는 과도한 쏠림을 방지한다[1,2]. 이에 많은 제조사들은 주행 성능과 승차감이 중요시되는 고성능 및 고급 차량에 스트럿 바를 장착하여 판매하고 있다. 스트럿 바는 완성차 시장뿐만 아니라 애프터 마켓 및 튜닝 시장에서도 저렴한 가격과 쉬운 구조 변경(승인 미 필요)으로 인해 오랜 기간 많은 관심을 받아왔다. 최근 스트럿 바는 내연기관 대비 무거운 전기차의[3] 차체 강성을 높여 비틀림을 줄이기 위한 대안 중 하나로 많은 관심을 받고 있다.
스트럿 바에 대한 관심이 증가함에 따라, 현재 시중에는 다양한 제품들이 판매되고 있다. 다만, 판매되고 있는 대부분의 제품들은 강성 및 주행 성능 향상에 관한 정량적인 정보 및 근거 없이 판매되고 있는 상황이다. 스트럿 바에 대한 정량적인 정보는 차량의 안정성에 직접적인 연관 관계가 있어 매우 중요하다[4,5]. 품질에 대한 명확한 규정과 법규 제정을 위해서는 스트럿 바에 대한 강도, 강성, 내구성, 내식성 등에 대한 정량적 평가가 제반[6]되어야 하나, 아직까지 해당 부분에 대한 연구는 많이 미비한 상황이다.
최근 몇몇 연구자에 의해 스트럿 바 관련 연구는 주로 소재 및 구조 변경에 중점을 두고 진행되고 있다. 소재 변경의 경우, Razak은 CFRP (Carbon Fiber Reinforced Polymer)를 활용하여 스트럿 바의 강성을 유지하되 무게 절감 성능을 분석하였다[7]. 다만, 소재 변경은 장기간의 개발 기간 및 제작 단가의 상승으로 인해 단기적으로 적용 확대가 쉽지 않다는 한계점을 지닌다. 구조 변경은 적용 주기가 짧고 원가 상승의 최소화와 더불어 응력 집중을 획기적으로 줄이는 등 다양한 이점을 지니고 있다[8,9]. 이에 개발 기간 및 제작 단가의 확보를 위해 스트럿 바의 개선 설계는 구조 변경을 통해 이루어졌다. 한문식은 스트럿 바의 구조 설계를 통해 피로하중에 따른 수명과 내구성을 분석하였다[10]. 또한, Mironenko는 스트럿 바의 정중앙부 구조를 ‘V’자형 요소로 변경하여 충격에 따른 응력 변화를 분석하였다[11].
비록 이전 스트럿 바의 개선 설계 연구를 통해 차량의 안정성을 향상시켰지만, 현재 스트럿 바 장착에 따른 차량의 안전성(Safety) 문제가 제기되고 있는 상황이다. 압축 강성이 높은 스트럿 바는 차체 측면 충돌에 유연하게 반응하지 못하게 하여 충격을 완화하지 못한 상태로 힘을 반대편 엔진 마운트로 전달되게 한다. 이로 인해 직접적으로 힘을 받은 부위뿐만 아니라 반대쪽 펜더(Fender) 또한 동시에 파손될 수 있다. 이는 차량의 안전성과 직결되므로 스트럿 바는 과도한 압축에 유연하게 반응할 수 있도록 설계되어야 한다. 이에 따라, 스트럿 바는 굽힘 강성을 고려하여 차량의 안정성을 높일 뿐만 아니라 압축 강성을 고려하여 차량의 안전성 또한 높일 수 있는 설계가 필수적이다.
본 연구는 다양한 몸체 형상에 따른 스트럿 바의 굽힘과 압축을 고려한 구조적 거동을 상대적으로 분석하는 것을 목표로 한다. 이를 위해 본 연구는 시중에서 판매 및 사용되고 있는 6가지 서로 다른 형상의 스트럿 바를 연구 모델로 선정하였고 이를 3차원 CAD 모델로 구현하였다. 그리고 유한요소해석 기반 스트럿 바의 굽힘과 압축 발생 시나리오를 구현하여 각 형상별 구조적 거동을 상대적으로 분석하였다.
2. 본론
2.1 연구 모델 선정
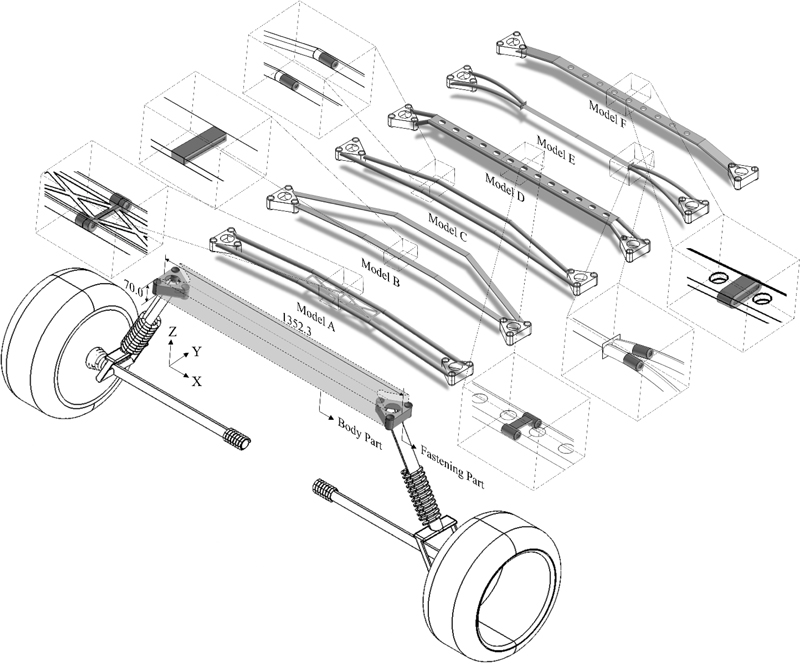
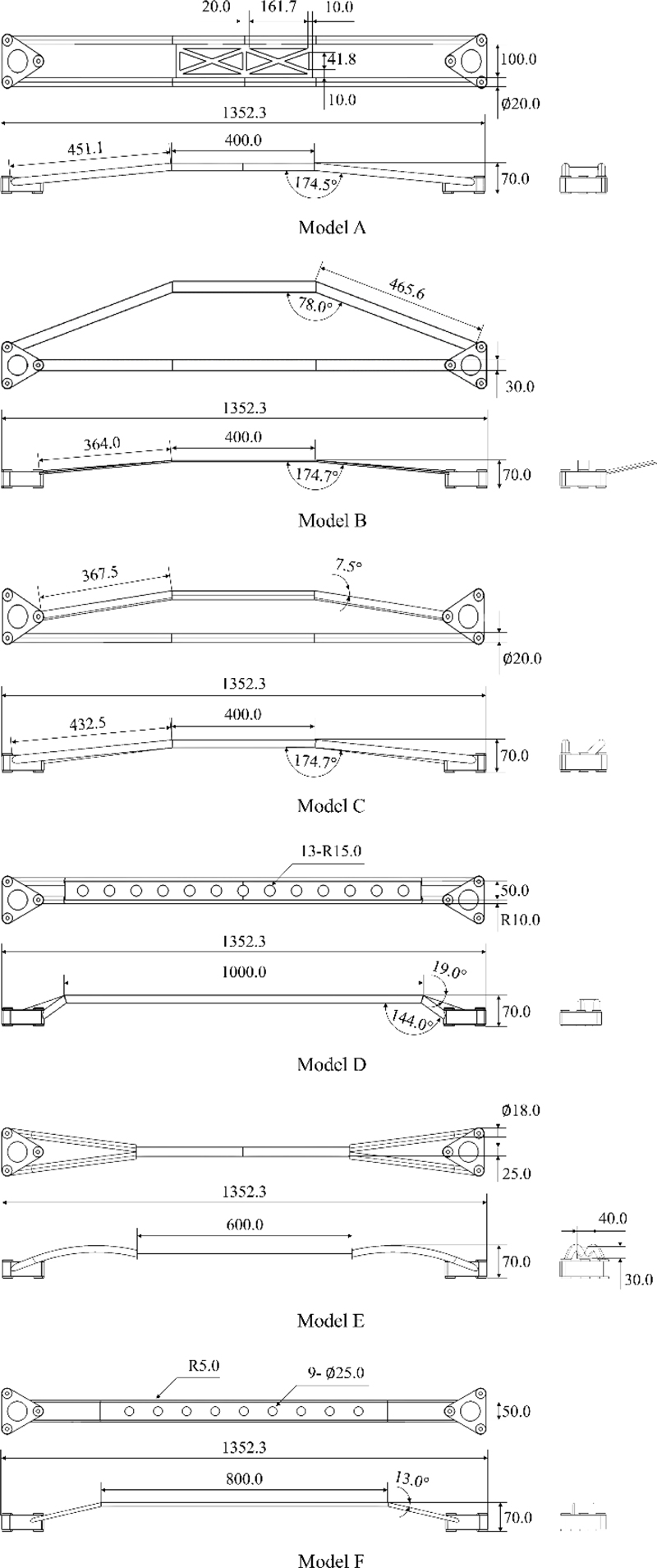
본 연구는 시중에 판매되는 6가지 서로 다른 형상의 스트럿 바를 연구 모델로 선정하였다. Fig. 1은 선정한 모델들의 3차원 CAD 모델 및 주요 치수를 나타낸다. 본 연구에서 선정한 모델들은 국내 및 해외 시장에서 활발히 판매 및 활용되고 있으며, 모두 일반 차량(사용자)을 타깃으로 하는 브랜드들의 대표 제품들이다. 이 모델들의 공통점은 굽힘 강성을 높이기 위하여 모두 위로 휘어지는 구조로 형성 되어있으며, 체결 부위 상단부에 결합해 있다. 또한, 아반떼 AD 차량에 장착가능한 모델로 체결 부위를 포함하여 가로길이는 1,352.3 mm이고 높이는 70.0 mm이다. 다만, 각 모델은 구성하는 축의 단면 형상과 축의 개수가 다르고, 보강 정도 또한 차이가 있다. 이에 따라 해당 사항을 스트럿 바의 주요 구조로 판단하고, 이를 기준으로 각 모델을 평가했다.
첫 번째 모델(Model A)은 중공 원형 단면 형상의 축으로 형성되어 있으며, 몸체 중심에 트러스 형상의 판이 보강되어 있고 이중 축으로 구성되어 있는 구조이다. 두 번째 모델(Model B)은 중공 사각 단면 형상의 축으로 형성되어 있으며, 몸체 중심에 추가적인 보강 구조가 없고 이중 축으로 구성되어 있는 구조이다. 세 번째 모델(Model C)은 중공 원형 단면 형상의 축으로 형성되어 있으며, 몸체 중심에 추가적인 보강 구조가 없고 이중축으로 구성되어 있는 구조이다. 네 번째 모델(Model D)은 중공 원형 단면 형상의 축으로 형성되어 있으며, 몸체 중심에 원형으로 타공된 플레이트가 길게 보강되어 있고 이중 축으로 구성되어 있는 구조이다. 다섯 번째 모델(Model E)은 하이브리드 구조로, 중공 원형 단면 형상의 이중 축으로 형성되어 있고 몸체 중심에 사각 단면 형상의 빔 형태로 변경되는 구조이다. 여섯 번째 모델(Model F)은 중공 사각형을 기반으로 옆면에 필렛이 된 단면 형상의 축으로 형성되어 있으며, 몸체 중심은 타공된 단일 축으로 구성되어 있는 구조이다.
본 연구는 스트럿 바 몸체의 형상에 따른 구조적 거동을 효과적으로 분석하기 위해 6가지 모델의 체결 부위를 동일하게 생성하였으며, 몸체의 부피는 143,650 mm³으로 동일하게 유지하였다. Table 1은 각 모델별 초기 부피 및 비율을 동일하게 생성하였을 때의 몸체 두께를 나타낸다.
2.2 유한요소해석 기반 구조적 거동 분석
본 연구는 유한요소해석 상용소프트웨어인 ANSYS 2022 R1의 Workbench를 사용하여 6가지 모델에 대한 구조적 거동을 분석하였다. 모든 모델은 세장비(Slenderness) 0.3 이하의 구조로 이루어져 있다. 본 연구는 솔리드 요소 대비 계산 효율성을 높이기 위해 4절점 2차원 쉘 요소를 활용하여 모델을 생성하였다[12]. 체결 부위는 1 mm 크기의 Quadrilateral Dominant 쉘 요소로 구성하였으며 두께는 1 mm로 설정하였다. 해당 두께는 내부 방향으로 커지도록 설정하였다. 몸체 부분은 1 mm 크기의 Quadrilateral Dominant 쉘 요소로 구성하였다. 두께는 각 모델별 설정한 두께를 부여하였으며, 해당 두께 또한 내부 방향으로 커지도록 설정하였다. 또한, 모델의 정확도를 보장하기 위해 자코비안(Jacobian) 값과 가로세로비(Aspect Ratio)를 측정하여 요소의 품질(Mesh Quality)을 평가하였다[13,14]. Table 2는 각 모델에 대한 유한요소모델의 총 절점수(평균 68 만 개) 및 요소수(평균 22 만 개)와 자코비안 값(평균 0.972) 및 가로세로비(평균 1.068)를 나타낸다.

The total number of nodes and elements for each FE model, and the average Jacobian value and aspect ratio
각 요소에는 강철, 알루미늄, 구리, 마그네슘의 합금인 두랄루민의 물성치(Young’s Modulus: 76.00 GPa, Poisson’s Ratio: 0.33, Yield Strength: 300.00 MPa)를 부여하였다.
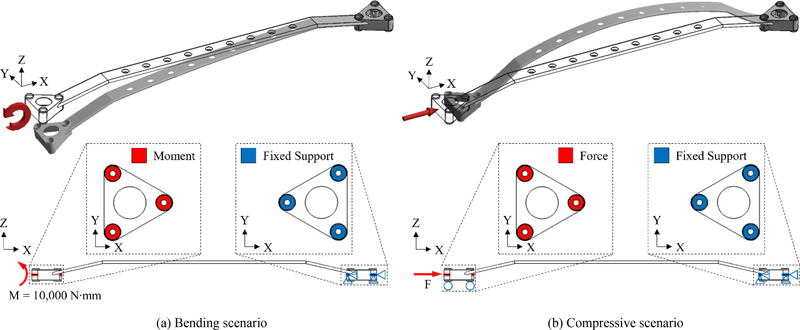
본 연구는 차량의 비틀림 상황을 스트럿 바의 굽힘 시나리오로, 차량의 측면 충돌 상황을 스트럿 바의 압축 발생 시나리오로 변환하여 각 형상별 구조적 거동을 상대적으로 분석하였다(Fig. 2). 해당 분석은 해석의 수렴성을 높이고 효율적인 계산 및 비용을 사용하기 위해 동적 상황을 정적 해석으로 변환하여 수행하였다[15].
스트럿 바의 굽힘은 차량의 비틀림 시 발생하며, 해당 비틀림으로 인해 스트럿 바는 반시계 방향으로 휨모멘트가 발생한다. 굽힘 발생 시나리오에서 스트럿 바의 구조적 거동은 스트럿 바의 높이(Z 축) 방향의 처짐(변형)량을 통해 상대 분석하였다. 이에 경계 조건으로는 한쪽 체결 부위를 완전히 고정(Fixed)하고 반대쪽 체결 부위에 Y축에 음의 방향으로 10,000 N·mm 크기의 모멘트를 부여했다. 10,000 N·mm의 모멘트는 각 스트럿 바의 굽힘 성능을 명확하게 구분할 수 있는 크기로, 모든 스트럿 바에 동일하게 부여되었다.
스트럿 바의 압축은 차량의 측면 충돌 시 발생하며, 해당 충돌로 인해 차량의 엔진 룸에서는 충돌 방향으로 침입이 발생된다. 이에 측면 충돌 상황은 압축 하중으로 변환하여 해석을 수행하였다. 압축 발생 시나리오에서 스트럿 바의 구조적 거동은 변형률 에너지를 통해 스트럿 바의 유연성을 분석하였고, 항복 발생 하중을 통해 파손성을 분석하였다. 첫 번째로, 총 변형률 에너지는 해당 구조물이 에너지를 얼마나 흡수할 수 있는지를 나타내는 지표로써 더 큰 변형률 에너지는 해당 구조물이 더 많은 에너지를 흡수하며 하중에 더 유연한 것을 나타낸다. 이에 경계 조건으로는 한쪽 체결 부위를 완전히 고정(Fixed)하고 반대쪽 체결 부위에 스트럿 바의 가로(X 축) 방향으로 1,000 N 크기의 하중을 부여했다. 굽힘의 경우와 동일하게, 압축 하중의 1,000 N은 각 스트럿 바의 압축 성능들을 명확하게 구분가능한 크기로 모든 스트럿 바에 동일하게 부여되었다. 또한, 압축 방향의 변위는 제약하지 않으며 압축 방향의 수직 방향으로의 변위는 고정하기 위해 하중이 부여되는 체결 부위에 Y와 Z 축 방향으로의 변위는 구속하였다. 두 번째로, 더 낮은 항복 발생 하중은 해당 구조물이 더 빨리 소성 변형으로 전환되며 이는 파손으로 이어져 힘을 반대편으로 전달하지 않는 것을 나타낸다. 이에 경계 조건으로는 한 쪽 체결 부위를 완전히 고정(Fixed)하고 반대쪽 체결 부위에 스트럿 바의 가로(X 축) 방향으로 항복 응력(300.0 MPa) 발생시키는 하중을 부여했다. 또한, 유연성을 분석할 때와 동일하게 하중이 부여되는 체결 부위에 Y와 Z 축 방향으로 변위를 구속하였다.
해석은 개인용 PC (Intel i9-12900K, GPU: GEFORCE RTX 3080, RAM: 64GB)를 이용하여 수행하였으며, 평균 21.8 GB의 메모리를 사용하였다.
3. 결과 및 고찰
본 연구는 스트럿 바의 몸체 형상에 따른 굽힘과 압축에 대한 구조적 거동을 예측하였다. 이에 따라 먼저, 사용한 요소 종류와 크기에 대한 검증 및 이전 연구[7]와의 비교를 통해 연구 방법을 검증하여 결과의 타당성을 검토하였다. 이후, 연구의 목적인 스트럿 바의 구조적 거동을 효과적으로 분석하기 위해 굽힘 시나리오에서는 높이(Z 축) 방향 처짐량을, 압축 시나리오에서는 몸체 부위의 총 변형률 에너지 및 항복이 발생하는 최대 하중을 분석하였다.
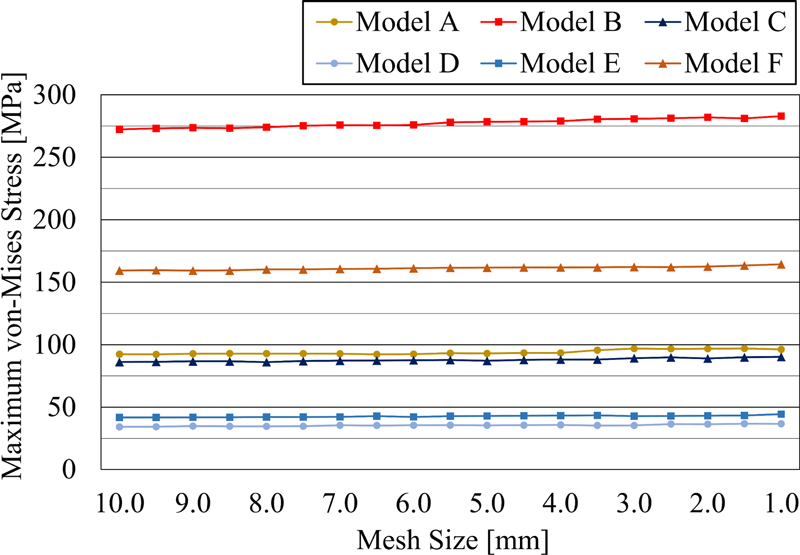
먼저 사용한 요소에 대한 검증은 요소의 크기에 따른 수렴성 평가를 통해 수행하였다. Fig. 3는 요소의 크기를 10에서 1 mm 까지 0.5 mm씩 줄여가며 최대 응력 값을 나타낸다. 또한 요소의 크기가 작아질수록 최대 응력이 증가하는 경향을 보였다. 다만, 요소 크기에 따른 최대 응력의 차이가 3.0% 미만으로 매우 적었으며, 응력의 크기가 수렴하는 것을 확인하였다.
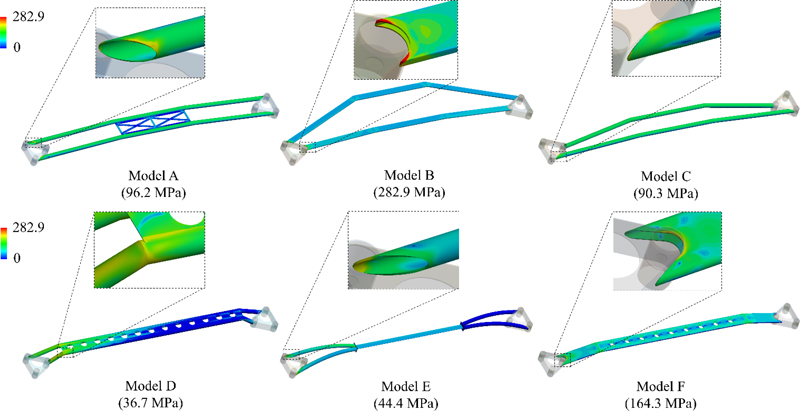
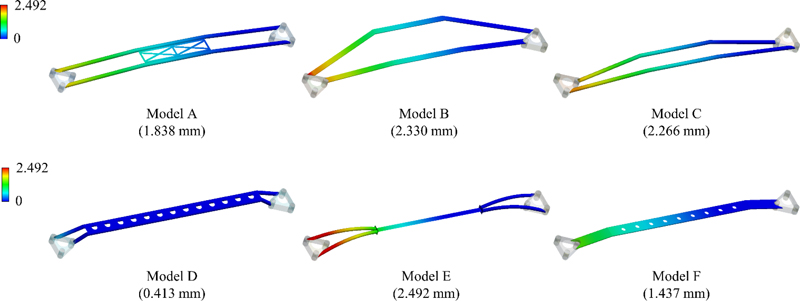
Fig. 4는 굽힘 발생 시 생성한 모델들의 응력 분포를 나타낸다. Model D를 제외한 모든 모델들의 최대 응력은 몸체와 체결 부위가 이어지는 연결부에서 발생하였으며, 이는 이전 연구[7]의 결과와 일치한다.
추가적으로, Model D는 몸체와 체결 부위가 이어지는 연결부에서도 상대적으로 높은 응력(18.0 MPa)이 발생하였지만 최대 응력(36.7 MPa)은 몸체의 보강판과 중공축이 만나는 위치에서 발생했다. 또한, 다른 모델들은 체결 부위와의 연결부에서 응력이 집중되어 발생한 것에 비해, Model D의 최대 응력은 다른 모델들에 비해 낮은 수치를 보였으며 응력 분포 역시 고르게 분산된 결과를 보였다. 이는 설계 시 보강재를 추가하지 않고도 구조 설계를 통해 최대 응력을 낮출 수 있고 응력 집중 현상을 완화할 수 있음을 의미한다.
3.1 스트럿 바의 굽힘 발생 시 구조적 거동 분석
본 연구는 굽힘 발생 시 몸체 형상에 따른 구조적 거동을 분석하였다. Fig. 5는 생성한 6개 모델들의 높이(Z축) 방향 처짐(변형)량을 나타낸다. 생성한 모델들은 각각 상이한 처짐량을 나타냈다. 이는 스트럿 바의 몸체 형상에 따라 스트럿 바의 굽힘 강성이 매우 상이하다는 것을 의미한다.
스트럿 바의 굽힘 발생 시 구조적 거동은 처짐량에 따라 정량적으로 분석했다. 먼저, Model C의 처짐량(2.266 mm)은 Model B의 처짐량(2.330 mm)에 비해 더 작은 결과를 나타냈다(Fig. 5). 이는 축을 구성하는 주요 단면의 형상 차이로 인해 발생했다. Model B와 C는 몸체 중심부에 보강 구조가 없는 이중축을 공통적인 특징으로 가지고 있으나, 주요 단면의 형상이 다르다. Model B의 주요 단면은 중공 원형 단면이고, Model C의 주요 단면은 중공 사각 단면으로 구성되어 있다. 이로 인해 주요 단면의 형상에 따라 Z축 기준의 단면 계수(Section Modulus)의 차이가 발생했다(Table 3). Model C의 단면계수는 286.0 mm3이며, 이는 Model B의 단면계수인 97.6 mm3보다 큰 수치를 나타낸다. 따라서 단면계수가 큰 Model C가 굽힘 발생 시 더 우수한 결과를 나타냈다. 이러한 결과는 스트럿 바를 구성하는 축의 주요 단면 형상이 단면계수의 차이를 발생시키며, 이러한 차이는 굽힘 강성에 중요한 영향을 준다는 것을 의미한다.
두 번째로, Model A의 처짐량(1.838 mm)과 Model D의 처짐량(0.413 mm)은 Model C의 처짐량(2.266 mm)에 비해 더 작은 결과를 나타냈다(Fig. 5). 이는 몸체 중심에 보강 구조 유무의 차이로 인해 발생했다. 해당 모델들은 축을 구성하고 있는 주요 단면의 형상과 이중 축을 공통적인 특징으로 가지고 있으나, 보강 구조에서 차이가 발생했다. Model A와 Model D는 몸체의 중심에 보강 구조가 있는 반면, Model C는 보강 구조가 없는 특징을 가지고 있다. 특히, Model D는 Model A보다 더 작은 처짐량을 보여 더 우수한 성능을 나타냈다. Model D는 보강 구조의 길이가 Model A에 비해 더 길게 형성되어 있어 굽힘 성능에 더 유리한 것을 알 수 있다. 또한, 몸체의 중심에 넓게 보강된 구조(A, D, F)가 중심이 보강되지 않은 모델(B, C, E)보다 낮은 처짐량을 나타냈다. 이러한 결과는 몸체의 중심이 보강된 구조가 차량의 안정성을 개선하는 데 더 효과적이라는 것을 의미한다.
추가적으로 생성한 모델 중 Model E가 가장 큰 처짐량인 2.492 mm을 나타냈다(Fig. 5). Model E는 원형 중공축과 빔 구조를 포함한 하이브리드 구조로, 원형 단면 형상의 단면계수는 456.2 mm3으로 상대적으로 높지만, 사각형 단면 형상을 기반으로 한 빔 구조의 단면계수는 9.7 mm3으로 생성한 모델 중 가장 낮은 수치를 나타낸다. 반면, 처짐량이 가장 작은 모델은 Model D로 0.413 mm의 처짐량을 발생하였으며 이는 가장 큰 처짐량의 16.6%에 해당한다. Model D는 원형 중공축을 기반으로 축 상단에 긴 타공판이 보강된 구조이다. 보강 구조가 축 상단에 추가되는 것은 도심을 기준으로 보강 구조가 최외곽에 추가되는 것이기에 단면계수 측면에서 우위를 확보할 수 있다. 이러한 결과를 통해, Model D는 굽힘 강성이 높아 차량의 비틀림에 강직하며, 이로 인해 해당 스트럿 바가 장착된 차량의 안정성(Stability)은 가장 우수할 것으로 예상된다. 또한, 앞서 언급한 응력 분포를 같이 고려하면 Model D는 차량의 선회 시 더 큰 하중을 견딜 수 있을 뿐만 아니라 내구성 또한 우수한 것을 의미한다. 이러한 결과는 스트럿 바의 주요 축이 굽힘 성능을 확보하는 데 매우 중요하지만, 몸체의 구조 및 보강 구조의 위치에 따라 굽힘 성능을 효과적으로 확보할 수 있음을 의미한다.
3.2 스트럿 바의 압축 발생 시 구조적 거동 분석
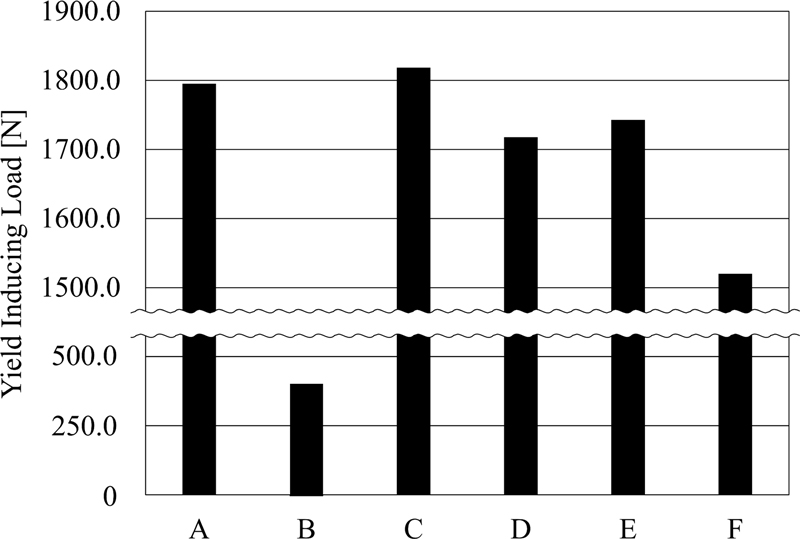
본 연구는 압축 발생 시 몸체 형상에 따른 구조적 거동을 분석하였다. Fig. 6은 생성한 6개 모델들에 대한 몸체 부분의 총변형률 에너지를 나타내고, Fig. 7은 생성한 모델들의 항복 발생(300.0 MPa) 시 하중을 나타낸다. 생성한 모델들은 각각 상이한 항복 발생 하중을 나타냈다. 이는 스트럿 바의 몸체 형상에 따라 스트럿 바의 압축 강성이 매우 상이하다는 것을 의미한다.
생성한 모델 중 Model B가 가장 큰 변형률 에너지인 3,378.20 mJ를 나타냈다. 반면, 변형률 에너지가 가장 작은 모델은 Model D로 222.89 mJ을 보였으며 이는 가장 큰 모델에 비해 1,515.6% 낮은 수치이다. 동일한 재료 내 변형률 에너지가 크다는 것은 형성되어 있는 구조가 충돌 하중에 대해 힘을 더 많이 흡수하는 것을 의미한다. 이러한 구조는 특정한 힘에 대해 에너지를 더 많이 흡수하므로 변형률 에너지가 클수록 이는 더 유연하게 반응하는 것을 의미한다. 또한, Model B는 측면 충격 발생 시 몸체 중심 부분이 넓어지며 힘을 흡수하는 데 유리한 것으로 나타냈다.
생성한 모델 중 Model B가 가장 작은 항복 발생 하중인 418.6 N을 나타냈다. 반면, 항복 발생 하중이 가장 큰 모델은 Model C로 1,818.3 N을 보였으며 이는 가장 작은 모델에 비해 434.4% 높은 수치이다. 동일한 재료 내 항복 발생 하중이 작다는 것은 형성되어 있는 구조가 충돌 하중에 대해 더 빨리 소성 변형으로 전환되는 것을 의미한다. 이에 해당 구조는 특정한 힘에 대해 더 빨리 변형되고 파손되어 충격을 반대편으로 전달하지 않는 것을 의미한다.
앞선 결과들을 종합해보면 Model B와 F가 압축 발생 시 우수한 결과를 나타냈다. 두 모델은 공통적으로 축의 단면 형상이 가로(Y축) 방향으로 길이가 긴 사각형 단면을 기반으로 설계되었다. 특히, Model B는 중심에 보강이 없음과 더불어 가장 낮은 단면 계수(97.6 mm3)를 지니고 있어 이러한 휨 현상을 가장 유연하게 반응하는 것으로 나타낸다(Table 3).
반면, Model F는 가장 큰 단면 계수(497.9 mm3)를 지니고 있지만, 해당 시나리오에서 우수한 결과를 나타냈다. 이는 스트럿 바를 구성하고 있는 축의 개수에 기인한다. Model F는 다른 모델들과 다르게 더 넓은 면적을 가진 단일 축으로 설계되었다. 이는 넓은 단면적을 가진 단일 축이 단면계수가 큼에도 불구하고, 단면계수가 작은 이중 축보다 압축 하중을 더 효과적으로 흡수하고 더 빨리 소성 변형으로 전환될 수 있음을 의미한다. 따라서, 압축 하중을 고려한 스트럿 바의 구조는 단면 형상의 단면계수에 대한 고려뿐만 아니라 단면의 넓이가 비교적 큰 단일 축을 통해 압축 성능을 효과적으로 확보할 수 있음을 의미한다. 이러한 결과를 통해, 해당 구조는 차량의 측면 충격에 유연하게 반응하는 것을 나타내며 이는 차량의 안전성(Safety)이 가장 우수할 것으로 예상된다. 또한, 이는 차량의 측면 충돌 시 작은 하중에도 유연하게 반응할 뿐만 아니라 오히려 파손되며 반대편 펜더에 충격을 전달하지 않기에 차량의 안전성 또한 우수할 것으로 예상된다.
3.3 스트럿 바의 굽힘과 압축을 고려한 구조적 거동 분석
본 연구는 굽힘과 압축 발생 시 몸체 형상에 따른 상대적인 구조적 거동을 동시에 고려하였다. 일체형 구조(Model F)는 굽힘과 압축 시나리오에서 모두 우수한 결과를 나타냈다. 각각의 시나리오에서 우수한 성능을 내는 모델과 그렇지 않은 모델의 가장 큰 차이점은 축의 개수이다. 특히, Model F는 단일 축을 기반으로 이중 축보다 넓은 단면 형상을 지니고 있다. 이로 인해, 사각형 단면 형상의 작은 단면계수를 보완하여 굽힘 성능을 높일 수 있다. 동시에 넓은 단면 형상의 단일 축은 많은 힘을 흡수하여 압축 성능을 높일 수 있다. 따라서, 가로로 넓은 사각 단면 형상을 활용하는 단일 축의 형태가 차량의 안정성 및 안전성 개선에 가장 효과적임을 의미한다.
추가적으로 굽힘과 압축 발생 시에는 결과의 우수한 순서가 다르게 나타났다. Model B는 굽힘에서 2번째로 취약한 결과를 나타냈지만 압축에서 가장 우수한 결과를 나타냈다. 이를 통해 굽힘과 압축 발생 시 스트럿 바의 성능은 상충관계(Trade-off)가 아니라고 볼 수 있다. 따라서, 이는 장착된 차량의 안정성과 안전성을 동시에 개선할 수 있는 스트럿 바의 설계가 가능하다는 것을 의미한다.
본 연구는 다음과 같은 한계점을 가진다. 첫째, 본 연구는 정적 해석을 기반으로 스트럿 바의 성능 비교를 하였다. 동적 상황에서 스트럿 바의 굽힘 및 압축 성능을 정확하게 평가하기 위해서는 동적 해석이 필수적이다. 다만, 본 연구에서는 동일한 크기와 패턴의 하중을 부여하여 스트럿 바들의 성능을 상대 비교하고자 하였다. 둘째, 스트럿 바에 대표적으로 발생하는 굽힘과 압축 하중에 대해서만 구조적 거동을 상대적으로 평가하였다. 하지만, 스트럿 바에는 피로 등 다양한 하중이 발생할 수 있기에 여러 하중 조건 아래 분석이 요구된다. 셋째, 스트럿 바의 전체적인 구조를 고려하지 않고, 체결 부위는 모두 동일하게 설정하였다. 넷째, 차량에 스트럿 바를 장착하여 주행 안정성에 대한 분석은 수행하지 못하였다. 다만, 이전 연구[7]에서 스트럿 바 장착에 따라 서스펜션 시스템의 움직임을 감소시켜 차체의 전체 비틀림을 감소시킬 수 있다는 연구 결과를 보여주었다. 이 차체의 비틀림은 차량의 주행 안정성과 밀접한 상관관계가 있다[1,2]. 따라서, 본 연구에서 굽힘 강성이 높은 스트럿 바는 차량의 주행 안정성을 높일 수 있을 것이라 예상된다. 그럼에도 불구하고 본 연구는 차량의 안정성과 안전성을 동시에 개선할 수 있는 스트럿 바의 설계 가능성을 명확히 보였다.
4. 결론
본 연구는 다양한 몸체 형상에 따른 스트럿 바의 굽힘과 압축에 대한 구조적 거동을 상대적으로 분석했다. 이를 위해 시중에서 판매 및 사용되고 있는 6가지 몸체 형상의 스트럿 바를 모델링 하였다. 이어 스트럿 바의 굽힘 및 압축 발생 시 구조적 거동을 분석하였다. 그 결과, 굽힘 발생 시 스트럿 바의 최대 응력은 일반적으로 몸체와 체결 부위 사이의 연결부에 집중되었다. 이에 구조 설계를 통해 집중된 응력을 고르게 분산시켰다. 또한, 스트럿 바의 몸체 형상에 따라 차량의 안정성(Stability)과 안전성(Safety)이 변화하는 것을 확인했다. 특히, 넓은 단면 형상을 활용하는 단일 축 형태의 구조가 가장 우수한 굽힘 및 압축 성능을 보였다. 더불어 굽힘과 압축을 동시에 고려한 스트럿 바의 성능은 상충관계가 아니므로, 차량의 안정성 및 안전성을 모두 고려한 스트럿 바의 개선 설계 가능성을 확인했다. 이로써 본 연구는 스트럿 바의 구조적 거동에 대한 이해를 높이고 차량의 안정성과 안전성을 향상시키는 데 기여할 수 있는 중요한 정보를 제공했다.
Acknowledgments
이 논문은 2024년도 산업통상자원부의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0021513, 2024년 산업혁신기반구축사업).
References
-
Mohan, R., Hariram, V., Subramanian, M., Padmanabhan, S., (2017), Improvements in vehicle stiffness by adding internal reinforcements, International Journal of Vehicle Structures and Systems, 9(2), 72-76.
[https://doi.org/10.4273/ijvss.9.2.02]

-
Chen, W., Zuo, W., (2014), Component sensitivity analysis of conceptual vehicle body for lightweight design under static and dynamic stiffness demands, International Journal of Vehicle Design, 66(2), 107.
[https://doi.org/10.1504/IJVD.2014.064546]

-
Beddows, D. C. S., Harrison, R. M., (2021), PM10 and PM2.5 emission factors for non-exhaust particles from road vehicles: Dependence upon vehicle mass and implications for battery electric vehicles, Atmospheric Environment, 244, 117886.
[https://doi.org/10.1016/j.atmosenv.2020.117886]

-
Jing, L., Wu, L., Li, X., Zhang, Y., (2017), Study on kinematic and compliance test of suspension, IOP Conference Series: Materials Science and Engineering, 231(1), 012186.
[https://doi.org/10.1088/1757-899X/231/1/012186]

-
Lukoševičius, V., Makaras, R., Rutka, A., Keršys, R., Dargužis, A., Skvireckas, R., (2021), Investigation of vehicle stability with consideration of suspension performance, Applied Sciences, 11(20), 9778.
[https://doi.org/10.3390/app11209778]

- Park, Y., Park, H. S., (1986), A study on improving the realiablity of a finite elements model and stiffness damage detection by dynamic characteristics measurements, Transactions of the Korean Society of Mechanical Engineers, 10(1), 157-163.
-
Ab Razak, M. S., Othman, M. N., Sulaiman, S. N., Ramli, R., Sanada, Y., (2021), Composite optimization of automotive carbon fiber strut bar using hyperworks optistruct, Journal of Physics: Conference Series, 1793(1), 012072.
[https://doi.org/10.1088/1742-6596/1793/1/012072]

-
Bendsoe, M. P., Guedes, J. M., Haber, R. B., Pedersen, P., Taylor, J. E., (1994), An Analytical model to predict optimal material properties in the context of optimal structural design, Journal of Applied Mechanics, 61(4), 930-937.
[https://doi.org/10.1115/1.2901581]

-
Gardner, L., Ashraf, M., (2006), Structural design for non-linear metallic materials, Engineering Structures, 28(6), 926-934.
[https://doi.org/10.1016/j.engstruct.2005.11.001]

-
Han, M., Cho, J., (2016), A study on fatigue durability through the structural analysis of strut bar, Transactions of the Korean Society of Automotive Engineers, 24(5), 504-511.
[https://doi.org/10.7467/KSAE.2016.24.5.504]

-
Mironenko, R. Y., Balaev, E. Y., Blednova, Z. M., (2018), Engineering design of safe automobile front strut tower brace with predetermined destruction, IOP Conference Series: Materials Science and Engineering, 327(3), 032039.
[https://doi.org/10.1088/1757-899X/327/3/032039]

-
Valeš, J., Stan, T.-C., (2017), FEM modelling of lateral-torsional buckling using shell and solid elements, Procedia Engineering, 190, 464-471.
[https://doi.org/10.1016/j.proeng.2017.05.365]

-
Bucki, M., Lobos, C., Payan, Y., Hitschfeld, N., (2011), Jacobian-based repair method for finite element meshes after registration, Engineering with Computers, 27(3), 285-297.
[https://doi.org/10.1007/s00366-010-0198-2]

- Nemade, A., Shikalgar, A., (2020), The mesh quality significance in finite element analysis, IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), 17(2), 44-48.
-
Kim, H.-G., Kim, E., Cho, M., (2013), Transformation of dynamic loads into equivalent static load based on the stress constraint conditions, Journal of the Computational Structural Engineering Institute of Korea, 26(2), 165-171.
[https://doi.org/10.7734/COSEIK.2013.26.2.165]

Appendix
APPENDIX

BS. candidate in the Department of Mechanical Engineering, Keimyung University. His research interest is design optimization for vehicle safety.
E-mail: willy600301@gmail.com

Assistance Professor in the Department of Mechanical Engineering, Keimyung University. His research interest is mechanical engineering based on optimization and artificial neural network.
E-mail: kjj4537@gmail.com