인공신경망을 활용한 재료 및 설계 변수에 따른 다공성 구조체의 탄성계수 예측

1. 서론

다공성 구조체는 가볍고 높은 에너지 흡수 능력과 같은 특성으로 인해 항공우주, 의료, 구조 공학 등 다양한 분야에서 중요한 역할을 하고 있다[1,2]. 이러한 다공성 구조체의 기계적 성능, 특히 탄성계수는 재료의 특성과 설계 변수에 따라 크게 달라진다[3]. 따라서 다공성 구조의 설계 변수에 따른 기계적 물성을 계산 및 예측하고자 하는 많은 시도가 이루어져 왔다[4-7]. 하지만 전통적인 방법으로는 재료 특성과 설계 변수 간의 복잡한 상관관계를 완전히 해석하는 데 한계가 있으며, 이는 정확한 탄성계수 예측을 어렵게 만드는 요인으로 작용하고 있다.

최근 인공신경망(Artificial Neural Networks, ANNs)이 복잡한 비선형 시스템의 예측 및 분석에 있어 강력한 도구로 부상하고 있다. 인공신경망은 대규모 데이터로부터 학습하여 다양한 변수 간의 복잡한 관계를 모델링할 수 있으며, 이를 통해 전통적인 방법보다 더 높은 예측 정확도를 제공할 수 있음이 여러 연구 결과를 통해 검증되어 왔다[8-11].

본 연구에서는 재료의 종류 및 설계 변수(예: 체적 분율, 구조의 종류)를 바탕으로 다공성 구조체의 탄성계수를 예측하기 위한 인공신경망 모델을 개발하고자 하였다. 공학 분야에서의 인공지능 연구에서 지속적으로 문제시되는 데이터 부족 문제를 해결하기 위해 유한요소해석(Finite Element Analysis, FEA) 시뮬레이션을 통하여 설계 변수-탄성계수 간의 커플링 된 대량의 데이터셋을 확보하였으며, 이를 활용하여 ANN 모델을 학습시키고, 별도의 테스트 데이터셋을 통해 모델의 성능을 평가하였다. 그 결과, 재료 종류와 설계 변수가 탄성계수에 미치는 영향을 면밀히 분석할 수 있었으며, 인공신경망 모델의 예측 능력을 검증하여 실제 설계에 적용 가능한 수준의 예측 정확도를 확보할 수 있음을 확인하였다.

2. 실험방법

2.1 유한요소해석 기반 탄성계수 데이터 구축

인공신경망 학습에 필요한 설계 변수-탄성계수 데이터 구축을 위해 유한요소해석을 기반으로 설계 변수에 따른 탄성계수를 계산하였다. 유한요소해석은 ANSYS Workbench의 Material Designer 모듈을 통해 수행하였다. 연구에 적용된 다공성 구조체는 Fig. 1과 같이 격자(Lattice) 및 TPMS (Triply Periodic Minimal Surfaces)로 이루어진 6가지 종류를 사용하였으며, 각각의 다공성 구조체는 5 mm 크기의 단위 셀(Unit Cell)로 설계 및 메쉬화를 수행한 뒤 탄성계수 계산에 적용되었다. 각 구조체의 체적분율(Volume Fraction, VF)은 0.2-0.8(0.1 간격)로 다양하게 하여 유한요소해석을 수행하였다. 다만, TPMS SchwarzP 형상의 경우, 다른 구조에 비해 체적 분율이 증가할수록 표면적과 곡률이 기하학적으로 복잡하게 변하면서 해석 도중 수렴문제를 유발하여 0.2-0.6으로 해석을 진행하였다. 6가지의 구조체와 체적분율 범위, 6종류의 재료를 조합하여 총 240개의 데이터를 유한요소해석을 통해 생성하였다. 이후 인공신경망 학습을 위한 충분한 데이터셋을 확보하기 위해 주어진 데이터로부터 2차 다항식 적합(Polynomial Fitting)을 수행한 뒤 체적 분율 범위에서 100개의 데이터를 추출하여 총 3,636개의 데이터를 얻을 수 있었다.

Fig. 1

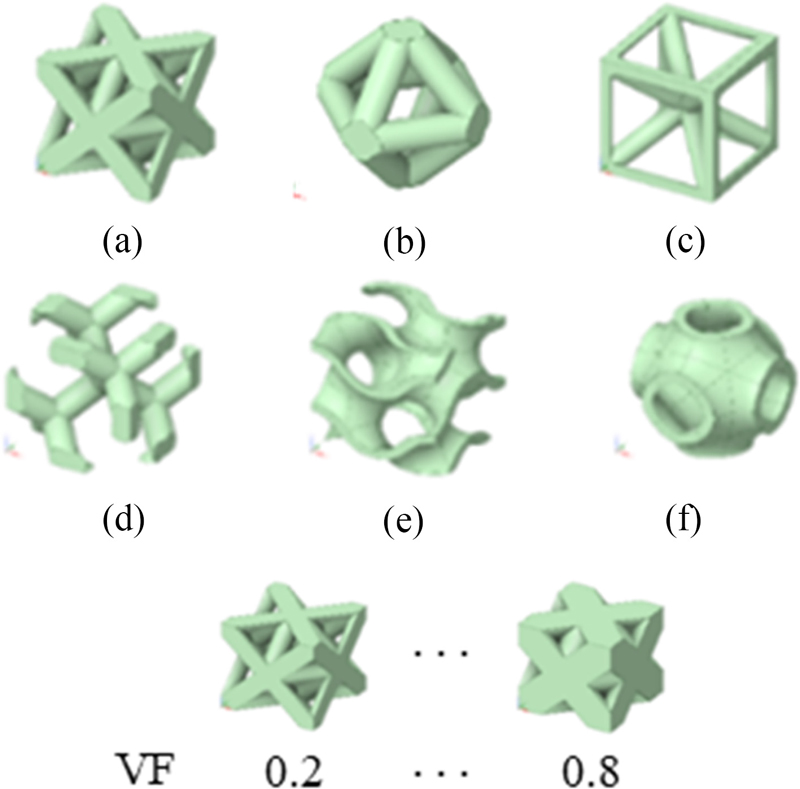
Schematic of porous structures for (a) octet, (b) double pyramid, (c) cubic with enter supports, (d) diamond, (e) TPMS Gyroid, and (f) TPMS SchwarzP

준비된 데이터는 학습, 테스트, 검증 데이터로 각각 70, 15, 15%씩 배분하여 인공신경망 최적화를 위한 훈련 및 검증에 사용하였다.

유한요소해석에 적용된 재료물성은 ANSYS Material Library에서 제공하는 6개의 대표적인 적층 제조 재료의 물성을 사용하였으며 사용된 재료 및 이에 대한 탄성계수 값을 Table 1에 나타내었다.

Table 1

Materials and their elastic modulus

2.2 인공신경망 모델 및 평가 방법

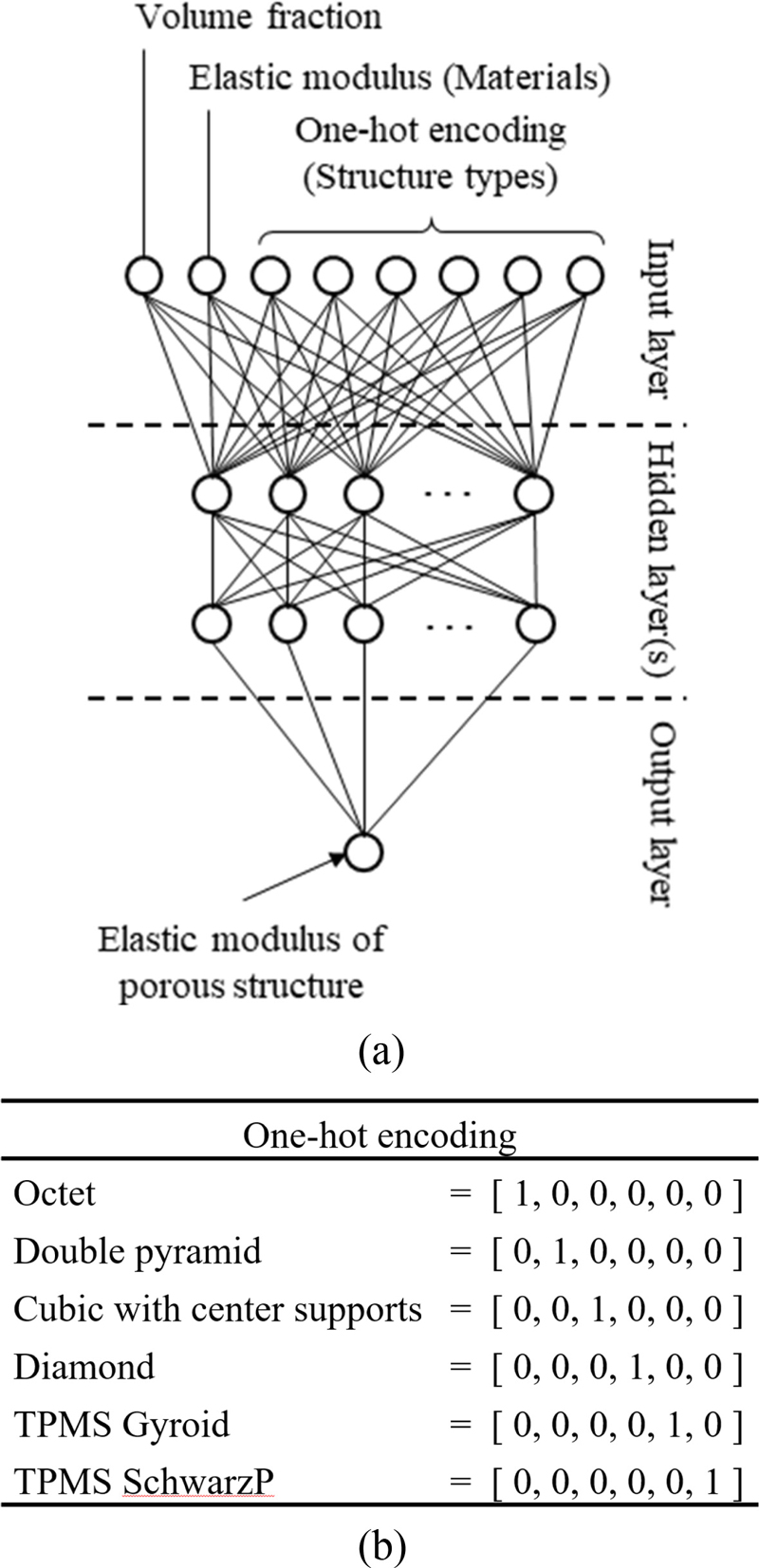
Fig. 2(a)는 본 연구에 사용된 인공신경망의 구조를 나타내고있다. 인공신경망은 크게 입력층(Input Layer), 은닉층(Hidden Layers), 그리고 출력층(Output Layer)으로 구분되어 있다. 입력층은 총 8개의 노드(Nodes)로 이루어져 있으며, 이 중 6개는 다공성 구조체의 종류를 구분하는 원-핫 인코딩(One-hot Encoding) 값이 (Fig. 2(b)), 나머지 2개는 체적 분율과 재료의 탄성계수 값이 입력되도록 구성하였다.

Fig. 2

Schematic depicting (a) architecture of the ANN and (b) onehot encoding for porous structures

은닉층의 경우 다양한 층수(3-8 Layers) 및 노드 수(4-128 Nodes)를 적용하여 학습을 수행하였으며, 그 결과를 분석하여 최적의 인공신경망 구조를 얻고자 하였다. 여기서 모든 은닉층은 동일한 노드 수를 갖도록 설계하였음을 알려 둔다. 출력층은 다공성 구조체의 탄성계수 값에 대응하는 하나의 노드로 구성되어 있다.

인공신경망에 적용되는 재료 및 다공성 구조체의 탄성계수 값은 아래 수식을 통해 0.1에서 0.9 사이의 정규화(Normalization)된 값으로 변환하여 사용하였다. 이는 모든 데이터의 범위를 균일하게 하여 일부 데이터가 모델 학습에 과도한 중요도를 갖게 하는 것을 방지하기 위함이다.

$\[ x^{\text{'}}=0.1+0.8\left(\frac{X-X_{min}}{X_{max}-X_{min}}\right) \]$

(1)

여기서, x′, X, X_min, 및 X_max는 각각 정규화된 값, 실제값, 데이터 최솟값 및 데이터 최댓값을 의미한다.

각각의 모든 완전 연결층(Fully Connected Layer) 뒤에는 Batch Normalization과 ReLu 활성화 함수를 추가하고, Huber 손실 함수 및 Adam Optimizer을 사용하여 최적화를 수행하였다. ReLu 활성화 함수 이후 Batch Normalization을 적용함으로써, 활성화된 데이터의 분포를 정규화하여 과도한 가중치 변동을 방지하고 학습 안정성을 높일 수 있었으며, 이 방식은 모델이 비선형성을 효과적으로 학습하면서도 데이터의 분포를 일정하게 유지하도록 하여, 기울기 소실 문제를 완화하였다. 또한 학습의 반복적 수행에도 더 이상의 손실함수의 향상이 없을 때 학습을 중지시키는 조기 종료 콜백 함수를 추가하여 모델 학습의 과적합(Over Fitting)을 방지하였다. 학습은 32 미니배치(Mini-Batch)로 10,000번의 Epoch동안 반복 수행되게 설정하였으며, GEFORCE RTX A6000 GPU (NVIDIA, Santa Clara, CA, USA)을 사용하여 훈련을 수행하였다.

학습이 완료된 인공신경망은 아래의 AE (Average Error)와 AARE (Average Absolute Relative Error)값을 계산하여 예측 성능을 평가하였다.

$\[ AE=\frac{1}{n}\sum _{i=1}^n \left|E_i-P_i\right| \]$

(2)

$\[ AARE =\frac{1}{n}{\Sigma }_{i=1}^n\left|\frac{E_i-P_i}{E_i}\right|\times 100 \]$

(3)

여기서 E_i, P_i, 및 n은 각각 다항식 적합 곡선으로부터 얻은 탄성계수, 인공신경망 모델의 예측 탄성계수, 그리고 평가에 사용된 데이터의 수를 의미한다. AE와 AARE는 각각 모델의 예측값과 실제값 간의 평균 및 상대오차를 나타내며, 이를 통해 모델의 성능을 객관적으로 평가하고자 하였다.

3. 결과 및 고찰

3.1 유한요소해석 결과

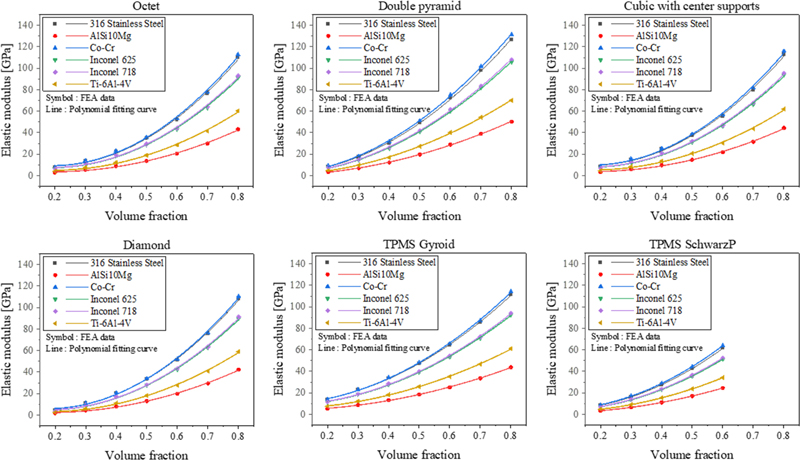
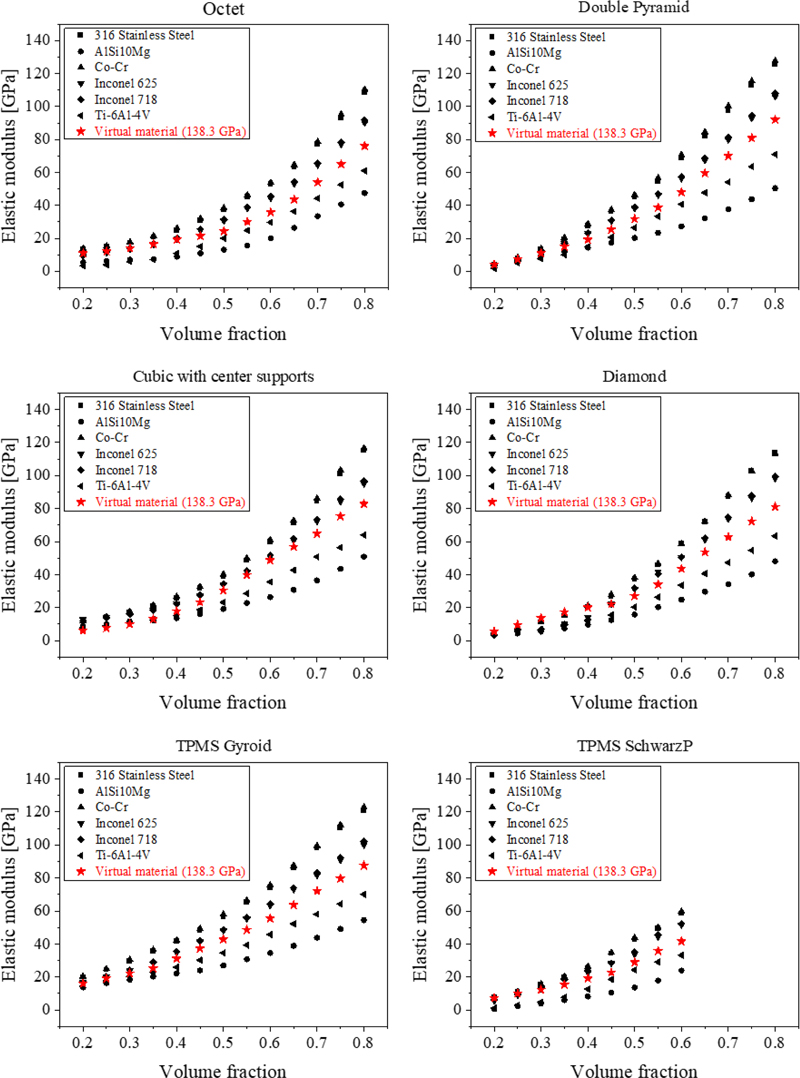
6가지 다공성 구조체의 재료 및 체적 분율에 따른 탄성계수에 대한 유한요소해석 결과를 Fig. 3에 나타내었다. 그림에서 알 수 있듯이, 모든 구조와 재료의 탄성계수는 체적 분율이 증가함에 따라 비선형 적으로 증가하는 경향을 보였으며, 재료의 탄성계수가 높아짐에 따라 다공성 구조체의 탄성계수 또한 높아지는 것을 확인할 수 있다. 또한 다항식 적합 곡선이 FEA결과(Symbol 데이터)와 정확히 교차하는 것을 확인할 수 있으며, 이를 통해 다항식 적합이 해석결과를 충분히 반영하는 곡선을 얻을 수 있음을 확인하였다. 2.1장에서 언급한 바와 같이 인공신경망 학습에 사용되는 데이터는 위 다항식 적합 곡선으로부터 얻은 값임을 알려 둔다.

Fig. 3

Results of elastic modulus calculation using FE-simulation

3.2 ANN 학습 결과

인공신경망 모델의 구조 최적화를 위해 다양한 층수와 노드수의 은닉층을 갖는 여러 모델을 학습시켰으며, 그 전체 결과를 Table 2에 나타내었다. 모델 성능에 대한 검토 결과, 5개의 층수와 4개의 노드를 갖는 모델이 가장 높은 정확도를 보임을 확인하였다. (AE: 1.39 GPa, AARE: 6.69%).

Table 2

Results of ANN prediction with respect to the number of layers and nodes

은닉층의 층수와 노드 수가 인공신경망 예측 성능에 미치는 영향을 직관적으로 분석하기 위해 인공신경망 구조에 따른 예측 성능 변화 추이를 Fig. 4에 나타내었다. 층수에 따른 예측 성능의 경우, 유의미한 경향성은 나타나지 않았으며 AE는 6개의 층수에서, AARE는 5개의 층수에서 가장 좋은 성능을 보였다.

Fig. 4

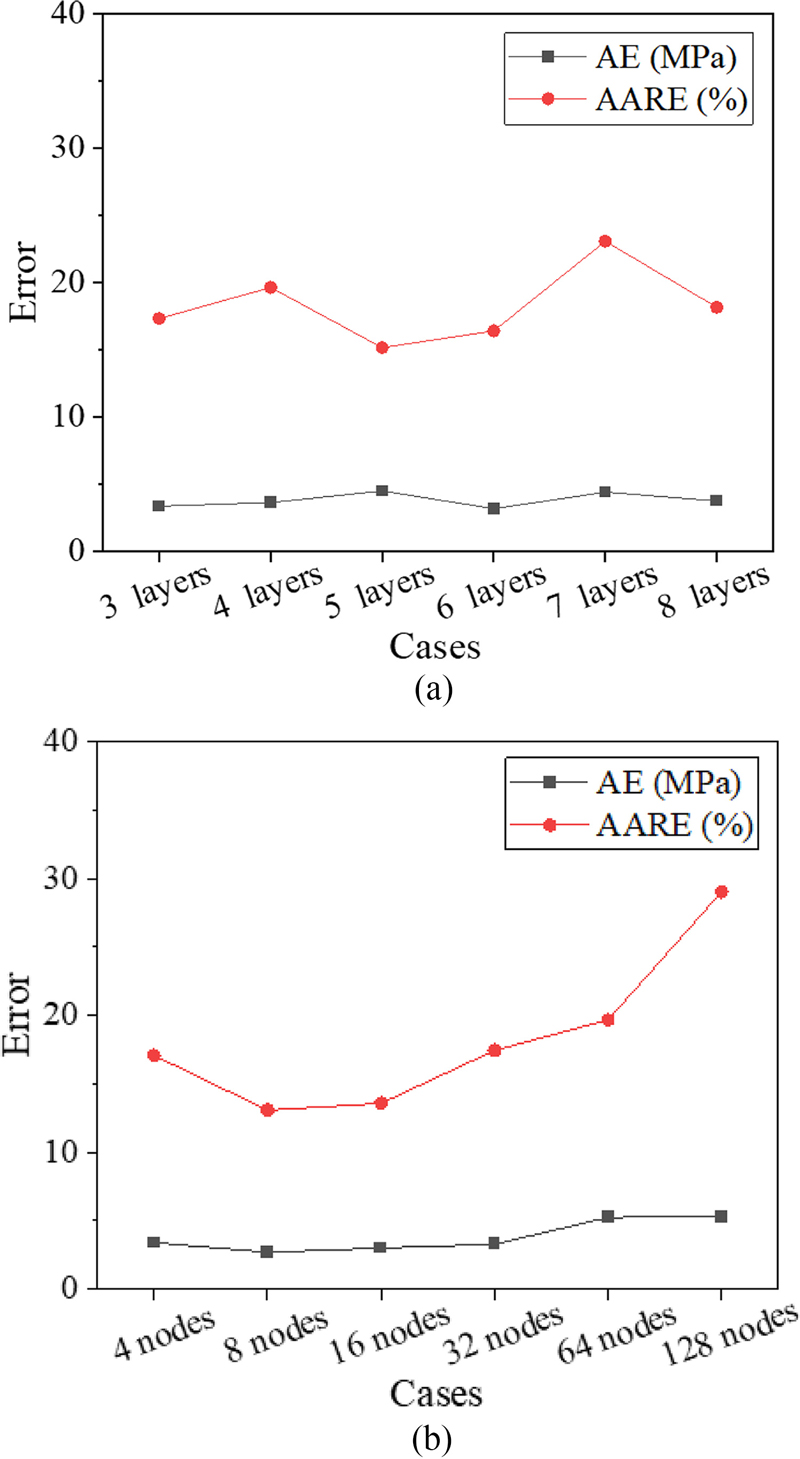
Graphs showing the results of AE and AARE calculation according to (a) the number of hidden layers and (b) the number of nodes

노드 수는 층수에 비해 모델의 예측 성능에 보다 많은 영향을 미치는 것으로 나타났다. 초기 4 노드에서 16 노드까지는 비교적 균일한 성능을 보였지만, 이후 노드가 128까지 증가됨에 따라 AARE가 급격히 악화됨이 확인되었다. 이는 과도한 노드수가 입력데이터의 중요도를 지나치게 희석시켜 예측 능력을 저하시킨 것으로 판단된다.

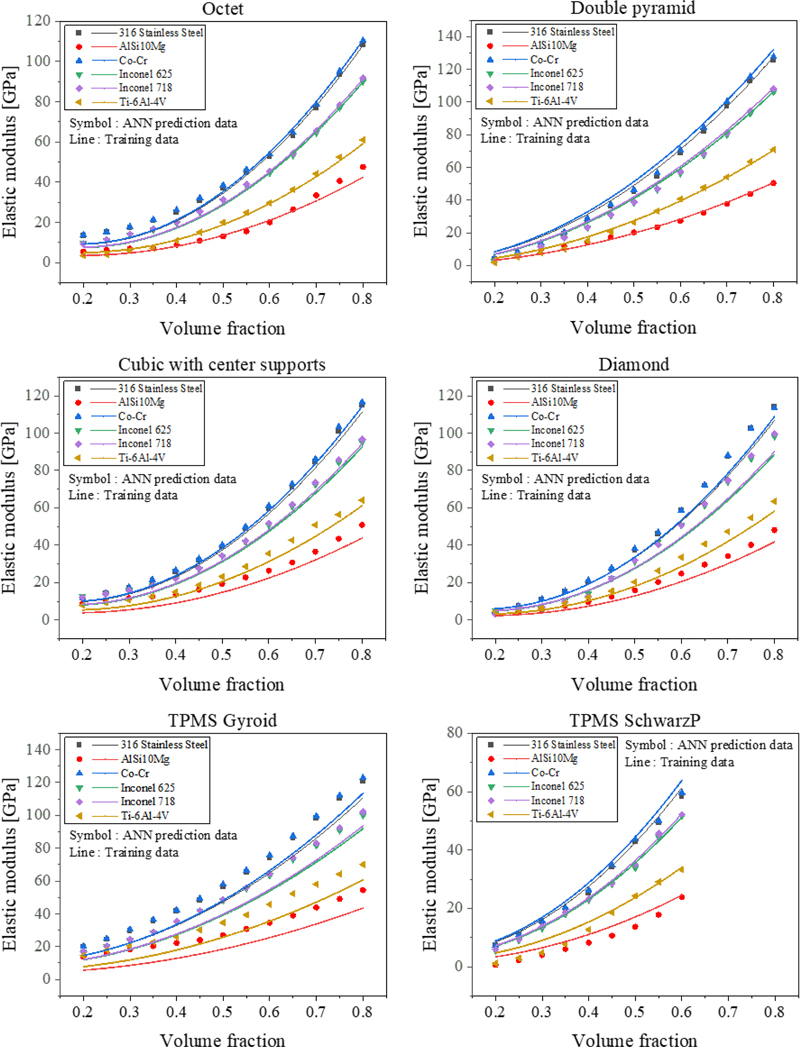
Fig. 5는 인공신경망으로부터 예측된 탄성계수 값을 다항식 적합 곡선으로부터 얻은 학습 데이터와 비교한 결과를 나타내고 있다. 전반적으로 인공신경망 모델이 모든 구조체 종류 및 재료에서의 체적 분율에 따른 탄성계수 변화 경향을 잘 모사하고 있음을 확인할 수 있다. 이는 해당 모델이 재료 특성 및 설계 변수와 탄성계수 간의 상관관계를 정확히 학습하였음을 의미한다. 하지만 TMPS Gyroid의 경우, 모든 재료 종류에서 학습 데이터에 비해 높은 탄성계수를 보이며 다른 다공성 구조에 비하여 예측 정확도가 낮았다. 이러한 특징은 TPMS Gyroid 구조가 다른 5가지 구조와는 다른 설계 변수-탄성계수 상관관계 특성을 갖고 있으며 이에 따라 일반화된 인공신경망이 정확한 예측을 하지 못한 것이라 판단된다. 실제로 TPMS Gyroid구조는 반복되는 곡면과 높은 표면적 대비 낮은 부피 분율을 가지는 구조이기 때문에 복잡성이 높으며 이로 인해 다른 구조체와는 다른 상관관계 특성을 가질 가능성이 있다고 판단된다[12].

Fig. 5

Comparison between ANN prediction and training data

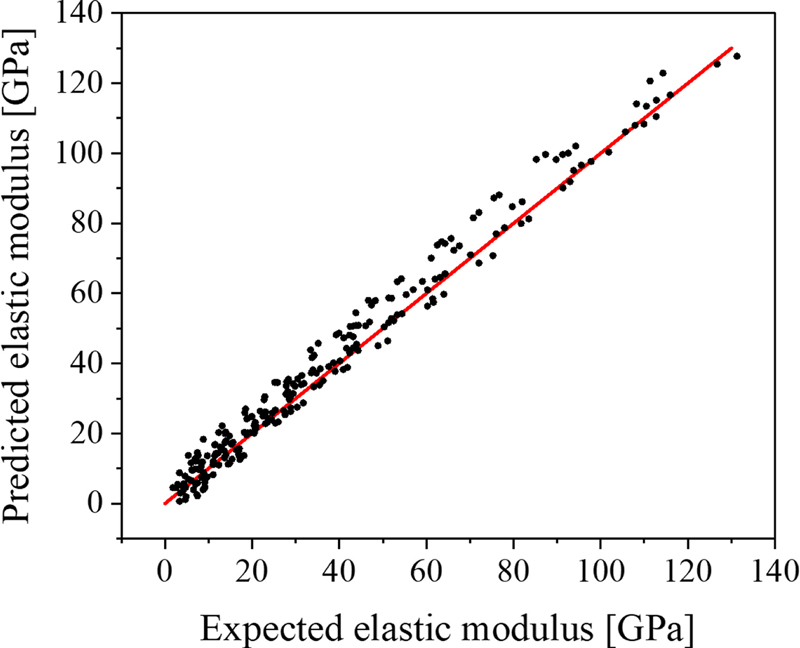
Fig. 6은 탄성계수의 수준에 따른 기댓값과 예측값 사이의 연관성 그래프를 나타내고 있다. 전체 범위에서 인공신경망은 기댓값 대비 높은 예측값을 나타냈지만 기준선(적색선)에서 크게 벗어나지 않는 결과를 보여주었다. 또한 탄성계수의 수준에 따른 예측 성능의 차이는 존재하지 않았다. 따라서 훈련된 인공신경망은 탄성계수 예측에 효과적으로 활용할 수 있음을 알 수 있다.

Fig. 6

Correlation relationship between the expected and predicted values using optimized ANN model

본 연구를 통해 개발된 탄성계수 예측을 위한 인공신경망을 새로운 재료에 대해 설계 변수에 따른 탄성계수 예측에 사용할 수 있다면 활용성 측면에서의 강점이 되리라는 것은 의문의 여지가 없다. 따라서 이러한 기능을 확인하기 위하여 탄성계수 138.3 GPa을 갖는 가상의 재료에 대해 구조체의 종류 및 체적 분율에 따른 탄성계수 예측을 수행하였으며 그 결과를 Fig. 7에 나타내었다. 그림에서 알 수 있듯이 가상의 재료에 대한 예측값(적색 별표)은 Inconel 625(162 GPa)과 Ti-6Al-4V(107 GPa) 사이에 위치함을 알 수 있다. 가상 재료의 탄성계수가 138.3 GPa이라는 것을 감안하였을 때 충분히 합리적인 결과라고 판단되며, 체적분율의 증가에 따른 탄성계수 증가 추세도 다른 재료와 같이 비선형적으로 증가되는 경향을 모사함을 확인할 수 있다. 따라서 본 연구를 통해 개발된 인공신경망은 훈련에 적용된 재료뿐만 아니라 새로운 재료에 대한 다공성 구조 설계에도 유용하게 활용될 수 있는 도구임을 확인할 수 있다.

Fig. 7

Results of elastic modulus prediction for virtual material according to structure types and volume fraction

4. 결론

본 연구에서는 인공신경망을 활용하여 다양한 재료 및 설계 변수를 고려한 다공성 구조체의 탄성계수를 예측하는 모델을 개발하였다. 유한요소해석 시뮬레이션을 통해 생성된 대규모의 데이터셋을 바탕으로 인공신경망 모델을 학습시키고, 그 과정에서 최적의 모델 구조를 제안하였으며, 이를 통해 전통적인 방법에 비해 더욱 정확하고 신뢰성 있는 예측이 가능함을 확인하였다. 학습된 인공신경망은 학습에 사용되지 않은 새로운 데이터에 대해서도 일반화된 예측 능력을 보여주었으며, 이는 다양한 다공성 구조 설계에 적용 가능함을 시사한다. 모델의 활용성 측면에서는 새로운 재료에 대해서도 추가적인 유한요소해석이나 인공신경망의 학습 없이도 구조체의 탄성계수를 신뢰성 있게 예측 가능함을 보였으며 이를 통해 설계 효율성을 크게 향상시킬 수 있음을 확인하였다.

Acknowledgments

본 논문은 한국생산기술연구원 기업수요기반생산기술 실용화사업(No. JA240011)의 지원을 받아 수행된 연구 결과입니다

REFERENCES

• Wang, X., Xu, S., Zhou, S., Xu, W., Leary, M., Choong, P., Qian, M., Brandt, M., Xie, Y. M., (2016), Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review, Biomaterials, 83, 127-141. [https://doi.org/10.1016/j.biomaterials.2016.01.012]
• Egan, P. F., Gonella, V. C., Engensperger, M., Ferguson, S. J., Shea, K., (2017), Computationally designed lattices with tuned properties for tissue engineering using 3D printing, PloS one, 12(8), e0182902. [https://doi.org/10.1371/journal.pone.0182902]
• Moon, I. Y., Song, Y., (2023), Design of lattice structure for controlling elastic modulus in metal additive manufacturing, Journal of the Korean Crystal Growth and Crystal Technology, 33(6), 276-281.
• Karamooz Ravari, M. R., Kadkhodaei, M., (2015), A computationally efficient modeling approach for predicting mechanical behavior of cellular lattice structures, Journal of Materials Engineering and Performance, 24, 245-252. [https://doi.org/10.1007/s11665-014-1281-4]
• Alwattar, T. A., Mian, A., (2019), Development of an elastic material model for BCC lattice cell structures using finite element analysis and neural networks approaches, Journal of Composites Science, 3(2), 33. [https://doi.org/10.3390/jcs3020033]
• Peng, C., Tran, P., Nguyen-Xuan, H., Ferreira, A. J. M., (2020), Mechanical performance and fatigue life prediction of lattice structures: Parametric computational approach, Composite Structures, 235, 111821. [https://doi.org/10.1016/j.compstruct.2019.111821]
• Ravari, M. K., Kadkhodaei, M., Badrossamay, M., Rezaei, R., (2014), Numerical investigation on mechanical properties of cellular lattice structures fabricated by fused deposition modeling, International Journal of Mechanical Sciences, 88, 154- 161. [https://doi.org/10.1016/j.ijmecsci.2014.08.009]
• Moon, I. Y., Jeong, H. W., Lee, H. W., Kim, S.-J., Oh, Y.-S., Jung, J., Oh, S., Kang, S.-H., (2022), Predicting high temperature flow stress of nickel alloy A230 based on an artificial neural network, Metals, 12(2), 223 [https://doi.org/10.3390/met12020223]
• Kim, B., Ha, S. H., (2023), Simulation-based material property analysis of 3D woven materials using artificial neural network, Journal of the Computational Structural Engineering Institute of Korea, 36(4), 259-264. [https://doi.org/10.7734/COSEIK.2023.36.4.259]
• Liu, X., Yan, Z., Zhong, Z., (2021), Predicting elastic modulus of porous La0.6Sr0.4Co0.2Fe0.8O3-δ cathodes from microstructures via FEM and deep learning, International Journal of Hydrogen Energy, 46(42), 22079-22091. [https://doi.org/10.1016/j.ijhydene.2021.04.033]
• Maurizi, M., Gao, C., Berto, F., (2022), Predicting stress, strain and deformation fields in materials and structures with graph neural networks, Scientific Reports, 12(1), 21834. [https://doi.org/10.1038/s41598-022-26424-3]
• Zhang, J., Zhao, J., Rong, Q., Yu, W., Li, X., Misra, R. D. K., (2022), Machine learning guided prediction of mechanical properties of TPMS structures based on finite element simulation for biomedical titanium, Materials Technology, 37(1), 1-8. [https://doi.org/10.1080/10667857.2021.1999558]