스트레인 웨이브 기어 플렉스플라인 반경 방향 강성 측정 방법
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Strain wave gears are widely used as reducers in robots, including collaborative and industrial robots. As a key component, they play a crucial role in determining overall robot performance. To enhance their effectiveness, various studies have focused on directly measuring the performance of assemblies or predicting the performance of individual components through analysis. However, there is a notable lack of research that experimentally measures and compares the physical properties of the circular spline, flexspline, and wave generator—the primary elements of strain wave gears. In this paper, we developed equipment to measure the radial stiffness of the flexspline, one of the key components, and validated its reliability through preliminary experiments. Furthermore, we measured and compared the radial stiffness of flexsplines produced by three different manufacturers. These findings are expected to provide valuable insights for improving the performance of strain wave gears and advancing robotics technology.
Keywords:
Strain wave gear, Flexspline, Radial stiffness키워드:
스트레인 웨이브 기어, 플렉스플라인, 반경 방향 강성1. 서론
산업용 로봇과 협동 로봇에 널리 사용되는 스트레인 웨이브 기어(Strain Wave Gear)는 웨이브 제너레이터(Wave Generator), 플렉스플라인(Flexspline), 서큘러 스플라인(Circular Spline)으로 구성 된다[1,2]. 스트레인 웨이브 기어 시장은 일본의 하모닉드라이브사가 전체 시장의 70% 이상을 점유하고 있어 국산화가 시급한 상황이다. 국내에서는 에스비비테크, SPG, 삼성전기, 현대트랜시스 등 다수의 기업에서 스트레인 웨이브 기어를 개발 중이며 그 일환으로 스트레인 웨이브 기어 성능 평가 장치에 대한 연구도 진행되었다[3-5]. 성능 평가 장치 개발에 관한 연구는 각도 전달 오차(Angular Transmission Error), 기동토크(Starting Torque), 히스테리시스 곡선(Hysteresis) 등 스트레인 웨이브 기어의 주요 성능 지표를 측정하는 장비를 만들고, 측정 결과를 해석하는 연구를 중심으로 진행되었다[6-8]. 현재 국내의 스트레인 웨이브 기어 제품 개발에 있어서 해결해야 할 현안은 스트레인 웨이브 기어의 제품화를 위해 제품 간 품질 편차 최소화와 제품의 내구성 향상이다. 품질 편차 문제의 해결을 위해 각 요소 부품의 물리적 특성의 측정을 통해 완제품의 성능에 관련된 상관관계를 밝히는 것이 필요하다. 그런데 스트레인 웨이브 기어의 성능평가장치에 관한 연구는 일부 있지만, 각 요소 부품의 물리적 특성을 측정하는 연구는 없었다[9-12].
스트레인 웨이브 기어가 작동할 때, 캠 형상의 웨이브 제너레이터가 플렉스플라인에 삽입되어 회전하면서 반경 방향으로 지속적인 탄성 변형이 발생한다. 플렉스플라인의 반경 방향 강성이 높으면 스트레인 웨이브 기어의 강성이 증가해 제어 측면에서는 유리할 수 있지만, 효율이 저하될 가능성이 있다. 플렉스플라인의 반경 방향 강성은 스트레인 웨이브 기어 성능을 결정하는 주요 요소 중 하나이다. 본 논문에서는 스트레인 웨이브 기어의 핵심 구성 요소인 플렉스플라인의 반경 방향 강성을 측정하기 위한 장비와 방법을 제안한다.
2. 반경 방향 강성 측정 장치
2.1 기구부 구성
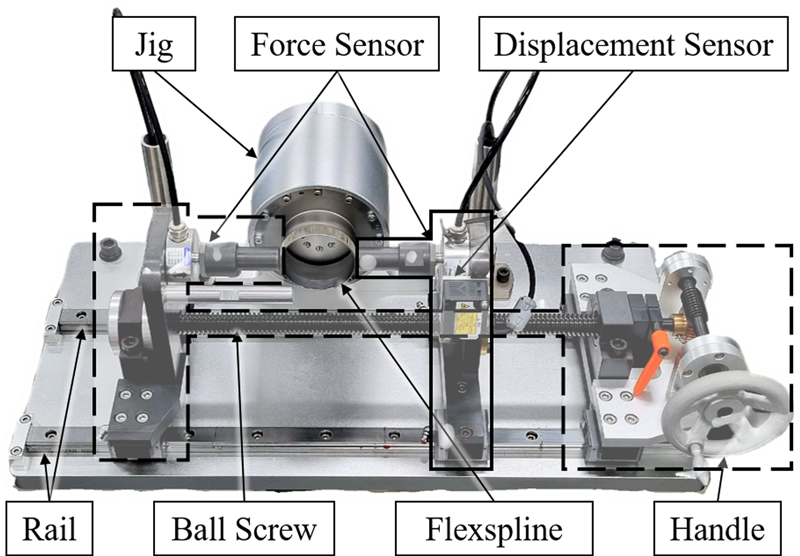
반경 방향 강성 측정 장치는 Fig. 1과 같이 플렉스플라인을 고정할 수 있는 지그와 반경 방향으로 양쪽에서 부하를 측정할 힘 센서(Force Sensor)와 플렉스플라인의 반경 방향 변형량을 측정할 수 있는 변위 센서(Displacement Sensor)를 부착할 수 있게 하였다. 레일(Rail)은 플렉스플라인의 축과 수직으로 설계하여 힘 센서가 반경 방향으로만 움직이도록 자유도를 제한하였다. 플렉스플라인 지그(Jig)는 형번과 형상에 따라 변경할 수 있도록 설계하여 다양한 형번과 타입의 플렉스플라인 반경 방향 강성을 측정할 수 있도록 하였다.
측정 순서는 다음과 같다. 먼저 플렉스플라인을 지그에 고정하고 핸들(Handle)을 시계방향으로 돌리면 실선으로 표시된 부분이 볼 스크루(Ball Screw)에 의해 레일을 따라 왼쪽으로 움직이며 플렉스플라인에 먼저 닿게 된다. 이후 점선으로 표시된 부분이 오른쪽으로 움직이며 왼쪽 힘 센서도 플렉스플라인에 닿게 된다. 핸들을 계속해서 돌리면 힘 센서가 반경 방향으로 플렉스플라인을 누르며 변형시켜 강성을 측정할 수 있게 된다.
2.2 센서 및 DAQ 구성
플렉스플라인의 반경 방향 강성(kr)은 훅의 법칙에 따라 식(1)과같이 변형된 변위(x)와 가해진 힘(F)으로 계산할 수 있다.
| (1) |
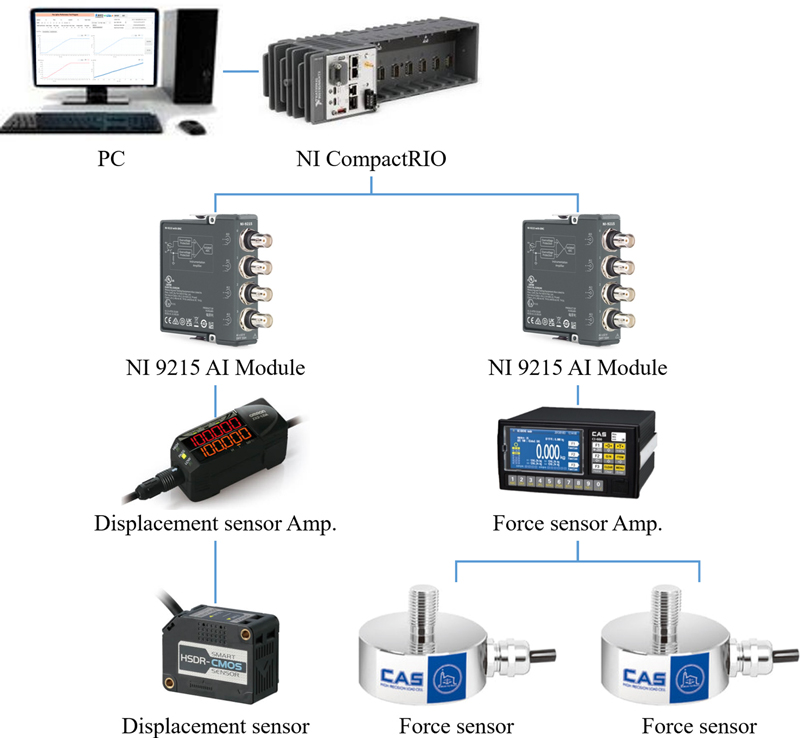
반경 방향 강성을 측정하기 위해 OMRON의 ZX2-LD100 변위 센서와 CAS의 MNT-100L 힘 센서를 이용하였다. 하드웨어 연결은 Fig. 2와 같이 각 센서를 통해 측정된 값은 앰프를 통해 아날로그 데이터로 변환한 뒤 DAQ (Data Acquisition)에서 수집 및 신호 처리 후 컴퓨터에서 확인할 수 있게 되어 있다. 측정에 사용된 센서와 DAQ의 성능은 Table 1에서 확인할 수 있다.
DAQ는 NI의 CompactRIO와 NI 9215 AI 모듈을 사용하였다. ADC의 분해능은 16 bits, 입력 전압은 ±10.0 V로 0.3 mV 레벨의 전압을 측정할 수 있어 변위 센서와 힘 센서의 앰프에서 출력하는 아날로그 출력을 충분히 측정할 수 있는 모델을 사용하였다.
3. 반경 방향 강성 측정 실험
3.1 반경 방향 강성 측정 방법
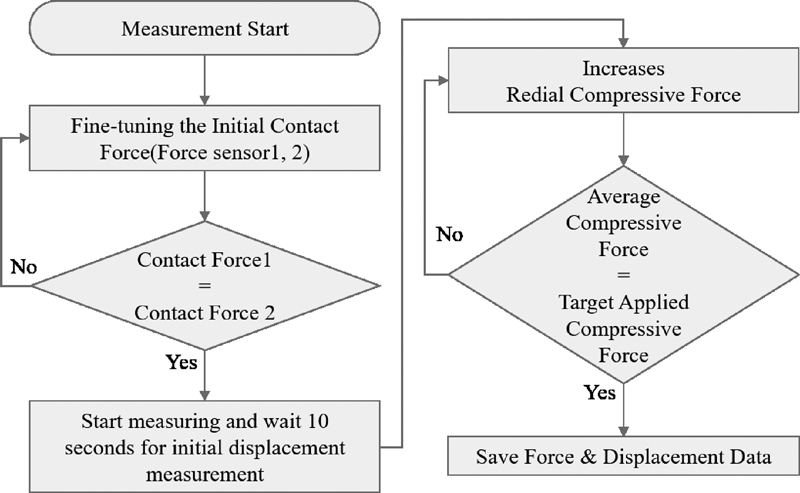
플렉스플라인 반경 방향 강성을 측정하는 방법을 Fig. 3에 나타냈다. 두 개의 힘 센서가 플렉스플라인의 기어 치에 닿도록 핸들을 조종하고 이후 힘 센서 1에서 측정되는 접촉력(Contact Force 1)과 힘 센서 2에서 측정되는 접촉력(Contact Force 2)이 같아지도록 레일을 조절한다. 힘 센서의 초기 접촉 힘이 같아지면 힘과 변위 데이터를 측정하기 시작한다. 초기 변위를 정확히 측정하기 위해 10초 동안 대기 후 핸들을 돌려 플렉스플라인을 반경 방향으로 눌러 설정한 값까지 부하를 올린다. 플렉스플라인이 탄성 변형되며 측정된 변위와 힘을 저장하고 반경 방향 강성을 계산하게 된다.
실험하려는 플렉스플라인의 종류는 실크 햇(Silk Hat) 형상, 25형번, 감속비 100을 사용하였다. 감속기 제조사 세 곳에서 3개씩 총 9개의 플렉스플라인을 준비하였다. 반경 방향 강성을 측정하기에 앞서 하중을 얼마나 가하여 강성을 측정할지 정해야 한다. 플렉스플라인의 반경 방향 변형은 타원형의 웨이브 제너레이터가 삽입되어 일어나게 된다. 따라서 플렉스플라인의 반경 방향 변형량은 웨이브 제너레이터의 장축과 단축 차이만큼 발생하게 된다.
세 제조사의 25형번 웨이브 제너레이터의 장축과 단축의 길이는 모두 62.0과 60.6 mm로 동일하다. 장축과 단축의 길이 차는 1.4 mm이다. 따라서 웨이브 제너레이터가 삽입될 때 플렉스플라인이 단축 방향으로 변위가 줄어들고 장축 방향으로는 변위가 늘어나 최종적으로 단축 방향의 변형량은 0.7 mm 근처일것으로 보이나, 실험에서 변형량의 충분한 차이를 보기 위해 A 제조사의 플렉스플라인이 반경 방향으로 1.4 mm 변형될 때의 힘을 기준으로 강성 측정을 진행하였다.
3.2 신호 처리
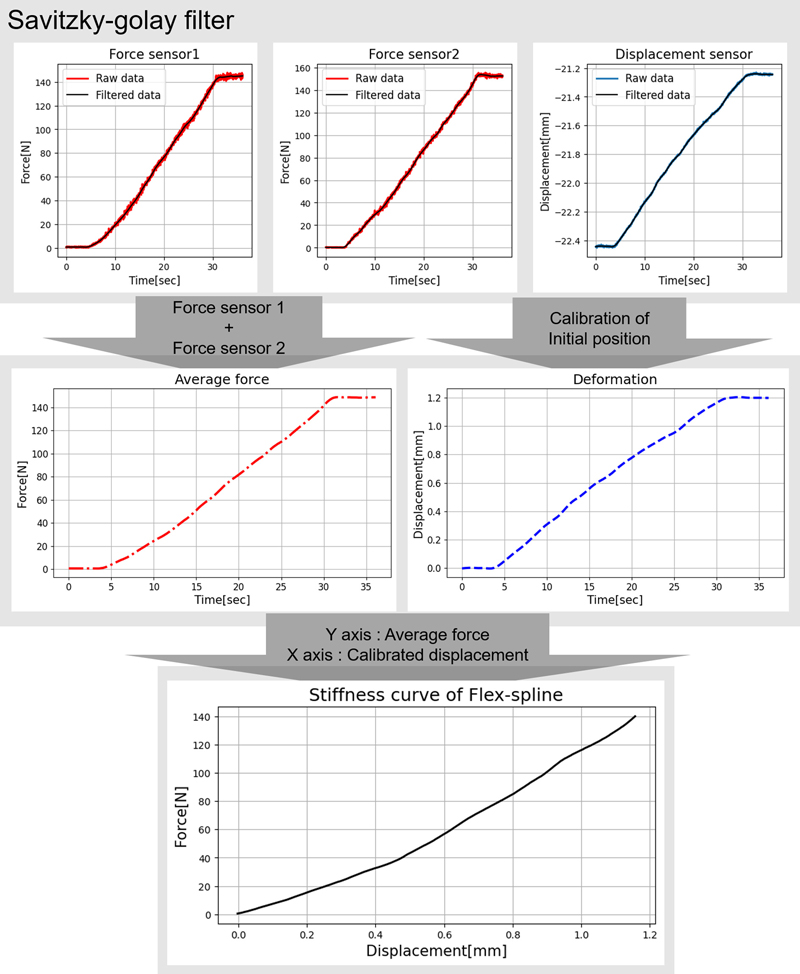
플렉스플라인의 반경 방향 강성 측정 값의 저장 주기는 25 ms로 설정하여 초당 40개의 데이터를 취득할 수 있도록 하였다. 취득한 데이터는 Fig. 4와 같이 Savitzky-golay 필터를 사용하여 노이즈를 제거하였다. 두 개의 힘 센서에서 취득한 데이터는 같은 시간에 측정된 두 값의 평균을 계산하여 평균 힘 데이터를 얻었다. 변위 센서로 획득한 데이터는 부하를 인가하기 전 두 힘 센서의 접촉력이 같을 때 측정한 값을 기준으로 초기 위치를 보정하고 변형량을 계산하였다.
3.3 예비 실험
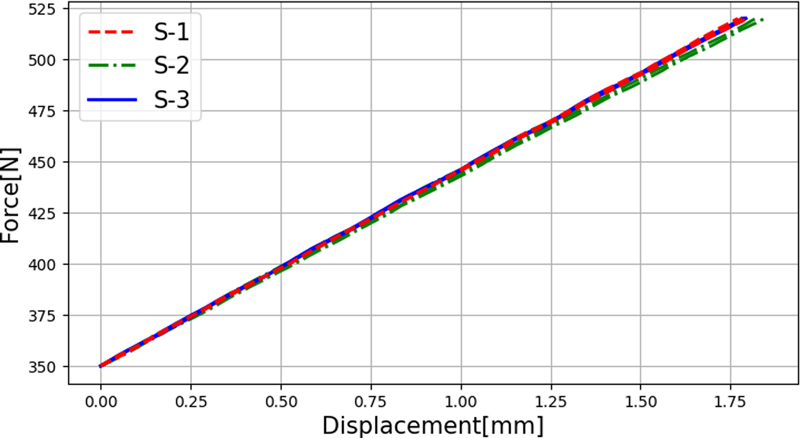
플렉스플라인의 반경 방향 강성을 측정하기 전에 제작한 측정 장비가 강성을 바르게 측정할 수 있는지 확인하기 위하여 예비 실험을 진행하였다. 결과의 정확도를 높이기 위해 JIS B5012 규격으로 제작된 강성이 같은 용수철 3개(S-1, S-2, S-3)를 준비하여 각각 3번씩 반복하여 강성을 측정하였다. 용수철의 특성은 다음과 같다. 강성은 96.30 N/mm로 하중이 520 N 걸리면 변형량은 자유 길이 25 mm에서 21.6% 줄어들어 5.4 mm 발생한다. 따라서 예비 실험은 제조사에서 제공하는 용수철의 사양에 따라 520 N까지 일정한 속도로 부하를 증가시키고, 힘과 변형량을 측정하여 Fig. 5와 같은 데이터를 획득하였다. 획득한 데이터 중 520 N까지의 기울기를 계산하여 Table 2과 같이 강성을 얻었다. 측정된 강성의 전체 평균은 94.35, 표준편차는 0.59 N/mm이다. 제조사에서 제공하는 강성 96.30 N/mm를 참값으로 가정하였을 때 오차율은 2.03%이다. 전체적으로 참값보다 강성이 모두 낮게 측정되어 상대적으로 정확도는 낮지만, 측정된 강성의 분포가 모여 있어 높은 정밀도로 측정되는 것을 확인하였다. 강성이 참값보다 낮게 측정된 원인은 용수철의 제조 오차나 측정 시 용수철을 지그와 정확히 동축에 장착하지 못하여 발생할 수 있을 것으로 예상된다. 용수철의 강성 측 시 발생한 문제는 플렉스플라인 전용 지그를 제작하여 힘이 항상 같은 위치에 가해질 수 있도록 하였다.
3.4 플렉스플라인 반경 방향 강성 측정 결과
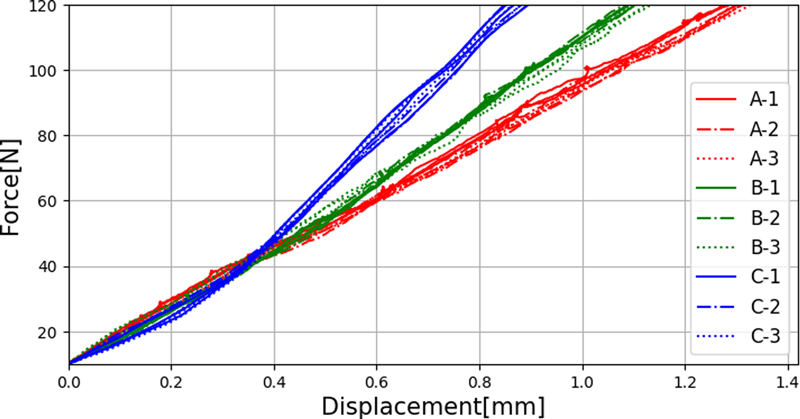
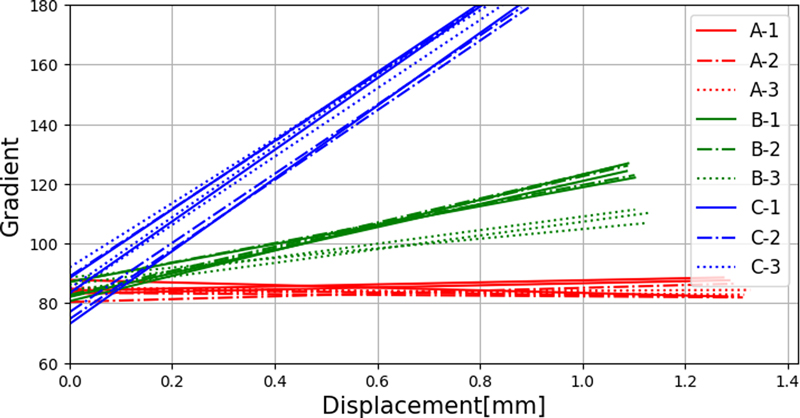
3개 회사의 동일한 형번(25형번)의 플렉스플라인에 대해 부품 별로 각각 3번씩 측정하여 위치 변화량에 따른 힘의 값을 Fig. 6에 제시하였다. 플렉스플라인의 반경 방향의 강성은 Fig. 6의 기울기 값이다. Fig. 6에 표시된 곡선의 선형성을 비교하기 위해 기울기의 변화량을 계산하였다. 측정된 강성 그래프로부터 다항회귀함수를 구하고, 그 함수의 기울기 변화량을 Fig. 7과 같이 구하였다.
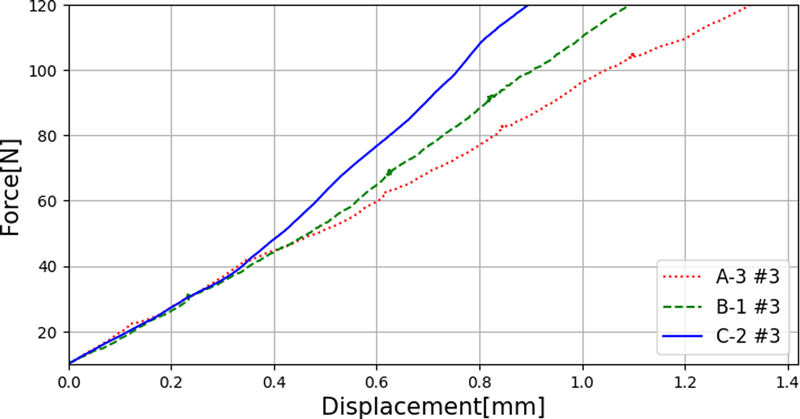
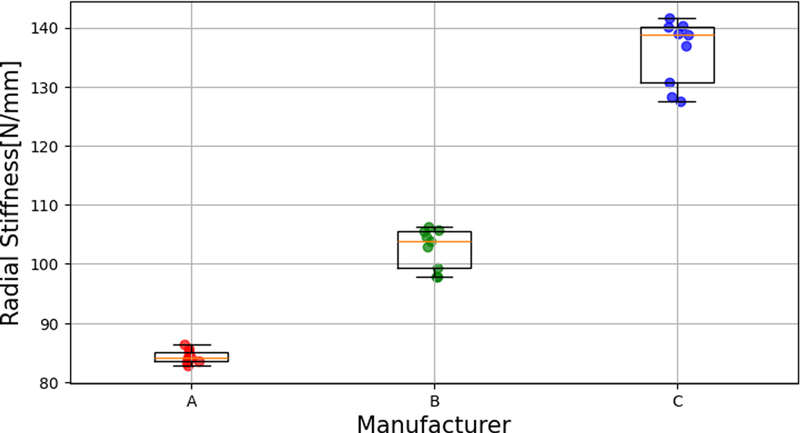
제조사별 플렉스플라인의 반경 방향 강성의 평균값을 Table 3에 보였다. A사의 반경 방향 강성이 낮고, B사와 C사는 A사 대비하여 강성이 높았다. 제조사 별로 측정한 플렉스플라인의 반경 방향 강성의 대푯값을 뽑아 한곳에 Fig. 8과 같이 표현하니 차이가 더 명확하게 보였다. 강성이 가장 큰 C사 제품의 기울기가 가장 가파르고 B사, A사 순서로 기울기가 작아지는 것을 확인 할 수 있다. 또한 플렉스플라인의 반경 방향 강성을 상자 수염 그림(Box and Whisker Plot)으로 나타내어 Fig. 9과 같이 분포를 확인하였다.
시장에서 품질이 우수하다고 평가되는 A사의 제품은 반경 방향 강성의 편차가 B와 C에 비해 작아 품질 균일성이 유지되고 있었다. 반면, B사와 C사의 플렉스플라인은 강성 값이 A사의 플렉스플라인보다 크고 편차도 크다. 알려진 바에 의하면 현재 B사와 C사의 스트레인 웨이브 기어는 A사의 제품에 비해 효율이 낮고 수명이 짧다. 일반적으로 플렉스플라인이 스트레인 웨이브 기어의 동력 전달 과정에서 탄성 변형을 하게 되는데 반경 방향의 강성치가 높으면 회전 시 플렉스플라인과 웨이브 제너레이터 사이에 압력이 커지고 두 개의 부품간 마찰력이 커지게 되면서 효율이 저하되고 수명이 줄게 된다. 따라서 플렉스플라인이 너무 큰 값의 반경 방향의 강성치를 가지는 것은 좋지 않은 것을 알 수 있다. 다른 한편으로 반경 방향의 강성 값을 낮추기 위한 소재를 사용할 경우, 소재의 물성에 의해 비틀림 방향의 강성도 또한 낮춰질 수 있으므로 반복적인 부하에 의해 부품 변형이 발생할 가능성이 커지고, 제어 정밀도가 떨어질 수 있는 문제가 발생할 수 있다. 따라서 스트레인 웨이브 기어의 플렉스플라인의 강성 값은 A사의 제품처럼 플렉스플라인의 적절한 강성 값을 균일하게 유지하는 것이 중요함을 알 수 있다.
4. 결론
본 연구에서는 스트레인 웨이브 기어의 플렉스플라인 반경 방향 강성을 측정하기 위한 장비와 방법을 제안하였다. 동일 모델의 플렉스플라인을 제조사별로 비교한 결과, A사의 플렉스플라인이 시장에서 고품질로 평가받는 것처럼 반경 방향 강성 값이 일정한 범위 내에서 균일하게 분포하는 것을 확인하였다. 이는 B사와 C사의 플렉스플라인이 개발 사양 및 품질에서 편차를 줄일 필요가 있음을 시사한다. 앞으로는 스트레인 웨이브 기어조립품의 비틀림 강성을 측정하여, 플렉스플라인과 조립체 간의 성능 상관관계를 연구할 계획이다.
NOMENCLATURE
| kr : | Radial Stiffness |
| x : | Deformation |
| F : | Force |
Acknowledgments
이 연구는 산업통상자원부 ‘소재부품기술개발사업’ 지원을 받아 연구 되었음(No. 20017498).
REFERENCES
-
Lee, B. J., Kim, G. T., Kim, H. C., Shin, Y. J., (2019), Static and dynamic friction characteristics analysis of actuation module for friction compensation of exoskeleton robot, Journal of the Korean Society for Precision Engineering, 36(10), 929-935.
[https://doi.org/10.7736/KSPE.2019.36.10.929]

-
Pham, A.-D., Ahn, H.-J., (2018), High precision reducers for industrial robots driving 4th industrial revolution: state of arts, analysis, design, performance evaluation and perspective, International journal of precision engineering and manufacturinggreen technology, 5, 519-533.
[https://doi.org/10.1007/s40684-018-0058-x]

-
Tjahjowidodo, T., Al-Bender, F., Van Brussel, H., (2013), Theoretical modelling and experimental identification of nonlinear torsional behaviour in harmonic drives, Mechatronics, 23(5), 497-504.
[https://doi.org/10.1016/j.mechatronics.2013.04.002]

-
Kim, J. Y., Bea, D. S., Jang, J. D., (2021), Torsional performance analysis of oldham coupling for harmonic drive, Journal of the Korean Society for Precision Engineering, 38(9), 701-705.
[https://doi.org/10.7736/JKSPE.021.041]

- Kim, I. K., Park, I. G., Choi, W., (2015), A study of the frequency response according to torsional stiffness of the harmonic drive, Proceedings of the Korean Society of Precision Engineering Srping Conference, 349-350.
-
Rhéaume, F. E., Champliaud, H., Liu Z., (2009), Understanding and modelling the torsional stiffness of harmonic drives through finite-element method, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 223(2), 515-524.
[https://doi.org/10.1243/09544062JMES949]

- Ha, D. S., Kim, J. H., Lee, M. S., (2021), A numerical analysis a flex spline for flat type harmonic drive, Proceedings of the Korean Society of Precision Engineering Autumn Conference, 327.
- Yeon, H. K., Lee, M. S., Kim, J. H., (2022), Establishment of finite element model for wave generator stiffness analysis considering contact nonlinearity, Proceedings of the Korean Society of Precision Engineering Autumn Conference, 338.
- Koh, D. G., Kim, J. G., Shin, J. S., Jin, M., (2021), Development of torsional stiffness measurement equipment for flex-spline of strain wave gear, Proceedings of the Autumn Conference on Drive and Control, 74.
- Koh, D. G., Kim, J. G., Shin, J. S., Jin, M., (2021), Development of stiffness measurement equipment for wave generator of strain wave gear, Proceedings of the Korean Society of Precision Engineering Autumn Conference, 277.
- Lee, S., Kim, J. G., Shin, J. S., Jin, M., (2021), Development of experimental device for measuring flex-spline radial stiffness of strain wave gear, Proceedings of the Korean Society of Precision Engineering Autumn Conference, 278.
- Kim, J. G., Shin, J. S., Koh, D. G., Lee, S., Jin, M., (2022), Stiffness evaluation of harmonic reducer flex spline, Proceedings of the Korean Society of Precision Engineering Autumn Conference, 353.

Graduated from Kumoh Institute of Technology, Department of Mechanical Engineering, M.S. degree. He is currently a researcher at the Korea Institute of Robotics and Convergence (KIRO). His research interests include robotics.
E-mail: woong2479@kiro.re.kr

Graduated from Gwangju Institute of Science and Technology, Department of Mechanical Engineering, M.S. degree. He is currently a researcher at the Korea Institute of Robotics and Convergence. His research interests include Fault Diagnosis of Robots.
E-mail: daegwon@kiro.re.kr

Principal Researcher in Korea Institute of Robotics and Technology Convergence. His research interest is robot manipulator, hydraulic robots, disaster response robots and commercial robots.
E-mail: ps100@kiro.re.kr

Director and Chief Researcher with the Human-centered Robotics R&D Division of the KIRO, Pohang, South Korea. His research interests include robust control of nonlinear plants, time-delay control, robot motion control, electro-hydraulic actuators, winding machines, collaborative robots, disaster robotics, and factory automation. Dr. Kim serves as an associate editor of the International Journal of Control, Automation, and Systems, Journal of Drive and Control, and Journal of the Korean Society for Precision Engineering.
E-mail: mulimkim@kiro.re.kr