강화학습 기반 레이저 경로의 제어시스템
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the field of optical engineering, the laser position control system has important role in many applications, such as measurement, communication, fabrication. Traditional methods to solve laser position control system often face the problems of insufficient generalization, such as configuration or singular solution. In this study we proposed a novel model-free reinforcement learning approach based Proximal Policy Optimization (PPO) for laser position control system. To control the position of laser, we develop an efficient representation of environmental inputs and outputs. Position error of Position Sensing Detector (PSD), and three kinds of distance parameters are applied our environmental parameters. To overcome the challenges associated with training in real worlds, we developed training environment in simulation. The simulation to evaluate performance of our approach, we perform several times of experiments in both simulated and real world system.
Keywords:
Laser, Position control system, Beam path, PPO, Model-free키워드:
레이저, 위치 제어 시스템, 광경로, 근사정책최적화, 무모델1. 서론
최근 레이저를 활용한 다양한 응용 기술이 개발되고 있다. 기존 정밀가공, 의학과 같은 실생활 적용 분야를 넘어, 고도의 정밀도와 정확성이 요구되는 위성통신, 방위산업, 항공기 통신 등 다양한 분야에 걸쳐 광범위하게 확대되고 있다[1-3]. 이에 따라 레이저 광경로 위치 제어 기술의 중요성이 대두되고 있으며, 구동기를 비롯한 광경로 분석에 대한 연구가 활발히 진행되고 있다[4-10].
전통적인 레이저 광경로 위치 제어 기술은 두 가지 방법이 존재한다. 기하학적인 해석 방법은 레이저 위치 인식 센서의 결과로부터, 각 구동기의 명령각을 역산하여 해를 구한다[3]. 해당 방법의 경우 구동기의 위치와 레이저 위치 인식 센서의 배치에 따라 해가 존재하지 않을 수 있다. 또한 모델링 기반의 기하학을 해석하기 때문에, 실제 광경로 구성 시 장비 설치 오차나 구동 오차에 대한 극복이 어렵다.
이를 해결하기 위하여 수치적인 해석 방법이 사용되었다[7-9]. 해당 방법은 구동기의 구동각과 레이저 위치 센서의 결과를 여러 번 취득한 후 최적화 방법을 통하여, 위치와 구동각을 매핑 할 수 있는 야코비안 행렬을 구성하여 사용하는 방법이다. 해당 방법은 모델링 오차를 줄일 수 있는 장점은 있지만 특이해를 발생시킬 수 있는 문제가 존재한다.
최근 이러한 모델링 기반의 문제 풀이 방법을 해결하기 위하여, Model Free 기반의 강화학습을 이용한 제어 방안이 연구되고 있다. Model Free 기반의 강화학습은 역동적인 환경에서 반복적인 시행착오와 상호작용을 통하여, 목표 정책을 구하는 학습 방법으로 데이터 수집 방법에 따라 On-policy와 Off-policy로 구분된다. On-policy 기반 강화학습은 현재 정책과 이전 샘플로 생성된 정책이 같은 경우로, 학습데이터의 효율성은 떨어지나 구현이 간결하고, 여러 정책을 사용할 수 있는 장점이 있다[18-20]. Off-policy 기반 강화학습 알고리즘은 현재 정책과 이전 샘플 정책이 다른 경우로, 수집 데이터의 효율은 높지만, Offline에서 적절한 데이터로 생성된 정책이기에 평가가 어렵다[21-23]. 특히 강화학습 중 하나인 Proximal Policy Optimization (PPO)[20]은 대표적인 On-policy 방식의 강화학습으로 기존 Advanced Actor Critic (A2C) 알고리즘을 일반화[24]하여 정책 최적화를 수행하며, CLIP 함수를 통해 목적 함수의 발산을 막을 수 있어, 안정적인 학습이 가능하다. 또한 기존의 Trust Region Policy Optimization (TRPO)[18]이나 Asynchronous Advantage Actor Critic (A3C)[19]와 같은 알고리즘에 비하여 구조가 단순하여 계산의 부하가 적고, 구현이 간단하다. 이러한 장점을 바탕으로 다양한 분야에서 PPO를 활용한 제어를 연구 개발하고 있다[11-14].
본 논문에서는, PPO를 활용하여, 레이저 빔의 위치 제어 시스템을 제안한다. 해당 제어 시스템은 레이저가 발생할 수 있는 병진오차, 회전오차를 보상하기 위하여 총 4 자유도의 구동축과, 4 자유도의 위치 센서로 구성된다. 본 시스템은 레이저 발생지역을 기준 좌표로 정의하고, 이를 바탕으로 시스템 모델링을 수행한다. 수행한 모델링을 바탕으로 PPO에 보상함수, 행동, 상태를 결정하였고 이를 시뮬레이션과 실제 실험을 통하여 결과를 분석하였다. 해당 시스템의 장점은 PPO 알고리즘을 통한 레이저 경로 제어의 자동화와 일반화에 있다. PPO 알고리즘을 통하여 형성되는 목적함수와 이를 통한 제어를 학습으로 수행할 수 있다. 일반화의 관점에서는 기존 기하학적인 해석해나 수치적인 해석해의 한계점인 경로 구성 제한과 특이해를 극복하여, 단일해를 구할 수 있는 장점이 있다.
2. 시스템 모델링
2.1 레이저 위치 제어 시스템 구성
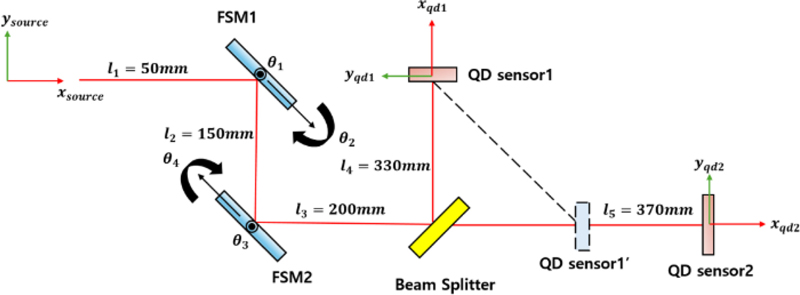
본 논문에서 구성한 레이저 위치 제어 시스템은 Fig. 1과 같으며, 2개의 Fast Steering Mirror (FSM)와 2개의 QD 센서, 1개의 Beam Splitter로 구성되어 있다. 이는 레이저가 진행 축인 X축을 제외한 Y축과 Z축으로 병진, 회전 오차를 보정하기 위하여 설계된 구조이다. 레이저의 최종 위치와 회전각을 알아내기 위하여, 2기의 QD 센서의 설치 거리에 차이를 두었다. QD 센서1은 QD 센서1’와 동일한 좌표로 볼 수 있으며, 각 QD 센서에서 측정한 위치정보를 기반으로 레이저의 회전 값을 알 수 있게 구성하였다[7]. 해당 QD 구성을 통하여 시스템적으로 레이저의 입사 각도 정보도 내포할 수 있도록 구성을 하였다. 2기의 FSM은 각각 2축으로 구동할 수 있으며, 최소 구동단위가 마이크로라디안이다. QD 센서는 각 셀의 조도 전압값을 위칫값으로 환산을 하여 레이저의 최종 X-Y의 위치를 확인할 수 있다. QD센서의 정보를 위치로 변환하는 방법은 식(1) 및 식(2)와 같다[18].
| (1) |
| (2) |
Q 값은 QD 센서에 맺히는 레이저의 조도를 의미하며, K는 전압과 위치 간 변환 상수를 의미한다.
BeamSpliiter는 레이저를 각 QD 센서로 레이저를 분광하는 역할을 한다.
2.2 기구학 해석
각 QD 센서에 맺힌 레이저의 위치정보는 QD 센서의 중앙위치를 기준으로 생성된 위치 좌표이다. 이는 FSM들이 구동 시, 광경로의 병진 운동 및 회전 운동에 대한 정보를 파악할 수 없으며, 학습 성능에 영향을 끼친다. 이에, 레이저 좌표계를 기준으로, 각 QD 센서의 중심 좌표를 알기 위하여 정기구학 해석을 수행한다. Fig. 1의 레이저 광경로는 Denavit-hartenberg (DH) 변수[15]로 표현이 가능하며 이는 Fig. 2와 같다. 해당 DH-parameter를 기반으로 QD 센서1과 QD 센서2의 전달 행렬은 다음 식(3)과 같이 계산이 가능하다.
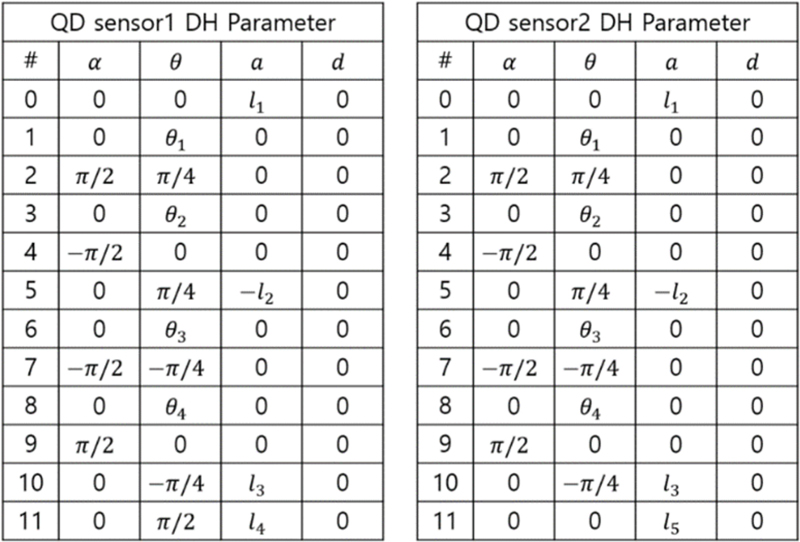
DH parameters of PSDs; (a) Laser beam frame to QD sensor1 frame and (b) Laser beam frame to QD sensor2 frame
| (3) |
R은 3차원상 회전행렬이고, p는 3차원 위치벡터이다. 해당 정기구학을 통하여 QD 센서에서 계산된 위치 정보는 레이저 좌표계 기준으로 이동량을 측정할 수 있다.
3. 강화학습 기반 제어
본 논문에서 적용한 PPO는 대표적인 Online 강화학습으로 다양한 환경에서 안정성과 효율성을 가지고 있다[20]. PPO는 정책 기울기 학습 방법의 하나로, 취득된 데이터를 기반으로 만들어진 환경의 상호작용과 제한된 대체목적함수를 사용하여 학습을 수행한다. 제한된 대체목적함수는 학습의 단계마다 정책변화를 제한하며, 이는 학습의 발산을 억제하고 안정적인 학습을 가능토록 한다. 식(4)는 PPO의 대체목적함수이고, 초월변수 ε는 이점함수 A를 양수일 때 1 + ε, 음수일 때 1 − ε만큼 발산을 억제한다.
| (4) |
| (5) |
| (6) |
이점 함수 A는 높은 분산 에러를 가지기에, 식(5)과 같이 시작시간 t부터 종료시간 T까지 Generalized Advantage Estimation (GAE)을 수행한다. 이때, KL Divergence에 대한 제한값은 가치함수 V와 할인율 γ로 표현될 수 있으며, 이는 식 (6)과 같다.
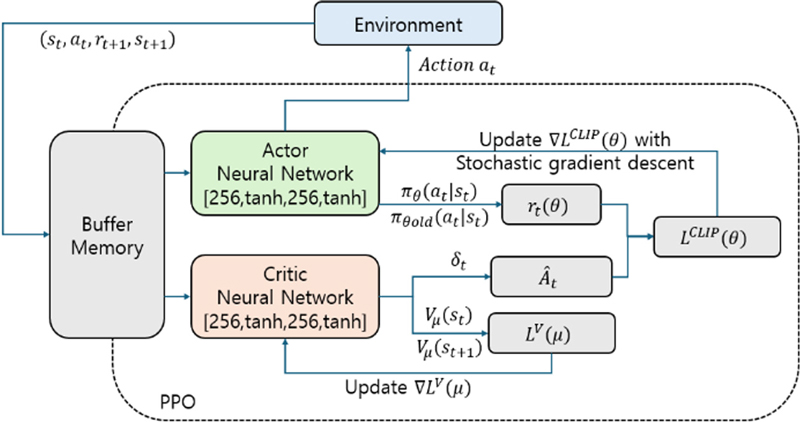
본 논문에서 제시하는 PPO의 전체 구조는 Fig. 3과 같으며, Actor 네트워크와, Critic 네트워크는 각각 2 레이어로 구성되어 있다. 각 레이어의 내부 구조는 256개의 뉴런과 Tanh의 활성함수로 구성되어 있다.
3.1 행동 및 상태 정의
레이저 최종 위치는 FSM들의 각도에 따라 변화하게 된다. 이에 식(7)과 같이 FSM들의 각도 변화량 벡터를 행동으로 정의하였다.
| (7) |
상태의 경우, 각도 정보와 위치오차, 유클리드 거리, 코사인 유사도, 혼합 거리를 기반으로 구성하였고 식(8)과 같이 정의한다.
| (8) |
θ는 각 시간별 FSM의 각도벡터이고, pe1과 pe2는 각각 QD 센서에서 발생한 위치 오차값이다. d1과 d2는 각 QD 센서에서 발생한 위치 오차들의 유클리드 거리값이다. c1과 c2는 QD 센서중심위치 벡터와 현재 레이저의 위치 벡터간 코사인 유사도[16]로, 벡터간 유사성을 나타낸다. 이는 식(9)와 같다.
| (9) |
pqdc는 QD 센서 중심위치 벡터이며, pqdl은 현재 QD 센서에 위치한 레이저의 위치이다. 이는 두벡터간 방향의 유사성을 의미하며 범위는 [-1 1]이다. m은 레이저의 위치와 방위를 표현하는 혼합 거리로, 유클리드 거리와 코사인 유사도를 통하여 식(10)과 같이 표현된다.
| (10) |
코사인 유사도의 범위는 [-1 1]이며, -1에 가까울수록 적을수록 두 벡터간 유사도는 떨어지게 된다. 이에 1 − c1으로 구성하여, 코사인 유사도가 [0 2]의 범위가 나올 수 있도록 표현하였다. 혼합거리는 유클리드 거리가 작고 코사인 유사도의 값이 커질수록 QD 센서의 중심점에 가깝도록 설계되었다.
3.2 보상함수 구성
보상함수 구성은 DRL 성능에서 중요한 요소이다. 레이저가 PSD 상 목표 위치에 도달하였을 때의 보상함수 구성은 식(11)과 같다.
| (11) |
ω는 혼합거리의 자연로그값에 대한 가중치이다. 해당 보상함수의 구성으로 혼합거리의 길이가 짧아질수록 보상의 크기는 증가하게 된다. 본 논문에서 ω의 값은 -0.5로 설정하였다.
FSM의 과도한 이동으로 QD 센서의 인식범위를 벗어나면, -10의 벌점을 부여하였고, 빠른 학습 결과를 도출하기 위하여, 매 스텝마다 벌점으로 -0.005를 부과하였다.
이전 혼합거리보다 큰 경우가 발생하면 추가적인 벌점으로, 혼합거리의 오차를 주었다. 이와 반대로 이전 혼합거리보다 작은 경우는 혼합거리의 오차를 보상으로 주었다.
4. 실험
4.1 시뮬레이션 실험 및 결과
시뮬레이션 학습은 Fig. 1과 동일 구성으로 수행하였다. 해당 구성에 맞게 광경로의 길이를 할당하였으며, 각 FSM은 2 자유도의 구동각으로 구성하였다.
학습용 PC성능은 Intel i9(5.1 Ghz), 32 GB RAM, RTX4070 그래픽 카드의 하드웨어로 구성되었다. 소프트웨어 개발 환경은 Pybullet[17]과 Stable-baseline3[18]로 구성을 하였다. 각 FSM이 임의의 구동각에서 시작하여, 레이저 위치가 QD 센서좌표 중심점까지 가도록 학습을 시켰으며, 좌표 중심점까지 거리가 50 um 이하가 되면, 해당 에피소드를 종료하고, 보상을 하였다. 각 스텝에서 이동의 최소 명령단위는 2.5 urad으로 설정하였고, 한 에피소드당 106 스텝 동안 학습을 수행하였다. 총 10번의 에피소드 동안 학습을 수행하였고, 총 107의 스텝을 학습하였다. 실험 환경에 대한 설정과 결과는 Fig. 4와 같다.
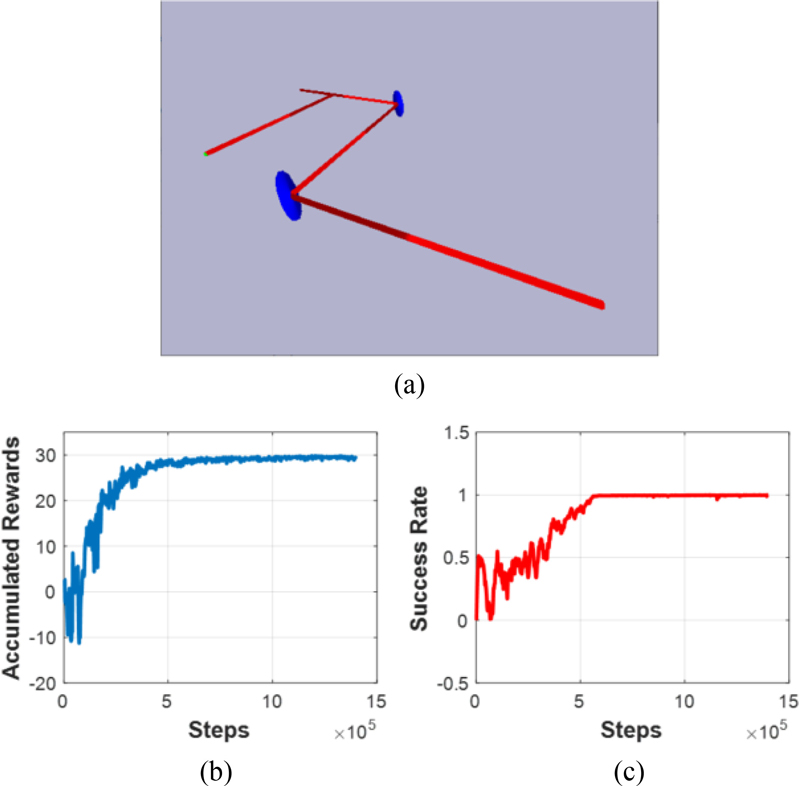
Scene of PPO Learning and training result; (a) Scenery of simulation environment, (b) Accumulated Reward while training and (c) Success rate while training
학습한 결과 보상함수는 약 -11.78에서 시작하여, 최종 30지점에서 수렴하였다. 총 학습 시간은 3시간 48분이 소요되었다.
학습 시, 설정된 전체 초월 변수는 Table 1과 같다.
4.2 실환경 실험 및 결과
실제 레이저 위치 제어 시스템에 실험은 Fig. 5와 같이 구성하여 실험을 수행하였다. 레이저는 Thorlab사의 LP515-SF3를 사용하였으며, 해당 레이저는 515 nm 파장에 3 mW의 규격이다. FSM 2기는 CEDRAT사의 DTT60-SM을 사용하였고, 크기는 64 × 36 mm이고, -5~5 mrad의 구동각을 가지고 있다. FSM에 부착된 거울의 크기는 50 × 5 mm이다. FSM 제어기는 CEDRAT사의 CCBu20을 사용하였으며, 내장된 폐루프 위치 제어기를 사용하였다. QD 센서는 OSI사의 QD50-0를 사용하였고, 50 mm2, 8 mm의 인식범위를 가지고 있다. QD 센서 데이터는 A/D 변환기를 통하여 데이터를 취득했다. BeamSplitter의 경우 Thorlab사의 BP233을 사용하였고, Lens의 경우 레이저의 초점을 맞추기 위하여 사용되었으며, Edmund Optics사의 #48-237과 #48-236을 사용하였다. 레이저발생기로부터 발생된 레이저는 FSM1과 FSM2를 거쳐 BeamSplitter로 도달하며, BeamSpliiter에 도달한 레이저는 각각 QD 센서1, QD 센서2로 전달되도록 구성하였다.
실제 레이저 위치 제어 시스템에서도 시뮬레이션과 동일한 설정으로 학습이 수행하였으며, 학습 결과는 Fig. 6과 같다. 학습결과 보상함수는 -15.7에서 시작하여, 27지점에서 수렴하였다. 총 학습 시간은 8시간 48분이 소요되었다.
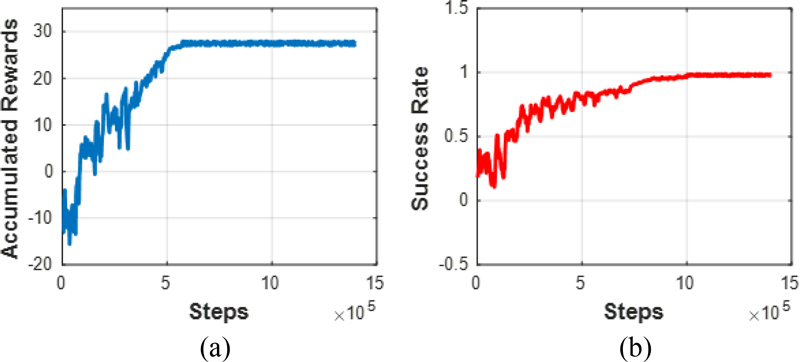
Scene of Realworld PPO training result; (a) Accumulated Reward while real world training and (b) Success rate while real world training
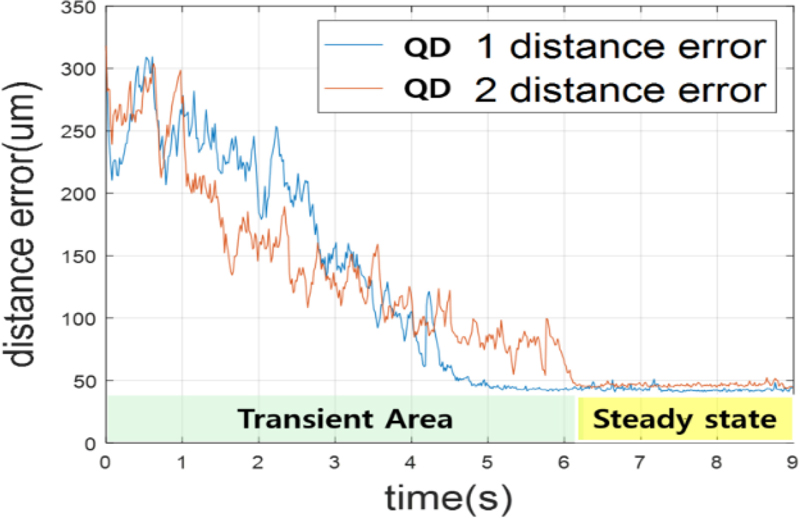
학습 완료 후 실제 시스템 구동 시, QD 센서 중심 위치에 대한 추종 능력을 실험하였다. 전체 1,000회를 독립적으로 수행하였으며, 실제 실험 또한 시간 스텝 별 각 FSM이 이동하는 최소의 단위는 2.5 urad으로 설정하였다. 해당 실험 결과는 Fig. 7과 같다.
처음 FSM의 관절 위치는 임의의 값을 주며 QD 센서의 50 um 이내로 레이저가 들어오면 다음 임의의 위치에서 실험을 수행하도록 구성하였다. QD 센서1과 QD 센서2는 1,000회 중 970회인 97%의 확률로 50 um내로 위치 제어가 되었다. QD 센서1은 평균 6.78초(±0.78초), QD 센서2는 7.13초(±0.62)의 시간이 소요되었다. 최대 레이저 위치 제어에 7.75초의 시간이 소요되었다.
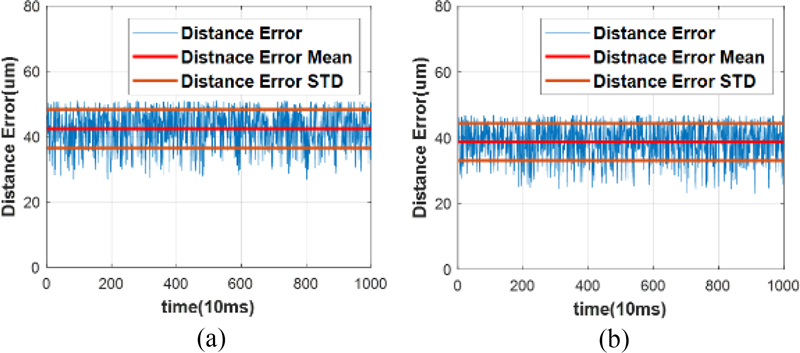
50 um내에서 정상상태의 위치 오차는 Fig. 8과 같다. QD 센서1은 평균 42.42 um(±5.95 um)로 나왔으며, QD 센서2는 평균 38.71 um(±5.68 um)의 결과로 도출되었다.
5. 결론
본 연구에서는 PPO를 활용한 레이저 빔의 위치 제어시스템을 개발하고 제안한다. 레이저의 자유도를 고려한 광경로를 구성하였고, 레이저 좌표계를 기준으로 레이저 위치센서의 값을 매핑하였다. 매핑된 정보와 구동기의 정보, 레이저 위치에서 발생하는 거리 오차들을 바탕으로 행동, 상태, 보상함수를 구성하였다. 정의된 행동, 상태, 보상함수를 기반으로 PPO를 학습시켰으며, 학습 결과에 대한 분석은 시뮬레이션과 실제 시스템을 통하여 이루어졌다. 시뮬레이션 실험 결과 50 um 이하의 위치 오차를 100%로 추정하였고, 실제 환경에서는 50 um 이하의 오차를 97%로 추정하였다. 이러한 추정의 차이는 실제 환경에서 요인되는 FSM의 게인값이나, QD 센서의 민감도로 발현되는 요인으로 사료된다.
본 연구는 기존의 기하학적인 해석방법이나 수치적인 해석방법과는 다르게 단일해가 나오는 방식으로 광경로를 제어하였다. 또한 별도의 제어기 구성 없이 구동기의 구동각과 위치센서의 정보만으로 위치 제어를 수행할 수 있기에 모델링에서 발생하는 오차에 대한 고려가 필요 없는 장점이 존재한다.
하지만 다량의 학습 시간으로 인하여 실제 환경에서 적용까지 많은 시간이 소요되는 단점이 있으며 목표 위치까지 수렴 시간이 오래 걸린다는 단점이 있었다. 이에 향후 본 연구를 확장하여, 학습 시간을 줄이고, 목표 시간까지 빠른 수렴 시간을 확보한 강화학습 제어기 연구를 수행할 계획이다.
NOMENCLATURE
| H : | Transformation Matrix |
| R : | Rotation Matrix |
| p : | Position Vector |
| ε : | Hyper Parameter |
| r : | Reward Parameter |
| A : | Advantage Function |
| θ : | Policy Neural Network |
| γ : | Discount Factor |
| V : | Value Function |
| s : | State Space |
| δ : | KL Divergence Limi |
| μ : | Critic Policy Function |
| π : | Actor Policy Function |
| a : | Action Space |
| Q : | Diode Voltage |
| ω : | Weight Factor |
| FSM : | Fast Steering Mirror |
REFERENCES
-
Pinkerton, A. J., (2016), Lasers in additive manufacturing, Optics & Laser Technology, 78, 25-32.
[https://doi.org/10.1016/j.optlastec.2015.09.025]

-
Lee, H., Lim, C. H. J., Low, M. J., Tham, N., Murukeshan, V. M., Kim, Y.-J., (2017), Lasers in additive manufacturing: A review, International Journal of Precision Engineering and Manufacturing-Green Technology, 4, 307-322.
[https://doi.org/10.1007/s40684-017-0037-7]

-
Wang, J., Huang, L., Hou, L., He, G., Ren, B., Zeng, A., Huang, H., (2013), The beam delivery modeling and error sources analysis of beam stabilization system for lithography, Proceedings of International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, 9046.
[https://doi.org/10.1117/12.2036313]

-
Juqing, Y., Dayong, W., Weihu, Z., (2017), Precision laser tracking servo control system for moving target position measurement, International Journal of Optik, 131, 994-1002.
[https://doi.org/10.1016/j.ijleo.2016.11.214]

-
Abdalla, N., Liu, S., Abdelrahim, A., (2020), Precision laser tracking for beam path control with PSD fuzzy controller, Proceedings of Asia Energy and Electrical Engineering Symposium (AEEES), 440-447.
[https://doi.org/10.1109/AEEES48850.2020.9121403]

-
Qin, F., Zhang, D., Xing, D., Xu, D., Li, J., (2017), Laser beam pointing control with piezoelectric actuator model learning, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50(3), 1024-1034.
[https://doi.org/10.1109/TSMC.2017.2754863]

-
Chang, H., Ge, W.-Q., Wang, H.-C., Yuan, H., Fan, Z.-W., (2021), Laser beam pointing stabilization control through disturbance classification, Sensors, 21(6), 1946.
[https://doi.org/10.3390/s21061946]

-
Li, Z., Liu, B., Wang, H., Yi, H., Chen, Z., (2022), Advancement on target ranging and tracking by single-point photon counting lidar, Optics Express 30(17), 29907-29922.
[https://doi.org/10.1364/OE.464070]

-
Marti, S., Mustafa, E., Bisson, G., Anand, P., Fabritius, P., Esslinger, T., Akin, A., (2023), FPGA-based real-time laser beam profiling and stabilization system for quantum simulation applications, Proceedings of Euromicro Conference on Digital System Design (DSD), 8-15.
[https://doi.org/10.1109/DSD60849.2023.00012]

-
Xie, Y., Praeger, M., Grant-Jacob, J. A., Eason, R. W., Mills, B., (2022), Motion control for laser machining via reinforcement learning, Optics Express, 30(12), 20963-20979.
[https://doi.org/10.1364/OE.454793]

-
Blake, X. J., Aphiratsakun, N., (2024), Reinforcement learning for PID gain tuning in ball-and-beam systems: A Comparative study, International Conference on Robotics, Engineering, Science, and Technology 2024, 187-190.
[https://doi.org/10.1109/RESTCON60981.2024.10463594]

-
Wang, G., Yang, F., Song, J., Han, Z., (2024), Dynamic laser inter-satellite link scheduling based on federated reinforcement learning: An asynchronous hierarchical architecture, IEEE Transactions on Wireless Communications, 14273-14288.
[https://doi.org/10.1109/TWC.2024.3411169]

-
Li, C., Yu, R., Yu, W., Wang, T., (2023), Reinforcement learning-based control with application to the once-through steam generator system, Nuclear Engineering and Technology, 55(10), 3515-3524.
[https://doi.org/10.1016/j.net.2023.06.001]

-
Murray R. M., Li. Z., Sastry S. S., (2017), A mathematical introduction to robotic manipulation, CRC Press.
[https://doi.org/10.1201/9781315136370]

- Tan, P.-N., (2006), Introduction to data mining 2ed edition, Springer.
- Coumans, E., Bai, Y., (2016), Pybullet, a python module for physics simulation for games, robotics and machine learning. https://docs.google.com/document/d/10sXEhzFRSnvFcl3XxNGhnD4N2SedqwdAvK3dsihxVUA/edit?tab=t.0
- Raffin, A., Hill, A., Gleave, A., Kanervisto, A., Ernestus, M., Dormann, N., (2021), Stable-baselines3: Reliable reinforcement learning implementations, Journal of Machine Learning Research, 22(268), 1-8.
- Schulman, J., Levine, S., Moritz, P., Jordan, M. I., Abbeel, P., (2015), Trust region policy optimization, arXiv preprint arXiv:1502.05477, .
- Mnih, V., Puigdomènech Badia, A., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., Silver, D., Kavukcuoglu, K., (2016), Asynchronous methods for deep reinforcement learning, arXiv preprint arXiv:1602.01783, .
- John, S., Wolski, F., Dhariwal, P., Radford, A., Klimov, O., (2017), Proximal policy optimization algorithms, arXiv preprint arXiv:1707.06347, .
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., Riedmiller, D., (2013), Playing atari with deep reinforcement learning, arXiv preprint arXiv:1312.5602, .
- Haarnoja, T., Zhou, A., Abbeel, P., Levine, S., (2018), Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor, International Conference on Machine Learning, 1861-1870.
- Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., Wierstra, D., (2019), Continuous control with deep reinforcement learning, arXiv preprint arXiv:1509.02971, .
- Huang, S., Kanervisto, A., Raffin, A., Wang, W., Ontañón, S., Dossa, R. F. J., (2022), A2C is a special case of PPO, arXiv preprint arXiv:2205.09123, .

Senior Researcher of Hanwha systems Infra Technology R&D Center. His research interest is Robotics engineering.
E-mail: geemin@hanwha.com

Senior Researcher of Hanwha systems Infra Technology R&D Center. His research interest is control engineering.
E-mail: pys419@hanwha.com

Senior Researcher of Hanwha systems Infra Technology R&D Center. His research interest is motion planning.
E-mail: arccircle@hanwha.com

Principal Researcher of Hanwha systems Infra Technology R&D Center. His research interest is LOS stabilization control.
E-mail: Daegyu.choi@hanwha.com

Chief Researcher of Hanwha systems Infra Technology R&D Center. His research interest is optical engineering.
E-mail: chikyung.ahn@hanwha.com

Senior Researcher of Agency for Defense Development. His research interest is beam/image path stabilization control.
E-mail: yeyoon@add.re.kr