[ REGULAR ]

Journal of the Korean Society for Precision Engineering - Vol. 36, No. 11, pp.1017-1023

ISSN: 1225-9071 (Print) 2287-8769 (Online)

Print publication date 01 Nov 2019

Received 16 Apr 2019 Revised 24 Jun 2019 Accepted 03 Jul 2019

DOI: https://doi.org/10.7736/KSPE.2019.36.11.1017

볼-스크류 서보시스템의 정밀운동을 위한 비선형 외란관측기를 갖는 Super-Twisting 슬라이딩 모드 제어기 설계

한성익¹^{, #}

1동국대학교 경주캠퍼스 기계시스템공학과

Design of a Super-Twisting Sliding Mode Controller with a Nonlinear Disturbance Observer for Precise Motion of a Ball-Screw Servo System

Seong Ik Han¹^{, #}

1Department of Mechanical System Engineering, Dongguk University, Gyeongju Campus

Correspondence to: ^#E-mail: skhan@dongguk.ac.kr, TEL: +82-54-770-2222

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this study, a super-twisting sliding mode controller with a non-linear disturbance observer for a ball-screw servo system was designed to obtain a precise motion and fast convergent control performance. Unknown dynamics of the servo system were approximated into pre-assumed diagonal constants for rapid controller design in the real industry to avoid expensive and time consuming experimental identification process. Moreover, uncertainties due to nonlinear friction, axis misalignment and dead zone were estimated by a nonlinear disturbance observer, which is combined with the designed super-twisting controller. The designed controller and observer systems were applied to the 2-axis ball screw servo system to verify the efficacy of the proposed control system via simulation and experiment.

Keywords:

Ball-Screw servo system, Precise motion, Super-Twisting sliding mode control, Nonlinear disturbance observer

키워드:

볼-스크류 서보시스템, 정밀운동, Super-Twisting 슬라이딩 모드제어, 비선형 외란관측기

1. 서론

산업현장에서 정밀한 모션시스템 제어기를 설계하기 위해서는 서보시스템의 동적 특성에 대한 정확한 모델 구축이 필요하고 미소한 운동영역에서 제어기 성능에 크게 영향을 주는 비선형 마찰을 모델링을 해야하며 볼 회전 축과 선형 가이드(LM Guide) 사이의 비대칭성, 작동 온도에 따른 회전축 팽창, 구동모터와 회전축 사이의 회전 중심 불일치 및 연결 커플링부의 사역대(Deadzone) 비선형 및 외부교란들을 종합적으로 고려해야 하며 이러한 특성들을 모두 실험적 측정과 분석을 통해 구하는 것은 매우 어려우며 경제적이나 시간적으로 많은 비용이 요구된다. 따라서 저비용으로 신속하고 외란에 강인하며 정밀한 이송 운동을 보장하는 제어기를 설계하는 것이 매우 효율 적인 방법이다.

슬라이딩 모드 제어(Sliding Mode Control, SMC)^1,2는 비교적 제어기 구조가 간단하면서 가변 구조 특성을 이용 하여 외란에 강인한 장점이 있어서 로봇과 서보시스템, 운송시스템의 제어에 많이 사용되었다. 그러나 채터링 문제로 인해 이를 회피하는 기법들이 등장하였으나 1차 슬라이딩 모드의 단점들이 근본적으로 해결된 것은 아니었다. 그래서 2차 슬라이딩 모드³의 일종으로 채터링을 줄이면서 빠른 응답을 보장할 수 있는 Super-Twisting 슬라 이딩 모드 제어기법이 연구되었다.^4,5 그리고 선형시스템에 대한 관측기는 많이 연구되었으나 선형시스템에 국한되므로 미지의 비선형 외란을 추정하는 관측기는 Chen^6,7 등에 의해 연구되었으나 Super-Twisting 슬라이딩 모드와 결합한 제어는 아직 연구되지 않았으며 산업용 서보시스템에 대해 적용하는 실용적인 연구가 많이 진행 되지 않았다.

그리고 산업 현장에서는 신속하고 편리하게 설계할 수 있으면서도 어느정도의 제어 성능을 보장할 수 있는 경제적이고 효율성이 뛰어난 제어 방법을 필요로 한다. 따라서 본 연구에서는 동적 특성을 사전에 가정하는 시행 착오법과 미지의 비선형 동특성, 모델링 오차, 외부 교란 들을 실시간으로 추정할 수 있는 비선형 외란 관측기를 이용하여 추정하여 비용과 시간이 소요되는 실험적인 식별(Idenfication) 과정이 필요없으며 외란에 강인하며 채터링이 적은 Super-Twisting 제어기법을 적용하여 위치 추종성능이 우수한 제어기를 설계하고 시뮬레이션과 실험을 통해 성능을 검증하여 제안한 제어기법을 산업체에서 효과적으로 활용할 수 있도록 한다. 본 연구에서 제안한 방법과 Chen^6,7 등이 제안한 방법과 비교하면 본 연구는 2차 슬라이딩 모드 제어기법을 적용하여 채터링이 감소하고 외란에 대해 더 강인하고 관측기 설계를 위한 플랜트 비선형 동역학에 대한 정확한 식별과정을 요구하지 않고 신속한 제어기 설계 및 외란에 대한 강인 성을 보장하는 장점을 보여준다.

2. 비선형 외란관측기 및 제어기 설계

2.1 비선형 외란관측기 설계

서보시스템 동적 모델은 다음 식(1)과 같이 주어진다.

M q q ¨ + C q, q ˙ q ˙ + G q + F d t = τ

(1)

여기서 $q, q ˙, q ¨ ∈ R n × 1$ 는 위치, 속도, 가속도 벡터 M(q)∈R^n×n는 관성행렬, $C q, q ˙ ∈ R n × n$ 는 Coriolis 행렬, G(q)∈R^n×1는 중력 벡터, F_d(t)∈R^n×1는 외란, 축비대칭, 축변형, 마찰, 사역대등을 포함하는 불확실성, τ(t)∈R^n×1는 토크입력을 각각 나타낸다. 식(1)은 다음과 같은 고유 성질을 갖는다.⁸

성질 (1) 대칭(Symmetric)이고 양의 한정(Positive Definite) 인관성 행렬 M(q)는 모든 q에 대하여 ∥M(q)∥≤K_M을 만족하며, K_M은 양의 상수 대각행렬이다.

성질 (2) $C q, q ˙$ 의 정의로부터 $M ˙ q - 2 C q, q ˙$ 는 왜대칭(Skew Symmetric) 행렬이므로 $q ˙ T M ˙ q - 2 C q, q ˙ q ˙ = 0$ 가 항상 성립한다.

성질 (3) $C q, q ˙$ 와 G(q)는 각각 $C q, q ˙ ≤ K C q ˙, G q ≤ K G$ , 를 만족하고, K_C, K_G는 각각 양의 상수 이다.

위에서 정의된 동특성 파라미터들은 다음의 조건을 만족 한다고 가정한다.

가정 (1) 다음 조건을 만족하는 근사화 오차 Δ_M, Δ_C, Δ_G가 존재한다고 가정한다.

M q - Ξ M ≤ Δ M C q, q ˙ - Ξ C q ˙ ≤ Δ C G q - Ξ G ≤ Δ G

여기서, Ξ_M∈R^n×n, Ξ_C∈R^n×n, Ξ_G∈R^n×1는 각각 상수대각 행렬을 나타낸다. 동특성 파라미터 Ξ_M∈R^n×n, Ξ_C∈R^n×n, Ξ_G∈R^n×1는 시행착오법을 통하여 근사화 될 수 있다. 이는 많은 비용과 시간이 요구되는 실험을 통한 파라미터 식별과 복잡한 적응기법이나 퍼지 혹은 신경망 근사를 이용한 설계를 고려하지 않아도 제어기 설계 과정을 신속 하게 할 수 있다. 근사화 오차는 외란관측기와 강인 슬 라이딩 모드 제어기를 이용하면 충분히 보상할 수 있다. 식(1)을 식(2)와 같이 표현할 수 있다.

Ξ M q ¨ + Ξ C q ˙ q ˙ + Ξ G + U + F d = τ

(2)

여기서 $U = M q - Ξ M q ¨ + C q, q ˙ - Ξ C q ˙ q ˙ + G q - Ξ G$

식(2)를 상태 공간모델로 표현하면 다음 식(3)과 같다.

x ˙ 1 t = x 2 t, x ˙ 2 t = f 0 x + g 0 u t + d x, t

(3)

여기서 $x 1 = q, x 2 = q ˙, f 0 x = - Ξ M - 1 Ξ C x 2 x 2 + Ξ G, g 0 = - Ξ M - 1, u = τ, d = - Ξ M - 1 U + F d$ 를 각각 나타낸다. 서보시스템에 대한 비선형 관측기는 다음과 같이 주어진다.⁶

d^= φ + p x

(4)

φ ˙ = - η x φ - η x p x + f 0 x + g 0 u

(5)

여기서 p(x)는 비선형 설계함수이고 η(x) = ∂p(x)/∂x₂, p(x)는 모든 x ∈ Rⁿ에 대해 η(x) = ∂p(x)/∂x₂>η>0가 되도록 선정한다.

가정 (2) 식(2)에 주어진 불확실성 d(x, t)는 식(4), 식(5)의 관측기 동역학에 비해 느리게 변한다. 즉 $d ˙ x, t$ 이다.

외란 추정오차를 $d d ~ x, t = d x, t - d^x, t$ 로 정의하면 가정 (2)에 의해 $d ~ ˙ x, t = d ˙ x, t - d^˙ x, t = - d^˙ x, t$ 로 표현된다. 따라서 식(4), 식(5)를 고려하면 식(6)의 결과를 얻을 수 있다.

d ~ ˙ x, t = - d^˙ x, t = - φ ˙ - ∂ p x ∂ x 2 x ˙ 2 = η x φ + η x p x + f 0 x + g 0 u - η x ˙ 2 = - η d ~ x, t

(6)

그러므로 식(5)는 식(7)과 같은 오차 동역학식으로 표현 되고

d ~ ˙ x, t = η d ~ x, t = 0

(7)

$d ~ x, t = d ~ x 0, 0 e - η t$ 이며 t→∞에 따라 전역적으로(Globally) $d ~ x, t → 0$ 으로 수렴하며 $d^x, t = d x, t$ 가 된다. 수렴속도는η(x) 값에 의해 조절된다.

2.2 Super-Twisting 슬라이딩 모드 제어기 설계

원하는 위치를 x_1d로 선정하고 추정 위치오차 신호를 e = x₁ − x_1d로 정의하면 1차 슬라이딩면을 다음 식(8)과 같이 정의한다.

s = e ˙ + c 1 e

(8)

여기서 c₁> 0은 대각 상수행렬이다. 다음과 같은 새로운 오차 상태변수를 정의한다.

ξ 1 = k 1 s + s 1 / 2 s i g n s

(9)

ξ 2 = - k 2 ∫ 0 t k 12 s + 32 k 2 s 1 / 2 s i g n s + 12 s i g n s d τ

(10)

여기서 k₁> 0, k₂> 0는 대각상수행렬이다. 식(8), 식(9)를 각각 미분하면

ξ ˙ 1 = k 1 + 12 s - 1 / 2 s ˙ = χ c 1 e ˙ + f 0 x + g 0 u + d x, t - x ˙ 1 d

(11)

ξ ˙ 2 = - k 2 k 12 s + 1 + γ k 2 s γ s i g n s + γ s i g n s = - χ k 2 ξ 1

(12)

여기서 $χ = k 1 + 12 s - 1 / 2$ 제어입력을 다음과 같이 선정한다.

u = g 0 - 1 - k 3 ξ 1 - ξ 2 - c 1 e ˙ - f 0 x - d^x, t + x ˙ 1 d

(13)

식(13)을 식(11)에 대입하면

ξ ˙ 1 = - χ k 3 ξ 1 + χ d ~

(14)

가정 (3) 식(14)에서 추정오차 $d ~ x, t$ 는 다음의 조건을 만족한다고 가정한다.

d ~ x, t = ρ x, t ξ 1

(15)

여기서 |ρ(x,t)≤δ|이고 δ는 미지의 양의 상수. 식(15)를 고려 하면 식(12), 식(14)은 식(16)과 같은 행렬 형태로 표현된다.

ξ ˙ = - χ A ξ

(16)

여기서 오차 상태벡터 ξ=[ξ₁ ξ₂]^T이고 행렬 A는 식(17)과 같다.

A = k 3 - ρ 1 0 k 2

(17)

3. 제어시스템 안정도 해석

앞 절에서 설계한 외란관측기와 제어기에 대한 폐루프시스템의 안정도를 해석하기 위해 Lyapunov 함수를 다음과 같이 선정한다.

V = 12 ξ T P ξ

(18)

여기서 $P = β + 4 κ - 2 κ - 2 κ 1$ , β > 0와 κ > 0은 설계상수이다. 식(18)을 미분하면 식(19)와 같다.

V ˙ = ξ T P ξ = - χ ξ T A T P + P A ξ ≤ - χ ξ T Q ξ

(19)

여기서 대칭행렬 Q는 다음과 같다.

Q = 2 k 3 - δ β + 4 κ 2 - 4 k 2 κ - 2 κ k 3 - δ + k 2 - β + 4 κ 2 - 2 κ k 3 - δ + k 2 - β + 4 κ 2 4 κ

만일 제어 게인을 $k 2 = 2 κ k 3 - δ, k 2 > δ + β 8 κ + 2 κ 3 β + κ$ 조건을 만족하도록 선정하면 대칭행렬 Q는 양의 한정행렬(Positive Definite Matrix)이 된다. 그리고 다음과 같은 부등 식조건들을 얻을 수 있다.

ξ 2 = ξ 12 + ξ 22 = k 12 s 2 + 2 k 1 s s i g n s + s + ξ 22

(20)

12 λ min P ξ 2 ≤ 12 ξ T P ξ ≤ 12 λ min P ξ 2

(21)

식(20)의 조건을 식(21)에 대입하면 식(22)와 결과를 얻을 수 있다.

s 1 / 2 ≤ ξ ≤ 2 V 1 / 2 λ min 1 / 2 P

(22)

$χ = k 1 + 12 s - 1 / 2$ 와 식(22)를 고려하면 식(19)는 다음과 같이 주어 진다.

V ˙ ≤ - χ λ min Q ξ 2 = - k λ min Q ξ 2 - s - 1 / 2 2 λ min Q ξ 2 ≤ - k 1 2 λ min Q λ max P V - 2 λ min Q λ min P V 1 / 2 = - Λ 1 V - Λ 2 V 1 / 2

(23)

여기서 $Λ 1 = 2 k 1 λ min Q / λ max P, Λ 2 = 2 λ min Q / λ min P$ . 따라서 ξ = 0로 수렴하는 시간은 다음과 같이 주어진다.⁹

t f = t 0 + 2 Λ 1 ln ⁡ Λ 1 V 1 / 2 ξ 0 + Λ 2 Λ 2

(24)

유한 시간 t_f 이내로 ξ→0이면 s→0, e→0으로 수렴함을 의미한다.

4. 시뮬레이션 및 실험

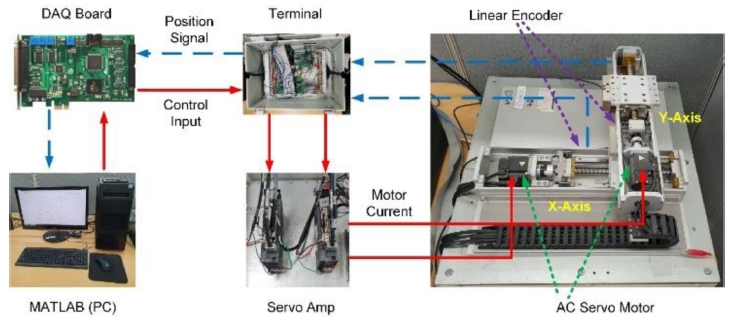
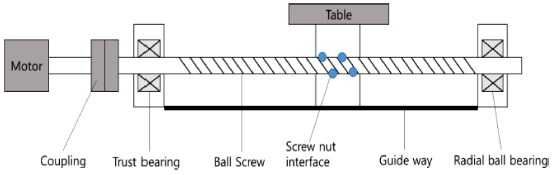
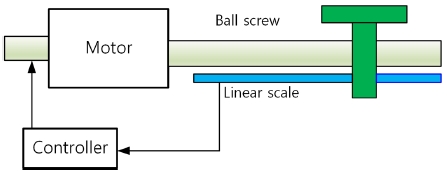
본 연구의 실험에 사용된 이송 테이블 제어시스템, 피드백 제어 구조 및 볼-스크류 시스템은 다음의 Figs. 1-3에 주어져 있다. 이 시스템은 볼-스크류(Ball-Screw) 방 식으로 구동되는 2자유도 직교좌표 형태의 서보시스템 이다. 구동장치로는 Mitsubishi AC 서보 모터가 장착되어 있으며, 모터 구동을 위한 인버터는 Mitsubishi 범용 드라이버를 사용한다. 이송테이블의 위치를 측정하기 위한 계측장치로는 Reinishaw사의 비접촉식 리니어 엔코더를 사용하며, 이송기구로는 Samick THK사의 볼-스크류 및 Linear Guide가 장착되어 있다. Windows 기반 실시간 제어를 위한 데이터 수집 장치로는 HUMUSOFT사의 MF-634 DAQ Board (PCI-Express Type)를 사용하였고, 제어기 설계는 MATLAB Simulink Package를 사용하였다. 볼스크류 구동계의 파라미터들은 Table 1에 제시되어 있다. 시뮬레이션 및 실험에 사용된 2축 이송 테이블은 수평으로 움직이므로 중력항은 무시하고 미지의 외란에는 마찰, 사역대, 축 편심, 열팽창 등에 의한 토크들을 포함한다. 제안한 제어시스템의 성능을 평가하기 위하여 3개의 제어기가 설계되었다: 슬라이딩 모드 제어기(SMC), Super-Twisting 슬라이딩 모드 제어기(STSMC), 외란관측기를 갖는 Super-Twisting 슬라이딩 모드 제어기(STCNDO). 설계된 제어기는 1 kz의 샘플링 주파수로 MF634 보드를 사용하여 Simulink Desktop Real Time 라이브러리를 통하여 구현되었다.

Fig. 1

Components of the ball-screw transfer table control system

Fig. 2

Feedback control with the linear scale

Fig. 3

Structure of the ball-screw driver system

Table 1

Parameter of the ball-screw drive system

4.1 시뮬레이션 결과

각 축의 원 위치 추종 명령입력은 다음과 같이 선정 하였다: x_d = 5 sin(1.2566 t) (mm), y_d = 5 cos(1.2566 t) (mm). 제어기 게인들은 각 제어기들의 성능비교와 적절한 성능 보장을 위해 다음과 같이 선정하였다: c_x1 = 1, c_y1 = 1는 1차 슬라이딩면의 기울기를 정의하도록 선정하였고, k_x1 = 8, k_y1 = 8, k_x2 = 10, k_y2 = 10는 Super-Twisting 제어 파라미터로 선정하였으며, k_x3 = 5, k_y3 = 5, β_x = 35, β_y = 20, κ_x = 0.7, k_y = 0.5는 식(19)의 불확실성에 대한 안정도 조건을 만족하도록 선정하였다. 동특성 파라미터는 Ξ_Mx = 0.035, Ξ_My = 0.006, Ξ_Cx = 0.005, Ξ_Cy = 0.002로 시행착오 과정을 거쳐 각각 선정하였으며 마찰력은 쿨롱마찰로 가정하였고 가상의 외부교란은 F_d = −0.01 cos(0.5 t)로 설정하였다.

Fig. 4는 각 제어시스템의 원위치 추종 결과를 나타낸다. SMC의 경우 위치오차가 전체적으로 큰 것을 확인할 수 있다. STSMC는 추종성이 향상 되었으나 방향전환 구간 에서 여전히 큰 오차가 존재한다. 그리고 STCNDO는 더 개선된 추종 성능을 확인할 수 있다. 추종 오차를 나타 내는 Figs. 4(b)와 4(c)를 참고하면 성능차이를 더욱 확실하게 알 수 있다. 그리고 이러한 오차를 정량적으로 비교하기위하여 Table 2에 추종오차의 RMS 값을 나타내었다. STSMC가 방향전환 구간에서 오차가 커지는 이유는 비선 형 마찰 모델이 백래쉬와 사역대 같은 불확실성 효과를 내기 때문이라고 판단한다. 그리고 STCNDO는 이러한 불확실성을 적절하게 보상을 할 수 있기 때문에 방향전환간에서도 90% 이상 개선된 추종 성능을 보여 준다. Figs. 4(d)와 4(e)에서 NDO가 계산된 외란 신호를 완벽하게 추정하지는 못하지만, 전체적으로 유사하게 추정하는 것을 확인할 수 있다. 급격하게 변하는 노치 형상의 비선형 마찰을 신속하게 추정하지 못하는 것은 NDO를 설계할 때, 외란이 관측기 동역학에 비해 천천히 변한다고 가정하고 설계하였기 때문이다. 이러한 점은 빠른 유한시간수렴 외란관측기를 필요로 하며 추후 고려하기로 한다.

Fig. 4

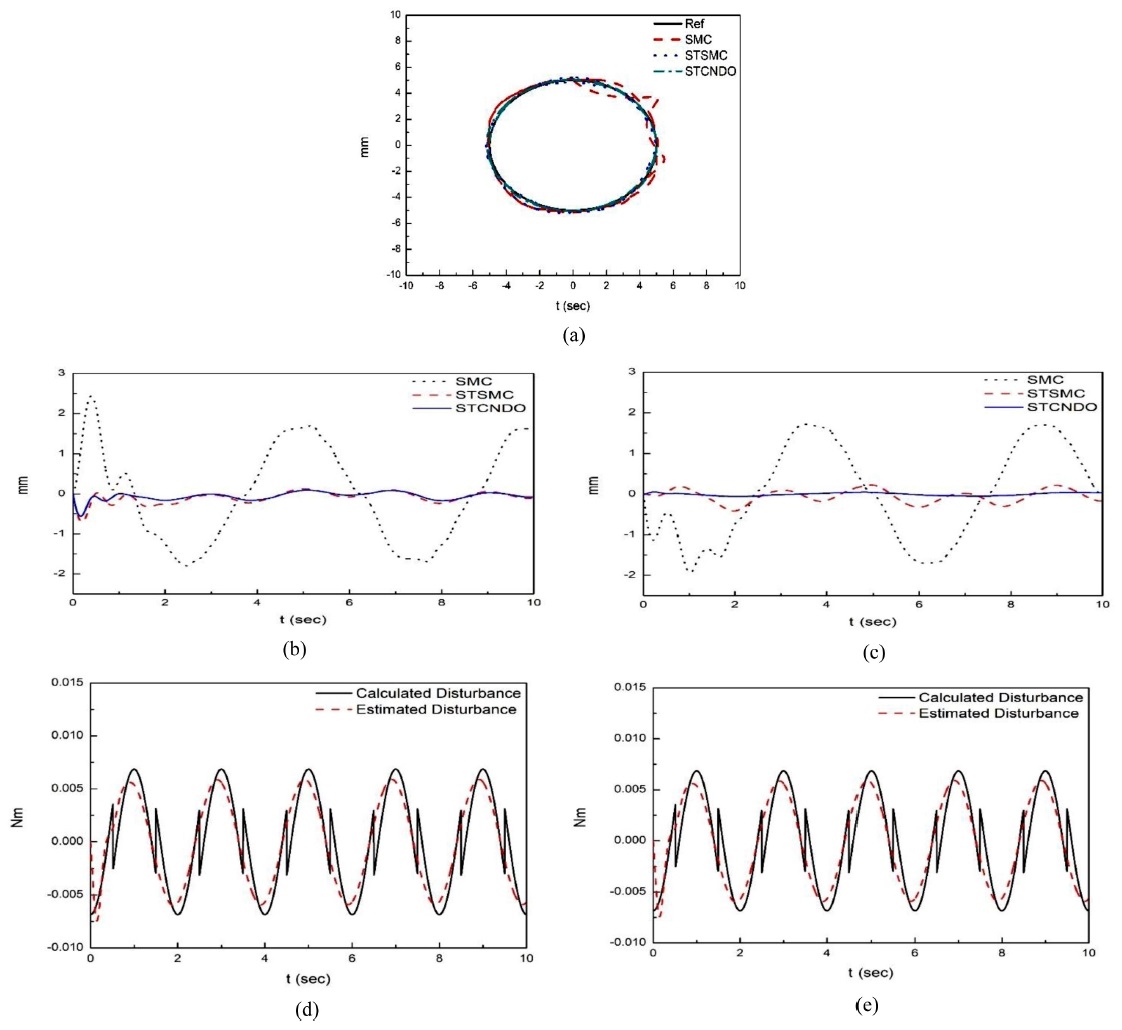
Simulation results. (a) The circle position tracking output. (b) Tracking error of the X-axis, (c) Tracking error of the Y-axis, (d) Disturbance estimation results of the STCNDO system in the X-axis, and (e) Disturbance estimation results of the STCNDO system in the Y-axis

Table 2

RMS value of the tracking error (Simulation)

4.2 실험 결과

시뮬레이션과 유사하게 원위치 명령입력을 선정하였다: x_d = 5 sin (1.2566 t) (mm), y_d = 5 cos(1.2566 t) (mm). 제어기 게인은 다음과 같이 선정하였다: c_x1 = 15, c_y1 = 15, k_x1 = 20, k_y1 = 20, k_x2 = 10, k_y2 = 10, k_x3 = 7, k_y3 = 4, β_x = 5, β_y = 5, κ_x = 0.5, k_y = 0.5. 동특성 파라미터는 Ξ_Mx = 0.035, Ξ_My = 0.006, Ξ_Cx = 0.005, Ξ_Cy = 0.002로 각각 선정하였다. 시뮬레이션의 게인 값들과 다른 이유는 시뮬레이션에서는 유도전동기 자체의 동특성을 고려하지 않았으며 정확한 마찰과 사역대에 대한 정보를 사전에 고려할 수 없기 때문이었다. SMC의 경우 실험 시 제어 게인 값들이 시뮬레이션 경우보다 큰 값으로 선정되었기 때문에 시뮬레이션의 경우 보다는 적지만 위치오차가 전체적으로 큰 것을 확인할 수 있다. 이송 테이블이 위치를 전환하는 경우에는 일시적으로 입력 토크가 작아지므로 이 때 운동 마찰과 사역대는 작은 토크일 때 영향이 크게 나타나게 된다. 방향전환 시 STSMC는 추종성이 SMC에 비해 향상되었으나 시뮬레이션에서와 마찬가지로 방향전환 구간에 사역대와 백래쉬에 의한 영향이 커지고 이러한 외란을 추정하고 보상할 수 없으므로 여전히 증가되며 Figs. 5(d)와 5(e)에서 실험신호의 최대, 최소 진폭부 돌출 및 지연 신호로 나타난다. 그리고 STCNDO는 시뮬레이션과 마찬가지로 가장 개선된 추종 성능을 보여준다. 이러한 오차를 정량적으로 비교하기 위하여 Table 3에 추종오차의 RMS 값을 나타내었다. STCNDO는 시뮬레이션보다 추종 오차가 크게 나타나는 것을 확인할 수 있는데, 이는 불연속적으로 빠르게 변하는 미지의 마찰이 시뮬레이션보다 더 영향이 크기 때문이라고 판단된다.

Fig. 5

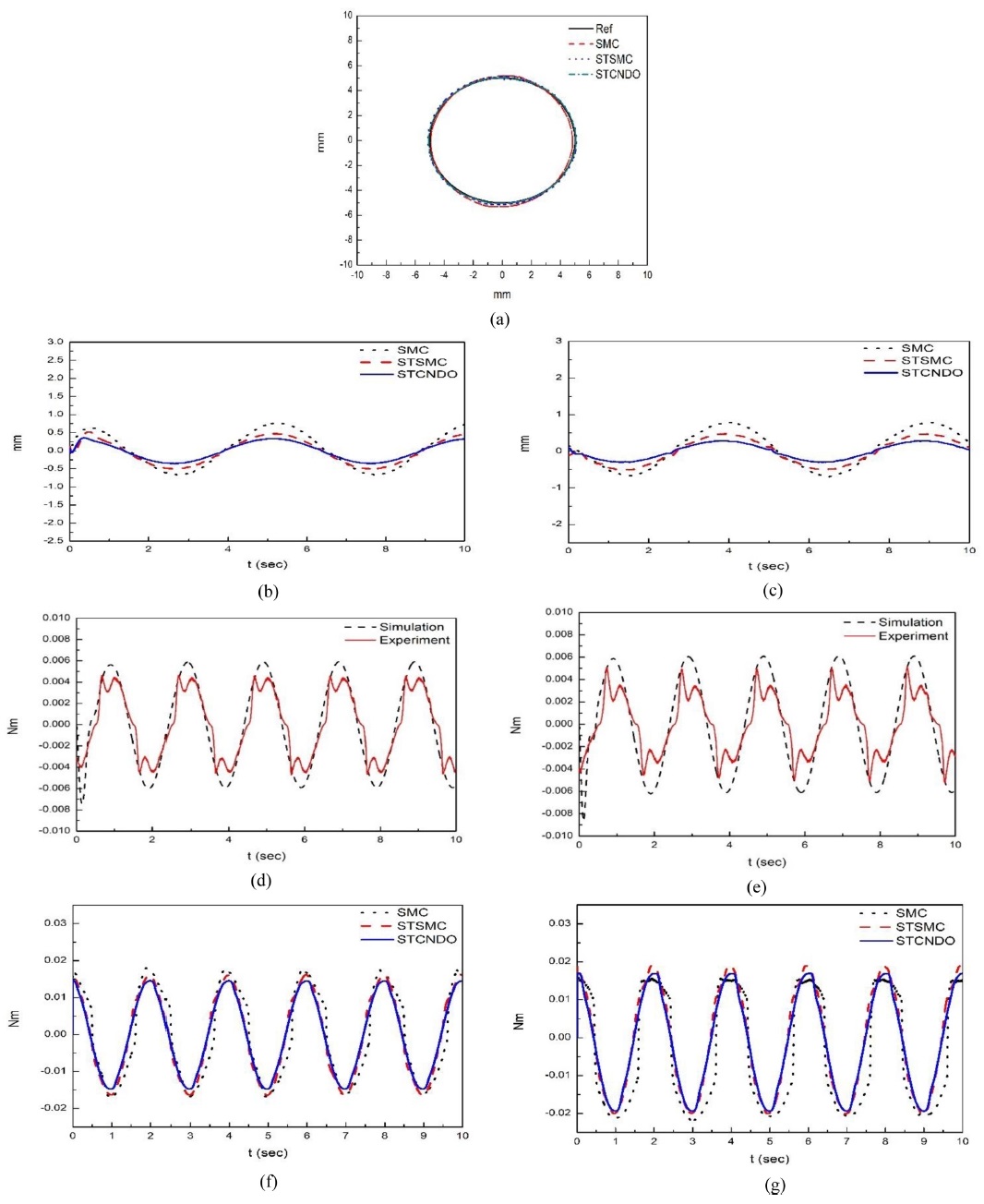
Experimental results. (a) Circle command tracking output, (b) Tracking error of the X-axis, (c) Tracking error of the Y-axis, (d) Disturbance estimation result of the X-axis of the STCNDO system, (e) Disturbance estimation result of the Y-axis of the STCNDO system, (f) Control input of the X-axis of each system, and (g) Control input of the Y-axis of each system.

Table 3

RMS value of the tracking error (Experiment)

5. 결론

본 연구에서는 비선형 서보시스템의 정밀한 위치제어를 위하여 비선형 외란 관측기를 결합한 Super-Twisting 슬라이딩 모드제어기(Super-Twisting Sliding Mode Control With Nonlinear Disturbance Observer, STCNDO)를 제안하고, 산업용 서보시스템의 위치 제어에 적용하여 다음과 같은 결론을 얻었다.

(1) 실제 산업용 서보시스템에 대해 파라미터와 비선형 특성 및 외란에 대한 모델링을 요구하지 않고 간단한 시행 착오적인 기법을 통해 신속하고 강인한 제어기를 설계하는 기법을 제시하였다.

(2) 기존의 1차 슬라이딩 모드 제어기법을 개선한 STSMC를 설계하였으며 비선형 외란을 추정할 수 있는 비선형 관측기를 결합한 STCNDO 시스템을 설계하였다.

(3) 설계된 제어시스템을 산업용 서보시스템에 대한 시뮬레이션과 실험을 통해 기존의 제어시스템에 비해 개선된 위치 추종성능을 보여줌을 검증하였다.

추후 연구로서는 외란의 변화에 빠르게 대응하는 유한 시간 비선형 외란관측기를 연구하여 적용할 예정이다.

Acknowledgments

본 연구는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2018R1A2B6005128).

REFERENCES

Slotine, J. J. E. and Li, W, “Applied Nonlinear Control,” Prentice Hall, 1991.
Edwards, C. and Spurgeon, S. K., “Sliding Mode Control: Theory and Applications,” CRC Press, 1998. [https://doi.org/10.1201/9781498701822]
Levant, A., “Principles of 2-Sliding Mode Design,” Automatica, Vol. 43, No. 4, pp. 576-586, 2007. [https://doi.org/10.1016/j.automatica.2006.10.008]
Moreno, J. A. and Osorio, M., “Strict Lyapunov Functions for the Super-Twisting Algorithm,” IEEE Transactions on Automatic Control, Vol. 57, No. 4, pp. 1035-1039, 2012. [https://doi.org/10.1109/TAC.2012.2186179]
Gonzalez, T., Moreno, J. A., and Fridman, L., “Variable Gain-Super Twisting Sliding Mode Control,” IEEE Transactions on Automatic Control, Vol. 57, No. 8, pp. 2100-2105, 2012. [https://doi.org/10.1109/TAC.2011.2179878]
Chen, W. H., Balance, D. J., Gawthrop, P. J., and O’Reilly, J., “A Nonlinear Disturbance Observer for Robotic Manipulator,” IEEE Transactions Industrial Electronics, Vol. 47, No. 4 pp. 932-938, 2000. [https://doi.org/10.1109/41.857974]
Yang, J., Chen, W. H., and Li, S., “Nonlinear Disturbance Observer based Robust Control for Systems with Mismatched Disturbances/Uncertainties,” IET Control Theory & Applications, Vol. 5, No. 18, pp. 2053-2062, 2011. [https://doi.org/10.1049/iet-cta.2010.0616]
Vidyasagar, M. and Spong, M. W., “Robot Dynamics and Control,” John Wiley & Sons, 1989.
Yu, S., Yu, X., Shrinzadeh, B., and Man, Z., “Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode,” Automatica, Vol. 41, No. 11, pp. 1957-1964, 2005. [https://doi.org/10.1016/j.automatica.2005.07.001]

Seong Ik Han

Assistant Professor in the Department of Mechanical System Engineering, Dongguk University Gyeongju Campus. His research interest is robot & servo system control.

E-mail: skhan@dongguk.ac.kr

Servo motor	X-axis	HF-KP23
Servo motor	Y-axis	HF-KP13
Servo amplifier	MR-J3-20B
Lead of ball-screw	X-axis	1 mm
Lead of ball-screw	Y-axis	2 mm
LM guide	X-axis	SR15W
LM guide	Y-axis	SRS15WM
Motor power	X-axis	200 W
Motor power	Y-axis	100 W

	SMC	STSMC	STCNDO
x-axis	1.20 (100%)	0.17 (14%)	0.12 (10%)
y-axis	1.18 (100%)	0.17 (15%)	0.03 (3%)

	SMC	STSMC	STCNDO
x-axis	0.24 (100%)	0.09 (38%)	0.05 (21%)
y-axis	0.21 (100%)	0.12 (57%)	0.06 (29%)