틸팅하는 추진기를 지닌 수중로봇의 추력벡터 분해와 구동범위 제한 알고리즘으로 구성된 제어기의 제어 이득 최적화

1. 서론

수중로봇이 물 속에서 작업을 하기 위해서는 안정적인 호버링 능력이 매우 중요하며, 수중에서의 위치 및 자세 제어 성능을 보장할 수 있는 제어기 설계가 필요하다. Kim¹은 Manta 타입의 UUV에 대해 PID 제어, Fuzzy 제어를 적용하였고, Kim²은 6자유도 ROV의 견실한 호버링 제어를 위한 백스테핑 제어기를 설계하였다. Hong³은 AUV의 제어 모드를 구분하여, 모드에 따라 LQ 제어기, PID 제어기, 슬라이딩 모드 제어기를 설계한 바 있다. 하지만 이런 연구의 대부분은 제어기를 설계하는 과정에서 추진기의 물리적 한계인 포화(Saturation)를 고려하지 않았으며 추진기의 포화를 고려한다면 이 로봇들의 제어 성능을 더 향상시킬 수 있을 것이다.

비례-적분-미분 제어 기법(PID Control)은 제어기의 구조가 간단하고, 파라미터 조정을 비교적 쉽게 할 수 있으며, 제어 성능 또한 우수하여 가장 많이 사용되는 대표적인 형태의 제어 기법이다. 최근 현대 제어 이론의 급격한 발전에도 불구하고 실제 산업현장에서는 여전히 신뢰성이 높은 PID 제어기가 널리 사용되고 있다. 그러나 앞서 말한 추진기의 포화 때문에 제어기에서 도출된 출력의 거동이 느려지는 경우가 존재한다. 이 경우 제어기의 적분 부분이 매우 빠르게 증가하게 되고 최종값에 도달하는 시간이 늘어나 제어 능력이 떨어지게 된다. 이런 포화상태를 회피하는 방법을 안티 와인드업이라고 하며 Clamping, Back-Calculation 및 Observer Approach등의 방법이 있다.⁴

많은 분야에서 이러한 제어기의 제어 이득을 적절하게 조정하는 연구를 활발히 진행 중이다. 근궤적법을 이용한 방법⁵이 널리 알려져 있으며, Ziegler와 Nichols⁶는 단위 계단 입력에 대한 플랜트의 응답을 보면서 변수를 구하는 방법과 비례 이득의 증가에 의해 처음으로 진동이 발생하였을 때의 제어 이득과 주파수에 기초를 둔 방법을 제시하였다. 시간지연을 모델링 하여 Tuning하는 방법⁷ 또한 연구되었으나 이러한 방법들은 입출력을 분리시키기 어려운 다중입출력 시스템에는 적용하기 어려운 점이 있다.

다중 입출력 시스템에 대한 제어 이득 선정 연구도 진행되고 있다. Seo⁸는 가변 저항의 전압을 이용하여 3자유도 마이크로 병렬 기구의 제어 이득을 실험계획법을 통해 최적화 하였으며, Lee⁹는 다구치 방법론을 이용하여 다축 동시 PID 제어시스템의 제어 이득을 조정하는 연구를 수행하였다. 그러나 이들의 연구는 모델의 정보를 사용하지 않고 실험을 통해 제어 이득을 조정하기 때문에 실험을 하는 과정이 번거롭고 시간이 많이 걸린다는 단점이 존재한다.

본 연구에서는 틸팅하는 추진기를 가진 수중로봇의 제어 이득 선정을 다룬다. 제어기의 이득은 성능, 안정성, 견실성 등에 큰 영향을 미친다. 각각의 이득은 서로 상관관계가 있기 때문에 총 24개의 적절한 제어 이득을 동시에 선정하는 것은 쉽지 않다. 본 논문에서는 최적화된 18개의 PID 제어 이득을 먼저 선정한 후 6개의 안티 와인드업 제어 이득을 최적화한다. 로봇의 추진기 모델을 반영한 제어기의 이득을 네 가지 오차에 따른 성능지수에 따라 최적화를 수행하였으며, 각 성능지수를 최소화하는 제어 이득을 선정하였다. 이를 통해 얻은 제어 이득을 사용하여 시뮬레이션을 수행하였고, 이를 통해 결과를 분석한다.

본 논문의 구성은 다음과 같다. 2장에서는 수중로봇 TTURT를 소개하며 모델링과 제어 알고리즘에 대해 설명한다. 3장에서는 최적화 문제정의, 방법 및 최적화 결과를 나타내었다. 4장에서는 최적화를 통해 얻은 제어 이득을 이용하여 시뮬레이션을 수행한 결과를 다루었으며, 마지막으로 5장에서는 최종 결론을 제시한다.

2. Tilting Thruster Underwater Robot (TTURT)

2.1 TTURT의 모델

서울대학교 견실설계공학연구실에서 개발한 수중 로봇 TTURT¹⁰는 4개의 틸팅하는 추진기만으로 6자유도를 구현하는 것이 특징이다. Fig. 1의 TTURT는 추진기 개수를 줄임으로써 로봇의 크기와 무게 그리고 전력소모를 줄일 수 있는 것이 큰 장점이다. 로봇의 동역학 모델은 식(1)과 같다.

Fig. 1

Tilting thruster underwater robot (TTURT)

$\[ \mathbf{\text{M}}\dot{v}+\mathbf{\text{C}}\left(v\right)v+\mathbf{\text{D}}\left(v\right)v\text{+}g\left(\eta \right)=\tau \]$

(1)

여기서 M은 Inertia 행렬이고 C(v)는 코리올리 행렬, D(v)는 댐핑 행렬이다. g(η)는 중력과 부력벡터이며 중성부력이 되도록 설계되었다. 틸팅하는 추진기의 추진력은 f₁, f₂, f₃, f₄로 나타낼 수 있으며, α, β는 추진기의 틸팅 각도이다. 좌변의 η는 로봇의 위치, 자세 벡터이며, v는 η의 미분 값이다. 로봇의 앞쪽의 추진기 2개는 α, 뒤의 추진기 2개는 β의 각도로 동시에 회전한다.

TTURT는 수중에서 다양한 작업을 수행할 수 있도록 로봇 본체의 윗면과 아랫면에 매니퓰레이터를 장착할 수 있는 도킹메커니즘으로 설계되었으며 수중구조물의 밸브를 돌리는 작업¹¹ 및 불가사리 채집¹² 등을 연구한 바가 있다.

2.2 TTRUT의 제어 알고리즘

틸팅하는 추진기에 의해 발생되는 추력벡터의 비선형성 때문에 로봇의 위치와 자세를 유지하는 것은 쉽지 않다. 따라서 추력 벡터를 하나의 상수 행렬과 8개의 입력으로 나누어 6자유도를 제어할 수 있는 제어기를 설계하였다.¹³ 먼저 원하는 위치와 자세를 얻기 위한 추력은 간단한 PID 제어를 통해 얻을 수 있으며, 이렇게 도출된 추력을 각각의 추진기가 만들어내야 할 추력과 틸팅 각도로 변환하게 된다.

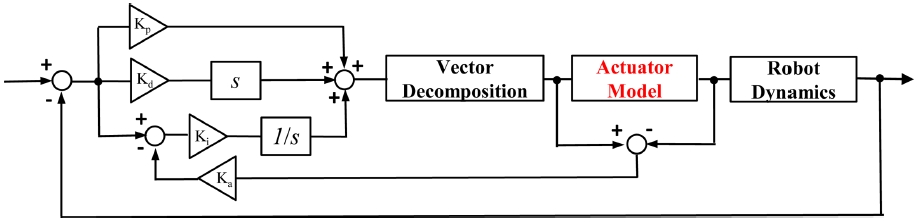
그러나 실제 추진기는 이렇게 도출된 제어 입력이 매우 빠르게 변할 때 그 속도를 따라가지 못하는 한계가 존재한다.¹⁴ 이런 추진기 속도 포화를 극복하기 위해 실제 틸팅메커니즘 모델을 구했으며, 이를 반영하여 와인드업현상을 줄일 수 있는 제어기를 Fig. 2와 같이 설계하였다.

Fig. 2

Block diagram of PID-Anti windup control system

로봇의 Error Dynamic와 제어 입력은 다음 식(2)와 같다.

$\[ \mathbf{\text{M}}\left(\eta \right)\ddot{e}+\mathbf{\text{C}}\left(v,\eta \right)\dot{e}+\mathbf{\text{D}}\left(v,\eta \right)\dot{e}={\mathbf{\text{J}}}^{-T}\left(\eta \right)\mathbf{\text{A}}u \]$

(2)

$\[ u={\mathbf{\text{A}}}^{+}\left[{\mathbf{\text{J}}}^T\left\{{\mathbf{\text{K}}}_{p}e+{\mathbf{\text{K}}}_d\dot{e}+{\mathbf{\text{K}}}_i\underset{0}{\overset{t}{\int }}\left(e\left(\tau \right)-{\mathbf{\text{K}}}_a{e}_a\left(\tau \right)\right)d\tau \right\}\right] \]$

(3)

여기서 J는 자코비안 행렬이며, e는 위치 자세 오차벡터이다. A는 추력벡터를 분해하여 얻은 상수행렬이며, K_p, K_d, K_i는 제어를 위한 비례, 미분, 적분 이득행렬, K_a는 안티 와인드업에 영향을 주는 이득행렬이다.

3. 제어 이득 최적화

3.2 제어 이득 최적화 결과

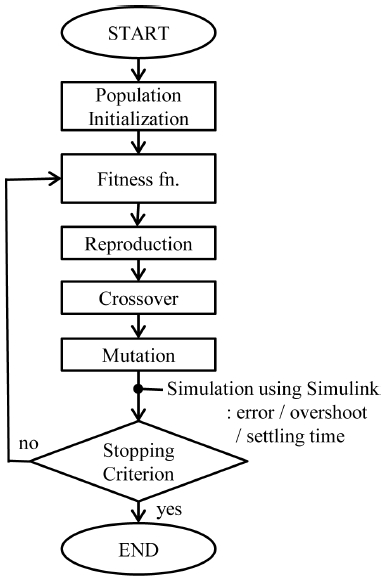
유전알고리즘은 유전적인 계층과 적자생존이라는 진화의 원리를 이용하며, 확률적인 방법으로 최적 해를 찾아가는 최적화 기법 중의 하나이다. MathWork의 상용프로그램인 Matlab의 최적화 툴박스의 ga 함수를 이용하여 이를 쉽게 구현할 수 있다. 유전알고리즘은 Fig. 3과 같은 순서로 진행된다. 제어 이득 값들이 업데이트 될 때마다 Simulink를 호출하여 그 때의 제어 이득을 적용한 시뮬레이션을 실행한 후, 에러와 정착시간, 오버슈트 등을 계산한다. 이 과정을 반복하여 최적값을 탐색하도록 하였다.

Fig. 3

Flow chart of genetic algorithm optimization method

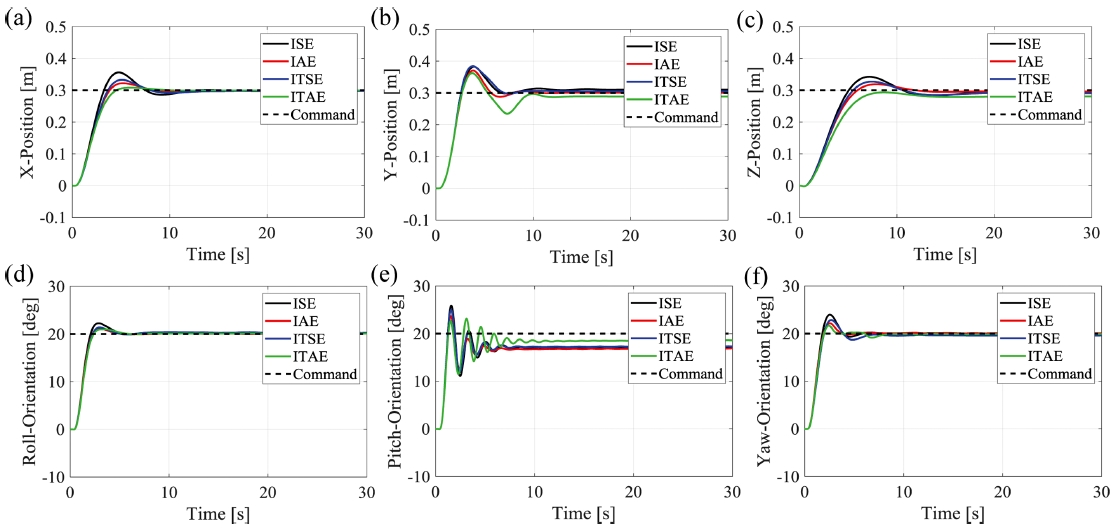
4가지의 시스템 오차를 대입하여 각 목적함수를 최소화하는 최적화 결과를 Table 1에 도시하였으며 이 때 각각의 계단 응답을 Fig. 4에 나타내었다.

Table 1

Optimization results

Fig. 4

Step responses of four optimized gains; (a) X-Position; (b) Y-Position; (c) Z-Position; (d) Roll-Orientation; (e) Pitch-Orientation; and (f) Yaw-Orientation

4. 시뮬레이션 결과 및 분석

4.1 추진기의 포화를 고려한 제어기의 시뮬레이션

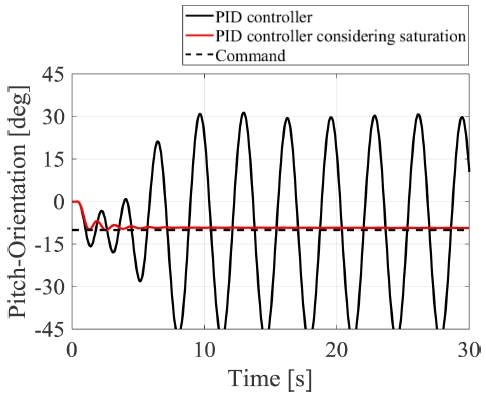
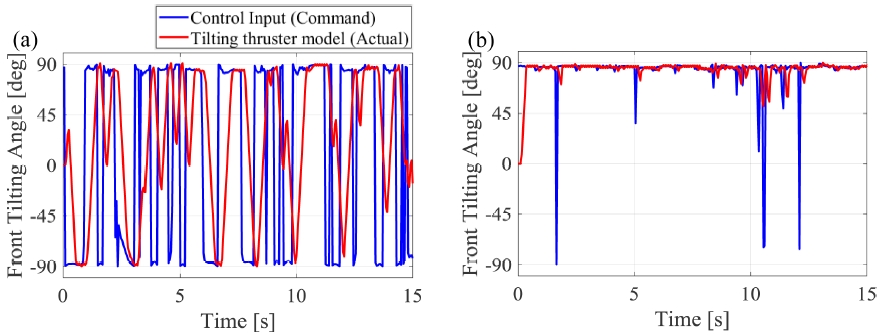
추진기의 포화를 고려하지 않고 튜닝한 PID 제어 이득만을 제어기에 적용한 경우와 추진기의 포화를 고려하기 위하여 추진기 모델을 반영한 제어기의 성능을 비교해 보았다. 최적화 수행 중 Pitch 방향은 제어 이득의 작은 변화에도 진동하거나 발산하는 양상을 보여 가장 민감한 자세로 여겼으며 따라서 가장 좋지 않은 성능을 보인 Pitch 방향에 -10° 입력을 인가하였다. Fig. 5를 보면 추진기의 포화를 고려하지 않은 제어기는 진동 발산하는데 반해 포화를 고려한 제어기의 경우 원하는 값에 수렴하는 것을 알 수 있다. Fig. 6은 실제 추진기의 거동을 나타낸 것이며, 추진기의 포화를 고려하지 않았을 경우에는 추진기가 제어기에서 나오는 제어 입력을 따라가지 못하는 것을 알 수 있다. 반면 Figs. 6(b)는 6(a)에 비해 잘 쫓아가는 경향을 확인할 수 있다. 이를 통해 추진기의 포화를 함으로써 제어기의 성능이 향상되는 것을 확인하였다.

Fig. 5

Step response in pitch angles with and without considering saturation

Fig. 6

Tilting angle of front thrusters; (a) without considering saturation; and (b) with considering saturation.

4.2 최적화된 제어 이득에 따른 시뮬레이션

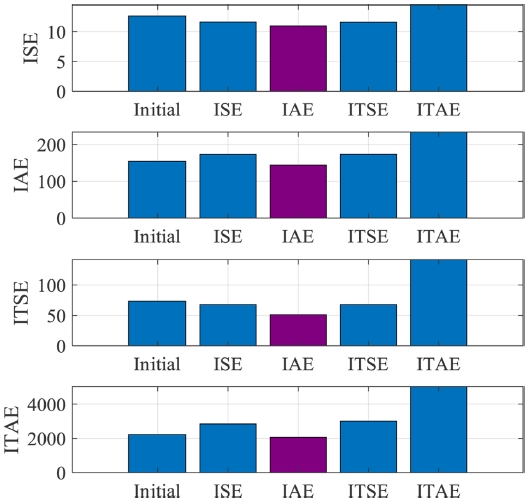
앞서 구한 네 가지의 시스템 오차에 따른 제어 이득을 제어기에 적용하여 임의의 경로를 추종하게 하는 입력을 로봇에 가하였다. 먼저 z방향으로 -0.2 m, 10초 뒤 x방향으로 0.1 m 이동 후, Pitch 방향으로 -30° 기울이는 자세를 입력으로 넣어주었으며 그 결과는 Fig. 7과 같다. 네 가지 경우 모두 명령을 잘 따르는 것을 확인하였으며 정량적인 오차를 구하였다. 선정된 네 가지의 제어 이득에 따라 6자유도 오차의 합을 계산하여 비교 분석한 결과는 Table 2와 Fig. 8을 통해 확인할 수 있다. 절대 오차 적분값(IAE)을 목적 함수의 오차에 대입하여 최적화를 수행한 결과로 선정된 제어 이득이 평가 기준 모두에서 가장 좋은 제어기 성능을 가지는 것을 확인하였다. 이 때에 계산한 오차, 즉 ISE, IAE, ITSE, ITAE가 처음 시뮬레이션 결과에 비해 각각 13.03%, 6.18%, 29.38%, 7.38%만큼 감소한 것을 알 수 있다.

Fig. 7

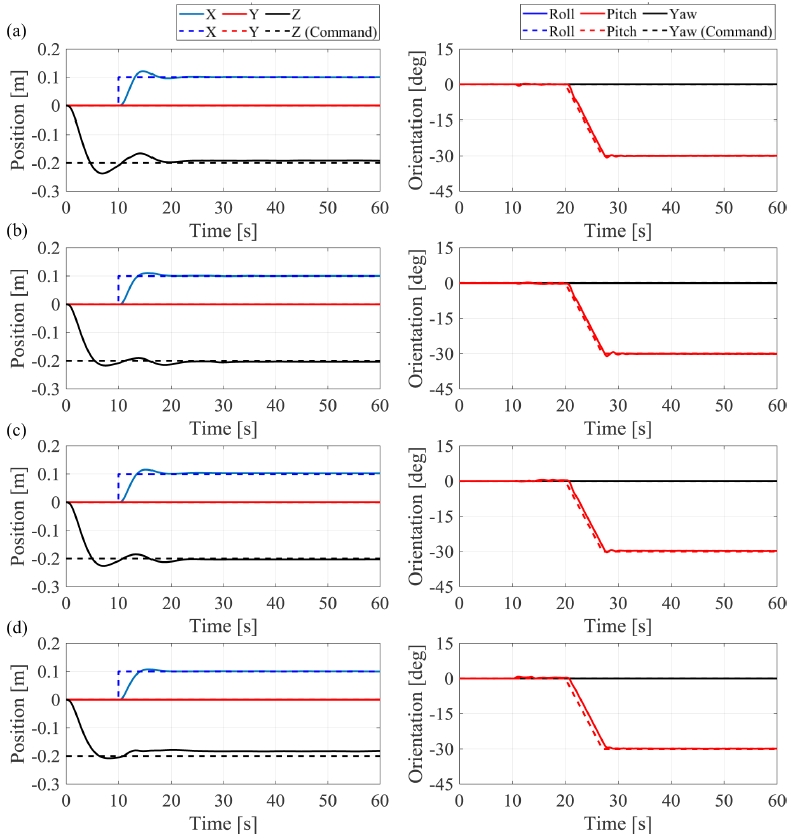
Position and orientation of TTURT according to four control gains optimized with performance index; (a) ISE; (b) IAE; (c) ITSE; and (d) ITAE

Table 2

Errors with optimized control gains

Fig. 8

Comparison of errors with optimized control gains

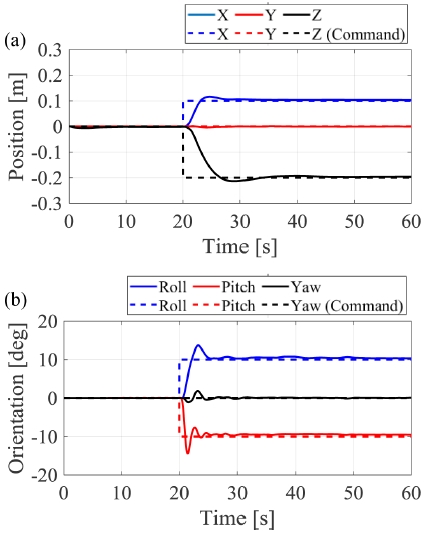
추가적으로 여러자유도에 계단 입력을 동시에 가한 시뮬레이션을 수행해 보았다. 20초가 되는 순간 동시에 x방향으로 0.1 m, z방향으로 -0.2 m, Roll 방향으로 10°, Pitch 방향으로 10°의 계단 입력을 인가하였으며 그 때의 로봇의 위치와 자세를 Fig. 9에 나타내었다. 입력을 가한 그 순간 약간의 오버슈트가 생기는 것을 알 수 있으나 동시에 여러 입력을 가한 경우에도 로봇이 잘 수렴하는 것을 확인하였다.

Fig. 9

Position and orientation of TTURT when the step input applied at the same time

5. 결론

본 논문에서는 틸팅하는 추진기를 가진 수중 로봇의 안정적인 호버링 제어를 위해 추진기의 포화를 반영한 제어기의 이득을 선정하는 연구에 대해 다루고 있다. 틸팅 추진기의 추력 벡터 분해와 구동 범위 제한 알고리즘으로 구성된 PID 제어기의 총 24개 이득을 구하기 위한 최적화를 수행하였다. 총 24개의 제어 이득이 x, y, z, Roll, Pitch, Yaw의 6개 계단응답에서의 오차를 최소화하는 방향으로 선정되었다. 4가지의 시스템 오차에 기반한 목적함수에 따라 최적화된 제어 이득을 비교, 분석하여 절대 오차 적분값(IAE)을 성능 지수로 하여 얻은 결과가 가장 좋은 성능을 보이는 것을 확인하였다. 처음에 선정된 임의의 제어 이득을 사용한 결과와 비교하였을 때 로봇의 6자유도 오차가 각각 13.03%, 6.18%, 29.38%, 7.38%만큼 줄어든 것을 알 수 있다.

본 연구를 통해 제어기 설계 시 추진기의 포화를 고려하여야 하고, 제어 이득의 최적화가 수행되어야 제어기의 성능을 향상시킬 수 있다는 것을 확인하였다. 이렇게 얻은 최적의 제어 이득을 적용하여 향후 실제 수조에서 실험을 수행할 예정이며 호버링 성능을 검증할 계획이다.

Acknowledgments

본 연구는 2017학년도 부산대학교 교내학술연구비 (신임교수 연구정착금)에 의한 연구임.

REFERENCES

• Kim, H.-D., Kim, J.-Y., Kim, S.-H., and Lee, S.-K., “A Study of the Control System on the Manta-Type UUV,” Journal of Navigation and Port Research, Vol. 35, No. 5, pp. 359-363, 2011. [https://doi.org/10.5394/KINPR.2011.35.5.359]
• Kim, J., Kim, J.-W., Jin, S., Seo, T., and Kim, J., “Gain Optimization of a Back-Stepping Controller for 6-DOF Underwater Robotic Platform,” Journal of the Korean Society for Precision Engineering, Vol. 30, No. 10, pp. 1031-1039, 2013. [https://doi.org/10.7736/KSPE.2013.30.10.1031]
• Hong, S. W., Oh, S. R., Seo, S. T., Lee, J. K., Park, Y. I., et al., “Development of Technologies for Navigation and Manipulator System of a Semi-Autonomous Underwater Vehicle,” Korea Ocean Research and Development Institute, 2000. (in Korean)
• Azar, A. T. and Serrano, F. E., “Design and Modeling of Anti Wind Up PID Controllers,” in: Zhu, Q. and Azar, A., (Eds.), Complex System Modelling and Control through Intelligent Soft Computations, Springer, pp. 1-44, 2015. [https://doi.org/10.1007/978-3-319-12883-2_1]
• Franklin, G. F., Powell, J. D., Emami-Naeini, A., and Powell, J. D., “Feedback Control of Dynamic Systems,” Prentice Hall, 6th Ed., pp. 243-336, 2009.
• Ziegler, J. G. and Nichols, N. B., “Optimum Settings for Automatic Controllers,” Transaction of ASME, Vol. 64, No. 11, pp. 759-768, 1942.
• Skogestad, S. and Postlethwaite, I., “Multivariable Feedback Control: Analysis and Design,” Wiley, pp. 359-368, 2007.
• Seo, T.-W., “Control Gain Tuning of the 3-DOF Micro Parallel Mechanism Platform via Design of Experiment Methodology,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 11, pp. 1207-1213, 2012. [https://doi.org/10.7736/KSPE.2012.29.11.1207]
• Lee, K. and Kim, J., “Controller Gain Tuning of a Simultaneous Multi-Axis PID Control System Using the Taguchi Method,” Control Engineering Practice, Vol. 8, No. 8, pp. 949-958, 2000. [https://doi.org/10.1016/S0967-0661(99)00201-4]
• Jin, S., Kim, J., Kim, J., and Seo, T. W., “Six-Degree-of-Freedom Hovering Control of an Underwater Robotic Platform with Four Tilting Thrusters via Selective Switching Control,” IEEE/ASME Transaction on Mechatronics, Vol. 20, No 5, pp. 2370-2378, 2015. [https://doi.org/10.1109/TMECH.2014.2378286]
• Bae, J., Bak, J., Jin, S., Seo, T. W., and Kim, J., “Optimal Configuration and Parametric Design of an Underwater Vehicle Manipulator System for a Valve Task,” Mechanism and Machine Theory, Vol. 123, pp. 76-88, 2018. [https://doi.org/10.1016/j.mechmachtheory.2018.01.014]
• Kim, J., Jin, S., Kim, J.-W., Seo, T. W., and Kim, J., “Optimal Design of a Four-Bar Linkage Manipulator for Starfish-Capture Robot Platform,” Journal of the Korean Society for Precision Engineering, Vol. 30, No. 9, pp. 961-968, 2013. [https://doi.org/10.7736/KSPE.2013.30.9.961]
• Bak, J., Nguyen, H.-N., Park, S., Lee, D., Seo, T., et al., J., “Positioning Control of an Underwater Robot with Tilting Thrusters via Decomposition of Thrust Vector,” International Journal of Control, Automation and Systems, Vol. 15, No. 5, pp. 2283-2291, 2017. [https://doi.org/10.1007/s12555-016-0298-x]
• Jin, S., Kim, J., Kim, J.-W., Bae, J. H., Bak, J., et al., “Back-Stepping Control Design for an Underwater Robot with Tilting Thrusters,” Proc. of 2015 International Conference on Advanced Robotics (ICAR), pp. 1-8, 2015. [https://doi.org/10.1109/ICAR.2015.7251425]
• Peace, G. S., “Taguchi Methods,” Addison-Wesley, pp. 273-291, 1993.