외골격 로봇의 마찰보상제어를 위한 구동 모듈의 정적 및 동적 마찰 특성 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Actuators for exoskeleton robots comprise various types such as electric, hydraulic, and pneumatic and it is necessary to apply the correct actuator according to the purpose. Most exoskeleton robots mainly use electric actuators, and some special-purpose robots, such as for heavy-load transport requiring large force, use hydraulic actuators. In this paper, friction of the actuation module consisting of a harmonic drive and a brushless DC motor is measured through experiments. And the friction characteristics of the actuation module are analyzed. The harmonic drive transmission system has various advantages, but it also has hysteresis and nonlinear friction characteristics. The friction compensation control of the actuation module enables precise control of the exoskeleton robot, and improves the robot’s performance. Appropriate friction model selection and design affects friction compensation performance. In this study, static and dynamic friction models are designed and analyzed based on the friction data of the actuation module.
Keywords:
Exoskeleton robot, Friction compensation, Friction model, Electronic actuation module, Harmonic drive키워드:
외골격 로봇, 마찰 보상, 마찰 모델, 전기식 구동 모듈, 하모닉 드라이브1. 서론
전 세계적으로 민·군 분야에서 외골격 로봇에 대한 연구가 활발히 진행되고 있다. 외골격 로봇은 주로 민간 분야에서 노약자 보행 보조, 재활 치료와 같은 의료 재활용으로 개발되어 여러 의료 및 재활 기관에서 사용 중이다.1,2 또한 산업계에서는 현장 근로자를 위한 외골격 로봇이 특정한 자세를 유지하거나 고중량물의 운반 및 무거운 공구를 지지하는 등의 근골격계를 지원하는 형태로 개발되었다.3 최근에는 다양한 형태와 목적의 군용 외골격 로봇에 대한 연구개발이 진행되고 있다.
다양한 외골격 로봇 중 하드 타입 외골격 로봇은 인체의 뼈와 유사한 역할을 수행하는 뼈대를 통해 지면으로의 부하 경로(Load Path)를 통해 체중 또는 등짐과 같은 신체에 가해지는 하중을 로봇이 분담한다. 이러한 외골격 로봇은 지원 가능한 인체 관절의 범위에 따라서 하지형, 상지형, 전신형 외골격 로봇 등이 있다.4,5 또한 외골격 로봇에 사용되는 구동기는 전기식, 유압식, 공압식, 케이블식 구동기와 스프링과 같은 탄성체를 이용한 구동기가 있다.6-9
본 연구의 외골격 로봇은 하지형 외골격 로봇이며 전기식 구동기를 사용한다. 전기식 구동기는 브러시리스 DC모터와 하모닉 드라이브로 구성되어 있다. 하모닉 드라이브는 높은 기어비를 통해 작은 모터로 큰 토크를 발생시킬 수 있어 구동기의 크기를 줄일 수 있으며, 기어의 백래시가 거의 없어 정밀한 위치 제어가 가능하고 효율이 높은 장점이 있다.10 이러한 장점들로 인하여 하모닉 드라이브는 산업, 의료, 항공우주 등의 다양한 분야에 적용되어 있다. 하지만 하모닉 드라이브는 동마찰 특성이 비선형적이고 히스테리시스가 있으며 마찰 손실이 크다는 단점이 있다.11 이러한 단점들이 구동기의 성능 저하를 야기하므로 마찰 손실에 대한 적절한 보상제어를 통해 운동의도 추종제어성능을 더욱 향상시킬 수 있다. 운동의도 추종제어 성능저하 시, 착용자와 로봇 간 운동 또는 자세 불일치로 인해 착용자의 불편함과 저항감을 야기하며, 심각할 경우 착용자의 부상을 유발할 수 있다.
마찰 보상을 수행하는 방법은 두 가지가 있다. 첫번째는 기설정된 마찰 모델을 통하여 예측된 마찰 보상 값을 제어기로 피드 포워드 입력하는 것이고, 두 번째는 구동 시스템에 포함된 로드셀 등에 의하여 측정된 값을 이용하여 마찰 보상을 수행하는 것이다.12 그러나 시스템의 구성과 구동 모듈에 작용하는 부하에 의해 영향을 받는 실제 마찰력은 정확하게 측정할 수 없으므로 마찰 모델을 통한 근사치를 도출하여 마찰 보상을 수행한다.13 따라서 마찰 모델에 따라 마찰 보상 제어 성능의 차이가 커지므로 적절한 마찰 모델의 선정이 중요하다.
기존 외골격 로봇 중 ALEX13와 HUMA14는 각각 쿨롱과 점성 마찰 모델의 조합 및 점성 마찰 모델과 같은 정적 마찰 모델을 이용하여 마찰 보상을 수행하였다. 정적 마찰 모델을 이용하여 마찰 보상을 수행할 경우 구동기의 히스테리시스, 스틱-슬립(Stick-Slip) 등의 동적 특성을 표현할 수 없으므로 마찰 보상 제어 시 한계가 있다.
본 연구에서는 외골격 로봇에 사용된 전기식 구동 모듈의 정적 및 동적 마찰 특성을 실험을 통해 획득하고 이에 대하여 분석하여 다양한 마찰 모델을 이용한 마찰 특성의 모델링을 수행하였다. 또한 마찰 모델의 모델링 결과에 대하여 착용자의 저항감을 최소화할 수 있는 마찰 모델에 관하여 논의한다.
2. 외골격 로봇
2.1 외골격 로봇 소개
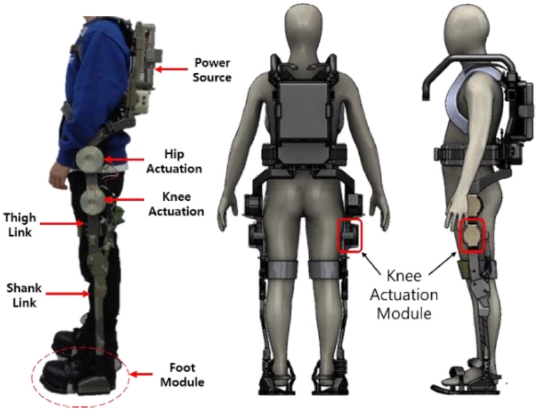
Fig. 1은 본 연구에 사용된 하지형 외골격 로봇이다. 외골격 로봇은 총 18자유도를 가지며, 이 중 무릎관절 에만 구동 모듈이 적용되어 있다. Fig. 1을 보면, 엉덩이를 기준으로 두개의 구동 모듈이 상하로 배치되어 있다. 상부의 구동 모듈은 엉덩관절을 보조하기 위하여 토션스프링을 이용하는 탄성 모듈이 적용되었고, 하부의 구동 모듈은 무릎관절을 지원하기 위한 전기식 구동 모듈이다. 무릎관절 구동 모듈은 하지 저관성 설계를 위해 멀티 링크 구조를 통하여 무릎관절의 구동에 보조력을 지원한다.
외골격 로봇은 다양한 신체 크기에 대응하기 위하여 골반 폭 및 대퇴와 정강이 부분의 길이 조절이 가능하도록 설계되어있다.
3. 마찰 모델
마찰 모델은 정적 마찰 모델과 동적 마찰 모델이 있다. 쿨롱, 점성, Stribeck 마찰 모델 등이 정적 마찰 모델이고, Dahl, LuGre 마찰 모델 등이 동적 마찰 모델이다.
3.1 쿨롱 및 점성 마찰 모델
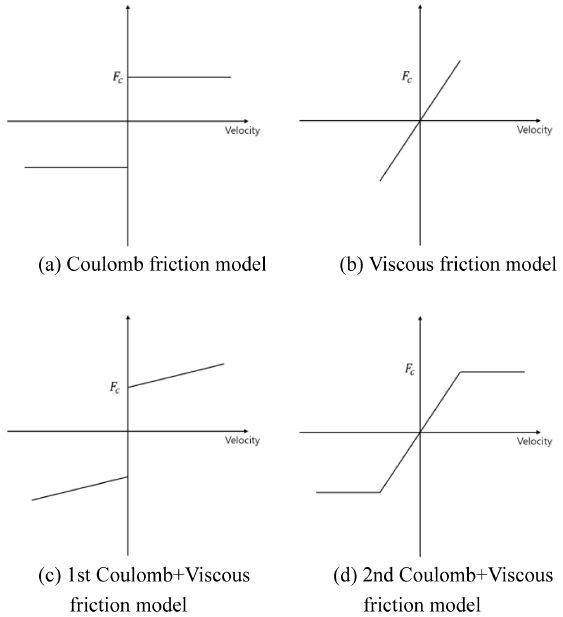
Fig. 2(a)의 쿨롱(Coulomb) 마찰 모델은 가장 기본적인 마찰 모델이며 이를 수식으로 표현하면 아래 식(1)과 같다.15
| (1) |
식(1)에서 마찰력은 속도의 크기와는 상관없이 속도의 방향에만 영향을 받는다. 따라서 쿨롱 마찰 모델에서 마찰력은 Fc의 크기만큼 움직임을 방해하는 방향으로 작용한다는 것을 나타낸다. 쿨롱 마찰력인 Fc는 아래 식(2)과 같다.
| (2) |
식(2)에서 μ는 쿨롱 마찰 계수이며 익히 알고있는 동마찰 계수와 동일하다. Fn은 접촉면에 수직한 방향의 힘을 나타낸다.
Fig. 2(b)의 점성 마찰 모델은 단독으로 거의 사용되지 않고 주로 쿨롱 마찰 모델과 조합되어 사용된다. 점성 마찰 모델은 아래 식(3)과 같다.
| (3) |
식(3)에서 η는 점성 마찰 계수를 나타내고, 은 속도를 나타낸다. 식(3)에서 점성 마찰력은 속도와 선형적인 관계임을 알 수 있다. 즉 점성 마찰 계수를 기울기로 하는 마찰력과 속도의 선형 방정식이다.
앞서 언급하였듯이 점성 마찰 모델은 쿨롱 마찰 모델과의 조합으로 주로 사용되며, 두 가지 방법으로 조합할 수 있다. 첫 번째는 수식으로 표현하면 식(1)과 식(3)의 합으로 표현될 수 있으며 아래 식(4)와 같다.
| (4) |
식(4)를 도식으로 표현하면 Fig. 2(c)와 같다. 점성 마찰 모델은 마찰 특성을 나타내기에 부족하여 사용이 제한적이고, 쿨롱 마찰 모델 및 쿨롱과 점성 마찰 모델의 조합 중 첫 번째 모델은 속도가 0인 지점에서 마찰력이 정의되어 있지 않다. 즉 속도가 0 근처의 저속 구간에서 왕복 운동을 하는 경우 구동기의 떨림(Chattering) 현상을 야기할 수 있다. 이러한 단점을 보완하기 위하여 Fig. 2(d)와 같이 쿨롱과 점성 마찰 모델의 두 번째 조합 모델이 제시되었으며 수식으로 표현하면 아래 식(5)와 식(6)과 같다.
| (5) |
| (6) |
식(5)와 식(6)에서 알 수 있듯이 속도가 0 이상의 구간에서는 쿨롱 마찰력과 점성 마찰력 중 작은 값이 마찰력이 된다. 반대로 속도가 0 미만인 구간에서는 음의 쿨롱 마찰력과 점성 마찰력 중 큰 값이 마찰력이 된다. 따라서 Fig. 2(d)와 같이 쿨롱과 점성 마찰 모델의 두 번째 조합 마찰 모델을 이용할 경우 속도가 0 근처의 저속 구간에서 구동기의 떨림 현상을 해결할 수 있다.
3.2 Stribeck 마찰 모델
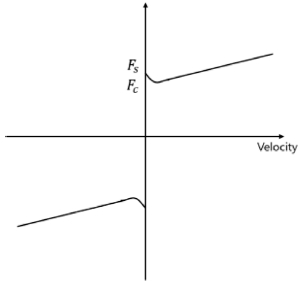
Stribeck은 마찰에 관한 실험 중 특정 속도 영역에서 속도는 증가하지만 마찰력은 오히려 감소하는 현상을 발견했다. 이를 Stribeck 효과라고 하며 식(7)과 같다.15
| (7) |
Stribeck 마찰 모델에서 Fs는 정 마찰력, vs는 Stribeck 속도, j는 Stribeck 곡선 형상을 나타내는 지수이며, Stribeck 마찰 모델은 Fig. 3과 같다.
Stribeck 마찰 모델 또한 속도가 0일 때 마찰력이 정의되어 있지 않기 때문에 속도가 0 근처인 저속 구간에서 구동 시 구동기의 떨림 현상을 야기할 수 있다.
3.3 LuGre 마찰 모델
Dahl은 물체에 아주 작은 힘을 가했을 때 물체가 움직이지 않고 제자리로 돌아오는 현상을 발견했다.16 이러한 스프링과 같은 탄성체와 유사한 거동을 통해 마찰력이 단순히 속도의 영향을 받는 것이 아니라 변위의 영향도 있을 것이라 판단하여 마찰 모델을 제시하였으며, 이를 수식으로 나타내면 다음 식(8)과 같다.
| (8) |
식(8)에서 σ0는 강성 계수를 나타내며, i는 히스테리시스의 형상을 표현하는 지수이다. Dahl 모델을 단순화하기 위하여 i = 1로 설정하며, 이 경우 Dahl 모델은 다음 식(9)과 같이 표현된다.
| (9) |
Dahl은 식(9)의 마찰 모델의 통하여 속도가 0 부근에서 운동할 때의 마찰력과 히스테리시스를 표현할 수 있는 새로운 마찰 모델을 개발하였으며, 이를 통하여 Stribeck 마찰 모델의 단점을 보완할 수 있었다. 하지만 식(9)의 Dahl 마찰 모델을 통해서는 Stribeck 효과와 스틱-슬립 운동을 표현할 수 없었으며, 단순히 전 미끄럼(Presliding) 운동에 대한 근사치만 표현할 수 있었다. 하지만 Dahl 모델은 추후 LuGre 마찰 모델의 기초가 되었다.
LuGre 마찰 모델은 Dahl 마찰 모델에서 표현할 수 없었던 Stribeck 효과와 스틱-슬립 운동을 표현할 수 있다. 따라서 LuGre 마찰 모델은 미소 변위에서의 스프링과 유사한 거동 특성, 히스테리시스, 스틱-슬립 운동 등을 모두 표현 가능하다는 장점으로 인하여 많이 사용된다. LuGre 마찰 모델을 수식으로 표현하면 아래 식과 같다.17
| (10) |
| (11) |
| (12) |
LuGre 마찰 모델에서 z는 마찰 상태를 의미하며, 이를 이용하여 브리슬(Bristle)의 평균적인 변형을 설명할 수 있다. σ0는 강성 계수, σ1은 브리슬의 댐핑 계수, σ2는 점성 마찰 계수를 나타내며 은 Stribeck 효과, vs는 Stribeck 속도를 나타낸다. Dahl 모델과 비교하여 LuGre 모델은 속도에 대한 함수 을 적용하였고, 초미세변위와 관련된 댐핑 σ1 등이 추가되었다. 또한 j는 Stribeck 곡선 형상 계수를 나타내며 0.5, 1, 2를 주로 사용한다. 본 연구에서는 Stribeck 곡선 형상 계수를 2로 설정하여 구동 모듈의 마찰 특성을 모델링 하였다.
4. 실험 및 결과
4.1 구동 모듈 소개 및 실험 환경 구성
본 연구에 사용된 무릎관절 구동 모듈은 Fig. 4와 같이 모터, 하모닉 드라이브, 절대각 엔코더, 베어링 등으로 구성되어있으며 하우징은 자체적으로 제작하였다. 구동 모듈에 사용된 모터는 Allied Motion 사의 MF0076008-A 모델이며, 하모닉 드라이브는 SBB 사의 SCSD25-100-2A 모델이다. 구동 모듈은 총 중량이 개당 약 1.4 kg이고 100 : 1의 기어비를 가진다. 모터를 제어하기 위한 드라이버로는 Elmo 사의 G-beeR50100 모델을 사용하였다.
구동 모듈의 마찰 데이터를 획득하기 위하여 Fig. 5와 같이 실험 환경을 구성하였다. 실험 과정은 먼저 전원공급기를 이용하여 구동 모듈과 모터 드라이버에 각각 48 V, 5 V를 입력한다. 그 후 모터 드라이버 전용 소프트웨어를 이용하여 모터 드라이버의 기어비, 극 쌍 등 구동 모듈의 정보 입력, 게인 튜닝 등의 설정을 진행한 후 마찰 데이터 획득 실험을 진행하였다. 또한 전용 소프트웨어를 통해 구동 모듈에 명령을 인가하고 데이터를 획득할 수 있다. 마찰 데이터를 획득하기 위하여 1000 RPM의 속도와 0.1 Hz의 주기를 갖는 사인파 명령을 인가하였다.
4.2 마찰 데이터
구동 모듈의 단순한 동역학 모델은 다음 식(13)과 같이 모델링하여 나타낼 수 있다.
| (13) |
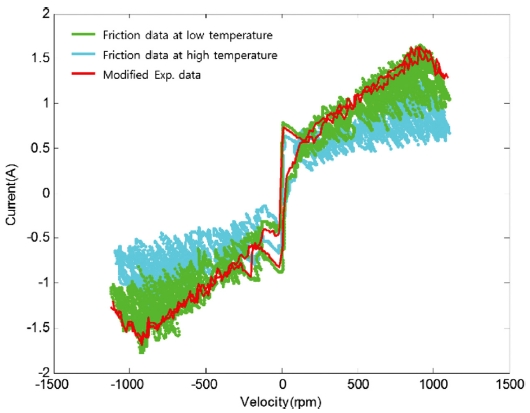
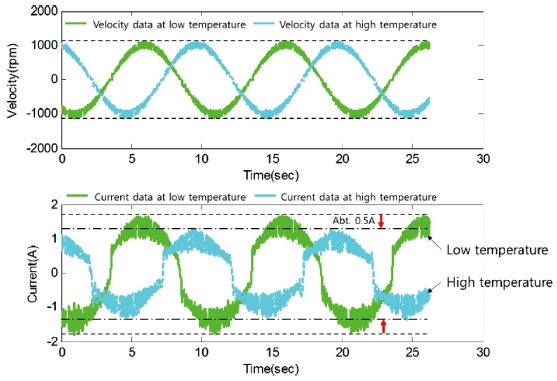
식(13)에서 J는 관성을 나타내고, 는 각각 마찰과 부하에 의한 토크를 나타낸다. 구동 모듈의 마찰 특성 획득 시 관성의 영향이 포함된 시간 도메인에서의 마찰 특성 데이터는 Fig. 6과 같다.
관성의 영향으로 인하여 구동 모듈의 속도가 증가하였다가 감소할 때, 즉 구동 모듈의 회전 방향이 반대가 될 때 마찰 데이터의 변화폭이 큰 것을 Fig. 6을 통해 확인할 수 있다. 따라서 구동 모듈의 관성의 영향을 보상해야 한다. 그 후 마찰 데이터의 보간을 수행하면 Fig. 7과 같은 마찰 모델을 설계하기 위한 마찰 데이터를 획득할 수 있다.
Fig. 6을 통하여 우리는 본 연구에 사용된 구동 모듈이 온도가 상승함에 따라 마찰력이 감소한다는 것을 확인하였다. 실험결과에 따르면 구동 모듈의 온도가 상온에서 약 40°C로 20°C 가량 상승했을 때 약 0.5 A 감소하는 것을 확인할 수 있다. 따라서 실제 마찰 모델을 이용한 마찰 보상을 수행할 때 온도의 영향을 고려해야 할 것으로 판단된다.
Fig. 7과 같이 구동 모듈의 관성의 영향을 보상한 후 보간을 수행하여 획득한 마찰 데이터를 이용하여 앞서 3장에서 소개하였던 마찰 모델들을 이용하여 모델링을 수행하였으며, 실제 적용 가능성을 살펴보았다.
4.3 마찰 모델링 결과
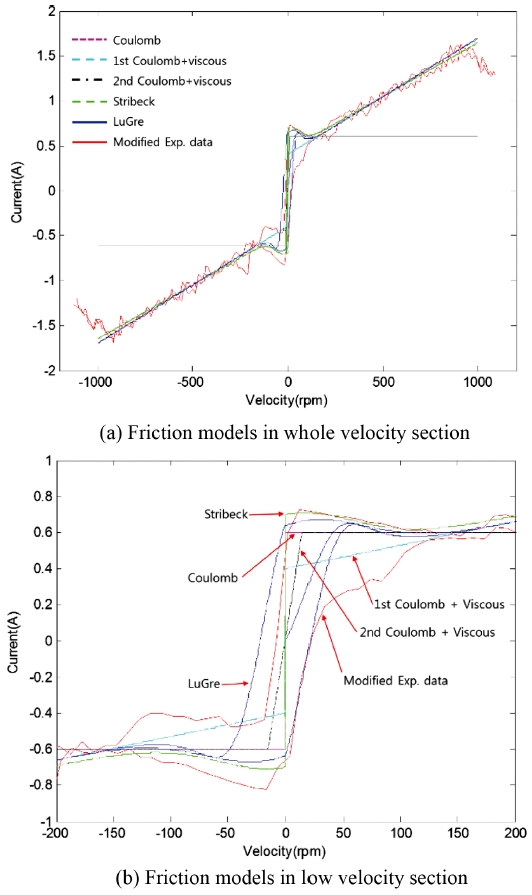
Fig. 8을 통해 쿨롱 마찰 모델 단독으로는 구동 모듈의 마찰 특성을 표현하기에는 매우 부족하다는 것을 확인할 수 있다. 저속 영역에서 떨림 현상을 야기할 뿐 아니라 점성 마찰 영역에서도 속도가 증가할수록 구동 모듈과 모델의 마찰 차이가 점점 증가한다.
두 종류의 쿨롱과 점성 마찰 모델의 조합 모델 중 첫 번째 마찰 모델은 속도가 0 근처의 저속 구간에서 구동 모듈의 떨림이 발생하겠지만 구동 모듈 마찰 데이터의 점성 마찰 영역을 비교적 잘 추종하는 것을 확인할 수 있다. 두 번째 마찰 모델에서는 속도가 0 근처의 저속 구간에서 기울기가 가파르지만 구동 모듈의 떨림은 발생하지 않을 것이다. 하지만 점성 마찰 영역을 전혀 추종하지 못하는 결과를 보인다.
Stribeck 마찰 모델은 앞의 모델들과 비교하였을 때 구동 모듈의 마찰 데이터를 가장 잘 추종하는 것을 확인할 수 있다. 하지만 마찰 데이터에 존재하는 히스테리시스를 표현하지 못하며 쿨롱 마찰 모델과 마찬가지로 속도가 0인 지점에서 마찰력이 정의되어 있지 않으므로 구동 모듈의 떨림을 야기할 것이다. 또한 속도가 양인 구간에 대해서는 마찰 데이터와 거의 일치하는 결과를 보여주지만 속도가 음인 구간에서 구동 모듈의 마찰 데이터와 약간의 오차가 발생하는 것을 확인할 수 있다. 이는 구동 모듈의 회전 방향에 따른 마찰 데이터의 차이로 인한 결과인 것으로 판단된다.
정적과 동적 마찰 모델의 차이는 저속구간에서 구동 모듈의 마찰 특성 반영 여부이다. Fig. 8(a)에서 약 200 RPM 이상의 점성 마찰 영역에서는 마찰 모델의 특성이 선형으로써 정적 및 동적 마찰 모델이 유사한 것을 알 수 있다. 실제 구동 모듈 마찰은 회전 방향이 바뀌는 저속구간(-150~150 RPM)에서 히스테리시스가 존재하지만 정적 마찰 모델은 히스테리시스를 표현하지 못한다. Fig. 8(b)에서 정적 마찰 모델과 달리 동적 마찰 모델인 LuGre 마찰 모델은 쿨롱, 점성, Stribeck 효과와 히스테리시스 등 대부분의 마찰 특성을 표현 가능하다. 특히 속도가 양에서 음으로 변화하는 일부 저속구간에서 마찰 특성 데이터와 거의 일치하는 것을 확인할 수 있다. 따라서 LuGre 마찰 모델이 본 논문의 마찰 모델 중 구동 모듈의 마찰 특성과 최소한의 오차를 가지는 것을 확인할 수 있었다.
5. 결론
본 논문에서는 BLDC 모터와 하모닉 드라이브로 구성된 외골격 로봇의 구동 모듈의 마찰 특성을 다양한 마찰 모델을 활용하여 분석하였다. 구동 모듈의 마찰 특성 데이터로부터 히스테리시스, Stribeck 효과 등을 확인하였으며, 다양한 마찰 모델 중 LuGre 마찰 모델이 이러한 특성들을 모두 반영하므로 착용자의 저항감을 최소화하는 마찰 모델일 것으로 판단된다. 향후 실제 외골격 로봇에 각각의 마찰 모델을 적용한 마찰 보상 제어를 수행하여 착용자의 저항감을 최소화하는 최적 마찰 모델의 식별 및 검증이 필요하다.
NOMENCLATURE
| F : | Friction force |
| Fc : | Coulomb friction force |
| Fs : | Static friction force |
| z : | Average deflection of the contacting asperities |
| x : | Relative displacement |
| : | Sliding velocity |
| : | Stribeck effect |
| σ0 : | Contact stiffness |
| σ1 : | Damping coefficient |
| σ2 : | Viscous friction |
| vs : | Stribeck velocity |
| j : | Stribeck curve shape factor |
REFERENCES
-
Kawamoto, H. and Sankai, Y., “Power Assist Method based on Phase Sequence and Muscle Force Condition for HAL,” Advanced Robotics, Vol. 19, No. 7, pp. 717-734, 2005.
[https://doi.org/10.1163/1568553054455103]

-
Zeilig, G., Weingarden, H., Zwecker, M., Dudkiewicz, I., Bloch, A., et al., “Safety and Tolerance of the RewalkTM Exoskeleton Suit for Ambulation by People with Complete Spinal Cord Injury: A Pilot Study,” Journal of Spinal Cord Medicine, Vol. 35, No. 2, pp. 96-101, 2012.
[https://doi.org/10.1179/2045772312Y.0000000003]

-
De Looze, M. P., Bosch, T., Krause, F., Stadler, K. S., and O’Sullivan, L. W., “Exoskeletons for Industrial Application and Their Potential Effects on Physical Work Load,” Ergonomics, Vol. 59, No. 5, pp. 671-681, 2016.
[https://doi.org/10.1080/00140139.2015.1081988]

-
Schiffman, J. M., Gregorczyk, K. N., Bensel, C. K., Hasselquist, L., and Obusek, J. P., “The Effects of a Lower Body Exoskeleton Load Carriage Assistive Device on Limits of Stability and Postural Sway,” Ergonomics, Vol. 51, No. 10, pp. 1515-1529, 2008.
[https://doi.org/10.1080/00140130802248084]

-
Hong, M., Kim, G., and Yoon, H., “ACE-Knee, a Novel Modularized Knee Exoskeleton: Concept Design and Analysis of Design Requirements by Knee Motion Analysis,” Journal of the Korean Society for Precision Engineering, Vol. 36, No. 4, pp. 373-381, 2019.
[https://doi.org/10.7736/KSPE.2019.36.4.373]

-
Zoss, A. B., Kazerooni, H., and Chu, A., “Biomechanical Design of the Berkeley Lower Extremity Exoskeleton (BLEEX),” IEEE/ASME Transactions on Mechatronics, Vol. 11, No. 2, pp. 128-138, 2006.
[https://doi.org/10.1109/TMECH.2006.871087]

-
Yun, S. S., Kang, B. B., and Cho, K. J., “EXO-Glove PM: An Easily Customizable Modularized Pneumatic Assistive Glove,” IEEE Robotics and Automation Letters, Vol. 2, No. 3, pp. 1725-1732, 2017.
[https://doi.org/10.1109/LRA.2017.2678545]

-
Gerez, L., Chen, J., and Liarokapis, M., “On the Development of Adaptive, Tendon-Driven, Wearable EXO-Gloves for Grasping Capabilities Enhancement,” IEEE Robotics and Automation Letters, Vol. 4, No. 2, pp. 422-429, 2019.
[https://doi.org/10.1109/LRA.2019.2890853]

-
Ulrey, B. L. and Fathallah, F. A., “Biomechanical Effects of a Personal Weight Transfer Device in the Stooped Posture,” Proc. of the Human Factors and Ergonomics Society Annual Meeting, Vol. 55, No. 1, pp. 1052-1056, 2011.
[https://doi.org/10.1177/1071181311551220]

-
Ghorbel, F. H., Gandhi, P. S., and Alpeter, F., “On the Kinematic Error in Harmonic Drive Gears,” Journal of Mechanical Design, Vol. 123, No. 1, pp. 90-97, 2001.
[https://doi.org/10.1115/1.1334379]

-
Wolf, S. and Iskandar, M., “Extending a Dynamic Friction Model with Nonlinear Viscous and Thermal Dependency for a Motor and Harmonic Drive Gear,” IEEE International Conference on Robotics and Automation, pp. 783-790, 2018.
[https://doi.org/10.1109/ICRA.2018.8460613]

-
Armstrong-Helouvry, B., Dupont, P., and De Wit, C. C., “A Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction,” Automatica, Vol. 30, No. 7, pp. 1083-1138, 1994.
[https://doi.org/10.1016/0005-1098(94)90209-7]

-
Banala, S. K., Agrawal, S. K., and Scholz, J. P., “Active Leg Exoskeleton (ALEX) for Gait Rehabilitation of Motor-Impaired Patients,” Proc. of IEEE 10th International Conference on Rehabilitation Robotics, pp. 401-407, 2007.
[https://doi.org/10.1109/ICORR.2007.4428456]

-
Hyun, D. J., Park, H., Ha, T., Park, S., and Jung, K., “Biomechanical Design of an Agile, Electricity-Powered Lower-Limb Exoskeleton for Weight-Bearing Assistance,” Robotics and Autonomous Systems, Vol. 95, pp. 181-195. 2017.
[https://doi.org/10.1016/j.robot.2017.06.010]

-
Armstrong-Helouvry, B., Dupont, P., and De Wit, C. C., “A Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction,” Automatica, Vol. 30, No. 7, pp. 1083-1138, 1994.
[https://doi.org/10.1016/0005-1098(94)90209-7]

-
Dahl, P. R., “Measurement of Solid Friction Parameters of Ball Bearings,” Aerospace Corp El Segundo Ca Engineering Science Operations, No. TR-0077 (2901-03)-3, 1977.
[https://doi.org/10.21236/ADA042599]

-
De Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky, P., “A New Model for Control of Systems with Friction,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425, 1995.
[https://doi.org/10.1109/9.376053]


Junior researcher in Agency for Defense Development. His current research interest is friction compensation of exoskeleton actuator and exoskeleton control.
E-mail: bjlee@add.re.kr

Senior researcher in Agency for Defense Development. His research interests include exoskeleton control, nonlinear control, and control application.
E-mail: gtk@add.re.kr

Senior researcher in Agency for Defense Development. His current research interests include exoskeleton control and movement recognition.
E-mail: kimhc@add.re.kr

Received the Ph.D. degree in Department of Mechanical Engineering from Korea Advanced Institute of Science and Technology, Republic of Korea, in 2013. Since 2013, he has been a senior researcher in Agency for Defense Development. His research interest is design and control of exoskeleton and wearable robots.
E-mail: yjshin@add.re.kr