표적 방호력 및 반응장갑 비산거동 분석에 근거한 주탄두 기폭지연시간 결정방법

2.1 반응장갑 방호력 발생원리 및 반응체 비산속도

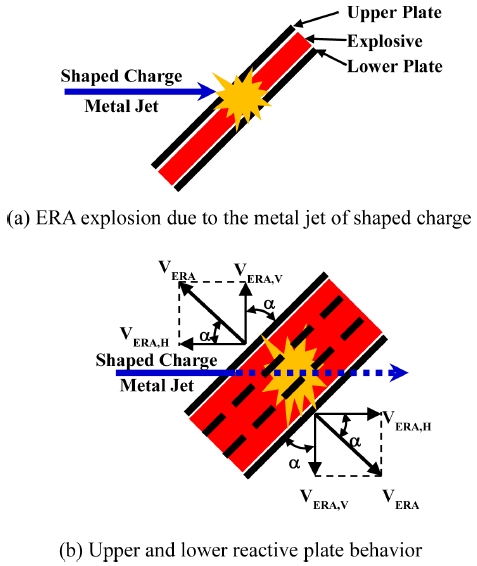
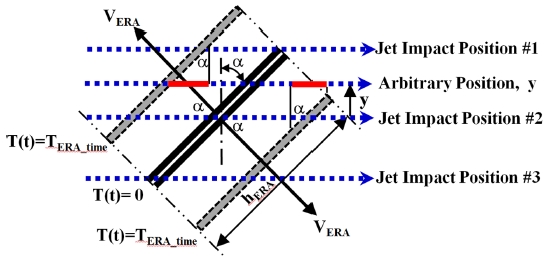
반응장갑의 경우 Fig. 1(a)에 나타낸 바와 같이 두 개의 금속판 사이에 화약이 충진 된 샌드위치 구조를 가지며 성형작약제트(Shaped Charge Jet, SCJ)나 철갑탄(Armor Piercing Bullet, AP) 충돌에 의해 내부 화약이 폭발하게 되며, 이때 발생하는 폭발력에 의해 반응장갑 상부판(Upper Plate)과 하부판(Lower Plate)은 각각 V_ERA 속도를 갖고 Fig. 1(b)에 나타낸 바와같이 비산하게 된다.⁹

Fig. 1

Activation concept of explosive reactive armor

참고로 상부판과 하부판이 제트를 지나갈 때 제트 관통력이 저하되는 이유는 미시적으론 서로 다른 두 유체 경계 면에서 생기는 마찰에 대한 켈빈-헬름홀츠 불안정성(Kelvin-Helmholtz Instability) 현상에 기인한 것이며,^10,11 거시적으로는 반응체가 제트 진행방향에 수직한 속도성분 V_ERA,V를 갖고 제트를 지나갈 때 성형작약탄두 기폭 시 발생한 메탈제트가 실제 반응장갑 반응체 두께보다 두꺼운 금속판을 통과하는 영향을 받게 되어 성형작약 제트의 관통성능이 감소하게 된다.

본 연구에서는 상부판과 하부판 두께와 재질이 동일한 반응장갑을 고려하였으며, 반응장갑 폭발 시 비산하는 반응체 비산 속도는 거니방정식(Gurney Equation)으로부터 식(1)과 같이 구할 수 있다.⁴

여기서, V_ERA는 반응장갑 반응체(상부판, 하부판) 비산속도(m/sec), $$ \sqrt{2E}$$는 화약종류에 따라 결정되는 거니상수(Gurney Constant) (m/sec), m_plate는 반응장갑 샌드위치 구조물의 반응체 질량(kg), m_exp는 샌드위치 구조물 사이에 충진 된 화약질량(kg)이다.

Fig. 1로부터 성형작약 제트의 진행방향에 수직한 축에서 반응장갑이 기울어진 각을 충돌각 α라 정의하고, 제트 진행방향에 수직, 수평한 방향의 반응체 비산속도를 구하면 식(2)와 같다.

여기서, V_ERA,V는 제트 진행방향에 수직한 방향의 반응체 비산속도성분(m/sec), V_ERA,H는 제트 진행방향과 수평한 방향의 반응체 비산속도성분(m/sec)이다.

2.2 반응장갑 충돌위치에 따른 반응체 비산소요시간

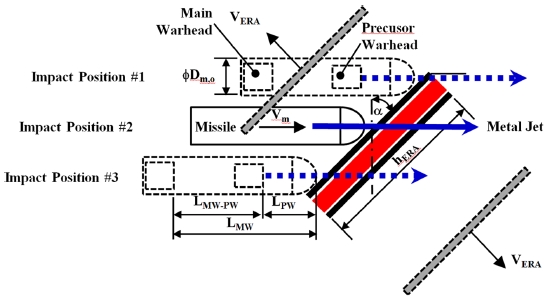
유도탄이 반응장갑을 장착한 표적과 충돌 시 Fig. 2와 같이 충돌위치 #1과 충돌위치 #3 사이의 임의 위치에서 충돌하게 되며, 충돌 후 선구탄두 기폭에 의해 발생하는 제트에 의해 폭발한 반응장갑 반응체가 유도탄 진행방향에서 완전히 사라지는데 소요되는 시간은 충돌 한 위치에 따라 달라지게 된다.

Fig. 2

Impact position between missile and ERA

상/하부 반응체가 자유롭게 비산할 수 있다고 가정하고 상/하부 반응체가 유도탄 진행방향에서 완전히 사라지는데 소요되는 시간을 비산소요시간이라 정의하였다. 또한, 선구탄두 제트가 반응장갑 양 끝 단을 통과할 때 반응체 비산에 소요되는 시간을 비산최대소요시간이라 정의하였으며, 제트가 반응장갑 중앙을 통과하는 경우 반응체가 사라지는데 소요되는 시간을 비산평균 소요시간이라 정의하였다. 유도탄 진행방향에서 반응체가 완전히 사라진다는 의미는 유도탄이 표적을 향해 비행 시 유도탄 직경범위 내에 반응체가 존재하지 않는 것을 의미한다.

비산최대소요시간을 T_{ERA_Rmv_max}라 정의하고, 비산평균소요시간을 T_{ERA_Rmv_avg}라 정의할 때 각각의 비산소요시간은 식(3) 및 식(4)와 같다.

이때, 반응장갑의 두께에 관한 영향은 무시하였으며, 유도탄 선두부 내 각종 구성품은 선구탄두 폭발과 동시에 비산되며 반응장갑 반응체 비산속도에 영향을 주지 않는다고 가정하였고, 충돌위치 #3의 하부판 비산소요시간은 충돌위치 #1의 상부판 비산소요시간과 동일하다고 가정하였다.

여기서, T_{ERA_Rmv_max}는 충돌위치 #1과 #3에서 반응장갑 반응체가 유도탄 진행방향에서 사라지는데 필요한 최대시간(sec), h_ERA는 반응장갑 반응체 길이(m)이고, D_m,o는 유도탄의 직경(m)이다.

여기서, T_{ERA_Rmv_avg}는 충돌위치 #2에서 반응장갑 반응체가 유도탄 진행방향에서 사라지는데 필요한 평균시간(sec)이다.

2.3 표적 충돌각 α과 유도탄 입사각 γ의 관계

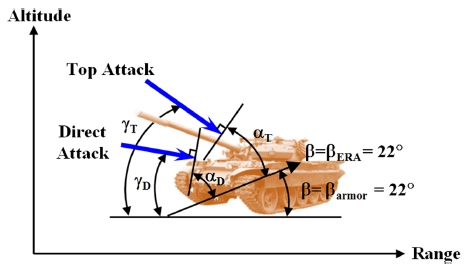
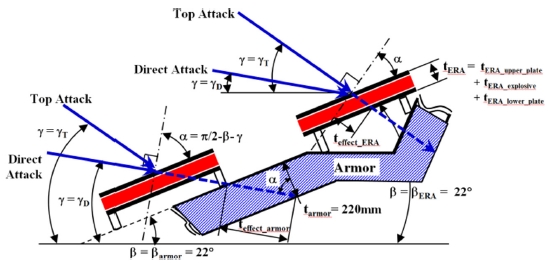
이중성형작약 유도탄이 표적을 공격 할 때 Fig. 3과 같이 표적을 직접 공격하는 직접공격(Direct Attack) 방식과 표적의 상부를 공격하는 상부공격(Top Attack) 방식이 있다. 유도탄이 표적에 충돌할 때 유도탄 진행방향은 유도제어(Guidance Control)에 의해 받음각(Angle of Attack)이 0^o가 된다고 가정하여 성형작약탄두에서 발생하는 제트의 방향은 유도탄 진행방향과 동일하다고 가정하였다.

Fig. 3

Relation between incidence angle γ and impact angle according to target attack mode

또한, 직접공격 시 유도탄 종말속도(Terminal Velocity)는 유도탄 최대비행속도를 갖고, 상부공격 시에는 최소비행속도를 갖는다고 가정하였다.

유도탄이 표적과 충돌할 때 지면과 이루는 각을 입사각 γ라 하고, 유도탄 진행방향에 수직한 면과 표적이 이루는 각을 충돌각 α이라 정의 할 때 입사각과 충돌각의 관계는 식(5)와 같다.

여기서, β는 전차 주장갑과 반응장갑의 기움각(Degree), α는 유도탄 진행방향에 수직한 면과 표적이 이루는 각이고, γ는 유도탄이 표적과 충돌할 때 지면과 이루는 각이다.

직접공격과 상부공격 시 유도탄 입사각 γ 범위는 식(6)과 같다.

여기서 γ_T와 γ_D는 각각 상부공격과 직접공격 시 유도탄과 제트의 입사각(Degree), α_T와 α_D는 각각 상부공격과 직접공격 시 유도탄 진행방향에 수직한 면이 표적과 이루는 충돌각(Degree)이고, Δα_T와 Δα_D는 각각 상부공격과 직접공격 시 충돌각의 가변범위(Degree)이다.

2.4 반응장갑 반응체와 주탄두 사이 수평/수직거리

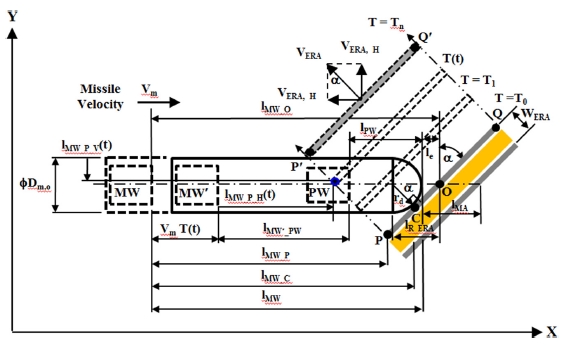
유도탄 선구탄두 제트가 반응장갑 충돌위치 #2인 중앙에 관통했을 때 반응장갑 거동은 Fig. 4에 나타내었다. 이때 반응체 거동은 강체운동으로 가정하였으며 제트는 단면적이 없는 1차원 제트로 가정하였다.

Fig. 4

The behavior of a reactive element

유도탄 선두부가 반응장갑의 점 C와 충돌하게 되면 유도탄 선구탄두 제트가 반응장갑의 중간인 점 O를 관통하며 상부 반응체는 V_ERA 속도로 비산운동을 하게 된다. 반응장갑 폭발 시 반응체의 끝점 P는 시간에 따라 점 P’으로 비산하게 되며 임의 시간 T(t) 에서 점 P(t) 와 주탄두 앞면까지의 수평거리와 유도탄 외경까지의 수직거리는 식(7)와 같다.

여기서, l_{MW_P_H}(t)는 임의 시간 T(t)에서 반응장갑 반응체 위의 점 P(t)와 주탄두 앞면까지의 수평거리(m)이고, l_{MW_P_V}(t)는 임의 시간 T(t)에서 반응장갑 반응체 위의 점 P(t)와 유도탄 외경까지의 수직거리(m), l_MW는 주탄두 설치 이격거리(m), r_d는 레이돔 곡률반경(m)이고, V_m는 유도탄 비행속도(m/sec)이다.

식(8)은 Fig. 2에 나타낸 바와같이 유도탄이 반응장갑 상단 끝에 메탈제트를 방출하는 충돌위치 #1인 경우에 임의 시간 T(t)에서 주탄두와 반응체 위의 점 P(t)의 거리 관계식을 나타낸다.

마찬가지로 식(9) 역시 충돌위치 #3의 경우 임의 시간 T(t)에서 주탄두와 반응체 위의 점 P(t)의 거리를 나타낸다.

참고로 Fig. 4에서 유도탄 정점(Missile Apex)와 반응장갑 후면 주장갑 시작점까지 거리 l_MA는 식(10)과 같다.

2.5 반응장갑 충돌위치에 따른 반응장갑 방호력

Fig. 5는 반응장갑 반응체 비산거동에 따른 반응장갑 방호력이 발생하는 원리를 도식화 한 것으로 반응장갑의 총 유효방호력은 제트가 반응장갑 관통 시 제트 흐름을 방해하는 정적 방호력과 반응체 비산에 의해 제트흐름을 방해하는 동적방호력의 합으로 제트충돌위치 #2인 경우 반응장갑 총 유효방호력은 식(11)와 같다.

Fig. 5

Protection capability of ERA according to the scattering distance of reactive elements

참고로 방호력은 균질압연강판(Rolled Homogenous Armor, RHA)의 등가두께로 표현하였다.

여기서, t_{effect_ERA_total}는 반응장갑의 총 유효방호력(m), t_{effect_ERA_S}는 제트가 반응장갑을 관통하는 시점(T(t) = 0)에서 반응장갑의 정적 방호력(m), t_{effect_ERA_D}는 반응장갑 반응체인 상부판과 하부판이 각각 T_{ERA_time} 동안 V_ERA의 속도로 비산하며 제트 진행을 가로지른 길이에 의한 동적방호력(m), T_{ERA_time}는 반응장갑 내 반응체가 제트를 가로지르며 제트 흐름을 방해한 시간(sec), t_{ERA_upper_plate}와 t_{ERA_lower_plate}는 각각 반응장갑 상부/하부 반응체의 두께(m), t_{ERA_house}는 반응장갑 하우징 두께(m), <>⁰는 특이점 함수(Singularity Function)이고,¹² y는 반응장갑 중앙에서 제트가 충돌하는 임의위치 까지의 수직거리(m)이다.

또한, 충분히 긴 반응장갑 반응체 비산시간 T_{ERA_time}가 주어진다면 제트를 가로지르는 반응체 상/하부판 길이의 합이 같아지므로 모든 충돌위치에서 반응장갑 방호력은 동일하게 되며 식(12)와 같다.

2.6 유도탄 입사각 γ에 따른 표적 총 방호력

Fig. 6은 반응장갑을 갖춘 표적을 공격하는 방식에 따라 반응장갑, 주장갑, 메탈제트 간의 기하학적 관계를 나타낸 개략도로 식(5)와 식(12)을 이용하여 전차의 총 방호력을 유도탄 입사각 γ에 대해 표현하면 식(13)와 같다.

Fig. 6

Schematic diagram of the armored tank with ERA

여기서, t_{total_effect_armor}는 전차의 총 방호력(m), t_{effect_armor}는 주장갑의 방호력(m), t_{effect_ERA_total}는 반응장갑의 총 방호력(m), t_armor는 주장갑의 두께(m)이다.

3.1 이중판넬 반응장갑을 갖는 전차 방호력 변화

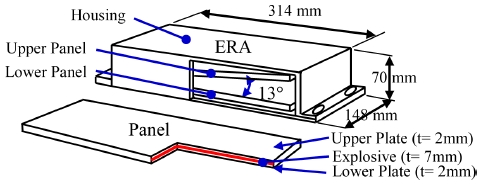
본 연구에서는 동일한 샌드위치 판넬 2장이 1개의 하우징 내에 13° 각도 차를 갖고 설치된 이중 판넬 반응장갑을 고려하였으며 이중판넬 반응장갑 개략도는 Fig. 7과 같다.

Fig. 7

Conceptual drawing of arbitrary ERA with two panels

단일판넬을 갖는 반응장갑의 총 방호력을 나타낸 식(11)을 Fig. 7에 나타낸 이중 판넬 반응장갑에 적용하면 이중판넬 반응장갑의 총 방호력은 식(14)와 같다.

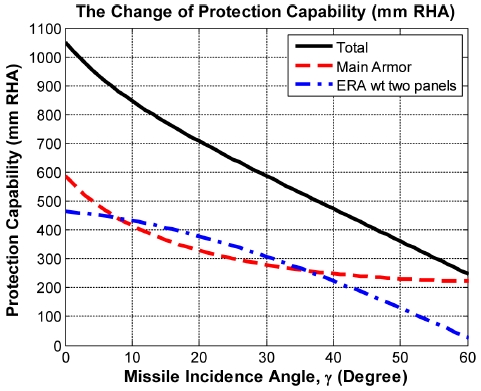
식(13)의 우변 두번째항을 식(14)로 대체하여 이중판넬 반응장갑을 장착한 표적의 총 방호력 변화를 유도탄 입사각 γ에 따라 구하면 Fig. 8과 Table 1와 같다.

Fig. 8

The change of protection capability of arbitrary target with two panels ERA

Table 1

Protection capability of arbitrary target with two panels ERA (mm RHA)

Fig. 8과 Table 1로 부터 유도탄 입사각 γ가 0°일 때 주장갑 방호력은 587 mm RHA이며, 입사각이 60°일 때(상부공격) 주장갑 방호력은 222 mm RHA로 감소함을 알 수 있다. 또한, 직접 공격 시 주입사각(Main Incident Angle)이 10°이고, 상부공격 시 주입사각이 50°일 때 전차 주장갑 방호력은 직접공격 방호력 보다 184 mm RHA 감소 함을 알 수 있다.

만일 표적에 장착된 반응장갑이 선구탄두에 의해 주탄두 관통성능 저하없이 완벽하게 제거되고, 주탄두 관통성능이 입사각 0°시 주장갑 관통을 위해 필요한 587 mm RHA 이상의 관통성능을 갖고 있다면, 모든 상부공격 입사각에서 표적의 총 방호력이 473 mm RHA 이하이므로 주탄두 제트가 반응장갑에 의해 방해를 받더라도 표적 파괴에 문제가 없을 수 있음을 알 수 있다.

3.2 직접공격 입사각의 경우

3.2.1 직접공격 시 주탄두 제트 방해방지를 위해 필요한 입사각별 반응체 비산소요시간

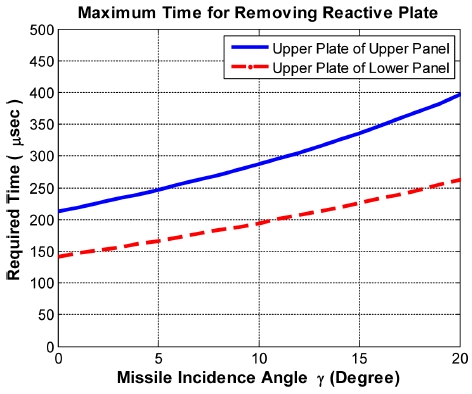
유도탄 내 선구탄두가 이중판넬 반응장갑을 기폭 시켰을 때 반응장갑 내부에 장착된 각 판넬의 상부 반응체 비산소요시간을 식(3)을 통해 구하면 Fig. 9와 Table 2와 같다. 이때 고려한 유도탄의 외경은 140 mm로 가정하였다.

Fig. 9

Required maximum time for removing reactive plate from the front of missile

Table 2

Required maximum time for removing reactive plate from the front of missile with ϕ140 mm diameter

Table 2를 살펴보면 직접공격 입사각에서 반응장갑 반응체의 방해를 방지하기 위해 선구탄두 기폭 후 주탄두 기폭은 최소 396 μsec 이상 지연시켜야 함을 알 수 있다.

3.2.2 직접공격 시 반응체와 주탄두 간 충돌발생 시점

선구탄두 기폭 후 주탄두는 기폭지연시간 동안 유도탄 최대 비행속도의 종말속도를 가지고 표적을 향해 계속 비행하므로 비산 중인 반응장갑 반응체와 충돌할 수 있다. 따라서, 본 절에서는 직접공격 시 반응체와 주탄두의 충돌발생 시점을 입사각별로 구하고자 한다.

Fig. 2에서 충돌위치 #1이 주탄두와 반응체 상의 끝단 P점과 수평거리가 가장 짧아 반응장갑 기폭 시 반응체와 주탄두 사이의 충돌발생 가능성이 가장 높으므로 식(8)을 이용하여 주탄두와 반응장갑 반응체의 상대거리가 0 m가 되는 시점을 Fig. 10과 Table 3에 나타내었다. 이때 고려한 유도탄 종말속도는 직접공격 시 유도탄 최대비행속도를 고려했으며, 544 m/sec (Mach 1.6)로 가정하였다.

Fig. 10

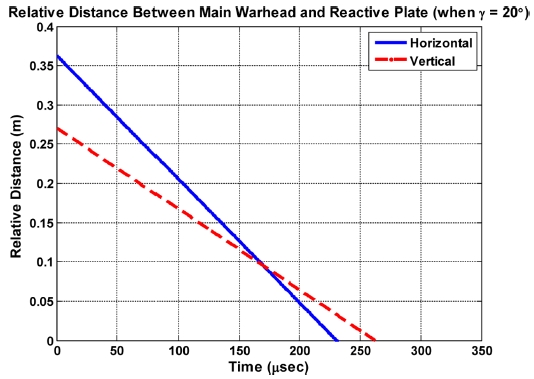
Relative distance between main warhead and reactive plate (when γ = 20°) in case of maximum terminal velocity

Table 3

Required time (μsec) when the relative distance is 0 m in case of maximum terminal velocity

Fig. 10에서 입사각 20°의 경우 수평방향 상대거리가 0 m인 시점(231 μsec)이 수직방향 상대거리가 0 m인 시간(262 μsec) 보다 작다는 의미는 반응체가 유도탄 비행방향에서 아직 벗어나지 않아 수평방향 상대거리가 0 m인 시점에서 반응체와 주탄두가 충돌한다는 것을 의미한다.

Table 3로부터 입사각 13° 이상에서는 수평방향 상대거리가 0 m가 되는 시점이 주탄두가 수직방향으로 사라지는데 소요되는 시점 보다 짧아 주탄두 기폭지연시간을 214 μsec 이상으로 할 경우 입사각 13° 이상에서는 주탄두와 반응체가 서로 충돌할 수 있음을 알 수 있다.

따라서, 주탄두 제트 방해 방지를 위해 주탄두 기폭지연시간을 3.2.1절에서 언급한 반응체 비산소요시간인 396 μsec 이상으로 설정할 경우 직접공격 입사각 13° 이상에서 주탄두와 반응체의 충돌은 불가피해지게 된다.

만일 주탄두와 반응체의 충돌을 방지하고자 주탄두 기폭지연시간을 214 μsec 이하로 할 경우에는 주탄두 제트는 396 μsec와 214 μsec의 차인 182 μsec동안 비산 중인 반응장갑 반응체에 방해를 받게 되어 주탄두 제트의 관통력은 감소하게 된다.

Table 1에 나타낸 바와 같이 직접공격 입사각에서는 표적의 총 방호력이 최소 708 mm RHA 이상으로 상부공격과 비교해 상대적으로 높으므로 반응장갑에 의해 주탄두 제트가 방해받는 것은 바람직하지 않다.

따라서, 직접공격 시 주탄두 기폭지연시간은 반응장갑 반응체가 주탄두 진행방향에서 완전히 벗어나는데 소요되는 시간인 396 μsec 이상으로 설정하고 반응체와의 충돌로부터 선구탄두와 주탄두 사이에 보호벽을 설치 하여 주탄두를 보호하는 것이 바람직해 보인다.^6,8

3.3 상부공격 입사각의 경우

3.3.1 상부공격 시 주탄두 제트 방해방지를 위해 필요한 입사각별 반응체 비산소요시간

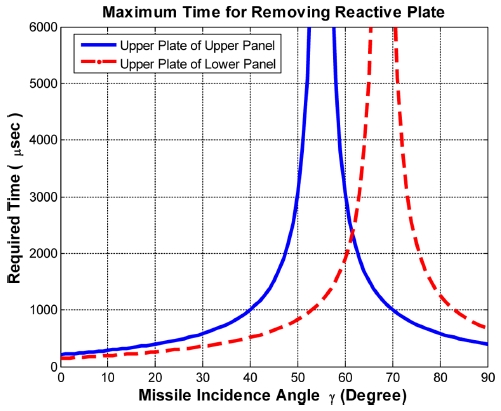
3.2절과 마찬가지로 식(3)를 이용하여 상부공격 시 반응장갑 내 각 판넬의 상부 반응체 비산소요시간을 구하면 Fig. 11 및 Table 4와 같다.

Fig. 11

Required maximum time for removing reactive plate from the front of missile

Table 4

Required maximum time for removing reactive plate from the front of missile with ϕ140 mm diameter

Fig. 11에 나타낸 바와같이 상부공격 입사각 55°와 68°의 경우 반응장갑 반응체 비산방향과 유도탄 진행방향이 서로 마주 보게 되어 반응체와 주탄두 충돌은 피할 수 없으므로 상부공격에 있어서도 주탄두를 보호할 수 있는 방법을 고려해야 함을 알 수 있다.

또한, 상부공격에서는 직접공격과 달리 반응체가 상대적으로 긴 시간 동안 유도탄 비행방향에 머무르나 제트를 가로지르는 반응체 속도 및 이동거리가 상대적으로 작다. 따라서, 감소되는 제트 관통력은 작으며, 작아지는 크기는 Table 1에 나타낸 상부공격 시 반응장갑 방호력을 통해 알 수 있다.

3.3.2 상부공격 시 반응체와 주탄두 간 충돌발생 시점

상부공격 주입사각인 50°의 경우 시간에 따른 주탄두와 반응체 간의 상대거리를 Fig. 12 및 Table 5에 나타내었으며, 유도탄 종말속도는 최소비행속도인 170 m/sec (Mach 0.5)로 가정하였다.

Fig. 12

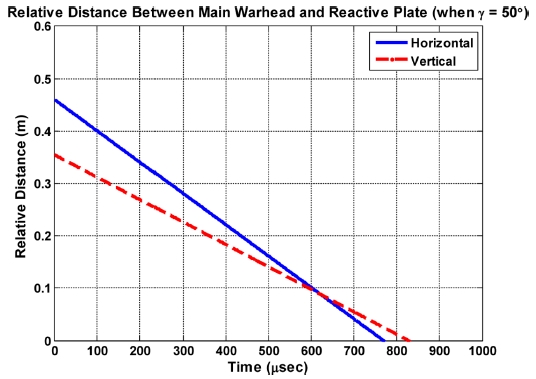
Relative distance between main warhead and reactive plate (when γ = 50°) in case of minimum terminal velocity

Table 5

Required time (μsec) when the relative distance is 0 m in case of minimum terminal velocity

Table 5로부터 입사각 40° 이상의 상부공격의 경우 주탄두와 반응장갑 반응체 사이의 수평방향 상대거리가 0 m가 되는 시점이 수직방향 상대거리가 0 m가 되는 시점 보다 짧아 476 μsec 이상의 주탄두 기폭지연시간에서는 반응체와 주탄두와 충돌하게 되며, 수평/수직방향 상대거리가 0 m가 되는 시점간의 차이 시간 동안 주탄두 제트는 반응체에 의해 방해를 받을 수 있다.

예를 들어 주입사각 50°의 충돌발생시점인 734 μsec를 주탄두 기폭지연시간으로 결정한다면 주탄두 제트 지속가능시간에 따라 달라지지만 반응체가 유도탄 비행방향에서 벗어나는 시점인 827 μsec와의 시간 차이인 93 μsec 동안 주탄두 제트는 반응체의 방해를 받게 되며, 입사각이 커질 수록 수평/수직방향의 시점 차이도 커짐을 Table 5를 통해 알 수 있다.

따라서, 주탄두 제트 방해 영향을 최소화하고 반응체와 주탄두의 충돌을 방지하기 위해 선구탄두 기폭 후 주탄두 기폭지연시간은 476 μsec 이내로 설정하는 것이 적절해 보인다.

3.4 주탄두 기폭지연시간 결정 시 추가고려사항

앞 3.2절과 3.3절로부터 본 연구에서 고려한 유도무기 체계의 경우 주탄두 제트 관통력 저하를 최소화할 수 있는 주탄두 기폭지연시간은 주탄두 보호벽 등의 별도 구조물이 주탄두 앞 단에 설치되어 있다는 가정 하에 396-476 μsec임을 알 수 있었다.

그러나, 주탄두 기폭지연시간 결정에 영향을 주는 추가 인자로는 선구탄두 기폭 시 발생하는 파편과 주탄두 기폭지연시간 동안 감소하는 주탄두-주장갑 사이의 이격거리 감소에 의한 주탄두 관통력 저하를 꼽을 수 있다.

선구탄두 파편 영향의 경우 선구탄두와 주탄두 사이에 별도 주탄두 보호 구조물을 설치하여 영향을 배제하거나 파편이 주탄두에 도달하기 전에 주탄두를 기폭시키는 방법이 있으나, 일반적으로 파편속도가 1,000-2,500 m/sec 이상으로 빠르고⁶ 유도탄 내 배치된 선구탄두와 주탄두 거리가 가까워 파편이 주탄두에 도달하기 전에 주탄두를 기폭하는 방법은 유용하지 않다. 참고로 본 연구에서 고려한 유도탄의 경우 선구탄두 기폭 시 발생하는 파편최대속도는 거니방정식에⁴ 의해 2,874 m/sec이며, 선구탄두와 주탄두 배치간격 0.21 m를 지나 선구탄두 파편이 주탄두에 도달하는 시간은 73 μsec이다.

따라서 본 연구에서 고려한 유도탄의 경우 별도의 주탄두 보호구조물을 추가하는 것이 선구탄두 기폭 시 발생하는 파편 영향을 배제하는 효과적인 방법이라 생각된다.

그리고, 주탄두 기폭지연시간 동안 감소하는 주탄두-주장갑 이격거리의 경우 직접공격 시 유도탄 종말속도와 상부공격 시 유도탄 종말속도가 서로 달라 동일한 주탄두 기폭지연시간으로 두 충돌조건 모두 주탄두 관통성능 저하를 최소화하는 것은 가능하지 않다.

직접공격의 경우 일반적으로 상부공격 대비 유도탄 종말속도가 높아 표적에 가해지는 충격에너지가 높고, 보편적인 운용개념 상 상부공격이 주로 사용되므로 본 연구에서는 상부공격에서 주탄두 관통성능이 제대로 발휘되기 위한 주탄두 기폭지연시간을 구하였다.

본 연구에서는 주탄두 기폭지연시간 동안 감소하는 주탄두-주장갑 이격거리에 기인한 주탄두 관통성능 저하가 없도록 하기위해 주탄두 비행으로 감소하는 이격거리 허용량을 Fig. 4와 식(10)에 나타낸 유도탄 정점(Apex)으로부터 반응장갑 후면 주장갑 시작점까지 거리, l_MA로 하였다.

또한, 상부공격 시 유도탄 종말속도는 가정에 따라 170 m/sec로 하였고, Fig. 4에 나타낸 반응장갑 전체 두께, W_ERA는 Fig. 7에 나타낸 반응장갑의 두께 0.07 m로 하였다. 이 경우 주탄두 관통성능 저하가 발생하지 않도록 하기 위한 주탄두 기폭지연 최대허용시간은 Fig. 13과 Table 6과 같다.

Fig. 13

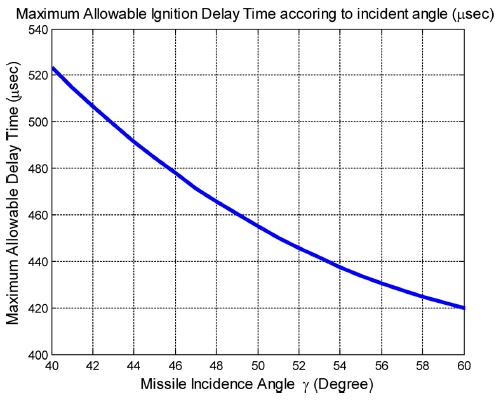
Maximum allowable delay time of main warhead ignition according to incidence angle in case of top attack

Table 6

Maximum allowable delay time (μsec) of main warhead detonation and the initial distance lMA between missile apex and main armor according to incidence angle in case of top attack

Table 6에서 주탄두가 유도탄 종말속도로 주장갑을 향해 비행하여 감소되는 주탄두-주장갑 간의 상대거리 감소 허용량은 입사각 60°에서 0.071 m로 가장 짧으며, 이 상대거리를 주탄두가 비행할 때 소요되는 시간은 418 μsec이다.

주탄두 기폭지연시간이 418 μsec일 경우 입사각 60°에서 주탄두-주장갑 사이의 상대거리는 유도탄 내 주탄두 최초 탑재거리였던 주탄두 이격거리와 동일하게 되어 주탄두 관통성능 발휘에 영향이 없게 된다.

주탄두 이격거리란 최초 유도탄 내 탑재된 주탄두 앞 단에서 유도탄 정점까지의 거리를 의미하며, 일반적으로 주탄두 목표관통성능은 주탄두 이격거리에서 발휘되도록 설계되어 있다.

동일한 주탄두 기폭지연시간으로 상부공격 모든 입사각에서 주탄두 관통성능 저하를 방지하려면 주탄두 기폭지연 최대시간은 418 μsec 이하로 설정해야 주탄두-주장갑 상대거리가 주탄두 이격거리 보다 작아지는 것을 방지하여 주탄두 관통성능 저하를 방지할 수 있다.

따라서, 본 연구에서 고려한 표적과 유도탄의 경우 최종적인 주탄두 기폭지연시간은 396 μsec와 418 μsec 사이의 값이며, 단일 값을 결정할 경우 두 값의 평균값인 407 μsec로 설정하는 것이 이중성형작약 유도탄이 이중판넬 반응장갑을 장착한 표적 파괴를 위한 관통성능을 최대화 할 수 있는 주탄두 기폭지연시간이라 판단된다.