레이저 간섭계를 이용한 대형 체적 레이저 가공 로봇의 평행도 오차 보정

1. 서론

4차 산업의 확산과 기존 정형화된 공정에서 탈피한 다양한 하이브리드(Hybrid) 공정의 요구가 증가하면서, 로봇 매커니즘의 공정 기계가 많이 활용되고 있다. 산업현장에서 널리 사용되고 있는 용접(Welding), 조립 공정(Assembly Process)뿐 아니라, 금속 적층제조(Additive Manufacturing), 절삭 공정(Cutting Process)에도 로봇의 활용이 확산되고 있다.^1,2 로봇의 경우 말단 장치에 작업 시 필요한 기본적인 자유도가 있기 때문에, 갠트리 등의 확장축에 연결하여 대형 부품 가공이 가능하다.

가공물의 품위를 위해 가공 로봇의 강성 확보가 중요하기 때문에, 절삭 가공에 활용 가능한 다양한 로봇 구조가 개발되고 있다. 특히 이동 질량(Moving Mass)이 적고 하중 분산에 유리한 병렬 메커니즘(Parallel Mechanism)의 기계들이 연구되고 있다.^3-9 Hexapod^3-6는 대표적인 병렬 메커니즘으로 절삭 가공에도 활용되고 있지만, 틸트 각(Tilt Angle) 제한 및 작업영역(Workspace)이 협소하여 사용제약이 있다.⁶ 구조적인 제약을 극복하고자 병렬 플랫폼과 틸팅 로터리 테이블 또는 XY 구동 테이블을 구비한 하이브리드 구조의 로봇 가공기도 개발되었다.^7-9 Neumann¹⁰은 3축 병렬 플랫폼에 2개의 회전축이 연결되어 공구가 5자유도 운동을 할 수 있는 하이브리드 구조인 Exechon 메커니즘을 개발하였다. 이 구조는 기존 병렬구조에 비해 넓은 작업영역과 확장성이 높은 장점이 있고, 볼 조인트(Ball Joint)없이 회전 조인트(Revolution Joint)으로만 구성하여 가공에 충분한 강성을 갖도록 하였다.^11-14

이러한 가공 로봇은 정밀 기계로 분류된다. 다축 정밀 기계는 위치 정확도가 중요한 성능 지표이며, 위치 정확도는 기하학적 오차(Geometric Error), 열 오차(Thermal Error), 동적 오차(Dynamic Error) 등에 의해 영향을 받게 된다.^15,16 이러한 오차들은 레이저 간섭계, 레이저 트래커, 볼바를 활용하여 측정하고 있다.^17-19 작업영역 확장을 위한 축(확장축)과 연결된 가공 로봇의 경우, 전 작업영역에서의 정확도를 확보하기 위해 확장축과 로봇좌표계의 정렬 작업이 필요하다. 단일 기계에 대한 기하학적 오차를 측정하는 방법은 많이 알려져 있지만, 확장축과 연결된 로봇의 위치 종속적 오차를 측정하는 방법은 연구가 필요한 실정이다.

본 연구에서는 레이저 간섭계를 활용하여 대형 부품 가공을 위한 레이저 복합 가공 로봇의 평행도 오차를 측정하고 보정하는 방법을 소개한다. 이 로봇은 Exechon 메커니즘 기반의 병렬기구 기계(Parallel Kinematic Machine, PKM)와 2개의 작업영역 확장축을 포함하고 있다. PKM좌표계의 기구학적 구동축과 2개의 확장축 간의 평행도 오차는 4개의 직각도 오차를 측정 및 보정하여 개선한다. 확장축과 PKM 간의 직각도 오차는 (1) 평행한 두 축의 진직도 측정, (2) 면대각 거리오차 측정을 기반으로 추정한다. PKM은 로봇 자체의 구속 운동이 있어 레이저 측정용 광학계 정렬이 변동되기 때문에, 구속 운동이 발생하는 PKM 이동축과 확장축 간의 평행도는 직접 측정이 어렵다. 따라서, 면대각 거리오차로부터 직각도를 추정한다. 평행도 오차 보정은 추정된 직각도 반영하여 기준좌표계에 대한 PKM 기본좌표계 조정을 통해 실시한다. 2장에서는 확장축과 PKM이 결합된 대형 체적 가공 로봇의 기하학적 오차 및 기구학 모델을 소개한다. 3장에서는 레이저 간섭계를 활용하여 병렬 기구 로봇과 확장 축과의 직각도 오차를 측정 방법을 제시하고, 평행도 오차 보정 방법을 제안한다. 4장에서는 레이저 복합 가공이 가능한 대형 체적 가공 로봇에서의 실험 결과를 통해 제안한 방법을 검증한다.

2. 대형 체적 가공을 위한 로봇의 기구학 모델

2.1 기계 구조

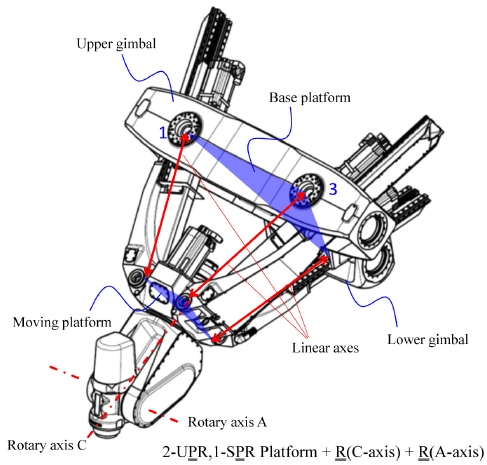
Exechon 메커니즘의 병렬 기구 기계는 Fig. 1과 같이 직선 축 3개가 병렬로 결합된 구동 플랫폼에 2개의 회전축이 직렬로 연결되어 있는 구조이다. 상부 외부 짐벌(Upper Outer Gimbal) 회전축과 1, 3번 회전 조인트의 회전축의 교차점, 하부 짐벌(Lower Gimbal) 회전축과 2번 회전 조인트 회전축의 교차점은 기계 구동 중 고정된 위치에 있다. 3개의 교차점으로 이뤄진 평면을 기저 플랫폼(Base Platform)으로 설정한다. 공구의 이동경로를 고려하여 기저플랫폼 좌표계에 대한 공구좌표계(Tool Coordinate System)를 역기구학을 통해 산출하여 PKM 각 축을 구동한다. 대형 체적 가공 로봇은 확장축을 활용하여 PKM을 직접 이동시키거나, 작업테이블(Work Table)을 이동시켜 작업영역을 확장한다. 이 연구에서는 대형 부품 가공을 위해 x-, y-방향 확장축을 구비한 PKM을 예시 구조로 설명한다. 확장축 X2는 PKM을 장착하여 PKM의 x-방향 작업공간을 확장한다. 확장축 Y2는 작업테이블을 장착하여 PKM과의 상대 운동에 의한 y-방향 작업공간을 확장하는 역할을 한다.

Fig. 1

Structural configuration of the parallel kinematic machine (PKM)

2.2 기구학 체인과 오차 모델

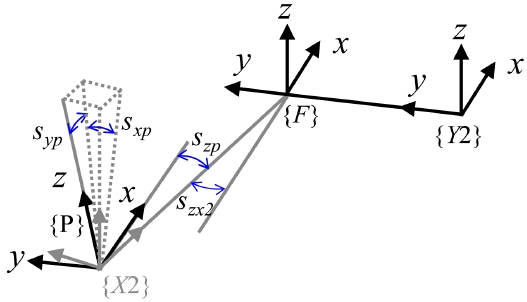
PKM의 기구학은 Bi²⁰ 등에 의해 연구되었다. 대형부품 가공 로봇의 기구학 모델을 수립하기 위하여 각 로컬좌표계는 Fig. 2와 같이 설정한다. 기준좌표계 원점은 PKM, X2-축, Y2-축이 원점일 때, 공구 중심점(Tool Center Point, TCP)에 설정한다. 그리고, 기준좌표계의 y-방향을 Y2-축 방향으로 설정하면, 기구학 체인은 동차변환 행렬(Homogeneous Transformation Matrix, HTM)으로 다음과 같이 나타낼 수 있다.

Fig. 2

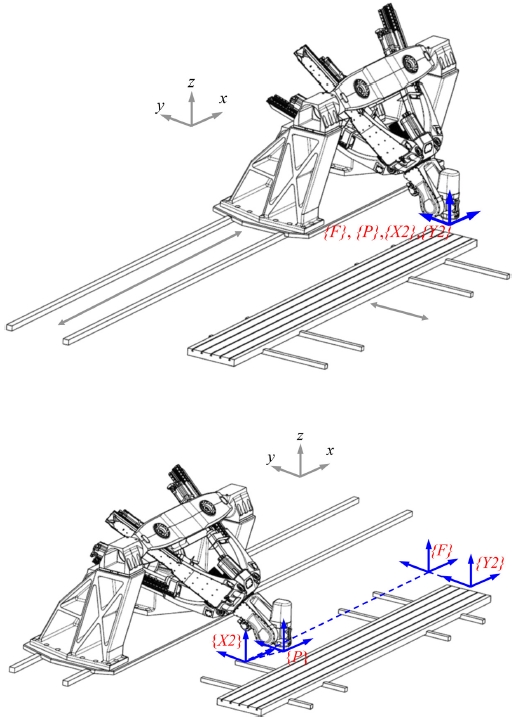
Coordinate systems of the large volume laser machining robot for (top) initial position, (bottom) temporary position

$\[ {{}^{F}T}_{Y2}{{}^{Y2}T}_w{}^w{T}_t={}^F{T}_{X2}{}^{X2}{T}_P{}^P{T}_t \]$

(1)

여기서, ^AT_B는 A좌표계에 대한 B좌표계의 좌표변환을 나타내는 4 × 4 행렬이다. F, P, w, t는 기준좌표계, PKM좌표계, 공작물좌표계, 공구좌표계를 의미한다.

원점 설정 정의에 따라 각 로컬좌표계 간의 오프셋 오차는 고려하지 않는다. PKM은 일반 직렬 3축 기계와는 달리, 물리적 직선축이 아닌 기구학적 직선 3축으로 표현한다. PKM, X2-축, Y2-축은 각 구동 위치에서 6자유도의 위치 종속적 기하학적 오차(Position Dependent Geometric Error, PDGE)가 발생한다. PKM의 PDGE는 단 방향 구동에도 모든 구동축이 구속되어 움직이기 때문에 3차원 좌표에서 고려해야 한다. 기준좌표계의 y-방향을 Y2-좌표계의 y-방향으로 설정하면, X2-좌표계는 불완전한 조립으로 인하여 기준좌표계(Reference Coordinate System)에 대한 위치독립적 기하학적 오차(Position Independent Geometric Error, PIGE)인 직각도 오차(Squareness Error)를 포함한다. Y2-축과 X2-축에 의해 기준좌표계의 z-방향이 결정된다. X2-좌표계에 대한 P-좌표계의 PIGE는 3개의 직각도 오차로 Fig. 3과 같이 표현할 수 있다. HTM을 활용하여 표현한 각 로컬좌표계 간의 관계는 다음 식(2)과 같다.

Fig. 3

Position independent geometric errors of the large volume laser machining robot

$\[ \begin{array}{l}{F}_{T_{Y2}}=\left(\begin{array}{cccc}1& -{\epsilon }_{zy2}& {\epsilon }_{yy2}& {\delta }_{xy2}\\ {\epsilon }_{zy2}& 1& -{\epsilon }_{xy2}& y2+{\delta }_{yy2}\\ -{\epsilon }_{yy2}& {\epsilon }_{xy2}& 1& {\delta }_{zy2}\\ 0& 0& 0& 1\end{array}\right),\\ F_{T_{X2}}=\left(\begin{array}{cccc}1& -s_{zx2}-{\epsilon }_{zx2}& {\epsilon }_{yx2}& x2+{\delta }_{xx2}\\ s_{zx2}+{\epsilon }_{zx2}& 1& -s_{xx}-{\epsilon }_{xx2}& {\delta }_{yx2}\\ -{\epsilon }_{yy2}& s_{xx}+{\epsilon }_{xx2}& 1& {\delta }_{zx2}\\ 0& 0& 0& 1\end{array}\right),\\ X{2}_{T_P}=\left(\begin{array}{cccc}1& -s_{zP}-{\epsilon }_{zP}& s_{yP}+{\epsilon }_{yP}& x+{\delta }_{xP}\\ s_{zP}+{\epsilon }_{zP}& 1& -s_{xP}-{\epsilon }_{xP}& y+{\delta }_{yP}\\ -s_{yP}-{\epsilon }_{yP}& s_{xP}+{\epsilon }_{xP}& 1& z+{\delta }_{zP}\\ 0& 0& 0& 1\end{array}\right),\\ {P_T}_t=\left(\begin{array}{cc}I& \mathbf{t}\\ 0& 1\end{array}\right),\mathbf{t}={\left(\begin{array}{ccc}tx& ty& tz\end{array}\right)}^T, Y{2}_{T_W=}\left(\begin{array}{cc}I& 0\\ 0& 1\end{array}\right).\end{array} \]$

(2)

여기서, d_ij는 j-좌표계의 i방향 위치오차를 의미하고, e_ij는 j-좌표계의 i방향 각도오차를 의미한다. 직각도 s_zx2는 X2-축과 Y2-축이 직각에서 벗어난 정도로 나타내며, X2-좌표계가 Y2-좌표계의 z-방향으로 일정 각도의 회전오차로 표현한다. s_xp, s_yp, s_zp는 X2-좌표계에 대한 P-좌표계의 3방향 직각도 오차를 의미한다.

기하학적 오차에 의한 체적오차 Δp는 기구학 체인으로부터 다음 식(3)과 같은 좌표변환으로 계산한다.

$\[ \begin{array}{l}{}^w{T}_t={\left({}^F{T}_{Y2}{}^{Y2}{T}_w\right)}^{-1}{}^F{T}_{X2}{}^{X2}{T}_P{}^P{T}_t,\\ where, {}^w{T}_t=\left(\begin{array}{cc}{}^w{R}_t& \mathbf{p}\\ 0& 1\end{array}\right),\\ ∆\mathbf{p}=\mathbf{p}-\overline{\mathbf{p}}={\left(\begin{array}{ccc}∆\mathit{x}& ∆\mathit{y}& ∆\mathit{z}\end{array}\right)}^{\mathrm{T}},\overline{\mathbf{p}}={\left(\begin{array}{ccc}\mathit{x}& \mathit{y}& \mathit{z}\end{array}\right)}^{\mathrm{T}}.\end{array} \]$

(3)

여기서, $$ \overline{\text{p}}$$, p는 공칭위치와 오차가 포함된 위치를 의미한다.

3. 레이저 간섭계를 활용한 평행도 오차 측정과 직각도 오차 추정

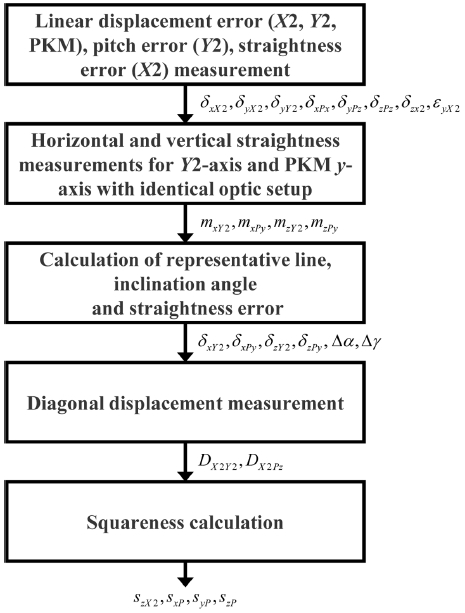
본 논문에서는 PKM과 확장축 간 평행도 오차를 유발하는 주요인인 직각도를 측정 및 보상하여 평행도 오차를 보정하는 방법을 제안한다. 대형 체적 가공 로봇의 PKM과 확장축 좌표계 간 직각도 오차는 평행한 두 축 구동에 의한 진직도 측정, 대각거리오차 측정을 활용하여 추정할 수 있다. 일반 직선3축 기계의 직각도 측정은 레이저 간섭계, 볼바, 마스터 등을 활용하여 대각 측정으로 측정하는 방법이 연구되어 왔다.^17,19,21 PDGEs 측정 데이터와 면대각 거리오차 측정 데이터를 활용하면, 광학 스퀘어(Optical Square)없이도 정확한 직각도를 측정할 수 있다. 확장축과 동일한 방향으로 구동하는 PKM 축은 진직도 측정만으로 간단하게 직각도를 측정할 수 있다. 따라서, 효율적인 직각도 추정을 위한 직각도 측정 절차는 진직도 및 대각거리 측정을 통해 Fig. 4와 같고, 측정된 직각도를 보상하여 평행도 오차 보정을 수행한다.

Fig. 4

Squareness measurement procedure based on the straightness and diagonal displacement measurement

3.1 진직도 측정을 활용한 평행도 오차 측정

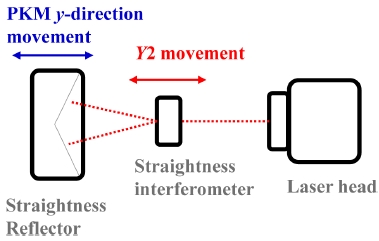
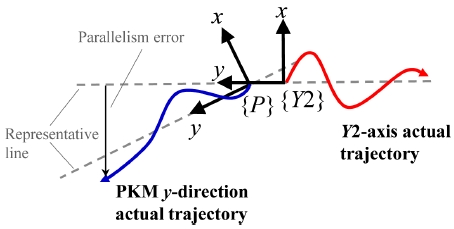
평행도 오차는 기준축에 대하여 평행해야 하는 한 축이 벗어난 정도를 나타내는 척도이며, 레이저 간섭계의 진직도 측정을 통해서 산출할 수 있다. Fig. 5와 같이 Y2-축에 대한 레이저 빔 정렬 및 수평/수직 진직도를 측정하여 데이터 m_xY2, m_zY2를 취득한다. 빔 정렬을 유지한 상태로 PKM의 y-방향(PY-축) 구동을 통해 수평/수직 진직도 측정 데이터 m_xPy, m_zPy를 취득한다. PY-축의 Y2-축에 대한 평행도 오차는 Fig. 6과 같이 Y2-축 진직도 측정 데이터의 대표 직선으로부터 벗어난 위치오차이다. 양끝점 또는 최소자승직선으로 m_xY2, m_zY2의 대표직선 기울기(γ_Y2, α_Y2)를 계산한 후, m_xPy, m_zPy에서 대표직선을 제거하면 다음과 같이 Y2-축에 대한 PY-축의 x, z-방향 평행도 오차 e_xPy, e_zPy가 계산된다.

Fig. 5

Parallelism error measurement via straightness measurement of the laser interferometer

Fig. 6

Parallelism error and representative lines of two straightness measurements

$\[ \begin{array}{c}{e}_{xPy}\left(Py\right)=m_{xPy}\left(Py\right)-{\gamma }_{Y2}\times Py,\\ e_{zPy}\left(Py\right)=m_{zPy}\left(Py\right)-{\alpha }_{Y2}\times Py.\end{array} \]$

(4)

m_xPy, m_zPy의 대표직선 기울기(γ_Py, α_Py)를 계산하면, 두 대표직선 간의 기울기 차이는 Δγ, Δα가 되고, 이 값은 직각도 계산에 사용된다. Exechon 메커니즘의 PKM의 경우 x-방향 구동 시에 구속 운동으로 인해 스핀들 축 방향이 종속적으로 회전하게 되며, 이는 진직도 광학계의 정렬이 벗어나도록 한다. 따라서, 평행도 오차를 직관적으로 측정하기 어렵다.

4. 실험

제안한 방법 검증을 위하여, 실험은 Table 1과 같이 대형부품의 레이저 공정 및 절삭 가공용으로 사용되고 있는 맥스로텍 社의 PKM 로봇 MXT700S 모델(Fig. 7)의 평행도 오차를 대상으로 실시하였다. 평행도 및 직각도 측정을 위해 Renishaw 社의 XL-80과 거리측정, 진직도 측정, 각도측정 광학계를 사용하였다. 모든 측정 데이터에 포함된 아베 오차는 기 측정된 각도오차 데이터와 아베 오프셋 값을 활용하여 계산하였고 측정 데이터로부터 제거하였다.

Table 1

Specification of the measured machine and measuring instrument

Fig. 7

Experimental setup for measuring the PDGEs

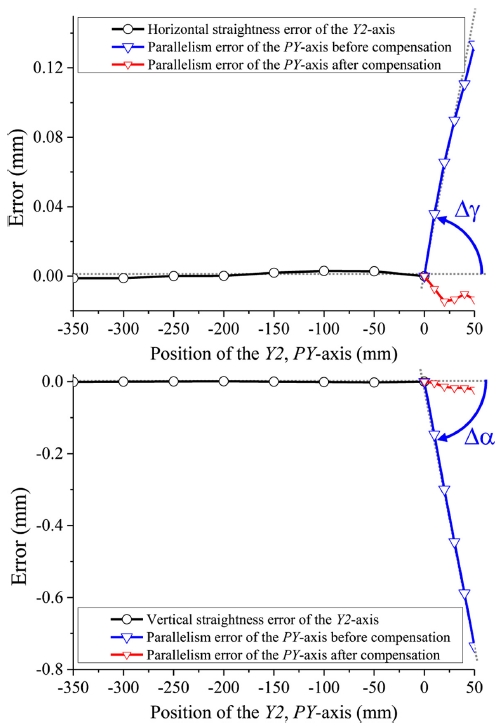
Y2-축과 PY-축의 평행도 오차는 Fig. 8과 같이 동일한 설치 조건의 진직도 측정을 통해서 Fig. 10과 같이 측정되었다. Y2-축은 0~-350 mm 구간에서 측정을 실시 하였으며, PY-축의 경우 평행도 오차가 진직도 측정 범위를 벗어나지 않도록 0~50 mm 구간에 제한하여 측정을 실시하였다. 수평 진직도 측정에서 x-방향의 평행도 오차는 0.133 mm였고, PY-축과 Y2-축의 대표직선 기울기 차이 Δγ는 2.81 mrad으로 측정되었다. 수직 진직도 측정에서 y-방향 평행도 오차는 -0.735 mm였고, 대표직선 기울기 차이 Δα는 -14.7 mrad으로 측정되었다. 3장에서 언급한 바와 같이 PKM의 x-방향 구동 시에 구속 운동으로 인해 진직도 측정 광학계 정렬이 틀어지기 때문에 X2-축과 PX축의 평행도 오차는 측정할 수 없었다.

Fig. 8

Parallelism error measurement using the straightness measurement optics

Fig. 9

Face diagonal displacement measurement (DX2PZ) for estimating the squareness error

Fig. 10

Straightness error and parallelism error before/after squareness error compensation

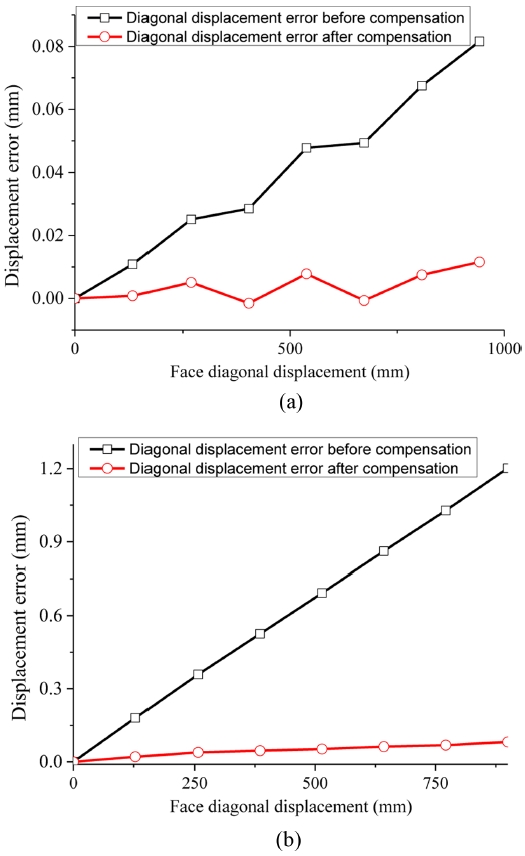
4개의 직각도 측정하기 위해, 면대각 거리측정 실험을 실시하였다. 먼저, 직각도 추정에 필요한 각 축의 PDGEs는 Table 2와 같이 측정하였다. 모든 측정은 3회 반복, 왕복으로 수행하였고, 결과는 평균 값으로 표시하였다. 면대각 거리 D_X2Y2는 X2와 Y2-축 구동을 통해 측정하였고, Fig. 11(a)와 같이 최대 0.082 mm의 거리오차가 확인되었다. 직각도 s_zX2는 -0.034 mrad으로 계산되었다. 면대각 거리 D_X2PZ는 직각도 s_yP를 추정하기 위해 Fig. 9와 같은 광학계 설치를 통해서 측정하였으며, Fig. 11(b)와 같이 최대 1.216 mm의 거리오차가 있었다. 추정된 직각도는 s_yP 4.35 mrad이다. 앞서 측정한 평행도 오차 데이터로부터 나머지 직각도 s_xP, s_zP는 각 -14.74, -2.85 mrad으로 계산되었다.

Table 2

Measured position dependent geometric errors for estimating squareness error from the face-diagonal displacement error

Fig. 11

Face-diagonal displacement errors of (a) DX2Y2 and (b) DX2PZ before/after squareness compensation

PKM의 기본좌표계를 회전변환하여 기준좌표계에 대한 PKM 좌표계 조정을 실시하였다. Y2-축에 대한 PY-축의 평행도는 Fig. 10, Table 3과 같이 x-방향은 최대 0.134 mm에서 0.014 mm로 90.4%, z-방향은 -0.735 mm에서 -0.022 mm로 97% 감소함을 확인하였다. X2-축에 대한 PX-축의 평행도는 PKM의 구속 운동으로 직접적으로 진직도 측정을 통해 확인할 수 없기 때문에, 면대각 거리오차 측정을 통해 X2-축과 PZ-축의 직각도 오차가 보정됨을 확인하였다. 면대각 거리오차 ΔD_X2PZ는 보정 전 1.216 mm에서 0.082 mm로 93% 줄어들었다. X2-축과 Y2-축의 직각도 오차는 G-code 보정을 통해서 실시하였고, 면대각 거리오차는 보정 전 0.082 mm에서 보정 후 0.011 mm로 87% 줄어든 것을 확인하였다. PKM 자체의 정확도가 개선되면, 더 정확한 보정 결과가 예상된다.

Table 3

Parallelism errors and diagonal displacement errors w/wo the squareness error compensation

5. 결론

본 논문에서는 대형 체적 가공이 가능한 레이저 복합 가공용 로봇의 PKM과 작업영역 확장을 위해 추가된 확장축 간의 평행도 오차 측정 및 보정 방법을 제안하였고 결론은 다음과 같다.

(1) 레이저 간섭계의 진직도 측정을 활용하여 확장축과 평행한 PKM 축간의 평행도 오차를 측정하고, 직각도 산출에 사용

(2) 진직도 측정을 활용하면 간편하게 직각도를 산출할 수 있으며, 구속 운동으로 PKM의 x-방향 진직도는 레이저 간섭계로 측정이 어렵기 때문에, 대각거리 오차 측정을 통해 직각도를 추정

(3) 추정된 PKM의 3개 직각도 오차는 기준좌표계에 대한 기본좌표계에 반영하여 좌표변환으로 보상하고, 평행도 오차가 보정됨

(4) 평행도 오차 보정을 통해 대형부품의 형상 정확도를 향상시킬 수 있고, PKM 자체 오차의 개선을 통해서 더 정확한 평행도 오차 보정 가능

Acknowledgments

이 논문은 2018학년도 경북대학교 연구년 교수 연구비에 의하여 연구되었음.

REFERENCES

• Brunete, A., Gambao, E., Koskinen J., Heikkila, T., Kaldestad, K. B., et al., “Hard Material Small-Batch Industrial Machining Robot,” Robotics and Computer-Integrated Manufacturing, Vol. 54, pp. 185-199, 2018. [https://doi.org/10.1016/j.rcim.2017.11.004]
• Barnfather, J. D., Goodfellow, M. J., and Abram, T., “A Performance Evaluation Methodology for Robotic Machine Tools used in Large Volume Manufacturing,” Robotics and Computer-Integrated Manufacturing, Vol. 37, pp. 49-56, 2016. [https://doi.org/10.1016/j.rcim.2015.06.002]
• Neugebauer, R., Schwaar, M., Pritschow, G., Eppler, C., and Garber, T., “New Approaches to Machine Structures to Overcome the Limits of Classical Parallel Structures,” CIRP Annals, Vol. 51, No. 1, pp. 293-296, 2002. [https://doi.org/10.1016/S0007-8506(07)61520-0]
• Weck, M. and Staimer, D., “Parellel Kinematic Machine Tools – Current State and Future Potentials,” CIRP Annals, Vol. 51, No. 2, pp. 671-683, 2002. [https://doi.org/10.1016/S0007-8506(07)61706-5]
• Pritschow, G., “Parallel Kinematic Machines (PKM) – Limitation and New Solutions,” CIRP Annals, Vol. 49, No. 1, pp. 275-280, 2000. [https://doi.org/10.1016/S0007-8506(07)62945-X]
• Lee, M. K., Kim, T. S., and Park, K. W., “Study on Kinematic Calibration of a Parallel-typed Machining Center Tool,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 26, No. 11, pp. 2237-2244, 2002. [https://doi.org/10.3795/KSME-A.2002.26.11.2237]
• Kanaan, D., Wenger, P., and Chablat, D., “Kinematic Analysis of a Serial-parallel Machine Tool: The VERNE Machine,” Mechanism and Machine Theory, Vol. 44, No. 2, pp. 487-498, 2009. [https://doi.org/10.1016/j.mechmachtheory.2008.03.002]
• Son, S., Kim, T., Sarma, S. E., and Slocum, A., “A Hybrid 5-Axis CNC Milling Machine,” Vol. 33, No. 4, pp. 430-446, 2009. [https://doi.org/10.1016/j.precisioneng.2008.12.001]
• Tian, W., Yin, F., Liu, H., Li, J., Li, Q., et al., “Kinematic Calibration of a 3-DOF Spindle Head Using a Double Ball Bar,” Mechanism and Machine Theory, Vol. 102, pp. 167-178, 2016. [https://doi.org/10.1016/j.mechmachtheory.2016.04.008]
• Neumann, K. E., “Parallel-Kinematical Machine,” US Patent, 8783127 B2, 2009.
• Jin, Y., Bi, Z. M., Liu, H. T., Higgins, C., Price, M., et al., “Kinematic Analysis and Dimensional Synthesis of Exechon Parallel Kinematic Machine for Large Volume Machining,” Journal of Mechanisms and Robotics, Vol. 7, No. 4, Paper No. 041004, 2015. [https://doi.org/10.1115/1.4029499]
• Bi, Z. M., “Kinetostatic Modeling of Exechon Parallel Kinematic Machine for Stiffness Analysis,” The International Journal of Advanced Manufacturing Technology, Vol. 71, Nos. 1-4, pp. 325-335, 2014. [https://doi.org/10.1007/s00170-013-5482-z]
• Kim, T., Kim S., Nah, S., and Kim, K., “Design of a Machine Tool Containing a 3-Strut Parallel Kinematic Structure,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 8. pp. 878-885, 2011.
• Bi, Z. M. and Wang, L., “Optimization of Machining Processes from the Perspective of Energy Consumption: A Case Study,” Journal of Manufacturing Systems, Vol. 31, No. 4, pp. 420-428, 2012. [https://doi.org/10.1016/j.jmsy.2012.07.002]
• Schwenke, H., Knapp, W., Haitjema, H., Wecken-Mann, A., Schmitt, R., et al., “Geometric Error Measurement and Compensation of Machines-An Update,” CIRP Annals, Vol. 57, No. 2, pp. 660-675, 2008. [https://doi.org/10.1016/j.cirp.2008.09.008]
• Mayr, J., Jedrzejewski, J., Uhlmann, E., Donmez, M. A., Knapp, W., et al., “Thermal Issues in Machine Tools,” CIRP Annals, Vol. 61, No. 2, pp. 771-791, 2012. [https://doi.org/10.1016/j.cirp.2012.05.008]
• Lee, H., Lee, D., and Yang, S., “Squareness Estimation for Coordinate Measuring Machine using the Laser Interferometer based on the Face-Diagonal Method,” Journal of the Korean Society Precision Engineering, Vol. 33, No. 4, pp. 295-301, 2016. [https://doi.org/10.7736/KSPE.2016.33.4.295]
• Lee, H., Son, J., and Yang, S., “Techniques for Measuring and Compensating for Servo Mismatch in Machine Tools Using a Laser Tracker,” The International Journal of Advanced Manufacturing Technology, Vol. 92, Nos. 5-8, pp. 2919-2928, 2017. [https://doi.org/10.1007/s00170-017-0382-2]
• Yang, S.-H., Lee, H.-H., and Lee, K.-I., “Face-And Body-Diagonal Length Tests Using a Double Ball-Bar for Squareness Errors of Machine Tools,” International Journal of Precision Engineering and Manufacturing, Vol. 19, No. 7, pp. 1039-1045, 2018. [https://doi.org/10.1007/s12541-018-0123-y]
• Bi, Z. M. and Jin, Y., “Kinematic Modeling of Exechon Parallel Kinematic Machine,” Robotics and Computer-Integrated Manufacturing, Vol. 27, No. 1, pp. 186-193, 2011. [https://doi.org/10.1016/j.rcim.2010.07.006]
• Kruth, J. P., Zhou, L., Bergh, C. V., and Vanherck, P., “A Method for Squareness Error Verification on a Coordinate Measuring Machine,” The International Journal of Advanced Manufacturing Technology, Vol. 21, Nos. 10-11, pp. 874-878, 2003. [https://doi.org/10.1007/s00170-002-1408-x]