반경-축 방향 링 롤링 공정의 정의 및 제어를 위한 분석적인 접근법

1. 서론

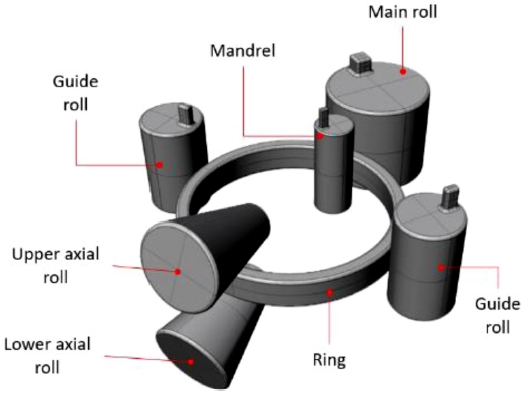
링 롤링이란 이음매 없는 링모양의 제품을 만드는 공정을 말한다. 링 롤링으로 생산할 수 있는 제품은 기차 바퀴, 우주 항공 부품 및 마찰 방지 베어링, 자동차 바퀴용 외륜 등과 같은 여러 산업 분야의 제품 제작에 사용되고 있다.¹ 링 롤링 공정의 복잡성으로 인해 높은 치수의 정확도와 우수한 기계적 성질을 가진제품을 생산하기 위해서는 계획 및 선행 연구가 수행되어야 한다.² 문헌에서 몇몇 연구자들은 링의 확장과 같은 중요한 제어에 대한 공정 변수의 영향을 이해하기 위한 목적으로 수치적 관점에서 링 롤링 공정 Fig. 1의 분석에 관심을 기울였다.

Fig. 1

Schematic representation of the radial-axial ring rolling process

Qian et al.³ 및 Zhou et al.⁴는 ABAQUS의 3차원 열-역학적(Thermo-Mechanical) 수치모델을 개발하고, 반경-축 방향의 링 롤링 공정에서의 링 및 롤 크기의 영향을 실험과 높은 일치성을 보임으로 검증하였다. 그 외에도 Zhou et al.⁵는 크기가 큰 스틸링에 대하여 링의 확장과 공정 하중을 예측할 때 제안한 모델을 실험결과와 비교하여 검증함으로써 신뢰성을 입증하였다.

Wang et al.⁶은 롤링 시간을 단축하기 위하여 링 롤링 과정을 먼저 최적화한 통합 수치모델을 제시한 다음 최적화된 공정 조건을 이용하여 자체 시뮬레이션 했다. 개발된 수치모델 결과를 티타늄 합금 링에 관한 문헌의 결과와 비교하여 일치성을 검증하였다. 뿐만 아니라, Qian et al.⁷는 링의 제작에 필요한 단조 및 피어싱(Piercing) 공정을 포함한 링 압연 공정의 전체적인 분석을 위해 상업용 소프트웨어인 Simufact Forming 14를 사용하여 수치모델을 개발하였다. 연구 결과 링의 변형률, 온도 및 응력 분포의 불균일성이 링 압연 공정에서 링의 최종 결정립 크기 및 기계적 성질과 상관 관계가 있음을 입증하였다.

롤과 링 사이의 복잡한 열-기계적 상호 작용으로 인하여 해석 시간은 항상 반경-축 방향 링 롤링 공정의 연구를 위해 개발된 수치모델에서 큰 취약점이 된다. 이를 위해 일부 저자들은 전체적인 계산 시간 단축에 주목했다.

Davey and Ward⁸, Kim et al.⁹은 실제로 변형이 일어나고 있는 링의 국소영역에만 Fine Mesh를 나머지 영역에서는 Rough Mesh를 사용하는 Dual-Mesh 시스템을 소개하였다.

Davey and Ward⁸은 반경-축 방향 링 롤링의 경우 모델에 Mesh를 생성하는데 필요한 노드의 수를 17.5%로 감소시켰고 반경 방향 링 롤링의 경우 25%까지 감소시켰다. 이에 따라 ALE(Augmented Lagrangial-Eulerin) 업데이트 방법과 함께 Dual-Mesh 시스템의 적용은 계산 시간을 단축할 수 있다는 명백한 이점을 제공하였다. 또한 Kim et al.⁹에서 Fine-Course Dual-Mesh 방식에 대한 정확도의 편차는 링이 처음으로 세분화된 영역의 개수 관점에서 분석되어 어떻게 세분화를 해야 더 높은 정밀도 또는 계산 시간의 단축으로 이어질 지를 나타냈다. 링 롤링 수치 시뮬레이션의 계산 시간을 단축하기 위해 다른 저자들이 진행한 추가적인 방안은 Standard Material Mesh System(MMS)를 대신하여 계산 부하를 줄이는 Spatial Mesh System(SMS)를 적용하는 것이었다. Yea et al.¹⁰은 스프레드, 압력 분포 및 하중의 예측을 위해 자체 개발 프로그램인 SHAPE-RR®에 SMS/MMS 기술을 적용하였고 Kim et al.¹¹은 최적의 공정 조건을 결정하기 위해 성형 하중을 최소화하였다.

Han et al.¹²는 링의 외경이 아닌 높이의 확장에 대한 특별한 유형의 링 롤링 공정의 정의 개발이라는 실험적 관점에서 볼 때 흥미로운 연구를 진행하였다. 이 방법을 활용하여 링 높이의 185% 확장이라는 놀라운 결과를 보여주었다.

반경-축 방향 링 롤링 공정의 연구를 위한 분석모델의 개발과 관련하여 몇 가지 중요한 방법이 간략하게 수년에 걸쳐 게재되고 있다. Hua and Zhao¹³에 의해 Slip Line 분석 이론에 근거한 Feeding, Biting-In 조건이 제안되었고 그 뒤 연구결과에 근거하여 Zhou et al.⁴와 Guo et al.¹⁴는 초기 및 최종 맨드릴과 축 방향 상부 롤의 속도를 선택할 수 있는 범위를 포함한 알고리즘을 제안했다. Berti et al.¹⁵는 Zhou et al.⁴와 Guo et al.¹⁴에서 제안된 모델에서 맨드릴과 축 방향 상부 롤 모두에 대해 압축 속도 정의에 대한 필요성을 검증하고 개선하였다.

Berti et al.¹⁵에 제시된 결과에 따라 Quagliato and Berti¹⁶는 반경-축 방향 링 롤링 공정에서 링의 단면적의 3D 변형 텐서를 예측하기 위한 분석모델을 제시하였으며, 이는 링의 형상 변화에 영향을 미쳤다. 또한 Quagliato and Berti¹⁷는 전도성, 대류성 및 복사 열교환 현상의 결과로 공정 중 링의 평균 온도가 내려가는 것을 예측하기 위한 분석모델을 개발했다. Berti et al.,¹⁵ Quagliato and Berti,¹⁶ Quagliato and Berti¹⁷의 결과에 따르면 Hill¹⁸에 의해 제안된 slip line 솔루션과 Hawkyard¹⁹에 의해 반경 방향 링 롤링 공정에 적용된 소재의 활용, 특정 링 형상의 제한사항을 보여줬다. 반경-축 방향 공정에서의 하중 예측을 위한 해석 모델의 개발과 관련하여 많은 논문들의 대부분이 반경 방향 하중 예측이고 축 방향 하중에 대한 내용은 극 소수로 다루고 있다. 최근 Quagliato et al.^20,21는 CAD 해석과 Slip Line 이론에 기초한 반경-축 방향 하중의 예측을 위한 두가지 방법을 추가 개발하였으며 실험 결과와 수치 시뮬레이션의 결과를 비교하여 검증되었다.

반경-축 방향 링 롤링 공정을 위한 분석모델뿐만 아니라 수치모델 개발에도 많은 노력이 있었지만 어떠한 연구자들도 공정 중 다중선형(Multi-Linear) 맨드릴 이송속도의 변화로 인해 링의 확장에서의 영향을 연구한 바가 없다.

이를 위해 본 논문에서는 Berti et al.¹⁵의 연구를 기반으로 반경-축 방향 링 롤링 공정동안 맨드릴 이송속도의 다양한 변화에 따른 플랫 링의 확장을 예측하기 위한 분석적인 알고리즘을 정의하는 것을 목표로 한다. 링의 확장 단계에서 맨드릴의 이송속도의 변화는 D(t) 곡선의 기울기의 변화를 가져온다. 여기에서 D는 링의 외경이다. 링의 비정상적 확장은 다음과 같은 여러 요인와 관련이 있다.

(1) 공정 초기에 의도적으로 느린 이송속도로 진행 후 특정 시점에서 빠른 이송속도로 변화.

(2) 공정 초기에 의도적으로 높은 이송속도로 진행 후 특정 시점에서 느린 이송속도로 변화.

(3) 일정한 맨드릴 이송속도에서 링의 점진적 혹은 급진적인 온도 변화에 따른 링 확장의 변화.

이 외에도, 공정 중에 발생할 수 있는 링과 롤 사이의 슬립현상을 보다 잘 예측하기 위해, 윤활 조건을 링의 시간에 따른 확장 속도와 관련시키는 방법도 제안하였다. 이 제안된 기능의 목적은 링과 롤 사이의 슬립현상으로 인한 링 확장에서 지연되는 부분을 계산하는 것이다. 슬립현상은 링 롤링 공정에서 일반적으로 존재하지만 수치 시뮬레이션으로는 예측하기가 어렵다.

이후 결과에서 볼 수 있듯이 제안된 형상 예측 알고리즘은 링의 확장 단계에서 맨드릴 이송속도가 여러 번의 변화가 있는 경우에도 링의 확장을 정확하게 예측할 수 있다.

2. 분석 모델 정의

앞서 언급한 바와 같이 제안된 알고리즘은 Berti et al.¹⁵에서 진행된 연구를 기반으로 하며, 다음 두가지 중요한 주제가 설명된다.

(1) 메인 롤(Main-Roll) 회전속도, 맨드릴(Mandrel)과 축 방향 상부 롤(Upper Axial Roll)의 이송속도, 축 방향 롤의 회전속도.

(2) 단일 맨드릴 이송속도를 위해 개발된 링 형상 예측 알고리즘.

이번 장의 다음 두 절에서는 Berti et al.¹⁵에서 정의된 공정 매개 변수 및 링 형상 예측 방법에 대하여 요약을 하였다. 이후 2.3절에서는 확장 단계 중 맨드릴 이송속도가 변화하는 경우 링의 확장 예측을 위한 새롭게 정의된 알고리즘을 제시하였다.

2.1 롤의 공정변수 정의

이 절에서는 맨드릴, 축 방향 상부 롤의 이송속도 및 메인 롤 회전 속도의 선택 범위를 결정하기 위한 식은 형상 예측 방식의 배경을 더 잘 이해할 수 있도록 요약된다.

메인 롤의 회전 속도와 관련하여, Zhou et al.⁴는 공정 중에 안정성을 확인하기 위하여 식(1)에서 메인 롤의 반경 R_R와 회전속도 ω_R를 활용하였다. 이 식은 공학 계산보다는 경험에 근거하고 있지만 이전의 여러 저자의 연구에서 입증된 것처럼 균일한 링의 확장을 얻을 수 있다.

$\[ \frac{400}{R_R}\le {\omega }_R\le \frac{1600}{R_R} \]$

(1)

맨드릴 이송속도와 관련하여 Berti et al.¹⁵에서처럼 두 개의 다른 범위가 정의되어야 한다. 식(2)는 공정 중 초기 이송속도의 범위, 식(3)은 최종 속도의 범위이다. Berti et al.¹⁵에서 제안된 것처럼 이 범위안에서 두 속도를 선택한 후에 선택된 맨드릴 이송속도는 선형적으로 감소되어야 하고 링은 균일한 확장을 해야 한다.

(2)

(3)

$$ K_1=\frac{1}{R_R}+\frac{1}{R_M},K_2=\frac{1}{R_r}+\frac{1}{R_M}+\frac{1}{R_0}-\frac{1}{r_0},K_3=\frac{1}{R_r}+\frac{1}{R_M}+\frac{1}{R_F}-\frac{1}{r_F}$$이며 각각 링 롤링 공정, 초기 형상, 최종 형상의 변수로 정의된다. R_R, R_M은 각각 메인 롤, 맨드릴의 반경을 의미한다.

식(2)과 식(3)는 Penetration(왼쪽 항)과 Biting-In(오른쪽 항) 조건을 기반으로 하며, 이는 차례로 변형하는 동안 링의 부분에서 발생하는 소성 변형장을 기반으로 한다. 맨드릴 이송속도의 초기 및 최종 범위안에서 선택한 이송속도에 따라서 축 방향 상부 롤의 이송속도도 마찬가지로 초기 및 최종 범위가 동일하게 Keaton’s Rule²²를 사용하여 정의될 수 있으며, 결과적으로 식(4), 식(5)와 같다.

(4)

(5)

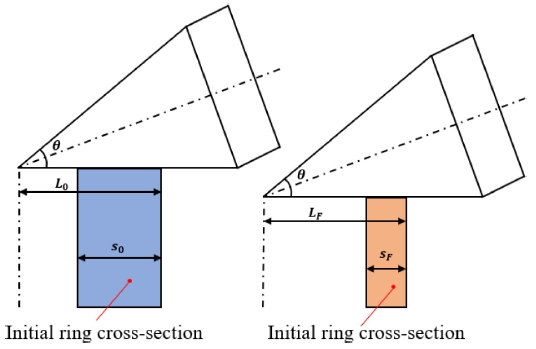
식(2)부터 식(5)까지, R₀, r₀, h₀는 초기 링의 바깥반경, 안쪽반경, 높이이고 R_F, r_F, h_F는 최종 링의 바깥반경, 안쪽반경, 높이이다. β_R와 β_A는 맨드릴과 메인 롤사이 마찰각과 축 방향 롤사이의 마찰각을 각각 나타낸다. 마지막으로 식(4) 및 식(5)에서, L₀, L_F, s₀, s_F와 θ는 Fig. 2와 같이 정의된다.

Fig. 2

Axial roll-ring contact variable definition

2.2 링 형상 예측 알고리즘

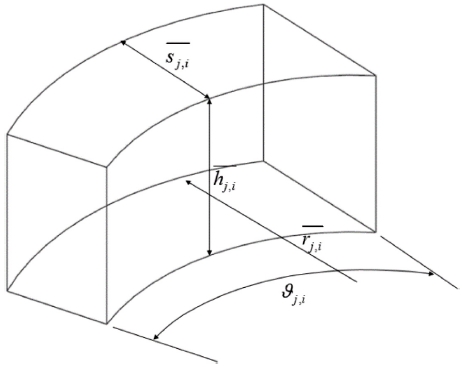
개발된 일련의 알고리즘에서 계산은 링을 여러 개로 분할한 부분에서 수행된다. 링 분할에 대한 정의는 Berti et al.¹⁵와 그 밖에 몇몇 다른 저자의 연구에 이용되었다. 링의 원주 방향으로 분할하였으며, 몇 개로 분할할 것인지를 선택할 수 있다. 분할된 링 조각은 Fig. 3에 나타냈으며 여기서 첨자 “i”는 라운드(공정 중 링의 한바퀴 회전)수를 “j”는 i-라운드에서의 분할된 링의 조각 번호를 의미한다. 이후로 분할된 링 조각을 조각이라 명명하도록 한다.

Fig. 3

Slice concept and parameters

링 형상 예측의 시작점은 식(6)과 같이 맨드릴 이송속도 식으로 나타낸다. 여기서 t_M은 실제 맨드릴 롤링시간을 나타내며, t는 일반적인 시간 변수이다. 또한 식(6)을 활용하여 시간이 지남에 따른 링의 두께는 식(7)로 계산할 수 있다.

$\[ v_M\left(t\right)={\left[v_M\right]}_0+\left(\frac{{\left[v_M\right]}_F-{\left[v_M\right]}_0}{t_M}\right)t \]$

(6)

$\[ \begin{array}{c}{s}_j\left(t\right)={\text{s}}_{\text{0}}-\underset{0}{\overset{t_j}{\int }}{v}_M\left(t\right)dt\hfill \\ ={\text{s}}_{\text{0}}\left[\left(\frac{{\left[v_M\right]}_F-{\left[v_M\right]}_0}{t_{cycle-M}}\right)\frac{{t_j}^2}{2}+{\left[v_M\right]}_0{t}_j\right]\hfill \end{array} \]$

(7)

링의 초기 형상에 기초하여 링과 롤 사이에 슬립현상이 없다고 가정하면, 공정의 첫 번째 라운드에 필요한 시간 t₁은 식(8)과 같이 계산될 수 있다.

$\[ t_1=\frac{2\pi }{{\omega }_s}\frac{R_{j,0}}{R_s} \]$

(8)

Fig. 3과 같이 γ_j = δ · j로 정의된 조각에서(여기서 j = 1...n이며 δ는 조각의 분할각이다.) 링이 시계 방향으로 회전하는 경우 두 가지 현상이 발생할 수 있다. 조각이 링의 오른쪽방향에 위치하면 맨드릴-메인 롤 사이와 축 방향 롤 사이를 통과하게 된다. 그러므로 두께는 식(7)에 의해 정의된 것과 같아야 하고 높이는 Keaton’s Rule에 의해 식(9)과 같이 계산될 수 있다

$\[ h_{j,1}=\sqrt{\left({h_0}^2-{s_0}^2\right)-{s_{j,1}}^2} \]$

(9)

반면에 분할된 조각이 링의 왼쪽방향에 위치한다면, 맨드릴과 메인 롤의 사이를 통해서만 통과할 것이고, 그 결과 두께변형만이 발생한다. 이 경우 식(7)만을 사용해야 하며 링의 높이는 초기 h₀와 동일하게 유지된다.

두께와 높이를 계산한 후에 초기 분할된 모든 조각에 대해 공정(L_f,j,1)의 첫번째 라운드에서 각 조각의 Linear Length의 변화는 식(10)에 따라 계산될 수 있다. 여기서 V_j는 조각의 부피를 나타내며 $$ \overline{S_{J,i}}$$와 h_j,i는 j-조각의 평균 두께와 높이를 각각 나타낸다. 링의 분할의 정의에 따라, 계산에서 V_j는 일정하고 조각들은 공정 중에 다른 변형을 받을 수 있지만 계산의 시작과 끝 사이에는 차이가 없는 것으로 간주된다.

$\[ L_{f,j,i}=\frac{V_{j,0}}{\overline{s_{J,i}}\cdot \overline{h_{J,i}}} \]$

(10)

원칙적으로 각 조각의 오른쪽과 왼쪽면은 반경-축 방향 링 롤링 공정의 특성으로 인해 다른 변형을 받는다.

각 조각의 평균 반경의 계산에 필요한 첫 번째 라운드에서의 전체 링의 평균 반경은 식(11)과 같이 계산될 수 있다. 이것은 최대 반경과 최소 반경 사이의 평균을 나타낸다.

$\[ \overline{r_1}=\frac{{\sum }_{j=1}^n{L}_{f,j,i}}{2\pi } \]$

(11)

최대값은 $$ \overline{r_{1,\text{max}}}=2\overline{r_1}-r_0$$로 계산되고, 최소값 중 하나는 링의 평균 반경으로 정의되며 $$ \overline{r_{1,mm}}=\overline{r_0}=\left(R_0+r_0\right)/2$$로 계산된다. 공정 중에 링 반경이 일정하지 않은 것은 링 롤링 공정 특성에 대한 영향이며 원칙적으로 공정 전후의 조각 형상은 다르다.

마지막으로 링의 각 조각의 평균 반경은 링의 위치와 두께 및 높이에 따라 식(12)과 같이 정의된다. 여기서 $$ {\sum }_{k=1}^j{L}_{f,j,1}$$는 고려한 조각까지 모든 조각의 Linear Length의 합을 나타낸다.

$\[ \overline{r_{j,1}}=\frac{\left(\overline{r_{J,max}}-\overline{r_0}\right){\sum }_{k=1}^j{L}_{f,j,1}}{{\sum }_{k=1}^n{L}_{f,j,1}}+\overline{r_0} \]$

(12)

지금까지 요약된 알고리즘에 따르면 공정의 첫 번째 라운드의 형상만 정의되었으므로 나머지 모든 공정 라운드를 정의하기 위해선 몇 가지 사항을 추가해야 한다.

첫 번째 라운드 이후 메인 롤 방향으로 맨드릴이 점진적으로 움직여 링이 확장된다. 이에 따라, 맨드릴 롤링시간은 각 조각의 길이가 서로 다른 것을 고려하여 수정되어야 한다. 이것은 식(13)에 나타내었다. 링 외경과 메인 롤 사이의 기어비가 고려되며, 여기서 k는 교정단계를 제외한 공정 중 링의 총 라운드 수를 나타낸다.

$\[ t_i={\sum }_{i=2}^k\frac{R_{j-1,i}+R_{j,i}}{{\omega }_R{R}_R}\frac{L_{f,j,i}}{\overline{r_{J-1,i}}+\overline{r_{J,i}}} \]$

(13)

그 밖에도 i-라운드의 경우, 평균과 최대 링의 반경이 계산됨을 식(14)과 식(15)에서 보여준다. i-1라운드에서 링의 최대 반경은 $$ \overline{r_{i-1,\text{max}}}=\overline{r_{i,mm}}$$와 같이 다음 i-라운드의 최소 반경으로 정의된다.

$\[ \overline{r_i}=\frac{{\sum }_{j=1}^n{L}_{f,j,i}}{2\pi } \]$

(14)

$\[ \overline{r_{i,max}}=2\overline{r_i}-\overline{r_{i-1,max}} \]$

(15)

따라서 이전의 식(12)에서 제시된 것과 동일한 이론적 근거에 따라 각 라운드의 두번째에서 마지막 조각까지의 조각의 평균반경은 식(16)로써 예측될 수 있다.

마지막으로 링의 내경과 외경은 식(17), 식(18)으로 각각 계산된다.

$\[ \overline{r_{J,i}}=\frac{\left(\overline{r_{i,max}}-r_{i,min}\right){\sum }_{k=1}^j{L}_{f,j,1}}{{\sum }_{k=1}^n{L}_{f,j,1}}+\overline{r_{i-1,max}} \]$

(16)

$\[ r_{j,i}=\overline{r_{J,i}}-\frac{\overline{s_{J,i}}}{2} \]$

(17)

$\[ R_{j,i}=\overline{r_{J,i}}-\frac{\overline{s_{J,i}}}{2} \]$

(18)

Berti et al.¹⁵에서 정의된 바와 같이, 제시된 알고리즘은 공정 전반에 걸쳐 링 형상 확장을 계산할 수 있게 하고, 2.3절에서는 원래의 식에 대하여 개선된 점이 상세히 설명된다.

2.3 다중선형 이송속도의 링 확장 예측 알고리즘

반경-축 방향 링 롤링 공정에서는 앞서 언급했듯이 여러 개의 맨드릴 이송속도가 필요로 할 수 있다.

초기 맨드릴 이송속도 [V_M]₀로 시작하여 단일 맨드릴 이송속도만 설정하면 최종 맨드릴 이송속도 [V_M]_F는 Fig. 4(a)처럼 선형적으로 속도가 감소한다. 이에 따르면, 링 외경의 확장은 Fig. 4(b)와 같이 도식화될 수 있는데 여기서 초기 기울기는 외경의 확장단계를, 두번째 기울기는 교정단계를 나타낸다.

Fig. 4

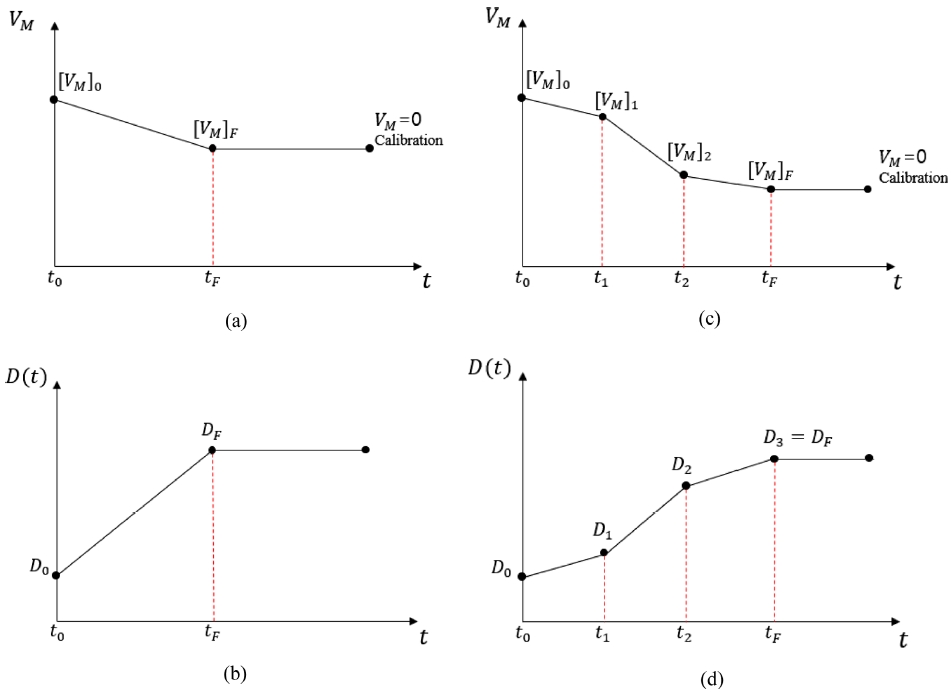
(a) Mandrel feeding speed, (b) time-based ring outer diameter expansion for single mandrel feeding speed, (c) multilinear mandrel feeding speed, and (d) consequent variation of the ring outer diameter expansion rate

또한 초기 및 최종 맨드릴 이송속도 사이에서 Fig. 4(c)과 같이 맨드릴 이송속도의 변화를 주어 시간에 따른 링의 확장에 변화를 줄 수 있다(Fig. 4(d)). 공정 중 의도적으로 이송속도의 변화를 주기도 하는데 링의 온도 변화에 의해서도 변화가 생길 수 있다. 이는 맨드릴로 인한 링의 변형량을 감소시킴으로써 궁극적으로 링의 확장 속도를 감소시킨다.

맨드릴 이송속도의 변화는 기울기가 서로 다른 확장단계를 만들며, 이송속도가 변하는 각각의 지점은 이전 맨드릴의 최종 속도와 동일하다. 실제로 맨드릴 이송속도의 값은 링의 확장속도와 관련이 있고 초기와 최종 맨드릴 이송속도 간의 차이도 링의 확장에 있어 매우 중요하다.

이를 분석하면 맨드릴 이송속도의 변화에 따라 링의 두께가 감소되는 속도의 변화하며 식(7)로부터 식(19)과 같이 정의할 수 있다.

$\[ \mathrm{s}\left(t\right)=s_0-{\sum }_{i=1}^n\underset{t_{i=1}}{\overset{t_i}{\int }}{v}_{M_i}\left(t\right)dt \]$

(19)

식(19)에서 v_Mi(t)는 초기시간 t_i-1 및 최종시간 t_i로부터 계산된 맨드릴 이송속도의 선형 감소를 나타낸다. N= 3 케이스인 경우, 세가지 다른 맨드릴 이송속도를 나타내며 결과적으로 링 두께의 변화는 Fig. 5(a)에 나타낸 것과 같고, 링의 두께의 변화에 의하여 예측된 외경은 Fig. 5(b)와 같다.

Fig. 5

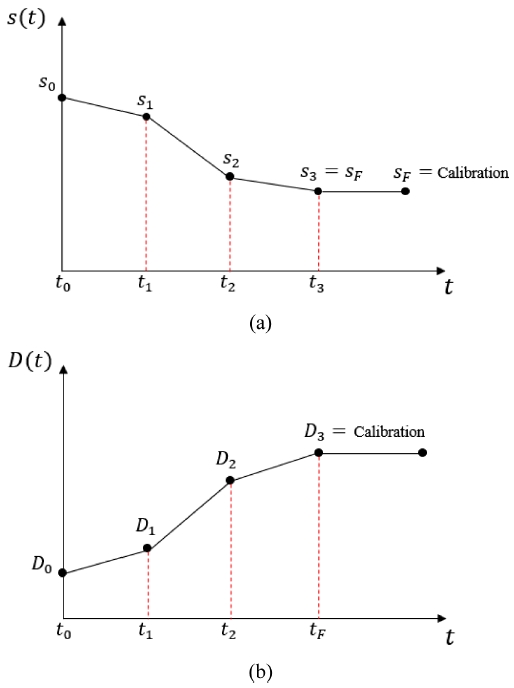
Multilinear variation of (a) thickness and (b) outer diameter of the ring for the case of n = 3 mandrel feeding speeds

식(19)에 따라 두께변화는 서로 다른 맨드릴 이송속도 변화에 따라 달라지며 Berti et al.¹⁵에서 정의된 형상 예측 알고리즘은 여전히 사용할 수 있지만 이를 반복적으로 사용하는 방식으로 적용하여야 한다. 여러 개의 다른 기울기를 가진 s(t) 또는 D(t) 계산의 각 단계에서 초기 링 형상에 대한 관련 값을 다르게 사용하여야 한다. 다시 말하면 계산의 각 단계에서 링의 초기 형상은 이전 확장단계에서 온 것임으로 링의 최종 형상 또는 중간 형상 중 하나가 될 수 있다.

3. 실험 검증

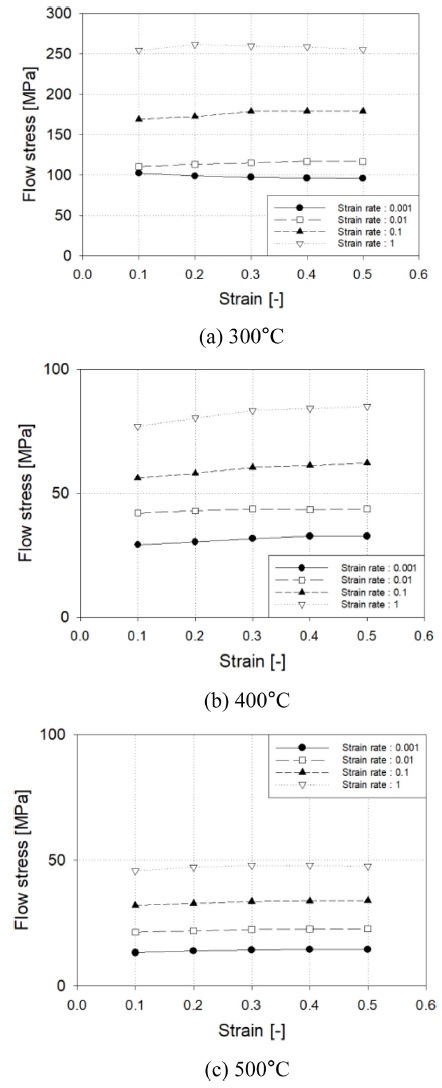
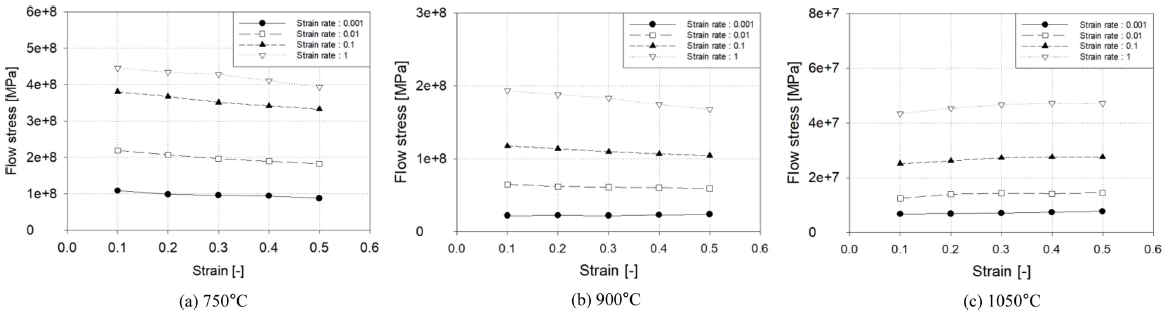
개발된 분석모델과 수치 시뮬레이션, 실험 결과의 검증을 위해 링 롤링 시험기로 AA6061 합금 소재에 대하여 연구를 진행하였다. 링 롤링 시험기는 Fig. 6(a)와 같다. 장비의 구성은 구동력을 공급하는 메인 롤과 공회전을 하면서 링의 반경 방향에 대한 성형 하중을 제어하는 맨드릴, 그리고 축 방향 성형하중을 제어하는 축 방향 상부 롤 등으로 이루어져 있다. 링은 메인 롤과 맨드릴 사이에 놓이며 메인 롤을 회전시키면서 맨드릴로 하중을 가하여 롤 간의 거리를 좁힘에 따라 링의 두께를 감소시킴과 동시에 반경 방향으로 확장한다. 링 롤링 실험에 사용된 시험기의 치수 및 초기, 최종 링 치수와 같이 실험 관련 설정 값은 Table 1에 나타내었다. 링의 외경 변화를 측정하기 위하여 Fig. 6(b)과 같이 링의 옆면에 붙어 같이 회전하는 Scale Sensor를 사용하여 실시간으로 링의 크기 변화를 측정하였다. AA6061 소재 링의 물성은 Table 2, 온도에 대한 유동응력 곡선은 Fig. 7에 나타내었다. 실험 결과와 해석 결과를 공정하게 비교하기 위하여 실제 실험의 공정 변수가 수치 시뮬레이션과 분석모델의 설정에 활용되었다.

Fig. 6

Laboratory-size ring rolling machine utilized for the experiments (a), Scale sensor for measuring the outer diameter during radial-axial ring rolling process (b)

Table 1

AA6061 ring dimensions, ring rolling test machine data and process conditions

Table 2

AA6061 Aluminum alloy material properties

Fig. 7

Temperature dependent flow stress curves for the AA6061

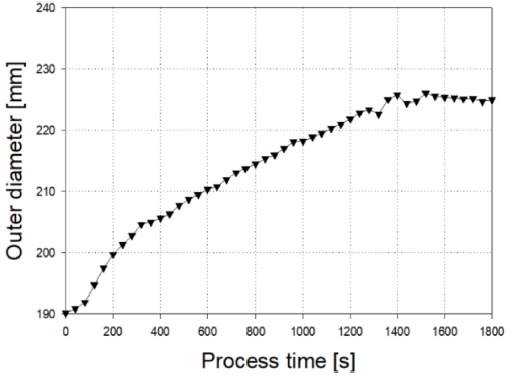
실험에서 링의 균일한 확장을 위해 쌍선형 맨드릴 이송속도를 사용하였다. 실험 전 링을 오븐으로 150^oC까지 가열 후 진행하였다. 실험 초기 링의 온도가 높은 이유로 인해 빠른 이송속도를 사용하면 큰 형상 변화가 일어난다. 이송속도의 변화를 주어 롤과 링 사이의 마찰력이 낮아 맨드릴과 메인 롤 사이를 링이 통과하지 못하고 헛도는 현상이 생김을 방지하였다. 이후에 링의 온도가 빠르게 낮아져 이송속도를 높여 원하는 치수까지 링을 확장시킬 수 있었고, 그렇게 진행한 결과는 Fig. 8에 나타내었으며, 링의 초기 형상과 최종 형상은 Fig. 9과 같다.

Fig. 8

AA6061 time-dependent ring outer diameter experimental result

Fig. 9

Initial and final ring shapes of AA6061 ring

4. 수치모델 구현 및 검증

4.1 수치모델의 특성

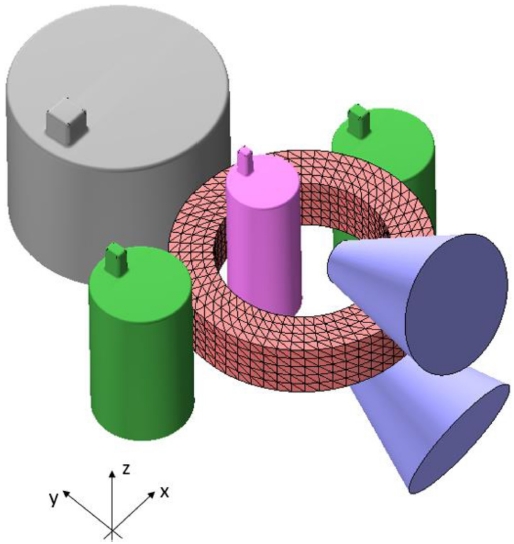
본 논문에서 제안된 분석모델의 검증을 위하여 상용 소프트웨어인 Simufact Forming 14로 수치 시뮬레이션이 진행 되었으며 시뮬레이션과 관련된 모든 정보와 수치모델 검증 결과는 이 절에서 설명된다. 수행된 수치모델은 Fig. 10과 같다.

Fig. 10

Numerical simulation implemented in Simufact Forming 14

수치 시뮬레이션에서는 이전 다른 저자의 연구에서 수행된 것처럼 식(20)와 같은 전단응력 마찰모델이 활용되었다. 링과 맨드릴-메인 롤 간의 마찰계수를 m = 0.85, 링과 축 방향 롤 및 가이드 롤 사이의 접촉에 대한 마찰계수를 m = 0.6으로 설정했다.

수치 시뮬레이션과 분석모델에는 동일한 마찰 계수가 사용되었다. 공정 중 롤과 링사이의 마찰에 대한 마찰 값의 정의는 Sun et al.²³의 연구에서 사용 가능한 범위에 따라 수행하였고 일반적으로 높이감소보다 두께감소가 더 크기 때문에 맨드릴-메인 롤 사이의 마찰이 축 방향 롤 사이보다 더 크다. 이러한 이유로, 링의 옆면에 스케일 제거(Descaling)를 진행하게 되는데 이는 맨드릴-메인 롤과 링으로 하여금 더 큰 마찰력을 갖게 만든다. 이와 달리 축 방향에서는 변형이 적기 때문에 링의 윗면과 아랫면은 스케일 제거를 하지 않으므로 마찰 계수가 낮아진다. 가이드 롤은 공정에서 링의 중심을 잡는 역할과 정상적으로 접촉을 하게끔 만들어주는 역할을 하며 일반적으로 윤활이 잘 되어있다. 이러한 이유로 수치모델에서는 링과 맨드릴-메인 롤 사이는 높은 마찰계수를 설정하고 축 방향 롤, 가이드 롤에는 낮은 마찰 계수를 설정하였다.

$\[ m=\frac{{\tau }_i}{k} \]$

(20)

절점 위치 전개는 링 롤링 공정에서와 같이 큰 변형의 경우에 적합한 Updated Lagrangian Approach에 따라 제어된다. FE 모델은 8개의 절점을 갖는 정육면체 Mesh를 사용하였으며, 검증을 위한 시뮬레이션에는 4.0 (Axial), 4.0 (Radial), 4.0 mm(Tangential)와 같은 Mesh 사이즈를 사용하였다. 5절에서 제시된 검증사례에서는 Mesh 사이즈는 16.0 (Axial), 12.0 (Radial), 16.0 mm (Tangential)이다. 절점의 위치가 Mesh들 중 가장 작은 Mesh의 측면 길이 1/20보다 작으면 표면과 접촉한 것으로 간주된다. 또한 두 Mesh 사이의 상대 속도가 0.001 mm/s보다 작으면 두 Mesh 사이를 접착 조건으로 간주한다. 수치모델에서 계산의 연속 반복에 대하여 두 가지 수렴 조건(변위: 0.25 mm, 절점력: 0.35 N)이 사용된다. 마지막으로 링의 초기온도는 150^oC, 공정 환경 온도는 50^oC로 일정하게 설정하였다.

4.2 소재 물성

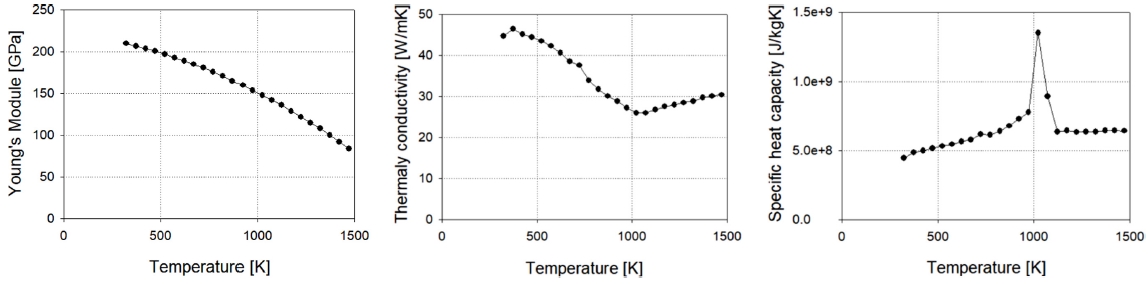
수치모델은 42CrMo4 합금, Ti6Al4V 합금 및 AA6061 합금, 이 세가지 소재를 사용하였다. 42CrMo4 합금의 물성 및 열 물성, 유동응력 식인 식(20)과 관련 상수는 각각 Table 4, Fig. 11, Table 3에 나타내었다.

Table 3

42CrMo4 alloy material model constants and validity ranges

Fig. 11

Thermal properties of the 42CrMo4 alloy

Table 4

42CrMo4 alloy material and simulation setting information

$\[ \sigma =C_1{e}^{\left(C_2\cdot T\right)}{\epsilon }^{\left(n_1\cdot T+n_2\right)}{e}^{\left(\frac{L_1\cdot T+L_2}{\epsilon }\right)}{\dot{\epsilon }}^{\left(m_1\cdot T+m_2\right)} \]$

(21)

AA6061 합금의 기계적 물성은 이전 절에서 작성되었으며 Ti6Al4V 합금의 물성은 Table 5, 온도에 대한 유동응력 곡선은 Fig. 12에 나타내었다.

Table 5

Ti6Al4V alloy mechanical and thermal properties

Fig. 12

Temperature dependent flow stress curves for the Ti6Al4V alloy

4.3 수치모델 설정

서로 다른 치수에 대한 분석모델의 신뢰성을 검증하기 위해 세 가지 서로 다른 초기 링 치수로 시뮬레이션을 진행하였다. 이 외에도 동일한 수치모델을 사용하여 4.2절에서 정의된 세 가지 소재를 사용하였다. 각각의 링은 쌍선형(Bilinear) 및 삼선형(Trilinear)의 속도를 갖는 두 가지 이송속도 조건으로 시뮬레이션을 진행하였다. 이 방법을 통해 개발된 분석모델에 대한 확실한 유효성을 검증할 수 있다. 링의 초기 및 최종 형상과 롤의 이송속도 및 회전속도에 대한 설정 값은 아래 표에 나타내었다. Table 6은 쌍선형 이송속도를 갖는 Ti6Al4V 합금 링의 초기 및 최종 외경, 내경, 높이의 치수이며, Table 7은 이송속도를 나타내었다. Table 8은 삼선형 이송속도를 갖는 Ti6Al4V 합금 링의 초기 및 최종 외경, 내경, 높이의 치수이며, Table 9는 이에 대한 이송속도를 나타내었다.

Table 6

Case 1-1–Initial and final geometry setting

Table 7

Case 1-1–Bilinear velocities tools settings

Table 8

Case 1-2–Initial and final geometry setting

Table 9

Case 1-2–Trilinear velocities tools settings

Tables 10과 11은 삼선형 이송속도를 갖는 AA6061, 42CrMo4 합금 링의 초기 및 최종 외경, 내경, 높이의 치수이며, Table 12는 이에 대한 이송속도를 나타내었다.

Table 10

Case 2-1–Initial and final geometry setting

Table 11

Case 2-2–Initial and final geometry setting

Table 12

Case 2-1, 2-2–Initial and final geometry setting

Tables 13, 15는 링의 최종 외경 치수가 1300에서 1500 mm안에 있는 Ti6Al4V 합금 링의 초기 및 최종 외경, 내경, 높이의 치수이다. Table 14는 쌍선형 이송속도를 Table 16은 삼선형 이송속도를 나타내었다.

Table 13

Case 3-1–Initial and final geometry setting

Table 14

Case 3-1–Bilinear velocities tools settings

Table 15

Case 3-2–Initial and final geometry setting

Table 16

Case 3-2–Trilinear velocities tools settings

4.4 수치모델 검증

이번 절에서는 4.1절과 동일한 수치모델을 사용하며, 3장에서 설정한 실험 조건을 똑같이 사용하여 개발된 수치모델의 유효성을 검증하기위한 목적으로 수치 시뮬레이션을 수행하였다.

검증을 위해 초기 온도조건 뿐만 아니라 실험과 동일한 쌍선형 이송속도로 진행되었고 롤의 이송속도 및 회전속도 설정 값을 Table 17에 나타내었다. 또한 AA6061 소재의 링을 실험 전 150 ^oC로 가열 후 실험을 진행하였다.

Table 17

AA6061 validation simulation tools settings

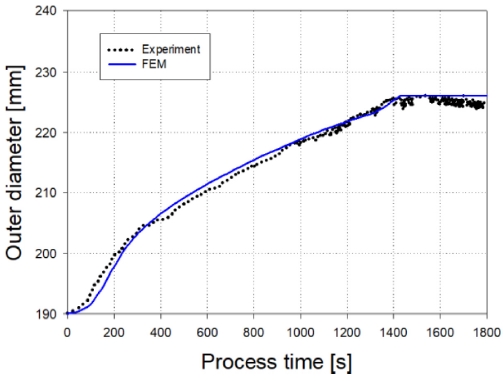
수치모델과 실험간 비교 결과는 Fig. 13와 같이 좋은 결과를 얻었으며 오차율은 Table 18에 나타내었다. 이로써 수치모델은 검증이 되었으며 다음 장에서 개발된 형상 예측 알고리즘의 검증에 활용되었다.

Fig. 13

Experiment and simulation results

Table 18

AA6061 time-based error calculation between simulation and experiment result

5. 결과 및 검증

이 장에서는 4장에서 진행한 시뮬레이션 결과와 새로운 모델과의 비교 검증을 진행하였다. 검증단계에서의 목표는 다음 세 가지 경우에 따른 개발된 모델의 신뢰성 검증이다.

(1) 초기, 최종 링 치수가 다른 경우(2) 맨드릴 이송속도의 개수가 다른 경우(3) 다른 소재 사용의 경우

(3)의 경우에 개발된 모델은 순수 분석 및 운동학적인 개념만을 기반함으로, 유동응력 식은 링 형상 예측에 포함되지 않는다. 이 부분은 이전 저자의 연구 Berti et al.¹⁵에서 강조되었지만 입증된 적이 없다. 이러한 이유 때문에 앞서 강조한 것처럼 개발된 모델은 소재만 변경된 동일한 시뮬레이션 모델에 적용하여 링 형상의 확장에 대한 영향만이 연구되었다.

최종적으로, 링 형상 예측의 정확도에 대한 실험 중 윤활이 공정에 미치는 영향도 고려해야 한다. 이와 같은 고려 사항은 이전 3장의 실험 결과를 기반으로 한다.

5.1 초기-최종 링 치수와 이동속도에 대한 형상 예측

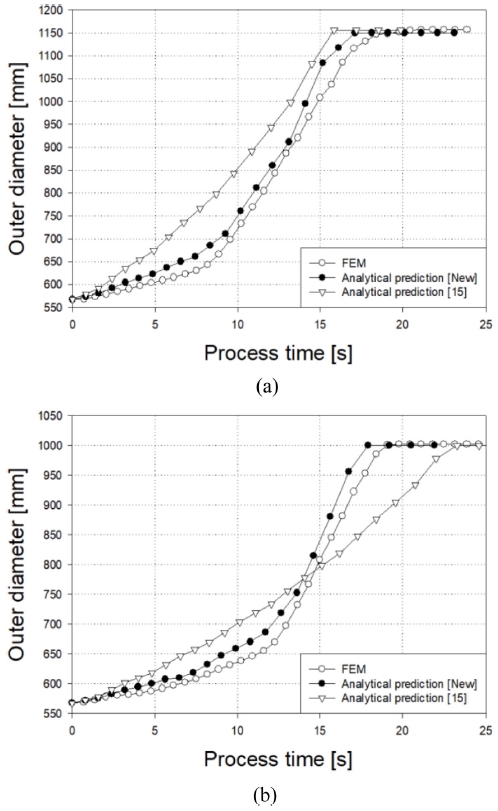
앞선 4장의 시뮬레이션 설정에 따라 7Case의 모든 연구 결과가 작성이 되었고, 최대 및 평균 오차율에 대한 부분도 포함되었다. Fig. 14(a)는 Ti6Al4V 합금 링에 쌍선형 맨드릴 속도를, Fig. 14(b)는 삼선형 맨드릴 속도를 적용한 해석결과와 새로운 모델, 이전 모델의 비교를 나타냈다.

Fig. 14

(a) Case 1-1 and (b) Case 1-2 outer diameter analytical prediction vs numerical results

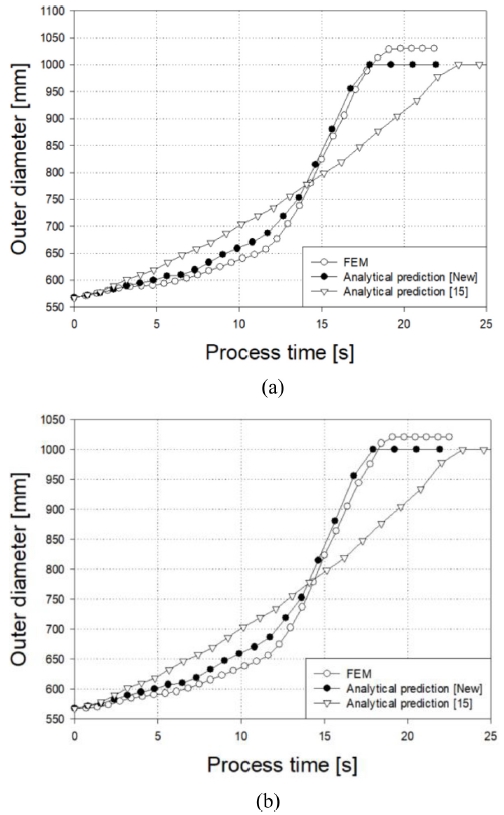
Fig. 15(a)는 AA6061 합금 소재 링에 삼선형 맨드릴 이송속도를, Fig. 15(b)는 42CrMo4 합금 소재 링에 삼선형 맨드릴 이송속도를 설정한 해석결과와 새로운 모델, 이전모델의 비교를 나타내었고, 오차율은 Table 19와 같다.

Fig. 15

(a) Case 2-1 and (b) Case 2-2 outer diameter analytical prediction vs numerical results

Table 19

Case1, 2 Analytical prediction [New]-FEM error [%], Analytical [15]-FEM error [%]

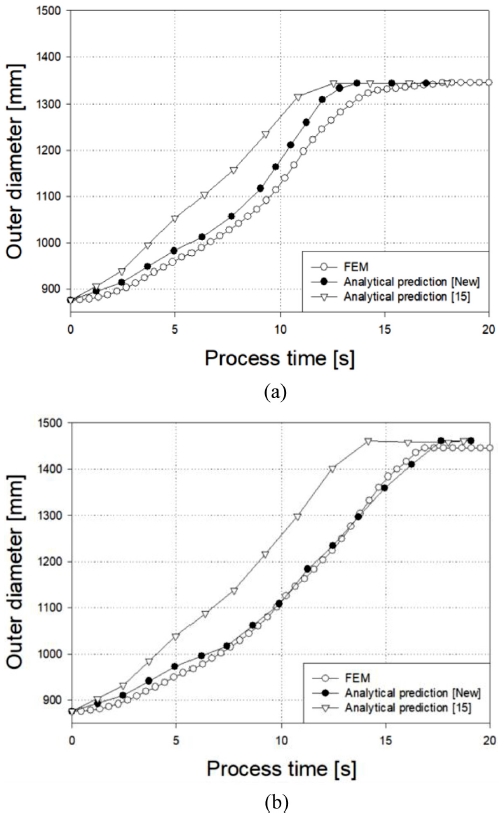
Figs. 16(a)과 16(b)는 초기 외경이 876.2 mm인 Ti6Al4V 합금 소재의 링을 각각 쌍선형, 삼선형 맨드릴 이송속도를 설정하여 진행한 결과이며, 오차율은 Table 20과 같다.

Fig. 16

(a) Case 3-1 and (b) Case 3-2 outer diameter analytical prediction vs numerical results

Table 20

Case3 Analytical prediction [New]-FEM error [%], Analytical [15]-FEM error [%]

5.2 슬립현상 예측

제조 공정 산업에 종사하는 모든 엔지니어 및 연구원들은 링과 롤 사이의 슬립현상이 있다는 문제점을 잘 알고 있다. 슬립현상은 잘 알려진 문제이지만 정량적인 공정변수와 상관시키는 것이 쉽지 않기 때문에 본 논문에서는 제외되었다. 하지만 이 연구에서 저자는 윤활 조건과 관련하여 슬립현상을 해석하려 시도하였다. 이전 3장에서 진행된 실험에서 많은 양의 DW-40 윤활제가 맨드릴-메인 롤 사이에서 링의 걸림을 방지하는데 사용되었다. 이 부분에 대해선 Fig. 17에 나타내었다.

Fig. 17

Lubricant on the ring during the 6061 laboratory experiments

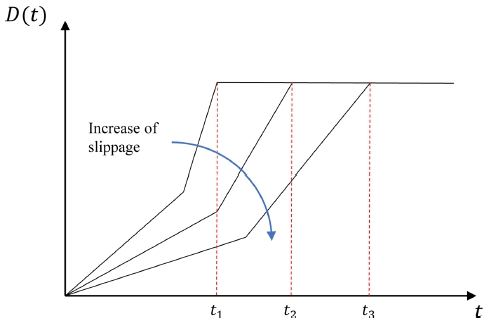
슬립현상의 문제에 대하여 분석 및 이론적 설명은 쉽지 않지만 Fig. 18에 나타낸 것과 같이 저자는 이것을 링의 확장을 지연시키는 영향이라고 정의하였다. 시간 t₁은 미끄러짐이 없는 경우의 최종 확장시간을 나타내며, t₂와 t₃는 슬립현상으로 인해 목표 직경에 도달하는데 필요한 시간이 증가함을 나타낸다.

Fig. 18

Effect of the slippage on a bilinear expansion curve

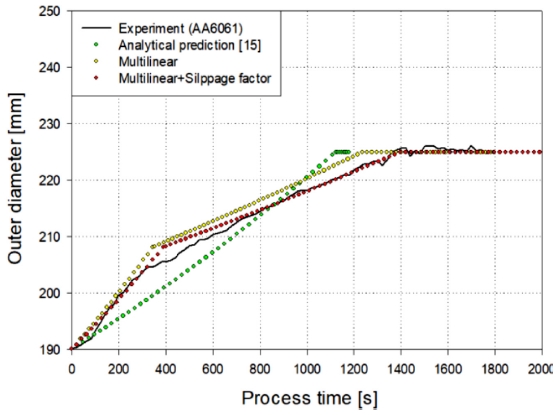
위에 언급한 부분에 대한 타당성은 분석적인 예측과 실험의 결과의 비교에 의해 확인할 수 있다. Fig. 19에서 보다시피 2.3절에서 정의된 모델을 기반으로 한 다중선형(Multilinear) 값은 실험결과와 유사한 경향성을 보이지만 슬립현상에 대한 인자값인 1.3을 공정시간에 곱하게 되면 다중선형+슬립현상 인자값(Multilinear+Slippage Factor)이 되고 확장 단계간 링의 치수도 매우 잘 예측이 되는 것을 확인할 수 있었다.

Fig. 19

Slippage factor consideration in the ring geometrical prediction

슬립현상의 인자 값에 대한 수학적 또는 물리적인 설명은 아직 찾지 못하였지만 이 문제는 링 형상의 확장을 정확하게 예측하는데 매우 중요하다. 링 롤링 공정에서 링과 롤사이의 슬립현상은 가장 진보된 수치모델에서도 예측할 수 없으며 공정 중 윤활 조건을 추측함으로만 평가할 수 있다. 링 롤링 공정에서의 슬립현상에 대한 결과는 이 문제를 다루는 연구자에게 도움이 될 수 있으며, 복잡하고 예측하기 어려운 공정 요소에 대한 추가 연구의 기반이 될 수 있을 것으로 사료된다.

6. 결론

Berti et al.¹⁵의 알고리즘에서는 맨드릴 이송속도가 2개 이상인 공정에서는 오차율이 증가하였다. 본 논문에서는 맨드릴 이송속도가 2개의 이상인 경우에 형상 예측 오차율을 줄이기위해 새로운 모델을 개발하였다. 개발모델의 검증을 위해 링 롤링 시험기의 맨드릴 이송속도를 2개로 설정하고, AA6061 알루미늄 합금 소재를 압연하였다. 실험 결과와 예전 모델에 비해 새로운 모델의 결과의 오차율이 감소되는 것을 확인하였다. 또한, 실험에서 슬립현상이 발생함에 따라 새로운 모델과 실험과의 차이가 나타났기 때문에 수치모델을 이용한 예측에서 중요한 변수임이 확인되었다.

개발한 새로운 모델의 교차검증을 위해, 초기 세 가지 링 치수와 공정변수를 조절하여 최종 링의 치수가 800에서 2000 mm까지의 다양한 해석결과를 확보하였다. 실험결과를 이전 모델과 비교하였고 2.16%의 최대 오차율과 1.42%의 평균 오차율은 보였다. 새로운 모델과 비교하였을 때의 1.7%의 최대 오차율과 0.97%의 평균 오차율을 보였다. 해석결과와 비교했을 때 이전 모델은 최대 21.91%, 평균 8.27%의 오차율을 보였으며 새로운 모델은 최대 6.82%, 평균 2.68%의 오차율을 보여 이전모델보다 개선된 것을 검증하였다. 따라서 개발된 새로운 모델을 사용함으로써 산업 엔지니어 또는 연구자들이 반경-축 방향 링 롤링 공정의 제어에 큰 기여를 할 수 있을 것이다.

REFERENCES

• Eruç, E. and Shivpuri, R., “A Summary of Ring Rolling Technology—I. Recent Trends in Machines, Processes and Production Lines,” International Journal of Machine Tools and Manufacture, Vol. 32, No. 3, pp. 379-398, 1992. [https://doi.org/10.1016/0890-6955(92)90009-6]
• Eruç, E. and Shivpuri, R., “A Summary of Ring Rolling Technology—II. Recent Trends in Process Modeling, Simulation, Planning, and Control,” International Journal of Machine Tools and Manufacture, Vol. 32, No. 3, pp. 399-413, 1992. [https://doi.org/10.1016/0890-6955(92)90010-E]
• Qian, D., Zhou, G., Hua, L., Shi, D., and Li, H., “3D Coupled Thermo-mechanical FE Analysis of Blank Size Effects on Radial-Axial Ring Rolling,” Ironmaking & Steelmaking, Vol. 40, No. 5, pp. 360-368, 2013. [https://doi.org/10.1179/1743281212Y.0000000048]
• Zhou, G., Hua, L., and Qian, D., “3D Coupled Thermo-Mechanical FE Analysis of Roll Size Effects on the Radial–Axial Ring Rolling Process,” Computational Materials Science, Vol. 50, No. 3, pp. 911-924, 2011. [https://doi.org/10.1016/j.commatsci.2010.10.029]
• Zhou, G., Hua, L., Lan, J., and Qian, D., “FE Analysis of Coupled Thermo-Mechanical Behaviors in Radial–Axial Rolling of Alloy Steel Large Ring,” Computational Materials Science, Vol. 50, No. 1, pp. 65-76, 2010. [https://doi.org/10.1016/j.commatsci.2010.07.008]
• Wang, Z., Fan, J., Hu, D., Tang, C., and Tsui, C., “Complete Modeling and Parameter Optimization for Virtual Ring Rolling,” International Journal of Mechanical Sciences, Vol. 52, No. 10, pp. 1325-1333, 2010. [https://doi.org/10.1016/j.ijmecsci.2010.06.008]
• Qian, D. and Pan, Y., “3D Coupled Macro–Microscopic Finite Element Modelling and Simulation for Combined Blank-Forging and Rolling Process of Alloy Steel Large Ring,” Computational Materials Science, Vol. 70, pp. 24-36, 2013. [https://doi.org/10.1016/j.commatsci.2012.12.035]
• Davey, K. and Ward, M., “A Practical Method for Finite Element Ring Rolling Simulation Using the ALE Flow Formulation,” International Journal of Mechanical Sciences, Vol. 44, No. 1, pp. 165-190, 2002. [https://doi.org/10.1016/S0020-7403(01)00080-7]
• Kim, B., Moon, H., Kim, E., Choi, M., and Joun, M., “A Dual-Mesh Approach to Ring-Rolling Simulations with Emphasis on Remeshing,” Journal of Manufacturing Processes, Vol. 15, No. 4, pp. 635-643, 2013. [https://doi.org/10.1016/j.jmapro.2013.05.002]
• Yea, Y., Ko, Y., Kim, N., and Lee, J., “Prediction of Spread, Pressure Distribution and Roll Force in Ring Rolling Process Using Rigid–Plastic Finite Element Method,” Journal of Materials Processing Technology, Vol. 140, Nos. 1-3, pp. 478-486, 2003. [https://doi.org/10.1016/S0924-0136(03)00721-0]
• Kim, N., Kim, H., and Jin, K., “Optimal Design to Reduce the Maximum Load in Ring Rolling Process,” International Journal of Precision Engineering and Manufacturing, Vol. 13, No. 10, pp. 1821-1828, 2012. [https://doi.org/10.1007/s12541-012-0239-4]
• Han, X., Hua, L., Zhou, G., Lu, B., and Wang, X., “FE Simulation and Experimental Research on Cylindrical Ring Rolling,” Journal of Materials Processing Technology, Vol. 214, No. 6, pp. 1245-1258, 2014. [https://doi.org/10.1016/j.jmatprotec.2013.12.020]
• Lin, H. and Zhi, Z. Z., “The Extremum Parameters in Ring Rolling,” Journal of Materials Processing Technology, Vol. 69, Nos. 1-3, pp. 273-276, 1997. [https://doi.org/10.1016/S0924-0136(97)00029-0]
• Guo, L. and Yang, H., “Towards a Steady Forming Condition for Radial–Axial Ring Rolling,” International Journal of Mechanical Sciences, Vol. 53, No. 4, pp. 286-299, 2011. [https://doi.org/10.1016/j.ijmecsci.2011.01.010]
• Berti, G., Quagliato, L., and Monti, M., “Set-Up of Radial–Axial Ring-Rolling Process: Process Worksheet and Ring Geometry Expansion Prediction,” International Journal of Mechanical Sciences, Vol. 99, pp. 58-71, 2015. [https://doi.org/10.1016/j.ijmecsci.2015.05.004]
• Quagliato, L. and Berti, G. A., “Mathematical Definition of the 3D Strain Field of the Ring in the Radial-Axial Ring Rolling Process,” International Journal of Mechanical Sciences, Vols. 115-116, pp. 746-759, 2016. [https://doi.org/10.1016/j.ijmecsci.2016.07.009]
• Quagliato, L. and Berti, G. A., “Temperature Estimation and Slip-Line Force Analytical Models for the Estimation of the Radial Forming force in the RARR Process of Flat Rings,” International Journal of Mechanical Sciences, Vol. 123, pp. 311-323, 2017. [https://doi.org/10.1016/j.ijmecsci.2017.02.008]
• Hill, R., “The Mathematical Theory of Plasticity,” Oxford University Press, 1998.
• Hawkyard, J., Johnson, W., Kirkland, J., and Appleton, E., “Analyses for Roll Force and Torque in Ring Rolling, with Some Supporting Experiments,” International Journal of Mechanical Sciences, Vol. 15, No. 11, pp. 873-893, 1973. [https://doi.org/10.1016/0020-7403(73)90018-0]
• Quagliato, L., Berti, G. A., Kim, D., and Kim, N., “Contact Geometry Estimation and Precise Radial Force Prediction for the Radial-Axial Ring Rolling Process,” International Journal of Material Forming, Vol. 11, No. 6, pp. 789-805, 2018. [https://doi.org/10.1007/s12289-017-1388-x]
• Quagliato, L., Berti, G. A., Kim, D., and Kim, N., “Slip Line Model for Forces Estimation in the Radial-Axial Ring Rolling Process,” International Journal of Mechanical Sciences, Vol. 138, pp. 17-33, 2018. [https://doi.org/10.1016/j.ijmecsci.2018.01.025]
• Keeton, C. R., “Ring Rolling, in: ASM Metals Handbook: Forming and Forging, Metals Park,” ASM International, pp 108-127.
• Sun, Z.-C., He, Y., and Ou, X.-Z., “Thermo-Mechanical Coupled Analysis of Hot Ring Rolling Process,” Transactions of Nonferrous Metals Society of China, Vol. 18, No. 5, pp. 1216-1222, 2008. [https://doi.org/10.1016/S1003-6326(08)60207-1]