유도초음파를 활용한 경사각 결함의 각도 변화에 따른 산란 신호 해석 연구


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The guided ultrasonic wave has the advantage of diagnosis on a wide area within in a short time due to the long distance propagation characteristic. However, there are many difficulties in signal analysis due to the mode conversions in the reflection from the defect and boundaries. In the use of guided waves for structure monitoring, it is necessary to understand the relation between the propagation mode and the mode of variation according to the shape of the defect. In this study, the characteristics of induced ultrasonic mode conversion is analyzed in taper defects formed from the surface of an aluminum plate. The defect depths of the plate thickness are 20, 50, and 80% and the characteristics of the reflection and transmission modes are analyzed on various defect widths, depending on the angle of change of the tapered shape. The A0 and S0 modes were selected as the excitation mode of the guided waves, the transmission and reflection coefficient amplitudes are analyzed. It is confirmed that the wavelength of the excitation mode having a large influence on the amplitude of the transmission and reflection signals generated by the taper defects depend on the shape of the defect.
Keywords:
Guided waves, Scattering signal, Wave signal analysis, Defect shape, Mode conversion, Tapered defect키워드:
유도초음파, 산란 신호, 신호해석, 결함형상, 모드변이, 테이퍼형 결함1. 서론
현대사회에서 안정적인 전력 수급을 위하여 원자력 발전의 가동률 향상과 발전량을 유지하기 위해 가혹한 환경에서 원자력 발전 설비들이 지속적으로 사용되고 있다. 또한 항공기의 경우 대형 수송을 위해 대형 항공기가 제작되고 운행되고 있으며, 고속철도도 수송 효율 향상을 위해 탑승 인원을 증가시키고 주행 속도를 향상시키기 위해 많은 노력을 하고 있다. 원자력 발전을 비롯한 대형 항공기, 고속열차의 안전에 대한 관심은 점점 높아지고 있다. 고속열차의 운행 안전에 영향을 주는 레일과 휠의 접촉으로 인해 표면 결함이 생성되고, 사고의 위험성이 증가하는 등의 문제가 발생하고 있다.1 또한 작동 유체로 인해 감육 발생으로 완만한 경사의 결함에서 일부 와류현상으로 인해 깊이가 지속적으로 깊어지는 현상이 발생하고 있다.2 초음파를 활용한 비파괴 진단(Nondestructive Testing, NDT)과 구조물 상태 진단(Structural Health Monitoring, SHM)을 위해서는 초음파의 전파 특성과 결함으로 인해 발생되는 산란 신호에 대한 이해가 중요하다. 특히 유도초음파를 활용하여 대형 구조물의 넓은 영역을 진단 및 평가하는 경우 유도초음파 모드특성과 모드 변이에 대한 이해가 반드시 필요하다. 유도초음파를 활용한 구조물 상태 평가 및 진단에 대한 연구는 다양한 분야에서 많은 연구가 수행된 바 있다.3-7 특히나 대부분의 구조물에서 쉽게 찾아볼 수 있는 평판형 구조물에서 전파하는 유도초음파의 전파 특성과 모드 변이에 대한 연구는 Y. Cho,8-10 Y. Lu11에 의해 연구된 바 있다. 결함의 형상과 유도초음파의 모드 변이 현상에 대한 정확한 이해가 있어야 신호에 대한 정량적인 해석이 가능하다. 다양한 결함에 대한 산란 모드 변이 현상을 실험적으로 증명하기에는 시험편 제작에 많은 한계점이 존재하므로 수치 모델링을 통한 연구가 필요하다.
평판에서 발생된 결함으로 인해 생성된 모드 변이 현상에 대해 실험적인 검증12-14과 경계요소법(Boundary Element Method, BEM)15과 유한요소법(Finite Element Method, FEM)16을 활용한 수치 모델 해석을 활용한 선행연구가 있었으나 결함의 형상이 삼각형, 사각형, 계단형 등 물리적으로는 의미를 가지나 실제 발생 가능성이 낮은 경우에 대한 연구가 대부분이었다. 경사각을 가지는 형태의 결함에 대한 연구가 수행된 사례가 있으나 산란 신호와 결함의 형상에 대한 다양한 사례에 대한 연구가 미흡하다.17
본 연구에서는 선행 연구 사례의 단순한 형상의 결함의 한계를 뛰어넘어 발생 가능한 테이퍼형 결함과 결함의 형상 변화와 유도초음파 모드 변이 현상에 대한 상관관계를 분석하였다. 유한요소 모델 해석을 활용하여 테이퍼형 결함의 경사각 변화에 따라 입사되는 A0, S0 모드에서 결함으로 인해 발생되는 반사, 투과 되는 모드 변이를 분석하였다.
2. 유도초음파 이론과 유한요소 모델
2.1 유도초음파 분산 특성
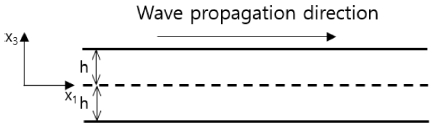
유도초음파 이론은 많은 연구 논문과 교재에서 상세히 설명되어 있어 본 연구 논문에서는 간략히만 설명한다. 유도초음파는 파장 대비 두께가 얇은 경우 발생되는 특수한 형태의 초음파로 체적파와 다르게 원거리를 전파할 수 있는 특징을 가지고 있다. 유도초음파 모드에는 구조물의 중심축을 기준으로 대칭형으로 거동하는 대칭 모드(S-Mode)와 서로 반대로 거동하는 반대칭 모드(A-Mode)가 있으며 각 모드 별로 기준 모드가 되는 차수가 0인 모드부터 무한대까지 존재한다.18 Fig. 1은 해석 모델의 좌표계와 평판형 구조를 나타낸 그림이다.
평판형 구조물에서는 평면변형조건을 활용하여 3차원 파동방정식을 2차원으로 해석할 수 있으며, 이때의 종파와 횡파의 파동 방정식 각각 식(1), 식(2)와 같다.
| (1) |
| (2) |
식(1)과 식(2)의 파동방정식을 자유경계면의 경계 조건을 적용하여 풀이하면 식(3)과 식(4)와 같이 정리할 수 있다. 식(3)은 대칭 모드를 식(4)는 반대칭모드의 특성을 나타내는 특성방정식을 의미한다.
| (3) |
| (4) |
이때, k는 파수(Wave Number), h는 Fig. 1에 표현된 것과 같이 두께의 절반이고, p와 q는 다음과 같이 정의한다.
| (5) |
| (6) |
p와 q를 정의하는데 사용된 ω는 입사된 유도초음파의 각주파수이고, CL과 CT는 전파 매질에서의 종파와 횡파 속도를 의미한다.
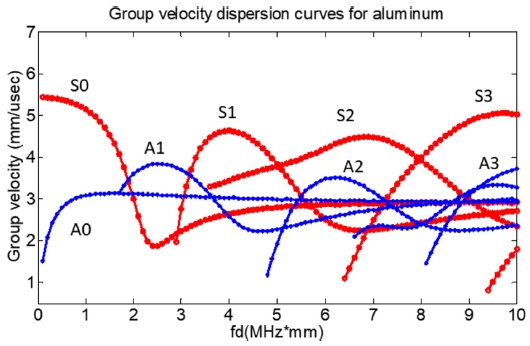
식(3)과 식(4)를 통해 계산된 위상속도로부터 실제 유도초음파가 모드 별로 군집하여 전파하는 군속도를 계산할 수 있다. 군속도의 분산 선도는 Fig. 2와 같다. 유도초음파 전파 특성을 해석하기 위한 모델을 설정하는데 위상 속도 분산 선도의 전파 특성을 활용하고, 실제 전파 신호를 분석하는데 군속도 분산 선도를 활용하여 모드 확인을 한다.
2.2 유도초음파 전파 해석 모델
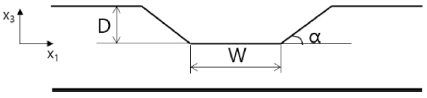
유도초음파 전파 모드 해석을 위해서는 모델 설정에 위상 속도 분산 선도를 활용하여 입력 모델을 설정한다. 본 연구에서는 표면에서부터 테이퍼형으로 발생된 결함을 대상으로 경사각을 변화하며 해석을 수행하였다. 결함은 1 mm 두께의 알루미늄 평판에서 표면에서부터 결함의 깊이가 0.2, 0.5, 0.8 mm에 대한 모델을 해석하였다. 테이퍼 결함의 경사각은 5°에서부터 5°씩 변화하여 수직 결함인 90°까지 해석을 수행하였다. 유도초음파 모드는 기준 모드인 A0와 S0를 1.0 MHz를 활용하여 가진하여 해석을 수행하였다. 결함의 형상을 정의하는 변수로는 결함의 깊이 D, 경사각 α, 결함의 기준 폭 W를 활용하였으며, Fig. 3과 같다.
결함의 각도가 90°인 경우 전체 결함의 폭은 W이고, α가 작아질수록 표면 쪽 결함의 폭이 급격하게 커지게 되며, 완만한 경사각의 결함 형상을 갖게 된다. 해석 모델의 W는 5 mm로 고정하고 각 결함의 깊이에서 경사각 변화에 따른 반사, 투과 모드 변이를 해석하였다.
해석 모델에 활용된 알루미늄의 재질은 Table 1과 같다. 1MHz, 4 Cycle의 톤버스트 신호를 형성하고, 모델의 가진 지점에 각각 대칭, 반대칭 형태로 부가하였다. 유도초음파 전파 모델을 해석할 때 Comb Type 또는 집중하중방식으로 가진을 할 경우 유도초음파의 전파 방향을 제한하기 어려운 한계점이 있어 양방향으로 전파하는 초음파를 흡수하여 불필요한 모델경계에서 생성되는 반사 신호를 상쇄시켜야 한다. 일반적으로 Fig. 4와 같이 모델의 경계를 무한 요소로 설정하여 반사 신호를 상쇄시킨다.
초음파 전파 모델 해석을 위해서는 유한 요소의 크기는 초음파의 파장의 1/10 이하가 되어야 초음파 전파 특성을 정확하게 분석할 수 있다. 본 연구에서는 요소의 크기를 파장의 1/15을 기준으로 선정하여 요소를 생성하였다.
3. 테이퍼 결함 영역의 유도초음파 전파 신호 해석
해석 모델의 결함 깊이는 각 0.2, 0.5, 0.8 mm이고, 결함의 경사각이 완만한 5°에서부터 5°씩 증가하여 수직 사각 결함의 형상이 되는 90°까지 경사각과 결함의 깊이에 따른 반사와 투과되는 유도초음파 모드 변이 현상의 상관관계를 찾기 위한 모델 해석을 수행하였다. 유도초음파의 모드가 충분히 생성되고, 결함 영역에서 투과, 반사 후 모드 변이 현상을 관찰하기 위해 충분한 결함영역에서 충분한 거리를 확보하여 모델을 생성하였다. 유도초음파가 가진되는 위치와 결함 영역을 투과, 반사한 후 수신되는 위치를 각각 결함 영역의 가운데를 기준으로 각각 200 mm 떨어진 위치에 데이터를 수집하도록 설정하였다.
Fig. 5(a)는 대칭형 모드를 가진한 후 결함 영역에서 반사, 투과가 일어난 후 모드 변이 현상이 발생하는 것을 볼 수 있다. Fig. 5(b)는 반대칭형 모드를 가진하여 전파하는 현상을 보여준다. 반대칭형 모드의 경우 대칭형 모드보다 모드 변이 현상이 광범위하게 발생하는 것을 확인할 수 있다. 유도초음파의 모드변이 현상은 Fig. 2의 분산 특성 선도의 가진 주파수 성분에서 발생 가능한 모드로 변이가 일어나며, 전파 거리가 증가함에 따라 종파와 횡파 등 전파 거리에 따라 급격하게 감쇠되는 초음파 모드는 국부적으로만 존재하고 측정위치에는 영향을 주지 않는다.
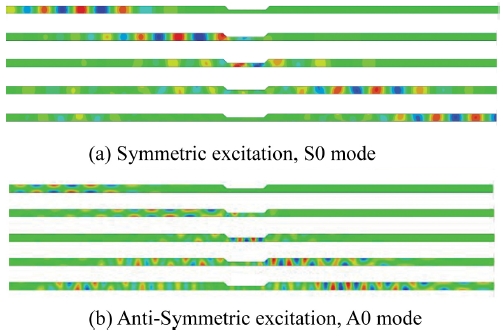
Displacement distribution of Symmetric (a), Anti-Symmetric (b) guided wave propagation and mode conversion at tapered defect region
3.1 A0 모드의 모드 변이 해석
평판 모델에서 반대칭형으로 입력 변위를 발생시켜 A0 모드만 선택적으로 가진하여 모델 해석을 수행하였다. Fig. 6은 결함 깊이 0.5 mm일 때 테이퍼 결함 각도가 45°인 경우의 대표 해석 신호이다. Fig. 6(a)는 초음파를 가진하는 위치에서 수집한 신호이다. 초기 가진 신호의 진폭이 나타난 이후 결함에서 반사되어 모드 변이가 일어난 S0 모드가 나타나고, 그 뒤로 A0 모드가 발생한다. 모델의 반대쪽 끝에서 반사된 신호가 수신된 것은 무한 요소로 설정하였으나 반사되는 신호가 발생하여 전파되는 신호와 함께 중첩 증폭되어 나타나는 것을 확인할 수 있다. 가진 모드로 A0 모드를 선택하여 모델 해석을 수행하였으나 S0 모드가 먼저 나타나는 이유는 Fig. 2의 분산 특성 선도와 같이 1 mm 두께의 시험편에 1 MHz로 가진된 A0 모드에서 모드 변이 현상으로 S0 모드가 발생되고, 이 때 S0 모드는 A0 모드보다 전파속도가 빨라 수신 위치에 먼저 도달하였기 때문이다. Fig. 6(b)는 결함 영역을 투과한 후 모드 변이 현상에 따른 S0 모드와 A0 모드의 진폭을 확인할 수 있다. 측정된 초음파 패킷의 최대 진폭을 기준으로 투과, 반사 신호의 진폭을 선정하였다. 테이퍼 결함의 각도 변화에 따른 반사, 투과 신호의 크기를 표현하였다. 이때, A0 모드를 가진하여 시험편을 전파하는 과정에서 테이퍼형 결함으로 인해 발생된 반사, 투과 신호의 크기를 결함 두께와 각도에 따른 크기 비교를 위해 Figs. 7과 8에 표현하였다. Fig. 7은 A0 모드를 가진하여 결함으로 인해 발생된 반사 신호 중 A0 모드와 S0 모드의 신호를 테이퍼형 결함의 각도에 따라 비교한 결과이며, Fig. 8은 A0 모드를 가진하여 결함을 통화한 후 발생된 A0 모드와 S0 모드의 신호 크기를 나타낸 결과이다.
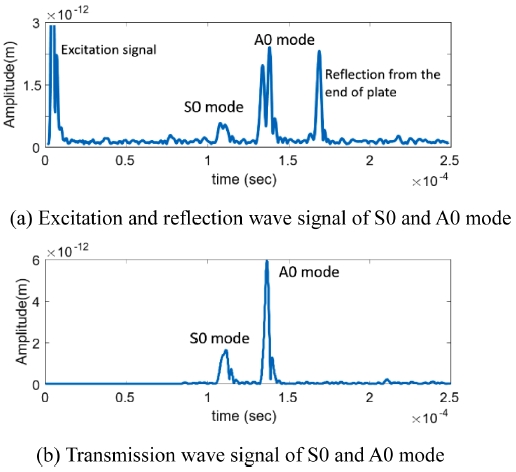
A0 excitation and reflection signal (a) and transmission signal (b) of 45° taper angle and 0.5 mm defect depth
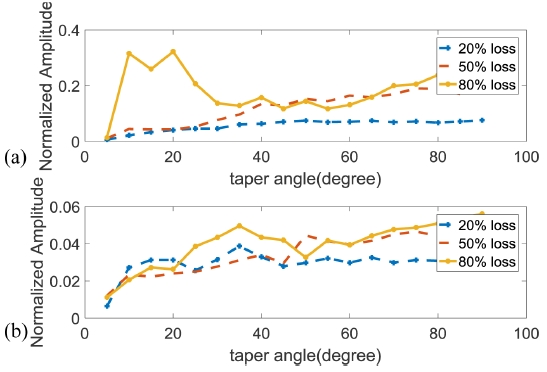
Reflection amplitude comparison at A0 incident and A0 mode conversion (a) and S0 mode conversion (b) at various defect depth
3.2 S0 모드의 모드 변이 해석
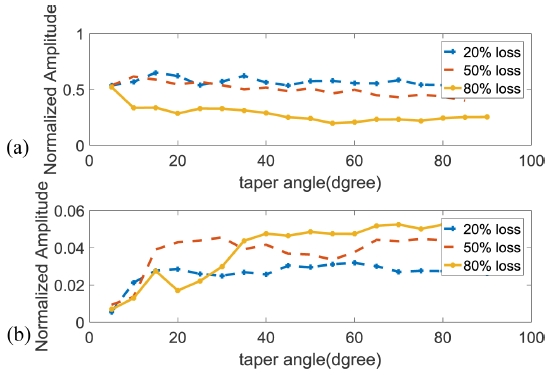
3.1절의 반대칭형 모드 해석과 동일한 조건에서 입력 변위를 대칭형으로 발생시켜 대칭형 모드만 가진하였을 때 발생된 신호는 Fig. 9과 같다. 제시된 조건으로 S0를 가진한 경우 전파 속도가 A0 모드보다 빨라 Fig. 6에서 나타나는 신호의 위치보다 앞선 곳에 나타나며, 속도 계산을 하였을 때 모드 성분을 정확하게 확인할 수 있었다. 테이퍼 결함의 각도 변화에 따른 반사, 투과 신호는 Figs. 10 및 11과 같다. 결함의 깊이가 0.2 mm일 때, 결함의 경사각의 변화에 따라 반사신호는 완만하게 변화하는 반면, 투과신호는 급격하게 줄어드는 것을 확인할 수 있다.
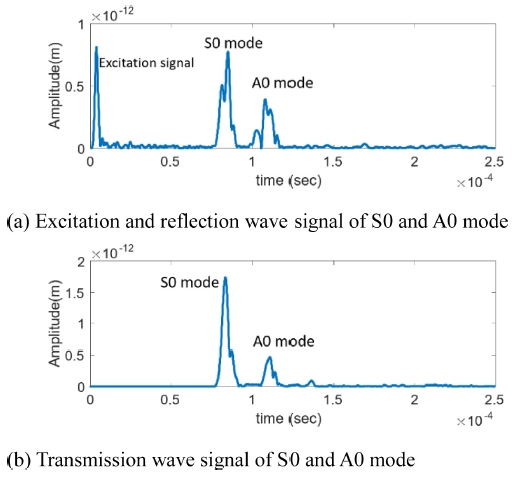
S0 excitation and reflection signal (a) and transmission signal (b) of 45° taper angle and 0.5 mm defect depth
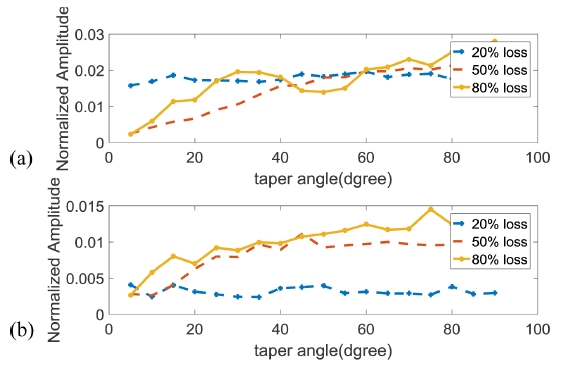
Reflection amplitude comparison at S0 incident and A0 mode conversion (a) and S0 mode conversion (b) at various defect depth
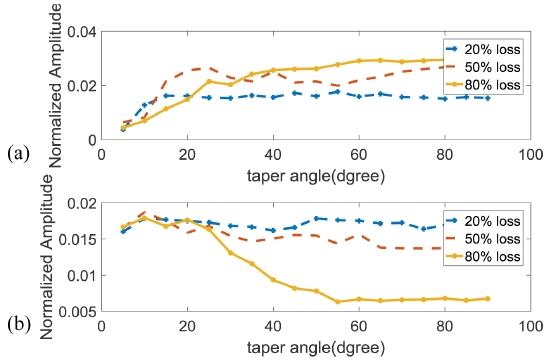
Transmission amplitude comparison at A0 incident and A0 mode conversion (a) and S0 mode conversion (b) at various defect depth
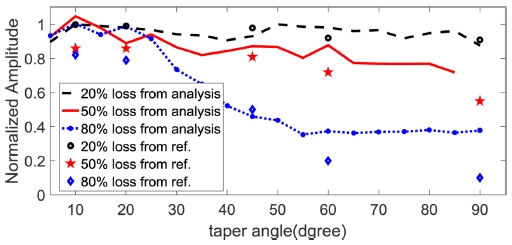
Comparison result of previous reference (black, red, blue symbols) and analysis data (black, red, blue lines) on S0 mode incident and S0 mode transmission
계산된 결과는 선행연구논문17의 결과와 비교하였을 때, 전체적으로 결과의 양상은 동일하게 나타나는 것을 확인할 수 있으며, 결함의 깊이가 깊고 결함의 각도가 작은 경우 결함 해석 모델의 크기로 인해 차이가 나타나는 것을 확인할 수 있다. 결함으로 인해 발생되는 유도초음파의 산란 신호는 결함의 형상과 크기에 민감하게 반응하는 것을 확인할 수 있으며, 다양한 형상과 크기에 대한 일반화할 수 있는 형태의 데이터 분석이 추가적으로 필요하다.
4. 결론
평판형 구조물의 테이퍼형 결함의 경사각 변화에 따른 반사, 투과 신호 진폭을 모델 해석을 통해 분석하였다. 유도초음파의 특성 중 다양한 모드에 따라 전파하는 특성이 달라지는 현상을 반영하기 위해 대칭, 반대칭 모드 중 특정 모드만 가진될 수 있도록 모델을 설정하였으며, 이를 바탕으로 전파하는 모드를 확인하였다. A0 또는 S0 모드를 선택 가진하여 테이퍼형 결함으로 인해 발생된 반사, 투과 신호의 크기를 가진 진폭으로 정규화 하여 분석하였다. 결함의 깊이가. 0.2에서 0.8 mm로 커짐에 따라 반사되는 신호의 진폭은 증가하고, 투과되는 진폭의 크기는 감소하는 것을 볼 수 있다. 테이퍼 결함의 각도가 증가함에 따라 A0 모드 가진 조건에서 측정된 A0 모드와 S0 모드의 투과, 반사 신호의 크기의 변화율은 크지 않은 것을 볼 수 있다. 이런 경우 실제 현장에서 A0 모드를 활용하여 구조물에 발생된 결함을 진단할 경우 테이퍼 결함 각 변화에 민감하게 변화하지 않으므로 신호 분석에 어려움이 있을 수 있다. 하지만 S0 모드 가진 조건을 활용하였을 경우 결함 깊이가 0.2 mm인 경우에도 테이퍼 결함 각의 변화에 민감하게 반응하는 것을 볼 수 있다. 따라서 산업현장에서 유도초음파를 활용한 구조물 진단을 할 경우, 신호 분석을 통해 결함의 상태를 파악하는데는 S0 모드를 활용하는 것이 결함 상태를 파악하는데 더 유리하다.
모델 해석 결과를 바탕으로 평판 구조물의 표면에 발생한 결함 분석을 통해 결함의 크기를 정량적으로 검출할 수 있다고 판단된다. 추후 연구에서는 실험적 검증과 표면의 미세 결함에 대한 정량적 결함 형상 예측 연구에 응용할 수 있을 것이라 기대된다.
NOMENCLATURE
| CL : | Longitudinal wave velocity |
| CT : | Shear wave velocity |
| φ : | Scalar potential |
| ψ : | Vector potential |
| k : | Wave number |
| α : | Taper angle |
Acknowledgments
논문은 2018년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과임.
REFERENCES
-
Fan, Y., Dixon, S., Edwards, R. S., and Jian, X., “Ultrasonic Surface Wave Propagation and Interaction with Surface Defects on Rail Track Head,” NDT & E International, Vol. 40, No. 6, pp. 471-477, 2007.
[https://doi.org/10.1016/j.ndteint.2007.01.008]

-
Xie, S., Chen, Z., Takagi, T., and Uchimoto, T., “Quantitative Non-Destructive Evaluation of Wall Thinning Defect in Double-Layer Pipe of Nuclear Power Plants Using Pulsed ECT Method,” NDT & E International, Vol. 75, pp. 87-95, 2015.
[https://doi.org/10.1016/j.ndteint.2015.06.002]

- Cho, Y.-H., “Understanding and Application of Ultrasonic Guided Waves,” Journal of the Korean Society for Nondestructive Testing, Vol. 21, No. 4, pp. 446-460, 2001.
-
Lee, J. and Cho, Y., “Using Lamb Waves to Monitor Moisture Absorption in Thermally Fatigued Composite Laminates,” Journal of the Korean Society for Nondestructive Testing, Vol. 36, No. 3, pp. 175-180, 2016.
[https://doi.org/10.7779/JKSNT.2016.36.3.175]

-
Choi, J. and Cho, Y., “Feasibility Study on Diagnosis of Material Damage Using Bulk Wave Mixing Technique,” Journal of the Korean Society for Nondestructive Testing, Vol. 36, No. 1, pp. 53-59, 2016.
[https://doi.org/10.7779/JKSNT.2016.36.1.53]

-
Rose, J. L., Pilarski, A., and Ditri, J., “An Approach to Guided Wave Mode Selection for Inspection of Laminated Plate,” Journal of Reinforced Plastics and Composites, Vol. 12, No. 5, pp. 536-544, 1993.
[https://doi.org/10.1177/073168449301200504]

-
Michaels, J. E. and Michaels, T. E., “Guided Wave Signal Processing and Image Fusion for in Situ Damage Localization in Plates,” Wave Motion, Vol. 44, No. 6, pp. 482-492, 2007.
[https://doi.org/10.1016/j.wavemoti.2007.02.008]

-
Cho, Y. and Rose, J. L., “A Boundary Element Solution for a Mode Conversion Study on the Edge Reflection of Lamb Waves,” The Journal of the Acoustical Society of America, Vol. 99, No. 4, pp. 2097-2109, 1996.
[https://doi.org/10.1121/1.415396]

-
Cho, Y., Hongerholt, D. D., and Rose, J. L., “Lamb Wave Scattering Analysis for Reflector Characterization,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 44, No. 1, pp. 44-52, 1997.
[https://doi.org/10.1109/58.585189]

-
Cho, Y., “Estimation of Ultrasonic Guided Wave Mode Conversion in a Plate with Thickness Variation,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 47, No. 3, pp. 591-603, 2000.
[https://doi.org/10.1109/58.842046]

-
Lu, Y., Ye, L., Su, Z., and Yang, C., “Quantitative Assessment of Through-Thickness Crack Size Based on Lamb Wave Scattering in Aluminium Plates,” NDT & E International, Vol. 41, No. 1, pp. 59-68, 2008.
[https://doi.org/10.1016/j.ndteint.2007.07.003]

-
Benmeddour, F., Grondel, S., Assaad, J., and Moulin, E., “Experimental Study of the A0 and S0 Lamb Waves Interaction with Symmetrical Notches,” Ultrasonics, Vol. 49, No. 2, pp. 202-205, 2009.
[https://doi.org/10.1016/j.ultras.2008.08.002]

-
Lowe, M. and Diligent, O., “Low-Frequency Reflection Characteristics of the S0 Lamb Wave from a Rectangular Notch in a Plate,” The Journal of the Acoustical Society of America, Vol. 111, No. 1, pp. 64-74, 2002.
[https://doi.org/10.1121/1.1424866]

-
Lowe, M. J., Cawley, P., Kao, J., and Diligent, O., “The Low Frequency Reflection Characteristics of the Fundamental Antisymmetric Lamb Wave A0 from a Rectangular Notch in a Plate,” The Journal of the Acoustical Society of America, Vol. 112, No. 6, pp. 2612-2622, 2002.
[https://doi.org/10.1121/1.1512702]

-
Cho, Y., “Estimation of Ultrasonic Guided Wave Mode Conversion in a Plate with Thickness Variation,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 47, No. 3, pp. 591-603, 2000.
[https://doi.org/10.1109/58.842046]

-
Wang, S., Huang, S., and Zhao, W., “Simulation of Lamb Wave’s Interactions with Transverse Internal Defects in an Elastic Plate,” Ultrasonics, Vol. 51, No. 4, pp. 432-440, 2011.
[https://doi.org/10.1016/j.ultras.2010.11.009]

-
Park, J. W., Cho, Y. H., and Lee, J. S., “Finite Element Analysis of Scattering Signal from Slope Angle of Notch Type Defects on the Plate Surface,” Journal of the Korean Society for Nondestructive Testing, Vol. 37, No. 3, pp. 139-147, 2017.
[https://doi.org/10.7779/JKSNT.2017.37.3.139]

-
Rose, J. L., “Ultrasonic Guided Waves in Solid Media,” Cambridge University Press, 2014.
[https://doi.org/10.1017/CBO9781107273610]


Assistant Professor in the School of Mechanical Engineering, Changwon National University. His research interest is wave propagation analysis for NDE and SHM
E-mail: jaesun@changown.ac.kr