압축 및 내압을 받는 고무 오링의 거동 특성에 관한 연구

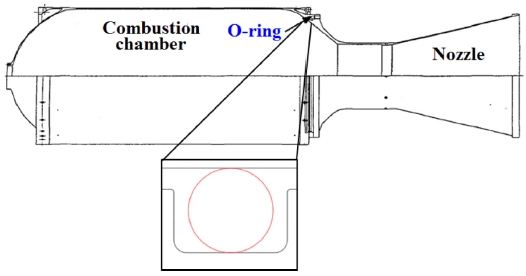
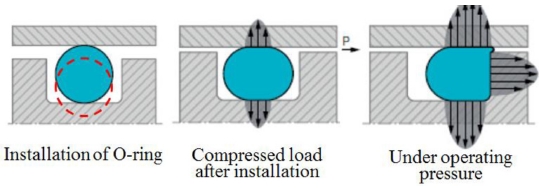
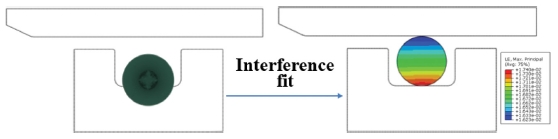
Fig. 1은 일반적인 고체추진기관에 적용된 오링의 모습을 나타내고, Fig. 2는 오링의 작동 개념을 나타낸다. 오링은 초기에 사각형 그루브에 위치하게 된다. 이때 그루브 직경보다 오링의 내경이 작기 때문에 오링은 어느 정도의 신장률(Stretch Ratio)를 갖게 된다. 이 상태에서 오링이 장착된 Nozzle이 연소관에 조립되면서 오링은 압축하중을 받게 된다. 이후 연소관에서 발생된 고압의 가스에 의해 오링은 추가적인 압력하중을 받게 되어 최종적인 밀봉을 위한 접촉응력을 발생시키게 된다.

Fig. 1

O-ring part of solid rocket motor11 (Adapted from Ref. 11 on the basis of open access)

Fig. 2

Operating principle of O-ring3 (Adapted from Ref. 3 on the basis of open access)

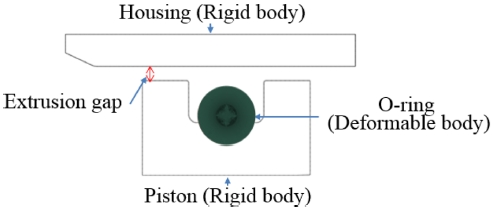
본 논문에서는 압축 및 내압을 받는 오링의 거동 특성 분석을 위해 Fig. 3에서 보는 바와 같이 구조해석 상용 S/W인 ABAQUS의 2D 축대칭 모델을 이용하였다. Housing과 Piston은 강체요소(Rigid Body)로 모델링 하였고 오링은 CAX4H (4-Node Bilinear Axisymmetric Quadrilateral, Hybrid, Constant Pressure) 요소 타입으로 Deformable Body로 구성하였으며 Node 수는 8,239, Element 수는 6,417개이다. 특히 오링 소재인 고무의 비압축성 거동 모사를 위해 Hybrid Element를 사용하였다.

Fig. 3

2D axisymmetric model of O-ring for FEM

고무의 초기 신장률은 약 1.8%가 되도록 설정하였고 Extrusion Gap은 0.1, 0.08, 0.05 mm로 각각 설정하였다. 또한 오링과 Housing, Piston과의 마찰계수로는 0.2, 0.15, 0.13 등으로 변경해 가면서 접촉응력에 대해 미치는 영향에 대해 검토 하였고, 작동 압력으로는 13 MPa를 적용 하였다. 오링 소재인 고무의 점탄성(Viscoelastic) 특성을 구현하여 응력 완화(Stress Relaxation) 현상이 미치는 영향에 대해서도 분석하였다.

본 논문에서는 Fig. 2에 나와있는 오링의 작동 개념을 구현하기 위하여 아래와 같은 단계로 해석을 수행하였다.

Step #1 : 피스톤 그루브에 오링 장착(Interference Fit)
Step #2 : Compression Load 부가
Step #3 : Stress Relaxation
Step #4 : 작동압력 13 MPa 부가
*Step #3은 오링의 점탄성 특성 고려시에만 적용

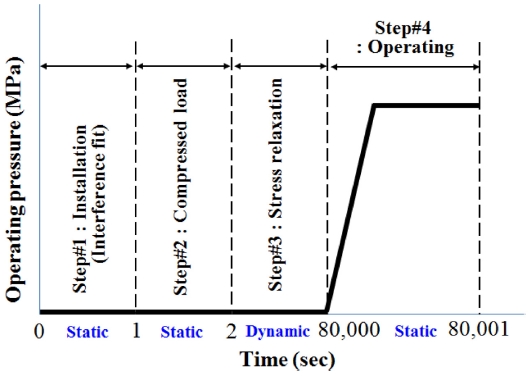
Fig. 4는 해석 단계별 Time Curve를 나타낸다.

Fig. 4

Time curve of the analysis

고체추진기관의 경우 Nozzle이 연소관에 조립되어 오링이 압축하중을 받은후 일정기간 제품을 보관하게 된다. 이때 오링 소재인 고무의 점탄성(Viscoelastic) 특성으로 인해 오링에는 응력완화(Stress Relaxation) 현상이 발생하게 된다. 이후 고체추진기관이 작동할 때 작동압력 13 MPa이 작용하게 된다. Step #1은 정적(Static) 해석으로 이때 오링의 내경은 사각형 그루부 내경보다 작기 때문에 Fig. 5에서 보는 바와 같이 중첩(Overlap)이 발생되게 된다. 이 경우 해석에서는 오링과 그루브 내경이 접촉을 이루게 하기 위해 초기 중첩된 부분을 점진적으로 제거하여야 한다. 이때 오링에는 그에 따른 응력과 변형률이 발생하도록 설정 하여야 한다. 본 논문에서는 이를 구현하기 위해 ABAQUS S/W 2016에서 제공하는 Interference Fit 기능을 이용하였다. Fig. 5는 오링의 초기 위치 및 피스톤에 조립되었을 때, 즉 Interference Fit이 적용된 후의 형상을 나타낸다.

Fig. 5

Results of interference fit

Step #2는 정적(Static) 해석으로 Nozzle이 연소관에 장착될 때 발생되는 압축하중을 부가 하였다. 압축하중은 Fig. 3에서 Extrusion Gap이 각각 0.1, 0.08, 0.05 mm가 되도록 변위제어를 통해 구현하였다. Step #4는 동적(Dynamic) 해석으로 오링 고무의 점탄성(Viscoelastic) 특성을 고려하여 응력완화(Stress Relaxation) 해석을 수행 하였다. Step #5는 정적(Static) 해석으로 오링에 작동 유체의 작동압력을 부가하여 오링의 거동을 분석 하였다.

초탄성 물질은 응력과 변형률 사이의 관계를 변형률 에너지 밀도 함수(Strain Energy Density Function)을 통해 얻는다. 이를 통해 변형률이 100-700%에 이르는 대변형에 대해서도 응력과 변형률의 관계를 구할 수 있다. 따라서 각 상황에 맞는 적절한 변형률 에너지 밀도함수를 선정하는 것이 중요하다. 변형률 에너지 밀도 함수에는 크게 미소 구조 관점에서 접근하는 물리적 모델로 Arruda-Boyce와 Van der Waals 모델이 있고, 연속체 역학의 관점에서 접근하는 현상학적인 모델로 Polynomial, Ogden 및 Marlow 모델이 있다. Polynomial 모델 중 1차 Full Polynomial 모델을 Mooney-Rivlin 모델이라고 하며, 2nd Stretch Invariant의 영향을 제거한 Reduced Polynomial 모델의 1차는 Neo-Hooken 이라고 하며, 3차를 Yeoh 모델이라고 한다. 본 논문에서는 관련 논문³에 발표된 NBR (Nitrile Butadiene Rubber) 고무의 단축인장 시험(Uniaxial Tension Test), 이축인장시험(Biaxial Tension Test), 순수전단시험(Pure Shear Test) 결과를 이용하여 Ogden Model을 이용하였다. Ogden 모델은 다음과 같이 연신률의 함수로 표현된다.

본 연구에서는 고무 재료를 비압축성 물질로 가정하여 J = 1이 되고, 3차항까지 고려하여 아래와 같은 모델을 사용 하였다.

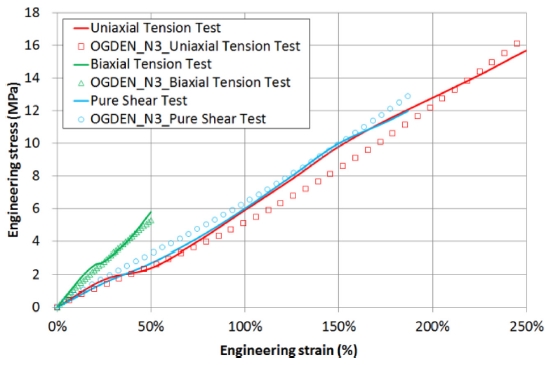
Fig. 6은 본 논문에서 사용할 NBR 고무의 시험결과를 나타내며 Ref. 3에서 발췌하여 적용하였다. 본 연구에서는 Ref. 3의 데이터를 이용하여 Ogden 모델로 Curve-Fitting하여 적용 하였고 Table 1은 도출된 Ogden 모델의 상수 값을 나타낸다.

Fig. 6

Results of curve-fitting for NBR3 (Adapted from Ref. 3 on the basis of open access)

Table 1

Ogden strain energy function of NBR

Lindley^6,7와 Karaszkiewicz⁸는 헤르츠 접촉이론(Hertzian Contact Theory)을 이용하여 오링의 압축하중을 아래 식(3)과 식(4)로 제시하였다.²

여기서, D는 오링의 평균 직경(Mean Diameter), d는 오링 단면적의 직경(Cross-Section Diameter), E는 탄성계수, C = e/d로 압축변위와 오링 단면적의 직경의 비이다. 또한 Lindley^6,7와 Karaszkiewicz⁸는 접촉폭(Contact Width) b을 식(5)와 식(6)으로 제시하였다.²

Lindley^6,7는 최대접촉응력 및 접촉응력 분포를 식(7)과 식(8)로 제시하였다.

여기서 x는 고무 오링의 반경 방향 위치를 나타낸다. 식(7) 및 식(8)에서 볼 수 있듯 접촉응력의 분포식은 재료 물성치로는 탄성계수 E만 사용하고 있음을 알 수 있다.² 고무 오링의 점탄성(Viscoelastic) 특성을 고려한 응력완화(Stress Relaxation) 연구에서도 탄성계수 E 값만 완화된 값을 쓰면 식(7) 및 식(8)이 동일하게 적용될 수 있다. 완화된 탄성계수 E 값은 식(9), 식(10)으로 나타낼 수 있다.²

식(10)을 식(9)에 대입하면 완화된 탄성계수는 식(11)로 나타낼 수 있다.²

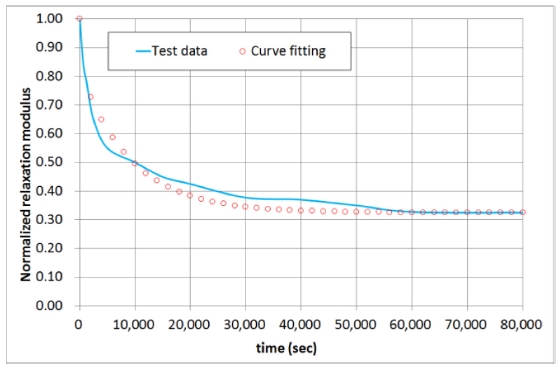
여기서 α_j는 Proney 계수이고, τ_j 값과 함께 완화된 탄성 계수 데이터로부터 구한다. 본 논문에서는 Ref. 5의 완화 탄성계수(Relaxation Modulus) 시험 데이터를 이용하였다. Fig. 7은 Ref. 5에서 발췌한 응력완화 탄성계수 시험 데이터에 대해 Curve-Fitting을 수행한 결과이며, Table 2는 이로부터 구한 α_j와 τ_j값을 나타낸다. Fig. 7에서 보는 바와 같이 응력 완화(Stress Relaxation)는 점탄성 특성을 가지고 있는 고무 오링에 힘을 가하여 그 상태를 유지하고 있더라도 오링 내부의 응력이 시간과 더불어 감소하는 특성을 의미한다.

Fig. 7

Results of curve-fitting for relaxation modulus5 (Adapted from Ref. 5 on the basis of open access)

Table 2

Material constant for relaxation modulus

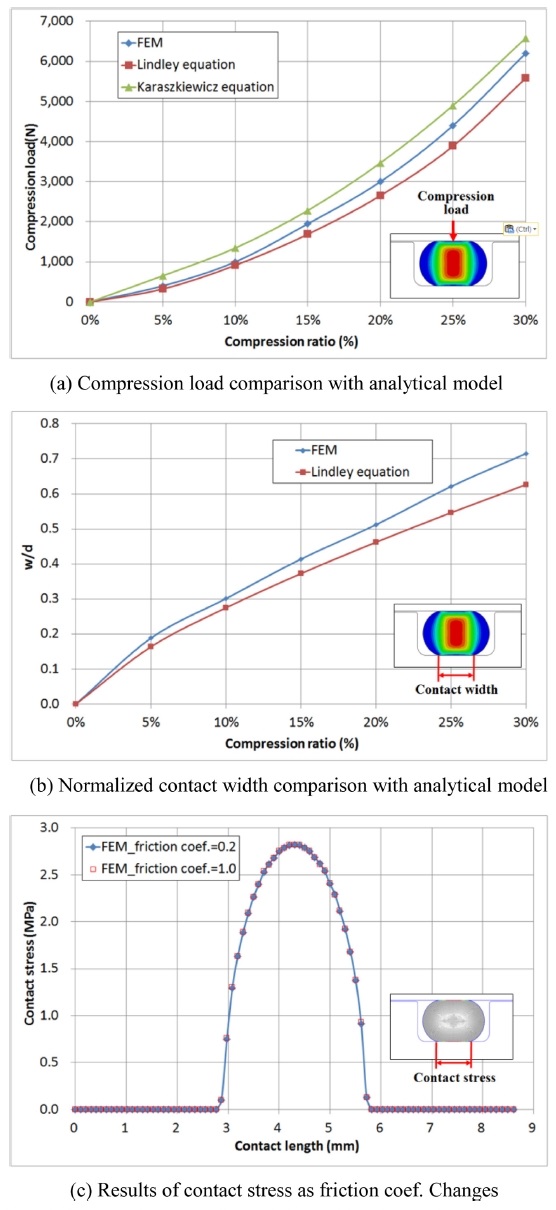
해석 모델의 검증을 위하여 측면부는 구속되어 있지 않고 작동 내압이 가해지지 않은 상태에서 단순히 축 방향으로만 압축이 가해질 때 유한요소 해석 결과와 2.2.2절에서 제시한 Lindley,^6,7 Karaszkiewica⁸의 모델로 예측한 결과를 비교하였다. Fig. 8(a)는 압축률에 따른 압축하중을 비교한 것이다. Karaszkiewica⁸의 모델은 FEM 해석결과 대비 전 압축 영역에서 전체적으로 크게 나타났으며 Lindley^6,7의 모델은 10% 압축률까지는 FEM과 유사 하였으나 10% 이상의 압축률에서는 FEM 대비 조금 낮은 경향을 나타내었다. Fir. 8(b)는 압축률에 따른 접촉폭을 비교한 것으로 FEM 해석결과 대비 Lindley^6,7 모델의 값이 압축률이 증가할수록 조금 더 작게 나타났다.

Fig. 8

FEM results comparison with analytical model

Fig. 8(c)는 압축률이 20%일 때 마찰계수 변화에 따른 접촉응력 분포도를 나타낸다. 접촉응력의 해석 결과는 전형적인 Hertz 응력 분포를 잘 나타내고 있음을 확인할 수 있다. 마찰계수를 0.2에서 1.0까지 변화 시켰을 때에도 단순히 압축하중만을 부가했을 경우에는 접촉 응력에 큰 변화를 가져오지 않는 것을 확인할 수 있다. Fig. 8의 결과를 종합해 볼 때 해석모델과 이론적 예측 모델의 값이 일부 차이는 있으나 오링 소재인 고무의 비선형적 특성, 접촉 응력의 비선형적 특성 등을 고려할 때 해석모델은 타당성을 확보하고 있는 것으로 보인다.

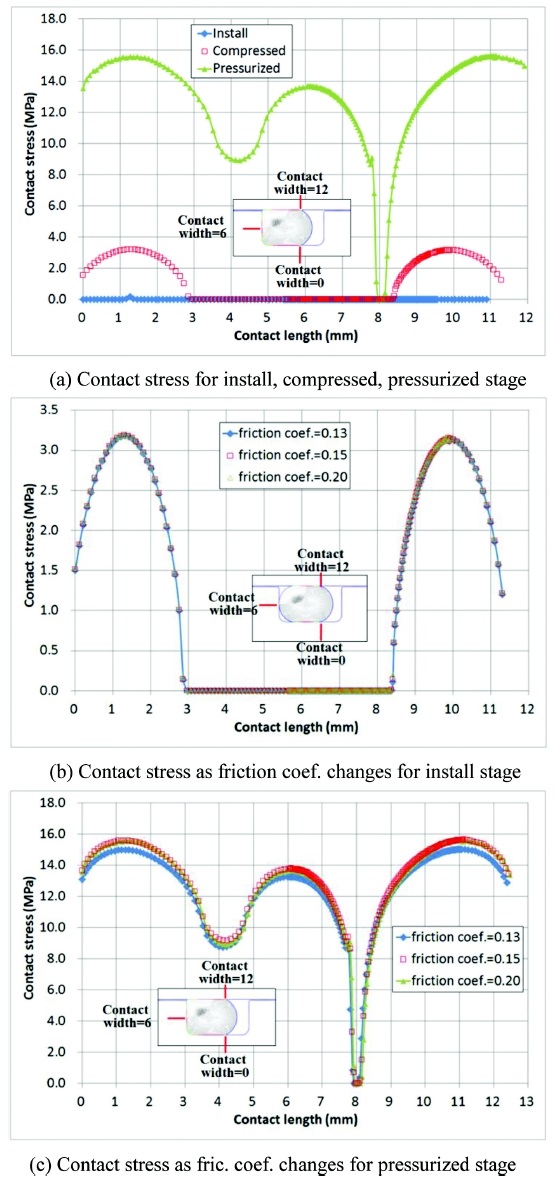
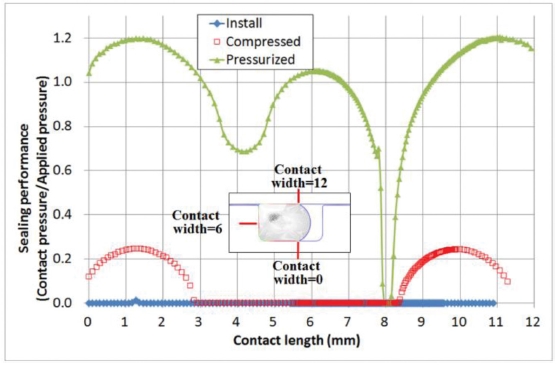
Fig. 9(a)는 오링이 Fig. 2에 나와있는 각 단계, 즉 Install, Compressed, Pressurized 각 단계별 접촉응력의 분포도를 나타낸다. 오링이 초기 위치에 장착되는 Install 단계에서는 매우 낮은 접촉응력을 형성하게 되고, 압축하중을 받는 Compressed 단계에서 전형적인 Hertz 응력분포를 나타내고 있다. 이후 내압이 작용되는 Pressurized 단계에서는 오링이 그루브 상하면과 측면부에 접촉이 되면서 Hertz 응력분포가 조금씩 일그러 짐을 확인할 수 있다.

Fig. 9

Contact stress for install, compressed, pressurized stage

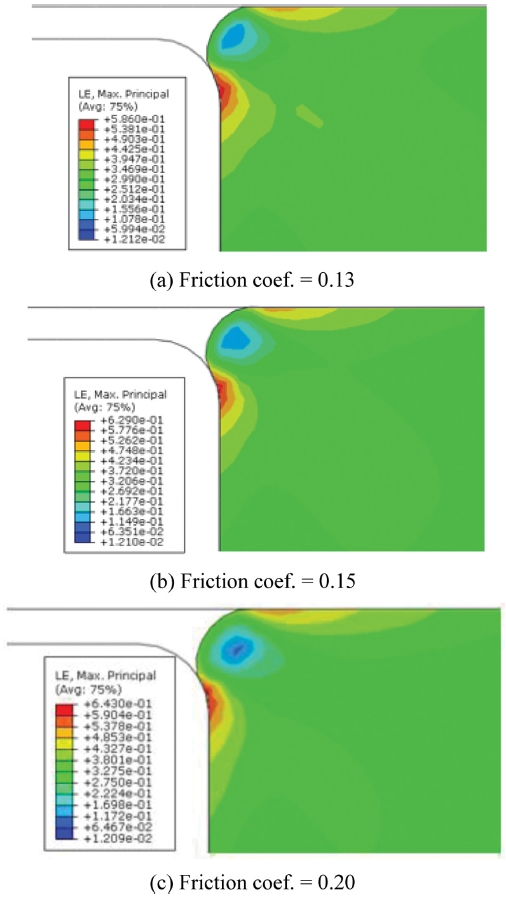
Fig. 9(b)는 Install 단계에서 마찰계수에 따른 접촉응력의 분포를 나타낸다. Install 단계에서는 오링의 접촉 상, 하면 모두에서 마찰계수가 0.13에서 0.20까지 변할 때 접촉응력의 변화는 미미함을 확인할 수 있다. Fig. 9(c)는 Pressurized 단계에서 마찰계수에 따른 접촉응력의 분포를 나타낸다. 마찰계수가 0.13일 때보다 0.15, 0.20일 때 접촉 응력은 소폭 상승 함을 알 수 있다. 그리고 Fig. 10에서 볼 수 있듯 마찰계수가 0.13, 0.15, 0.20으로 증가할 때 Extrusion Gap 부근에서 오링에서 발생하는 최대 Strain 값은 0.59, 0.63(7% 상승), 0.64(8.5% 상승)로 상승함을 확인할 수 있다. 이는 마찰계수가 증가함으로써 Extrusion Gap으로 빠져나가는 고무를 피스톤 면이 잡아주는 영향이 더 크기 때문인 것으로 분석 된다.

Fig. 10

Max. principal strain as fric. coef. changes

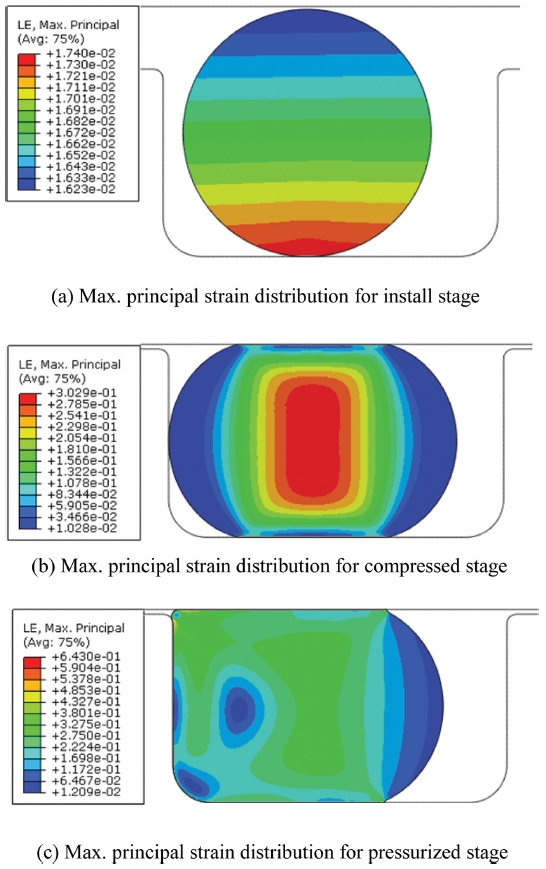
Fig. 11은 Install, Compressed, Pressurized 각 단계별 오링의 Max. Principal Strain 분포를 나타낸다. Install 단계에서는 그루부와 접촉되는 면 부위에서 최대 값이 나타나며, Compressed 단계에서는 오링 내부에서 최대값이 나타난다. 이후 Pressurized 단계에서는 Strain 최대값 위치가 Extrusion Gap 부근으로 이동함을 확인할 수 있다.

Fig. 11

Max. principal strain for install, compressed, pressurized

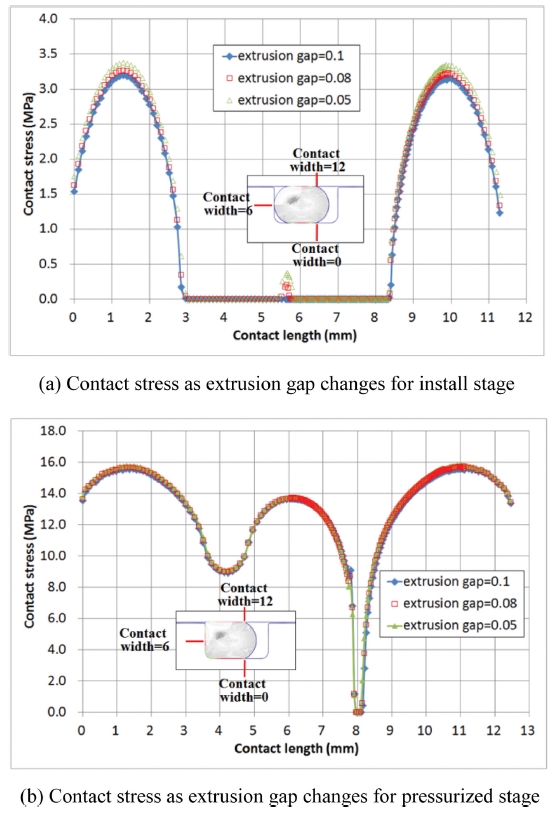
Fig. 12는 Install, Pressurized 단계별 Extrusion Gap을 0.05 mm에서 0.08 mm, 0.1 mm로 변화시켰을 때의 접촉응력 분포를 나타낸다. Install 단계에서는 Gap이 0.1 mm에서 0.05 mm로 작아짐에 따라 최대 접촉 응력이 소폭 상승함을 확인할 수 있다. 이는 Gap이 작아짐에 따라 오링의 압축률이 높아지기 때문인 것으로 분석된다. 하지만 Pressurized 단계에서는 Gap 변화에 따라 접촉응력의 변화가 거의 발생 하지 않았다. Fig. 13은 오링이 장착, 구동되는 각 단계별 밀봉 성능을 나타낸다. 오링이 작동압력에 대해 밀봉 성능을 발휘 하기 위해서는 작동압력보다 접촉 압력이 높아야 한다. 따라서 y축에는 작동압력 대비 접촉응력의 비를 나타내어 각 단계별 밀봉 성능 수준을 확인할 수 있도록 하였다.^1,4 Fig. 13에서 볼 수 있듯 Install과 Compressed 단계에서는 밀봉성능 지수가 0.3 이하 수준으로 낮음을 알 수 있다. 하지만 작동압력이 오링에 작용하게 되면 오링과 피스톤, 하우징과의 접촉면에서 밀봉성능 지수가 1 이상으로 정상적인 밀봉기능을 하고 있음을 확인할 수 있다.

Fig. 12

Contact stress as extrusion gap changes

Fig. 13

Sealing performance for install, compressed, pressurized

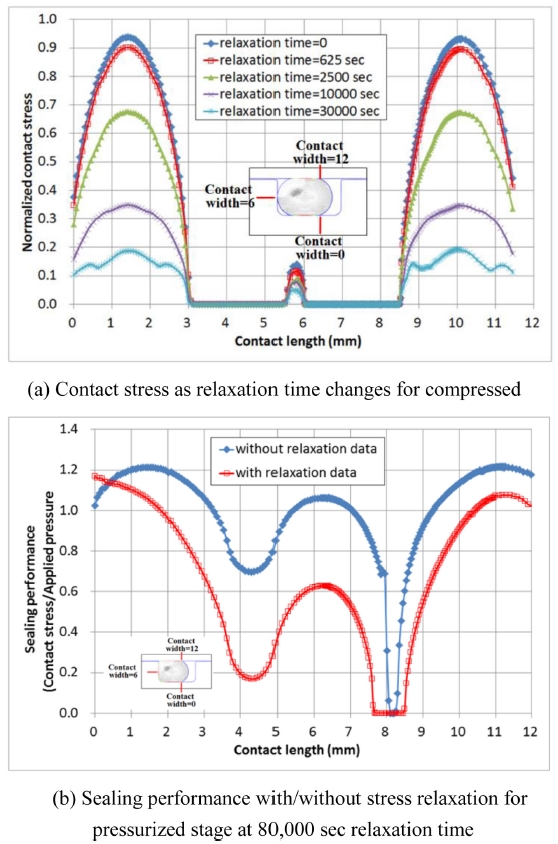
Fig. 14(a)는 오링 고무의 점탄성(Viscoelastic) 특징인 응력완화(Stress Relaxation) 효과를 고려했을 때의 Compressed 단계에서 나타나는 접촉응력의 변화를 응력완화 시간대별로 나타낸 것이다. 완화 시간이 2,500 sec일 때 접촉응력 지수가 완화시간 0초 대비 0.94에서 0.67로 약 29% 감소하고, 완화시간이 10,000 sec 경과하면 접촉응력 지수는 0.34 수준으로 64% 이상 감소함을 확인할 수 있다. Fig. 14(b)는 Pressurized 단계에서 오링 고무의 응력완화가 오링의 밀봉 성능에 미치는 영향을 나타낸 것으로 완화시간 80,000 sec에서의 값을 나타낸다. Contact Length 6 mm 위치에서 밀봉성능은 응력완화를 고려하지 않았을 경우 1.06에서 응력완화를 고려했을 때 0.63으로 약 42% 감소함을 확인할 수 있다. 또한 응력완화를 고려했을 때 Contact Length 일부 구간을 제외하고 전체적으로 밀봉성능 지수가 1 이하로 오링이 밀봉기능으로서의 제기능을 수행하지 못함을 확인할 수 있다. 따라서 기계구조물에 대한 오링 설계시 고무의 점탄성(Viscoelastic) 특성에서 기인한 응력완화(Stress Relaxation) 효과를 반드시 고려야 함을 알 수 있다.

Fig. 14

Contact stress change with/without stress relaxation