자기교란에 의한 방위각 추정 오차 최소화를 위해 기구학적 구속조건을 투영한 칼만 필터

1. 서론

이동체의 3차원 자세를 추정하기 위하여 저가의 초소형 관성/자기센서, 즉 IMMU (Inertial And Magnetic Measurement Unit)가 유비쿼터스 센싱, 재활의학, 스포츠 그리고 이동형 로봇 등 다양한 분야에서 사용되고 있다.^1-5 여기서, IMMU는 3축 가속도계, 3축 자이로스코프 그리고 3축 지자기센서로 이루어져 있다. 보편적인 IMMU기반 자세 추정 방법은 자이로스코프로 측정된 각속도 적분을 통한 예측 과정과 적분 과정에서 발생하는 표류오차(Drift Error)를 억제하기 위해 가속도계와 지자기센서를 통해 얻은 수직 및 수평 참조벡터를 이용한 보정 과정을 거친다. 이때, 수직 및 수평 참조벡터는 중력가속도 벡터와 지구자기장 벡터이며, 각각은 물체의 기울기(Tilt)와 방위각(Yaw)을 보정하기 위해 사용된다.^6,7

하지만 동적 조건이나 자기적으로 균등하지 않은 환경에서는 각각 외부가속도와 자기교란과 같은 교란성분들로 인해 정확한 참조벡터를 얻기 어렵다. 이로 인해 자세 추정 정확성이 저하될 수 있으며, 특히 주변 자성체에 의해 흔히 발생할 수 있는 자기교란으로 인한 방위각 추정 정확성 저하 문제는 매우 심각하다.^8-10

이에 대한 해결책으로서 다양한 자기교란 보상 메커니즘을 가지는 방위각 추정 알고리즘들이 제안되었다.^11-14 Ligorio 등¹¹은 자기교란 보상을 위해 1차 마르코프 체인(Markov Chain)기반의 자기교란 모델링을 사용한 방위각 추정 칼만 필터를 제안하였다. Lee와 Park¹²은 자기교란의 크기에 대한 문턱값(Threshold)을 설정하여 벡터교환을 통해 자기교란에 대응하였으며, 최미진과 이정근¹³은 더 나아가 자기교란 크기에 따라 1차 및 2차 마르코프 체인 기반 모델을 선택적으로 사용하는 방위각 추정 칼만 필터를 통해 자기교란 보상을 구현하였다. Madgwick 등¹⁴은 자기교란보상을 위해 최적화 기법인 경사 강하법(Gradient Descent)을 적용하였다.

이러한 기존의 자기교란 보상 메커니즘들은 단 시간 동안의 강하지 않은 자기교란에 대하여 뛰어난 보상 성능을 보이기도 하였다. 하지만, 이들은 근본적으로 마르코프 체인 등의 확률론적 모델을 사용하거나 또는 이미 훼손된 지자기센서의 측정 신호를 기반으로 한 최적화 기법을 사용함으로써 보상성능의 한계가 있을 수 밖에 없다. 즉, 이들 방법으로는 심각한 자기교란으로 인해 야기되는 방위각 추정 정확성의 급격한 저하문제를 해결할 수 없다.

기존 방법들은 대부분 구속되지 않은 단일물체를 대상으로 하고 있는 반면, 실제 대부분의 시스템들은 인간의 신체 또는 로봇과 같이 기구학적으로 구속되어 있다는 점에 주목할 필요가 있다. 이때, 시스템이 가지고 있는 기구학적 구속조건은 주로 조인트로 연결된 두 링크 각각의 자세 추정 정확성을 높이기 위함이 아니라 두 링크의 상대적인 자세에 해당하는 조인트 각도 추정 정확성을 높이기 위해 사용된다.^15,16 하지만, 기구학적 구속조건은 각 링크의 자세 추정 정확성을 높이기 위해 사용될 수 있으며, 최미진과 이정근¹⁷은 기구학적 구속조건을 이용하여 외부가속도로 인한 부정확성을 근본적으로 제거하고, 이를 통해 가속조건에서도 강건한 기울기 추정 칼만 필터를 제안한 바 있다.

본 논문에서는 자기교란에 의한 방위각 추정 오차를 최소화하기 위해 기구학적 구속조건을 투영한 새로운 방위각 추정 칼만 필터를 제안한다. 제안 알고리즘은 구면 조인트(Spherical Joint)로 연결된 2링크 시스템을 대상으로 하며, 자기교란보상 메커니즘을 지닌 기존의 방위각 추정 칼만 필터¹¹에 기구학적 구속조건을 투영한 칼만 필터다. 이때 사용되는 기구학적 구속조건은 구면 조인트의 가속도 구속조건으로 지자기센서 신호를 사용하지 않고 가속도계와 자이로스코프 신호를 이용하여 자기교란을 보상한다. 제안 칼만 필터의 성능을 구면 조인트로 연결된 두 링크에 임의의 자기교란을 가하는 다양한 자기교란 조건에서의 실험을 통해 검증하였다.

2. 방위각 추정 칼만 필터

2.2 방위각 추정 칼만 필터

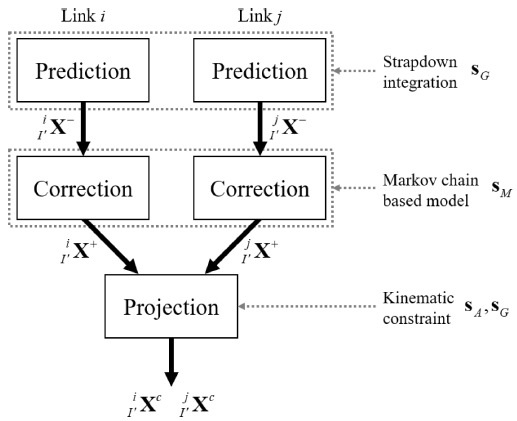
제안하는 칼만 필터는 기존의 방위각 추정 칼만 필터¹¹를 기반으로 하며, 자기교란으로 인한 부정확성을 감소시키기 위해 추가적으로 기구학적 구속조건을 폐루프 투영 방법¹⁹을 이용하여 기존 칼만 필터에 투영하였다(Fig. 1 참조). 이때 제안 칼만 필터는 예측, 보정 그리고 투영 과정을 거치며, 이산시간 t에 대한 칼만 필터식은 다음과 같다.

Fig. 1

Structure of the proposed Kalman filter

$\[ {\mathbf{\text{x}}}_t^{-}={\mathbf{\text{F}}}_{t-1}{\mathbf{\text{x}}}_{c,t-1} \]$

(5.1)

$\[ {\mathbf{\text{P}}}_t^{-}={\mathbf{\text{F}}}_{t-1}{\mathbf{\text{P}}}_{c,t-1}{\mathbf{\text{F}}}_{t-1}^T+{\mathbf{\text{Q}}}_{t-1} \]$

(5.2)

$\[ {\mathbf{\text{K}}}_t={\mathbf{\text{P}}}_t^{-}{\mathbf{\text{H}}}^T{\left(\mathbf{\text{H}}{\mathbf{\text{P}}}_t^{-}{\mathbf{\text{H}}}^T+{\mathbf{\text{R}}}_t\right)}^{-1} \]$

(6.1)

$\[ {\mathbf{\text{x}}}_t^{+}={\mathbf{\text{x}}}_t^{-}+{\mathbf{\text{K}}}_t\left({\mathbf{\text{z}}}_t-\mathbf{\text{H}}{\mathbf{\text{x}}}_t^{-}\right) \]$

(6.2)

$\[ {\mathbf{\text{P}}}_t^{+}=\left(\mathbf{\text{I}}-{\mathbf{\text{K}}}_t\mathbf{\text{H}}\right){\mathbf{\text{P}}}_t^{-} \]$

(6.3)

$\[ {\mathbf{\text{K}}}_{c,t}={\mathbf{\text{P}}}_t^{+}{\mathbf{\text{C}}}_t^T{\left({\mathbf{\text{C}}}_t{\mathbf{\text{P}}}_t^{+}{\mathbf{\text{C}}}_t^T+M_t\right)}^{-1} \]$

(7.1)

$\[ {\mathbf{\text{x}}}_{c,t}={\mathbf{\text{x}}}_t^{+}+{\mathbf{\text{K}}}_{c,t}\left(b_t-{\mathbf{\text{C}}}_t{\mathbf{\text{x}}}_t^{+}\right) \]$

(7.2)

$\[ {\mathbf{\text{P}}}_{c,t}=\left(\mathbf{\text{I}}-{\mathbf{\text{K}}}_{c,t}{\mathbf{\text{C}}}_t\right){\mathbf{\text{P}}}_t^{+} \]$

(7.3)

여기서, x는 상태벡터, F는 천이 행렬(Transient Matrix), P는 오차 공분산 행렬(Error Covariance Matrix), Q는 진행잡음에 대한 공분산 행렬(Covariance Matrix), K는 칼만이득, H는 관측 행렬(Observation Matrix), R은 측정잡음에 대한 공분산 행렬이며, z는 측정벡터이다. 식(5)와 식(6)은 각각 예측과 보정 과정의 칼만 필터식으로 기존 칼만 필터¹¹와 동일하며, –와 +표기는 각각 예측값과 보정값을 의미한다. 그리고, 투영 과정인 식(7)의 요소들은 기구학적 구속조건식에 의해 결정된다.

기존 칼만 필터의 경우 상태벡터 $$ \mathbf{\text{x}}={\left[\begin{array}{cc}{{}_{I^{\text{'}}}{}^S\mathbf{\text{X}}}^T& {{}^S\mathbf{\text{d}}}^T\end{array}\right]}^T$$를 사용하며, 이산시간 t에 대하여 다음과 같은 1차 마르코프 기반 자기교란 모델을 사용한다.¹¹

$\[ {{}^S\mathbf{\text{d}}}_t=c_{d1} {{}^S\mathbf{\text{d}}}_{t-1}+c_{d2}{\mathbf{\text{ε}}}_{d,t-1} \]$

(8)

여기서, c_d1와 c_d2는 자기교란 모델 파라미터이며, ε_d는 자기교란 모델 잡음이다.

천이 행렬 F와 관측 행렬 H는 1차 스트랩다운 적분식과 식(8)에 의해 다음과 같이 정리된다. ¹¹

$\[ {\mathbf{\text{F}}}_{t-1}=\left[\begin{array}{cc}{\mathbf{\text{I}}}_{3\times 3}-{}^S{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_{t-1}∆t& {\mathbf{\text{0}}}_{3\times 3}\\ {\mathbf{\text{0}}}_{3\times 3}& {\mathbf{\text{I}}}_{3\times 3}\cdot c_{d1}\end{array}\right] \]$

(9.1)

$\[ \mathbf{\text{H}}=\left[\begin{array}{cc}{\mathbf{\text{I}}}_{3\times 3}& {\mathbf{\text{I}}}_{3\times 3}\end{array}\right] \]$

(9.2)

여기서 틸드(~) 표기는 해당벡터의 외적 행렬을 의미하며, Δt는 센서의 샘플링률을 나타낸다.

기구학적 구속조건 투영 과정에서의 상태벡터 x_c는 다음과 같다.

$\[ {\mathbf{\text{x}}}_c=\left[\begin{array}{c}{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}\\ {}_{I^{\text{'}}}{}^j\mathbf{\text{X}}\end{array}\right] \]$

(10)

기존 칼만 필터에서 상태벡터로 사용되는 자기교란의 경우는 투영 과정을 거쳐 추정된 $$ {}_{I^{\text{'}}}{}^S\mathbf{\text{X}}$$값에 의해 다음과 같이 추정된다.

$\[ {}^S\mathbf{\text{d}}={\mathbf{\text{s}}}_M-‖\mathbf{\text{m}}‖{}_{I^{\text{'}}}{}^S\mathbf{\text{X}} \]$

(11)

기구학적 구속조건을 투영하는 과정에서 사용되는 구면 조인트의 가속도 구속조건식은 다음과 같다.

$\[ {}^I{\mathbf{\text{a}}}_i+{}_i{}^I\ddot{\mathbf{\text{R}}}{}^i{\mathbf{\text{p}}}_i={}^I{\mathbf{\text{a}}}_j+{}_j{}^I\ddot{\mathbf{\text{R}}}{}^j{\mathbf{\text{p}}}_j \]$

(12)

여기서, a는 외부가속도, $$ {}^S{\mathbf{\text{p}}}_S$$는 각 센서좌표계에서 바라본 센서좌표계의 원점에서 조인트 중심까지의 위치벡터이다. 식(12)를 방향 코사인행렬의 미분 공식 $$ {}_S{}^I\dot{\mathbf{\text{R}}}={}_S{}^I\mathbf{\text{R}}{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_S$$을 이용하면 다음과 같이 정리된다.

$\[ \begin{array}{c}{}_i{}^I\mathbf{\text{R}}\left\{{}^i{\mathbf{\text{a}}}_i+\left({\stackrel{~}{\dot{\mathbf{\text{ω}}}}}_i+{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_i{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_i\right){}^i{\mathbf{\text{p}}}_i\right\}\\ ={}_j{}^I\mathbf{\text{R}}\left\{{}^j{\mathbf{\text{a}}}_j+\left({\stackrel{~}{\dot{\mathbf{\text{ω}}}}}_j+{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_j{\stackrel{\mathrm{~}}{\mathbf{\text{ω}}}}_j\right){}^j{\mathbf{\text{p}}}_j\right\}\end{array} \]$

(13)

이를 식(2.2)와 $$ {}^S\mathbf{\text{a}}={\mathbf{\text{s}}}_{AS}-‖\mathbf{\text{g}}‖{}_I{}^S\mathbf{\text{Z}}-{\mathbf{\text{n}}}_A$$을 이용하여 $$ {}_I{}^S\mathbf{\text{X}}$$에 대한 식으로 정리하면 다음과 같다.

$\[ {\left({\mathbf{\text{f}}}_i-{\mathbf{\text{ε}}}_i\right)}^T {}_I{}^i\mathbf{\text{X}}={\left({\mathbf{\text{f}}}_j-{\mathbf{\text{ε}}}_j\right)}^T {}_I{}^j\mathbf{\text{X}} \]$

(14)

여기서, $$ {\mathbf{\text{f}}}_S={\mathbf{\text{s}}}_{AS}+\left({\overline{\dot{\mathbf{\text{s}}}}}_{GS}+{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS}{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS}\right){{}^S\mathbf{\text{p}}}_S$$이며, $$ {\mathbf{\text{ε}}}_S=-{{}^S\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_S{\dot{\mathbf{\text{n}}}}_G+\left({{}^S\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_S{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS}-2{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS} {{}^S\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_S\right){\mathbf{\text{n}}}_G+{\mathbf{\text{n}}}_A$$이다. 위 식을 식(4)를 이용하여 $$ {}_{I^{\text{'}}}{}^S\mathbf{\text{X}}$$에 대한 식으로 재정리하면 다음과 같다.

$\[ \begin{array}{c}{\left({\mathbf{\text{f}}}_i-{\mathbf{\text{ε}}}_i\right)}^T\left({}_{I^{\text{'}}}{}^i\mathbf{\text{X}}+\text{sin}{\theta }_i{}_I{}^i\mathbf{\text{Z}}\right)/\text{cos}{\theta }_i\\ ={\left({\mathbf{\text{f}}}_j-{\mathbf{\text{ε}}}_j\right)}^T\left({}_{I^{\text{'}}}{}^j\mathbf{\text{X}}+\text{sin}{\theta }_j{}_I{}^j\mathbf{\text{Z}}\right)/\text{cos}{\theta }_j\end{array} \]$

(15)

식(15)를 이산시간 t에 대하여 정리하면 다음과 같다.

$\[ \begin{array}{c}\cos {\theta }_{j,t}\sin {\theta }_{i,t}{\mathbf{\text{f}}}_{i,t}^T{{}_I{}^i\mathbf{\text{Z}}}_t-\cos {\theta }_{i,t}\sin {\theta }_{j,t}{\mathbf{\text{f}}}_{j,t}^T{{}_I{}^j\mathbf{\text{Z}}}_t\\ =-\cos {\theta }_{j,t}{\mathbf{\text{f}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t+\cos {\theta }_{i,t}{\mathbf{\text{f}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t+{\nu }_t\end{array} \]$

(16)

여기서, 구속 잡음(Constraint Noise)에 해당하는 v_t를 $$ {{}_{I^{\text{'}}}{}^S\mathbf{\text{X}}}_t={{}_{I^{\text{'}}}{}^S\mathbf{\text{X}}}_t^{+}-{{}_{I^{\text{'}}}{}^S\mathbf{\text{X}}}_{\epsilon ,t}^{+}$$을 이용하여 정리하면 다음과 같다.

$\[ \begin{array}{c}{\nu }_t=\cos {\theta }_{j,t}\sin {\theta }_{i,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_I{}^i\mathbf{\text{Z}}}_t-\cos {\theta }_{i,t}\sin {\theta }_{j,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_I{}^j\mathbf{\text{Z}}}_t\\ +\cos {\theta }_{j,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t^{+}-\cos {\theta }_{i,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t^{+}\\ -\cos {\theta }_{j,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_{\epsilon ,t}^{+}+\cos {\theta }_{i,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_{\epsilon ,t}^{+}\end{array} \]$

(17)

여기서, $$ -\cos {\theta }_{j,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_{\epsilon ,t}^{+}$$와 $$ \cos {\theta }_{i,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_{\epsilon ,t}^{+}$$는 오차의 곱으로 이루어져 있기 때문에 0으로 취급하며, 구속잡음 v_t의 나머지 성분들은 각각 $$ {\mathit{\nu }}_{1,t}=\cos {\theta }_{j,t}\sin {\theta }_{i,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_I{}^i\mathbf{\text{Z}}}_t$$, $$ {\mathit{\nu }}_{2,t}=-\cos {\theta }_{i,t}\sin {\theta }_{j,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_I{}^j\mathbf{\text{Z}}}_t$$, $$ {\mathit{\nu }}_{3,t}=\cos {\theta }_{j,t}{\mathbf{\text{ε}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t^{+}$$ 그리고 $$ {\mathit{\nu }}_{4,t}=\cos {\theta }_{i,t}{\mathbf{\text{ε}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t^{+}$$라고 한다. 이때 구속 잡음은 공분산 $$ M_t\left(=E\left({\nu }_t{\nu }_t^T\right)\right)$$을 갖는다. $$ E\left({\nu }_t{\nu }_t^T\right)$$는 구속 잡음의 각 성분들의 기대값의 합과 동일하며, 각 성분들은 모두 스칼라이므로 aa^T = a^T a를 만족한다. 이에 따라 $$ E\left({\nu }_t{\nu }_t^T\right)=E\left({\nu }_t^T{\nu }_t\right)$$이며, 각 성분들의 기대값은 다음과 같다.

$\[ \begin{array}{c}E\left({\nu }_{1,t}^T{\nu }_{1,t}\right)={\cos }^2{\theta }_{j,t}{\sin }^2{\theta }_{i,t}\left\{{\sigma }_A^2{\left({{}_I{}^i\mathbf{\text{Z}}}_t\right)}^T{{}_I{}^i\mathbf{\text{Z}}}_t\right.\hfill \\ \left.+{\sigma }_G^2{\left({{}_I{}^i\mathbf{\text{Z}}}_t\right)}^T{\mathbf{\text{λ}}}_{i,t}{\mathbf{\text{λ}}}_{i,t}^T{{}_I{}^i\mathbf{\text{Z}}}_t+{\sigma }_{Gdot}^2{\left({{}_I{}^i\mathbf{\text{Z}}}_t\right)}^T{{}^i\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_i{{}^i\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_i^T{{}_I{}^i\mathbf{\text{Z}}}_t\right\}\hfill \end{array} \]$

(18)

$\[ \begin{array}{c}E\left({\nu }_{2,t}^T{\nu }_{2,t}\right)={\cos }^2{\theta }_{i,t}{\sin }^2{\theta }_{j,t}\left\{{\sigma }_A^2{\left({{}_I{}^j\mathbf{\text{Z}}}_t\right)}^T{{}_I{}^j\mathbf{\text{Z}}}_t\right.\hfill \\ \left.+{\sigma }_G^2{\left({{}_I{}^j\mathbf{\text{Z}}}_t\right)}^T{\mathbf{\text{λ}}}_{j,t}{\mathbf{\text{λ}}}_{j,t}^T{{}_I{}^j\mathbf{\text{Z}}}_t+{\sigma }_{Gdot}^2{\left({{}_I{}^j\mathbf{\text{Z}}}_t\right)}^T{{}^j\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_j{{}^j\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_j^T{{}_I{}^j\mathbf{\text{Z}}}_t\right\}\hfill \end{array} \]$

(19)

$\[ \begin{array}{c}E\left({\nu }_{3,t}^T{\nu }_{3,t}\right)={\cos }^2{\theta }_{j,t}\left\{{\sigma }_A^2{\left({{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t\right)}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t\right.\hfill \\ \left.+{\sigma }_G^2{\left({{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t\right)}^T{\mathbf{\text{λ}}}_{i,t}{\mathbf{\text{λ}}}_{i,t}^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t+{\sigma }_{Gdot}^2{\left({{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t\right)}^T{{}^i\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_i{{}^i\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_i^T{{}_{I^{\text{'}}}{}^i\mathbf{\text{X}}}_t\right\}\hfill \end{array} \]$

(20)

$\[ \begin{array}{c}E\left({\nu }_{4,t}^T{\nu }_{4,t}\right)={\cos }^2{\theta }_{i,t}\left\{{\sigma }_A^2{\left({{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t\right)}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t\right.\hfill \\ \left.+{\sigma }_G^2{\left({{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t\right)}^T{\mathbf{\text{λ}}}_{j,t}{\mathbf{\text{λ}}}_{j,t}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t+{\sigma }_{Gdot}^2{\left({{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t\right)}^T{{}^j\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_j{{{}^j\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_j}^T{{}_{I^{\text{'}}}{}^j\mathbf{\text{X}}}_t\right\}\hfill \end{array} \]$

(21)

여기서, $$ {\mathbf{\text{λ}}}_S={{}^S\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_S{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS}-2{\stackrel{\mathrm{~}}{\mathbf{\text{s}}}}_{GS}{{}^S\stackrel{\mathrm{~}}{\mathbf{\text{p}}}}_S$$이며, σ_A, σ_G 그리고 σ_Gdot는 각각 n_A, n_G 그리고 $$ {\dot{\mathbf{\text{n}}}}_G$$의 표준편차이다.

식(16)에 의해 식(7)의 C_t와 b_t가 다음과 같이 정리된다.

$\[ {\mathbf{C}}_t=\left[\begin{array}{cc}-\text{cos}{\theta }_{j,t}{\mathbf{\text{f}}}_{i,t}^T& \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i,t}{\mathbf{\text{f}}}_{j,t}^T\end{array}\right] \]$

(22)

$\[ b_t=\cos {\theta }_{j,t}\text{sin}{\theta }_{i,t}{\mathbf{\text{f}}}_{i,t}^T{{}_I{}^i\mathbf{\text{Z}}}_t-\cos {\theta }_{i,t}\text{sin}{\theta }_{j,t}{\mathbf{\text{f}}}_{j,t}^T{{}_I{}^j\mathbf{\text{Z}}}_t \]$

(23)

기구학적 구속조건은 두 링크의 상대적인 자세만 만족하면 성립되지만, 구속조건 투영 과정에서는 양쪽 링크의 $$ {}_{I^{\text{'}}}{}^S\mathbf{\text{X}}$$가 모두 보정된다는 점을 명심해야 한다. 다시 말해, 투영 과정에서 $$ {}_{I^{\text{'}}}{}^i\mathbf{\text{X}}$$와 $$ {}_{I^{\text{'}}}{}^j\mathbf{\text{X}}$$가 함께 상태벡터로 설정되어 있기 때문에, 자기교란이 발생하지 않은 링크, 즉 기존 칼만 필터만을 사용하여도 방위각 추정 오차가 크지 않은 링크의 오차가 오히려 증가할 수 있다. 이에 대한 해결책으로 제안 방법에서는 투영 과정에서 구해진 칼만이득 K_c,t를 그대로 사용하지 않고, 자기교란 조건에 따라 식(24)와 같이 설정한 $$ {\mathbf{\text{K}}}_{c,t}^{+}$$를 사용한다. 이때 자기교란 조건은 자기교란의 크기 $$ ‖{{}^S\mathbf{\text{d}}}_t^{+}‖$$ Au (Arbitrary Unit)를 통해 구분되었다.

(24)

여기서, th_d는 문턱값(Threshold Value)이며, 본 논문에서는 실험 환경의 자기조건을 고려하여 0.2 Au를 사용하였다.

제안 및 기존 칼만 필터에 사용되는 자기교란 모델 파라미터는 모두 동일하게 설정하였다(c_d1= 0.1, c_d2 = 0.02). 또한, 센서좌표계의 원점에서 조인트 중심까지의 위치벡터를 센서좌표계에서 바라본 위치벡터는 T. Seel 등²⁰의 알고리즘을 통해 구하였으며, 각각 $$ {{}^i\mathbf{\text{p}}}_i={\left[\begin{array}{ccc}51.7& 0.3& -2.5\end{array}\right]}^T$$, $$ {{}^j\mathbf{\text{p}}}_j={\left[\begin{array}{ccc}50.6& 0.1& -2.9\end{array}\right]}^T$$로 단위는 cm이다.

3. 검증실험 및 결과

3.1 검증실험

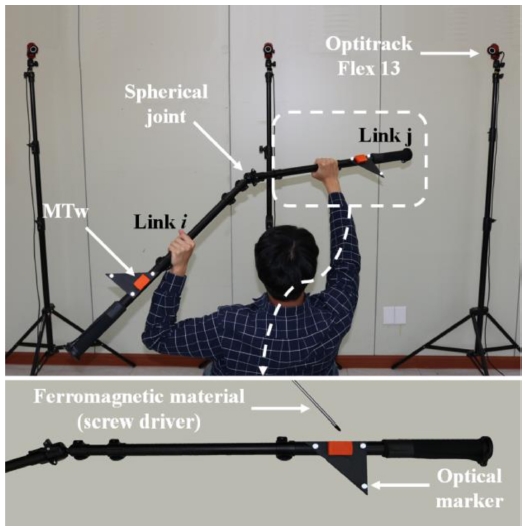
제안 칼만 필터의 성능 검증실험을 위해서 IMMU인 MTw(Xsens Technologies B. V.)와 방위각에 대한 참조값을 얻기 위해 광학식 모션 캡처 시스템인 OptiTrack Flex 13 (NaturalPoint, Inc.)을 사용하였다. 제안 칼만 필터의 성능 검증을 위해 구면 조인트로 연결된 2링크 시스템을 약 2분간 3차원적으로 움직이며, 각각 다른 자기 조건에서 총 3가지 실험을 실시하였다. 실험마다 자기 조건을 다르게 하기 위해서 자성체인 자석드라이버를 이용하여 각 링크에 임의의 자기교란을 가하였다(Fig. 2 참조).

Fig. 2

Experimental setup

Test 1은 링크 i에만 임의의 자기교란을 가하며, 다른 쪽 링크에는 자기교란을 가하지 않았다. Tests 2와 3은 링크 i와 j에 자기교란을 번갈아 가하였으며, 두 실험의 차이는 각 링크에 자기교란을 가하는 시간과 임의의 자기교란을 한 쪽 링크에 가한 후 다른 쪽 링크에 자기교란을 가하기까지의 시간, 즉 두 링크에 모두 자기교란이 가해지지 않는 시간을 다르게 하였다. 이때 Test 2의 경우 자기교란을 가하는 시간은 약 10초이며, 두 링크에 자기교란이 가해지지 않는 시간을 10초로 하였다. Test 3의 경우 자기교란을 가하는 시간은 약 30초이며, 두 링크에 자기교란이 가해지지 않는 시간을 30초로 하였다.

물체의 기울기에 해당하는 $$ {}_I{}^S\mathbf{\text{Z}}$$는 OpriTrack Flex 13을 통해 얻은 값을 사용하였으며, 이는 방위각 추정 성능을 확인하는데 있어 물체의 기울기에 대한 오차가 영향을 미칠 수 있기 때문이다. 이때, 제안 및 기존 칼만 필터¹¹의 요 추정 평균 제곱근 오차(Root Mean Square Error, RMSE)를 비교하였다.

3.2 결과 및 고찰

Fig. 3은 Test 3에서 구면 조인트로 연결된 두 링크에 임의로 가해진 자기교란의 크기와 요 추정 결과 그래프이다. Table 1은 자기 조건이 다른 3가지 실험에서 제안 및 기존 칼만 필터를 사용할 경우 각 링크에 대한 요 추정 RMSE 값이다. 이때, Fig. 3과 Table 1에서 Conventional과 Proposed는 각각 기존 및 제안 칼만 필터를 나타낸다.

Fig. 3

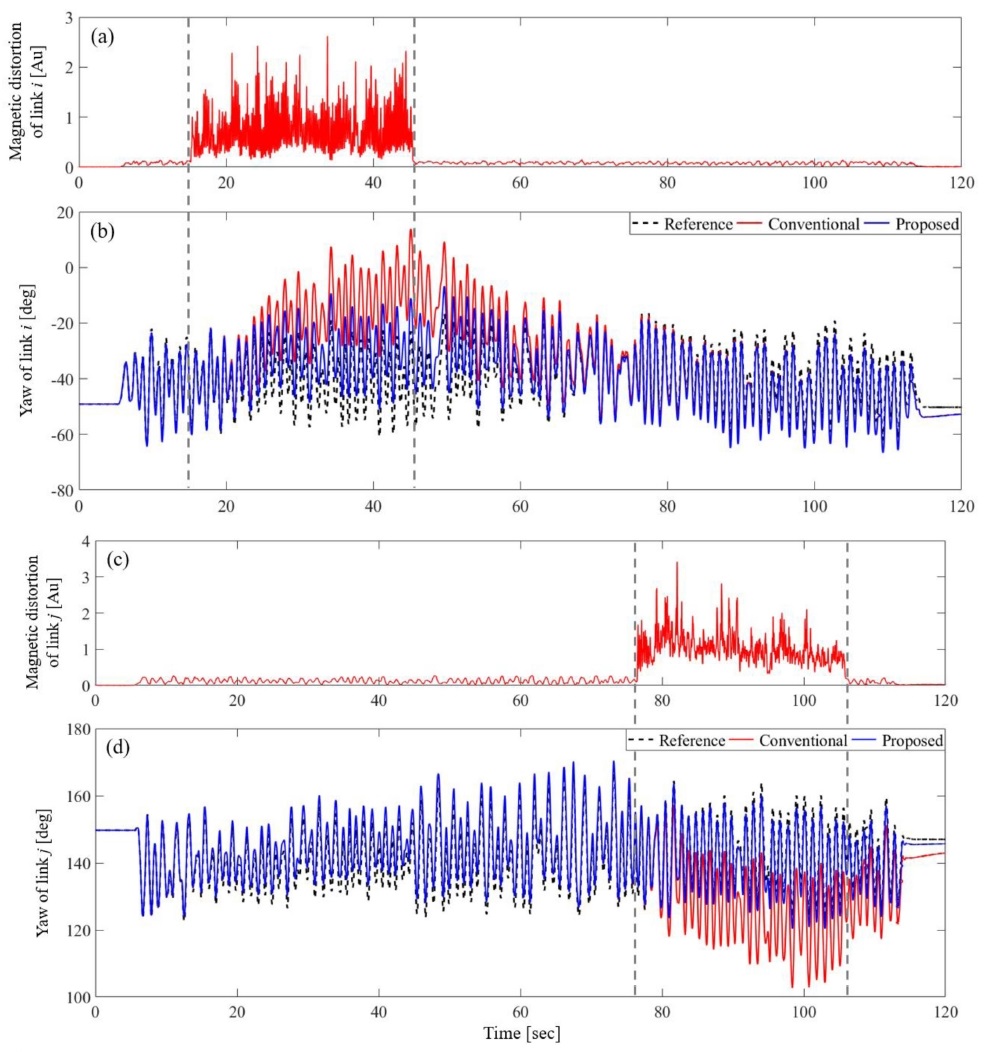
(a) and (c) the applied magnetic distortion magnitudes and (b) and (d) the yaw estimation results, for the links i and j, respectively, from Test 3

Table 1

RMSEs of yaw estimation for the links i and j in Tests 1-3(unit: degree)

Test 1에서 링크 i와 j에 대한 기존 칼만 필터의 요 추정 RMSE는 각각 9.70°, 1.20°로, 자기교란이 가해진 링크 i의 경우 큰 오차를 보이는 것을 확인할 수 있다. 제안 칼만 필터의 링크 i와 j에 대한 요 추정 RMSE는 각각 4.63°, 1.23°로 기존 칼만 필터와 비교하여 자기교란이 가해진 링크 i에 대한 오차가 5° 이상 감소하였다.

두 링크에 모두 자기교란이 가해진 Test 2에서는 기존 칼만 필터의 요 추정 RMSE는 각각 링크 i 6.02°, 링크 j 8.75°로, 두 링크에 모두 자기교란이 가해짐에 따라 두 링크의 요 추정 오차가 모두 6° 이상으로 큰 오차를 보였다. 이에 비해 제안 칼만 필터의 링크 i와 j에 대한 요 추정 RMSE는 각각 2.40°, 3.26°로, 두 링크의 요 추정 오차가 기존 칼만 필터에 비해 각각 3.62°, 5.49° 감소하였다.

Test 3에서 기존 칼만 필터의 요 추정 RMSE는 각각 링크 i13.41°, 링크 j8.74°로 두 링크의 요 추정 오차가 모두 8° 이상으로 큰 오차를 보였다. 제안 칼만 필터의 요 추정 RMSE는 각각 링크 i5.41°, 링크 j2.89°로 자기교란이 길게 가해졌음에도 불구하고 구속조건을 투영함에 따라 각 링크의 요 추정 성능이 각각 링크 i는 8.00°, 링크 j는 5.85° 개선되었다.

위 결과에서 확인할 수 있듯이 구속조건을 투영하지 않은 기존 칼만 필터의 경우 자기교란보상 메커니즘을 가지고 있으나, 강한 자기교란이 발생하는 경우 요 추정 성능이 심각하게 저하 될 수 있다. 이에 비해 제안 칼만 필터는 지자기센서 신호가 아닌 가속도계와 자이로스코프의 신호를 이용하는 구면 조인트의 가속도 구속조건을 사용하여 자기교란으로 인해 발생하는 요 추정 오차를 추가적으로 보정하였다.

이때, 식(24)에 따라 자기교란이 가해지지 않는 구간에서는 투영 과정에서의 칼만이득값이 0으로 지정된다는 점을 고려할 필요가 있다. 예를 들어, Test 3의 링크 i측에 자기교란이 가해진 구간에서(15-45 s 구간) 링크 j측에 문턱값을 넘지 않는 자기교란으로 인한 추정 오차는 링크 i의 추정성능에 영향을 미치게 된다. 또는 링크 i에서는 45 s이후 자기교란이 사라지고 나면 칼만이득값이 0이 되므로 구속조건 투영은 더 이상 적용되지 않는다. 따라서, 지자기센서 신호 및 마르코프 체인모델에 의한 보정에만 의존하게 된다. 이 지점에서 성공적으로 교란 보정이 이루어 지지 않는다면, 링크 i측의 잔류 추정 오차는 링크 j측에 자기교란이 가해진 구간에서(75-105 s 구간) 링크 j의 추정성능에도 영향을 미치게 된다. 이에 대한 추가적인 연구가 필요하다. 무엇보다, 제안 칼만 필터는 구면 조인트의 가속도 구속조건을 사용하므로 동적인 구간에서만 적용가능하다는 제한이 있다.

4. 결론 및 의의

본 논문에서는 자기교란으로 인해 발생하는 방위각 추정 오차를 최소화하기 위해 기구학적 구속조건을 투영한 방위각 추정 칼만 필터를 제안하였다. 제안된 필터는 기존 칼만 필터에 기구학적 구속조건을 폐루프 투영 방법을 이용하여 투영함으로써 추가적인 방위각 보정 과정을 거친다. 이때, 사용되는 구속조건은 구면 조인트의 가속도 구속조건으로 제안 칼만 필터는 지자기센서 신호가 아닌 가속도계와 자이로스코프 신호를 이용하여 자기교란을 보상한다.

제안 칼만 필터의 성능 검증을 위해 각기 다른 자기 조건을 갖는 3가지 실험에서 기존 칼만 필터와 방위각 추정 성능을 비교하였다. 검증실험결과, 제안 칼만 필터는 자기교란이 가해진 링크의 방위각 추정에 있어 구속조건을 투영하지 않은 기존 칼만 필터에 비해 52-67% 개선된 성능을 보였다. 제안된 칼만 필터는 동적조건에서만 작동한다는 한계는 있지만, 극심한 자기교란이 발생하는 환경에서도 추정성능이 크게 훼손되지 않으며 기존 칼만 필터보다 우수한 방위각 추정 성능을 보였다. 따라서, 제안 필터는 자기적으로 악조건시에도 강건한 방위각 정보를 제공하므로써, 불특정 자기환경에 노출될 수 있는 웨어러블 센싱분야나 이동형 보행 분석을 위한 조인트각도 추정 등의 분야에서 효율적으로 활용될 수 있다.

Acknowledgments

이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단 기초연구사업(No. 2018R1D1A1B07042791)의 지원을 받아 수행됨.

REFERENCES

• Min, S. J. and Kim, J., “Inertial Motion Sensing-Based Estimation of Ground Reaction Forces during Squat Motion,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 4, pp. 377-386, 2015. [https://doi.org/10.7736/KSPE.2015.32.4.377]
• Kim, Y. W., Cho, W. H., Jeon, Y. Y., and Lee, S. M., “Research on Classification of Sitting Posture with a IMU,” Journal of Rehabilitation Engineering and Assistive Technology Society, Vol. 11, No. 3, pp. 261-270, 2017.
• Lim, J. H. and Kang, S. K., “Non-Inertial Sensor-Based Outdoor Localization for Practical Application of Guide Robots,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 5, pp. 315-321, 2017. [https://doi.org/10.7736/KSPE.2017.34.5.315]
• Hwang, Y. J. and Choi, S. B., “Vehicle Orientation Estimation by Using Magnetometer and Inertial Sensors,” Journal of the Korean Society of Automotive Engineers, Vol. 24, No. 4, pp. 408-415, 2016. [https://doi.org/10.7467/KSAE.2016.24.4.408]
• Song, K. W., Song, Y. E., and Jung, H. R., “IMU Based Walking Position Tracking Using Kinematic Model of Lower Body and Walking Cycle Analysis,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 10, pp. 965-972, 2018. [https://doi.org/10.7736/KSPE.2018.35.10.965]
• Lee, J. K. and Park, E. J., “Minimum-Order Kalman Filter with Vector Selector for Accurate Estimation of Human Body Orientation,” Journal of IEEE Transactions on Robotics, Vol. 25, No. 5, pp. 1196-1201, 2009. [https://doi.org/10.1109/TRO.2009.2017146]
• Jeon, T. H. and Lee, J. K., “IMU-Based Joint Angle Estimation Under Various Walking and Running Conditions,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 12, pp. 1199-1204, 2018. [https://doi.org/10.7736/KSPE.2018.35.12.1199]
• Ligorio, G. and Sabatini, A. M., “Dealing with Magnetic Disturbances in Human Motion Capture: A Survey of Technique,” Journal of Micromachines, Vol. 7, No. 3, pp. 1-17, 2016. [https://doi.org/10.3390/mi7030043]
• Yi, C., Ma, J., Guo, H., Han, J., Gao, H., et al., “Estimating Three-Dimensional Body Orientation Based on an Improved Complementary Filter for Human Motion Tracking,” Journal of Sensors, Vol. 18, No. 11, pp. 1-19, 2018. [https://doi.org/10.3390/s18113765]
• He, Z., Chen, Y., and Shen, Z., “Attitude Fusion of Inertial and Magnetic Sensor under Different Magnetic Field Distortions,” Journal of ACM Transactions on Embedded Computing Systems, Vol. 17, No. 2, Article No. 48, 2018. [https://doi.org/10.1145/3157668]
• Ligorio, G. and Sabatini, A. M., “A Linear Kalman Filtering-based Approach for 3D Orientation Estimation from Magnetic/Inertial Sensors,” Proc. of IEEE Multisensor Fusion and Integration for Intelligent Systems, pp. 77-82, 2015. [https://doi.org/10.1109/MFI.2015.7295749]
• Lee, J. K. and Park, E. J., “A Fast Quaternion-Based Orientation Optimizer via Virtual Rotation for Human Motion Tracking,” Journal of IEEE Transactions on Biomedical Engineering, Vol. 56, No. 8, pp. 1574-1582, 2009. [https://doi.org/10.1109/TBME.2008.2001285]
• Choi, M. J. and Lee, J. K., “An Order-Switching Magnetic Distortion Compensation Mechanism for Accurate Azimuth Estimation,” Journal of Institute of Control Robotics and Systems, Vol. 23, No. 7, pp. 552-558, 2017. [https://doi.org/10.5302/J.ICROS.2017.17.0047]
• Madgwick, S. O., Harrison, A. J., and Vaidyanathan, R., “Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm,” Proc. of IEEE International Conference on Rehabilitation Robotics, pp. 1-7, 2011. [https://doi.org/10.1109/ICORR.2011.5975346]
• Laidig, D., Schauer, T., and Seel, T., “Exploiting Kinematic Constraints to Compensate Magnetic Disturbances When Calculating Joint Angles of Approximate Hinge Joints from Orientation Estimates of Inertial Sensors,” Proc. of International Conference on Rehabilitation Robotics, pp. 971-976, 2017. [https://doi.org/10.1109/ICORR.2017.8009375]
• Bonnet, V., Joukov, V., Kulić, D., Fraisse, P., Ramdani, N., et al., “Monitoring of Hip and Knee Joint Angles Using a Single Inertial Measurement Unit during Lower Limb Rehabilitation,” Journal of IEEE Sensors, Vol. 16, No. 6, pp. 1557-1564, 2016. [https://doi.org/10.1109/JSEN.2015.2503765]
• Choi, M. and Lee, J., “Inertial Sensor-Based Attitude Estimation Combining a Kinematic Constraint for Elimination of Acceleration-Induced Inaccuracy,” Journal of the Korean Society of Mechanical Engineers, Vol. 42, No. 3, pp. 263-269, 2018. [https://doi.org/10.3795/KSME-A.2018.42.3.263]
• Lee, J. K. and Choi, M. J., “A Sequential Orientation Kalman Filter for AHRS Limiting Magnetic Disurbance to Heading Estimation,” Journal of Electrical Engineering and Technology, Vol. 12, No. 4, pp. 1675-1682, 2017.
• Simon, D., “Kalman Filtering with State Constraints: A Survey of Linear and Nonlinear Algorithms,” Journal of IET Control Theory and Applications, Vol. 4, No. 8, pp. 1310-1318, 2010. [https://doi.org/10.1049/iet-cta.2009.0032]
• Seel, T., Schauer, T., and Raisch, J., “Joint Axis and Position Estimation from Inertial Measurement Data by Exploiting Kinematic Constraints,” Proc. of IEEE International Conference on Control Applications, pp. 45-49, 2012. [https://doi.org/10.1109/CCA.2012.6402423]